Evaluation of the performance of accommodating IOLs using a paraxial optics analysis

Abstract

Purpose

We employed an analytical approach to evaluate the key parameters for the potential design optimisation of accommodating intra-ocular lenses (AIOL) and to use these parameters to predict their accommodative performance.

Methods

Paraxial thin-lens equations to predict the accommodative performances of single-element (1E) and two-element (2E) AIOLs were developed. 2E-AIOLs with either mobile front or back lens elements were analysed as well as 1E-AIOL for their accommodative performance. A paraxial model including key ocular components (corneal surfaces, pupil and retina) as well as AIOL was used to evaluate the key control parameters and optimal design configurations. A range of variants of the model, representing varying powers of front and back optical elements and with either front or back optical element mobile was tested.

Results

Optimal accommodative performance of 2E-AIOL is governed by the power combinations of its optical elements; design variants with higher positive front element power produced greater accommodative efficacy, while mobility of the front element contributed more to the accommodative performance than the back element. The performance of 1E-AIOL is primarily governed by the power of the AIOL; the higher the AIOL power, the better the accommodative performance.

Conclusions

From an accommodative performance standpoint, the optimal design of 2E-AIOL should comprise a high plus power front element. Considering the maximum potential amounts of element translation available clinically, 2E-AIOLs are predicted to offer higher accommodative performance compared to 1E-AIOL.

Introduction

A breakthrough in vision correction occurred in 1949 when Sir Harold Ridley implanted the first intraocular lens (IOL). While far from perfect, the early devices worked well enough to encourage further developments and today, virtually all cataract patients receive the benefit of an IOL customized to the required power and design. While single-vision IOL offer near-perfect vision for a fixed distance, pseudophakic presbyopia remains a challenge. Demand for optimum near vision among pseudophakic patients, and a concurrent preference for good cosmesis is driving the development of innovative IOL designs that also afford near vision.

Developments in multifocal IOLs represented an early attempt to improve near vision for pseudophakic presbyopes. These IOLs employ multiple optical zones; or power progressions; or zones with diffractive optics, to simultaneously provide near and distance images. Due to the simultaneous presentation of images for a range of viewing distances to achieve near and distance focus, these devices typically compromise on some aspects of visual performance including subjective vision complaints such as glare, halos, poor contrast and ghosting (Artal et al., 1995; Dick et al., 1999; Manns et al., 2004). But the main weakness of such devices is that they do not reproduce the high-amplitude and continuously variable change in focus afforded by natural accommodation and enjoyed by the pre-presbyopic eye.

Studies using non-human primate models have convincingly validated the Helmholtz theory of accommodation (von Helmholtz, 1909; Glasser and Kaufmann, 1999). This theory provides the basis for the lenticular theory of presbyopia which postulates that presbyopia is primarily due to the progressive increase in the rigidity of the crystalline lens with ageing (Glasser and Kaufmann, 1999). From the clinical standpoint, these findings suggest that any strategy for restoring accommodation to the presbyope should ideally target the crystalline lens. Within this philosophy, a range of ‘lens-centric’ strategies for restoring accommodation, such as lens refilling (Kessler, 1964; Parel et al., 1986; Nishi and Nishi, 1998; Nishi et al., 1998, 2008; Koopmans et al., 2006) and photomodulation (Myers and Krueger, 1998; Krueger et al., 2001, 2005; Ripken et al., 2008) are currently being developed.

Ahead of these developments, accommodating IOLs (AIOLs) have emerged with rapid progress in development, and while single vision IOLs remain the most implanted post-cataract device by far, AIOLs are becoming one of the more preferred devices for restoring accommodation to pseudophakic presbyopes (Leaming, 2004). Within this family of AIOL, a range of designs and configurations have been proposed and developed (Assia, 1997; Dick, 2005; Doane and Jackson, 2007). The most prominent of the designs and configurations is represented by the single-element AIOL (1E-AIOL) and two-element AIOL (2E-AIOL) (Waring, 1992; Assia, 1997). These AIOL designs operate on the principle of changing effective power by shifting the axial position (a process often called ‘translation’) of one or more lens elements of the AIOL within the eye under the influence of physiological accommodation.

Typically, 1E-AIOLs consist of peripheral mechanical design features that facilitate antero-posterior translation of the optic during accommodation (Cumming et al., 2001; Küchle et al., 2002; McLeod et al., 2003; Dick and Dell, 2006; Doane and Jackson, 2007). The 2E-AIOL is a more complex device whose efficacy depends on the interplay between the optical and mechanical parameters of the AIOL and ocular components combined. With the rapid pace of development, however, it is known that at least one design of 2E-AIOL has been in clinical trials (McDonald et al., 2003; McLeod et al., 2003; Ossma et al., 2007; US National Institutes of Health, 2007).

Given the significant role AIOLs are anticipated to play in the clinical management of pseudophakic presbyopes, detailed considerations of their optical performance, and in particular, their accommodative performance, would be of benefit to understanding and optimising their design.

From the optical design standpoint, the empirical or clinical studies reported in the literature provide incomplete information regarding the optical performance of AIOL although a wide range of techniques has been used in those studies (Lesiewska-Junk and Kaluzny, 2000; Auffarth et al., 2002a,b; Findl et al., 2003; Langenbucher et al., 2003a). Limited literature exists around the objective measurement of the performance of AIOL based on direct quantification of accommodation amplitude. The majority of studies rely on subjective vision testing while some have employed indirect measurements of accommodation such as the amount of translation effected in an AIOL using special microscopy observational or ultrasonographic techniques (Auffarth et al., 2002a,b). A few studies have employed theoretical analytical approaches to model or predict the accommodative performance of AIOLs. Langenbucher et al. (2003b) used the matrix method to calculate changes in anterior and posterior focal points of the eye with change in axial position of commercially available 1E-AIOL. This calculation was used in determining the amount of accommodative amplitude achievable. This study however, did not analyse the effect of corneal power or axial length on accommodative performance. Later, Langenbucher et al. (2004), again using the matrix method, evaluated and compared the accommodative performance of 1E and 2E-AIOLs. In that study they considered one specific power combination (+32D front element) of 2E-AIOL with a fixed amount of translation (1 mm). While it effectively compared the performance of two types of AIOLs, the study was not intended to identify the optimal design in terms of all power combinations and directions of translation of the AIOL. Similar to the earlier study, the effect of corneal power or axial length was not extensively examined. Missotten et al. (2004) used vergence equations to predict the accommodative performance of 1E-AIOL. They explained the effect of corneal power, anterior chamber depth and axial length on accommodative performance but the study did not evaluate 2E-AIOLs or attempt to identify optimal designs of AIOLs.

To understand the performance of AIOL especially with a view to optimising their designs, approaches that can consider all possible design configurations within the entire design space (that is, the collection of every possible combination of values for all relevant design variables) would be more comprehensive than those employing modelling of certain specific design configurations. Studies which only consider existing or available designs would be limited in their scope of evaluation and may not identify the ultimate optimum design configuration. Similarly, studies which employ finite ray-tracing techniques (Nawa et al., 2003; Ho et al., 2006) would in practice, be limited to evaluate only selected design examples. Extrapolation of the findings from such studies risks losing validity. Thus, to explore the entire design space of AIOLs and to identify an optimum design, an analytical approach is required.

In this study, we extend the knowledge gained by the previous studies with an objective to understand, in an analytical manner, the control variables relevant to the design optimisation of AIOL in terms of their accommodative performance. We employed a paraxial optics approach to derive key equations describing the performance of 1E-AIOLs and 2E-AIOLs.

Methods

An analytical approach to evaluating the performance of AIOLs under the two design configurations mentioned (1E-AIOL and 2E-AIOL) was developed by employing a paraxial, first-order theory, model of the eye and AIOL. Several model eyes have been described (Bakaraju et al., 2008) in the literature which could be used in our study, however to ensure comparability with a previous study (Ho et al., 2006) that evaluated some similar design configurations (but using a computer-assisted ray-tracing method of evaluation) we selected the finite model eye of Navarro et al. (1985). The aspheric ocular surfaces of the model eye were modified and simplified to be spherical paraxial refracting surfaces. The crystalline lens was replaced by a model of a 2E-AIOL or 1E-AIOL consisting of two idealised thin lens elements. For the 1E-AIOL, one of the elements in the 2E-AIOL model was assigned a null refractive power.

The 2E-AIOL operates based on both the shifting of axial position and separation of the two lens elements. In practice, both elements of the AIOL would translate during accommodation due to the various forces exerted by the ciliary body, zonules and capsule, as well as the hydraulic and mechanical resistance from the vitreous and iris (Crawford et al., 1990; Heatley et al., 2004). For simplicity, we adopted the same simplified conditions as employed in an earlier study (Ho et al., 2006). Hence, in this study: Configuration 1 comprised an AIOL with a mobile front element in which the back element is maintained in a fixed position; and Configuration 2 comprised an AIOL with a mobile back element where the front element remained fixed.

Due to the tedious algebraic expressions that may be encountered in this optical model, we employed metrical methods (Long, 1974, 1976; Colliac, 1990; Gerrard and Burch, 1994) in the derivation of equations depicting the models. Under the matrix method, an optical system comprising the eye and two elements of AIOL (Table 1) can be described by the matrix system

$$\mathbf{M}=\mathbf{K}\cdot {\mathbf{T}}_{\mathrm{c}}\cdot {\mathbf{T}}_{\mathrm{f}}\cdot {\mathbf{R}}_{\mathrm{f}}\cdot {\mathbf{T}}_{\mathrm{s}}\cdot {\mathbf{R}}_{\mathrm{b}}\cdot {\mathbf{T}}_{\mathrm{b}}\cdot {\mathbf{T}}_{\mathrm{r}},$$ (1)

where

• K denotes the ray-transfer matrix representing the vergence of light at the posterior corneal surface, used to calculate amplitude of accommodation,

• T denotes ray-transfer matrices,

• R denotes refraction matrices, and suffixes

• b refers to the back reference plane,

• c refers to the cornea and anterior chamber,

• f refers to the front reference plane,

• s refers to the separation between A-IOL elements, and

• r refers to the vitreous chamber.

Table 1.

Prescription of parameter values for the eye model used in computational analyses modified from Navarro et al. (1985)

Surface	Radius	Thickness	Medium	Index
Front Cornea	7.72 mm	0.55 mm	Cornea	1.376
Back Cornea	6.50 mm	3.05 mm	Aqueous	1.336
Pupil (stop)	-	0 mm	Aqueous	1.336
Front reference	-		Aqueous	1.336
Front element	Thin lens	4.00 mm	Aqueous	1.336
Back element	Thin lens	total	Vitreous	1.336
Back reference	-	16.34 mm	Vitreous	1.336
Retina	-		Vitreous

For the AIOL model, both elements are represented by ideal thin lenses.

As employed in an earlier study (Ho et al., 2006), the introduction of the fixed-position reference planes to this model simplifies derivation of the paraxial formulae as it provides a fixed point of reference from which the position of either the front or back element of 2E-AIOL can be defined as a function of lens element translation.

For simplification, it is noted that the effect of refraction by the cornea merely changes the vergence between the visual object space and the vergence at the anterior chamber by a fixed amount. Thus, the refraction matrix for the cornea was ignored as we are primarily interested in a change in vergence (i.e., accommodation) as a result of translation of one of the lens elements; and in the case of 2E-AIOL, their separation.

Since the system is operating principally at finite conjugate ratio, the ray vergence, K, at the plane of the posterior corneal surface can be obtained by setting element m₁₂ of matrix M to zero and solving for K (see derivation in Appendix).

To evaluate the performance of AIOLs, we employed an indicator derived previously (Ho et al., 2006) and defined accommodative performance (P_k) as the rate of change in vergence of the rays with translation of the mobile lens element. A large value represents greater amount of accommodation induced by a given amount of translation. Mathematically, accommodation performance is the first derivative of the ray vergence at the corneal plane with respect to the amount of translation undertaken by the mobile element (Ho et al., 2006).

In addition to derivation and analysis of paraxial equations describing the performance of the two design configurations of AIOLs, by way of illustration of relationships between control parameters and performance, we computed the accommodative performance for specific configurations using the derived paraxial equations. The computation included determining the change in ray vergence at the corneal plane K, as defined by Equations A7 and A12 in the Appendix, when the front or back element of the 2E-AIOL was translated from its initial position. Different variants of the design configurations were tested by varying the power combinations of the elements. In this series of computations, we constrained the refractive power of both lens elements to be less than approximately ±40D. We also constrained the total power of the AIOL so that it rendered the combined ocular system emmetropic (i.e., the posterior focal plane of the model eye with AIOL at distance focus setting resides on the retina). Table 1 provides the prescription of parameter values for the eye model. A basic optical layout of the eye model with a 2E-AIOL has been given previously (see Figure 1 in Ho et al., 2006).

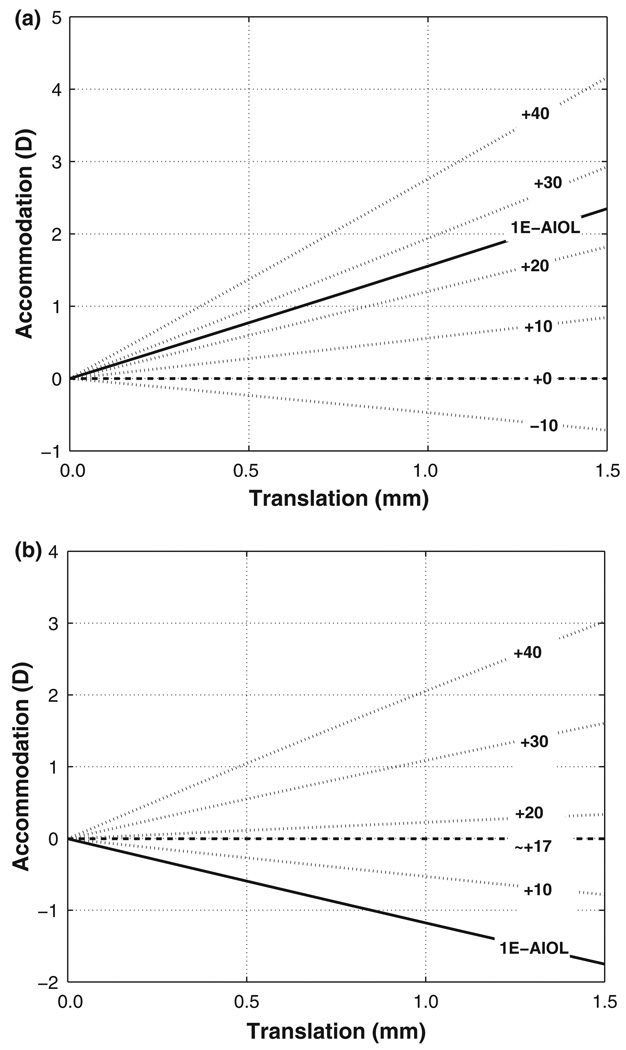
Figure 1.

Paraxial optics prediction of change in accommodation (D) with axial position of the mobile element for seven design variants (different front and back element power) of a two-element 2E-AIOL with (a) Configuration 1 (mobile front element) and (b) Configuration 2 (mobile back element). For both (a) and (b), power of the front element is indicated by the labels. Solid line represents the variant corresponding to a 1E-AIOL and long dashed line represents the variant portraying an immobile (single-vision) IOL. Accommodation in negative scale indicates de-accommodation (decrease in power) with element translation.

Results

Equations for vergence and accommodation performance were derived separately for the two configurations. Appendix details their derivation.

For Configuration 1 of a 2E-AIOL with a mobile front element, the ray vergence at the plane of the posterior cornea is given by

$$\mathrm{K}=(\mathrm{n}(\mathrm{n}{\mathrm{F}}_{\mathrm{f}}({\mathrm{t}}_{\mathrm{r}}+\mathrm{Z})+{\mathrm{F}}_{\mathrm{b}}(\mathrm{n}-{\mathrm{F}}_{\mathrm{f}}\mathrm{Z}){\mathrm{t}}_{\mathrm{r}}-{\mathrm{n}}^2)).{({\mathrm{n}}^2({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}+{\mathrm{t}}_{\mathrm{r}})-\mathrm{n}{\mathrm{F}}_{\mathrm{b}}({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}){\mathrm{t}}_{\mathrm{r}}\dots +{\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}-\mathrm{Z})\mathrm{Z}{\mathrm{t}}_{\mathrm{r}}-\mathrm{n}{\mathrm{F}}_{\mathrm{f}}(\mathrm{Z}+{\mathrm{t}}_{\mathrm{r}})({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}-\mathrm{Z}))}^{-1}$$ (2)

and for a 2E-AIOL with a mobile back element (Configuration 2) is given by

$$\mathrm{K}=(\mathrm{n}(\mathrm{n}{\mathrm{F}}_{\mathrm{f}}(\mathrm{D}+{\mathrm{t}}_{\mathrm{r}})-{\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}(\mathrm{D}-\mathrm{Z}+{\mathrm{t}}_{\mathrm{r}})\mathrm{Z}+\mathrm{n}{\mathrm{F}}_{\mathrm{b}}(\mathrm{D}-\mathrm{Z}+{\mathrm{t}}_{\mathrm{r}})-{\mathrm{n}}^2)).{({\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}({\mathrm{t}}_{\mathrm{r}}+\mathrm{D}-\mathrm{Z})\mathrm{Z}{\mathrm{t}}_{\mathrm{a}}\dots +{\mathrm{n}}^2({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}+{\mathrm{t}}_{\mathrm{r}})-\mathrm{n}{\mathrm{F}}_{\mathrm{f}}({\mathrm{t}}_{\mathrm{r}}-\mathrm{D}){\mathrm{t}}_{\mathrm{a}}-\mathrm{n}{\mathrm{F}}_{\mathrm{b}}({\mathrm{Z}}^2-{\mathrm{t}}_{\mathrm{a}}\mathrm{D}-{\mathrm{t}}_{\mathrm{r}}\mathrm{Z}+{\mathrm{t}}_{\mathrm{a}}\mathrm{Z}-\mathrm{D}\mathrm{Z}-{\mathrm{t}}_{\mathrm{a}}{\mathrm{t}}_{\mathrm{r}}))}^{-1}$$ (3)

where suffixes correspond to foregoing usage, and n is the refractive index of the aqueous and vitreous (considered equal for simplicity)

K is the ray vergence referenced at the posterior corneal surface in dioptres,

D is the maximum total thickness expressed in metres of the 2E-AIOL (set to 4.0 mm),

Z is the translation expressed in metres of the mobile element (varying from 0.0 mm being the initial position, to 1.5 mm being at the extreme position),

t denotes optical thicknesses between surfaces measured in metres, and

F denotes the refractive power of the elements measured in dioptres.

Accommodation performance, P_k, for Configuration 1 is given by the approximate formula

$${\mathrm{P}}_{\mathrm{k}}\approx \frac{1}{2}[2\mathrm{n}\frac{{\mathrm{F}}_{\mathrm{f}}}{{\mathrm{t}}_{\mathrm{r}}}-2{\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}-\mathrm{F}\frac{2}{\mathrm{f}}],$$ (4)

and for Configuration 2 is given by

$${\mathrm{P}}_{\mathrm{k}}\approx \frac{1}{\mathrm{n}}\left[{\mathrm{F}}_{\mathrm{b}}^2-2\mathrm{n}\frac{{\mathrm{F}}_{\mathrm{b}}}{{\mathrm{t}}_{\mathrm{r}}}\right].$$ (5)

From Equations 2 and 3, and more clearly in Equations 4 and 5, it can be observed that some design variants increase in power (i.e., accommodate) when the mobile element translates anteriorly (towards the cornea) while other design variants accommodate when the mobile element translates posteriorly. This provides some flexibility in the mechanical design of the AIOL supporting mechanical features for effecting accommodation relative to the dynamics of the ciliary body, zonule and lens capsule. Accommodation or de-accommodation effects with axial translation of selected design variants of AIOL are shown in Figure 1 to illustrate these relationships.

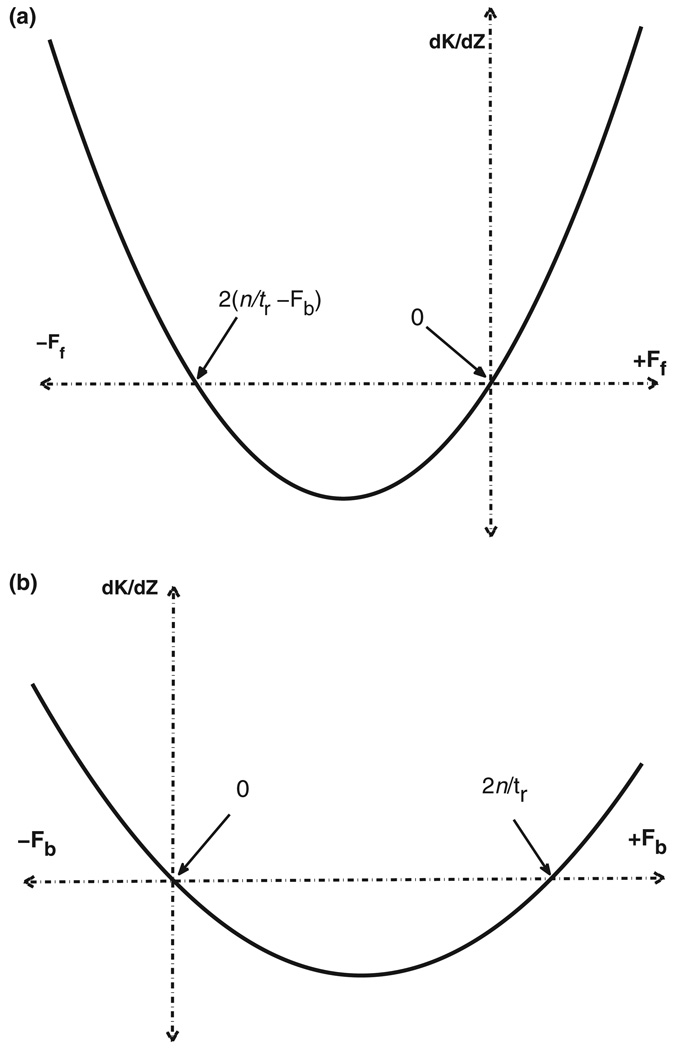
Equation 4, corresponding to Configuration 1 AIOLs, is a second-order function that concaves upward and has zero values at F_f = 2(n/t_r – F_b) and F_f = 0 (Figure 2a). Any value of F_f bracketed by these two points produces ‘negative’ accommodation (i.e., de-accommodation with ciliary body constriction and zonular relaxation – actions that are normally, physiologically, associated with accommodation) whereas values outside these points produce positive accommodation (i.e., normal accommodative behaviour with physiological accommodative process). However, values of F_f beyond the point defined by F_f = 2(n/t_r – F_b) represent extremely high negative powers which, from the device thickness and mechanical standpoints, would not be advantageous for an AIOL.

Figure 2.

Accommodative performance (dK/dZ) of a 2E-AIOL of (a) Configuration 1 with mobile front element and (b) Configuration 2 with mobile back element versus mobile element power (front power F_f for Configuration 1, back power F_b for Configuration 2). Practically, good accommodative performance can be achieved more efficiently with positive power front elements and/or negative power back elements. Otherwise, an extremely high negative power front, or positive power back, element is required to produce a matching amount of accommodation. Between the two zero-points, forward (Configuration 1) or backward (Configuration 2) translation results in de-accommodation.

As the fixed equivalent power of the AIOL (F_iol) for distance focus (i.e., with accommodation relaxed) is approximately the sum of F_f and F_b, the first zero of Equation 4 can be rewritten as F_f ≈ 2F_iol – 2n/t_r. Since refraction at the cornea contributes to the focusing of light to the retina, F_iol has a less positive value than n/t_r. Thus 2F_iol – 2n/t_r is negative and any positive F_f gives greater accommodative performance P_k (Figure 2a) than a negative F_f of the same absolute value. Therefore, selecting a design based on the practical range of power as discussed in the previous paragraph, greater accommodative performance can be realised when a positive-powered front element is used rather than a negative-powered one.

Similarly, the curve described by Equation 5 for Configuration 2 AIOL concaves upward and is disposed approximately symmetrically about F_b = n/t_r with zero values at F_b = 2n/t_r and F_b = 0 (Figure 2b). Following the same considerations as for Equation 4, that F_f + F_b ≈ F_iol, Equation 5 indicates that greater accommodative performance can be realised with a negative value of F_b.

When the power of the immobile back (F_b) or front (F_f) element is set to zero in Equations 4 and 5 respectively, a 1E-AIOL is modelled. In these design variants, accommodation performance is equal to

$${\mathrm{P}}_{\mathrm{k}}\approx -\frac{1}{\mathrm{n}}\left[{\mathrm{F}}_{\mathrm{i}\mathrm{o}\mathrm{l}}^2-2\mathrm{n}{\mathrm{F}}_{\mathrm{i}\mathrm{o}\mathrm{l}}/{\mathrm{t}}_{\mathrm{r}}\right],$$ (6)

where F_iol is the power of the single mobile lens of the 1E-AIOL.

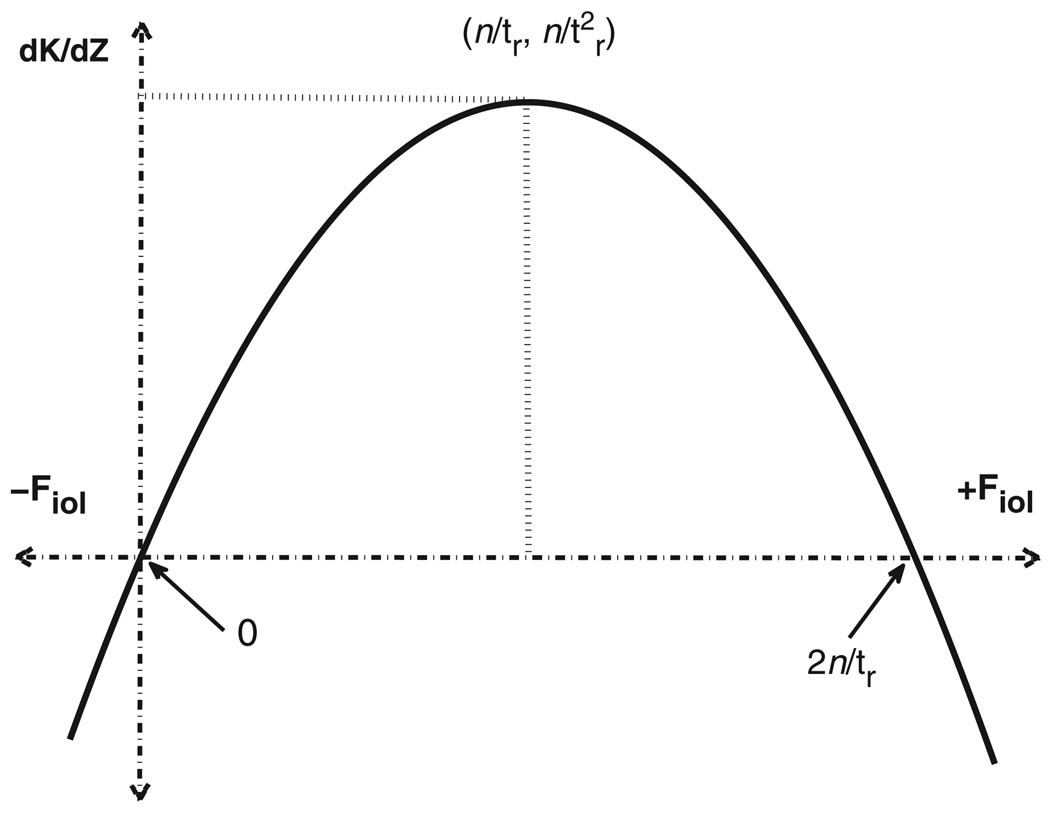
Equation 6 describes a curve that concaves downward and has zero values at F_iol = 0 and F_iol = 2n/t_r. From this equation and corresponding Figure 3, it can be seen that any power of the 1E-AIOL beyond these points on either side produces a negative accommodation effect with translation. The global maximum of the curve is at the coordinate $(\mathrm{n}/{\mathrm{t}}_{\mathrm{r}},\mathrm{n}/{\mathrm{t}}_{\mathrm{r}}^2)$ suggesting that the maximum accommodation is obtained when F_iol = n/t_r (Figure 3). However, this is an impractical case as this power would require the cornea to be effectively plano for the eye to be emmetropic. Since F_iol must be fixed to a value that renders an eye emmetropic, the accommodation performance of a 1E-AIOL is also fixed for a given eye. Yet, the relationship portrayed by Equation 6 shows that the lower the corneal power (i.e., hyperopes), the greater the amount of accommodation that can be derived with 1E-AIOL.

Figure 3.

A plot of accommodative performance (dK/dZ) versus total IOL power (F_iol) for 1E-AIOL. Good performance can be achieved more efficiently for higher positive power of the AIOL reaching a maximum when it is equal to the equivalent dioptric value of the vitreous chamber depth.

To be exhaustive, when the refractive power of the mobile element is set to zero (dashed horizontal line in Figure 1) we obtain the accommodation performance for the trivial design variant of a conventional (single-vision) IOL without translation, which does not produce any accommodation effect.

Discussion

Results of our paraxial analysis are in good agreement with those from finite ray-tracing. For an emmetropic eye with typical dimensions, Nawa et al. (2003) predicted that 1 mm translation of a 20 D 1E-AIOL would bring about 1.30 D of accommodation. Ho et al. (2006) also predicted a similar value (1.25 D.mm⁻¹) employing a ray tracing model. The small differences in predicted accommodation can be readily accounted for by the differences in model eye parameters as well as the starting axial position of the 1E-AIOL. A larger range of accommodation amplitude (up to 4 D) has been predicted for 2E-AIOL depending on the design (Ho et al., 2006). These predicted values are in close agreement with the values reported from a clinical study where accommodation of 1.06 D with 0.88 mm of translation (equivalent to 1.2 D.mm⁻¹) was reported (Langenbucher et al., 2003b). The analysis from this study predicted a value of 1.25 D.mm⁻¹ which is in good agreement.

Our model of 1E-AIOL also verified earlier computational studies (Nawa et al., 2003; Missotten et al., 2004) which predicted that individuals with shorter axial length, i.e., typically hyperopes, would enjoy greater accommodation amplitude for the same translation in 1E-AIOL. More precisely, the hyperopic eye, which is typically associated with a shorter axial length, demands a higher power of the IOL for distance refractive correction; and it is this greater power of the AIOL that brings greater accommodation. However, the power of the IOL and the accommodative performance does not depend merely on the vitreous chamber depth but also on the corneal power and the anterior chamber depth (Equations 2 and 3). For example, an eye with high corneal power and high natural lens power would require a correspondingly higher power for a 1E-AIOL resulting in a greater amount of accommodation. Conversely a myopic eye (often associated with higher corneal power) would require relatively lower 1E-AIOL power, resulting in a lesser amount of accommodation.

Studies of the performance of 2E-AIOL appear in a few articles (Hara et al., 1990, 1992;MSC Software Corporation, 2001; McDonald et al., 2003; Nataloni, 2003). One 2E-AIOL tested in vivo using a primate model (McDonald et al., 2003) achieved as high as 6 D of accommodation. Computer-assisted modelling (MSC Software Corporation, 2001; Nataloni, 2003) predicted that such a 2E-AIOL could deliver 4 D of accommodation assuming translation of 1.9 mm. Predictions from the present study agree with the results quoted above. For example, according to the analytic results of this study, 4 D of accommodation can be achieved by a 2E-AIOL of Configuration 1 with approximately a +35 D front element and a −15.50 D back element when translated by 1.7 mm. Calculations based on another design variant for a 2E-AIOL suggest that accommodation amplitudes of 2.2–2.4 D may be achieved with a +30 D to +35 D front lens element (McLeod et al., 2003).

It was noted that both elements in a 2E-AIOL are likely to translate simultaneously with the effort of accommodation in the eye (Ho et al., 2006; Lin, 2006b). Though we did not model simultaneous translation of both elements explicitly, its effect can be readily extrapolated by combining the analytical results of models for Configurations 1 and 2. It is clear from our 2E-AIOL model that the optimal performance is achieved when a plus lens moves forward (towards the cornea) or when a minus lens moves backward (towards the retina). Therefore, relative to normal physiological behaviour, maximum accommodation would be obtained when a 2E-AIOL contains a positive front element that moves in the forward direction and a negative back element that moves in the backward direction. This prediction has been noted in a previous paper (Lin, 2006a).

Mathematically, a desired equivalent power of the 2E-AIOL can be obtained from any of an infinite number of combinations of front and rear element powers. From consideration of Equations 4 and 5 it is observed that the accommodative performance of the 2E-AIOL is similarly dictated by the combination of power of the elements. Thus, unlike for 1E-AIOL, accommodative performance of a 2E-AIOL does not depend directly on the refractive state of the eye. For example, a myopic eye may be corrected by using a less positive front element power or a more negative back element power. The first configuration would produce a lower accommodative performance while the latter a higher performance. Therefore, the choice of element power combination is of greater consideration to accommodative performance than the actual refractive state to be corrected. However, from an implementation and optical engineering standpoint, the refractive state of the eye (and hence the individual element powers) may have a slight effect on the thicknesses of the AIOL elements which consequently may somewhat affect the final performance. For example, for the same accommodative performance, a hyperopic eye would require a thicker front element (plus lens) of 2E-AIOL (compared to the one required for myopic eye) for a given power of the rear element which occupies greater axial space. Such an embodiment in turn reduces the inter-element space available for translation and consequently, would reduce the accommodative performance.

As we employed only paraxial approaches in our modelling, the physical limitations of AIOL elements (thickness, surface shapes and manufacturing practicalities) and physiological aspects of AIOL performance (e.g., maximum achievable amount of translation, issues of lens surface design from the point-of-view of lens epithelial cell migration and potential iris irritation) could not be considered in our study. Investigations of these additional variables would be required to complete our understanding of the performance of AIOLs. A number of these variables (physical lens constraints such as lens form, thickness, diameter, etc) may be investigated using standard optical engineering principles (e.g., evaluating outcome optical performance within the feasible range of parameter values using optomechanical modelling tools such as computer-assisted lens-design software). Other more subjective or clinical variables (such as restriction of translation due to lens epithelial cell growth) can only be evaluated by undertaking well-controlled physical experimentation to reveal the underlying mechanisms of those variables.

Further, optical aberrations (both the AIOL alone and in combination with the eye) and magnification effects have been identified as possible factors influencing the performance of AIOL (Ho et al., 2006). Other aspects of optical performance include the performance of AIOL in the presence of astigmatism, its depth of focus, as well as factors such as errors in decentration and tilt of either individual elements or the AIOL as a whole. While beyond the scope of this study, analytical optics approaches, along the lines of those applied in this study, may be applied to investigating the impact of those other optical factors to acquire a more comprehensive understanding of the overall performance of AIOL and to explore designs for optimising the visual outcome for patients. The evaluation of these and other optical factors provides a worthwhile basis for future studies in this area.

From the clinical standpoint, this study has addressed only one specific aspect of AIOLs, that of accommodative efficiency (rate of change of accommodative power with a given amount of translation) and accommodation amplitude (total amount of accommodation available given the total range of translation). The results suggest that while the accommodative performance of 1E-AIOLs is dictated by the refractive state of the eye, with the greater degrees of freedom (a large range of front and back lens element power combinations) to achieve the correct power, the performance of 2E-AIOL is determined by the choice of lens element powers selected by the manufacturers in their design. Since the accommodative performance of 2E-AIOL is linked to the element powers, manufacturers should be encouraged (or perhaps induced by regulations or standards) to provide such data with the devices. Further, it may be of assistance to the practitioners advising their patients to provide information about the accommodative efficiency (i.e., the amount of accommodation achievable for a unit amount of translation). Of course, it must be cautioned that accommodation amplitude and efficiency are only two specific selection criteria for a device that will be responsible for providing the patient’s overall vision long-term. Optically, the performance with respect to visual quality (e.g., the impact of aberrations), field of view along the entire focusing range, stability of focus, etc, are also important factors in the selection of an AIOL. Non-optical factors are of great importance including any issues or difficulties associated with implantation, alignment and centration, etc; as well as longer-term issues such as the ability of the AIOL design to ward off lens epithelial cell regrowth that may interfere with its accommodative functionality. Many of these factors critical to the selection of an AIOL for the patient are only starting to be identified and investigated. Clearly, to benefit the patient, more work is required in all aspects of this important technology.

In conclusion, in this study, we have employed a paraxial optics approach to evaluating the accommodative performance of 1E-AIOL and especially 2E-AIOL. We developed equations suitable for the analytical description of the efficiency of an AIOL, its accommodative performance, as a function of lens element power, and position, separation and translation of elements for mobile front or back element AIOL. Consistent with the previous theoretical results, our model suggests that 2E-AIOL produce higher amplitudes of accommodation compared to 1E-AIOL. By mathematical approximation, closed-forms of the predictive equations for accommodative performance were derived. These derivations provide the basis for optical design optimization of AIOL from the point of view of maximising accommodation amplitude.

Appendix

Derivation of equations for paraxial thin-lens models

The optical system detailed in Table 1 can be described by the following matrix system

$$\mathbf{M}=\mathbf{K}\cdot {\mathbf{T}}_{\mathrm{c}}\cdot {\mathbf{T}}_{\mathrm{f}}\cdot {\mathbf{R}}_{\mathrm{f}}\cdot {\mathbf{T}}_{\mathrm{s}}\cdot {\mathbf{R}}_{\mathrm{b}}\cdot {\mathbf{T}}_{\mathrm{b}}\cdot {\mathbf{T}}_{\mathrm{r}},$$ (A1)

(see Methods for explanation of symbols). or more explicitly in terms of matrix elements m_i.j,

$$\left[\begin{array}{cc}{\mathrm{m}}_{11}& {\mathrm{m}}_{12}\\ {\mathrm{m}}_{21}& {\mathrm{m}}_{22}\end{array}\right]=\left[\begin{array}{cc}1& 1/K\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& t_c\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{t}}_{\mathrm{f}}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ -{\mathrm{F}}_{\mathrm{f}}& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{t}}_{\mathrm{s}}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ -{\mathrm{F}}_{\mathrm{b}}& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{t}}_{\mathrm{b}}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{t}}_{\mathrm{r}}\\ 0& 1\end{array}\right]$$ (A2)

where suffixes correspond to foregoing usage, and t denotes optical thicknesses (t/n) between surfaces measured in metres where n is the refractive index of aqueous and vitreous,

F denotes refractive powers of components or surfaces measured in dioptres, and

K is the relative accommodative state in dioptres.

Since refraction at the cornea only serves to add a fixed vergence to the relative accommodative state, K, and we are only concerned with changes in vergence (i.e., amplitude of accommodation) relative to the unaccommodated state, we can omit the corneal refraction matrix from the system matrix to simplify derivation. The actual amount of accommodation will be calculated from the difference between the value of K without translating and after translating of the AIOL element.

Configuration 1 Equations

For Configuration 1 AIOL, the back element is fixed in position at the back reference plane. Hence, t_b = 0, and matrix T_b may be ignored.

In addition, given the mobile front element in this configuration, t_s, the separation between the two elements and t_f, the distance of the front element from the front reference plane, may be defined in terms of the amount of axial shift of the front element Z_f, as well as the maximum separation of the two elements D. We therefore have

$${\mathrm{t}}_{\mathrm{f}}=\mathrm{D}-{\mathrm{Z}}_{\mathrm{f}},$$ (A3)

and

$${\mathrm{t}}_{\mathrm{s}}={\mathrm{Z}}_{\mathrm{f}},$$ (A4)

Since the system is operating principally at finite conjugate ratios (as vergence produced by corneal refraction has been ignored), the accommodative state, K, may be obtained by setting m₁₂ = 0 (Gerrard and Burch, 1994). On evaluating (2) and substituting (3) and (4), the solution for K becomes (Equation 2 in the main text)

$$\mathrm{K}=(\mathrm{n}(\mathrm{n}{\mathrm{F}}_{\mathrm{f}}({\mathrm{t}}_{\mathrm{r}}+\mathrm{Z})+{\mathrm{F}}_{\mathrm{b}}(\mathrm{n}-{\mathrm{F}}_{\mathrm{f}}\mathrm{Z}){\mathrm{t}}_{\mathrm{r}}-{\mathrm{n}}^2)).{({\mathrm{n}}^2({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}+{\mathrm{t}}_{\mathrm{r}})-\mathrm{n}{\mathrm{F}}_{\mathrm{b}}({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}){\mathrm{t}}_{\mathrm{r}}\dots +{\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}-\mathrm{Z})\mathrm{Z}{\mathrm{t}}_{\mathrm{r}}-\mathrm{n}{\mathrm{F}}_{\mathrm{f}}(\mathrm{Z}+{\mathrm{t}}_{\mathrm{r}})({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}-\mathrm{Z}))}^{-1}$$ (A5)

where suffixes correspond to foregoing usage, and n is the refractive index of the aqueous and vitreous (considered equal for simplicity)

K is the ray vergence referenced at the posterior corneal surface in dioptres,

D is the maximum total thickness expressed in metres of the 2E-AIOL (set to 4.0 mm),

Z is the translation expressed in metres of the mobile element (varying from 0.0 mm being the initial position, to 1.5 mm being at the extreme position),

t denotes optical thicknesses between surfaces measured in metres, and

F denotes the refractive power of the elements measured in dioptres.

Accommodation performance P_k is defined as the rate of change of ray vergence K with respect to axial shift Z_f of the mobile element (Ho et al., 2006). Thus P_k has units of D.mm⁻¹ and mathematically, it is the first derivative of K with respect to Z_f. The exact formula for P_k is a rather protracted equation. However, the equation may be simplified by approximation as follows. In the optical system of the combined eye and AIOL described, terms relating to refractive power are typically of the order of many tens of dioptres (i.e., 10² m⁻¹), while terms relating to distances are typically of the order of a few millimetres (10⁻³ m). Thus, in the expansion of the equation, groupings involving distance terms t_c, D and Z_f, may be considered negligible. Subsequently, an approximate formula for P_k may be derived as

$${\mathrm{P}}_{\mathrm{k}}\approx \underset{\mathrm{D}\to 0,\mathrm{Z}\to 0,{\mathrm{t}}_{\mathrm{c}}\to 0}{\text{lim}}\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}{\mathrm{Z}}_{\mathrm{f}}}.$$ (A6)

This approximation yields the following simplified formula (Equation 4 in the main text)

$${\mathrm{P}}_{\mathrm{k}}\approx \frac{1}{\mathrm{n}}\left[2\mathrm{n}\frac{{\mathrm{F}}_{\mathrm{f}}}{{\mathrm{t}}_{\mathrm{r}}}-2{\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}-{\mathrm{F}}_{\mathrm{f}}^2\right],$$ (A7)

Configuration 2 Equations

A similar approach can be employed for Configuration 2 AIOL where the back element is mobile and the front element is fixed in position. Here, t_f = 0, and matrix T_f may be ignored.

With this configuration, t_s, the separation between the two elements and t_b, the distance of the back element from the back reference plane, may be defined in terms of the amount of translation of the back element Z_b, as well as the maximum separation of the two elements D such that

$${\mathrm{t}}_{\mathrm{b}}=\mathrm{D}-{\mathrm{Z}}_{\mathrm{b}},$$ (A8)

$${\mathrm{t}}_{\mathrm{s}}-{\mathrm{Z}}_{\mathrm{b}}.$$ (A9)

By substituting (8) and (9) into (2), the ray vergence at the plane of the corneal back surface now equates to (Equation 3 in the main text)

$$\mathrm{K}=(\mathrm{n}(\mathrm{n}{\mathrm{F}}_{\mathrm{f}}(\mathrm{D}+{\mathrm{t}}_{\mathrm{r}})-{\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}(\mathrm{D}-\mathrm{Z}+{\mathrm{t}}_{\mathrm{r}})\mathrm{Z}+\mathrm{n}{\mathrm{F}}_{\mathrm{b}}(\mathrm{D}-\mathrm{Z}+{\mathrm{t}}_{\mathrm{r}})-{\mathrm{n}}^2)).{({\mathrm{F}}_{\mathrm{f}}{\mathrm{F}}_{\mathrm{b}}({\mathrm{t}}_{\mathrm{r}}+\mathrm{D}-\mathrm{Z})\mathrm{Z}{\mathrm{t}}_{\mathrm{a}\cdots }+{\mathrm{n}}^2({\mathrm{t}}_{\mathrm{a}}+\mathrm{D}+{\mathrm{t}}_{\mathrm{r}})-\mathrm{n}{\mathrm{F}}_{\mathrm{f}}({\mathrm{t}}_{\mathrm{r}}-\mathrm{D}){\mathrm{t}}_{\mathrm{a}}-\mathrm{n}{\mathrm{F}}_{\mathrm{b}}({\mathrm{Z}}^2-{\mathrm{t}}_{\mathrm{a}}\mathrm{D}-{\mathrm{t}}_{\mathrm{r}}\mathrm{Z}+{\mathrm{t}}_{\mathrm{a}}\mathrm{Z}-\mathrm{D}\mathrm{Z}-{\mathrm{t}}_{\mathrm{a}}{\mathrm{t}}_{\mathrm{r}}))}^{-1}$$ (A10)

with all symbols as defined previously.

An approximation for P_k derived from the rate of change of K with respect to Z_b can be found by employing the same approach for approximation used for the Configuration 1 equations. A simplified equation for accommodative performance for Configuration 2 is found as

$${\mathrm{P}}_{\mathrm{k}}\approx \underset{\mathrm{D}\to 0,\mathrm{Z}\to 0,{\mathrm{t}}_{\mathrm{b}}\to 0}{\text{lim}}\frac{\mathrm{d}\mathrm{K}}{\mathrm{d}{\mathrm{Z}}_{\mathrm{b}}},$$ (A11)

which yields the following simplified formula (equation 5 in the main text)

$${\mathrm{P}}_{\mathrm{k}}\approx \frac{1}{\mathrm{n}}\left[{\mathrm{F}}_{\mathrm{b}}^2-2\mathrm{n}\frac{{\mathrm{F}}_{\mathrm{b}}}{{\mathrm{t}}_{\mathrm{r}}}\right].$$ (A12)

When the power of the immobile element for each configuration (i.e., F_bfor Configuration 1 and F_ffor Configuration 2) is set to zero in Equations A7 and A12 respectively, a 1E-AIOL is modelled. In these design variants, accommodation performance is equal to (Equation 6 in the main text)

$${\mathrm{P}}_{\mathrm{k}}\approx -\frac{1}{\mathrm{n}}\left[{\mathrm{F}}_{\text{iol}}^2-2\mathrm{n}{\mathrm{F}}_{\text{iol}}/{\mathrm{t}}_{\mathrm{r}}\right],$$ (A13)

where F_iol is the power of the single mobile lens of the 1E-AIOL.