Canine Hip Dysplasia is Predictable by Genotyping

Summary

Objective

To establish a predictive method using whole genome genotyping for early intervention in canine hip dysplasia (CHD) risk management, for the prevention of the progression of secondary osteoarthritis (OA), and for selective breeding.

Design

Two sets of dogs (6 breeds) were genotyped with dense SNPs covering the entire canine genome. The first set contained 359 dogs upon which a predictive formula for genomic breeding value (GBV) was derived by using their estimated breeding value (EBV) of the Norberg angle (a measure of CHD) and their genotypes. To investigate how well the formula would work for an individual dog with genotype only (without using EBV or phenotype), a cross validation was performed by masking the EBV of one dog at a time. The genomic data and the EBV of the remaining dogs were used to predict the GBV for the single dog that was left out. The second set of dogs included 38 new Labrador retriever dogs, which had no pedigree relationship to the dogs in the first set.

Results

The cross validation showed a strong correlation (r>0.7) between the EBV and the GBV. The independent validation showed a strong correlation (r=0.5) between GBV for the Norberg angle and the observed Norberg angle (no EBV was available for the new 38 dogs). Sensitivity, specificity, positive, and negative predictive value of the genomic data were all above 70%.

Conclusions

Prediction of CHD from genomic data is feasible, and can be applied for risk management of CHD and early selection for genetic improvement to reduce the prevalence of CHD in breeding programs. The prediction can be implemented before maturity, at which age current radiographic screening programs are traditionally applied, and as soon as DNA is available.

Introduction

Hip dysplasia (HD) is a common inherited trait that affects the wellbeing of humans and dogs and imposes a heavy financial and emotional burden[1]. The disease is characterized by hip instability, which leads inexorably to painful, debilitating secondary hip osteoarthritis (OA) [2-4]. Canine hip Dysplasia (CHD) is a major veterinary problem occurring with a frequency up to 75% in mixed and pure breed dogs of approximately 70 million dogs in American households [5]. The prevalence in a hospital population is about 20% [5]. Human HD, referred to as developmental dysplasia of the hip (DDH), occurs with a frequency ranging from 5.4% to 12.8%. Hip OA prevalence was 4.4–5.3% for individuals over 60 years old [6, 7]. Developmental dysplasia of the human hip significantly influenced the prevalence of hip OA [7]. Radiographic surveys have found that 20% to 50% of human patients diagnosed with idiopathic hip OA had antecedent DDH[6].

Canine HD and DDH are homologous conditions from a clinical perspective with identical sequelae due to subluxation which results in focal overload of the articular surface and hip OA [6-9]. Current treatment options for human and canine HD or OA are limited to symptom management and hip replacement at end-stage degeneration. No data is available for the number of canine hip replacements undertaken each year but 82% of human hip replacements are due to end-stage OA [10]. The number of human total hip replacements is about a quarter million and this number is expected to double in the next twenty years [11]. The challenge is to develop predictive tools to identify the risk of CHD, DDH and hip OA at an early age so that more efficient and cost effective management can be applied.

Selective breeding of dogs has proven to be effective in reducing the prevalence of CHD [12]. In a previous study [13], we showed that the selective breeding program operated by Guiding Eyes for Blind (in Yorktown Heights, New York, USA) was able to achieve stable genetic improvement in hip morphology. Nationwide, the Orthopedic Foundation for Animals (OFA) has been scoring hip radiographs and releasing some of the records publicly over the last 40 years. In a previous study, we showed that a consistent genetic improvement has accumulated [14]. The genetic improvement was limited by the fact that the selection criteria of the majority of the breeding dogs had low accuracy. Even when an estimated breeding value (EBV) of an individual derived from raw phenotypes of itself and its relatives was available, it only reached reasonable accuracy if it was based on hundreds of progeny who were in a comparable group which also contained progeny from other dogs [14-16]. Producing this large number of progeny takes several years. The number of such accurate dogs was limited. Thus, improved methods of identifying dogs susceptible to HD are required to implement earlier preventative methods for allaying secondary hip OA. Because pure breed dogs must have documented pedigrees to be registered as pure by the American Kennel Club (AKC), EBVs can be calculated and these can be correlated with genomic breeding values (GBVs) composed of single nucleotide polymorphisms (SNPs) or sequence variants.

Here we present data for the first time to demonstrate that CHD is predictable from genomic data so that selection decisions can be made for a dog at puppy age. This implies that human HD could also be predicted at an early age and suitable preventative management could be applied to identify susceptible individuals who may be missed by physical screening and ultrasound and reduce the prevalence hip OA by preemptive intervention.

Materials and Methods

Dog samples

Two sets of dogs were genotyped for this study. The first set (359 dogs) was sampled from a pool of dogs with breeding values reported from our previous study [13]. The second set (53 Labrador retrievers) contained 15 dogs that were in the first set for the purpose of data quality control (e.g. genotyping error) and imputation of missing SNPs across genotyping platforms. The rest of the dogs (38) were newly admitted patients to the Cornell University Hospital for Animals. They either had hip pain and lameness or were being radiographed as a screening tool prior to breeding. There was no known pedigree relationship between the 38 new dogs in the second sample and the 359 dogs in the first sample. Cornell Institutional Animal Care and Use Committee Protocol approval numbers are 2005-0151 (DNA Bank) and 2006-0187 (Hip Dysplasia and Osteoarthritis Genetics).

Radiographic methods and estimated breeding value

The four measurements used for hip evaluation were the Norberg angle (NA), Orthopedic Foundation for Animals (OFA) score, the distraction index (DI) and the dorsolateral subluxation score (DLS) [17]. The former two are evaluated from the extended hip projection and are phenotypically and genetically correlated while the latter two are evaluated on different projections and are phenotypically and genetically correlated [14]. No measure alone completely represents hip morphology. The hips of the Baker Institute dogs were commonly radiographed at 8-12 months of age. The Guiding Eyes for the Blind radiographed their dogs’ hips at 14-18 months of age. The age of dogs admitted to the CUHA varied but were 2 years of age on average. All radiographic measurements except the OFA score have achieved their maximal accuracy when the dogs are 8 months old which is skeletal maturity. The DI and the DLS score reveal more hip laxity than the NA and the OFA score. The DLS imaging position reveals maximum subluxation which can be masked by the extended hip imaging position. The OFA score increases in accuracy as a dog ages because the secondary OA progresses and is more evident radiographically [17]. Estimated breeding values (EBV) were derived by using a multiple trait mixed linear model from our previous study [13]. As NA correlated to OFA score and most dogs had NAs measured, NA was chosen for this study.

Single Nucleotide Polymorphism Genotyping

The first set of dogs was genotyped on the Infinium Canine SNP20 BeadChip (Illumina Inc., San Diego CA) with ~22,000 SNPs across the genome (http://www.illumina.com/documents/products/datasheets/datasheet_canine_snp20.pdf). The second sample of dogs was genotyped on an Affymetrix platform (Canine 127K SNP array version 2) of which ~50,000 SNPs were reliable. The majority (92.3%) of the Illumina SNPs had completed calls. There was 99.46% SNPs with call rate above 95%. For the Affymetrix SNP array, there were 71.65 % and 43.24% of SNPs with call rate above 90% and 95% respectively.

SNPs with missing calls above 45% were removed. We also removed SNPs with minor allele frequency (MAF) below 1% [18]. The final analysis contained 21,455 SNPs for the Illumina array and 48,431 for Affymetrix array. For the Illumina SNP array, the mean and median MAF were 0.2589 and 0.2399, respectively. For the Affymetrix SNP array, the mean and median MAF were 0.2589 and 0.2641, respectively. There were 13,465 SNPs in common between the two sets of SNPs. The concordance rate was 99.9% of the common SNPs genotyped on 15 dogs.

Principal component analysis (PCA) was performed based on the numeric genotypes that were 0 and 2 for the two homozygotes and 1 for the heterozygotes. Two analyses were performed on different dogs with different SNPs. The first PCA was performed on the 359 dogs in the first sample by using the 21,455 Illumina SNPs. The second PCA was performed on the 359 plus the additional 38 new dogs by using the common 13,465 SNPs. The 359 dogs, including the 15 common dogs, used the Illumina genotypes and the 38 additional dogs used the Affymetrix genotypes.

Genomic prediction model

We used the EBV and Illumina SNPs on 359 dogs to derive the predictive formula. The model to predict the genomic breeding values based on m bi-allelic markers with m=21,455 was

$$y=\mu +\sum _i\sum _j{\mathrm{X}}_{ij}{\beta }_{ij}+e(i=1tom\text{and}j=1to2),$$ (1)

where y is the vector of the dependent variable (EBV), μ is a general mean, X_ij is a design vector for the jth allele of marker i, β_ij is the allele substitution effect of the jth allele of marker i, and e is a residual vector, which by default is $e~N(0,\mathrm{I}{\sigma }_e^2)$. In this model, the allele effects are modeled as random effects with ${\beta }_{ij}~N(0,{\phi }_i^2)$, where φ_i is a scaling factor that models the variance explained at the ith marker. The scaling factors can be interpreted as a standard deviation of allele substitution effects. The variance of allele effects is estimated using an informative prior distribution. We chose a prior common normal distribution on the scaling factors φ_i, e.g. ${\phi }_i~N(0,{\sigma }_s^2)$, where ${\sigma }_s^2$ was variance of φ_i. The ${\sigma }_s^2$ parameter was estimated from the data so that it would properly adjust to the correct level and apply the optimal shrinkage [19]. The ${\sigma }_s^2$ parameter could roughly be described as the expected average fitted variance per marker. The parameter of the common prior was given a starting value as ${\sigma }_s^2=0.0001$, and then was estimated simultaneously with other unknown parameters.

For all parameters, single chain Gibbs samplers were implemented. A Markov Chain Monte Carlo (MCMC) sampler was used to generate samples from the joint posterior distribution of the model parameters. The MCMC was performed with IBAY [20] for 50,000 cycles. The first 10,000 cycles were used as the burn-in period. One sample was saved for every 5 cycles in the rest of the 40,000 cycles. The averages and variances of unknown parameters from the 8,000 posterior samples were used as the final estimates and their dispersion parameters. The genomic breeding value (GBV) was estimated as follows:

$$\mathrm{GBV}=\sum _i\sum _j{x}_{ij}{\widehat{\beta }}_{ij}$$ (2)

where ${\widehat{\beta }}_{ij}$ was the average of the estimates of β_ij over 8,000 samples. Prediction error variance (PEV) [13] was derived for the GBV of each individual and genomic variance (${\sigma }_a^2$) was calculated from GBVs of all individuals.

Reliability (r), or accuracy, of the GBV of an individual, defined as the correlation between true and predicted values, was calculated from PEV and ${\sigma }_a^2$ as follows:

$$\mathrm{r}=\sqrt{1-\frac{PEV}{{\sigma }_a^2}}$$ (3)

We calculated GBV from all the SNPs based on the scaling factor and a subset of the most influential k SNPs (k=20, 50, 100, 200, 500, 1000, 5000 and 10000) selected for the largest scaling factors.

Imputation of missing SNPs

The Illumina SNPS that were not on the Affymetrix array were imputed by using a software tool (MACH) [21, 22].

Validation of predictive formula

We performed two types of validations: cross validation and independent validation. The cross validation was performed by masking an EBV of a dog one at a time (Jackknife cross validation). Its GBV was calculated based only on its genotypes by using the formula derived from the EBV and genotype on the rest of the 358 dogs. The process was repeated for each of the 359 dogs. We calculated GBV from all the SNPs based on the scaling factor and subsets of the most influential SNPs.

The independent validation was performed on 38 Labrador retriever dogs that had no pedigree relationship to the 359 dogs. The predictive formula was derived from the 359 dogs. The GBVs of the 38 dogs were calculated by using the formula in two ways. The first way used all the 21,455 Illumina SNPs with the missing SNPs imputed. The second way used the 13,465 common SNPs. The rest of the SNPs were discarded from the predictive formula. The correlations between GBV and EBV/phenotype within breed/cross were used as the criteria of validation.

Sensitivity, Specificity, Positive and Negative Predictive Value

Canine hip dysplasia is a complex disease and NA measurement is continuous. The range of NA is usually between 70 and 120 degrees, and the low degree indicates severe HD. No obvious cutoff was defined a priori to distinguish dysplastic and non-dysplastic hip. In this study, the cutoff was determined to maximize the minimum of the four diagnostic statistics; sensitivity, specificity, positive predictive value and negative predictive value [23, 24].

Results

Estimated breeding value

Canine hip dysplasia was measured using the Norberg angle. Its EBV for each dog were obtained from a multiple trait model in our previous study[13]. Breed was included as a co-factor. The average EBV was restricted to zero for each breed. Table 1 displays the averages and standard deviations of the 359 dogs sampled from various breeds and crosses. The 7 Greyhounds did not show HD and the standard deviations within this breed were small. The standard deviations within breed were about the same among other pure breeds. The variations among the crosses between Greyhounds and Labrador retrievers were between their parental variations (Table 1). The EBV of each dog was accompanied with a reliability score indicating the degree to which the EBV correlated with the true genetic effect, with 1 and 0 as the closest and farthest, respectively (Table 1).

Table 1.

Estimated Breeding Values (EBV) and reliabilities of hip dysplasia for 359 genotyped dogs^*

	Breed	N	Average	SD	Min	Max
EBV	LR	182	0.81	6.1691	−20.42	9.96
	G	7	−0.65	2.0233	−4.31	2.20
	LR × G	8	−1.15	2.0455	−4.50	1.54
	F1×LR	68	−0.66	4.4654	−14.71	6.40
	F1×G	17	−0.84	2.1344	−5.19	4.06
	(F1×LR) × (F1×LR)	13	−3.78	2.7547	−8.73	0.92
	German Shepherd	17	−1.24	8.0438	−19.70	6.98
	Golden Retriever	15	0.30	6.7509	−15.40	7.42
	Newfoundland	18	0.39	6.9325	−16.41	9.27
	Rottweiler	14	1.22	6.8150	−10.93	8.89
Reliability	LR	182	0.91	0.0343	0.70	0.97
	G	7	0.90	0.0121	0.89	0.92
	LR×G	8	0.92	0.0169	0.89	0.94
	F1×LR	68	0.90	0.0064	0.89	0.93
	F1×G	17	0.88	0.0051	0.88	0.89
	(F1×LR) × (F1×LR)	13	0.89	0.0065	0.87	0.89
	German Shepherd	17	0.87	0.0461	0.76	0.94
	Golden Retriever	15	0.87	0.0113	0.86	0.91
	Newfoundland	18	0.83	0.0221	0.86	0.91
	Rottweiler	14	0.86	0.0354	0.76	0.92

^*The number of dogs (N), average, standard deviation (SD), the minimum and maximum of EBV and reliability were given for each pure breed and crosses between Labrador retriever (LR) and Greyhound (G). The crosses included the first cross between retriever and Greyhound (F1), backcross to LR (F1×LR), backcross to Greyhound (F1×G), and a third generation cross: (F1×LR) × (F1×LR).

Genomic prediction

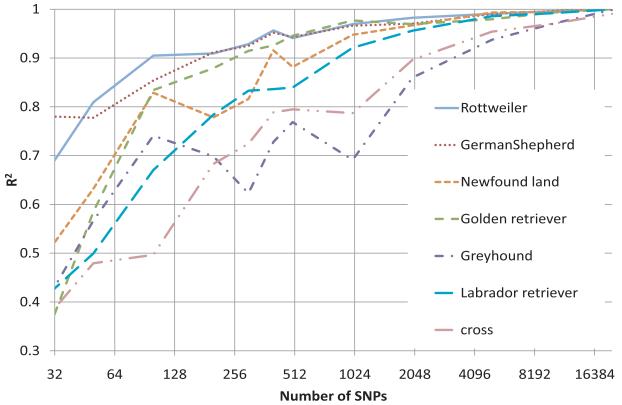
The training data set contained 359 dogs which were genotyped with the Illumina CanineSNP20 BeadChip containing ~22,000 SNPs (Figure 1). The prediction formula was built in a Bayesian framework [16, 19, 25]. When both genomic data and EBV were used to formulate the model for each dog, the correlation coefficient between the EBV and the predicted GBV was almost 1.00 which indicated that the model was over-parameterized. When the SNPs with least contribution (smallest scaling factors) to the GBV were gradually removed from the formula, the correlation decreased slowly and steadily. Even when 5,000 SNPs remained in the formula, the correlation was still above 0.98. However, the correlation decreased when the total number of SNPs in the GBV model was less than 100-500 (Figure 2). In addition to the agreement between EBVs and GBVs, a moderate correlation (R=0.47) was observed between the reliabilities of EBVs and GBVs. As expected, the more reliable the EBV, the more reliable the corresponding GBV.

Figure 1.

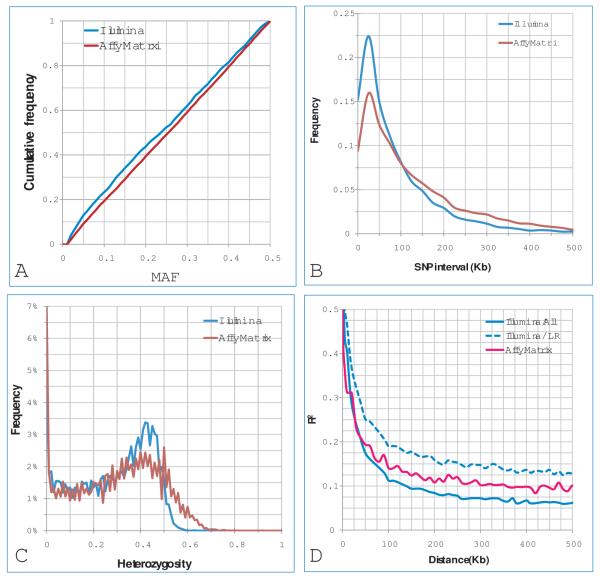
The properties of single nucleotide polymorphisms (SNPs). The SNP were genotyped with the Illumina array on 359 dogs and Affymetrix array on 53 dogs. A: Cumulative distribution of minor allele frequencies B: The density of the SNPs; C: Distribution of heterozygosity; D: Linkage disequilibrium (LD) decay (R²) over physical distance. The LD was calculated with all breeds and Labrador retriever (LR) respectively.

Figure 2.

Model fit of genomic breeding value and estimated breeding value. The model fit (R²) was displayed for each breed/cross over different number of the most influential SNPs. The cross included the first cross (F₁) between Labrador retriever and Greyhound (G), backcross to LR (F₁×LR), backcross to G (F₁×G), and third generations cross: (F₁×LR) × (F₁×LR).

Cross validation

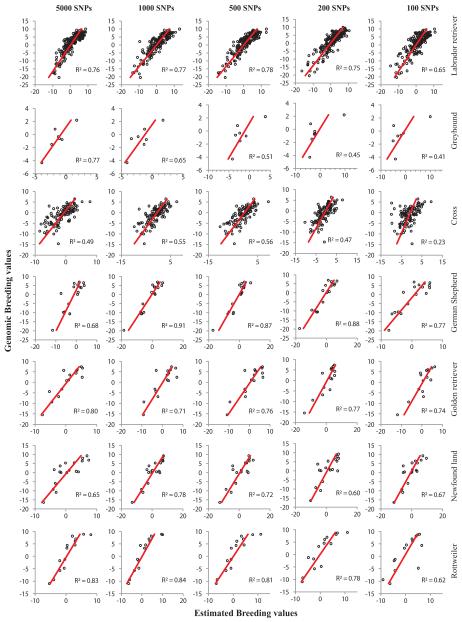
To examine how well the genomic prediction would work for an individual dog without an EBV or any phenotype, we removed one dog at a time from the set with 359 and then used the rest of the set to build a new prediction formula and then used that new formula to predict the GBV for the excluded dog. We repeated this process (Jackknife cross validation) for each dog until every dog had its own GBV estimated only with its genotype. During the process of calculating GBV, we used the most influential k SNPs (k=5000, 1000, 500, 200, 100, 50 and 20). Interestingly, the correlation (r) for using the top 5,000 SNPs dropped from ~0.98 to ~ 0.60 for the lowest number of SNPs when each dogs’s EBV was not used to predict the GBV of itself in the cross validation, no longer observing the over parameterization as before (Figure 3). The cross validation showed a strong correlation (r>0.70) between EBV and GBV by using all the SNPs.

Figure3.

Accuracy of genomic prediction from cross validation. Linear regression lines and R² are given for each plot of genomic breeding value (GBV) vs. estimated breeding value (EBV). The GBV of a dog was calculated from its genotypes by using the predictive formula derived from the genotype and EBV of all the other dogs (Jackknife cross validation). The plots were classified by breed/cross and number of the most influential SNPs used to calculate GBV. The cross included the first cross (F1) between Labrador retriever and Greyhound (G), backcross to LR (F1×LR), backcross to G (F1×G), and third generations cross: (F1×LR) × (F1×LR).

More interestingly, the correlation was well maintained even when the prediction formula was based on the most influential 100-500 SNPs. The correlation reduction for using less than 100-500 SNPs reflected the loss of SNPs in linkage disequilibrium (LD) with the quantitative trait nucleotides (QTNs) underlying the EBVs. In general, reasonable correlation was achieved when the top 100-500 SNPs were included.

Independent validation

Our final goal was to test whether the predictive formula could be applied to a naïve set of dogs outside the 359 dogs from which the original formula was derived, especially for the dogs that were unrelated to the original set. We genotyped another set of Labrador retriever dogs (53) with the Affymetrix Canine Array. One third of these dogs (15) were part of the 359 used for the purpose of data quality verification (e.g. genotyping error) and imputation of missing SNPs. The other 38 dogs were from among those admitted to the Cornell Hospital and had no known pedigree relationship to the dogs in the first set. Each of these dogs only had a single Norberg angle measurement on each hip. The worst hip angle (the minimum) from the two hips was used as the phenotype for each dog. No EBV was available on these dogs due to lack of pedigree information.

The Affymetrix SNP array contained ~50,000 informative SNPs, including the 13,465 from the Illumina array. The genotype calls on the 15 dogs genotyped with both arrays showed a very strong agreement (concordance rate was 99.9%).

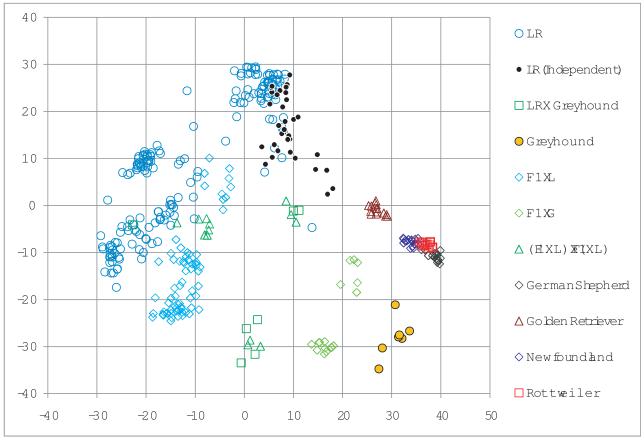
We performed PCA by using the common SNPs. The population structure of these dogs was clearly revealed by the first two principal components (PC). All the dogs within a pure breed were clustered together in the scatter plots (Figure 4). All the F₁ dogs of Greyhound/Labrador retriever breedings were positioned between their respective parental breeds. The backcross of the F₁ to Labrador retriever was closer to Labrador retriever and the backcross of F₁ to Greyhound was closer to Greyhound as expected. The substructure within the Labrador retriever breed reflected the multiple sources of Labrador retriever for these studies. The scatter plot of the first two PCs revealed the dispersion of the relationship of the new 38 Labrador retriever dogs with other dogs (Figure 4).

Figure 4.

Genetic relationship among dogs in the reference and independent sample. The genetic relationship was characterized by the first principal component (PC, X axis) and the second principal component (Y axis) of the SNP genotypes. The PCs were derived from the common 13,465 SNPs shared by the Illumina array and AffyMetrix Array. The Illumina array was used to genotype the reference population (359 dogs) and the Affymetrix SNP array was used to genotype the independent validation population (38). Fifteen dogs were genotyped on both platforms for the purpose of data quality control and imputation of missing SNPs. Different pure breeds and crosses are displayed separately. The crosses between Labrador retriever (LR) and Greyhound (G) include the first cross (F1), backcross to LR (F1×L), backcross to G (F1×G), and third generations cross: (F1×L) × (F1×L). The Labrador retrievers from the reference population and the independent validation population are also displayed separately to show the diversity between the two subgroups. The Labrador retrievers from the reference sample are displayed as LR and the ones from the independent sample is displayed as LR (Independent).

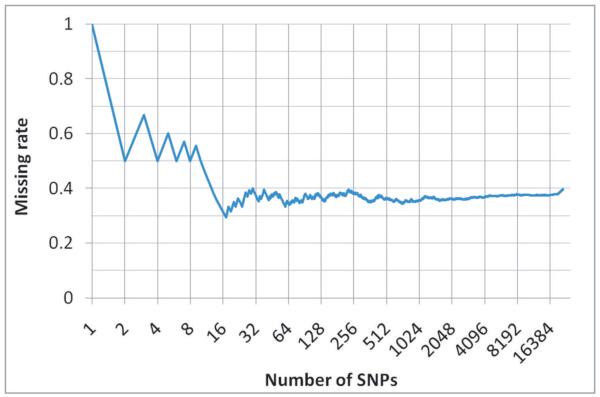
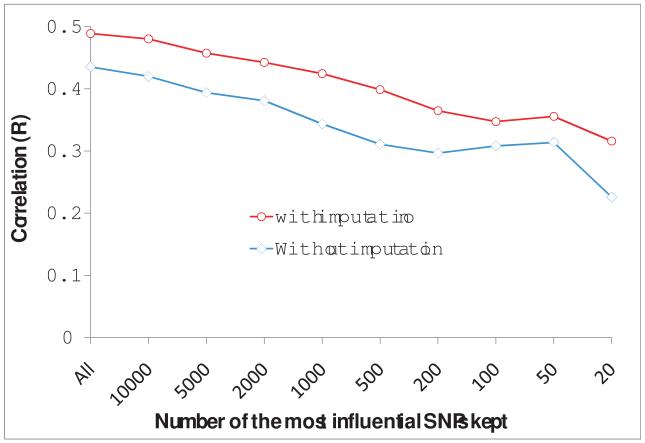
Among the Illumina 21,455 SNPs used to derive the predictive formula, 40% were not on the Affymetrix SNP array, including the most influential SNPs (Figure 5). We imputed the Illumina SNPs missing on the Affymetrix array. We applied the predictive formula to the 38 dogs by using the common SNPs (without imputation) and all of the Illumina array SNPs (with missing SNPs imputed). This independent validation showed strong correlations (r=0.5 with imputation and r=0.45 without imputation) between their known NA phenotype and GBV (Figure 6).

Figure 5.

Missing rate of single nucleotide polymorphisms (SNPs). There were 21,455 SNPs on Illumina array that was used to derive the predictive formula. About ~40% of these SNPs were not present on the Affymetrix array that was used to genotype the dogs for independent validation (including the first and the forth most influential SNPs on the Illumina array). The cumulative missing rates of SNPs are plotted against their order (descending log scale) based on their scaling factor.

Figure 6.

Accuracy of genomic prediction from independent validation. The validation was performed on 38 Labrador retrievers with the Norberg angle phenotype and SNPs from the Affymetrix array. The accuracy is displayed as the correlation coefficient between the phenotype and genomic breeding value (GBV). GBV was calculated by using the formula derived from 359 dogs genotyped with the Illumina SNP array. As 40% of SNPs on the Illumina array were not on the Affymetrix array, GBV was calculated with the common SNPs shared by the two arrays and all the SNPs on the Illumina array with missing SNPs imputed. The calculation of GBV was performed with a different number of the most influential SNPs.

Clinical diagnosis/prediction

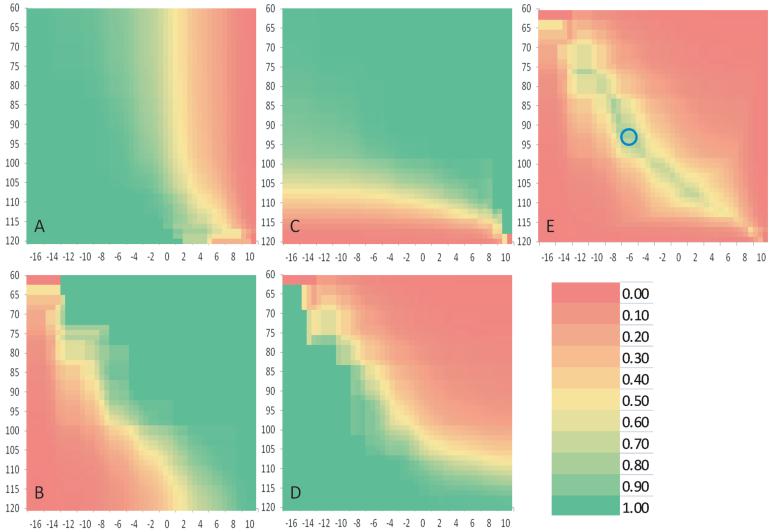
The cutoffs on NA and GBV were set at 105 degree and -6 respectively to define and diagnose dysplastic and non-dysplastic hips. These cutoffs maximized the minimum of the four clinical diagnostic statistics (sensitivity, specificity, positive predictive ability and negative predictive ability) in the reference population with 359 dogs (Figure 7). The corresponding sensitivity, specificity, positive predictive ability and negative predictive ability were 72.22%, 75.00%, 72.22% and 75.00%, respectively, among the 38 dogs in the independent validation.

Figure 7.

Precision of genomic prediction. The dichotomous status of hip dysplasia was defined by the cutoff of NA (X axis) and diagnosed by GBV (Y axis) among 359 dogs in the reference population. The color at each combination of the two cutoffs indicates the corresponding values of sensitivity (A), specificity (B), positive predictive value (C) and negative predictive value (D) and the minimum among the four values (E). The optimized cutoffs were 94 for NA and -6 for genomic breeding value indicated by the blue circle. The corresponding sensitivity, specificity, positive predictive ability and negative predictive ability were 98.77%, 75.00%, 96.97% and 88.23%, respectively.

Discussion

This is the first report showing a repeatable prediction of CHD from genomic data. A reliable prediction was achieved with as few as the most influential 100-500 SNPs. This prediction could be used for risk management of CHD or as a better alternative selection criteria than phenotype [26]. The correlation between GBV and observed NA (R²=0.5²=0.25) in the independent validation population was close to the correlation level between phenotype and true breeding value represented by heritability, reported as 0.24~0.25 [27] and 0.31~0.35 [28].

Furthermore, higher selection response may be achieved using GBV compared to using EBVs [25, 29, 30] suggesting that genomic selection would therefore be the method of choice to improve hip conformation most efficiently. It would have special use in small breeding programs for which breeders do not have deep and extended pedigrees upon which to estimate breeding values because the pool of reference individuals for a breed would house the genetic information needed for any dog of the same breed. In chickens, an almost four-fold increase in the accuracy of prediction of yet-to-be observed phenotypes for food conversion rate in broilers was reported when genomic prediction of phenotype was used compared with pedigree prediction of phenotype [31]. In mice, genomic predictions, including both additive and dominant SNP effects, produced a higher accuracy of phenotype prediction for various traits than using pedigree information alone [32].

In addition to the financial burden of progeny testing, the time delay to phenotyping at maturity means that many dogs are bred or bought by owners at weaning time without knowledge of their genetic potential for good hip conformation. Genomic prediction could be applied at birth even prior to weaning and purchase of pups by owners. Nevertheless, reliable phenotype or EBVs are essential for prior to developing GBV. Our result showed that there was a significant correlation (P<0.01) between the reliability of EBV and the accuracy of GBV. The correlation between the reliability of EBV and reliability of GBV was 0.47 (R²=0.22). The more reliable the EBV, the more reliable the corresponding GBV. This was consistent with the previous results that GBV was more accurate when it was derived from EBV than that derived from the raw phenotype as the EBV was more reliable than the raw phenotype.

The qualities of genotyped markers in this study were reasonably good with respect to polymorphism and heterozygosity. The minor allele frequency (MAF) of these SNPs followed a uniform distribution after removing the SNPs with MAF<1%. Heterozygosities had a bimodal distribution with one peak toward zero and one toward 0.5. The distribution was similar to both practical [33-35] and theoretical observations [36] under the assumptions of the neutral theory in a random mating population.

The accuracy of GBV could be higher if the genotyped markers had better coverage of LD by inclusion of more densely spaced markers [37-39]. The LD in our study population decayed very rapidly. A useful LD [40] (r²>0.3) only occurred at distances shorter than 30 kilobase pairs in Labrador retrievers and 20 kilobase pairs across the 6 breeds and the crosses. The dog genome is similar in size to the genomes of humans and other mammals, containing approximately 2.5 billion DNA base pairs [41]. This requires at least 125,000 informative SNPs to capture the LD intervals among breeds. The average and median marker interval from the Illumina CanineSNP20 BeadChip were 107 Kb and 70, respectively. This implied that we could have missed many QTNs.

GBV for hip conformation will become available for most breeds of interest. However, a continued effort at progeny testing to obtain reliable EBV, even as the new technology is applied, is necessary to retrain the predictive formula and to improve the accuracy of genomic prediction. There will always be impetus to expand the reference panel for a breed and across breeds, such as combining the naïve 38 dogs with our original 359 to use as the next reference population. As more dogs and breeds which have undergone genome wide genotyping are added to the reference population, the subset of SNPs used in the prediction set would be recalculated to capture more SNPs in LD with the causal QTN or genes.

The majority of the 359 dogs we used were Labrador retrievers and their crosses with Greyhounds, yet the other minor breeds were well predicted. This indicated that multiple breeds could be integrated together although they were remarkably diversified from a phenotypic and genotypic point of view. We derived PCs from all the SNPs. Similar to previous reports, we were able to separate the breed structure of the dogs in our study based on a plot of the first and second PCs (Figure 4).

For the four traits that collectively define CHD, there are at least 10-20 QTLs [42-44]. In the current study, we identified the most 100-500 influential SNPs providing the most information to the GBV through Bayesian analysis which jointly estimates their contribution. As the number of SNPs in the reference panel dropped below 50, the SNPs failed to bracket some of the QTN and thus the accuracy of the GBV would decrease.

Our previous genome wide association study identified 4 SNPs associated with CHD and 2 SNPs associated with hip OA [45]. These SNPs were identified through individual SNP associations. Further, the GWAS [45] included many more dogs and breeds which were genotyped within 8 previously identified QTL [44]. Genomic prediction could be enhanced by the finding the causal genes through genome wide association studies [45]. Positional cloning of candidate genes will provide opportunities to add intragenic informative SNPs in mutated genes to the genomic prediction panel [46, 47]. However, this may take some time as only one gene, fibrillin 2, has been shown to associated with CHD to date [48].

Our study indicated that genomic prediction could be effective with the most influential 100-500 SNPs chosen from ~22,000SNPs. If genotyping of these SNPs with customized array, or sequencing whole genome becomes cost effective for public use, genomic prediction can become a vital and integral part of improving canine breeding practices for CHD and become a routine part of personalized canine genetic medicine.