Abstract
Elementary flux mode (EFM) analysis is a powerful tool to represent the metabolic network structure and can be further utilized for flux analysis. The method enables characterization and quantification of feasible phenotypes in microbes. EFM analysis was employed to characterize the phenotype of Corynebacterium glutamicum to yield various amino acids. The metabolic network of C. glutamicum yielded 62 elementary modes by incorporating the accumulation of amino acids namely, lysine, alanine, valine, glutamine and glutamate. The analysis also allowed us to compute the maximum theoretical yield for the synthesis of various amino acids. These 62 elementary modes were further used to obtain optimal phenotypic space towards accumulation of biomass and lysine. The study indicated that the optimal solution space from 62 elementary modes forms a super space which incorporates various mutants including lysine producing strain of C. glutamicum. The analysis was also extended to obtain sensitivity of the network to variation in the stoichiometry of NADP in the definition of biomass.
Electronic supplementary material
The online version of this article (doi:10.1007/s11693-011-9073-8) contains supplementary material, which is available to authorized users.
Keywords: Elementary mode analysis, Corynebacterium glutamicum, Optimal phenotypic space, Stoichiometry, Flux analysis, Metabolic network
Introduction
Cellular networks are generally characterized by a set of properties associated with the interactions inherent between the large numbers of component parts. The interactions can be dynamic, non-linear interaction, self evolving/modifying with intrinsic/extrinsic noise and spatial organization. The interactions can be characterized at the genetic, signaling and metabolic levels. In the concept of the central dogma in biology, the hierarchical connectivity is between genes to mRNA, proteins, metabolic reactions and the phenotype. The phenotype can be well characterize by quantifying the metabolic pathways, where in the metabolic reaction just precedes the phenotypic response. Ideally a complete dynamic description of metabolism is necessary to fully characterize the phenotypic response. However, a dynamic description of the metabolism would require enzyme kinetics of several intracellular reactions and regulatory information which are hard to obtain. The most obvious and immediate strategy to overcome this bottleneck would be to analyze the dynamic system at steady state. In such an approach pseudo steady state is assumed for intracellular metabolites, thus eliminating the requirement of kinetic information. Stoichiometric network analysis (SNA) based on convex analysis to locate unique pathways for a system of linear pathways was developed on a chemical system, which laid the foundation for evolution of all future methods and development of algorithms for biological network analysis (Clarke 1988). Urbanczik and Wagner developed null space algorithm to calculate elementary mode fluxes of a chemical reaction system. This improved algorithm for SNA tackles the problem of combinatorial explosion which occur during the construction of elementary mode fluxes for studying large networks (Urbanczik and Wagner 2004). Urbanczik also developed a method for studying the set of alternative optima in the context of flux balance analysis (FBA) (Urbanczik 2007). Schuster and Hilgetag (1994) developed elementary flux mode (EFM) analysis for biochemical network applying the existing concept of convex analysis. Further, Schilling et al. (2000), modified the method of problem formulation to develop extreme pathway analysis which was also based on convex analysis, as applied by Clarke (1988) for SNA and Schuster and Hilgetag (1994) for EFM analysis (Schilling et al. 2000).
Elementary flux mode is one of the techniques of metabolic pathway analysis (Schuster and Hilgetag 1994; Urbanczik 2007; Schuster et al. 2007). Elementary mode analysis uses the metabolic network structure to evaluate the steady state flux distribution under varied media conditions. Each elementary mode is a non-decomposable stoichiometrically balanced pathway in the network, which can operate independently. If any of the reaction in the mode is eliminated, then the entire mode will cease to function (Papin et al. 2004). They connect extracellular metabolites through independent feasible routes represented by an elementary mode, which can be interpreted as an overall biochemical reaction. All the feasible modes represents the entire metabolic network present in organism (Poolman et al. 2004b), since each elementary mode takes into account the combined effect of all the individual reactions that participate in the entire pathway. Thus the approach of flux analysis through elementary modes is systemic in nature and captures a realistic picture of the phenotypic state that can reside in the organism.
Consequently elementary modes have been used to study structural properties of different metabolic networks such as synthesis of tryptophan from glucose (Schuster et al. 1999), combined glycolysis and pentose phosphate pathway (PPP) system in E. coli and Treponema pallidum (Schuster et al. 2000), adenine nucleotide metabolism (Schuster et al. 2002), plant metabolism (Poolman et al. 2004a), enzyme deficient human red blood cells (Cakir et al. 2004), and photosynthate metabolism in chloroplasts (Poolman et al. 2003). Apart from an understanding of the structural properties of metabolic networks using elementary mode analysis, there have been studies on pathway properties and phenotypic behaviour such as study of pathway alignment in glycolysis (Dandekar et al. 1999), use of decomposition algorithms to analyze sub-networks in the central metabolism of Mycoplasma pneumoniae (Schuster et al. 2002), robustness analysis by carrying out gene knockouts (Behre et al. 2008; Stelling et al. 2002; Wilhelm et al. 2004), and the study of pathway redundancy in human erythrocytes (Schuster and Kenanov 2005). EFMs can also be used in tandem with kinetic studies to build kinetic models for different systems as reported in the analysis of sucrose accumulation in sugarcane culm (Rohwer and Botha 2001), growth dynamics in Chinese hamster ovary cells (Provost et al. 2006), and yeast glycolysis (Schwartz and Kanehisa 2006). The use of elementary modes to design and engineer strains for the design of new pathways for producing desired metabolites such as the production of (poly)-hydroxybutyrate from recombinant Saccharomyces cerevisiae (Carlson et al. 2002), design and optimization of pathways for succinate production in E. coli (Cox et al. 2006), optimization of cyanophin production from Pseudomonas putida and Ralstonia eutropha (Diniz et al. 2006), designing the most efficient biomass producing strains (Trinh et al. 2006), increasing ethanol yields in E. coli (Xu et al. 2008), etc. are also well documented. These studies employed elementary modes to characterize the phenotypic behaviour of the organism and quantified the fluxes in the system. Although the method is used to specific objectivity, not much work has been carried out in the characterisation of complete cellular phenotypes. Here, we utilize elementary modes to characterize the broad phenotypic capability of Corynebacterium glutamicum to synthesize various amino acids.
Previous work on C. glutamicum by Gayen and Venkatesh (2006) focussed on the characterization of the optimal phenotypic space using elementary modes. The objective of the work was to analyze the metabolism towards production of lysine using elementary modes and the use of linear programming to evaluate constraints on nitrogen and oxygen uptake by the cell. However, the study only analyzed the case for the production of lysine and trehalose as the extracellular metabolites using a set of fourteen modes. In order to understand the phenotypic behaviour of the organism, it is important to incorporate all the amino acids that the microorganism accumulates. Therefore, in the present work, a set of elementary modes were generated to account for the production of the amino acids: lysine, alanine, valine, glutamate and glutamine, in addition to trehalose, lactate and pyruvate. Further, all feasible combinations of metabolites that can yield feasible elementary modes, i.e. elementary modes producing only external metabolites were mapped. These feasible modes, which lead to individual metabolites or their combinations thereof, can be viewed as subsets of the network mapped by a set of 62 elementary modes. A study of the optimal phenotypic space for biomass and lysine using the stoichiometries of the sets of elementary modes also revealed that the optimal space for 62 modes encompassed all other spaces. The first part of our analysis is based on the premise that the definition of the biomass that yields various elementary modes is invariant. In the second part of our analysis, the elementary modes were used to assess the impact of specific internal metabolites on the optimal biomass values. Further, the definition of biomass was varied by altering the stoichiometric coefficient of ATP, NAD and NADP in the definition of biomass. Thus the sensitivity of the stoichiometric coefficient in the definition of biomass on the phenotypic characterization was also evaluated.
Materials and methods
Construction of the reaction network and building of the stoichiometry matrix
The complete set of reactions involved in the amino acid producing Corynebacterium glutamicum are listed in Gayen and Venkatesh (2006). The major metabolic pathways including glycolysis, PPP, TCA cycle are present in the central metabolism of C. glutamicum. Glucose uptake in the organism occurs via the glucose phosphotransferase system whereas ammonia is assimilated through glutamate (Glutamate dehydrogenase) and glutamine (glutamine synthetase) synthesis reactions. Anaplerotic reaction involved in lysine synthesis, which convert phosphoenolpyruvate (PEP) into oxaloacetic acid (OAA) and oxidative phosphorylation reactions have been incorporated. The ATP dissipation reaction adjusts the excess ATP produced in the organism (Vallino 1991). The definition of the biomass included the stoichiometry of the internal metabolites assuming a balanced growth. However, all the coefficients are represented in integral form required for calculating the elementary modes using the software “ScrumPy—Metabolic Modelling in Python” (Poolman 2006). The synthesis reactions for glutamate, glutamine, lysine, pyruvate, alanine and valine are also listed (Gayen and Venkatesh 2006). It should be noted that, an elementary mode must produce only external metabolites to be considered as feasible (Poolman 2006). To analyze all possible combinations of the seven metabolites, viz alanine, valine, glutamate, glutamine, pyruvate, lactate and lysine, we tested 128 possible cases with glucose, ammonia, oxygen, trehalose and biomass being external metabolites. The metabolites were tested for two levels, i.e. their presence or absence, and the experimental design for studying these simulations was as per a two level full factorial design (Montgomery 2004).
Optimization
The set of elementary modes was utilized to obtain the optimal phenotypic space under different conditions. This was achieved using the ‘linprog’ module from MATLAB©. The molar mass balances for the metabolites can be written as:
 |
1 |
where, M is vector representing the accumulation rates of the external metabolites and S is the matrix, indicating the stoichiometry of the elementary modes. The elements of E {e1, e2, e3, ………en} represents the vector of unknown fluxes of the elementary modes. The elements of vector E can be evaluated for a given set of measurements of accumulation rates (elements of M). Due to the paucity of measurements, a linear optimization technique can be employed to converge onto a feasible solution. Mathematically, the linear optimization formulation can be represented as:
 |
such that,
 |
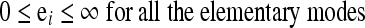 |
2 |
Mi is the accumulation rate of a specific metabolite (such as biomass). Also, S* is the stoichiometric matrix representing the elementary modes and M* is a known vector of the accumulation rates of extracellular metabolites, wherein the rows of the ith external metabolite are eliminated from S and M, respectively. It should be noted that the above approach of using linear programming to evaluate fluxes is similar to the methodology used in FBA. FBA uses the stoichiometry of the original network for the analysis, while we use the stoichiometries of the elementary modes. The unknown fluxes (E) of the elementary modes were obtained using linear programming. The flux vector E when multiplied with the stoichiometric matrix S, gives us the rate vector M, which is further used to map the phenotypic space (Gayen and Venkatesh 2006). The effect of varying the stoichiometric coefficients of the cofactors in the definition of the biomass on the optimal value of the metabolites was also studied. This helps to gauge the relative sensitivity of the metabolites to the cofactors NADP(H), ATP and NAD(H). The coefficient of ATP was first varied holding the coefficients of NADP(H) and NAD(H) constant. The same was repeated for NADP(H) and NAD(H). For each case the impact of varying the coefficient in the biomass definition on the optimal yield of the biomass was enumerated.
Results and discussion
The metabolic network of C. glutamicum was used to obtain elementary modes representing stoichiometric connectivity between various external metabolites. The analysis included three substrates, namely, glucose, ammonia and oxygen and ten products, namely, biomass, trehalose, lactate, pyruvate, lysine, alanine, valine, glutamate, glutamine and CO2. The analysis yielded 62 elementary modes connecting the substrates to the extracellular products (see Online Resource 1 for details).
Out of the 62 modes that were obtained, 35 yielded lysine, 19 yielded biomass, 15 yielded trehalose, 12 yielded valine and alanine, 10 yielded pyruvate and lactate, and 6 yielded glutamate and glutamine (see Online Resource 2 for details). The software “ScrumPy” lists the elementary modes both in terms of the stoichiometries of the external metabolites and in terms of the individual reactions which form the elementary mode. This information can be used to gain better understanding regarding the differences between various modes. For example, the modes leading to glutamate and glutamine were found to be similar except for the amount of ammonia they consume, also no mode led to both glutamate and glutamine. The additional ammonia in the modes leading to glutamine was required because of the conversion of α–ketoglutarate to glutamate which further consumes ammonia to form glutamine, resulting in the increased stoichiometric coefficient for ammonia. A similar balance on ammonia was observed for the metabolite pair of valine and alanine. The number of moles of alanine formed per mode was more than valine and the latter required NADPH and more carbon as compared to alanine. This imposes constraint on the formation of valine, which appears in the form of difference in the coefficients of alanine and valine in the elementary modes specific to these metabolites. However, in case of lactate and pyruvate, no specific mode contained both pyruvate and lactate as product. This is due to the net NADH balance and the fact that a reaction converting pyruvate to lactic acid using lactate dehydrogenase. Maximum yield of the metabolites were also obtained from the elementary modes directly as the ratio of the coefficient of the metabolite in the elementary mode to that of glucose in the same mode. Maximum yields of various metabolites obtained were 200, 63.65, 25 and 115.7 mM/100 mM of glucose consumed for lactate, lysine, trehalose and biomass, respectively. The maximum yields for the accumulation of alanine, valine, glutamate and glutamine were 171.43, 85.71, 100 and 100 mM/100 mM of glucose consumed, respectively. Elementary modes which give maximum theoretical yield of the metabolite produced by them are graphically presented in Fig. 1. Lysine yield reported in the literature varies substantially. This largely depends on the definition of the metabolic network under consideration. Maximum theoretical lysine yield obtained upon considering full set of available pathways in the central metabolism was 82% (Wittmann and Becker 2007), whereas if only the major pathways were considered, then lysine yield on glucose was 75% (de Graaf 2000; Schuster et al. 2007; Hollander 1994; de Graaf et al. 2001). Lysine yield obtained by Vallino was 64%, assuming pyruvate carboxylase flux to be zero (Vallino 1991), whereas, it was only 56% when limitation in succinyl-CoA supply was assumed (Gulik and Heijnen 1995). Lysine yield obtained in this study is close to the value obtained by Vallino since the metabolic network considered in the present study is similar to that reported by Vallino (1991). Both these studies considered the conversion of PEP to OAA through phosphoenolpyruvate carboxylase (PEPCx) as an anaplerotic reaction yielding 64% lysine. When the second anaplerotic reaction which converts pyruvate into OAA was incorporated, then the maximum theoretical yield was 75%, as reported elsewhere (results not shown) (Hollander 1994; Schuster et al. 2007; de Graaf 2000; de Graaf et al. 2001). It was also possible to obtain the bounds on oxygen and ammonia uptake rates for individual metabolites, directly from elementary modes. These bounds depict the feasible range of ammonia and oxygen uptake rates between which production of a particular metabolite was possible. Table 1 lists these bounds for the individual metabolites and it is clear that among the nitrogen containing metabolites, which includes amino acids and biomass, production of lysine, alanine and valine were more flexible as the feasible range for ammonia and oxygen uptake rates were wider as compared to that of other metabolites. On the contrary, the production of glutamate was restricted to a narrow range of ammonia and oxygen uptake rates. It was also evident from the table that the production of glutamate and glutamine by the organism was only practicable when ammonia uptake rate was high. For the remaining external metabolites—lactate, pyruvate, trehalose and CO2—ammonia and oxygen uptake rates were quite broad, portraying that the production of these metabolites were not under very stringent control of oxygen and ammonia, as it was for the nitrogen containing compounds.
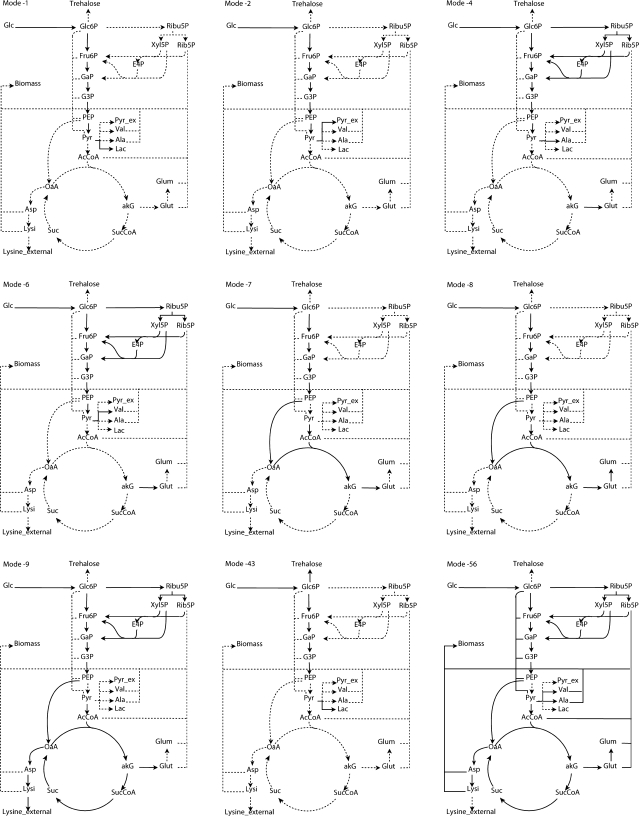
Fig. 1.
Graphical representation of selected elementary modes. These are the modes which give maximum theoretical yield of the metabolite produced by them. Active reactions in the mode are shown with solid lines. Number assigned to the mode is same as given in the Electronic Supplementary Material 1
Table 1.
The minimum and maximum uptake rates (mM/h) for ammonia and oxygen for a specific metabolite obtained directly from the stoichiometric coefficients of 62 elementary modes set
| Amino acid | Ammonia | Oxygen | ||
|---|---|---|---|---|
| Minimum | Maximum | Minimum | Maximum | |
| Lysine | 40 | 166.7 | 42.9 | 366.7 |
| Glutamate | 100 | 141.7 | 75 | 150 |
| Glutamine | 133.3 | 200 | 75 | 154.2 |
| Alanine | 50 | 171.4 | 50 | 300 |
| Valine | 25 | 150 | 50 | 300 |
| Biomass | 40 | 126.2 | 94.6 | 310.0 |
| Trehalose | 0 | 115.8 | 0 | 220 |
| Pyruvate | 0 | 133.3 | 50 | 124.9 |
| Lactate | 0 | 133.3 | 0 | 112.1 |
| CO2 | 25 | 200 | 42.9 | 366.7 |
Although 62 elementary modes were obtained to represent the metabolic network, it would be interesting to obtain modes with a subset of extracellular metabolites to obtain relationships between various metabolites. For example, one can obtain elementary modes with just the biomass, CO2 and lysine as the products. This implies that the organism can use 62 modes to obtain a steady (phenotypic) state yielding various metabolites present in the network. A two level factorial design was used to obtain elementary modes from the seven extracellular metabolites namely, the five amino acids, lactate and pyruvate. It should be noted that biomass, trehalose and the three substrates (O2, NH3 and glucose) were included in all the analysis. The analysis yielded elementary modes for 27 (=128) different combinations, out of which only 52 resulted in feasible elementary modes. Infeasible sets yielded elementary modes containing intracellular metabolites in the modes, indicating stoichiometric imbalance. When only one metabolite of the seven extracellular metabolites was considered, the analysis yielded feasible modes, except in the case of glutamine. However, feasible modes were not obtained when lactate, glutamine, glutamate, valine and alanine were individually internalized maintaining the other six metabolites external. It was also observed that when lactate was considered internal in combination with any of the other six metabolites (taking only one among these six at a time); the analysis resulted in an infeasible solution for every such combination. In order to understand the reason of obtaining infeasible solution for certain combinations, a case where internal metabolites were produced was investigated in a set of elementary modes. The case where lactate and lysine were deleted was considered. In this case a total of 23 elementary modes were obtained. However, a few of these modes included internal metabolites such as ATP, NADP, etc. in their elementary modes. By comparing the pathways for these modes with the corresponding 23 modes out of the set of 62 modes, it was observed that the reactions making up the elementary modes were identical, but for the stoichiometric coefficients. In these 23 modes the coefficients of the individual modes were not balanced indicating that the system was unable to attain a steady state. Another observation made was that the internal metabolites were observed only in some of the modes leading to biomass, whereas the rest leading to alanine, valine, glutamate, glutamine and pyruvate were identical to those appearing in the set of 62 modes. This indicated that the combination of extracellular metabolite could not balance the biomass definition resulting in a metabolite overflow. Online Resource 3 lists all the combinations of external metabolites which give feasible elementary modes.
To further explore the effect of deleting a particular metabolite, lysine was eliminated from the set of external metabolites to yield 27 elementary modes. Comparing this set of elementary modes with the original 62 modes, it was observed that the 27 modes were a subset of the 62 modes. Similarly 52 elementary modes were obtained, when pyruvate was deleted from the set of external metabolites, which were also a subset of the 62 modes. This indicated that the set of elementary modes obtained by including all metabolites was a superset from which the elementary modes for other subset of metabolites may be derived. This is in agreement with the invariance property for the elementary modes (Schuster et al. 2000) i.e., given two systems where one has a few reactions more than the other, the set of elementary modes of the lesser reaction will be conserved in the set of elementary modes for the larger system. Essentially, this signifies that the set of 62 modes represents all possible elementary modes for the organism and hence forms a superset mapping the prevailing metabolism. This also translates to the fact that the 62 elementary modes can represent a broader feasible phenotypic status of the organism. Thus, the set of 62 elementary modes can be further used to characterize the optimal phenotypic space of the organism.
Elementary modes and optimal phenotypic space
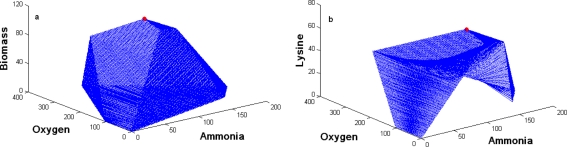
The set of 62 elementary modes was used to obtain the optimal phenotypic space for the uptake of glucose, ammonia and oxygen under various cellular objectives namely, maximization of biomass or lysine. Figure 2 shows the phenotypic space for maximization of biomass or lysine using the 62 modes.
Fig. 2.
Optimal phenotypic spaces using 62 modes for C. glutamicum: (a) maximization of biomass and (b) maximization of lysine. Three constraints glucose, O2 and NH3 were specified in each case. Circle on the plots shows maximum feasible yield of biomass (115.7) or lysine (63.5)
The analysis demonstrates that for a normalized glucose uptake rate of 100 mM/h, the feasible uptake rates of ammonia and oxygen were [0–200] and [0–366] mM/h, respectively. The organism accumulates only lactate and trehalose and yields of other metabolites were zero, when the uptake rates of oxygen and ammonia were zero. Under these conditions, yield of lactate was substantially higher than that of trehalose. This situation corresponds to elementary mode number 1 in the modes for trehalose/lactate. At the other extreme, when both ammonia and oxygen uptake rates were maximum, a feasible solution was not obtained. At a maximum oxygen uptake rate of 366 mM/h, corresponding ammonia uptake rate was only 67 mM/h. At these uptake rates, lysine formation rate was significant, while production rates of rest of the metabolites were close to zero. Similarly, for maximum ammonia uptake rate of 200 mM/h corresponding oxygen uptake rate was 150 mM/h and this condition was represented by homoglutamine condition, i.e. only glutamine was produced at these uptake rates. Uptake rates of ammonia and oxygen corresponding to maximum biomass yield of 115.5 mM/100 mM of glucose consumed were 85 and 171 mM/h, respectively, while the rate of formation of rest of the metabolites was close to zero.
We obtained a total of 22 elementary modes for a lysine over producing strain of C. glutamicum, wherein the extracellular secretion of pyruvate and other amino acids were negligible. Here apart from the substrates, the remaining external metabolites were lactate, lysine, trehalose, CO2 and biomass. For 22 modes, feasible uptake rates of ammonia and oxygen were [0–127] and [0–365] mM/h respectively, for a normalized glucose uptake rate of 100 mM/h. The organism produces lactate and trehalose at zero uptake rates of oxygen and ammonia as observed before. Where as, for the case with maximum oxygen or ammonia uptake rate, the lysine yield was high with the formation rate of rest of the external metabolites close to zero. This indicated that for lysine formation high oxygen and ammonia uptake rates were essential. Uptake rates of ammonia and oxygen corresponding to maximum biomass yield (115.5 mM/100 mM of glucose consumed) remained same as that for 62 modes.
Gayen and Venkatesh (2006) focussed on characterization of optimal phenotypic space for C. glutamicum, using 14 elementary modes. Here lactate was also considered as an internal metabolite. For these modes bounds on NH3 and O2 uptake rates were [40–127] and [155–365] mM/h, respectively, which were in the range observed for the ammonia and oxygen uptake rates obtained from 62 elementary modes set. At minimum uptake rate of ammonia (40 mM/h), no lysine was produced while all the other external metabolites were formed and a moderate uptake rate of oxygen was observed. At maximum oxygen or ammonia uptake rate, almost no trehalose and biomass were formed. In both the cases the production rate of lysine was large and maximum possible was observed i.e. 63.33 mM/h in the latter case. At ammonia and oxygen uptake rates of 85 and 174 respectively, rate of biomass formation was maximum (115.09 mM/h), while no trehalose and lysine formation was observed.
The characterization of the phenotypic space of an organism thus gives insight into the feasible ranges of the accumulation rates of various metabolites. It is thus possible to compute the nutrient (glucose, O2 and NH3) uptake rate at optimal production levels of various metabolites. In addition, the characterization of optimal phenotypic space allows determination of optimal/suboptimal behaviour of the organism under a given set of conditions. Specifically, if the solution lies below the optimal solution space, it can be inferred that although the solution is feasible, the organism is sub-optimal for the synthesis of the particular metabolite. We had employed stoichiometric coefficients of elementary modes to determine the thermodynamically feasible bounds on the nutrient uptake rates without going through the additional process of linear optimization. More significantly, the feasible uptake rates of different nutrients for each metabolite can be determined, which was not possible to evaluate from the optimal phenotypic space for a particular metabolite. However, the stoichiometry of elementary modes cannot yield all the optimal solutions and cannot infer sub-optimality in the phenotype.
Further, when the optimal phenotypic space for maximization of biomass and for lysine for the set of 22 modes was superimposed over the phenotypic space for 62 modes, it was observed that the optimal space for 22 modes was a subspace of phenotypic space for 62 modes (results not shown). The solution space for 62 modes was substantially bigger than that for 22 modes. This implied that if the system was modelled using 22 modes, then a large number of feasible solutions could be missed out. Thus, it was observed that not only the set of 62 elementary modes a superset for the other modes, even the phenotypic space that it spans was a super space representing a bigger phenotypic space.
Stoichiometric sensitivity
The analysis discussed above was based on the different sets of metabolites that could be produced by the organism, thus characterizing its various phenotypes, wherein the definition of the biomass remained the same. The biomass definition that was used for developing the stoichiometric matrix was based on the stoichiometric coefficients listed by Neihardt and Ingraham (Neidhardt et al. 1990), as given below Eq. 3.
 |
3 |
The above definition accounts for the various cofactors that are present in the organism and also includes data obtained by carrying out an elemental balance of the dry cell. The stoichiometric coefficient for the cofactors NADP, NAD and ATP can be noted to be 500, 350 and 3,100, respectively. Since these cofactors play an important role in the oxidative state and energetics of the cell, the effect of these stoichiometric coefficients on the elementary modes and maximum biomass yield were analyzed.
The upper and lower bounds of the ATP values were determined by estimating the elementary modes for each case and then selecting the phenotypically feasible options. The same was repeated for NAD and NADPH. In each case the optimal yield of biomass was determined. We then plotted the optimum biomass value against the coefficient of the specific cofactor. Finally, stoichiometric coefficient of ATP was altered to determine the feasibility of obtaining elementary modes. The stoichiometric coefficient for ATP was in the range of [0–4,100] to obtain feasible elementary modes. However, it was observed that irrespective of the stoichiometric coefficient of ATP, the maximum yield of biomass was 115.7 as noted before. This indicates that the stoichiometric coefficient of ATP in the definition of biomass does not have an effect on biomass yield. This may be due to the flexibility in the network offered by the ATP dissipation reaction, which independently converts ATP to ADP. To confirm this we obtained the flux distribution for various stoichiometric coefficients of ATP in the definition of biomass using experimental data obtained from literature (Vallino and Stephanopoulos 1993). The flux distribution for the system with altered stoichiometry of ATP was the same as for the original network with 3,100 ATP, 500 NADPH and 350 NAD in the biomass definition. This implies that the flux through the central carbon metabolism was not affected by the stoichiometry of ATP in the biomass definition. However, only the flux through the ATP dissipation reaction (that is, ATP - > ADP) reduced with increasing stoichiometric coefficient in the biomass definition. This indicates that the ATP dissipation reaction is capable of buffering the additional requirement of ATP in the biomass definition. Further, the optimal biomass formation itself is constrained by the stoichiometry of other cofactors and metabolites, which ensures that the excess ATP requirement is not a burden.
A similar result was obtained by altering the stoichiometric coefficient of NAD. A range of [0–4,000] was tested for the stoichiometry of NAD in the biomass definition to yield feasible elementary modes. The maximum yield of biomass was again independent of the stoichiometric coefficient of NAD. Here also flux distribution was obtained for various stoichiometric coefficients of NAD in the definition of biomass. Unlike, in case of ATP, the coefficient of NAD had a strong influence on the flux distribution of the central carbon metabolism with increasing coefficient of NAD in biomass definition, the flux through glycolysis and TCA pathway was reduced while the flux through oxidative phosphorylation was increased. However, the accumulation rates of the extracellular metabolites were not affected. This implies that the fluxes involving NAD internally rearrange to balance the cofactor requirement. It was also noted that a feasible solution was not obtained for coefficient of NAD greater than 1,200 in the biomass definition implying that this is the maximum coefficient that the network can balance. Thus, the network was sensitive to the coefficient of NAD in the biomass definition due to the balancing of additional cofactor requirement, while for ATP the network was robust to changes in the stoichiometric coefficient value.
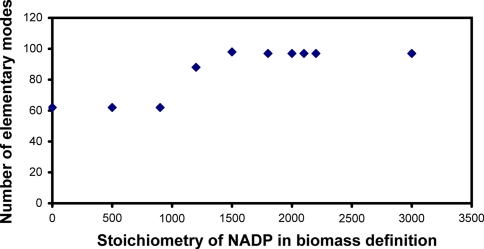
Further the effect of stoichiometric coefficient of NADP in the biomass definition was analyzed. The number of feasible elementary modes was a strong function of the stoichiometric coefficient of NADP in the biomass (see Fig. 3). It can be observed that feasible elementary modes were obtained in the stoichiometric coefficient range of [0–3,000] for NADP. Up to the NADP value of 900, the number of elementary modes obtained was 62. Beyond this as coefficient of NADP was increased, the number of elementary modes too increased. For instance at an NADP value of 1,200, the number of elementary modes obtained were 88 while at a value of 1,500, 98 elementary modes were obtained. At an NADP value of 1,800 the number of elementary modes dropped down from 98 to 97 and then it maintained at 97 up to NADP value of 3,000. Beyond this value of NADP, the number of elementary modes did not vary and remained at 97. However, the resulting elementary modes do not yield feasible solutions as they produce internal metabolites.
Fig. 3.
The number of feasible elementary modes with respect to change in the stoichiometric value of NADP in the biomass definition
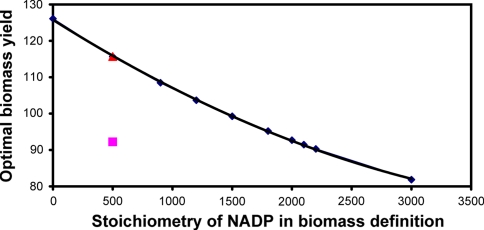
Analysis also revealed that optimal biomass yield was strongly related to the change in the stoichiometric coefficient of NADP in the biomass definition (see Fig. 4). It decreased with increase in the coefficient of NADP. For zero stoichiometric value of NADP, the optimal yield of biomass was 126.0 mM/100 mM of glucose consumed, an increase from the original 115.7 mM/100 mM of glucose consumed corresponding to stoichiometric coefficient of 500 for NADP. Further, as stoichiometry of NADP was increased, a gradual decrease in the optimal yield of biomass was observed, whereas the optimal yields of the other metabolites did not change. The decreasing trend in the biomass yield with respect to stoichiometric coefficient of NADP was observed until the upper limit of 3,000; at which point the biomass yield was 81.9 mM/100 mM of glucose consumed with respect to a normalized glucose value of 100.
Fig. 4.
Value of optimal biomass yield with respect to change in the stoichiometric value of NADP in the biomass definition filled diamond. Solid line shows the trend line. Filled triangle and filled square shows maximum theoretical and experimental biomass yields, respectively
The elementary modes obtained at NADP level of 1,500 and 2,000 were compared to understand the underlying difference, originating due to the variation in the stoichiometric coefficient of NADP. It was observed that there were modes leading to alanine, valine, lysine, lactate and pyruvate which were not present in the set of 97 modes. Similarly, when the NADP value was 1,800, there were modes leading to glutamate, glutamine and two additional modes leading to biomass formation which were not found in the set of 98 modes. Thus, there was a complete shift in the set of elementary modes obtained due to changes in the stoichiometry of NADP value. In order to accommodate for the increase in NADP value, the suboptimal pathways leading to certain metabolites were eliminated and the pathways leading towards biomass were added. But this was achieved by the cell at the expense of the maximal biomass production, which is clear from Fig. 4, which shows the maximum biomass yield due to variation in the stoichiometry of NADP. The figure also depicts a difference between experimental and theoretical optimal biomass yields. Theoretical biomass yield was around 115.7 mM while biologically feasible yield was around 92.25 mM for glucose uptake rate of 100 mM/h (Vallino 1991), which is 80% of the maximum. This difference in the yields may be attributed to the limitation in the substrate uptake capacity of the cell, although the yield of 92 for biomass remains in the optimal phenotypic space (Gayen and Venkatesh 2006).
Summary
Traditionally linear programming problem (LPP) has been widely used in order to obtain flux distributions in metabolic networks. One of the earliest work reported by Savinell and Palsson (1992) presented a mathematical formalism that focused on metabolites and not just on cofactors (Savinell and Palsson 1992). While there have been several approaches to analyze metabolic networks such as FBA (Kauffman et al. 2003; Varma et al. 1993) and MFA (Vallino and Stephanopoulos 1993), the newer approaches are based on mixed integer linear programming (Lee et al. 2000) and quadratic programming (Mahadevan and Schilling 2003). Gayen and Venkatesh (2006) used LP to study the optimal phenotypic space using the stoichiometry matrix from the set of elementary modes. Our work extends the scope of previously reported approaches by considering bigger matrices and larger spaces. The analysis on C. glutamicum yielded a set of 62 modes which acts as a superspace to represent the metabolic network. Similarly, the phenotypic space of the accumulation rates of biomass and the other metabolites obtained by considering 62 modes, acts as a superspace with respect to subsets of elementary modes. Analysis of stoichoimetric coefficients of elementary modes and characterization of the phenotypic space provide limits on uptake rates of each nutrient and maximum yield for each metabolite. While the former provides theoretical yields of extracellular metabolites and limits in uptake rates of substrates, the latter provides information about possible combinations of nutrient uptake rates to produce a specific metabolite optimally along with providing optimal/suboptimal behaviour of the organism under a given set of conditions. An advantage of using elementary modes is to obtain thermodynamically feasible bounds on the nutrient uptake rates through the stoichiometry of nutrients for the formation of extracellular metabolites. Thermodynamically feasible bounds for O2 and NH3 uptake rates for several metabolites (see Table 1) were obtained directly from the elementary modes. The advantage of using elementary mode analysis is to obtain such a property without resorting to either experimental methods or linear optimization of the network.
The study of stoichiometric sensitivities of the cofactors was carried out to extend the analysis to different definitions of biomass, whereas previous studies were restricted to the effect of externalization of various metabolites. Such a study is important as it gives insights about the thermodynamic bounds on the cofactors used to define biomass. The study demonstrated a strong linkage between stoichiometry of NADP in the biomass definition and maximum theoretical yield of biomass. Previous studies on C. glutamicum mutants have ascertained the role of NADPH for the production of lysine and its impact on the lysine biosynthesis pathway. It was observed that while NADPH does influence the enzymes in the biosynthetic pathway of lysine, its overall effect on the pathway flux was negligible (Hua et al. 2000; Yang et al. 1999). Also, the role of NADPH in the central metabolism was vital as it traverses between the TCA cycle and the pentose phosphate pathway as it gets recycled. Studies with C. glutamicum mutants (Park et al. 1997) have shown that perturbations in the pentose phosphate pathway can cause an overproduction of NADPH, thus increasing the reducing power of the cell. Analysis also demonstrated that the stoichiometry of NADP in biomass strongly influences the maximum biomass yield.
Elementary modes are important tools for metabolic pathway analysis and for rational strain design (Carlson et al. 2002; Schuster et al. 1999; Schuster et al. 2000). They can be used for evaluating robustness, optimality and enzyme subsets required for a specific phenotype (Klamt and Stelling 2003). The feasible elementary modes were evaluated for different combinations of metabolites to characterize the phenotype of C. glutamicum. The set of elementary modes obtained from the analysis maps all possible pathways within the organism. The method provided a systemic approach of mapping phenotypes using the set of elementary modes. This can further be used to obtain the optimal phenotypic spaces for different metabolites using linear programming under various objective functions. Cofactors play an important role in determining the optimal yields of biomass and have relative importance in the stoichiometric matrix. Further studies could include strategies to optimize the synthesis of various amino acids using C. glutamicum.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Footnotes
Devesh Radhakrishnan, Meghna Rajvanshi contributed equally.
References
- Behre J, Wilhelm T, Kamp A, Ruppin E, Schuster S. Structural robustness of metabolic networks with respect to multiple knockouts. J Theor Biol. 2008;252(3):433–441. doi: 10.1016/j.jtbi.2007.09.043. [DOI] [PubMed] [Google Scholar]
- Cakir T, Tacer CS, Ulgen KO. Metabolic pathway analysis of enzyme-deficient human red blood cells. BioSyst. 2004;78(1–3):49–67. doi: 10.1016/j.biosystems.2004.06.004. [DOI] [PubMed] [Google Scholar]
- Carlson R, Fell D, Srienc F. Metabolic pathway analysis of a recombinant yeast for rational strain development. Biotechnol Bioeng. 2002;79(2):121–134. doi: 10.1002/bit.10305. [DOI] [PubMed] [Google Scholar]
- Clarke B. Stoichiometric network analysis. Cell Biochem Biophys. 1988;12(1):237–253. doi: 10.1007/BF02918360. [DOI] [PubMed] [Google Scholar]
- Cox SJ, Levanon SS, Sanchez A, Lin H, Peercy B, Bennett GN, San KY. Development of a metabolic network design and optimization framework incorporating implementation constraints: a succinate production case study. Metab Eng. 2006;8(1):46–57. doi: 10.1016/j.ymben.2005.09.006. [DOI] [PubMed] [Google Scholar]
- Dandekar T, Schuster S, Snel B, Huynen M, Bork P. Pathway alignment: application to the comparative analysis of glycolytic enzymes. Biochem J. 1999;343:115–124. doi: 10.1042/0264-6021:3430115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Graaf A (2000) Metabolic flux analysis of Corynebacterium glutamicum. In: Bioreaction engineering, modelling and control. Springer, New York, pp 506–555
- de Graaf A, Eggeling L, Sahm H (2001) Metabolic engineering for L-lysine production by Corynebacterium glutamicum. In: Metabolic engineering, pp 9–29. doi:10.1007/3-540-45300-8_2 [DOI] [PubMed]
- Diniz SC, Voss I, Steinbuchel A. Optimization of cyanophycin production in recombinant strains of Pseudomonas putida and Ralstonia eutropha employing elementary mode analysis and statistical experimental design. Biotechnol Bioeng. 2006;93(4):698–717. doi: 10.1002/bit.20760. [DOI] [PubMed] [Google Scholar]
- Gayen K, Venkatesh KV (2006) Analysis of optimal phenotypic space using elementary modes as applied to Corynebacterium glutamicum. BMC Bioinform 7. doi:445 10.1186/1471-2105-7-445 [DOI] [PMC free article] [PubMed]
- Gulik WMv, Heijnen JJ. A metabolic network stoichiometry analysis of microbial growth and product formation. Biotechnol Bioeng. 1995;48(6):681–698. doi: 10.1002/bit.260480617. [DOI] [PubMed] [Google Scholar]
- Hollander JA. Potential metabolic limitations in lysine production by Corynebacterium glutamicum as revealed by metabolic network analysis. Appl Microbiol Biotechnol. 1994;42(4):508–515. doi: 10.1007/BF00173913. [DOI] [Google Scholar]
- Hua Q, Yang C, Shimizu K. Metabolic control analysis for lysine synthesis using Corynebacterium glutamicum and experimental verification. J Biosci Bioeng. 2000;90(2):184–192. [PubMed] [Google Scholar]
- Kauffman KJ, Prakash P, Edwards JS. Advances in flux balance analysis. Curr Opin Biotechnol. 2003;14(5):491–496. doi: 10.1016/j.copbio.2003.08.001. [DOI] [PubMed] [Google Scholar]
- Klamt S, Stelling J. Two approaches for metabolic pathway analysis? Trends Biotechnol. 2003;21(2):64–69. doi: 10.1016/S0167-7799(02)00034-3. [DOI] [PubMed] [Google Scholar]
- Lee S, Phalakornkule C, Domach MM, Grossmann IE. Recursive MILP model for finding all the alternate optima in LP models for metabolic networks. Comput Chem Eng. 2000;24(2–7):711–716. doi: 10.1016/S0098-1354(00)00323-9. [DOI] [Google Scholar]
- Mahadevan R, Schilling CH. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab Eng. 2003;5(4):264–276. doi: 10.1016/j.ymben.2003.09.002. [DOI] [PubMed] [Google Scholar]
- Montgomery DC. Design and analysis of experiments. 5. Singapore: Wiley; 2004. [Google Scholar]
- Neidhardt FC, Ingraham JL, Schaechter M (1990) Physiology of the bacterial cell: a molecular approach, vol 1, 1st edn. Sinauer Associates Inc, Sunderland
- Papin JA, Stelling J, Price ND, Klamt S, Schuster S, Palsson BO. Comparison of network-based pathway analysis methods. Trends Biotechnol. 2004;22(8):400–405. doi: 10.1016/j.tibtech.2004.06.010. [DOI] [PubMed] [Google Scholar]
- Park SM, Sinskey AJ, Stephanopoulos G. Metabolic and physiological studies of Corynebacterium glutamicum mutants. Biotechnol Bioeng. 1997;55(6):864–879. doi: 10.1002/(SICI)1097-0290(19970920)55:6<864::AID-BIT5>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Poolman MG (2006) ScrumPy: metabolic modelling with Python. In: IEE proceedings systems biology, pp 375–378. doi:10.1049/in-syb:20060010 [DOI] [PubMed]
- Poolman MG, Fell DA, Raines CA. Elementary modes analysis of photosynthate metabolism in the chloroplast stroma. Eur J Biochem. 2003;270(3):430–439. doi: 10.1046/j.1432-1033.2003.03390.x. [DOI] [PubMed] [Google Scholar]
- Poolman MG, Assmus HE, Fell DA. Applications of metabolic modelling to plant metabolism. J Exp Bot. 2004;55(400):1177–1186. doi: 10.1093/jxb/erh090. [DOI] [PubMed] [Google Scholar]
- Poolman MG, Venkatesh KV, Pidcock MK, Fell DA. A method for the determination of flux in elementary modes, and its application to Lactobacillus rhamnosus. Biotechnol Bioeng. 2004;88(5):601–612. doi: 10.1002/bit.20273. [DOI] [PubMed] [Google Scholar]
- Provost A, Bastin G, Agathos SN, Schneider YJ. Metabolic design of macroscopic bioreaction models: application to Chinese hamster ovary cells. Bioprocess Biosyst Eng. 2006;29(5–6):349–366. doi: 10.1007/s00449-006-0083-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohwer JM, Botha FK. Analysis of sucrose accumulation in the sugar cane culm on the basis of in vitro kinetic data. Biochem J. 2001;358(2):437–445. doi: 10.1042/0264-6021:3580437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savinell JM, Palsson BO. Network analysis of intermediary metabolism using linear optimization. 1. development of mathematical formalism. J Theor Biol. 1992;154(4):421–454. doi: 10.1016/S0022-5193(05)80161-4. [DOI] [PubMed] [Google Scholar]
- Schilling CH, Letscher D, Palsson BO. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J Theor Biol. 2000;203(3):229–248. doi: 10.1006/jtbi.2000.1073. [DOI] [PubMed] [Google Scholar]
- Schuster S, Hilgetag C. On elementary flux modes in biochemical reaction systems at steady state. J Biol Syst. 1994;2(2):165–182. doi: 10.1142/S0218339094000131. [DOI] [Google Scholar]
- Schuster S, Kenanov D. Adenine and adenosine salvage pathways in erythrocytes and the role of S-adenosylhomocysteine hydrolase—a theoretical study using elementary flux modes. FEBS J. 2005;272(20):5278–5290. doi: 10.1111/j.1742-4658.2005.04924.x. [DOI] [PubMed] [Google Scholar]
- Schuster S, Dandekar T, Fell DA. Detection of elementary flux modes in biochemical networks: a promising tool for pathway analysis and metabolic engineering. Trends Biotechnol. 1999;17(2):53–60. doi: 10.1016/S0167-7799(98)01290-6. [DOI] [PubMed] [Google Scholar]
- Schuster S, Fell DA, Dandekar T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat Biotech. 2000;18(3):326–332. doi: 10.1038/73786. [DOI] [PubMed] [Google Scholar]
- Schuster S, Hilgetag C, Woods JH, Fell DA. Reaction routes in biochemical reaction systems: algebraic properties, validated calculation procedure and example from nucleotide metabolism. J Math Biol. 2002;45(2):153–181. doi: 10.1007/s002850200143. [DOI] [PubMed] [Google Scholar]
- Schuster S, Kamp A, Pachkov M (2007) Understanding the Roadmap of Metabolism by Pathway Analysis. In: Metabolomics. Methods in molecular biology. Humana Press, Iotowa, N, pp 199–226 [DOI] [PubMed]
- Schwartz J-M, Kanehisa M. Quantitative elementary mode analysis of metabolic pathways: the example of yeast glycolysis. BMC Bioinformatics. 2006;7(1):186. doi: 10.1186/1471-2105-7-186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelling J, Klamt S, Bettenbrock K, Schuster S, Gilles ED. Metabolic network structure determines key aspects of functionality and regulation. Nature. 2002;420(6912):190–193. doi: 10.1038/nature01166. [DOI] [PubMed] [Google Scholar]
- Trinh CT, Carlson R, Wlaschin A, Srienc F (2006) Design, construction and performance of the most efficient biomass producing E. coli bacterium. Metab Eng 8(6): 628–638. doi: 10.1016/j.ymben.2006.07.006 [DOI] [PubMed]
- Urbanczik R. Enumerating constrained elementary flux vectors of metabolic networks. Iet Systems Biology. 2007;1(5):274–279. doi: 10.1049/iet-syb:20060073. [DOI] [PubMed] [Google Scholar]
- Urbanczik R, Wagner C (2004) An improved algorithm for stoichiometric network analysis: theory and applications. Bioinform:bti127. doi :10.1093/bioinformatics/bti127 [DOI] [PubMed]
- Vallino JJ (1991) Identification of branch point restrictions in microbial metabolism through metabolic flux analysis and local network perturbations. Thesis, Massachusets Institute of Technology, Boston
- Vallino JJ, Stephanopoulos G. Metabolic flux distributions in Corynebacterium glutamicum during growth and lysine overproduction. Biotechnol Bioeng. 1993;41(6):633–646. doi: 10.1002/bit.260410606. [DOI] [PubMed] [Google Scholar]
- Varma A, Boesch BW, Palsson BO. Biochemical production capabilities of Escherichia coli. Biotechnol Bioeng. 1993;42(1):59–73. doi: 10.1002/bit.260420109. [DOI] [PubMed] [Google Scholar]
- Wilhelm T, Behre J, Schuster S. Analysis of structural robustness of metabolic networks. Syst Biol. 2004;1(1):114–120. doi: 10.1049/sb:20045004. [DOI] [PubMed] [Google Scholar]
- Wittmann C, and J. Becker (2007) The l-lysine story: from metabolic pathways to industrial production. In: Amino acid biosynthesis: pathways, regulation, and metabolic engineering,Springer, Heidelberg, pp 39–70. doi:10.1007/7171_2006_089
- Xu XJ, Cao LM, Chen X. Elementary flux mode analysis for optimized ethanol yield in anaerobic fermentation of glucose with Saccharomyces cerevisiae. Chin J Chem Eng. 2008;16(1):135–142. doi: 10.1016/S1004-9541(08)60052-X. [DOI] [Google Scholar]
- Yang C, Hua Q, Shimizu K. Development of a kinetic model for l-lysine biosynthesis in Corynebacterium glutamicum and its application to metabolic control analysis. J Biosci Bioeng. 1999;88(4):393–403. doi: 10.1016/S1389-1723(99)80216-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Below is the link to the electronic supplementary material.