The mechanical response of the lumbar spine to different combinations of disc degenerative changes investigated using randomized poroelastic finite element models

Abstract

Degeneration of the intervertebral disc is related to progressive changes in the disc tissue composition and morphology, such as water loss, disc height loss, endplate calcification, osteophytosis. These changes may be present separately or, more frequently, in various combinations. This work is aimed to the biomechanical investigation of a wide range of clinical scenarios of disc degeneration, in which the most common degenerative changes are present in various combinations. A poroelastic non-linear finite element model of the healthy L4–L5 human spine segment was employed and randomly scaled to represent ten spine segments from different individuals. Six different degenerative characteristics (water loss in the nucleus pulposus and annulus fibrosus; calcification and thickness reduction of endplate cartilage; disc height loss; osteophyte formation; diffuse sclerosis) were modeled in 30 randomly generated models, 10 for each overall degree of degeneration (mild, moderate, severe). For each model, a daily loading cycle including 8 h of rest, 16 h in the standing position with superimposed two flexion–extension motion cycles was simulated. A tendency to an increase of stiffness with progressing overall degeneration was observed, in compression, flexion and extension. Hence, instability for mild degeneration was not predicted. Facet forces and fluid loss decreased with disc degeneration. Nucleus, annulus and endplate degeneration, disc height loss, osteophytosis and diffuse sclerosis all induced a statistically significant decrease in the total daily disc height variation, facet force and flexibility in flexion–extension. Therefore, grading systems for disc degeneration should include all the degenerative changes considered in this work, since all of them had a significant influence on the spinal biomechanics.

Introduction

Disc degeneration is related to progressive changes in the lumbar intervertebral discs, involving both tissue biology and mechanics [5]. Both genetic inheritance [9, 10] and high mechanical loading [1, 4, 26] were identified as possible causes of this pathology. Once the process is initiated, a cascade of inevitable cell-mediated responses starts, leading to further degenerative phenomena [5]. Some of these phenomena, such as osteophytosis and decreased cell density, may simply reflect a remodeling response to altered mechanical loading, spinal stability and impaired nutrition [8].

In degenerated discs, the different morphological changes may be present individually or, more frequently, in different combinations. As a matter of fact, several grading systems of disc degeneration were based on the identification of the observable degenerative changes, by means of radiography [24, 48], discography [2], magnetic resonance imaging [30] or macroscopic examination [25, 48].

In a pioneering work, Kirkaldy-Willis and Farfan [19] described an increase in the spinal flexibility for mild and moderate degenerative scenarios, defined as instability, and a stiffening only for severe degeneration. This idea, supported by more recent studies [20, 40] had a critical influence on the development of the therapeutic options, e.g. for dynamic stabilization, which is aimed to the reduction of the flexibility to physiological levels. A recent work based on an extensive database of in vitro experiments contradicted this concept [49], thus heating up the debate about this topic. The single degenerative changes which may be responsible of spinal instability may have different and contrasting effects on it, and have therefore a somewhat unpredictable relevance.

The finite element (FE) method appears to be the most powerful tool for the investigation of the mechanics of disc degeneration and was extensively used in previous studies (reviewed in [27]). In contrast to in vitro tests in which the occurrence of the different degenerative changes cannot be controlled, being highly dependent on the availability of the specimens which are usually in a limited number and often severely degenerated, a FE model may arbitrarily include individual degenerative changes or any combination of them, representing a wide range of clinical scenarios, to very mild to highly severe degeneration. Galbusera et al. [13] performed a FE evaluation of the influence of several degenerative changes on the spine mechanics, by using a biphasic model simulating a daily loading cycle. However, the focus of the previous work was on the significance of each single alteration, thus not representing really clinically relevant scenarios and excluding the possibility of interactions between the different changes. In other studies [33, 37], fixed combinations of degenerative phenomena, such as height loss, reduced water content and osteophytosis were investigated. Despite these fixed patterns may reflect frequent degenerative disc conditions, clinical scenarios including different combinations are even more common and may have different mechanical behaviors.

The present manuscript is aimed to study the mechanical response of various clinical scenarios possibly representing disc degeneration, including different combinations of common macroscopic degenerative changes, in daily loading cycles including flexion–extension motion. In particular, the relevance of spinal instability for mild and moderate disc degeneration and the possible role of the various degenerative parameters in its determination were investigated.

Materials and methods

Models of the non-degenerated spine segments

A poroelastic non-linear parametric FE model of the L4–L5 human spine segment described in previous papers [13, 38] was employed and scaled to represent spine segments from different individuals. FE software Ansys 12.0 (Ansys Inc., Canonsburg, PA, USA) was used for pre-processing; ABAQUS 6.9 (SIMULIA, Providence, RI, USA) was employed for running simulations and post-processing. The model included vertebral bodies, posterior structures, intervertebral disc and the seven major ligaments (Fig. 1). Membrane fiber-reinforced elements were employed for the representation of ligaments and annulus collagen fibers. Eight crisscross fiber layers [14] were defined in the radial direction and each layer contained tension-only fibers. The fiber angle varied from ±24° to the mid-plane of the disc ventrally to ±46° at the dorsal side, according to a previous study [18]. The non-linear elastic material properties, the cross-sectional areas and the orientation of the solid materials, collagen fibers and ligaments were the same used in previous poroelastic studies [13, 38]. Facet joints were modeled by using a frictionless surface-to-surface contact between cartilaginous layers having a thickness of 0.5 mm and an average gap of 0.4 mm.

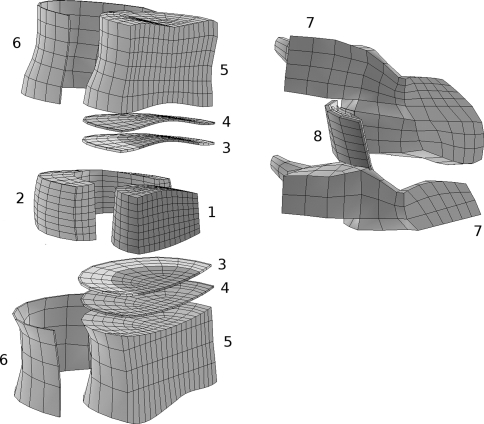
Fig. 1.

Exploded view of a FE model of the non-degenerated L4–L5 segment. For the sake of clarity, ligaments and half of the model are not shown. 1 Nucleus pulposus, 2 Annulus fibrosus, 3 cartilaginous endplates, 4 bony endplates, 5 trabecular bone, 6 cortical bone, 7 posterior elements, 8 facet joints

Poroelasticity was considered only for vertebral bodies, endplates and the intervertebral disc. Permeability values were the same used in a previous study [13] (Table 1) and were in turn derived from the paper by Ferguson et al. [11]. The strain-dependent permeability formulation developed by Argoubi and Shirazi-Adl [7] was employed. Partial saturation was allowed in the disc in order to avoid negative pressures during unloading [35], which were assumed as unrealistic.

Table 1.

Properties of the poroelastic materials employed in the FE models

Material	E (MPa)	υ	Initial permeability (m4/Ns)	Ref. elastic properties	Ref. permeability
Annulus ground substance	Non-linear		7.5 × 10−16	[38]	[11]
Nucleus	Non-linear		7.5 × 10−16	[38]	[11]
Cartilage	5.0	0.1	7.5 × 10−15	[7]	[11]
Cancellous bone	100.0	0.2	2.0 × 10−7	[7]	[11]
Cortical bone	10000.0	0.3	5.0 × 10−12	[7]	[11]

Ten models of the healthy spinal segment were created by randomly scaling the original model in order to obtain an antero-posterior diameter of the L4 body in agreement with values from literature (35.5 ± 0.88 mm for the L4 upper endplate [29]). The same value for the scale factor in all directions was assumed. Subsequently, for each scaled model the disc height value was randomly defined based on literature studies which correlated the disc height (h) to the actual antero-posterior vertebral diameter (D_ap):

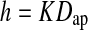1

where K is a normally distributed random variable having mean value 0.42 and standard deviation 0.05 ([48], in turn derived from [12]).

Models of the degenerated spine segments

The objective macroscopic grading system for intervertebral disc degeneration introduced by Wilke et al. [48] was used as the basis to build the models of the degenerated spine segments. This system estimates the overall degree of disc degeneration as the sum of six scores of different degenerative characteristics (appearance of nucleus pulposus, annulus fibrosus and endplate cartilage; height loss; osteophyte formation; diffuse sclerosis), which can be evaluated on mid-sagittal sections of lumbar specimens. A systematic sensitivity analysis individually considering these parameters was carried out in a previous study [13].

Thirty models of degenerated spine segments were randomly created, ten for each overall degree of degeneration (mild, moderate, severe). The size of the segments and the relevant disc height values were randomly selected using the method described in the previous paragraph. Discrete random variables were defined and used in the generation of the models (Table 2), in accordance to the previously described grading system. All variables were independent, uniformly distributed and contributed in average in the same way to the overall degree of degeneration.

Table 2.

Grading system and FE implementation of disc degeneration

Score	Random variable	0 points	1 point	2 points	3 points
Nucleus pulposus	Water content	80%	77%	74%	71%
Annulus fibrosus	Water content	70%	64%	58%	52%
	Presence of lesions	No lesions	No lesions	1 lesiona	2 or 3 lesionsa
Endplate cartilage	Thickness	0.5 mm	0.3 mm	0.3 mm thickness	0.3 mm thickness
	Calcification	No calcification	No calcification	50% calcification	100% calcification
Height loss	Height loss	No height loss	25%	50%	75%
Osteophyteb	Length	No osteophyte	1.5 mm	4.5 mm	7.5 mm
Diffuse sclerosis	Number of sclerotic regions	0	1–2a	3–4a	>4a

The overall degree of degeneration is assigned according to the sum of the six scores [0 points: degree 0 (no degeneration); 1–6 points: degree 1 (mild degeneration); 7–12 points: degree 2 (moderate degeneration); 13–18 points: degree 3 (severe degeneration)]

^aRandomly selected

^bReferred to a single osteophyte. The total osteophyte score is calculated by summing the points of the osteophytes in the four possible locations (total score 0: 0 points; 1: 1–4 points; 2: 5–8 points; 3: 9–12 points)

Degenerative conditions of the nucleus pulposus and of the annulus fibrosus were considered by reducing their water content by changing the initial void ratio, coherently with previous studies [16, 27]. Furthermore, three different types of annular lesions were considered: a rim lesion, a radial tear and a circumferential tear (Fig. 2a). In the lesion regions, nodes were duplicated to create a discontinuity in the mesh. Contacts were then created between the resulting facing surfaces [23]; the linear penalty formulation with a contact stiffness of 1,000 N/mm was used. The location and size of the lesions were similar to those considered in previous works [23, 41]. The number of the lesions included in each model assumed to be dependent on the model score concerning the annulus appearance (Table 2).

Fig. 2.

Positions of the rim (a-1), the radial (a-2) and the circumferential (a-3) lesions. Possible locations of the osteophytes (b) and of the sclerotic regions (c). d An admissible configuration for the locations of the sclerotic regions (gray) is depicted at L4; the configuration at L5 is not admissible because an inner region is sclerotic but the correspondent region closer to the endplate is not

Endplate cartilage degeneration was modeled by reducing the cartilage thickness from 0.5 to 0.3 mm and/or replacing the material properties of the cartilaginous elements with those of cortical bone, thus modeling cartilage calcification, depending on the specific score.

In the models including disc height loss, the disc height was reduced by 25, 50 or 75% with respect to the non-degenerative height value of the specific model. The buckling of the annular fibers was considered by offsetting the relevant stress–strain curves.

Osteophytes, when present, were modeled as solids having the same material properties of bone for the beaks and annulus fibrosus in the area between them, and random length of 1.5, 4.5 or 7.5 mm. The osteophytes were attached on four possible locations of the spine segment (Fig. 2b). All combinations of possible presence in each location and lengths were allowed.

Diffuse sclerosis was considered by replacing the material properties of trabecular bone with those of cortical bone in specific regions (Fig. 2c), randomly selected as follows. The lower half of L4 and the upper half of L5 were divided into four regions, each one of those randomly covered or not by sclerosis. The inner regions, farther from the endplates, could be sclerotic only if the correspondent region closer to the endplate was also sclerotic (example in Fig. 2d).

Boundary and loading conditions

In all simulations, the swelling of the disc due to the osmotic potential was simulated by imposing a pressure of 0.25 MPa [42, 43, 47] on the outer surfaces of all structures, as done in previous studies [7, 11, 28, 32]. The loading conditions represented a daily cycle (Fig. 3): 8 h of rest (defined as night, henceforth) modeled with a 200 N compressive load followed by a 500 N compression for 16 h (day, henceforth). A preconditioning cycle (swelling until equilibrium followed by 500 N compression for 16 h) was simulated before the night and day actually taken into account for data analysis. All loads were applied and removed in 10 s.

Fig. 3.

Time history of the compressive force (a) and of the flexion–extension moment (b) applied. After a preliminary preconditioning period, a compressive force representing a daily cycle was applied (200 N for 8 h, 500 N for 16 h). Flexion–extension cycles (moments of 7.5 Nm) were simulated 10 s and 15 h after the application of the compressive load during the day

In additional simulations, two flexion–extension cycles were considered during the day. Flexion and extension moments of 7.5 Nm were superimposed to the 500 N compressive load 10 s and 15 h after the application of the axial load, to model motion during the morning and the evening respectively. Each moment was applied and removed in 10 s. The ratio between the ranges of motion (RoMs) in the evening (15 h after load application) and in the morning (10 s after load application) was then calculated for each simulation.

Data analysis

The output variables of the study were the total daily axial displacement, the intradiscal pressure in the nucleus pulposus, the axial effective stress, i.e. in the solid phase, of the nucleus pulposus, the force transmitted through the facet joints, the daily fluid loss, the RoMs in flexion and extension, the ratios between the RoMs in the evening and those in the morning. The two-tailed Mann–Whitney test (p < 0.05) was employed to test the significance of the differences in the results between the models representing the four overall degrees of degeneration. Furthermore, the six scores contributing to the overall degree of degeneration and the output variables were correlated by calculating the Pearson coefficients and evaluating their significance.

Results

The total daily axial displacement was markedly reduced by increasing the overall degree of disc degeneration (Table 3), ranging in average from 1.51 mm for non-degenerated segments to 0.64 mm for severe degeneration. The same trend was observed for the force through the facet joints in compression, recorded at the end of the day (12.60 N in the right facet for degree 0 to 2.58 N for degree 3). The intradiscal pressures in the center of the nucleus at the end of the day considerably increased with disc degeneration, while the pressures at the end of the night were not significantly affected (Fig. 4). The axial effective stress in the nucleus at the end of the day generally increased with degeneration, with statistical significance only for the highest degeneration degree. The average relative diurnal fluid loss decreased (from 22.9% for degree 0 to 14.6% for degree 3), but without any statistical significance.

Table 3.

Average and standard deviation values of the predicted results for the different overall degrees of disc degeneration

Output parameter	Degree 0	Degree 1	Degree 2	Degree 3
Axial displacement (mm)	1.51 ± 0.09*(1)	1.26 ± 0.12*(2)	0.82 ± 0.21	0.64 ± 0.14*(0)
Facet force (N)	12.60 ± 1.52	10.41 ± 3.90*(2)	3.12 ± 3.78	2.50 ± 2.28*(0)
Pressure end day (MPa)	0.26 ± 0.001*(1)	0.28 ± 0.02	0.34 ± 0.08	0.40 ± 0.07*(0)
Pressure end night (MPa)	0.23 ± 0.004	0.23 ± 0.006	0.22 ± 0.02	0.22 ± 0.03
Axial effective stress (MPa)	0.13 ± 0.05	0.10 ± 0.10	0.14 ± 0.24*(3)	0.25 ± 0.29*(0)
Fluid loss (%)	22.91 ± 2.23	21.46 ± 7.08	20.10 ± 9.83	14.67 ± 8.00
Flexion RoM (°)	5.59 ± 0.54	5.10 ± 0.98*(2)	3.50 ± 0.93	3.37 ± 0.71*(0)
Extension RoM (°)	5.44 ± 0.65	5.09 ± 1.05*(2)	3.75 ± 1.25	3.57 ± 0.91*(0)
Flexion RoMevening/RoMmorning (−)	1.13 ± 0.05	1.15 ± 0.04*(2)	1.11 ± 0.03	1.09 ± 0.04*(0)
Extension RoMevening/RoMmorning (−)	1.05 ± 0.02	1.02 ± 0.06	0.98 ± 0.07	0.98 ± 0.05*(0)

*⁽ⁿ⁾ Significantly different from degree n

Fig. 4.

Predicted range of the intradiscal pressure in the nucleus pulposus for the different overall degrees of degeneration (average value of the ten models ± standard deviation), during the night (a) and the day (b)

The flexibility of the spinal segment in flexion–extension was generally notably reduced by disc degeneration (Table 3), in both flexion and extension. Spinal instability was hence not predicted. However, statistical significance for the differences between consecutive overall degeneration degrees was achieved only between degree 1 and 2. Severe degeneration did not induce a significant RoM reduction, probably due to the destabilizing effect of the annular lesions. The flexion RoMs were generally higher in the evening than in the morning, but the difference was reduced by increasing disc degeneration. The same trend was observed in extension, but with more variability in the results and no statistical significance, except for the difference between the highest degeneration degree and the non-degenerative condition.

The significance of the correlations between the six scores describing disc degeneration and the predicted results is reported in Table 4. All scores were strongly negatively correlated, i.e. an increase of the degenerative characteristic led to a decrease of the output, with the total daily axial displacement and the force through the facet joints (p < 0.001). A positive significant correlation with all scores was predicted for the intradiscal pressure at the end of the day; weaker correlations were found for the pressure at the end of the night. Coherently with the results of Table 3, the axial effective stress was not significantly correlated to any of the scores (p ≥ 0.05). The reduction of the RoMs in flexion and extension was also correlated to all scores; however, the degeneration of the nucleus pulposus had a lower significance level (p < 0.05) with respect to the other parameters. The scores had a mixed influence on determining the change in the RoMs between morning and evening (annulus degeneration, height loss, osteophytosis and diffuse sclerosis were significant in flexion, while endplate degeneration, height loss and osteophytosis in extension).

Table 4.

Statistical significance of the correlations between the input and the output parameters

	Overall deg.	Nucleus deg.	Annulus deg.	Endplate deg.	Height loss	Osteophytes	Diffuse sclerosis
Axial displacement	−−−	−−−	−−−	−−−	−−−	−−−	−−−
Facet force	−−−	−−	−−−	−−−	−−−	−−−	−−−
Pressure end day	+++	+++	+++	++	++	++	+++
Pressure end night	−	/	−−	/	/	−	−−−
Axial effective stress	/	/	/	/	/	/	/
Fluid loss	−−	−−	−−	/	/	–	−−−
Flexion RoM	−−−	−	−−−	−−−	−−−	−−−	−−−
Extension RoM	−−−	−	−−−	−−−	−−−	−−−	−−−
Flexion RoMevening/RoMmorning	−−	/	−−−	/	−−	−−	−−
Extension RoMevening/RoMmorning	−−−	/	/	−−	−−−	−−	/

+++/−: p < 0.001; ++/−−: p < 0.01; +/−: p < 0.05; /: p ≥ 0.05. +++/++/+: an increase of the input parameter leads to an increase of the output parameter; −−−/−−/−: an increase of the input parameter leads to a decrease of the output parameter

Discussion

In the present manuscript, the mechanical implications of specific degenerative characteristics when present in different combinations were evaluated by means of FE models. Results showed that disc degeneration induced a stiffening of the spinal segment in both compression and flexion–extension, lower fluid flow and weaker recovery in terms of intradiscal pressure after loading. Instability for mild disc degeneration was not predicted.

Many assumptions were done in developing the FE models of the degenerated spinal segments. Focal clefts and disruptions in the nucleus pulposus described in Wilke et al. [48] were neglected. Annular lesions were placed in fixed positions and had the same size in all models including them. In modeling endplate degeneration, which should be better considered as a degenerative change of the vertebra and not of the disc, a uniform thickness decrease over the entire surfaces was considered, in contrast to literature studies which reported irregular cartilage distributions [15, 48]. Elastic and permeability properties of the sclerotic endplates and vertebral bone were assumed to be equal to those of cortical bone, in the absence of specific experimentally measured data. The material properties of the structure attached to the annulus fibrosus between the osteophytes were equal to those of the annulus ground substance, coherently with Schmidt et al. [36] who reported a structural similarity between the two tissues, but not based on any in vitro measurement. Negative pore pressures in the disc upon unloading were assumed as unrealistic and avoided by introducing partial saturation. This is a controversial point which may require further investigations. Preliminary simulations not including partial saturation showed only marginal differences in the results, presumably due to the low difference between the load magnitudes imposed during the day and the night. The swelling pressure was considered as fixed and uniformly distributed, in contrast to previous studies which modeled its strain dependency [21, 22] and observed a non-uniform distribution of the fixed charge density [42]. Within the strain ranges of the present work, the swelling pressure was found to vary by 25% or less [11, 31, 44], thus possibly having a limited but not negligible influence on the predictions.

Many changes occurring in disc degeneration are biochemical in nature and were not included in the present models. The loss of proteoglycan content induces a disc depressurization [44], thus possibly influencing also the mechanical behavior. Water loss was simply modeled as a reduction on the initial void ratio, thus neglecting some aspects of the real phenomenon (increase in the type I collagen content and fibrotization of the nucleus and inner annulus [45]).

Simplifications were also made concerning the statistical distributions of the random variables, which were not chosen in order to represent a patient population. As a matter of fact, statistical data are available only for some of the degenerative characteristics, such as height loss [6] and osteophyte occurrence [39]. To circumvent this lack of knowledge, a wide range of possible degenerative patterns not representative of any specific population was considered, by assuming for all characteristics the same occurrence probability. This choice led to the impossibility of correctly evaluating the results in a probabilistic way. Therefore, probability density functions for the output parameters, though calculable with the present models, were not reported in the manuscript.

The validation of the present results is also problematic. As a matter of fact, experimental data about the impact of the single various degenerative changes are not currently available. Regarding FE studies, Rohlmann and coworkers [33] also found a decrease of the intervertebral mobility in flexion with decreasing disc height and nucleus water content. However, an increase of the extension range of motion was predicted for progressing disc degeneration, in contrast to the current results. This discrepancy may be due to the additional inclusion in the former model of facet joints degeneration, which was here not considered. Natarajan et al. [27] showed the same tendency to a stiffening of the intervertebral disc with a poroelastic FE model, although without showing results directly comparable with the present ones.

Some comparisons can be made concerning the models of the non-degenerated segments. The current average total daily axial displacement (1.51 mm) compared qualitatively well with previous experimental data published by Adams et al. [3] (1.53 mm after 6 h under a 1,000 N compressive load), and FE predictions by Ferguson et al. [11] (1.6 mm after 16 h under a 800 N load with a boundary pressure of 0.2 MPa) and Argoubi and Shirazi-Adl [7] (0.7 mm after 2 h under a 400 N load with a boundary pressure of 0.1 MPa). Wilke et al. [47] measured an intradiscal pressure of 0.24 MPa at the end of the night in vivo, clearly in agreement with the current results.

The output parameters were chosen in order to provide an extensive characterization of the mechanical response. Parameters related to the flexion–extension motion may give information about the possible spinal instability or stiffening. Axial displacement and fluid loss predictions describe the daily water loss and rehydration due to physiological loads, which was found to be compromised to some extent by disc degeneration. The intradiscal pressure in combination with the effective stress and the force in the facet joints may give qualitative indications about the possible progression of the pathology, in terms of disc failure phenomena or facet degeneration.

Disc degeneration generally induced a progressive stiffening of the spinal segment, both in compression and in flexion–extension. This effect was found to be significantly correlated with all scores, and is coherent with previous in vivo and in vitro data for high degrees of disc degeneration [20, 40, 49]. However, for mild degeneration instability was found in two studies [20, 40], while stiffening was observed in the other one [49]. The present work supported the findings of the latter. However, the assumed independence between the input random variables describing the various degeneration characteristics, which is not completely realistic, may have a role in this respect. For example, osteophytosis is generally the consequence of the destabilization due to annular lesions [17], while in the current models the two phenomena were independent. Therefore, for an accurate prediction of the effects of the progression of disc degeneration, relationships between the various degenerative changes should be considered. However, the introduction of such rules would require other assumptions, questioning the real significance of this possible modeling improvement.

A slower recovery of the intradiscal pressure during the day, related with decreasing fluid losses, was predicted with progressing disc degeneration. This result can be interpreted as an alteration of the capability of the spinal segment to transmit loads through fluid flow, when the fluid content decreases and endplate degeneration and sclerosis limit the possibility of imbibition. Coherently, significantly higher stresses in the solid phase were observed for the highest degeneration degree. This phenomenon may induce an increase of the risk of disc failure, thus possibly leading to disc herniation, which was found to be more frequent in young patients [34] and thus clinically more related to mild disc degeneration, and to delamination and tears, which exhibit higher occurrence rates in elderly patients [46]. This tendency of a more relevant role of the disc solid phase would also explain the decrease in the differences between the spine flexibility in the morning and in the evening with progressing disc degeneration.

Some of the discussed results have a direct clinical impact. The finding that mild degeneration does not generally induce instability may restrict the indications of dynamic stabilization systems to cases in which the instability is actually proven, e.g. with dynamic X-rays, or when decompression and the subsequent iatrogenic destabilization is necessary. Surgical implants, e.g. nucleus replacements, made of permeable materials may be useful in recreating a biomechanical condition more similar to that of the healthy disc. As a matter of fact, the loss of daily fluid flow predicted for degenerative conditions may be aggravated by the implantation of a non-permeable polymeric device, with possible consequences on the viability of cells in the remaining part of the disc. Grading systems for disc degeneration should include all the degenerative changes considered in the present work, since all of them definitely had an influence on the spinal biomechanics.

Further developments may be directed towards a fully probabilistic model of disc degeneration. The present parametric FE model may be directly employed in such a study from a technical point of view. However, as described above, statistical data about the occurrence of the individual degenerative characteristics are currently missing and should be gathered before setting up the model.