HLA*IMP—an integrated framework for imputing classical HLA alleles from SNP genotypes

Abstract

Motivation: Genetic variation at classical HLA alleles influences many phenotypes, including susceptibility to autoimmune disease, resistance to pathogens and the risk of adverse drug reactions. However, classical HLA typing methods are often prohibitively expensive for large-scale studies. We previously described a method for imputing classical alleles from linked SNP genotype data. Here, we present a modification of the original algorithm implemented in a freely available software suite that combines local data preparation and QC with probabilistic imputation through a remote server.

Results: We introduce two modifications to the original algorithm. First, we present a novel SNP selection function that leads to pronounced increases (up by 40% in some scenarios) in call rate. Second, we develop a parallelized model building algorithm that allows us to process a reference set of over 2500 individuals. In a validation experiment, we show that our framework produces highly accurate HLA type imputations at class I and class II loci for independent datasets: at call rates of 95–99%, imputation accuracy is between 92% and 98% at the four-digit level and over 97% at the two-digit level. We demonstrate utility of the method through analysis of a genome-wide association study for psoriasis where there is a known classical HLA risk allele (HLA-C*06:02). We show that the imputed allele shows stronger association with disease than any single SNP within the region. The imputation framework, HLA*IMP, provides a powerful tool for dissecting the architecture of genetic risk within the HLA.

Availability: HLA*IMP, implemented in C++ and Perl, is available from http://oxfordhla.well.ox.ac.uk and is free for academic use.

Contact: mcvean@stats.ox.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

An individual's Human Leukocyte Antigen (HLA) type, which describes the primary structure of the antigen-presenting classical HLA proteins, is an essential immunogenetic parameter, which influences susceptibility to many autoimmune and infectious diseases (Blackwell et al., 2009; Cooke and Hill, 2001), the risk of certain types of cancer (Brennan and Burrows, 2008; Wang et al., 2010), transplant compatibility (Szabolcs et al., 2010) and the likelihood of adverse drug reactions (Chung et al., 2007). In many autoimmune diseases, the HLA contributes the major fraction of genetic risk (Shiina et al., 2004). It is generally believed that this is related to variation in the HLA proteins' binding affinities, but the exact nature of the underlying mechanisms has remained elusive in most cases.

Because of the functional importance of the proteins, there is a considerable need for HLA type data in biomedical research, either as an explanatory variable (for example, in searching for factors influencing adverse drug reactions) or a covariate (for example, in looking for secondary risk factors in the HLA where there is a well-characterized primary classical risk allele). HLA type information can be useful in interpreting results from genome-wide association studies (GWAS). For example, a recent GWAS on psoriasis identified a SNP at the ERAP1 locus, which is associated with a significant increase in disease risk, but only in HLA-C*06:02 positive individuals (Strange et al., 2010).

However, lab-based HLA genotyping (through either direct sequencing, allele-specific amplification or hybridization) is typically slow and relatively expensive (costs are several hundred dollars per individual for high-quality allelic information at key class I and class II loci). In contrast, imputation of classical alleles from linked SNP data, while it can never achieve the degree of certainty of lab-based methods, is fast and inexpensive. This is particularly true for samples for which genome-wide SNP data have been collected as part of a GWAS. In such situations, imputation can be performed at no additional cost and with sufficient accuracy to enable the analysis of large-scale datasets (Leslie et al., 2008).

Imputation of classical HLA alleles is complicated by the genomic features of the HLA including extensive polymorphism (e.g. HLA-B with > 1600 alleles), long-range haplotype backgrounds and the influence of natural selection (Horton et al., 2008; Hughes, 2002; Traherne et al., 2006). de Bakker et al. (2006) have shown that while some classical alleles can be tagged by single SNPs, this is not generally true and experience has shown that standard SNP tagging approaches do not perform consistently well. To overcome these problems, we previously developed a probabilistic approach to classical HLA allele imputation (Leslie et al., 2008), here referred to as the LDMhc algorithm, which assesses the degree of relatedness between a chromosome with unknown HLA type but known SNP types in the region and a reference set of both SNP and HLA-typed chromosomes, based on SNP genotypes alone. Prior to the actual imputation procedure, the employed statistical model is constructed by iteratively selecting informative SNPs in the reference set from those that are typed in both the reference set and the sample to be typed. The performance of LDMhc is influenced by the size and diversity of the training set and the initial model building algorithm (Leslie et al., 2008).

Here, we present three developments of the LDMhc algorithm: a modification of the original SNP selection algorithm that leads to improved imputation call rates and accuracy; a parallelization of this algorithm that enables rapid analysis of large datasets; and an integrated software suite (HLA*IMP) that enables researchers to perform classical HLA allele imputation from genotype data collected from several available genome-wide SNP sets through reference to a reference dataset of over 2500 samples of European ancestry with dense SNP data and classical HLA allele types. We demonstrate that our framework produces highly accurate imputations (92–98% of imputations agree with lab-derived HLA types, at call rates of 95–99%) in an independent validation experiment and demonstrate the utility of the imputed genotypes in the context of a disease association analysis.

2 MATERIALS AND METHODS

2.1 Inference

The statistical model for inference is identical to the original implementation of LDMhc and based on the Li and Stephens Li and Stephens (2003) approximation to the coalescent (henceforth referred to as L&S). Given a set S_L of selected SNPs for HLA locus L and a set H_i,l (i = 1 .. # reference haplotypes, l = 1 .. # typed SNPs) of HLA-typed reference haplotypes, we define the probability that a phased SNP haplotype c with unknown HLA type carries allele A at locus L by

where T is the set of HLA alleles at L present in the reference dataset, H[X] is the set of haplotypes in H that carry allele X at L and P_L&S (c|S_L, H[X]) is the L&S emission probability of c based on the group H[X], reduced to the SNPs present in S_L and using a fine-scale recombination map for the SNPs in S_L (Myers et al., 2005). P_L&S (c|S_L, H[X]) can be interpreted as the probability that c is derived from a population consisting of chromosomes that carry the X allele. The model presented here assumes uniform priors on possible HLA alleles, but incorporating other priors (e.g. based on population frequency) is straightforward. The accuracy of P_L&S (c|S_L, H[A]) depends on the training set H, the alleles present in T and S_L, the set of SNPs used for inference. We thus seek a means of finding an optimal form of S_L.

2.2 SNP selection optimality measure

Before describing the SNP selection optimality measure used in our implementation, we outline the general SNP selection framework as described in Leslie et al. (2008). S_L is constructed iteratively, independently for each locus, in a forward-selection backward-elimination manner. For now, assume we have a loss function M. Let N_L be the set of SNPs already selected, possibly empty, and 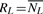, be the set of SNPs not currently in the imputation set. For the forward step, compute the loss function, M, for all possible additional SNPs to N_L, to find s_min, the SNP with the lowest score:

Set N_L = N_L ∪ s_min. In the backward elimination step, compute

and remove the SNP s_max with the highest score from N_L, unless s_min = s_max. Continue alternating forward and backward steps, until a predetermined maximum number of SNPs has been reached or the reduction in M for two subsequent added SNPs has fallen below a predefined threshold; then, set S_L = N_L.

Now, we describe the new SNP selection optimality measure. In our implementation, M is the sum of posterior error probabilities in a leave-one-out cross-validation analysis of all chromosomes in the reference set H:

with the dependence on locus L omitted here and V(c) being the known true HLA type of chromosome c. Our approach aims to maximize positive predictive power by optimizing the confidence in true calls during the model building procedure. In Leslie et al. (2008), optimality was measured by the product of call rate and accuracy conditional on a set threshold. Note that our definition removes the dependence on a set threshold for SNP selection. See Section 3.1 for an evaluation of the new SNP selection function's performance.

2.3 SNP selection parallelization

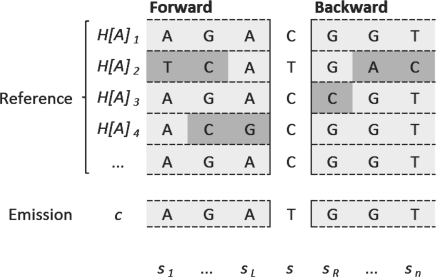
The SNP selection algorithm iteratively optimizes a sum of Hidden Markov Model (HMM) emission probabilities. The Markov property of the HMM leads naturally to parallelization as M can be calculated independently for each c and each s. To compute the L&S HMM emission probability P_L&S (c|S_L, H[X]), the position of s relative to the SNPs already in S_L is determined. s_l denotes the left neighbour of s, and s_r the right neighbour. Then, by the Markovian structure of the L&S approximation, the forward tables for P_L&S (c|S_L ∪ s, H[X]) and P_L&S (c|S_L, H[X]) are identical up to the state relating to s_l, and the same holds for the backward tables up to the state relating to s_r. Therefore, P_L&S (c|S_L ∪ s, H[X]) can be constructed from the forward- and backward-tables for P_L&S(c|S_L, H[X]) by adding the transition elements for s_l → s and s → s_r, as P_L&S (c|S_L, H[X]) is independent of s (Fig. 1). The state transition probabilities for s_l → s and s → s_r have to be set according to recombination probabilities; it is therefore natural to evaluate possible SNPs s in their chromosomal order, to be able to linearly move along the recombination map in use. With these modifications, it is possible to precalculate the forward and backward tables for P_L&S (c|S_L, H [X]) for ∀c and ∀A and propagate them over all computation nodes, then assign each node a linearly ordered subset of S. Finally, by applying the loss function M locally on each node, a local minimum is identified and sent to the controlling node, where the global minimum (best SNP) is determined. The backward elimination step is parallelized in a similar manner.

Fig. 1.

Visualization of the L&S Hidden Markov Model (HMM) states for a group of reference chromosomes carrying the A allele. Usually, the computation of an emission probability for a given chromosome c would involve filling the corresponding forward table (Rabiner, 1989) from s₁ to s_n and summing over the entries in s_n. However, the emission probability can also be calculated at any point s in the HMM, by combining the forward- and backward-tables up to s. In our parallelization approach, we compute both tables for each chromosome in advance (gray cells in the figure, polymorphisms highlighted in dark gray) and add the specific transition probabilities for any given SNP s (middle column), which can be performed in parallel without changing the precomputed table values.

2.4 SNP data preparation

The following cohorts were combined into a large reference set:

• the 1958 Birth Cohort (http://www.b58cgene.sgul.ac.uk/), typed both on the Illumina 1.2M and Affymetrix Genome-Wide Human SNP Array 6.0 chips (The Wellcome Trust Case Control Consortium, 2007). Where SNP genotype data overlapped, stringent thresholds for agreement were applied, resulting in 2420 genotype samples × 7733 SNPs (post QC, see below) in the extended HLA region.

• The HapMap CEU samples (The International HapMap Consortium, 2007) and CEPH CEU+ additional samples (de Bakker et al., 2006) (92 samples × 7733 BC58-overlapping SNPs)

A missing data threshold of 5% was applied to SNPs and individuals and all SNPs were checked for strand inconsistencies. SNP haplotypes for the 1958BC and CEU+ samples were phased using IMPUTE v2 (Howie et al., 2009) using the trio-phased HapMap samples as a reference dataset. Classically typed HLA genotypes were then phased into SNP haplotypes by using PHASE (Stephens and Scheet, 2005) applying standard settings for multiallelic loci. The combined reference dataset consists of 5024 haplotypes with data on 7733 SNPs in the HLA region. This splits up into 2474 (HLA-A), 3090 (HLA-B), 2022 (HLA-C), 175 (HLA-DQA1), 2629 (HLA-DQB1), 2665 (HLA-DRB1) locus-specific haplotypes which are used for inference.

Data for the validation experiment were generated by conducting a random 2/3 – 1/3 split of the set of reference data, using the 2/3 part as reference data to impute the HLA types of the remaining 1/3. For the validation experiment, the model is built using only the 2/3 part of the data to avoid overfitting to the 1/3 part, which is used as validation data. The 1/3 part of the data was not rephased; however, we established empirically that the phasing results from the internal haplotype imputation module of HLA*IMP are very similar to the results from IMPUTE.

The data for the disease association example presented in this article were prepared by the WTCCC2 and is described elsewhere (Strange et al., 2010).

2.5 HLA*IMP software implementation

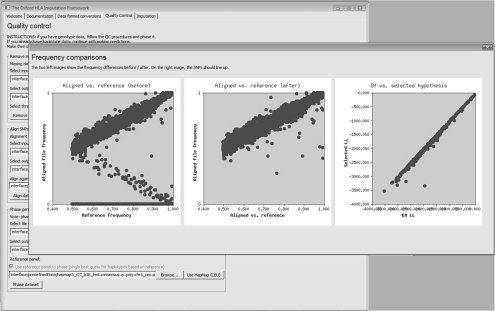
HLA*IMP is implemented in C++ and Perl. It consists of a front end and a back end. The front end is designed to assist end users in preparing their data—it has inbuilt modules for quality control, SNP strand alignment and haplotype phasing. Users are guided through these steps in a wizard-like sequential manner (Fig. 2). Output files from some popular genotype callers, including PLINK (Purcell et al., 2007), Birdsuite (Korn et al., 2008) and CHIAMO (Marchini et al., 2007), can be read in directly, as well as a simple generic format. The back end part, implemented as an online web service, carries out the computationally intensive parts of the imputation process. It can automatically process the files generated by the front end and notifies the end user via email of completed processes. As the result of the parallelized SNP selection depends on the initial set of available SNPs, we have preselected SNPs for some popular Affymetrix and Illumina SNP genotyping platforms; uploads from other platforms are currently not supported. HLA*IMP is free for academic use and available from http://oxfordhla.well.ox.ac.uk. The online resource includes detailed user information and a tutorial with a sample dataset.

Fig. 2.

The front end of HLA*IMP controls for missing data, aligns complementary SNPs and phases haplotypes in a largely automated manner. In this screen shot: graphical output from the alignment procedure, comparing SNP allele frequencies in the user dataset to HapMap allele frequencies, before (left) and after (middle) alignment. Complementary SNPs are aligned using an expectation-maximization (EM)-based procedure. A straight line of data points (right) indicates that there are no gross deviations between EM estimated and HapMap frequencies.

3 RESULTS AND DISCUSSION

3.1 Effects of modified SNP selection

To assess the effects of the new SNP selection function, we repeated one of the validation experiments from Leslie et al. (2008), using exactly the same datasets and exactly the same validation methodology. We find that the new SNP selection algorithm based on optimizing posterior probabilities typically outperforms the old SNP selection function, particularly when a threshold is applied to the certainty of calls (Supplementary Table S1). This effect is largely driven by an increase in call rate rather than any increase in accuracy, e.g. from 29% up to 75% for HLA-DQB1 at a call threshold of T = 0.9. At this threshold, the total number of correctly imputed alleles increases by 44% across all loci. At lower thresholds, this number is typically, though not consistently, increased. Note that much greater gains in accuracy are obtained by increasing the size of the reference panel (see below).

3.2 Cross-validation experiment

The new reference set of over 2500 samples was split in two parts and one of the two parts (2/3) was used to impute HLA types of the remaining part (1/3). Imputations were validated at the haplotype level and at four-digit (amino acid identity)/two-digit (sharing of serotypical features) resolution (see Table 1). A call threshold of T = 0.7 on the modes of the posterior HLA type distributions was employed, as our experience suggests that T = 0.7 represents a good compromise between accuracy and call rate. At two-digit resolution, between 97% (HLA-C) and 99% (HLA-DQB1) of calls are correct (i.e. they agree with the lab-based types), at call rates between 98% and 100%. At four-digit accuracy, call rates are from 95% (HLA-DRB1) to 99% (HLA-DQB1) and accuracy ranges from 92% (HLA-DRB1) to 98% (HLA-DQA1, HLA-DQB1). As the 1/3-part which was used for validation was completely excluded from model building, it can be regarded as if it had been sampled independently from the same population as the training data.

Table 1.

Accuracy and call rate for a 2/3 (training data) – 1/3 (validation data) cross-validation experiment, using a call threshold of T = 0.7 .

Locus	Number of validated	Call rate (2-digit)	Accuracy (2-digit)	Call rate (4-digit)	Accuracy (4-digit)
HLA-A	816	0.98	0.98	0.98	0.97
HLA-B	1009	0.98	0.98	0.98	0.96
HLA-C	635	0.98	0.97	0.97	0.97
HLA-DRB1	858	0.99	0.98	0.95	0.92
HLA-DQA1	51	1	0.98	0.98	0.98
HLA-DQB1	867	1	0.99	0.99	0.98

User datasets are always imputed using the full set of training data, which should result in greater accuracy.

3.3 Disease association experiment

To illustrate the utility of the imputed alleles in an empirical study, we imputed classical HLA types for case and control samples (where classical alleles were not available; note that the control samples include members of the 1958 Birth Cohort, for most of whom we have direct typing) within the WTCCC2 psoriasis disease association study (Strange et al., 2010). In psoriasis, the allele HLA-C*06:02 is well known to be the key genetic risk factor (Nair et al., 2006). Therefore, to assess the practical value of our methodology in realistic circumstances, we addressed the following two questions: would the association with C*06:02 be recovered from our imputed HLA types, and would a disease model based on imputed C*06:02 status be more predictive of disease (in terms of an associated model fit) than the most predictive SNPs? Table 2 summarizes the results. The C*06:02 association is clearly recognized as the strongest effect of any HLA allele, and it is also more significantly associated with psoriasis disease risk than any typed SNP. Using imputed HLA types in a conditional analysis also enabled the characterization of a novel interaction between HLA-C*06:02 and the ERAP1 locus (Strange et al., 2010).

Table 2.

P-values and odds ratios for imputed HLA-C*06:02 alleles and the most predictive SNP from Strange et al. (2010)

Locus/allele	P-value	Odds ratio
HLA-C*06:02	5.44E-221	5.55
rs10484554	3.05E-202	4.64

4 CONCLUSIONS

We have presented an integrated imputation framework for classical HLA types, based on a modified version of the LDMhc algorithm, a new parallelized model-building algorithm and a large set of carefully assembled training data. We have demonstrated that the accuracy of our approach at the four-digit level is >92%, at call rates >95%, where we note that our validation samples and reference set come from populations of similar (European) ancestry. Finally, we have shown that imputation of classical alleles can be used to identify and dissect genetic risk factors within the HLA in GWAS and related experimental designs. HLA*IMP is implemented as a user-friendly front end/back end system with inbuilt support for standard genotyping platforms. Our framework is freely available for academic use.