Spontaneous Cortical Activity Reveals Hallmarks of an Optimal Internal Model of the Environment

Abstract

The brain maintains internal models of its environment to interpret sensory inputs and prepare actions. While behavioral studies demonstrated that these internal models are optimally adapted to the statistics of the environment, the neural underpinning of this adaptation is unknown. Using a Bayesian model of sensory cortical processing, we related stimulus-evoked and spontaneous activities to inferences and prior expectations in an internal model and predicted that they should match if the model is statistically optimal. To test this prediction, we analyzed visual cortical activity of awake ferrets during development. Similarity between spontaneous and evoked activities increased with age and was specific to responses evoked by natural scenes. This demonstrates the progressive adaptation of internal models to the statistics of natural stimuli at the neural level.

Our percepts rely on an internal model of the environment, relating physical processes of the world to inputs received by our senses, and thus their veracity critically hinges upon how well this internal model is adapted to the statistical properties of the environment. For example, internal models in vision are used to extract the features, such as low-level oriented edges or high-level objects, that gave rise to the retinal image (1). This requires that the internal model is adapted to the co-occurrence statistics of visual features in the environment and the way they jointly determine natural images. Several aspects of perception (2, 3), motor control (4), decision making (5, 6) and higher cognitive reasoning (7, 8) are governed by such statistically optimal internal models. Yet, identifying the neural correlates of optimal internal models has remained a challenge (see supporting text online).

We addressed this problem by relating evoked and spontaneous neural activity (EA and SA) (9) to two key aspects of Bayesian computations performed with the internal model (Fig. 1A). The first key aspect is that a statistically optimal internal model needs to represent its inferences as a probability distribution, the Bayesian posterior P(features|input, model) (2, 10) describing the inferred probability that a particular combination of features may underlie the input. Thus, under the general assumption that the visual cortex implements such an optimal internal model, EA should represent the posterior probability distribution for a given input image (2, 11, 12), and SA should represent the posterior distribution elicited by a blank stimulus. The second key aspect of a statistically optimal internal model, under only mild assumptions about its structure, is that the posterior represented by SA converges to the prior distribution, describing prior expectations about the frequency with which any given combination of features may occur in the environment, P(features|model). This is because as the brightness or contrast of the visual stimulus is decreased, inferences about the features present in the input will be increasingly dominated by these prior expectations (for a formal derivation see supporting online text). This effect has been demonstrated in behavioral studies (3, 13), and it is also consistent with data on neural responses in V1 (14). Relating EA and SA to the posterior and prior distributions provides a complete, data-driven characterization of the internal model without making strong theoretical assumptions about its precise nature.

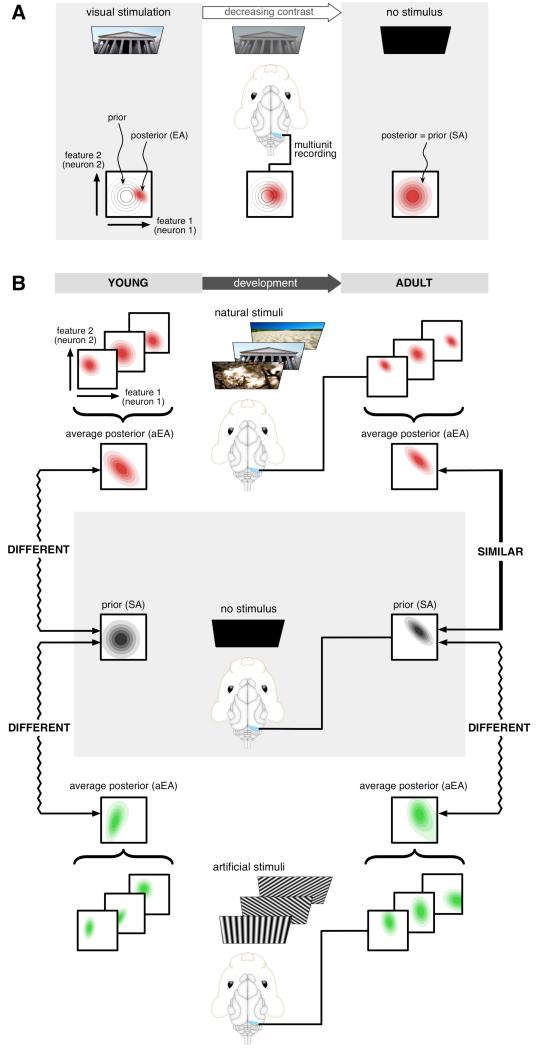
Fig. 1. Assessing the statistical optimality of the internal model in the visual cortex.

(A) The posterior distribution represented by EA (bottom, red filled contours show pairwise activity distributions) in response to a visual stimulus (top) is increasingly dominated by the prior distribution (bottom, gray contours) as brightness or contrast is decreased from maximum (left) to lower levels (middle). In the absence of stimulation (right), the posterior converges to the prior and thus SA recorded in darkness represents this prior. (B) Multiunit activity recorded in V1 (middle column) of awake, freely viewing ferrets either receiving no stimulus (middle) or viewing natural (top) or artificial stimuli (bottom) is used to construct neural activity distributions in young and adult animals. Under natural and artificial stimuli conditions, EA distributions represent distributions of visual features (red and green panels) inferred from particular stimuli. Average EA distributions (aEA) evoked by different stimuli ensembles are compared to the distribution of SA recorded in darkness (black panels), representing the prior expectations about visual features. Quantifying the dissimilarity between the SA distribution and the aEA distribution reveals the level of statistical adaptation of the internal model to the stimulus ensemble. The internal model of young animals (left) is expected to show little adaptation to the natural environment and thus aEA for natural (and also for artificial) scenes should be different from SA. Adult animals (right) are expected to be adapted to natural scenes and thus to exhibit a high degree of similarity between SA and natural stimuli-aEA, but not between SA and artificial stimuli-aEA.

Crucially, this interpretation of the EA and SA distributions allowed us to assess statistical optimality of the internal model with respect to an ensemble of visual inputs, P(input), using a standard benchmark of the optimality of statistical models (Fig. 1B) (15). A statistical model of visual inputs that is optimally adapted to a stimulus ensemble must have prior expectations that match the actual frequency with which it encounters different visual features in that ensemble (16). The degree of mismatch can be quantified as the divergence between the average posterior and the prior:

$$\mathrm{Div}\left[{\langle P\left(\text{features}\mid \text{input, model}\right)\rangle }_{P\left(\text{input}\right)}\parallel P(\text{features}\mid \text{model})\right]$$ (1)

where the angular brackets indicate averaging over the stimulus ensemble. A well-calibrated model will predict correctly the frequency of feature combinations in actual visual scenes, leading to a divergence close to zero. However, if the model is not adapted, or it is adapted to a different stimulus ensemble from the actual test ensemble, then a large divergence is expected. As we identified EA and SA with the posterior and prior distributions of the internal model, the statistical optimality of neural responses with respect to a stimulus ensemble can be quantified by applying Equation 1 to neural data, i.e., by computing the divergence between the average distribution of multi-neural EA (aEA), collected in response to stimuli sampled from the stimulus ensemble, and the distribution of SA (17) (Fig. 2A).

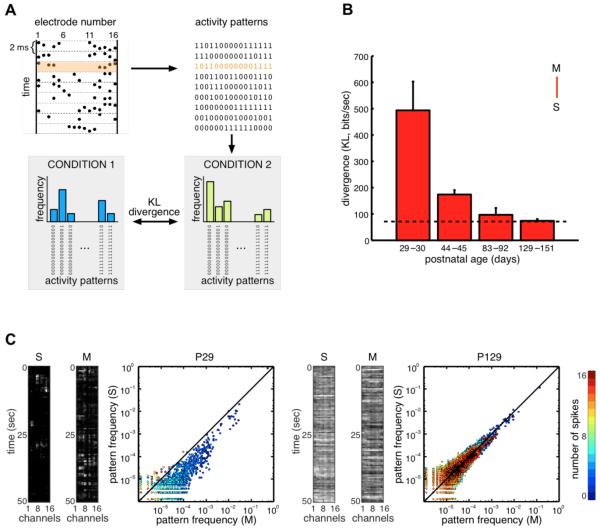
Fig. 2. Improving match between aEA and SA over development.

(A) Spikes were recorded on 16 electrodes, discretized in 2 ms bins, and converted to binary strings, so that each string described the activity pattern of cells at a given time point (top). For each condition, the histogram of activity patterns was constructed, and different histograms were compared by measuring their divergence (bottom). (B) Divergence between the distributions of activity patterns in movie-aEA (M) and SA (S), as a function of age (red bars). As a reference, the dashed line shows the average of the within-condition baselines computed with whithin-condition data split in two halves (Fig. S1). (C) Frequency of occurrence of activity patterns under SA (S, y-axis) vs. movie-aEA (M, x-axis) in a young (left) and adult (right) animal. Each dot represents one of the 2¹⁶ = 65536 possible binary activity patterns, color code indicates number of spikes. Black line shows equality. The panels at the left of the plots show examples of neural activity on the 16 electrodes in representative SA and movie-aEA trials for the same animals. Error bars on all figures represent SEM.

Because the internal model of the visual cortex needs to be adapted to the statistical properties of natural scenes, Equation 1 should yield a low divergence between aEA for natural scenes and SA in the mature visual system. We therefore measured the population activity within the visual cortex of awake, freely viewing ferrets in response to natural-scene movies (aEA) and in darkness (SA) at four different developmental stages: after eye opening at postnatal day (P) 29-30, after the maturation of orientation tuning and long-range horizontal connections at P44-45 (18), and in two groups of mature animals at P83-90 and P129-151 (n = 16 animals in total, Table S1). The divergence between aEA and SA decreased with age (Fig. 2B-C, Spearman’s, ρ = −0.70, p < 0.004) and the two distributions were not significantly different in mature animals (Fig. S1, P83-90: m = 5.74, p = 0.11; P129-151: m = 2.03, p = 0.25).

What aspects of aEA and SA are responsible for their improving match with age? Redundancy reduction, one prominent assumption regarding neural coding (19), would predict that neurons behave as sparse (20, 21) and uncorrelated information channels (22). To assess the importance of correlations between the activities of different neurons, we constructed surrogate distributions for aEA and SA that preserved single neuron firing rates but otherwise assumed that neurons fired independently (17). Thus, any divergence between a real and a surrogate distribution must be due to correlated neural activities (of second (23) or higher order). By computing this divergence, we found that the activity of neurons in both aEA and SA became increasingly correlated (Fig. 3A, Spearman’s ρ = 0.73, p < 0.002) and increasingly non-sparse with age (Fig. S2), arguing against redundancy reduction. Moreover, these increasing correlations were important for the match between aEA and SA because the surrogate SA did not converge to the true aEA (Fig. 3B, Spearman’s, ρ = 0.34, p = 0.22) excluding the possibility that the decreasing divergence between aEA and SA could be accounted for by changes in the firing rates of neurons alone.

Fig. 3. Contribution of spatial and temporal correlations to the match between aEA and SA.

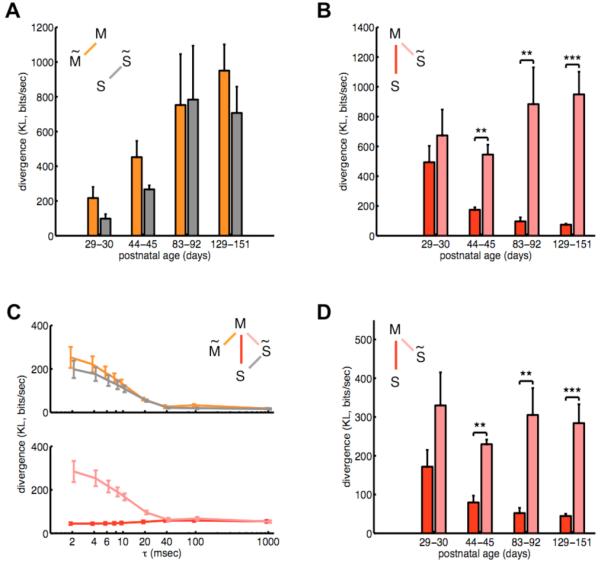
(A,B) The role of spatial correlations was quantified by the divergence between the measured distributions of neural activity patterns, movie-aEA (M) and SA (S), and the surrogate versions of the same distributions (M̃ and S̃), in which correlations between channels were removed, while keeping the firing rates intact (17). (A) The divergence between the measured and surrogate distributions increased significantly over age for both movie-aEA (orange) and SA (gray). (B) Enhanced match between movie-aEA and SA over development (red, cf. Fig. 2B) disappeared when spatial correlations were removed from SA (pink). (C,D) Divergence of transition probability distributions between measured neural activity patterns and their surrogate versions, in which temporal correlations were removed, while keeping firing rates and spatial correlations intact (17). (C) Temporal correlations in adult animals (P129-151) as a function of the time interval, τ. Within-condition divergences (top) show that temporal correlations decreased with time lag both in movie-aEA (orange) and in SA (gray). Across-condition comparison (bottom) of the divergence of aEA from the measured SA (red) and from the surrogate SA (pink) shows that temporal correlations in the two conditions were matched up to time intervals when they decayed to zero. (D) Temporal correlations at the shortest time interval (τ = 2 ms) as a function of age. The match of transition probabilities between movie-aEA and SA improved (red). Removing temporal correlations from SA eliminated this match (pink). In all figures, *p<0.05, **p<0.01, ***p<0.001, m-test.

An appropriate model of the visual environment should also capture its temporal dynamics. Therefore, we extended our analysis beyond the purely spatial domain to the temporal domain. We measured the probability of transitioning between any two patterns in a wide range of temporal delays for all conditions, and tested the strength and match of temporal correlations using surrogate distributions as was done in the spatial domain (17). The activity of neurons showed strong temporal correlations up to ~20 msec in both aEA and SA in adult animals (Fig. 3C). A strong prediction of the hypothesis that V1 neural activity reflects a statistically optimal internal model is that these transition probabilities should also be matched between aEA, when V1 processes temporally strongly structured visual input, and SA, when no visual stimulus is provided. Indeed, we found that the match between transition probabilities in aEA and SA significantly improved with age (Fig. 3D, Spearman’s ρ = −0.72, p < 0.003), such that in adult animals the temporal correlations were matched up to delays when they decayed to zero (Fig. 3C).

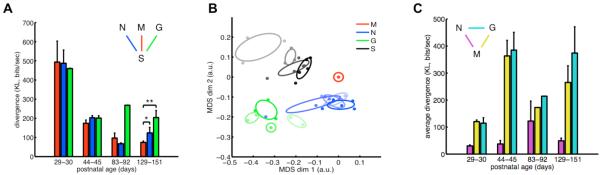
If the internal model reflected in V1 activity is tuned specifically to the natural visual environment, then the match between aEA and SA should also be specific to using a natural image ensemble for eliciting aEA, and other, “artificial”, stimulus ensembles should yield higher divergences between aEA and SA for mature animals. To test this prediction, aEA was collected with two other types of stimulus classes: drifting sinusoid gratings at different orientations and frequencies, and dynamic binary block noise that was updated at frame rate (17). Indeed, while in young animals there was no significant difference between the degree of match of SA and aEA, in the oldest age group SA was significantly better matched to neural activity evoked by natural images than that evoked by the two artificial stimulus ensembles (Fig. 4A-B, movie vs. noise: m = 16.47, p < 0.05; movie vs. grating: m = 943.07, p < 0.002). Furthermore, the divergence between different aEA distributions did not decrease significantly with age (Fig. 4B-C, movie vs. noise: ρ = 0.19, p = 0.49, movie vs, grating: ρ = 0.5, p = 0.21 , noise vs. grating: ρ = 0.67, p = 0.07) which ruled out the possibility that the decreasing divergence between aEA and SA was due to a general decoupling of V1 from sensory input (see also Fig. S3).

Fig. 4. Similarity between aEA and SA is specific to natural scenes.

(A) Divergence between neural activity patterns evoked by different stimulus ensembles (movie-aEA: red, M; noise-aEA: blue, N; gratings-aEA: green, G) and those observed in SA. In adult animals, SA was significantly more similar to movie-aEA than noise-aEA or gratings-aEA. (B) Two-dimensional projection of all neural activity distributions. Each dot represents one activity distribution in a different animal, colors indicate stimulus ensembles (movie-aEA: red, M; noise-aEA: blue, N; gratings-aEA: green, G; SA: black, S), intensity indicates age group (in the order of increasing intensity: P29-30, P44-45, P83-92, P129-151), ellipses delineate distributions belonging to the same age group. Positions of dots were computed by multi-dimensional scaling (MDS) to be maximally consistent with pairwise divergences between distributions. Movie-aEAs were defined to be at the origin. For young animals (faintest colors), SA was significantly dissimilar from all aEA distributions. Over development, SA moved closer to all aEAs; but by P129-151, SA was significantly more similar to movie-aEA than artificial stimuli-aEAs, as quantified in (A). (C) Divergences measured directly between different aEA distributions (noise-aEA and movie-aEA: magenta, gratings-aEA and movie-aEA: yellow, gratings-aEA and noise-aEA: cyan) showed no decrease in the specificity of the responses to different stimulus ensembles.

Our results suggest that V1 implements an internal model that is adapted gradually during development to the statistical structure of the natural visual environment and that SA reflects prior expectations of this internal model. While these findings do not address the degree to which statistical adaptation in the cortex is driven by visual experience or by developmental programs, they set useful constraints for both dynamical (24) and functional models (12) of sensory processing. We expect our approach to extend to other brain areas and to provide a general, quantitative way to test future proposals for computational strategies employed by the cortex.

One-sentence summary: The relation between spontaneous activity and activity evoked by natural stimuli in the primary visual cortex reveals that the cortical circuit progressively adapts its internal model to the statistical structure of the environment.