Relaxivity-iron calibration in hepatic iron overload: Probing underlying biophysical mechanisms using a Monte Carlo model

Abstract

Iron overload is a serious condition for patients with β-thalassemia, transfusion-dependent sickle cell anemia and inherited disorders of iron metabolism. MRI is becoming increasingly important in non-invasive quantification of tissue iron, overcoming the drawbacks of traditional techniques (liver biopsy). R2*(1/T2*) rises linearly with iron while R2(1/T2) has a curvilinear relationship in human liver. Although recent work has demonstrated clinically-valid estimates of human liver iron, the calibration varies with MRI sequence, field strength, iron chelation therapy and organ imaged, forcing recalibration in patients. To understand and correct these limitations, a thorough understanding of the underlying biophysics is of critical importance. Toward this end, a Monte Carlo based approach, using human liver as a ‘model’ tissue system, was employed to determine the contribution of particle size and distribution on MRI signal relaxation. Relaxivities were determined for hepatic iron concentrations (HIC) ranging from 0.5–40 mg iron/ g dry tissue weight. Model predictions captured the linear and curvilinear relationship of R2* and R2 with HIC respectively and were within in vivo confidence bounds; contact or chemical exchange mechanisms were not necessary. A validated and optimized model will aid understanding and quantification of iron-mediated relaxivity in tissues where biopsy is not feasible (heart, spleen).

INTRODUCTION

Iron overload is a life-threatening condition for patients with β-thalassemia, transfusion-dependent sickle cell anemia and inherited disorders of iron metabolism (1). Excess iron accumulates in liver, heart, spleen, and endocrine organs, causing oxidative damage. Liver biopsy is the prevailing clinical standard for monitoring total body iron stores; however, it is invasive, painful (2), expensive, prone to sampling error (3) and provides only indirect information regarding other inaccessible organs. As an alternative, MRI has gained importance in non-invasive quantification of tissue iron, overcoming the drawbacks of traditional techniques. Super-paramagnetic substances such as iron-oxide particles (ferritin and hemosiderin complexes) produce magnetic field disturbances that increase MRI relaxivities R2* (1/T2*) and R2 (1/T2), indirectly reflecting tissue iron loading. Recent studies by St. Pierre et al. (4) and Wood et al. (5) have demonstrated that MRI techniques can estimate hepatic iron content as accurately as liver biopsy. Due to success of these studies, MRI liver iron assessment has recently received FDA approval for clinical diagnosis.

In spite of recent success with studies showing good inter-machine and inter-study reproducibility for individual pulse sequences (4,6), relaxivity-iron relationships still vary between investigators in complicated ways. Iron calibration appears to vary with acquisition method (single spin-echo, multiple spin-echo or spectroscopic sequence (7–9)) as well as relaxation model (monoexponential, biexponential and nonexponential (10–12)). Recent animal studies have also indicated that different iron chelation therapies may mobilize or redistribute intrinsic iron stores differently, affecting the calibration curves (13). The variability seen across these factors remains unresolved. As a result, any pulse sequence modification must currently be re-validated in a patient population; an expensive, tedious, and time-consuming task. Lastly, with increasing popularity of 3T scanners, there is a need to translate relaxivity-iron relationships to higher field strengths (14).

It is also critical to understand incompletely explained phenomena, such as the nonlinearity of the R2-iron curve (unlike R2*) and the relevant iron “scales” imaged by R2 and R2* methods. Recent studies have demonstrated that R2 relaxivity of iron particles is critically size-dependent. In vivo R2 measurements reveal stronger R2 relaxivity than can be explained by dispersed ferritin particles. Aggregation of ferritin by 0.8 μm diameter liposomes or by enzymatic aggregation dramatically steepens the R2-iron relationship, making it closer to in vivo values (15,16). Morphology studies of iron deposits in human liver specimens have shown that iron deposits in human liver are on that same scale (12). Most lie in the range of 0.1–3.2 μm with a mode near 1 μm, however, the size and spacing vary with iron loading, Hence it is essential to systematically evaluate the contribution of various system parameters such as size and distribution of iron clusters, anatomical compartments and proton mobility on iron-related tissue R2 and R2*.

Toward this end, we hypothesized that Monte Carlo modeling can predict relaxivity-iron behavior in an iron overloaded tissue system given the knowledge of 1) iron scale and distribution, 2) intrinsic magnetic susceptibility of iron particles and 3) type of MRI experiment. Based on recently published work (17,18), realistic human liver mimics were simulated for this purpose, allowing a sensitivity analysis for particle size, distribution and proton mobility, to identify key contributors to iron-mediated MRI relaxation. A bridge between pathophysiology and intrinsic biophysics will help explain variability seen across the parameter-dependent calibrations, improving accuracy of diagnosis, management and care of patients with iron overload syndromes.

METHODS

Monte Carlo Model Outline

A flow diagram representing the model design is shown in Figure 1. A virtual liver geometry was constructed based on published statistics of hepatic iron scale and distribution and its magnetic properties (ferritin, hemosiderin). Given the hepatic iron concentration, the corresponding magnetic field was generated. Diffusion of protons was freely isotropic in three dimensions but constrained not to pass through the iron deposits. Diffusing water protons differentially accumulated phase according to their path through the magnetic disturbances. For each level of iron burden, the field induction decay (FID) was measured along with a single echo experiment to obtain predicted relaxivities R2* and R2, respectively.

Figure 1.

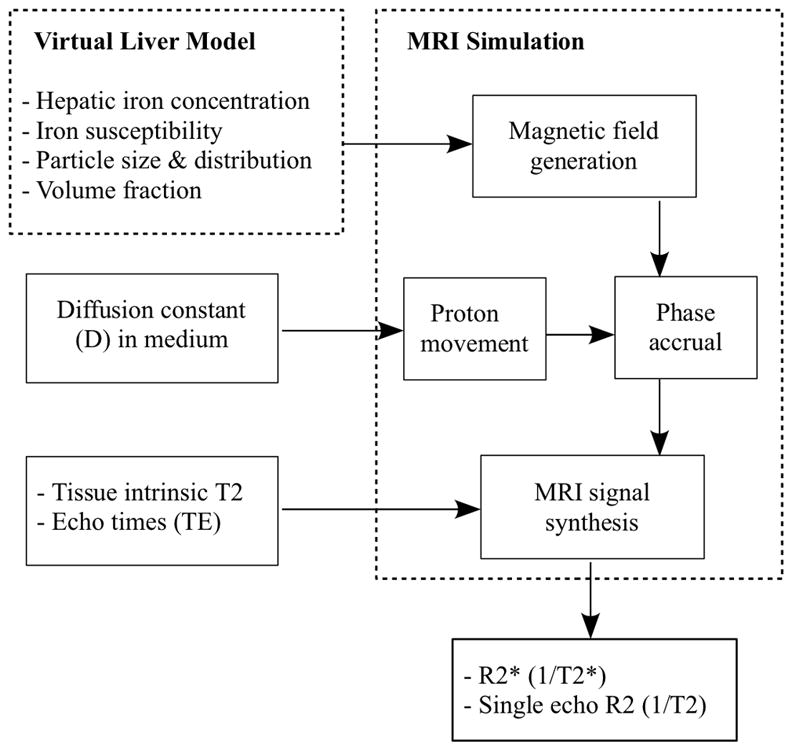
Schematic illustrating the flow of Monte Carlo simulations.

Virtual Liver Model

Tissue geometry

Human liver can be sub-divided into two primary compartments: hepatocyte and sinusoid. Synthetic liver geometry was generated similar to previously published model (17). An 80 μm side cuboidal liver volume was simulated with 64 hepatocytes in the form of cubes, each with a dimension of 20 μm. In addition, the sinusoidal compartment, which consists of iron-engulfing macrophages called Kupffer cells, was also incorporated. The sinusoids were represented by 18 cylindrical regions with a diameter of 10 μm (19) and height equal to a hepatocyte dimension. They were located at the intersection of adjacent hepatocytes, similar to that observed in liver parenchyma (20) constituting a volume of 6% (21). Figure 2 shows an illustration of the synthetic liver geometry; a third compartment of the liver, the portal tract, was ignored in the model.

Figure 2.

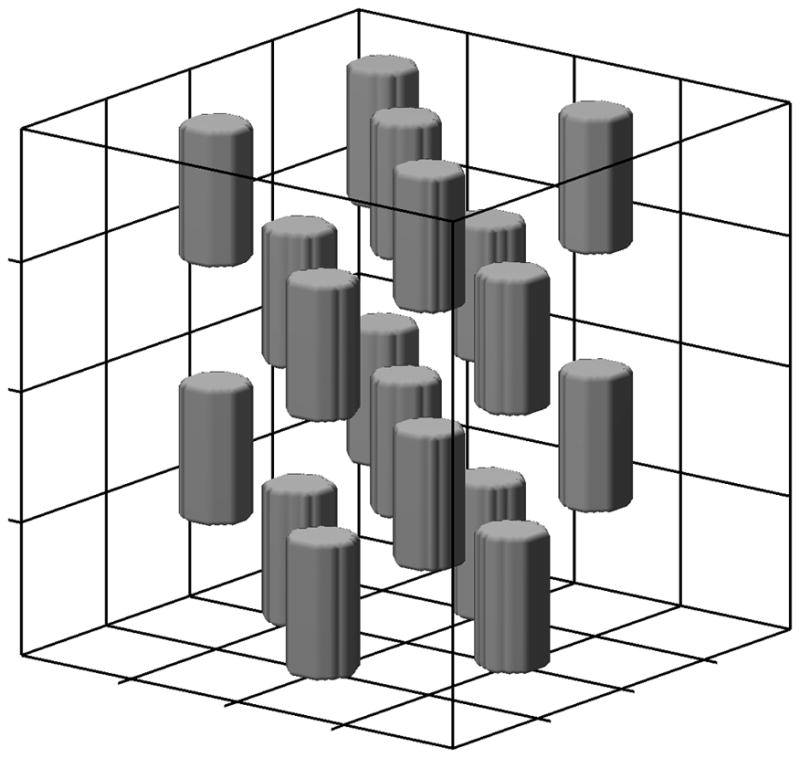
Illustration of virtual liver environment forming a 80 μm side cube with two anatomical compartments, hepatocytes and sinusoids. Grid lines represent boundaries of 64 hepatocytes each of 20 μm side while the 10 μm diameter cylinders form the sinusoidal compartment.

2. Iron morphology

Pattern of iron distribution within hepatocytes, as a function of total iron burden, has been described previously (18). Hepatic iron concentration in the range of 0.5–40 mg/g dry tissue was chosen for simulation purpose, representing the range for which in vivo human R2 and R2* calibration curves are known (4,5). Hemosiderin clusters were represented by homogeneous spheres with sizes in the range of 0.05–1.6 μm radius. A Gamma distribution function (GDF) has been shown to be a good description of size of cellular iron deposits (18), given by,

$$\mathit{GDF}(x)=\frac{1}{\beta \times \mathrm{\Gamma }(\gamma )}\times \left({\left(\frac{x-\mu }{\beta }\right)}^{(\gamma -1)}\times exp\left(-\frac{x-\mu }{\beta }\right)\right)$$ (1)

where, β>0 (Scale parameter), γ>0 (Shape parameter), x ∈ [0; ∞), x≥μ (location parameter) and Γ(γ) is the Gamma function given by,

$$\mathrm{\Gamma }(z)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt$$ (2)

Shape of a GDF controls the basic behavior of the function i.e. exponential, chi-squared or Weibull while scale alters its width. For a given HIC with a particle size range x, the corresponding GDF was computed by substituting appropriate scale and shape values. Volume fraction (VF) of spheres was calculated as a linear function of HIC (18), yielding a range of 0.43% to 5.46%. Two levels of particle grouping were incorporated into the model, both of which were also characterized by GDF’s (18): 1) inter-cellular iron anisotropy i.e. different hepatocytes have different amounts of iron, and 2) nearest neighbor criteria for inter-particle spacing. Table 1 summarizes the equations forming the statistical basis for the microscopic iron morphology of human liver. Using the equations in Table 1 and Eqn. 1, it was possible to generate the GDF for any iron concentration. Note that the units of β were in μm for particle size and nearest neighbor measures while it was dimensionless for iron anisotropy.

Table 1.

Iron Morphology description

Characterization	Equation	m [units]	c [units]	RMSE	R
Volume fraction	VF = m*HIC+c	0.00127 [(mg/g)−1]	0.00368 [%]	0.00716	0.93
Size distribution	β = m*HIC +c	0.000296 [μm.(mg/g)−1]	0.0935 [μm]	0.0245	0.17
	γ = m* β +c	2.188 [μm−1]	2.695 [ ]	0.0126	0.97
Nearest neighbor	γ = exp (m*log(HIC)+c)	0.476 [(mg/g)−1]	−0.131 [ ]	1.221	0.78
	β = exp (m*log(γ)+c)	−1.403 [μm]	0.740 [μm]	0.357	0.98
Cellular anisotropy	γ = m*HIC+c	0.0179 [(mg/g)−1]	1.025 [ ]	0.412	0.53
	β = exp (m*log(HIC)+c)	0.375 [(mg/g)−1]	−3.366 [ ]	0.0296	0.76

RMSE: Root Mean Square Error, R: Correlation coefficient, VF: Volume Fraction of spheres (%), HIC: Hepatic Iron Concentration (mg/g dry tissue weight), [ ]: Dimensionless

The relative iron loading of hepatocyte and sinusoidal compartments varies with the severity of total liver iron burden. Using quantitative histologic scoring from 70 liver biopsy specimens (17), we modeled compartmental loading by logistic functions, given by,

$$y=\frac{C}{1+{Ae}^{-Bx}}$$ (3)

where, x and y correspond to log(HIC) and iron scores respectively, C is the maximum value y can take, A reflects the ratio of C and y(x=0) and B represents how quickly y attains C. For a given HIC, hepatocyte iron score (HIS) was obtained by using A=5.2, B=0.57 and C=36 in Eqn. (3). In a similar manner, using A=5.1, B=0.57 and C=60 gave the total iron score (TIS) i.e. the summation of iron scores from all compartments. The volume fraction of iron spheres in the hepatocytes was thus computed using the ratio HIS/TIS. Since our Monte Carlo model neglected portal tracts, the remaining volume of spheres was assigned to sinusoids. The 18 sinusoids were filled equally with the allocated number of spheres.

3. Model generation

For a given HIC, a target sphere volume fraction was calculated from the equation given in Table 1. Spheres of different sizes were drawn using a HIC-matched particle size histogram until the specified volume fraction was attained. Each sphere was assigned a uniform iron density, ensuring conservation of total iron concentration. The spheres were then distributed throughout the simulation volume to produce specific iron distributions.

(a) Random distribution

This represented the simplest geometry. The spheres generated were placed in a non-overlapping manner within the tissue environment using a Gaussian random distribution. Collision was handled by placing the concerned sphere at the surface of the colliding sphere and overlap was checked until there was no collision or a specified number of attempts were reached. If collision had not been resolved by then, a new random position was generated and the process was repeated. Here, the entire liver environment was considered and hepatocyte and sinusoid compartments were presumed to be absent.

(b) Cellular anisotropy

In this model, particle distribution within hepatocytes remained Gaussian, but the amount of iron per hepatocyte followed experimentally-determined intercellular iron GDF, producing greater fluctuations in intercellular iron concentrations. Sinusoidal compartments were not modeled.

(c) Cellular anisotropy with nearest neighbor

Geometry was identical to (b) except that within each hepatocyte, spheres were placed in accordance to nearest neighbor GDF’s. The first sphere was placed randomly with every subsequent sphere being positioned at a histogram-drawn distance in relation to the previously placed one. Collisions were checked similar to that in (a) with modifications. If a collision could not be resolved, a new random position was generated maintaining the same distance criteria; this was repeated until there was no overlap. Finally, to avoid a deadlock, a new distance was generated if sphere could not be placed within 50 attempts and a new reference sphere was selected if no placement was found in 1000 attempts. Sinusoids were absent in this geometry.

(d) Cellular anisotropy with nearest neighbor along with sinusoids

The geometry criteria were the same as in (c) with the addition of the sinusoidal compartment. Based on the HIC, a fraction of the total volume of spheres was assigned to hepatocytes and the rest to sinusoids according to equation (3) and the constants provided earlier. Within the two compartments, spheres were placed as explained in (c).

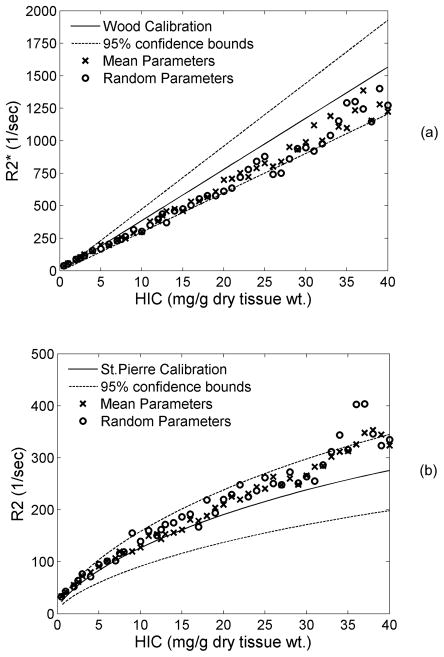
To access the sensitivity of MRI signal to perturbations in iron size and clustering, another version of this final model (d) was also generated where GDF parameters β and γ were allowed to randomly vary within 95% confidence bounds of their regression with HIC. The parameters were assumed to be Gaussian variables with ‘mean’ given by the equations described in Table 1 and ‘variance’ represented by the corresponding mean square error. Thus, for a given iron burden, iron morphology was allowed to alter freely within the observable variability in histological findings. This provides a sensitivity analysis for the accuracy of the histological characterization with respect to resulting relaxivity.

MRI Simulation

1. MRI signal synthesis and relaxation

The iron deposits were modeled as a collection of impenetrable spheres. The magnetic dipole field equation for a sphere is given by,

$$\frac{\mathrm{\Delta }B(r,\theta )}{B_0}=\left(\frac{1}{3}\right){\chi }_L{\left(\frac{R}{r}\right)}^3(3Co{s}^2\theta -1)$$ (4)

where, B₀ is the applied magnetic field (1.5T), R is the sphere radius, r is the radial distance from the center, θ is azimuthal angle to the magnetic axis. χ_L represents the particle susceptibility and is given by χ_L = (HIC/WDR)* χ_F/υ where υ is the sphere volume fraction, HIC is in terms of dry tissue weight and WDR is the tissue wet-to-dry weight ratio, set to 4.1 (22). χ_F is the intrinsic susceptibility of iron deposits and was assumed to be a 4:1 mixture of hemosiderin and ferritin using literature values of 1.1E-6 and 1.6E-6 m³/kg_Fe (23,24) yielding a composite estimate of 1.2E-6 m³/kg_Fe. The number of spheres distributed was given by N = υ.L³/(4/3.π.R³), where L is the side length of the cubic volume. Number of protons was optimally chosen to be 5000 since this produced a coefficient of variation of <2.5% for both R2 and R2*; based on test simulations, larger number of protons only increased simulation time without significant change in results.

Proton mobility was modeled as isotropic Gaussian diffusion with mean absolute displacement given by

$$\sigma =\sqrt{2\text{D}\delta }$$ (5)

where, D is the diffusion coefficient and d is the simulation time step; in 3D, the expected displacement in time t is given by E(r²) = 6Dt. We used a published value of D=0.76 μm²/ms determined for human liver (25). Proton random walk was interrogated over a time interval of 60 ms and constrained not to pass through the iron spheres; any proton that touched or entered a sphere was put back onto the surface. Time step for protons was d=0.5 μs; the expected distance traveled by a proton in this time interval is 0.048 μm that is less than the dimension of the smallest spatial perturbation (0.1 μm diameter). For a moving proton, the simulation volume followed a ‘periodic’ pattern i.e. a boundary crossing was mapped to the opposite side.

Phase accrual for each proton was then computed, reflecting local magnetic field fluctuations and the residence time in the field. At time step k, total phase accumulated is given by,

$$\mathrm{\Phi }(k)=\gamma \delta \sum _{i=1}^k(B_0+\mathrm{\Delta }B(p(i)))$$ (6)

where γ is the gyromagnetic ratio (2.675E8 sec⁻¹T⁻¹), p(i) = position of i^th proton and Φ(k) corresponds to the resultant spin angle with respect to the rotating frame. The NMR signal from a single proton can then be computed as:

$$S(t)=S(0)·e^{-t/T{2}_0+j\mathrm{\Phi }(t)}$$ (7)

where, T2₀ represents condition in an iron-free environment and was assumed to be 50 ms. Superposition of phase evolution of multiple protons yielded the envelope of the FID and R2* was calculated by exponential fitting.

The effect of 180° radiofrequency pulses for the single spin echo experiment was simulated by reversing the proton phase at half the echo time (TE). The resultant symmetric echo formation at TE was collected and peak complex magnitude was recorded. The experiment was repeated for multiple echo times, logarithmically spaced between 0.1–30 ms, to obtain a single-echo T2 decay curve. The envelope of the complex waveform was fit to a monoexponential plus a constant.

2. Implementation aspects

The magnetic field map within the virtual tissue was pre-calculated as a superposition of disturbances created by individual iron spheres. A 0.5 μm Nyquist sampling was used for the 80×80×80 μm³ volume forming a 160×160×160 point grid. In this way, the magnetic field at any given point in the environment could be computed by cubic interpolation within the field grid. Computational complexity of collision between protons with iron spheres was simplified by checking against only ‘nearby’ spheres i.e. which were within the envelope of expected motion in a 0.2 ms time interval. Thus, all spheres within a distance of twice the expected motion (6*D*0.2)^1/2 i.e. 2μm were considered as nearby spheres. To speed up computation of these highly parallelized procedures, custom MATLABR® (The Mathworks, Natick, MA) scripts were written using the distribution computing toolbox; infrastructure included a 16 node Linux-based cluster.

3. Sensitivity analysis

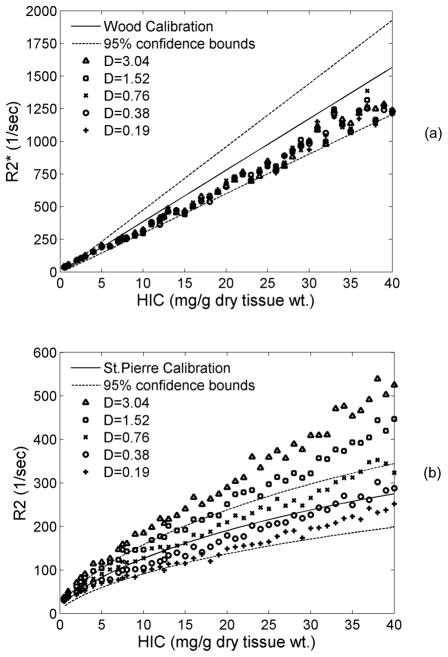
To evaluate the effect of anatomical boundaries on relaxivity, proton diffusion was modeled as 1) ‘unrestricted’ – free to move anywhere within the virtual environment and 2) ‘restricted’-constrained not to pass through hepatocyte or sinusoid boundaries. To access the sensitivity of relaxivity to proton mobility, simulations were repeated for D = 0.19, 0.38, 1.52 and 3.04 μm²/ms (octaves of nominal value of 0.76), the last one is close to that determined for water at 37° (26).

4. Bland Altman (BA) analysis

The Bland Altman statistic (BA) was employed to compare the predicted relaxivities across different model variants; BA=(A1−A2)/(average(A1+A2)), where A1 represented the model while A2 represented the reference in vivo calibration curves (4,5). The mean of the BA statistic reflected the offset of A1 from A2 while it’s standard deviation provided the intrinsic variability.

RESULTS

Tissue Geometry and Iron Morphology

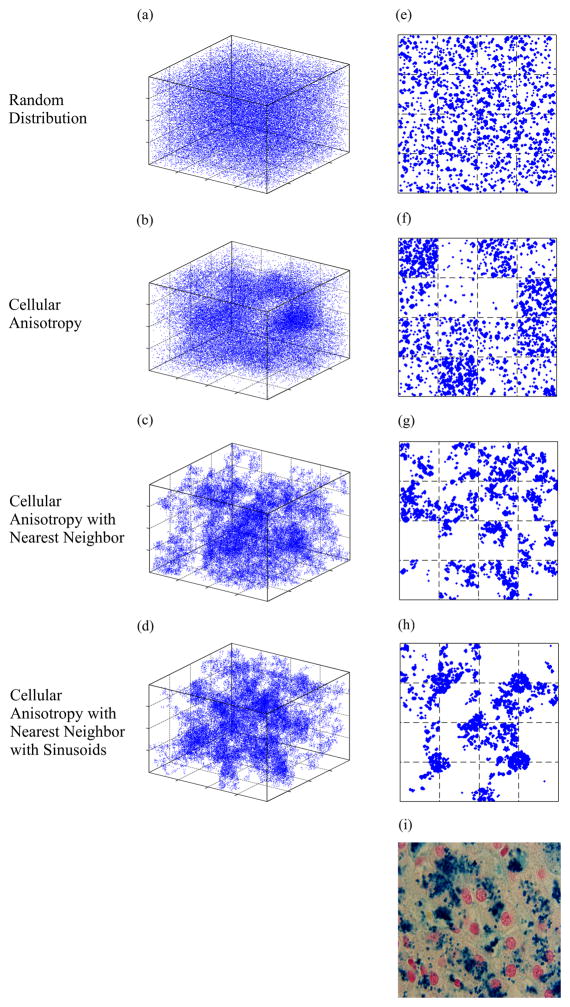
Figure 3 demonstrates three dimensional and cross sectional views of virtual liver geometry using four different iron distributions and an HIC of 20 mg/g dry tissue weight. The calculated (Table 1) volume fraction of iron spheres was 2.92%, leading to 41,200 spheres distributed in the simulated volume. Particle radii were drawn from the appropriate GDF (Table 1). Figure 3(a-d) are the representation of the sphere centers distributed in 3D with indicated morphology while (e-h) are the corresponding 4 μm thick random sections through the virtual volumes. Random distribution of the spheres does not produce a realistic simulated histology, even if inter-cellular anisotropy of iron loading is included (Figure 3e and 3f). Incorporation of nearest-neighbor information, within a cell, is essential to qualitatively match simulated iron distributions to tissue iron stains (Figure 3g and 3h, compared with 3i). For geometry in (h), ~30% of the spheres were placed equally in the sinusoids while others were distributed among hepatocytes based on anisotropy and nearest neighbor criteria. Clustering of iron can be seen occurring at intrahepatocyte, interhepatocyte, and compartmental (sinusoidal versus parenchymal) levels. The final geometry was the most accurate architectural and histological representation of human liver.

Figure 3.

Illustration of variants of virtual liver iron morphology that were generated for an iron concentration of 20 mg/g dry tissue weight. Panels (a-d) show the distribution of centers of iron spheres (blue) in the three dimensional tissue environment. Panels (e-h) are 4 μm thick random sections of the corresponding 3D volumes accounting for individual sphere dimensions. Panel (i) is a real histological section from a patient with 19.2 mg/g HIC; note the striking similarity between (h) and (i).

Iron Morphology and Relaxivity

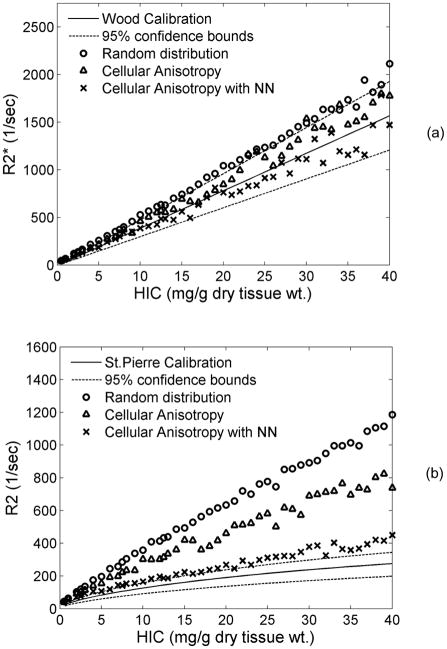
Figure 4 demonstrates model-predicted relaxivities overlaid on published in vivo calibration curves derived by Wood et al. and St. Pierre et al. (4,5). The plots show results for three different scenarios of iron morphology corresponding to those shown in Fig. 3(a–c). Here sinusoids were absent and proton diffusion was unrestricted. For random distribution, R2* values were outside the confidence bounds of in vivo calibration and overestimated the Wood calibration curve (5) by ~25% according to Bland Altman analysis. Adding simple cellular anisotropy to the iron morphology brought the prediction within the in vivo confidence bounds and decreased overestimation to 12%. When nearest neighbor criterion was applied, R2* values were only 4% below the Wood calibration curve.

Figure 4.

Plots compare model-predicted relaxivities with published in vivo calibrations for different patterns of iron distribution as indicated (where NN is nearest neighbor). Proton diffusion was unrestricted. (a) R2*-iron relationship is relatively insensitive to iron morphology, (b) R2-iron relationship changes from linear to curvilinear when inter-cellular iron anisotropy and nearest neighbor constraints are applied. This brings forth the importance of clustered nature of iron in vivo.

Iron aggregation had an even more dramatic effect on R2-iron calibration curve (Fig. 4b). For a random particle distribution without and including simple cellular anisotropy, the R2-iron relationship was close to linear and overestimated clinical calibrations by 102% and 80%, respectively. Once nearest neighbor information was included, however, calibration curvilinearity nature became evident, similar to in-vivo data(4). Inclusion of nearest neighbor information also lowered calibration bias to 34%.

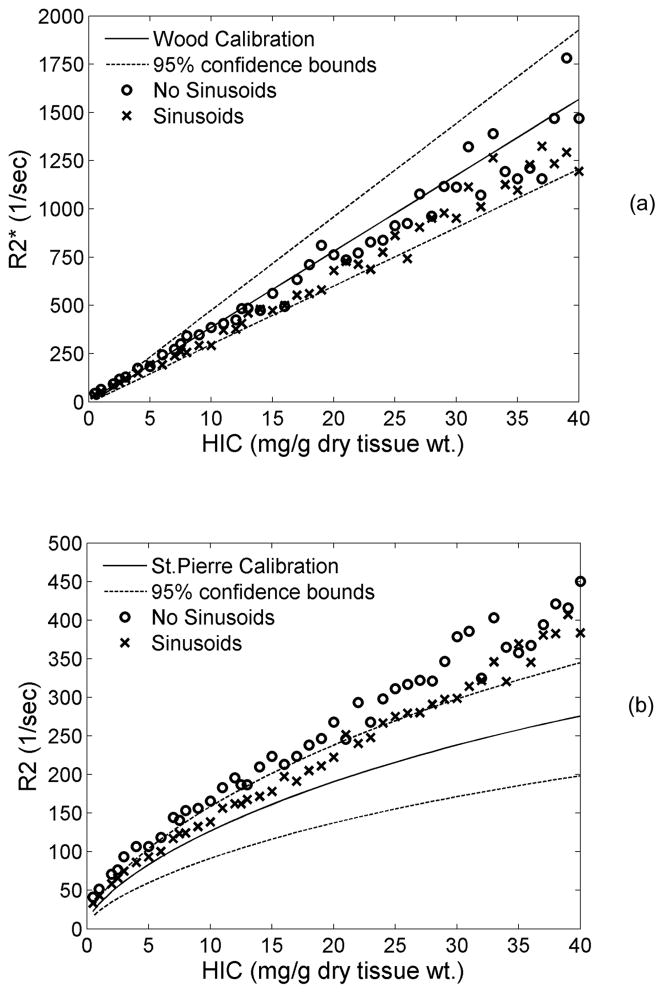
Effect of Sinusoidal Iron

Figure 5 shows a side-by-side comparison of predicted R2* and R2 with and without sinusoidal compartment modeling. Inclusion of sinusoids increased the negative bias of the predicted R2* calibration from −4% to −16% compared with hepatocyte modeling alone. Similarly, modeling the sinusoidal compartment caused R2 values to drop by an average of 14% when compared with purely-hepatocyte iron morphology, but the difference was not homogenous. Predicted iron curves matched observed data well for liver irons less than about 15 mg/g, but demonstrated larger deviation thereafter.

Figure 5.

Plots demonstrate the effect of loading iron in the sinusoidal compartment on R2* (a) and R2 (b). Proton diffusion was unrestricted. By including sinusoids, R2* dropped by 12% but remained within the confidence bounds of the calibration. R2 was brought closer to the calibration curve at low iron concentrations,; it exhibited an overall drop of 14%.

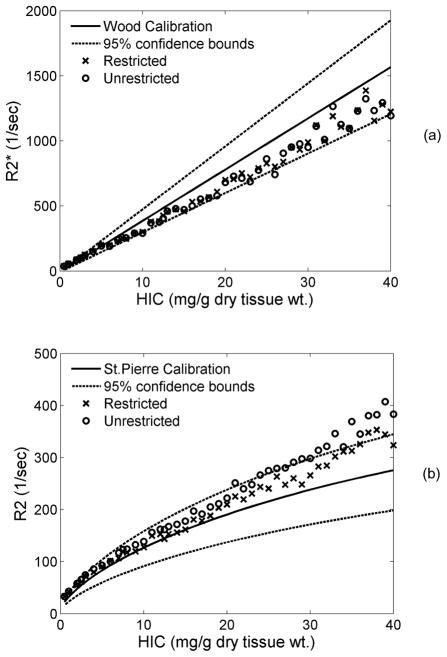
Restricted versus Unrestricted Diffusion

Simulations in Figures 4 and 5 allowed protons to pass freely through hepatocyte boundaries (unrestricted). Enforcement of restricted diffusion is shown in Figure 6; only the most realistic iron morphology is shown. As demonstrated in Figure 6a, impermeable anatomical boundaries (cell membranes) had no effect on R2*. In contrast, restricted diffusion decreased the R2-iron calibration curve an average of 8%. This effect was modest compared with changes in morphology, but further improved the match between observed and predicted R2-iron curves.

Figure 6.

Plots demonstrate the effect of the presence of anatomical boundaries on R2* (a) and R2 (b). In restricted diffusion, protons were not allowed to pass through cell boundaries. Sinusoids were included in the liver geometry. R2* was unaffected while R2 dropped by 8% when proton motion was restricted as compared to unrestricted.

Proton Diffusion Coefficient (D)

Figure 7 demonstrates sensitivity of R2* and R2 to changes in the estimated diffusion coefficient, D. Changes in proton mobility had no effect on R2* (7a). In contrast, proton mobility strongly influenced the R2-iron relationship (Figure 7b), with greater mobility producing greater R2 decay. On average, R2 decreased by ~16% as D was halved. For D=0.19–0.76 μm²/ms, R2 was within in vivo confidence interval.

Figure 7.

Plots show the sensitivity of proton diffusion coefficient (D) on R2* (a) and R2 (b). Over a wide range of D, R2* was unaffected while R2 dropped in a systematic manner with decrease in D.

Gamma Distribution Function Parameters

GDF parameters for Figures 4–7 were deterministic functions of HIC (Table 1), although resulting iron geometries and simulations represented random variables. In practice, our measurements of these parameters contained errors that could add additional variance into the predicted iron calibration curves. However, allowing the GDF parameters themselves to vary within their predicted 95% confidence intervals did not appreciably alter either R2* or R2 iron calibrations (Figure 8). Variability in the R2 calibration did increase slightly for HIC>30 mg/g, but other changes are imperceptible.

Figure 8.

Plots demonstrate changes in R2* (a) and R2 (b) when random β and γ parameters of the Gamma distribution function are used for generating iron size and distribution criteria. Both R2 and R2* remained unaffected, however variability increased at high iron concentrations.

Bland Altman Analysis

Table 2 summarizes the Bland Altman analysis for R2* and R2 predictions with respect to in vivo calibrations. Based on the trend of the BA statistic with HIC, R2* observations were split into two groups separated at HIC=5 mg/g. For HIC<5, the error term was invariant with respect to HIC and was therefore reported as an absolute disparity (in Hertz). In contrast, R2* error scaled linearly with HIC once it exceeded 5 mg/g. In this range, R2* error was more appropriately reported in relative terms (percent, error). R2 error scaled linearly with HIC throughout the entire HIC range, so only percent error is reported. All mean differences were significant at the level of p<0.003.

Table 2.

Bland Altman analysis for predictions

Figure	Type	R2* (HIC<5)		R2* (HIC>=5)		R2 (HIC>0)
		mean (Hz)	std (Hz)	mean (%)	std (%)	mean (%)	std (%)
4	Random distribution	48.37	12.14	25.17	3.16	102.99	16.02
	Cellular anisotropy	33.28	4.73	12.59	6.79	80.80	13.35
	Cellular anisotropy+NN	26.34	5.51	−4.28	8.94	34.21	7.91
5	No sinusoid	26.34	5.51	−4.28	8.94	34.21	7.91
	Sinusoid	14.14	9.07	−16.67	6.76	20.39	8.70
6	Unrestricted	14.14	9.07	−16.67	6.76	20.39	8.70
	Restricted	16.05	8.52	−16.37	6.34	12.07	8.28
7	D=3.04	16.91	8.51	−15.89	6.50	45.69	8.91
	D=1.52	15.46	7.88	−16.78	6.52	30.07	8.46
	D=0.76	16.06	8.52	−16.37	6.34	12.07	8.28
	D=0.38	16.14	7.24	−16.76	5.98	−5.16	10.01
	D=0.19	13.39	9.31	−16.83	6.12	−20.76	11.08
8	Mean params	16.06	8.52	−16.37	6.34	12.07	8.28
	Random params	14.31	8.71	−18.43	6.86	15.40	10.04

NN: Nearest Neighbor

DISCUSSION

Tissue iron is primarily stored as ferritin-clusters or insoluble hemosiderin deposits in cytoplasmic saccules known as lysosomes. Previous in vitro work has indicated that iron aggregation greatly amplifies local diffusion gradients, increasing transverse relaxivity six-fold compared with ferritin in solution or gel (15). Aggregation of ferritin by trypsin degradation produced similar amplification (16). The present observations further reinforce that clustering of lysosomal iron at multiple levels (individual particle size, particle grouping and inter-cellular anisotropy) is key to understanding in vivo R2 behavior. With increase in model complexity, R2 dropped and approached in vivo values for a given iron concentration, as demonstrated in Fig. 4b. This is consistent with prior theoretical and experimental work by Weisskoff et al. (27) which has shown that R2 initially increases with particle size, reaches maxima and then falls off for larger sizes. Since our operating range is in the descending part of this curve (sublinear), increasingly complex iron geometries increase the effective particle size via “clumping” and heterogeneous distribution, thereby producing lower R2 values. On the other hand, R2* was relatively insensitive to iron geometry (Fig. 4a); this is also consistent with the observations of Weisskoff et al. who demonstrated that the R2*-size relationship is a plateau for larger particle sizes, for a given particle magnetic susceptibility (χ_L).

In a similar manner, the influence of diffusion rate on relaxivity can be explained by its relationship with ‘effective iron scale’ or R²/D dependence; these relaxivity scaling properties have been extensively discussed by Weiskoff et al. (27). In our model, decreasing D, either by restricted diffusion through cell boundaries or absolute rate of proton diffusion, resulted in an increased R²/D thus shifting right on the relaxivity-size relationship. R2* was unaffected by changes in D (Fig. 6a, 7a) since we are on the plateau of the R2*-size curve. However, we observed a significant decrease in R2 with decreasing values of D (Fig. 6b, 7b) and this can be attributed to the sublinear nature of R2-size relationship. Lower proton mobility causes iron particles to appear magnetically “larger” to the diffusing proton because phase accrual is a combination of magnetic inhomogeneity and correlation time within the local magnetic influence. Intuitively, greater mobility increases motional averaging while lower mobility increases static refocusing; these observations are also consistent with prior work by Kennan et al. (28). Thus, physiologic fluctuations in diffusion, for example by temperature or hydration status, could potentially confound R2-iron calibrations. Fortunately, both temperature and body water are tightly controlled in humans.

R2 curvilinearity, or saturation, arises because static refocusing decreases R2 sensitivity to iron at larger iron scales. This has been documented in R2 liver iron assessments from both humans and gerbils (4,5,13). We had previously postulated that the static refocusing phenomenon was produced by the rightward shift of particle size with iron loading (5,12). However, Figure 4 clearly demonstrates that this effect is minimal compared with the static refocusing introduced at secondary larger scales. Both inter-cellular and intra-cellular iron scales are essential to explain in vivo behavior. In particular, magnetic field “fusion” from inter-particle grouping dominates the curvilinearity of in vivo R2 calibration curve. This is further in agreement with the relaxivity scaling properties discussed earlier (27). As iron concentration or χ_L is increased, the R2-size curve shifts up and to the left, however, as we are operating in the sublinear part of the curve, this upward shift is compensated by the increase in effective particle size. R2*-iron relationships were linear over the entire range of iron loads simulated (plateau effect) with a slope that was weakly determined by tissue iron distribution. In effect, R2* was governed primarily by magnetic susceptibility and would be expected to have closer correlations with biomagnetic susceptometer measurements than R2-based iron estimates (29).

One surprising finding was that the model even captured the strong curvilinearity at low iron concentrations (near the normal level of 1 mg/g) and had excellent asymptotic behavior despite its simplicity. Proton or chemical exchange mechanisms are required to explain ferritin relaxation in solutions (30), however our model did not include ferritin particles or any contact relaxivity mechanisms. Despite this, we were able to accurately describe both R2 and R2* iron calibrations simply by modeling susceptibility-based diffusion losses. Based on these observations, the known insolubility and compartmentalization of hemosiderin, and the relatively weak R2 relaxivities exhibited by ferritin solutions and gels, we conclude that dipole-dipole interactions are unimportant for single-echo R2 observations of iron-loaded tissues.

R2 and R2* values were well within in vivo confidence bounds when model incorporated sinusoids and restricted diffusion. In spite of this, uncertainty in some intrinsic variables still exists. Our model assumed a tissue wet to dry weight ratio of 4.1 (22), however it has been suggested that it may be as high as 5.5 (31). Another uncertain variable is the magnetic susceptibility of hepatic tissue iron deposits. Michaelis et al. made susceptibility measurements on horse spleen ferritin and hemosiderin observing values of 1.33E-6 and 1.1E-6 m³/kg_Fe respectively (23). Shoden et al. performed measurements on human ferritin and hemosiderin yielding values of 1.6E-6 m³/kg_Fe for ferritin and 1.2, 1.5 and 2.1 E-6 m³/kg_Fe for three hemosiderin samples (24). Based on these measurements we chose a susceptibility that was equivalent to a 4:1 mixture of hemosiderin and ferritin i.e. 1.1E-6 and 1.6E-6 m³/kg_Fe respectively yielding a model susceptibility of 1.2 E-6 m³/kg_Fe.

Since the effective susceptibility χ_L in Eqn. 4 is dependent on the ratio of intrinsic susceptibility and tissue wet to dry wt. ratio i.e (χ_F/WDR), we think that this combined factor is a more stable representation of the two. For our model, this factor was (1.2E-6/4.1) or 0.2926E-6 that agreed with the values used by Fischer et al. in their SQUID biosusceptometry measurements, (1.6E-6/5.5) or 0.2909E-6 (31). Since model-predicted R2* values were within the confidence bounds of the in vivo calibration, the assumed factor is probably very close to the ‘truth’.

Exact values for diffusion coefficient are difficult to measure in tissues in vivo. The only available in vivo human measurement for water diffusion in liver is 0.76 μm²/ms (25), however, the standard deviation for this measurement was 0.27, which defines a 95% confidence interval of 0.22–1.3. Furthermore, the measurement will vary depending on the time interval over which the proton motion has been interrogated. Based on Figure 7b, ‘effective’ in vivo diffusion coefficient could be anywhere between 0.19–0.76 μm²/ms. A recent study has also demonstrated a four-fold decrease in the apparent diffusion coefficient of water in injured brain tissue and that this may be due to kinetic changes occurring in the intracellular spaces.

The calibrations predicted by the model depend upon the accurate morphologic characterization of hepatic iron stores. Practical considerations, however, limited the number of patients studied (N = 20) (18) even though liver biopsy is known to have high sampling variability (3). Iron distribution histograms used in these simulations did not account for the stereological bias generated when approximating 3D structures using 2D information (32,33). Our algorithm to match the nearest neighbor histograms was also imperfect since we could not easily account for distance changes introduced by new particles upon the particles already placed. This slightly reduced the width of the final distribution, relative to the desired histogram, but the mode was unaltered. Lastly, particle spacing within sinusoids was assumed to be similar to that in hepatocytes, however, electron micrographs suggest that nearest neighbor distribution in sinusoids is narrower (particles are closer together) although more difficult to quantify. Nevertheless, the resulting simulated histology (Figure 3d, h) and calibration curves (Figure 5) were so similar to ‘truth’ that it is unlikely that these minor algorithmic imperfections were important. Furthermore, allowing histogram parameters to vary over their entire stochastic range produced little deviation from the mean behavior.

Future modifications of the model could include incorporating contributions from portal tract endothelial cells. Biliary and vascular endothelial cells in the portal system contain roughly 10–16% of the total iron concentration (17). Our present simulations did not explicitly model this compartment, instead placed its corresponding iron share into the sinusoidal spaces. However, the magnetic scale of such fluctuations is quite long and is likely to have smaller impact. A second modification could be to restrict proton mobility further by introducing other hepatocyte organelles such as the nucleus or inclusion bodies. The hepatic nucleus occupies ~7% of the hepatocyte (34) and is relatively iron-poor. These additional objects would further restrict proton diffusion within the hepatocyte, creating an “effective diffusion” constant lower than the assumed D. Rather than treating boundaries as absolute barriers, proton interactions with iron particles, cell nucleus, and cell boundaries (membranes) could be modeled as exchange times, which can be estimated from previous studies (10,12). Given the good agreement observed with simplified approaches, these additional complexities are unlikely to have a dramatic influence on R2* and single echo R2 measurements. However, they may influence CPMG sequences that are quite sensitive to the relative balance of proton mobility and iron scale, particularly at shorter interecho spacing.

While the present model provides important mechanistic insights, its real power lies in the ability to predict changes in relaxivity-iron calibration under various scenarios. For example, with the popularity of 3T MRI scanners, there is a need to translate the relationships to higher fields (14). Iron calibration curves obtained from CPMG sequences differ from single echo R2 measurements and may be echo-time dependent (9,12,35). Even single echo R2 calibration has only been validated for HIC < 40 mg/g. It is relatively straightforward to extrapolate the present model to these measurement conditions. Physiologic questions can be posed as well. Hereditary hemochromatosis types 1 and 4 load hepatocytes and sinusoidal cells independently of one another. Similarly, certain iron chelators deplete liver iron nearly selectively from hepatocyte stores. Intuitively, one would expect condition-specific liver iron calibration curves. All these conditions can be objectively tested, greatly reducing the need for rescanning patient cohorts.

Lastly, these data suggest that calibration curves in biopsy inaccessible organs can be derived from Monte Carlo simulations. The core knowledge of iron distribution and intrinsic susceptibility can be obtained from autopsy specimens. This knowledge is sufficient for R2* calibrations. R2 calibrations require measurements or estimates of proton mobility. This knowledge is more problematic but techniques for in vivo estimation are improving, as is our understanding of cellular proton mobility.

In summary, a thorough understanding of the physical interactions occurring at the microscopic level can definitely aid resolving 1) differences in calibration, 2) discrepancies in MRI techniques and 3) changes in calibration with change in iron distribution. Monte Carlo modeling (27,36) excels in this regard, turning complicated physical systems into number of smaller and simpler problems that are more tractable. Using iron particle size and scale information derived from liver biopsy specimens, we were able to accurately predict in vivo human R2 and R2* iron calibration curves. Iron scale variations at the particle, inter-particle, and inter-cellular level were critical in capturing the correct magnitude and curvilinearity of the R2-iron relationship; changes in proton mobility were analogous to changes in particle iron scale. R2* measurements were much more robust to changes in iron scale and proton mobility. These data clearly demonstrate that iron distribution, rather than iron speciation, is the critical determinant of R2 relaxivity. Further, they indicate that diffusion-mediated susceptibility losses dominate contrast mechanisms for clinical R2-iron determinations. Therefore, knowledge of iron susceptibility, iron distribution, and proton mobility is sufficient to characterize tissue iron relaxivities, at least at high iron loads. Thus, tissue-specific models can provide relaxation-iron calibration curves for inaccessible organs (heart, spleen, pancreas) where tissue biopsy is not an option.