Variance as a signature of neural computations during decision-making

Abstract

Traditionally, insights into neural computation have been furnished by averaged firing rates from many stimulus repetitions or trials. We pursue an analysis of neural response variance to unveil neural computations that cannot be discerned from measures of average firing rate. We analyzed single-neuron recordings from the lateral intraparietal area (LIP), during a perceptual decision-making task. Spike count variance was divided into two components using the law of total variance for doubly stochastic processes: (i) variance of counts that would be produced by a stochastic point process with a given rate, and loosely (ii) the variance of the rates that would produce those counts (i.e., “conditional expectation”). The variance and correlation of the conditional expectation exposed several neural mechanisms: mixtures of firing rate states preceding the decision, accumulation of stochastic “evidence” during decision formation, and a stereotyped response at decision end. These analyses help to differentiate among several alternative decision-making models.

Introduction

The quantitative study of cortical neural systems rests largely on establishing systematic relationships between changes in neural firing rate and changes in a stimulus attribute, motor response, or decision. For example, responses of neurons in primary somatosensory cortex lay the foundation for understanding vibrotactile sensation because mean firing rates are significantly higher for more intense tactile stimuli (Romo and Salinas, 2001). Likewise, responses in the middle temporal area (MT) are thought to underlie some aspects of motion perception, in part because their mean firing rates vary with motion strength in a manner that explains choice accuracy in a direction discrimination task (Britten et al., 1992). It follows that the variability of firing rate across repetitions might bear on the fidelity of these neural signals (Barlow, 1956; Bulmer et al., 1957; Tolhurst et al., 1983). Together, the mean and variance of neural responses furnish rich insight into the limits of perception, motor control and decision-making (Faisal et al., 2008; Glimcher, 2005; Parker and Newsome, 1998; Shadlen and Newsome, 1998).

Response variability can also furnish insight into the neural computations themselves. For example, the irregular discharge of neurons bears on theories of coding, synaptic integration and circuit function (Shadlen and Newsome, 1998; Softky and Koch, 1993). Recently, it has been suggested that the time course of the variance during a complex computation can expose properties of the signal transformation, such as a sign of a fixed point or attractor (Churchland et al., 2010). Here, we exploit a principled measure of response variability that identifies a component of variance that distinguishes various classes of neural computations. We apply this measure to study the responses of neurons in the lateral intraparietal area (LIP) of the macaque during a perceptual decision-making task (Fig. 1).

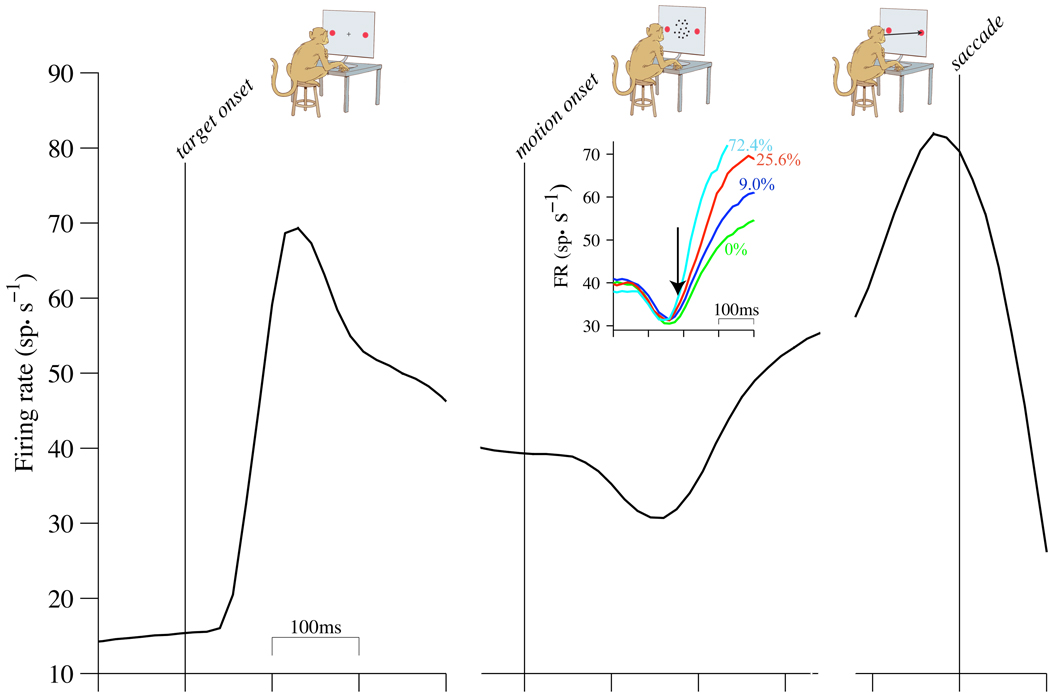
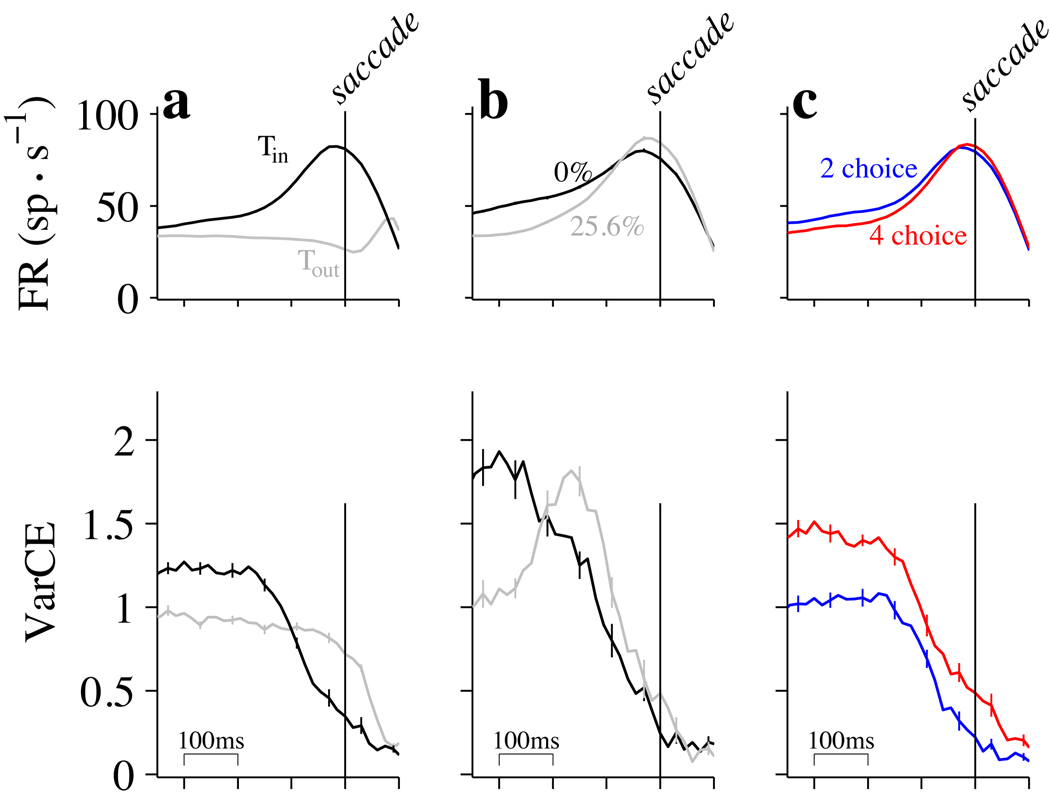
Figure 1. Overview of the task and neural responses.

Monkeys decided the net direction of motion in dynamic random dot displays and indicated their choices by making an eye movement to a peripheral choice target. Analyses of neural data focus on three epochs during the trials. Examples show subsets of data presented in subsequent figures. Left: Pre-decision epoch. Responses are aligned in time to the onset of choice targets (red circles in cartoons, above). Mean firing rates are from all 2-choice trials (16,444 trials). Mean rates are calculated from spikes counted in 60 ms bins (counting windows). Curves are running means; error bars are SEM from non-overlapping 60 ms windows (most are too small to be visible). Middle: Early decision formation. Responses are aligned to the onset of random dot motion. All 2-choice trials where motion was in the T_in direction are included (9,654 trials). Inset: responses grouped by motion strength (color, labels). Trials contribute to the averages up to 340 ms after motion onset or 100 ms before saccade initiation, whichever occurs first. Arrow indicates beginning of decision related activity, approximately 190 ms after motion onset. Right: End of decision. Responses are aligned to the initiation of the saccadic eye movement response. Averages reflect correct T_in choices only. All motion strengths are included (7008 trials).

Because the momentary evidence in the random-dot motion stimulus we use is noisy and temporally uncorrelated, a reasonable strategy for making decisions is to accumulate evidence over time. The time-dependent pattern of mean firing rates is consistent with a bounded integration mechanism (Fig. 1) (Gold and Shadlen, 2007; Smith and Ratcliff, 2004). After an initial dip, firing rates change gradually during decision formation at a rate that depends on stimulus strength (Fig.1, middle column). On trials when the monkey decides in favor of the choice target in the neuron’s RF (a T_in choice), mean firing rates reach a high value at the end of the decision (Fig.1, right column) that is similar for all motion strengths and reaction times (RT).

While bounded integration offers a parsimonious explanation of the choice and decision time, the mean response could be explained by a variety of alternative mechanisms that do not involve integration of noisy evidence. For example, the rise of mean firing rates to a threshold value could imply preparation for a saccadic eye movement (Hanes and Schall, 1996). Or, the rise might represent a change in the gain of a sensory representation of noisy momentary evidence, without appreciable integration (Cisek et al., 2009), possibly related to a gradual shift of attention to a choice target (Gottlieb and Balan, 2010). Or, the gradual rise might reflect the averages of step-like functions as the animal shifts from an uncommitted to a committed state.

We developed a technique to identify a component of neural response variability that can distinguish putative neural mechanisms. This technique exposed a mixture of states early in the trial, integration of noisy signals during decision formation, and a stereotyped threshold at decision end. An analysis of within-trial temporal correlations during decision-formation likewise constrains the type of mechanism that is at play. In addition to supporting particular mechanisms for perceptual decision-making, the analysis methods could provide useful tools for distinguishing classes of mechanisms that make similar predictions about mean firing rates.

Results

We analyzed neural recordings from LIP while monkeys performed a motion direction discrimination task (Fig. 1). A detailed analysis of the behavior and its connection to mean firing rates has been previously published (Churchland et al., 2008). The monkeys’ choices and RTs on this and similar tasks suggest that the decision is based on the accumulation of noisy samples of evidence (Bogacz et al., 2006; Gold and Shadlen, 2007; Ratcliff and Rouder, 1998). If the firing rate of LIP neurons represents such an accumulation, then the linear rise in mean response, evident in Figure 2, belies averaging over many random “diffusion” paths. These random paths ought to give rise to a distinct pattern in the variance of the neural response over multiple trials. We therefore set out to measure the response variance in a way that is informative about the underlying neural computations. We first provide a brief background on the principles that guide our analyses. Then, we describe our observations from neural data in LIP and argue that the variability at different times in the trial is suggestive of particular neural mechanisms.

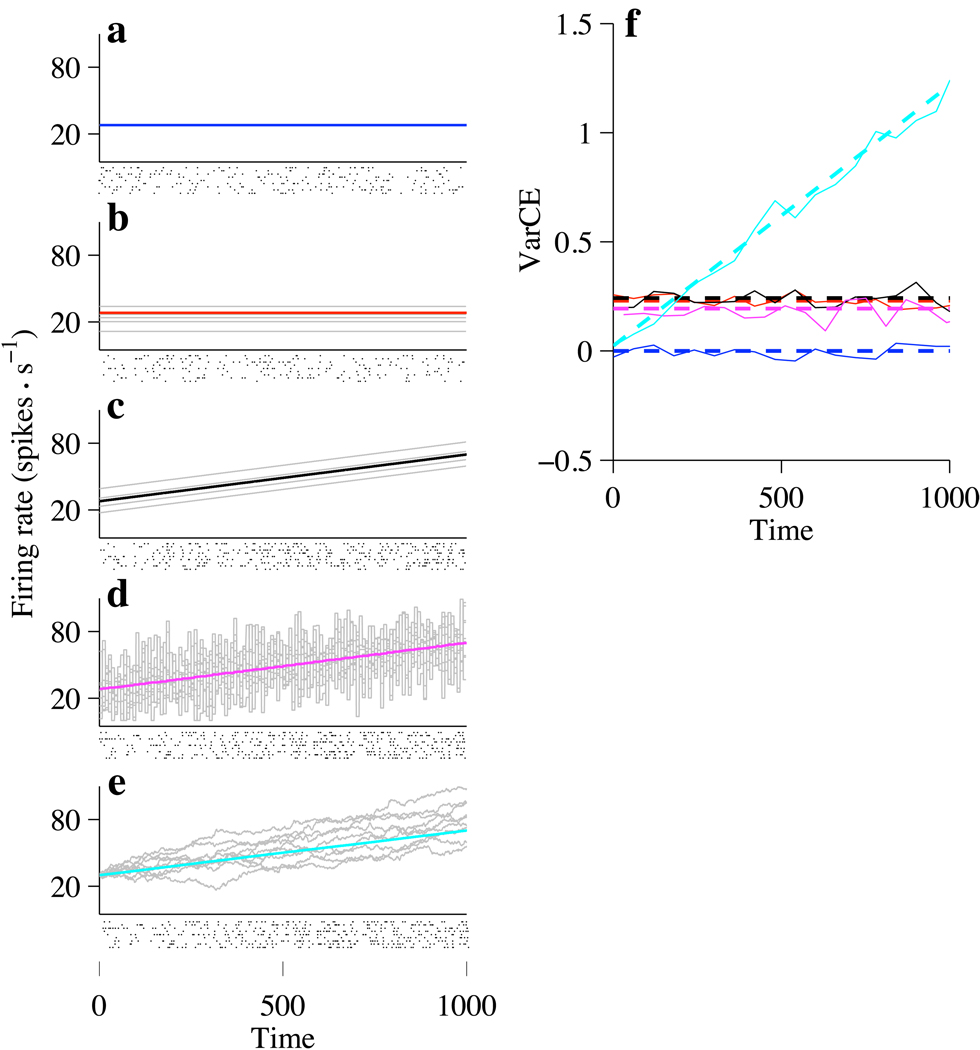
Figure 2. Examples of doubly stochastic point processes.

a–e, Each process is characterized by a rate function that may vary from trial to trial and a random point process that realizes that rate. Both sources of variability contribute to total spike count variance. For each process, theoretical rate functions are shown with simulations of a nonstationary Poisson point process. Mean spike rate and spike count variance are calculated in non-overlapping windows using the same method as for analysis of data in subsequent figures (60 ms; 20,000 simulated trials). Ten random spike trains are shown in the rasters below the panels. a. Constant rate without trial-to-trial variation. Spike count variability arises only from the stochastic point process (PPV), hence VarCE=0. b. Constant rate with trial-to-trial variation. A random value perturbs each rate function for the duration of the trial. Gray traces: examples of rate functions used to generate spikes. Total variance is comprised of PPV and VarCE. c. Same as b but with time varying rates. d. Same as c except that a new random perturbation is sampled every 10ms. e. Drift-diffusion. Rate is the sum of a deterministic “drift” function (same linear rise as in b and c) plus the cumulative sum of independent, random values drawn from a Normal distribution (mean=0). Individual rate traces resemble 1-dimensional Brownian motion (with drift). f. VarCE for the five examples. The VarCE captures the portion of total variance owing to variation in the rate functions across trials. Thick dashed lines show theoretical values $({\sigma }_{\langle N\rangle }^2)$ of VarCE for doubly stochastic Poisson point processes. Thin solid lines show VarCE estimates using the algorithm applied to the simulated spike trains $(s_{\langle N\rangle }^2)$. Counting window = 60 ms. Line color corresponds to the colors used in a–e.

Background 1. Doubly stochastic processes

We exploit a standard decomposition of the measured variance across observations into a variance of a random variable that depends on another hidden cause. In general, if a random value X depends on some other random variable Y, the law of total variance is

$$\mathit{\text{Var}}[X]=\underset{\begin{array}{c}\hfill \text{variance of conditional}\hfill \\ \hfill \text{expectation (VarCE)}\hfill \end{array}}{\underbrace{\mathit{\text{Var}}[\langle X|Y\rangle ]}}+\underset{\begin{array}{c}\hfill \text{expectation of}\hfill \\ \hfill \text{conditional variance}\hfill \end{array}}{\underbrace{\langle \mathit{\text{Var}}[X|Y]\rangle }}$$ (1)

where 〈…〉 denotes the expectation (or mean) of a random variable. Note that the conditional expectation has a variance because Y is itself a random variable.

It is useful to consider the neural response as a doubly stochastic process, such that the spike count in some epoch is a random realization of a stochastic point process, governed by a rate parameter, λ. The process is doubly stochastic because λ varies from trial to trial. For example, a “Poisson neuron” that receives a command to produce a spike rate λ_i in an epoch of duration T_i = τ_i+1 − τ_i will produce a random number of spikes, obeying a Poisson distribution with expectation 〈N_i〉 = λ_iT_i.

Corresponding to equation 1, the variance of that spike count can be described as

$$\underset{\begin{array}{c}\hfill \text{Total measured}\hfill \\ \hfill \text{variance}\hfill \end{array}}{\underbrace{{\sigma }_{N_i}^2}}=\underset{\mathit{\text{VarCE}}}{\underbrace{{\sigma }_{\langle N_i\rangle }^2}}+\underset{\begin{array}{c}\hfill \text{Point process}\hfill \\ \hfill \text{variance (PPV)}\hfill \end{array}}{\underbrace{\langle {\sigma }_{N_i|{\lambda }_i}^2\rangle }}$$ (2)

where N_i is the number of spikes in the epoch and λ_i is the firing rate. Note that means and variances are over trials, using the same time epoch. We refer to the first term on the right side of equation 2 as the “variance of the conditional expectation” (VarCE) because it represents the variance of a theoretical quantity that the neuron realizes through its spike discharge. We write ${\sigma }_{\langle N_i\rangle }^2$ as shorthand for ${\sigma }_{\langle N_i|{\lambda }_i\rangle }^2$ because the expectation of any count sample, given rate λ_i on that trial, is 〈N_i | λ_i〉 = λ_iT_i. The last term in equation 2 is the expectation of the conditional variance, but we shall refer to it as the “point process variance” (PPV) to convey the intuition: even if λ_i does not vary from trial to trial, the N_i would still vary from trial to trial according to some distribution.

For a Poisson neuron the PPV conforms to the Poisson distribution: the PPV equals the expectation of the counts (Daley and Vere-Jones, 2003). If the expectation is the same on every trial, then $\langle {\sigma }_{N_i|{\lambda }_i}^2\rangle ={\lambda }_i{T}_i=\langle N_i\rangle$ and the VarCE is zero. This case is illustrated in Figure 2a and the blue dashed trace in Figure 2f. Each point process (rasters) is produced by realization of the same rate. There is variability from trial to trial, but it is attributed solely to the PPV.

Next, consider an example in which the rate is different on each trial (Fig. 2b). For simplicity, suppose that the rate is stationary throughout the duration of each trial, but its value is drawn from some distribution. The VarCE captures this variance, ${\sigma }_{\langle N\rangle }^2=\mathit{\text{Var}}[\lambda T]$ (Fig. 2f, red lines >0), and the PPV becomes an average over variances associated with the variety of λ samples,

$$\langle {\sigma }_{N|\lambda }^2\rangle =\lambda T=\langle N|\lambda \rangle$$ (3)

Of course, the firing rate is typically not stationary throughout an epoch. If the time-varying rates were to differ by a random amount for the duration of each trial, as in Figure 2c, the VarCE is again greater than 0, and still remains constant as a function of time (Fig. 2c and black lines in Fig. 2f). A constant VarCE is still evident when the firing rate is perturbed by additive noise, as in a doubly stochastic Poisson process (Fig. 2d and magenta lines in Fig. 2f), also known as a Cox process (Cox and Isham, 1980).

The final example (Fig. 2e) is germane to the problem of decision-making. Consider rates that are generated by a drift-diffusion process: that is, the rate is the cumulative sum of independent random draws from a Normal distribution. Here, the mean firing rate is identical to the previous two examples. However, the VarCE is quite different: it grows over the course of the trial (Fig. 2f, cyan traces). For unbounded drift-diffusion, the VarCE is a linear function of time, like the variance of the position of a particle in Brownian motion.

Background 2. Estimate of VarCE from neurons

To obtain an estimate of the VarCE from neural data, we calculate the sample variance and subtract an estimate of the PPV. We do not assume that the point process is Poisson, but we make a simplifying assumption, based on renewal theory, that the count statistic, N_i, in epoch T_i obeys a distribution with variance proportional to the mean count:

$$\langle {\sigma }_{N_i|{\lambda }_i}^2\rangle =\varphi \langle N_i|{\lambda }_i\rangle$$ (4)

where ϕ is a constant (Geisler and Albrecht, 1995; Nawrot et al., 2008). This ratio is similar to the Fano factor, but it must be emphasized that ϕ is not the ratio of variance to mean counts measured from data. It is a theoretical quantity that characterizes an unknown process. It would equal the measured Fano factor were the VarCE equal to zero, which probably never occurs in vivo (see Discussion).

It should now be apparent that if we know ϕ, then the estimated VarCE, $s_{\langle N_i\rangle }^2$, is

$$s_{\langle N_i\rangle }^2=s_{N_i}^2-\varphi {\overline{N}}_i$$ (5)

where $s_{N_i}^2$ is the sample variance of the spike counts and N̅ is the sample mean (note that the s are estimators for the corresponding σ). For our purposes, fortunately, precise knowledge of ϕ is not essential. Because the VarCE must be nonnegative, we adopted the largest possible value of ϕ that ensured a positive VarCE throughout the trial. This is equivalent to the minimum value of the measured Fano factor (typically around the time of target onset). In the simulations in Figure 2, this implies that ϕ ≈ 1, consistent with the non-homogeneous Poisson point process we used for the simulations. The estimates for VarCE (Fig 2f, thin solid lines) are based on application of equation 5 to the simulated spikes (ϕ = 1). For the neural data, we estimated ϕ for each neuron.

Most of the analyses we pursue below concern the time dependent changes in the VarCE $(s_{\langle N_i\rangle }^2)$. We also examine the correlation between spike count expectations in different epochs within a trial. This correlation between conditional expectations (CorCE) is a useful complement to the time course of the VarCE for discerning the mechanisms at play during the prolonged period of decision formation (see below).

VarCE changes over the course of the trial

We analyzed the VarCE in three epochs during the trial: preceding motion onset, during decision formation, and just preceding the monkey’s saccadic eye movement response. VarCE is displayed in all three epochs together in Supp. Figs. 3 and 4. We propose that the VarCE in each epoch is suggestive of particular neural mechanisms.

VarCE preceding decision formation

We first examined responses during the time period after the choice targets appeared, before the onset of the random dot motion that informs the decision. The mean firing rate and VarCE from 70 neurons on the 2- and 4-choice tasks are shown (Fig. 3). For this period, responses were aligned to the onset of the choice targets (Fig. 3, vertical lines).

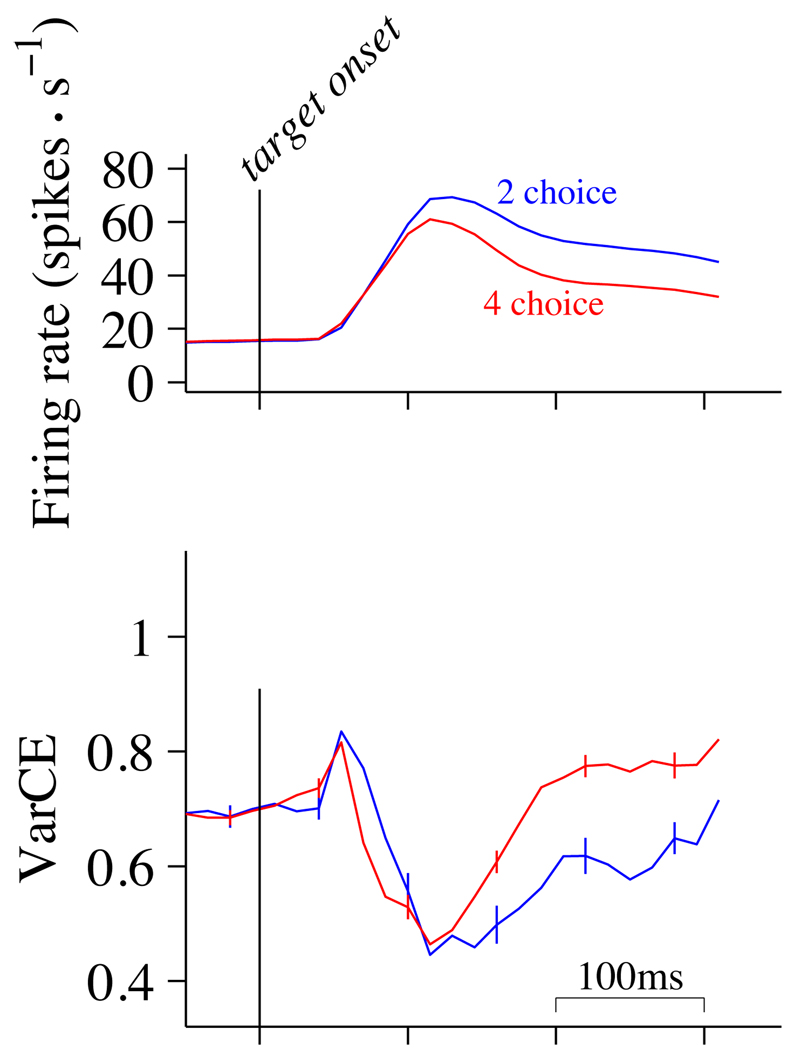
Figure 3. VarCE in the pre-decision epoch depends on number of alternatives.

Responses are aligned to the onset of the choice targets as in Fig. 1 (left panel). Mean and VarCE are calculated from spikes counted in a 60 ms sliding window. Top, mean firing rates for 2- and 4-choice conditions. Points include values from 70 neurons (2-choice, 16,444 trials; 4-choice, 32,882 trials). Error bars are SEM for non-overlapping windows (most are too small to be visible). Bottom, VarCE. Curves show the VarCE from the same 2- and 4-choice trials. Data from 70 neurons were combined using residual deviations from the means, respecting neuron identity. Error bars are SE (bootstrap; see Methods).

For both 2- and 4-choice trials, the appearance of the choice targets caused a transient increase in mean firing rate (Fig. 3, top), and then a return to a new, elevated firing rate. During the same time period, VarCE decreased sharply from the level during fixation, achieving a nadir around the time of the peak visual response (Fig. 3, bottom). The decrease in VarCE is in keeping with previous observations that the onset of a salient stimulus synchronizes neurons that were, up to that point, in a variety of states (Churchland et al., 2010).

On trials in which 4 choice targets were presented, the firing rates were lower than they were on the 2-choice trials (Fig. 3, top, blue trace above red), yet the VarCE was elevated on the 4-choice trials (Fig. 3, bottom, red trace above blue). This dissociation was pronounced in the epoch following the response transient as the monkey awaited onset of the random dot motion. The difference in VarCE first achieved statistical significance 160 ms after the onset of the choice targets (p<0.05, paired t-test) and remained significant through the duration that we analyzed. The difference was confirmed for a wide range of values for ϕ used to estimate the VarCE (see Discussion). We address the robustness of this and other findings in Supplementary Figures 1 and 5.

This analysis suggests that the weaker responses on the 4-choice task were associated with a greater variety of firing rates across trials. This insight, which cannot be ascertained from the mean responses, suggests that the effect of the extra two targets on the added uncertainty is probably not explained by a simple scaling of the firing rates, but rather a mixture of firing rate states that includes more low values, thereby reducing the mean (see Discussion).

VarCE during decision formation

Shortly after the onset of random dot motion, firing rates in LIP underwent a brief depression (Fig. 1, middle) followed by a more complex evolution that reflects the strength and direction of motion, as well as the monkey’s choice and RT. We consider decision-related activity to begin approximately 190 ms after the onset of stimulus motion, when the response averages first reflect the strength and direction of random dot motion (Churchland et al., 2008; Huk and Shadlen, 2005).

By the time of motion onset, the VarCE (Fig. 4, bottom row) was larger than the nadir attained after onset of the visual target and even the values in the ensuing 190 ms of the pre-decision period. This is consistent with a mixture of states, as noted above, and further compounded by alignment of the analysis epoch to motion onset, which occurs after a variable delay from target onset. Over the first ~100 ms of motion viewing, the VarCE declined to a new relative minimum. The relative minimum, which is associated with the dip in the firing rate averages, indicates that motion onset temporarily induces a more stereotyped level of activity. It is difficult to compare the degree of stereotypy with other epochs in which we observe a low VarCE, because the analysis window for counting spikes is wide enough to incorporate both the variability from the pre-decision period and the variability that grows in the ensuing period of evidence accumulation.

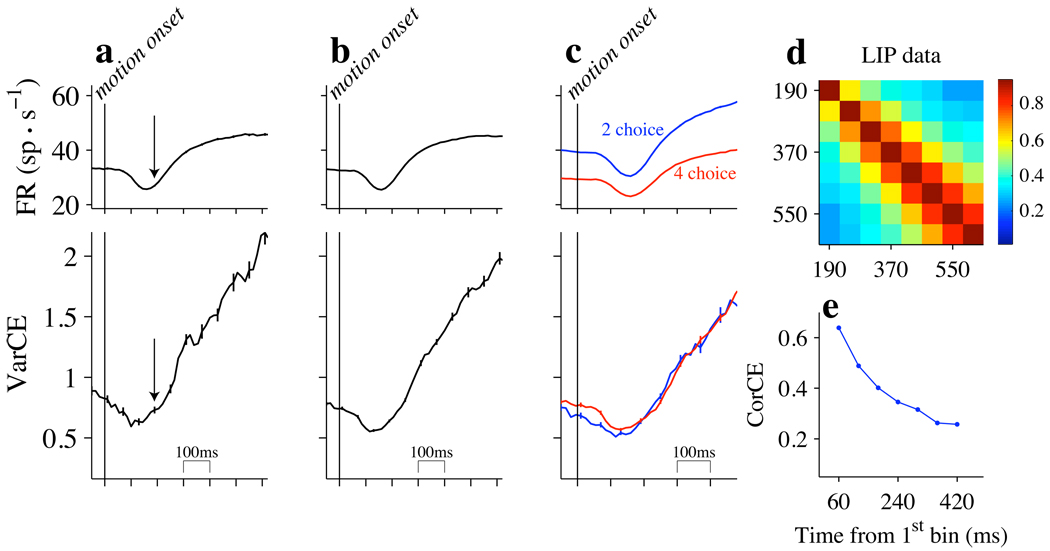
Figure 4. VarCE and CorCE during decision formation support a diffusion-like process.

Responses are aligned to the onset of stimulus motion (vertical lines), as in Fig. 1 (middle panel). a–c. Spike rates and count variance are derived from 60 ms counting windows. Top row: Mean firing rates. Error bars are SEM for nonoverlapping 60 ms bins. Bottom row: VarCE computed from the residual deviations from means, respecting neuron identity, motion strength, direction and number of choices. Error bars are SE (bootstrap); many are too small to be visible. a. 0% motion strength only (8,815 trials). Both panels: Arrow marks the time that mean responses begin to diverge as function of stimulus direction and motion strength, as indicated in Figure 1 (v). b. All motion strengths (50,326 trials). c. Comparison of 2- and 4-choice tasks; all motion strengths (16,444 and 33,882 trials, for 2- and 4-choice, respectively). d. Correlation of conditional expectations (CorCE) of counts as a function of time separation during decision formation. The matrix of CorCE values is displayed as a heat map (color bar to right; centers of the 60 ms counting windows are indicated by the axes). Data are from all trials, as in b, using the same residual deviations. e. Decay of correlation in time. Graph shows CorCE of the first time bin with each subsequent time bin (top row of the matrix in d).

After the initial dip, the VarCE underwent a linear rise. In light of the 60 ms counting window, we place the starting point roughly 170 ms after motion onset or ~20 ms before the mean firing rates begin to exhibit a dependency on the strength and direction of motion (Fig. 4a, bottom; arrow). The rise in VarCE was apparent when we analyzed only responses to 0% motion strength trials (Fig. 4a, bottom) and when we included all motion strengths and directions (Fig. 4b, bottom). The variance is thus associated with the decision variable in drift diffusion, which is intended to explain the process leading to correct as well as incorrect choices. A linear rise in VarCE is the expected pattern of Brownian variability associated with all possible diffusion paths, regardless of their ultimate destination.

The increase in VarCE was similar for 2- and 4-choice trials (Fig. 4c, bottom; 2 choice slope: 4.16±0.35; 4 choice slope: 4.19±0.16). It is notable that VarCE does not depend on number of choices: this implies that the noise is accumulated in a similar way regardless of whether the sensory evidence bears upon 2 or upon 4 choices. The effect of other deterministic task parameters (coherence and motion direction) had a more variable effect on the rate of rise of the VarCE as a function of time (Supp. Fig. 4, left), but for each motion strength and direction, we observed a linear rise consistent with an accumulation of a similar, statistically stationary source of noise.

Notice that the time dependent increase in mean firing rate depends on factors besides motion strength, direction, and the number of choices. This is evident from the mean firing rates on the 0% coherence trials (Fig. 4a, top), which contain balanced evidence for all directions. Although the animals’ decisions were unbiased, there is a time dependent increase in firing rate on these trials. For the competing accumulator mechanism, this time dependent rise would hasten decision termination (Churchland et al., 2008) because all competing accumulators would reach a termination bound by some time, even if the evidence were neutral.

If the response variance is explained by a diffusion (or Brownian) process, then the counts at different epochs during the course of a single trial ought to covary. This is because such a mechanism implies that the spike rate at a given time is determined by the spike rate at the previous time step plus one new random increment. A straightforward extension of the law of total variance allows us to estimate the degree to which the expectation of counts in separate epochs are correlated within a trial, the CorCE. As detailed in Methods, these correlation coefficients are obtained from the expectation covariance matrix, which is equivalent to the sample covariance matrix except that the $s_{\langle N_i\rangle }^2$ (i.e., VarCE) replace the diagonal (variance) terms. If spike rates are governed by a diffusion process, then the CorCE should be larger in adjacent counting epochs, and it should decrease as a function of the time separating the counting epochs. Moreover, for any given time separation, the CorCE should increase at later times, as trajectories wander to more extreme values.

This is the pattern observed in our data during decision formation (Fig. 4d). The CorCE is displayed as a pseudocolor matrix using a heat map to indicate the degree of correlation. Two features are notable. First, for any time separation (matrix elements along the same juxtadiagonal) the CorCE increases as a function of time (hotter colors in bottom right corner). Second, at any time (matrix elements along the same row) the CorCE is strongest in neighboring time bins and weaker with increasing separation in time. This is especially evident for the top row of the matrix, which displays the CorCE between the 1^st epoch (160 to 220 ms after motion onset) and each of the 8 subsequent epochs (Fig. 4e, blue trace). The observed pattern of CorCE was statistically reliable. Permuting the counts in each time bin, which preserves the VarCE, abolishes the pattern of CorCE seen in the data (p<0.0001 for weakest value in Fig. 4e). Together, the time dependent changes in VarCE and CorCE suggest that the firing rates of LIP neurons exhibit a component of variability from trial to trial that can be likened to the accumulation of random values. We will contrast this with several alternative models below, following a description of VarCE around the time of the choice.

VarCE at the time of the choice

We next examined VarCE around the time of the saccade (Fig. 5). Near the end of the decision, the mean firing rates indicated the direction of the subsequent eye movement (Fig. 5a, top). When the monkey chose T_in, firing rates reached a local maximum approximately 80 ms before the saccade, for all motion strengths (Fig. 5b, top; see also Supp. Fig. 4) and regardless of the number of alternatives (Fig. 5c, top). When the monkey chose the target in the opposite hemifield, firing rates decreased gradually until the time of the saccade (Fig. 5a, gray trace). For the analyses in figure 5, we grouped together all trials that ended in the same choice and aligned the spike counting windows to the time of saccade initiation.

Figure 5. VarCE declines at the end of decision formation.

Responses are aligned to the time of saccade initiation (vertical lines), as in Fig. 1 (right panel). Top row: Mean firing rates. Error bars are SEM. Bottom row: VarCE computed from the residual deviations. Error bars are SE (bootstrap). a. The decline in VarCE was faster and more pronounced for T_in choices (13,788 trials) than for T_out choices (13,724 trials). b. The decline in VarCE for T_in choices was apparent for strong and weak motion (2,815 and 2,838 trials; see Supplementary Figure 4 for comparison of all motion strengths). c. The decline in VarCE for T_in choices was apparent for 2- and 4-choice tasks (7235 and 6553 trials, respectively). Error trials for nonzero motion strengths are excluded in all panels.

For both sets of choices, there was a large VarCE in the approximately 300 ms preceding the saccade, reflecting a mixture of processes that have evolved for different durations from the beginning of decision formation. The deterministic components affecting drift, which undergo a stereotyped time course with respect to motion onset, are effectively sampled at different times when aligned to the end of the decision process, thereby exaggerating the VarCE. Diffusion for different durations also augments the VarCE, but restricting the analysis to trials that will end in one choice mitigates this contribution.

Nearer the end of the trial, the high VarCE gave way to a very different pattern that depended on the monkey’s choice. When the monkey chose T_in, the VarCE underwent a precipitous decline (Fig. 5a, bottom, black trace). For choices in the opposite direction, VarCE remained at a relatively stable value until the saccade was initiated (Fig. 5a, bottom, gray trace). The choice-dependent difference in VarCE was statistically significant 150 ms before the saccade and remained so until 50 ms after the saccade (p<0.05). This pattern was apparent for different motion strengths (Fig. 5b; see also Supp. Fig. 4) and for both 2- and 4-choice trials (Fig. 5c). The difference in VarCE for T_in and T_out indicates that the mechanism for terminating decisions resembles a threshold or bound for the winning choice only. Contrast this observation with bounded diffusion models, which depict a pair of decision termination bounds for positive and negative evidence (e.g. Gold and Shadlen, 2007). Whereas neurons with the chosen target in their response field show a common termination level, the competing processes are simply interrupted in a random state that is dependent on motion strength, time (e.g., urgency) and accumulated noise.

Models of decision formation

We next consider several candidate mechanisms that could explain the activity of LIP neurons during decision formation. In principle, each of these mechanisms can also explain the pattern of choices and RT measured in our experiments. Here, we do not attempt to achieve formal fits to the behavior and the physiology but to focus instead on the qualitative distinctions we can draw using the VarCE and CorCE.

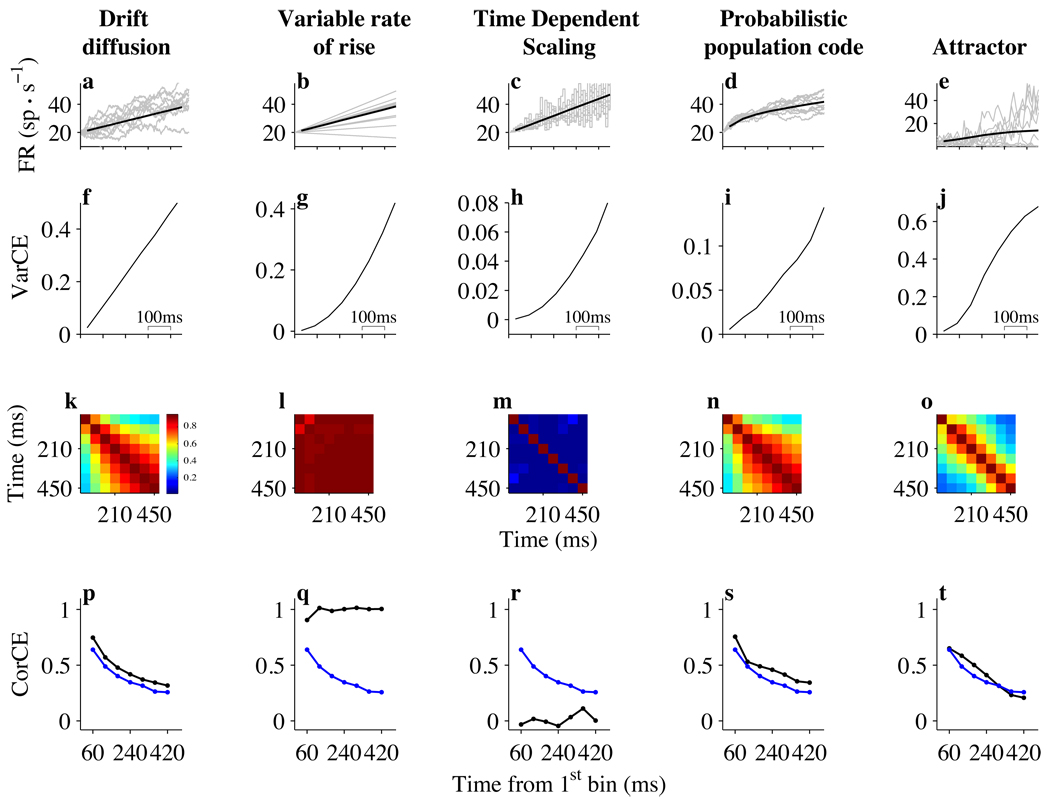
As previously mentioned, the time dependent changes in firing rate are consistent with a drift diffusion model (Fig. 2e and Fig. 6a). The “drift” refers to the deterministic effects on mean firing rate, namely the stimulus direction and coherence as well as a time dependent rise in firing rate that is independent of the stimulus properties. The “diffusion” refers to an accumulation of random values. Its signature is a linear rise in the VarCE as a function of time and CorCE that decays hyperbolically as a function of the separation between counting windows (Methods Eq. 10). These patterns are apparent in the VarCE and CorCE of LIP neurons during early decision formation (Fig. 6p, blue and black curves). The increase in overall correlation at late times (Fig. 6k, lower right corner) is subtler in data because responses near the RT are excluded.

Figure 6. Analysis of VarCE and CorCE in candidate models of decision-making.

Columns show analyses of simulated neural responses from five mechanisms in the epoch of early decision formation (corresponding to the epoch beginning ~190 ms after motion onset in the LIP data). a–e: Average firing rates (5,000 simulated trials). Gray traces: 10 randomly chosen trials. f–j: VarCE. k–o: CorCE matrices displayed as heat maps (scale bar near panel k). Same conventions as Fig. 4d, except for 190 ms delay of start time in LIP data. p–t: CorCE between first and subsequent time bins. Black: CorCE from the top row of the corresponding CorCE matrix in panels k–o. Blue: CorCE for the LIP data (same as Fig. 4e).

Alternatively, consider a mechanism in which the firing rates undergo a linear rise, or ramp, whose slope differs randomly from trial to trial (Fig. 6b). This “variable rate of rise” mechanism explains variation in simple motor RTs (Carpenter and Williams, 1995; Hanes and Schall, 1996) and some perceptual decisions (Reddi et al., 2003). The model predicts an increasing mean (Fig. 6b) and a quadratically increasing VarCE (Fig. 6g), which contrasts with the linear rise in the data. It also predicts nearly perfect correlation for all time windows (Fig. 6l). This is because there is just one source of variability, a random slope that affects the rate trajectory throughout its duration for each trial. If a rate happens to be above the mean at an early time, it will remain above the mean at all later times as well. The resulting CorCE is therefore perpetually high (Fig. 6q, black trace) unlike the data (Fig. 6q, blue trace).

Next, consider a mechanism that does not accumulate random numbers but simply scales random values as a function of time (Cisek et al., 2009). Consider a sequence of independent and identically distributed random values, which are multiplied by a linearly rising function of time. If the random values are positive, then multiplication will produce a monotonic increase in the mean firing rate (Fig. 6c, top), even though the random values themselves are statistically stationary (i.e., same mean and variance at all times). As in Figure 2d, we assume that the number of samples of independent random numbers is not enormous in any spike counting window. This mechanism would also predict a quadratic rise in VarCE. Moreover, the predicted CorCE from this model is negligible. This is because in time-dependent scaling, the variation about the mean originates from a random stream that is independent in time. This observation highlights the specificity of the CorCE as a signature of a process resembling accumulation.

The next model is based on the concept of a probabilistic population code (PPC) (Beck et al., 2008). Some features of the PPC are very similar to the DDM: firing rates of LIP neurons are produced by a mixture of deterministic and stochastic components, and independent samples of evidence from noisy, direction selective neurons are effectively summed at each time step. However, the PPC model differs from the DDM in some important respects: it is designed to represent a probability distribution over direction given the accumulated evidence. As a result, it contains more elaborate feedforward connectivity between MT and LIP neurons and lateral connectivity within LIP that controls the range of firing rates. Despite these extensions, the pattern of VarCE and CorCE contains the same signature of accumulation as seen in the DDM (Fig. 6i,n,s). This similarity argues that the key features of evidence accumulation are preserved when it is implemented in a more complex network designed to perform probabilistic inference.

Lastly, we consider a recurrent neural network that is exemplary of a class of dynamical “attractor” models of decision-making (e.g. Albantakis and Deco, 2009; Bogacz et al., 2006; Machens et al., 2005; Usher and McClelland, 2001; Wang, 2002). Here, we used a simplified firing-rate version of such a model (Wong et al., 2007). The VarCE for the attractor model undergoes quasi-linear time evolution for several hundreds of ms and then decelerates (Fig. 6j). The VarCE thus exposes the key features of this class of models: recurrent feedback that mimics integration and competition that leads to transitions toward more stereotyped decision states. The CorCE exhibits a pattern like diffusion early on (Fig. 6t), but signs of reaching the attractor states are not evident largely because the statistics were calculated only with traces that have not crossed a decision threshold (see Methods). When all time points were used, including those that have reached an attractor state, CorCE was larger and lasted longer at later times (lower right corner in the CorCE plot), reflecting strong correlation within an attractor state (data not shown).

State-like or gradual changes in firing rate

Together, the evolution of VarCE and CorCE suggest that LIP firing rates are affected by a mechanism that mimics the running sum of random increments to some termination bound. A plausible alternative, which we have yet to consider, is that the average firing rates represent mixtures of low and high firing rate states but do not meander in the manner of diffusion. If so, then for trials ending with a T_in choice, the gradual rise in firing rates observed in the data (Fig. 4, top) would reflect a mixture of two firing rate states: an uncommitted (low) and a committed (high) state. Accordingly, the change from the low to the high state occurs at a random time (i.e., “change point”) during each trial, such that the average rate reflects more high states as time elapses.

This is a difficult hypothesis to exclude using average firing rates, because it requires examination of the spike trains from individual trials: is the pattern of spikes consistent with a time-varying rate that undergoes a change from a low to a high state, or is it consistent with a realization of a random diffusion path that ends in an upper bound? The VarCE allows us to distinguish between these alternatives (Fig. 7).

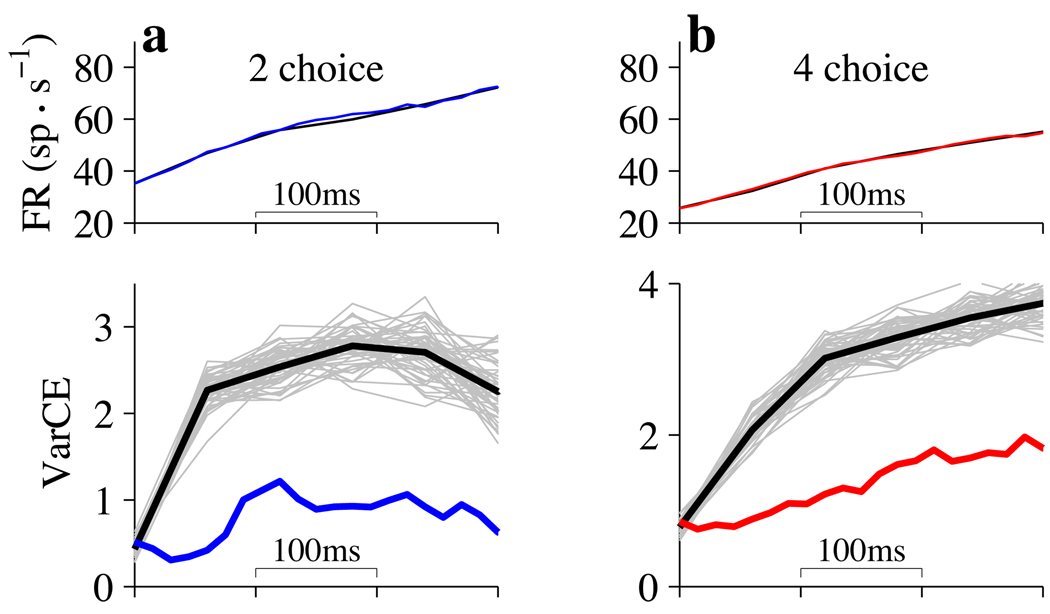
Figure 7. Use of VarCE to evaluate a mixture-of-states model.

Top, A mixture of low and high firing rate states can reproduce the mean firing rates from LIP in 2-choice (blue) and 4-choice (red) tasks. The analysis is for 0% coherent motion trials that culminate in a T_in choice. Black curves reconstruct average firing rates by mixing counts drawn from the start and end of the decisions (see Methods). Distributions of counts comprising these start and end sets were established separately for each neuron. Abscissae show time relative to the beginning of decision related activity in LIP, 190 ms after motion onset. Bottom, VarCE from the mixture model was estimated using a bootstrap procedure (600 samples). Each sample is a reconstruction of the mean firing rate, using the same number of trials as in the data. Black traces: average of the 600 VarCE values at each time point. Gray traces: individual sample reconstructions. VarCE from the data (blue and red curves) is outside the range associated with the mixture hypothesis. a. 2-choice. b. 4-choice. Note: VarCE associated with T_in choices is expected to rise initially, but then decrease owing to the exclusion of diffusion paths that lead to the alternative choices. This is evident in the 2-choice data (left) and would be evident in the 4-choice data (right) at later times (not shown).

We used Monte Carlo methods to estimate the expected VarCE if the spike counts in a time bin represent a mixture of two states: a “low state” represented by the counts from all trials at the beginning of decision formation (160 to 220 ms after motion onset) and a “high state” represented by the counts from all trials at the end of decisions for T_in (110 to 50 ms before saccade initiation). Unlike previous analyses, we include only trials in which the monkey chose T_in. We reconstituted the observed firing rate averages using random mixtures of the sets of counts comprising the low and high states (Fig. 7, top; black traces; see Methods). The VarCE for the mixture in the earliest time bins are indistinguishable from the data (colored traces), because the mixtures are comprised mainly from the low state. However, as time elapses, the mixture of low and high states required to produce the observed mean would be associated with a larger VarCE (Fig. 7, bottom; black traces).

The analysis leads us to reject the mixture (change point) model for trials ending in T_in choices (p=0.002 for both 2- and 4-choice). This conclusion is further supported by an analysis of the CorCE, which is predicted to be weaker under the mixture model (data not shown, p<0.001; bootstrap, Methods). We cannot perform such analyses on T_out choices because, as shown above, there is no evidence for a stereotyped state at the termination of these trials. Finally, we note that by restricting the analysis to T_in choices, the VarCE is not the one associated with diffusion (which must consider paths leading to all choices). The VarCE for T_in choices would ultimately decline as the responses approach the stereotyped high state before the saccade. There is a hint of this decline in Fig. 7a (bottom).

Discussion

Neural variability is frequently regarded as a nuisance: the highly variable discharge of cortical neurons necessitates collecting multiple repetitions of the same stimulus to generate a reliable estimate of the underlying mean firing rate, and it necessitates populations of neurons to transmit a reliable estimate of rate on one trial. However, variance itself, especially its time course, can be diagnostic of neural computations. Here too, the variable discharge of neurons is a nuisance, as it obscures the aspect of variance that is potentially diagnostic — the variance of the quantity that the neuron is supposed to represent. We have introduced a measure that allows us to look past one component of variance, the one associated with spiking, to gain insight about neural computations during decision-making.

Our main innovation is to depict the measured variance of spike counts as a reflection of a doubly stochastic process: a PPV associated with an idealized stochastic point process that would produce a random number of spikes even if some “intensity command” were identical on every repetition and a VarCE that describes the variance of that intensity command. This decomposition is a straightforward application of the law of total variance. We emphasize that the decomposition is a conceptual contrivance that does not conform to neurophysiological processes (e.g., synaptic integration and spike generation), at least not directly. Yet, it has the same intuitive appeal as the peristimulus time histogram (PSTH): it is a way of looking past the variability inherent in spike trains to infer the underlying computation. The PSTH recovers the mean intensity as a function of time, whereas the VarCE and CorCE recover properties of variance of that intensity across repetitions.

Comparison to other variance measures

Unlike the measured sample variance, the VarCE is intended to expose that component of variation that is tied to neural computation. By suppressing a component of the variance explained by irregular spiking, it reveals the trial-to-trial variance in the underlying rates. A larger VarCE implies greater heterogeneity of states across trials, and a linear increase in VarCE as a function of time is a hallmark of a diffusion or random walk process. The total variance cannot reveal such processes because all increases in firing rate are associated with larger total variance in cortex.

To large extent, the ratio of the variance-to-mean spike count (the Fano factor) achieves something similar to VarCE, because it normalizes the sample variance to the mean count. Both measures embrace the simplifying approximation that would liken spike trains to rate-modulated renewal processes: their intervals are independent and identically distributed once time is scaled to achieve the modulation of rate (Nawrot et al., 2008). In general the Fano factor and VarCE ought to be qualitatively consistent (but see, Supp. Fig. 2a). Indeed most of our conclusions would be supported by an analysis of the Fano factor (Supp. Fig. 2b–d).

The main advantage of VarCE is that it is principled. It captures the variance of the rates — actually the integrated rate across the counting window— from trial to trial. Therefore it has a natural link to standard dispersion measures (e.g., regression sum of squares as opposed to residual sum of squares, or the variance of the sum of independent random variables, as in diffusion). It is also a necessary first step in the calculation of the CorCE, which can be a highly diagnostic tool.

The main alternative to the CorCE is the spike autocorrelation function. The latter conflates variation in rate with variation in interspike interval, whereas CorCE isolates the former. Although it is beyond the scope of the present exercise, we anticipate that the CorCE could be adopted to better clarify the spike autocorrelation function in situations when rates undergo trial-to-trial variation. An extension to the cross correlation of firing rates (or spike cross-correlogram) is another potentially useful extension, especially when the rate is changing in time and from trial to trial (Aertsen et al., 1989; Vaadia et al., 1995).

Drawbacks of VarCE and CorCE

Since the VarCE is estimated by subtracting the PPV from the measured spike count variance, any uncertainty about the nature and magnitude of the PPV invites concerns about the validity of the VarCE and CorCE, and therefore about the conclusions we draw from these estimates. We have embraced three assumptions, which are incorrect but largely innocuous.

The first assumption is that PPV is proportional to the mean count. This holds if spike trains are properly characterized as rate-modulated renewal processes (Nawrot et al., 2008). For such a process, the variance of counts in an epoch is proportional to the mean. This is the inspiration for the expression for the PPV in equation 4. We recognize that neural spike trains do not conform exactly to this characterization. For example, when the firing rate changes, the refractory period does not scale in the way that the intervals do. Other violations of the renewal-like assumption are characterized in (Teich et al., 1997), although we suspect some are simply manifestations of VarCE and less exotic than these authors propose. For example, a change in Fano factor with window duration might be explained by mixtures or diffusion.

Important as they are, these caveats matter only to the degree that the PPV would be characterized erroneously as a value proportional to mean count, but this approximation appears secure. Only approximate conformity to the “rate-modulated renewal” assumption is required, and for this there is ample support (Nawrot et al., 2008). There is an approximately linear relationship between the mean and variance of the spike counts for neurons in several cortical areas for repetitions of identical stimuli (Britten et al., 1993; Churchland et al., 2006; Geisler and Albrecht, 1995; McAdams and Maunsell, 1999). These are conditions in which we would expect the VarCE to be minimal, and the same holds for LIP neurons when rates are relatively stationary, as in the delay period preceding a saccade to one target or during the late pre-decision period (cf. Maimon and Assad, 2009). These observations provide empirical support for the proportional relationship, PPV = ϕN̅, even if the magnitude of ϕ is unresolved.

The second assumption is that ϕ is fixed for the neuron — it does not depend on firing rate or state. This is unlikely to be true in all instances, and it could lead to inaccurate estimates of VarCE. For example, conditions favoring bursting in one epoch might affect our estimate of ϕ but fail to apply in other epochs, when the neuron is not bursting. That said, the observation of a roughly fixed ratio of variance to mean spike count and its near independence from conditions affecting the mean firing rate, such as motion strength, contrast and attentional state (Britten et al., 1993; Geisler et al., 2001; McAdams and Maunsell, 1999; Tolhurst et al., 1983), imply that ϕ is unlikely to vary systematically as a function of firing rate. Were ϕ a function of firing rate, then, to achieve a constant ratio of variance to mean count, the PPV and VarCE would necessarily contribute different proportions of the total variance when the firing rate changes. For example, if higher firing rates were associated with smaller ϕ (and hence a smaller PPV), then the constant ratio of variance to mean count could only be achieved if the decrease in PPV were offset by a concomitant increase in VarCE. This implies that the neuron’s spike discharge is less variable at higher rates, whereas the spikes comprising the input to the neuron are more variable. This seems highly implausible.

We favor a more consistent and parsimonious account of inputs and outputs: When a neuron is pushed to respond at a higher rate, both the variance of its inputs and the variance associated with its own spiking increase proportionately and thus preserve a consistent ratio of variance to mean spike count at low and high firing rates (Shadlen and Newsome, 1998). When this ratio changes, it is probably a reflection of a change in VarCE such as when conditions vary from trial to trial (i.e., mixture of states).

The third assumption is that ϕ can be approximated from neural data. This is truly suspect. Even if our own application of an upper bound is valid, it is unlikely to be helpful in data sets that do not furnish a plausible nadir in the measured Fano factor. Nonetheless, several practical heuristics serve to constrain estimates of ϕ. The VarCE must be nonnegative and less than the measured variance. Indeed it is unlikely that the VarCE is ever equal to zero in vivo, even under stable conditions in which variation in the “intensity command” ought to be minimal, because even highly stereotyped conditions do not remove all variability in synaptic inputs to neurons. This alone indicates that ϕ is less than the measured Fano factor. Similarly, the CorCE, which depends on the VarCE, must fall between ±1. This constrains ϕ to lower values.

Finally, theoretical considerations suggest an upper bound for ϕ, independent of the measured Fano factor. A Poisson process with refractoriness ensures ϕ<1 (Berry and Meister, 1998; Keat et al., 2001). For example, a 1.5 ms refractory period yields ϕ ≈ 0.8 over a range of firing rates commonly encountered in cortex. For cortical neurons that operate in a high input regime with balance of excitation and inhibition, a good choice for ϕ is in the range 0.4 to 0.7 (Nawrot et al., 2008; Shadlen and Newsome, 1998). Together, these heuristics might be applied judiciously in situations when the measured variance or Fano factor appear stationary as a function of time. Thus when a physiologist measures a Fano factor equal to 1.5, it may be reasonable to speculate that at least half of the measured variance is attributed to VarCE.

The above concerns serve mainly to reinforce the point that VarCE is useful mainly to compare responses when the neuron is likely to be in the same state, as when we compare responses in the pre-decision epoch in the 2- and 4-choice tasks, or when we examine the time course of VarCE during decision formation. We must exercise caution, however, when comparing the VarCE after target onset and before the saccade. In general, any conclusions that rest on the magnitude of VarCE and CorCE should be tested for robustness against variation in ϕ.

Importantly, the main conclusions of our study do not depend on precise knowledge of ϕ (Supp. Fig. 1). The linear rise in VarCE during decision formation is difficult to explain away, because it would require ϕ to change in just the right way to cancel the slope in Figure 4, bottom. Nevertheless, to evaluate this further, we repeated our analysis of the spike count variance using subsets of the data matched for firing rates (Churchland et al., 2010) (Supp. Fig. 5). These analyses provide reassurance that the time-dependent changes in VarCE and CorCE did not result from a misestimate of ϕ or because ϕ changed as a result of the time-varying firing rate.

VarCE during the pre-decision period, decision formation, and near the saccade

Previous analyses of the neural responses in LIP combined with analyses of choice and RT support a bounded integration mechanism for decision-making. The analyses of the VarCE and CorCE, presented here, lend independent support for this idea and expose new features of the neural computations that underlie the decision process: a mixture of firing rates associated with the pre-decision period, time-integration of a stochastic variable during decision formation and a threshold for terminating the decision.

During the pre-decision interval, we observed a higher VarCE on a 4-choice version of the task compared with a 2-choice version of the task. This observation suggests that the lower average firing rate on the 4-choice task belies a broader mixture of firing rates from trial to trial, most of which are lower in the 4-choice task. The lower average rate is probably not explained by a mechanism that invokes less excitation or greater suppression on all trials, owing perhaps to greater uncertainty (Basso and Wurtz, 1998), or normalization (Tolhurst and Heeger, 1997) or surround inhibition (Balan et al., 2008). Each of these mechanisms would simply scale the firing rate depending on the number of choices. They explain the lower firing rate on the 4-choice task, but they cannot explain the higher VarCE without additional assumptions.

During decision formation, the analysis of VarCE and CorCE provide direct support for stochastic accumulation by showing that the firing rates of LIP neurons are effectively sample-trajectories described by drift-diffusion. By perturbing the background of random dot motion displays, Huk and Shadlen (2005) demonstrated that LIP neurons represent the integral of motion evidence in the display, but these measurements did not demonstrate that spike trains from individual trials represent realizations of random walk or diffusion-like processes. An increase in variability during evidence accumulation is predicted by models of integration (Miller and Wang, 2006) but has not been demonstrated experimentally until now.

The pattern of VarCE and CorCE help to exclude several important alternatives to stochastic accumulation. For example a gradual shift in attention toward the choice target that simply follows a particular time course will not explain the increase in VarCE (Gottlieb and Balan, 2010). Similarly a change in the amplitude, or gain, of a signal (time-dependent scaling, Fig. 6, middle column) would not explain the pattern of CorCE that we observed during decision formation. A variable rate-of-rise model (Fig. 6, second column), where there is just one source of variability, a random slope that affects the rate trajectory for each trial, is also incompatible with the CorCE that we observed. The present exercise renders as unlikely any mechanism that lacks a Brownian component even if it gives rise to similar time dependent evolution in firing rates.

The increase in VarCE that we report during decision formation differs from the pattern of variability that is apparent in tasks that do not rely on the accumulation of evidence. For example, in dorsal premotor cortex, neural variability decreases gradually until the monkey’s movement, sometimes over a period as long as 400 ms (Churchland et al., 2006). Responses in LIP on a probabilistic reward task likewise decrease following the onset of a salient stimulus (Churchland et al., 2010). In light of the present work, our interpretation is that presenting a stimulus establishes experimental control and thus replaces a mixture of states across trials with greater consistency. We observed a similar decrease in variability in our data, following the presentation of choice targets, and again following the onset of random dot motion (Fig. 3) before the period of evidence accumulation. By contrast, during decision formation, the VarCE underwent a dramatic linear rise (Fig. 4, bottom) consistent with the accumulation over time of random samples of evidence.

These observations argue that the variability of neural responses, rather than simply hindering one’s ability to estimate the mean, can be exploited to constrain neural computations, particularly those that cannot be discerned from measures of average firing rate. This technique reveals that on decision-making tasks, LIP neurons reflect a mixture of states at the beginning of the trial, accumulation of evidence during decision formation, and a stereotyped level at decision end.

Methods

Behavior and physiology

All behavioral and neural data were previously published (see Churchland et al., 2008). Briefly, after a variable fixation period, two or four peripheral choice targets appeared to signal the direction alternatives on the trial. After a random delay (250–800 ms) dynamic random dot motion was displayed in a 5° diameter aperture centered at the fixation point. Task difficulty was controlled by varying the percentage of coherently moving dots on each trial (speed = 6°/s). The motion stimulus was extinguished when the monkey’s gaze moved outside the fixation window, thereby marking the time of saccade initiation. The data set consists of extracellular recordings from 70 well-isolated neurons in area LIPv (Lewis and Van Essen, 2000).

Data Analysis

Estimation of mean

We computed mean responses (Fig. 1 and top panels in Figs. 3,4, and 5) from the spike counts in 60 ms counting windows (bins) over repetitions of trials grouped by condition (motion strength, direction, etc). We used this brief counting window to facilitate examination of the response dynamics. Other window sizes yielded qualitatively similar results. All references to time refer to the midpoint of the counting window.

Estimation of variance of the conditional expectation (VarCE)

We estimated the VarCE in the same time windows used to estimate the mean. VarCE is estimated from a list of counts by subtracting an estimate of the PPV from the sample variance (Eq. 5). Its units are spikes². For each neuron, we obtain an estimate of the PPV by finding the time window with the smallest ratio of variance to mean (i.e., the Fano factor). Were VarCE=0 in this epoch, the measured variance would approximate the PPV. We take the Fano factor from this epoch as an upper bound estimate of ϕ for each neuron (median=0.46, IQR=0.23 to 0.70).

To enhance the power of most analyses, we combined data from several conditions (e.g., motion strength, neuron, etc.) that did not share the same mean count. To prevent this variation among the means from contributing to the combined variance, we estimated the variance using the residuals — that is, by subtracting from each sample count the mean for all trials sharing its condition. For example, in early decision formation, a condition would comprise all trials for one neuron that were obtained using the same motion strength, direction and number of choices.

The VarCE is then the variance of the union of residuals from all conditions, Z_◡, minus the weighted average of the PPV for the conditions:

$$s_{\langle N_i\rangle }^2=\mathit{\text{Var}}[z_{◡}]-{\displaystyle \sum _{i=1}^M\frac{n_i}{n_{◡}}{\varphi }_i{\overline{N}}_i}$$ (6)

where n_◡ is the total number of samples across all M conditions, n_i and N̅_i are the number of samples and the mean count for the i^th condition, respectively. Values of ϕ were the same for all conditions for a neuron: the largest value that ensures VarCE>0 for that neuron over all conditions and epochs. Standard error (SE) of $s_{\langle N_i\rangle }^2$ was estimated using a bootstrap procedure that preserved the number of trials in each condition (SE is the sample standard deviation from 200 samples). Similar results were obtained when we computed the VarCE separately for each condition and then averaged the values.

We computed the Fano factor in a similar way:

$${\mathit{\text{FF}}}_{\langle N_i\rangle }=\frac{\mathit{\text{Var }}\left[z_{◡}\right]}{{\displaystyle \sum _{i=1}^M\frac{n_i}{n_{◡}}{\overline{N}}_i}}$$ (7)

using the same conventions as equation 6. SEs were computed using a bootstrap procedure.

The trial groupings that define a condition depend on the analysis. In the pre-decision epoch (Fig. 3), we computed residuals using means from all trials from a neuron in either the 2- and 4-choice condition. For early decision formation (Fig. 4), we computed residuals using the means from each neuron, motion strength, motion direction, and number of choice targets. In this epoch, trials that ultimately led to any of the possible choices were grouped together. Each trial contributed data so long as the time of saccade initiation was at least 100 ms after the end of the bin (i.e., 130 ms after the time displayed on the abscissa). Therefore the numbers of trials contributing to each point in Figure 4 changes over time. Points on the plots in figure 4 indicate times when at least 25% of the trials were still contributing to the average (i.e. the RT for those trials was longer than the time point in question); varying this cutoff did not have a major impact on the time-dependent rise. The same time-dependent rise in VarCE was present when we restricted the analysis to trials with an RT > 700 ms and included all trials at each time point (data not shown). For responses in the perisaccadic epoch, we computed residuals using the means from each neuron, motion strength, motion direction, number of choice targets and choice. Note that the number of conditions contributing to each epoch’s analysis varied considerably. For example, when comparing 2- and 4-choice responses during the pre-decision period, all trials were included. For the same comparison around the time of the saccade, by contrast, trials that ended in a particular choice (i.e., T_in or T_out) were analyzed separately. As a result, many fewer trials contributed to each group.

Temporal correlations

The approach we use to estimate the VarCE extends naturally to pairwise measurements. Just as VarCE lends insight into the variance of an observed rate from trial to trial, the CorCE approximates the correlation between pairs of rates at different times during a trial. In both cases, we measure a total variance or covariance and correct for a portion that is caused by the point process. From the law of total covariance,

$$\mathit{\text{Cov}}[N_i,N_j]=\underset{\begin{array}{c}\hfill \text{covariance of}\hfill \\ \hfill \text{conditional expectations}\hfill \end{array}}{\underbrace{\mathit{\text{Cov}}[\langle N_i|{\lambda }_i\rangle ,\langle N_j|{\lambda }_j\rangle ]}}+\underset{\begin{array}{c}\hfill \text{expectation of}\hfill \\ \hfill \text{conditional covariance}\hfill \end{array}}{\underbrace{\langle \mathit{\text{Cov}}[N_i,N_j|{\lambda }_i,{\lambda }_j]\rangle }}$$ (8)

where the indices refer to epochs in time across the trial and the N and λ terms are spike counts and rates. As before, it is the first term on the right side of equation that interests us. The second term is the PPV when i=j. When i≠j, this term should be zero, because the variation associated with rendering a rate into a point process ought to be independent in two epochs. This reasoning is technically incorrect for adjacent bins because they share an interspike interval, but we saw nearly identical effects when we used bins that were separated by 30 ms (data not shown).

These considerations imply that the measured covariance is the covariance of the conditional expectation for the non-diagonal terms of the covariance matrix, and is simply the VarCE terms for the diagonal. The CorCE is obtained by writing the covariance matrix of conditional expectations as

$$\left(\begin{array}{ccc}\hfill s_{\langle N_1\rangle }^2\hfill & \hfill \dots \hfill & \hfill r_{1m}\sqrt{s_{\langle N_1\rangle }^2{s}_{\langle N_m\rangle }^2}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill r_{1m}\sqrt{s_{\langle N_1\rangle }^2{s}_{\langle N_m\rangle }^2}\hfill & \hfill \cdots \hfill & \hfill s_{\langle N_m\rangle }^2\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill {\mathit{\text{VarCE}}}_1\hfill & \hfill \dots \hfill & \hfill \mathit{\text{Cov}}[N_1,N_m]\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \mathit{\text{Cov}}[N_m,N_1]\hfill & \hfill \cdots \hfill & \hfill {\mathit{\text{VarCE}}}_m\hfill \end{array}\right)$$ (9)

and solving for the r_ij, where m is the number of epochs.

We computed the temporal correlations among spike counts in the data in m=9 successive time bins (width = 60 ms) beginning with the bin centered at 190 ms after motion onset. Like the analysis of VarCE in this epoch, we used the residual deviations to obtain a 9x9 total covariance matrix. The rise in VarCE in Figure 4b suggests that a process resembling diffusion begins ~20 ms earlier (i.e., ~170 ms after motion onset, based on fitting the VarCE samples in Fig. 4b by a constant followed by a ramp, smoothed with a 60 ms boxcar filter). Uncertainty regarding the start of this increase has little effect on the results. In particular, delaying the time of the first counting window to 220 ms does not affect the conclusions drawn from the CorCE analysis.

To facilitate comparison among different models, we plot the 1^st row of the CorCE matrix (Fig. 4d, Fig. 6p–t). For diffusion, the expected correlation of the underlying instantaneous rates at t_i and t_j is

$${\rho }_{\mathit{\text{ij}}}=\frac{t_i}{\sqrt{t_i{t}_j}}\text{ for }0<t_i<t_j$$ (10)

For a time-dependent scaling model, ρ_ij = 0. For the variable rise-rate model, ρ_ij = 1.

We established the distribution of CorCE under the null hypotheses {H₀ : ρ_ij = 0} by randomly permuting the counts within each epoch across the trials. This manipulation preserves the mean count, variance and VarCE at each time bin, but it breaks the correlations across time, within each trial. We used Monte Carlo methods (200 permutations) to assess the distribution of elements in the CorCE matrix under H₀. The p-value reported in the text is the largest for all elements of the top row of the matrix (the data plotted in Fig. 4e, blue symbols).

Models and simulations

The examples in Figure 2 are simulations of doubly stochastic point processes. For each trial, we generated a time-dependent rate function, λ(t), according to a set of model assumptions, and converted these rates into spikes by simulating a nonstationary Poisson point process. In 2a, the rate is a constant λ(t) = 20 Hz. In Figure 2b the rate is λ(t) = 20 + ε, where ε is a constant drawn from N {0, 8} (i.e., a Normal distribution with mean = 0 and standard deviation = 8). In 2c the rate is λ(t) = λ₀ + kt + ε, where ε is a constant drawn from N {0, 8}. In 2d, λ(t) = kt + ε(t), where ε(t) is a sequence of independent random values drawn from N {0, 18}, which are sampled (and held) every 10 ms. The 6 independent perturbations to λ(t) in each 60 ms counting window compensate partially for the larger standard deviation. In 2e, the rate undergoes drift and diffusion, as described below.

The examples in Figure 6 represent plausible mechanisms for decision-making, which are grossly compatible with the pattern of firing rates observed in LIP neurons. They can be configured to support decision making, typically by including competing units and by imposing a rule for terminating the process with a choice on each trial. However, with the exception of the “attractor” model, we do not analyze models that are configured with these features. Instead we focus on what would constitute the early portion of evidence accumulation, and we compare this to the responses recorded from LIP in a comparable epoch, from 190 to 670 ms after motion onset. Firing rate functions for each model were integrated across each 60 ms bin to obtain the expectations of spike counts from which VarCE and CorCE were calculated. All models were parameterized to approximate the firing rates of LIP neurons in Churchland (2008).

For the drift-diffusion model (Fig. 6, 1^st column; also Fig. 2e) the rate is λ(t) = λ₀ + f(t) + B(t), where λ₀=20 Hz, f(t) = 0.16t is a deterministic time-dependent drift, and $B(t)={\displaystyle {\sum }_{i=1}^{t/\mathrm{\Delta }t}}N\{0,\nu \sqrt{\mathrm{\Delta }t}\}$ is the accumulation of random numbers sampled at a rate of (Δt)⁻¹ from a Gaussian distribution with mean zero and standard deviation $\nu \sqrt{\mathrm{\Delta }t}$ (ν=21.8; see below).

To make decisions, we imagine that there are several neurons or pools of neurons; each accumulates noisy evidence in favor of one alternative and against the others. Decisions terminate when one of the accumulators reaches a stopping bound. This is the same as drift diffusion with an upper and lower stopping bound (Bogacz et al., 2006; Ratcliff and Rouder, 1998), so long as the evidence for one alternative is evidence against the other (Gold and Shadlen, 2007). In our implementation, we do not incorporate competing mechanisms or bounds. For drift diffusion, the VarCE should increase linearly as ν²t. The presence of a termination bound would distort this pattern in real data, but the effect should be negligible during the early epoch of decision formation, before many trials terminate.

For the variable rate-of-rise model (Fig. 6, 2^nd column), the rate is a ramp on each trial λ(t) = λ₀ + (k + ε)t, where k=0.03, and ε is drawn from N {0,ς = 0.02}. This model would also explain decisions using competing mechanisms (Reddi et al., 2003), although we did not implement this. For this model, the VarCE is a quadratic function of time: ${\sigma }_{\langle N\rangle }^2={\varsigma }^2{t}^2$.

For the time-dependent scaling (Fig. 6, 3^rd column), momentary evidence is drawn from a positive valued distribution, but the pieces of evidence are not summed together. Instead, each random value (of evidence) is weighted by a function, g(t), that increases gradually over time: λ(t) = λ₀ + g(t)ε(t), where ε(t) is a sequence of random values drawn from a stationary gamma distribution (mean = 20 sp/s and standard deviation ς = 0.47) that is sampled (and held) every 10 ms. These values approximate the average firing rate of a population of weakly correlated MT neurons to 0% coherent motion in a 10 ms sample (Britten et al., 1996). In an epoch from τ_i to τ_i+1, the expected count is the integrated rate:

$$\langle N_i\rangle ={\displaystyle \underset{{\tau }_i}{\overset{{\tau }_{i+1}}{\int }}}20g(t)\mathit{\text{dt}}$$ (11)

and the VarCE varies quadratically with the gain: ${\sigma }_{\langle N_i\rangle }^2\propto g^2(t){\varsigma }^2$. The multiple independent random samples in each counting window render this expression approximate. This model would make decisions via competition with other mechanisms, as in the previous two models.

The probabilistic population code (PPC, Fig. 6, fourth column) was implemented using an algorithm that has been described elsewhere (Beck et al., 2008). We simulated conditions approximating 0% coherence motion, and we analyze the response of a putative “right choice” LIP neuron during the early decision formation, regardless of the ultimate outcome of the trial. As in bounded integration, independent random samples of evidence from neurons in an MT layer are summed together at each time step in an LIP layer (for this paper, samples of evidence were generated independently at each time step, a change from Beck et al., 2008). The neurons also receive excitation and inhibition from other LIP neurons. Absent these inputs, the LIP firing rates would represent the sum of independent random numbers and would thus exhibit VarCE like the DDM.

The recurrent nonlinear dynamical “attractor” model (Fig. 6, right column) is described in (Wong et al., 2007). In the model, LIP neurons receive excitatory input from simulated MT neurons, recurrent excitation from other LIP neurons, and inhibition from interneurons, which themselves receive excitatory and inhibitory input from LIP neurons. The LIP neurons undergo dynamic changes resembling integration of evidence, followed by divergence into a stable attractor state in which only a subpopulation of neurons is active. Parameter values are the same as in (Wong et al., 2007) except for the following changes. (a) No target inputs were used (for simplicity). (b) The mean inputs representing random dots stimulus are smaller. I_motion = J_A,extμ₀ (1 ± fc′/100), where c′ is the motion coherence, μ₀ = 30 sp/s, J_A,ext = 1.83 × 10⁻⁴ nA/ sp/s, f = 7.2. The ± sign refers to the neural population for which the motion stimulus is the preferred or null direction, respectively. (c) The noise standard deviation is increased to 0.075 nA when the stimulus comes on. More details are available at: http://wanglab.med.yale.edu/webpages/codes.shtml

We analyzed only the early portion of the activity, corresponding to the period of evidence accumulation in the physiology. We checked that the psychometric function and chronometric function of the model are comparable to the monkey’s behavior (cf. Furman and Wang, 2008) but did not attempt to quantitatively fit the model to the behavioral data. Choice and RT on single trials were determined when one of the two neural pools crossed a firing rate threshold of 40 sp/s. Analysis at each time point was restricted to trials where both population firing rates were still below 40 sp/s.

For the mixtures (change-point) analysis (Fig. 7), we analyzed data from 0% coherence trials ending with a T_in choice, using all neurons. The method for producing mixtures of responses is described in the main text. Under the mixture model, the samples comprising the first time bin (centered 190 ms after motion onset) represent the low state. The Monte Carlo methods reproduce the mean as random samples (with replacement) from the same set of trials and therefore replicate the observed mean and VarCE. For all subsequent time bins, however, the rate is matched (on average) by sampling appropriate mixtures from this set of low state rates and the set of responses in a 60 ms bin centered 80 ms before saccade initiation (T_in choices). The VarCE for all 600 samples was larger than the observed VarCE in all but the first time bin, where they should be identical.