Shear Wave Velocity Imaging Using Transient Electrode Perturbation: Phantom and ex vivo Validation

Abstract

This paper presents a new shear wave velocity imaging technique to monitor radio-frequency and microwave ablation procedures, coined electrode vibration elastography. A piezoelectric actuator attached to an ablation needle is transiently vibrated to generate shear waves that are tracked at high frame rates. The time-to-peak algorithm is used to reconstruct the shear wave velocity and thereby the shear modulus variations. The feasibility of electrode vibration elastography is demonstrated using finite element models and ultrasound simulations, tissue-mimicking phantoms simulating fully (phantom 1) and partially ablated (phantom 2) regions, and an ex vivo bovine liver ablation experiment. In phantom experiments, good boundary delineation was observed. Shear wave velocity estimates were within 7% of mechanical measurements in phantom 1 and within 17% in phantom 2. Good boundary delineation was also demonstrated in the ex vivo experiment. The shear wave velocity estimates inside the ablated region were higher than mechanical testing estimates, but estimates in the untreated tissue were within 20% of mechanical measurements. A comparison of electrode vibration elastography and electrode displacement elastography showed the complementary information that they can provide. Electrode vibration elastography shows promise as an imaging modality that provides ablation boundary delineation and quantitative information during ablation procedures.

I. INTRODUCTION

Physicians widely use manual palpation in cancer detection because of known correlations between tissue stiffness and pathology [1]. For example, elastic modulus measurements of breast, prostate, and hepatic malignancies have been shown to be stiffer than the surrounding background tissue [2], [3]. Palpation can be subjective, however, and research has focused on developing more objective diagnostic techniques. Ultrasound is a good candidate because of its low cost, portability, and real-time imaging capabilities. Problems with ultrasound arise because cancers and ablated regions do not necessarily have different echogenic properties than the surrounding background tissue, as has been shown with partially ablated regions following radio-frequency (RF) ablation procedures [4], [5].

Ultrasound elastography, a method of imaging tissue elasticity, exploits the stiffness variations in tissue and provides similar information obtained by the physician during manual palpation. In this technique, pre-and post-deformation images are compared to generate a local displacement field. The gradient of the displacements produces a strain image [6], providing the physician with a more objective form of palpation. External quasistatic deformation has been applied to tissue using a transducer or plate as the compression device [7], [8]. This technique is effective for superficial organs such as the breast; however, problems arise with deep abdominal organs because of poor mechanical coupling, as well as lateral and out-of-plane motion [9].

A novel solution to this problem has been developed for abdominal RF and microwave (MW) ablation procedures, which are both minimally invasive techniques often used in place of surgical resection for isolated tumors less than 3 cm in diameter [10]. In this procedure, an RF electrode or MW antenna is inserted into the hepatic tumor under ultrasound guidance. Ionic agitation induces frictional heating in the vicinity of the electrode or antenna, causing coagulation necrosis and cell death in tissue heated above 42 °C [11]. Coincidentally, tissue heating also increases tissue stiffness. Bharat et al. developed a strain imaging technique for this procedure called electrode displacement elastography (EDE), where the ablation needle is cauterized to the ablated volume and used as a local deformation or displacement device [12]–[15]. Strain images generated with this technique provide excellent boundary delineation because of the “decorrelation halo” surrounding the stiffer inclusion [13]. However, a limitation of EDE and all strain imaging methods is that strain is not an inherent property of tissue. Quantitative information can be gained by estimating Young’s Modulus variations.

Recently, Young’s Modulus estimation techniques have been developed based on the relationship between the Young’s Modulus and shear wave velocity. In elastic materials, the shear modulus (µ) is related to the density (ρ) and the shear wave velocity (υ) of a material by

$$\mu =\rho {\upsilon }^2.$$ (1)

Under the assumption that the material is linear, isotropic, and incompressible, the Young’s Modulus (E) is related to the shear modulus by

$$E=3\mu .$$ (2)

Thus, Young’s Modulus is proportional to shear wave velocity. An obvious challenge to this work is generating shear waves in tissue.

External vibration has been one approach used. One dimensional (1-D) transient elastography, a technique incorporated in the FibroScan device (Paris, France), tracks a transient external vibration generated on the surface of the body into the liver, providing a shear wave velocity estimate along an ultrasound scan line (i.e., M-mode operation) [16]. FibroScan has shown that shear wave velocity correlates with the degree of fibrosis. Two-dimensional (2-D) transient elastography has also been investigated using external vibration and an ultrasound system capable of plane-wave insonification to provide the ultrafast frame rates necessary for shear wave tracking [17]. Magnetic resonance elastography (MRE) techniques have been developed that use continuous external vibration and have shown promise in detecting fibrosis [18], [19]. However, MRE may prove too costly for routine clinical exams. As with external quasistatic deformation techniques, transferring mechanical energy into deep tissue structures can be problematic. Propagating shear waves into the liver requires positioning of the vibration source between the ribs, which can be challenging. Excessive fat can also prevent shear waves from propagating into deep organs, making this technique impractical for obese patients.

Acoustic radiation force methods such as vibro-acoustography, supersonic shear imaging (SSI), and acoustic radiation force impulse (ARFI) imaging provide alternatives to external vibration. Vibro-acoustography has successfully imaged calcifications and fibroadenomas in the breast by detecting the mechanical response of tissue to oscillating radiation force [20], [21]. SSI uses radiation force to generate shear waves that are tracked at high frame rates using plane-wave insonification and has produced modulus maps in the liver in vivo [22], [23]. On systems with sequential scanning, ARFI has been developed [24]. Promising results have been obtained estimating the shear modulus in small regions of interest (ROIs) in human livers, and shear modulus has been coarsely mapped in a rat model of hepatic fibrosis [25], [26]. Spatially-modulated acoustic radiation force (SMURF) imaging, an offshoot of ARFI, applies an acoustic pulse of known spatial frequency and measures the resulting temporal frequency of the shear wave. This technique has been used to estimate the shear modulus in gelatin phantoms [27], [28]. Radiation force perturbation methods benefit from precise positioning of the perturbation: either by moving the transducer or changing the acoustic pulse location on the face of the transducer. However, acoustic pulses can generate shear wave amplitudes of only 20–30 µm in vivo, which can only be tracked a short distance laterally before they reach the noise floor. Patient safety must be considered for all radiation force techniques, as excessive acoustic energy can damage tissue [29].

Shear wave generation using internal mechanical vibration has also been investigated. Shear modulus estimates have been made with MRE while continuously vibrating an acupuncture needle in gelatin phantoms [30]. Needle vibration has also been used to estimate shear modulus with ultrasound, using Doppler to track motion in hydrogels [31]. These techniques benefit from the high amplitude shear waves generated within the material. High amplitude shear waves provide high signal-to-noise (SNR) displacement data; that is, high amplitude shear waves are less likely to be corrupted by motion artifacts present in vivo. Shear waves generated internally are also closer to the imaging ROI and propagate through fewer interfaces than shear waves generated externally [16].

We have developed an internal vibration method for RF and MW ablation applications. An extension of EDE, which we have coined electrode vibration elastography (EVE), applies transient perturbations to the ablation electrode, which are tracked across the face of the transducer. The time-to-peak (TTP) algorithm developed by Palmeri et al. is then used to reconstruct shear wave velocity [26]. We have previously demonstrated the feasibility of EVE using a 2-D finite element analysis (FEA) model of a stiff spherical inclusion bonded to an electrode in a soft background [32]. In the present study, we investigate EVE in FEA models incorporated into ultrasound simulations and compare EVE and EDE methods in tissue-mimicking (TM) phantoms and an ex vivo bovine liver ablation experiment. We show that high amplitude shear waves can be generated and tracked inside the RF ablation and in the surrounding background. EVE provides high SNR shear waves, good boundary delineation, and quantitative mechanical information. EVE, a marriage of transient mechanical vibration and ARFI tracking techniques, may hold promise for monitoring ablation procedures and detecting partially ablated regions post-procedure.

II. MATERIALS AND METHODS

A. Finite Element Analysis and Ultrasound Simulation

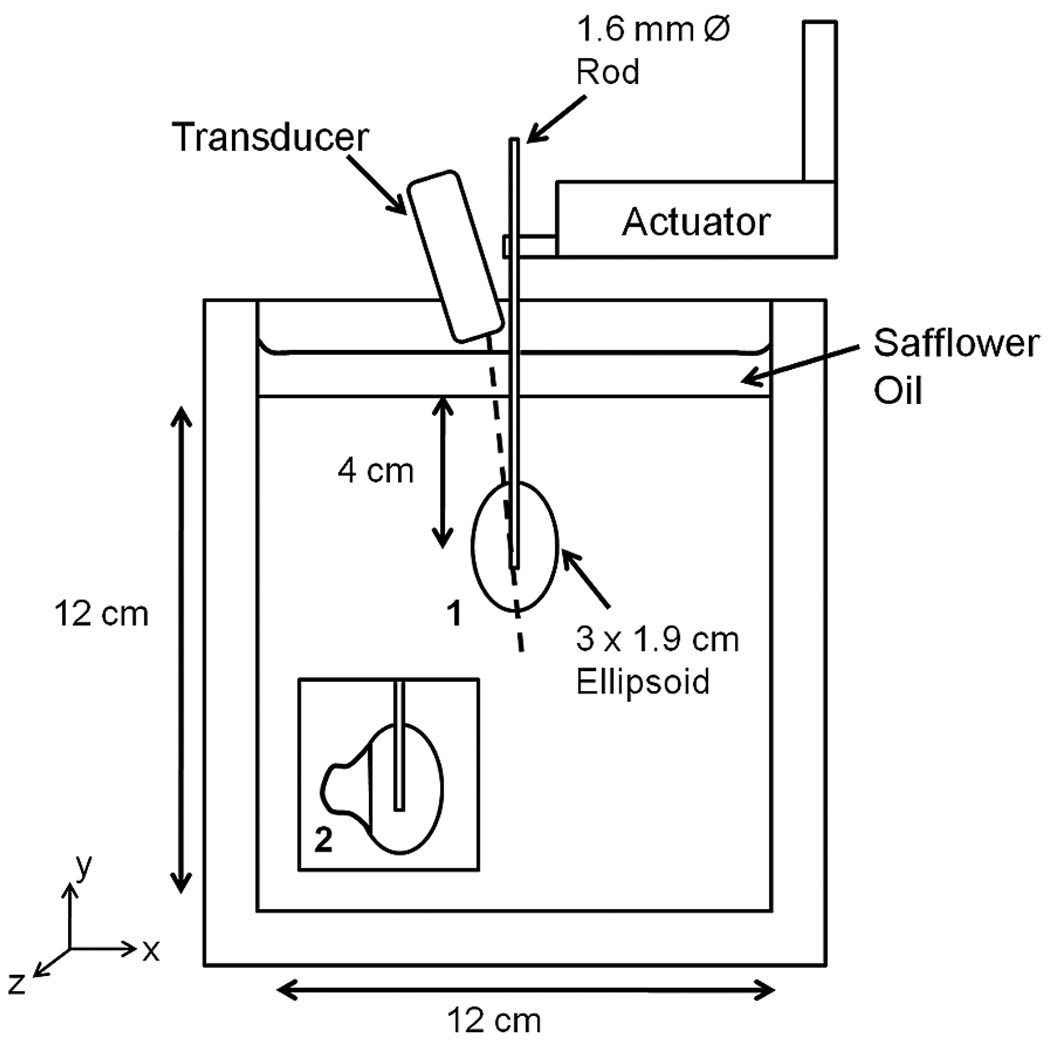
FEA models were used to test the feasibility of EVE. Two 2-D plane strain models based on actual phantoms (described in Section II-B) were created using ANSYS transient structural analysis (ANSYS Inc., Pittsburg, PA). Both phantoms modeled post-procedure RF ablations in a cirrhotic liver and are shown in Fig. 1. Phantom 1 contained a 3 × 1.9 cm stiff ellipsoidal mass in a softer background. Phantom 2 was similar but also contained a partially ablated region, as shown in the inset. Both FEA models were 12 × 12 cm with the electrode protruding 5.5 cm above the block. The bottom and sides of the FEA models were fixed in the x and y directions, while the top of the model was fixed only in the x direction. PLANE183 elements were used to model the tissue and electrode. The contact elements between the electrode and stiff ellipsoid were modeled as bonded. Some friction is present between the electrode and background. A friction coefficient of 0.15 is commonly used to model friction between lubricated metal plates [33]. The electrode above the inclusion was coated with petroleum jelly to minimize friction, but this lubricant wears off over time. Because of possible additional friction associated with the removal of lubricant from the electrode, the contact elements were modeled as frictional, with a friction coefficient of 0.2. A 3.5-cm sphere of influence mesh provided fine meshing in the ellipsoid and surrounding background and coarser meshing near the model boundaries. Simulations run with different mesh densities confirmed that no discretization artifacts were present. The material properties of the electrode were modeled as that for gold. The Young’s Modulus and material damping of the background, stiff ellipsoid, and partially ablated region were determined by dynamic compression testing of phantom material samples as described below. All phantom materials were considered nearly incompressible, i.e., Poisson’s ratio (υ) was 0.495.

Fig. 1.

Schematic diagram of TM phantom and testing setup. Phantom 1 contained a stiff ellipsoidal mass in a softer background, which was bonded to a stainless steel rod. Phantom 2 contained a partially ablation region, as shown in the inset. The FEA models of both phantoms were created using phantom dimensions and material properties that were estimated with dynamic compression tests. Note: Diagram is not to scale.

The FEA simulations modeled the EVE approach used in the TM phantom experiments. A Gaussian-shaped 100 µ amplitude transient perturbation 10 ms in duration (roughly half of a 50 Hz sine wave) was applied to the top edge of the electrode, similar to the EVE perturbation shown in Fig. 2. Simulations were run an additional 20 ms with no electrode motion to allow propagation of the shear wave through the stiff ellipsoid and into the surrounding background. 150 time points were simulated for the 30 ms simulation duration, for a sampling rate of 5000 Hz. Following simulation, the y displacements for each time point were exported from ANSYS. The TTP tracking algorithm [26] was implemented in an ROI surrounding the stiff ellipsoid and surrounding background using Matlab (The Math-Works, Natick, MA) to reconstruct the shear wave velocity, as described in Section II-E.

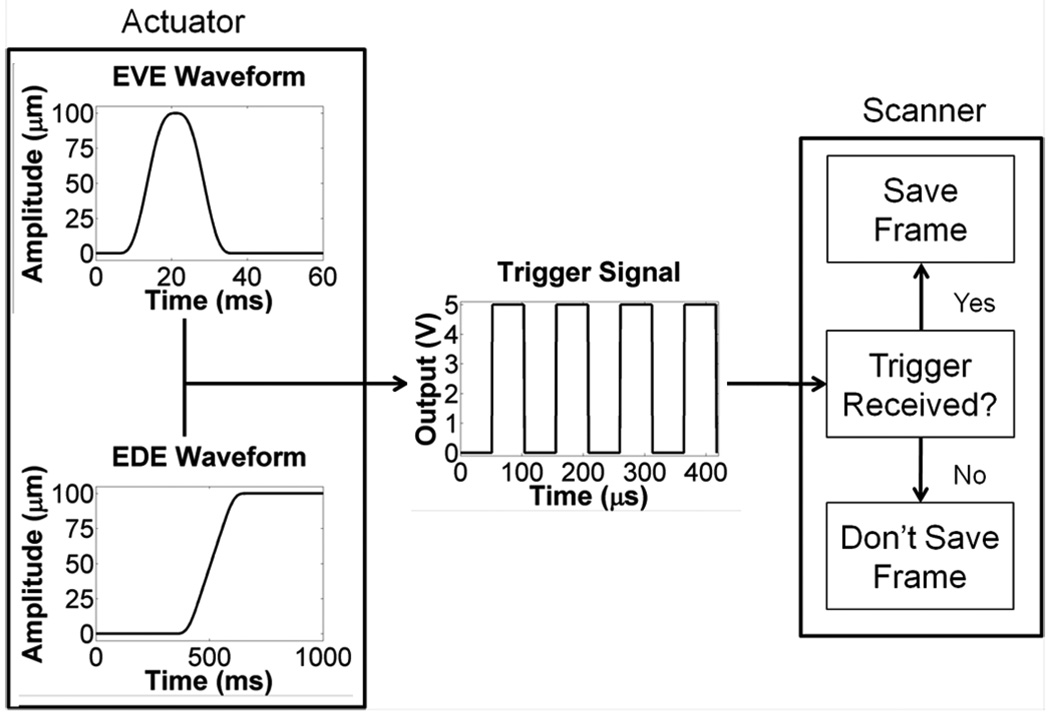
Fig. 2.

Data acquisition for EVE and EDE. For EVE acquisition, the piezoelectric actuator output a 100 µm, Gaussian-shaped perturbation, with sequences of zero displacement before and after the perturbation. The EDE waveform consisted of a 100 µm step displacement. For both waveforms, a trigger signal was output from the actuator controller approximately every 52 µs. The ultrasound scanner saves RF data frames acquired during a trigger reception.

The impact of ultrasonic speckle on our technique was also evaluated using a frequency domain based ultrasound simulation program [34]. Two sets of simulated radiofrequency echo-signals were generated from the FEA displacement fields. A 3.8 × 6.5 × 1.0 cm pre-displacement phantom was created with 10 scatterers/mm³. The scatterers were randomly distributed and included frequency-dependent backscatter [34]. The FEA displacements from phantom 1 or phantom 2 along the x and y directions were used to move the scatterers in the pre-displacement phantom for all 150 time points. Simulated radiofrequency echo-signals were generated from these deformed phantoms using the following parameters: 6.5 cm depth, 3.3 cm focus, 1490 m/s speed of sound, 5 MHz center frequency, 0.3 mm beam spacing, 2.0 F-number, 50% band-width, and 1 transmit cycle. Time sequences of displacements were estimated using 1-D cross-correlation implemented in Matlab, and the TTP algorithm was used to reconstruct the shear wave velocity (see Section II-E).

B. Tissue Mimicking Phantoms

Two TM phantoms were constructed for this study consisting of dispersions of microscopic safflower oil droplets in a gelatin matrix [35], [36]. The Young’s Modulus of these materials depends on the volume percent which is oil. The elastic properties of the ablations in both phantoms reflected a fully formed ablation. Phantom 1 contained a stiff ellipsoid (54% oil) simulating an RF ablation, which was bonded to a 1.6 mm stainless steel diameter rod simulating an RF electrode, shown in Fig. 1. This assembly was encased in a 12 × 12 × 12 cm block of softer background (80% oil) simulating cirrhotic liver tissue. The center of the ellipsoid was 4 cm from the top of the background cube and centered in the lateral and elevational dimensions. Differences in scatterer density between the ellipsoid and the background provided echogenic contrast on B-mode images. A layer of safflower oil on top of the phantom prevented desiccation. Phantom 2 contained a simulated partially ablated region. One side of the stiff ellipsoid was absent, and an irregularly shaped TM material simulating a tumor (70% oil) was bonded at this location. The speed of sound in all materials was approximately 1490 m/s, as measured using the substitution method.

The complex Young’s Modulus was measured at 1 Hz using a cylindrical sample of each TM phantom material; the diameter and thickness were 2.6 cm and 1.0 cm, respectively. Measurements were made on an Enduratec ELF 3200 (Bose Corporation; Eden Prairie, MN). Details of the measurement procedure are given in Madsen et al. [37]. Ten dynamic compression tests from 1% to 3% compression with a 1 Hz frequency were performed on each sample to determine the Young’s Storage Modulus (E’) and Young’s Loss Modulus (E”). Because the ratio E″/E′ was less than 0.10 for all materials, E’ was used as an approximation of the Young’s Modulus (E). In phantom 1, the Young’s Modulus was 7.75±0.18 kPa in the background and 27.95±1.30 kPa in the stiff ellipsoid, and in phantom 2, the Young’s Modulus was 8.66±0.42 kPa in the background, 15.23±1.51 kPa in the partially ablated region, 27.95±1.30 kPa and in the stiff ellipsoid. The shear wave velocity in these materials was estimated using (1) and (2).

C. ex vivo Bovine Liver

To investigate EVE in tissue, an ablation was formed in a piece of fresh bovine liver with a Valleylab Cool-tip RF ablation system (Valleylab, CO), using a 1.5-mm-diameter (17 gauge) electrode with a 3 cm active region. The generator was run for three minutes using the built-in impedance control algorithm. After the procedure, the electrode was cauterized to the ablation, the liver was encased in gelatin, and both EVE and EDE were performed. Fiducial markers were placed at both edges of the transducer directed into the imaging plane. Then, the transducer was removed, the sample was sliced, and the imaging plane was photographed. Approximately 1 cm³ of untreated liver was removed from either side of the ablation and from the center of the ablation on one side of the imaging plane. The untreated tissue was dynamically tested three times from 1% to 3% compression using the ELF system, while the ablation was only tested twice due to the instability of the ablated tissue. The Young’s Modulus was 103.6±24.8 kPa in the ablation, 1.37±0.09 kPa to the left of the ablation zone, and 1.90±0.12 kPa to the right of the ablation zone. The shear wave velocity was estimated in the tissue using (1) and (2).

D. Electrode Vibration Elastography and Electrode Displacement Elastography Techniques

Shear wave generation and tracking requires a vibration device and ultrasound scanner. A piezoelectric actuator (Physik Instrumente (PI) GmbH & Co. KG, Karlsruhe, DE) was attached to the phantom rod or RF electrode and transiently vibrated with a 100 µm amplitude, 10 ms duration perturbation, generating a shear wave that traveled through the ellipsoid or ablation and into the surrounding background. The shear wave was tracked using an Ultrasonix SonixTOUCH scanner and L14-5/38 transducer (Ultrasonix Medical Corporation; Richmond, BC, Canada). Both devices were controlled as shown in Fig. 2, using a custom Graphical User Interface (GUI) built using QT (Nokia Corporation, Espoo, Finland), PI libraries, and the Texo Software Development Kit (SDK) available from Ultrasonix.

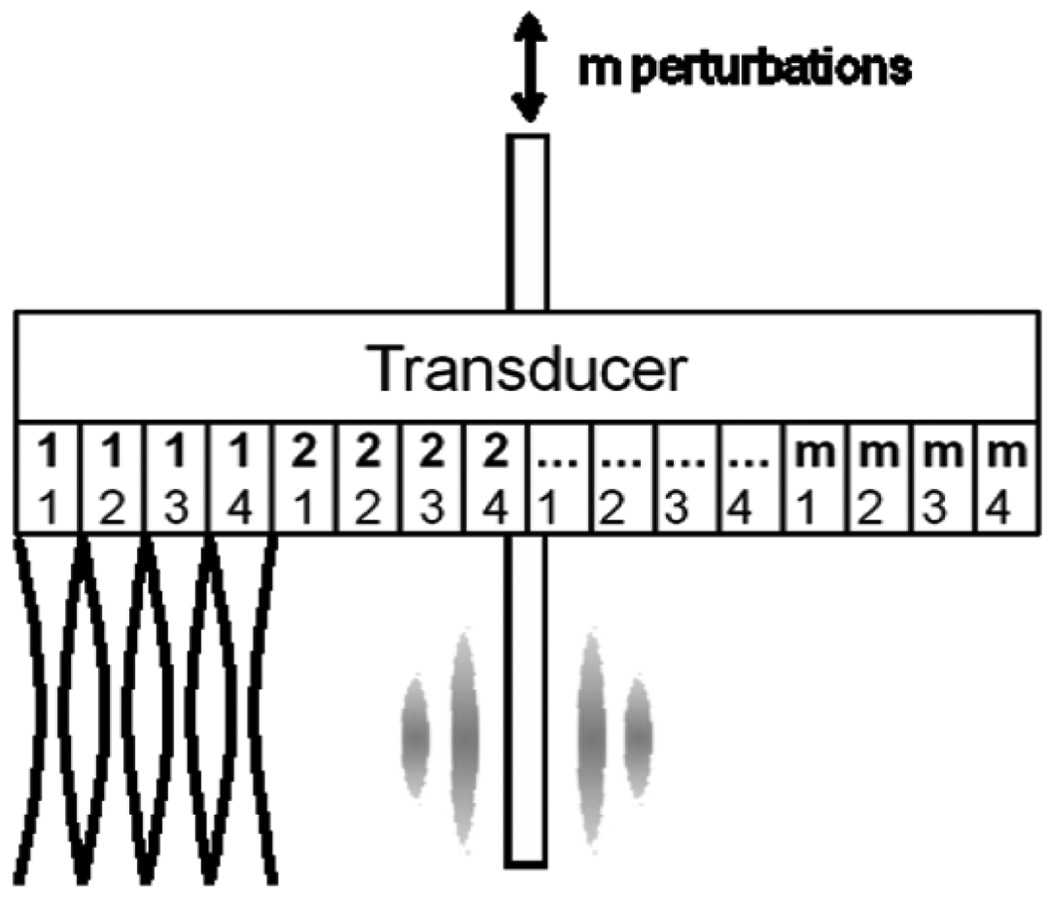
High frame rates are required to track the shear wave propagation. Because of the sequential scanning employed in most clinical scanners, a custom beam sequence was implemented using the Texo SDK and is shown in Fig. 3. A single A-line at a depth of 6.5 cm with an assumed speed of sound of 1490 m/s has an acquisition rate of 10 344 Hz. Thus, a frame of n lines scanned sequentially will be acquired at a rate of 10 344/n Hz. In phantom experiments, a frame composed of four locations tracked shear waves generated by one needle perturbation at 2586 Hz. Following the acquisition, the actuator was used to perturb the rod again, and the adjacent four locations were tracked. This process was repeated 30 times across the face of the transducer. In the ex vivo experiment, five tracking locations per perturbation were used, and the process was repeated 24 times.

Fig. 3.

Schematic diagram of an ultrasound scanning sequence for phantom experiments. Radiofrequency data were acquired sequentially at four tracking locations for each perturbation of the steel rod. The upper, bold numbers indicate locations scanned for each perturbation, and the lower numbers indicate scanning sequence. Five tracking locations per perturbation were used for the ex vivo experiment.

The actuator and scanner were synchronized during data collection. Frame acquisition occurred only on reception of an input trigger. A trigger was output by the actuator controller approximately every 52 µs during actuator motion, as shown in Fig. 2. Frames were acquired by the scanner approximately every 386 µs. Additional triggers received during a frame acquisition were ignored by the system. After each tracking sequence, data were saved to the scanner hard disk. Following all EVE tracking sequences, 128-line radiofrequency data frames covering the transducer’s field of view were acquired, which were used to generate traditional B-mode images. For phantom experiments, EVE and EDE data were collected with the following system settings: 6.5 cm depth, 5.0 cm focus, 1490 m/s speed of sound, 4.44 MHz transmit frequency, 2.6 transmit F-number, 33% −6 dB bandwidth, and 1 transmit cycle. Ten data sets were acquired for each of three transducer positions for both phantoms: the transducer centered over ablation, the transducer offset 1 cm to the right, and the transducer offset 1 cm to the left. For the ex vivo bovine liver, the following settings were used: 7.0 cm depth, 6.0 cm focus, 1540 m/s speed of sound, 4.44 MHz transmit frequency, 3.1 transmit F-number, 33% −6 dB bandwidth, and 1 transmit cycle. Three data sets were acquired for each of the three transducer positions.

Additionally, EDE was performed as a comparison to EVE for both the phantom and ex vivo experiments. A 100 µm step waveform was defined in the actuator controller and 128-line radiofrequency data frames were acquired during actuator motion, as in Fig. 2. Following acquisition of EDE data, RF data in the absence of deformation were acquired for B-mode images. As with EVE, ten data sets were acquired for the phantom experiments, and three data sets were acquired for the ex vivo experiment with the transducer centered on the ablation, offset 1 cm to the right, and offset 1 cm to the left.

E. Shear Wave Velocity, Strain, and Area Estimation

EVE displacements for the simulated and scanner radiofrequency data were estimated using 1-D cross-correlation because of the partial frame acquisitions method employed in the phantom and ex vivo experiments. Simulated radiofrequency data were in 128-line frames. Experimental radiofrequency data from the ultrasound scanner were in four- or five-line frames for each perturbation, which were parsed into one-line time sequences (i.e., M-mode) for each tracking location. Incremental displacements were calculated on adjacent frames or lines using a 2 mm window with 75% overlap. Summing estimates of a given pair with all preceding estimates for all time points provided displacement time sequences.

The TTP algorithm was used to calculate the shear wave velocity [26]. Displacement time sequences were upsampled by a factor of ten, and the time at which maximum displacement of the shear wave occurred, or TTP, was estimated for each pixel in the displacement plane or line time sequences. For scanner data, TTP lines from each tracking location were concatenated to form the TTP image. A 2 × 2 median filter was applied to TTP images, followed by a spline fit for each row to smooth the data laterally. The shear wave velocity was then estimated using a lateral five-point least-squares fit.

Strain images were created from the EDE data sets. Displacements were estimated from pre-and post-compression frames using 1-D cross correlation with a 2 mm window and 75% overlap, as with EVE. A 5 × 5 median filter and 3 × 3 moving average were used to smooth the displacement field. A five point axial least-squares fit was applied to estimate strain.

Shear wave velocity was estimated using 4 × 10 mm ROIs for FEA, ultrasound simulation, phantom, and ex vivo shear wave velocity images. In phantom 1, ROIs were in the left and right side of the ablation and the background. Background ROIs were 10 mm from the edge of the ablation in FEA and simulated radiofrequency data. The background ROIs were 3 mm from the ablation boundary in the phantom images because of the limited field of view of the transducer. In phantom 2, the shear wave velocity estimates used the same ROIs but also included an ROI in the partially ablated region. In the ex vivo experiment, ROIs were similar to phantom 1 ROIs. Young’s Modulus was estimated using (1) and (2). Strain was estimated in all images using the same ROIs as shear wave velocity.

The ablation area was also estimated for phantom and ex vivo experiments. The area of the stiff ellipsoid in phantom 1 and stiff ellipsoid/partially ablated region in phantom 2 were estimated from the B-mode, shear wave velocity, and strain images. Echogenic contrast was used to delineate the ellipsoid in the B-mode images. Velocity contrast was used in shear wave velocity images, recognizing that artifacts may be present above and below the ablated region. The decorrelation halo demarcated the ellipsoid boundary in strain images [13]. In ex vivo experiments, the ablation was delineated from the background from the shear wave velocity and strain images. No boundary was detectable on the B-mode images. Additionally, the ablation area from the gross pathology photograph was determined by delineating the white, necrotic tissue from the untreated tissue [38], [39].

F. Statistics

For phantom and ex vivo experiments, the significance of differences in shear wave velocity between imaging and mechanical testing estimates were assessed using a one-way analysis of variance (ANOVA; p < 0.001). Tukey multiple comparisons were then used to compare imaging ROIs to mechanical testing results (†, p < 0.05; ‡, p < 0.001). For phantom experiments only, significant differences between the shear wave velocity or strain and B-mode area estimates were also assessed (*, p < 0.05;**, p < 0.001). All data are presented as mean ± standard deviation.

III. RESULTS

A. Finite Element Analysis and Ultrasound Simulation

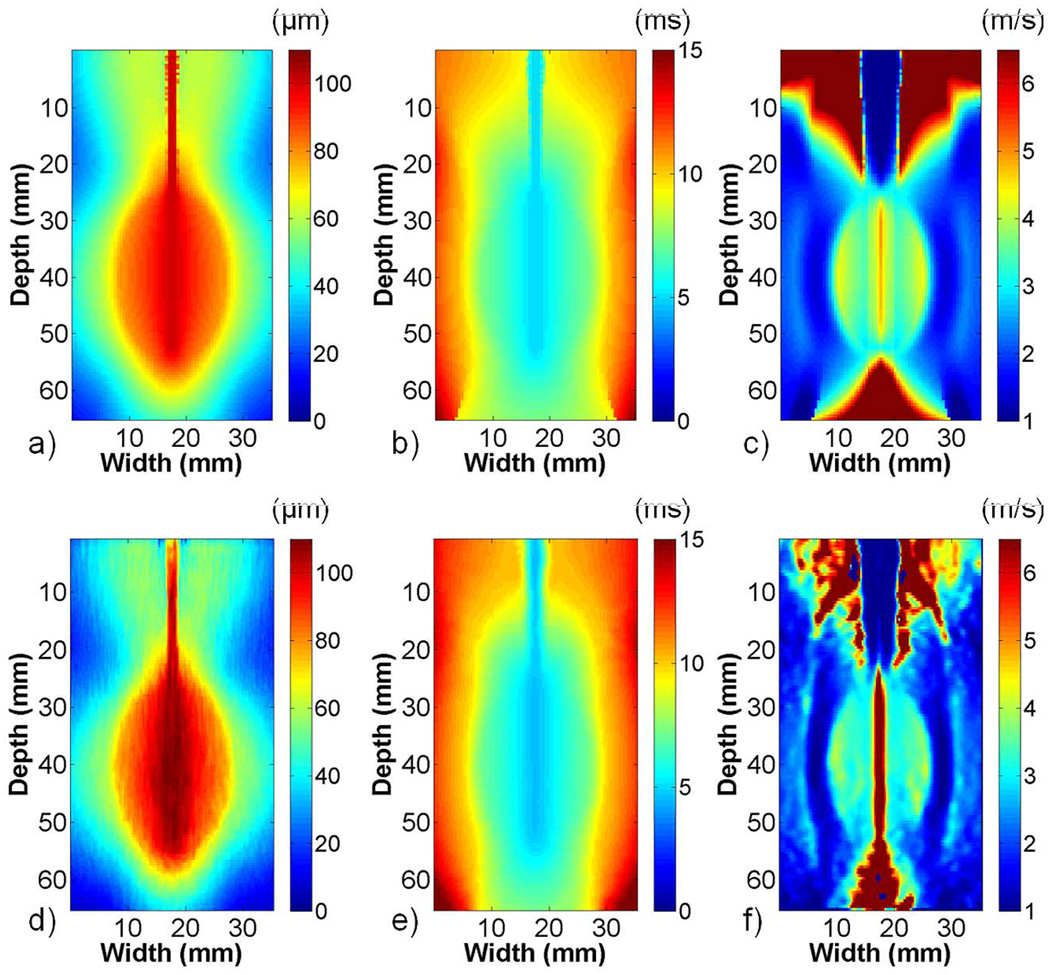
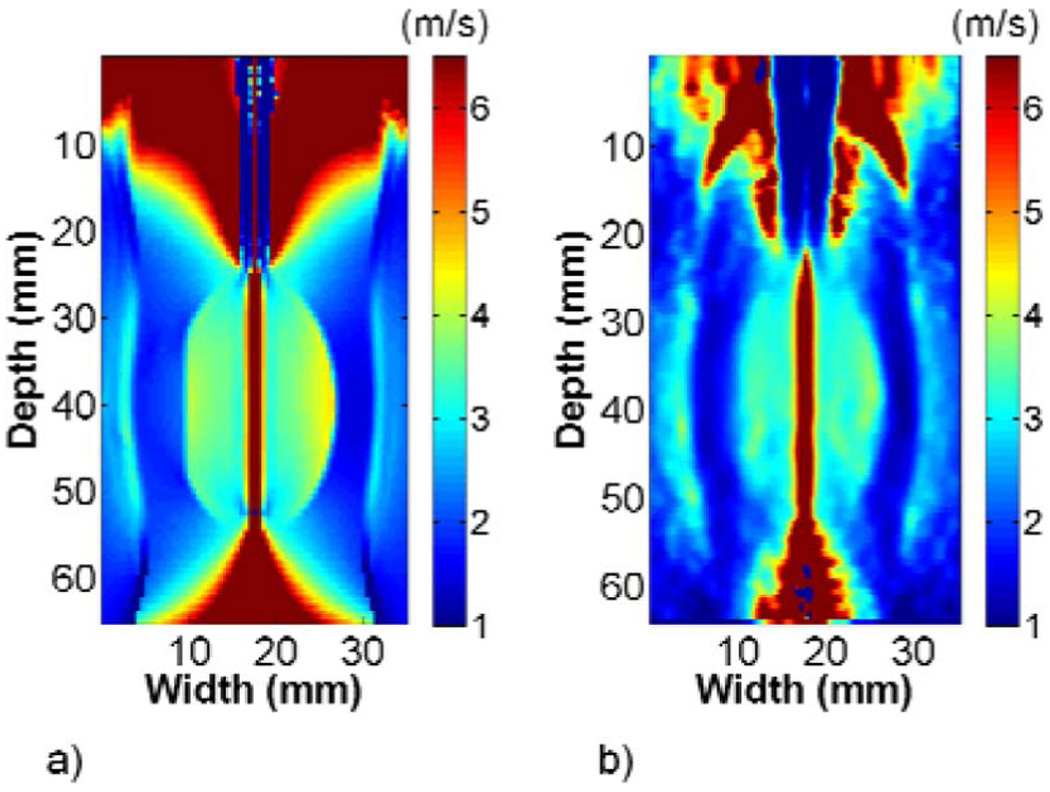
The FEA and ultrasound simulation images in phantom 1 showed good agreement. Fig. 4 shows the maximum displacement, TTP, and shear wave velocity images created using FEA (a)–(c) or 1-D cross-correlation (d)–(f) displacements. The maximum displacement at the center of the images approached the 100 µm electrode perturbation defined in the FEA model, and it decayed in the direction laterally away from the electrode. TTP increased with increasing distance from the electrode. The shear wave velocity image in Fig. 4(c) contained high shear wave velocity artifacts inside the stiff ellipsoid at the interface with the softer background, although not as prominently in the ultrasound simulation image in Fig. 4(f). Shear wave velocity artifacts were also present approximately 6 mm into the background on either side of the ellipsoid, as well as above and below the bonding between the electrode and ellipsoid in both FEA and ultrasound simulation images. The shear wave velocity and Young’s Modulus estimates in Table I from ROIs inside the ellipsoid and the surrounding background were higher than the values expected, given the Young’s Modulus values defined in the FEA model. The shear wave velocity and Young’s Modulus estimates from simulated radiofrequency data were closer to the anticipated values.

Fig. 4.

FEA and ultrasound simulation of EVE for phantom 1. Images present (a) and (d) maximum displacement, (b) and (e) TTP, and (c) and (f) shear wave velocity reconstructions for FEA (top) and ultrasound simulation (bottom). The images obtained using 1-D cross correlation on simulated radiofrequency data were similar to images obtained using FEA displacements. The shear wave velocity images show clear delineation between the stiff ellipsoid and surrounding softer background.

TABLE I.

Comparison of Imaging and Mechanical Testing Estimates

	ABLATION ONLY (PHANTOM 1)				PARTIAL ABLATION (PHANTOM 2)
	Shear Wave Velocity (m/s)				Shear Wave Velocity (m/s)
Image ROIs	B - L	B - R	A - L	A - R	B - L	B - R	A - L	A - R	PAR
FEA	1.86	1.86	3.69	3.69	1.94	1.97	3.58	3.60	2.09
US Sim	1.65	1.68	3.29	3.24	1.72	1.71	3.29	3.32	1.78
Phantom	1.53 ± 0.08†	1.60 ± 0.08	3.26 ± 0.16†	3.05 ± 0.19	1.64 ± 0.10	1.47 ± 0.08‡	2.95 ± 0.15	3.59 ± 0.23‡	2.06 ± 0.07†
Ex vivo	0.81 ± 0.03†	0.76 ± 0.01	13.49 ± 0.91†	23.78 ± 4.71†	--	--	--	--	--
ELF Testing	B		A		B		A		PAR
Phantom	1.61 ± 0.02		3.05 ± 0.07		1.70 ± 0.04		3.05 ± 0.07		2.25 ± 0.11
Ex vivo	0.68 ± 0.02	0.79 ± 0.03	5.9 ± 0.70		--		--		--
	Young' Modulus (kPa)				Young' Modulus (kPa)
Image ROIs	B - L	B - R	A - L	A - R	B - L	B - R	A - L	A - R	PAR
FEA	10.38	10.38	41.52	41.52	15.46	12.24	38.45	38.88	11.76
US Sim	12.48	12.00	33.67	32.67	13.23	12.85	32.47	33.07	7.68
Phantom	7.03 ± 0.75	8.06 ± 0.50	31.87 ± 3.07	28.06 ± 3.52	8.09 ± 1.00	6.52 ± 0.73	26.11 ± 2.67	38.84 ± 4.98	12.78 ± 0.81
Ex vivo	1.99 ± 0.17	1.71 ± 0.04	0.55e3 ± 0.07e3	1.74e3 ± 0.66e3	--	--	--	--	--
ELF Testing	B		A		B		A		PAR
Phantom	7.75 ± 0.18		27.95 ± 1.30		8.66 ± 0.42		27.95 ± 1.30		15.23 ± 1.51
Ex vivo	1.37 ± 0.09	1.90 ± 0.12	103.6 ± 24.8		--		--		--
	Strain (%)				Strain (%)
Image ROIs	B - L	B - R	A - L	A - R	B - L	B - R	A - L	A - R	PAR
Phantom	0.28 ± 0.03	0.25 ± 0.01	0.55 ± 0.01	0.56 ± 0.02	0.22 ± 0.03	0.32 ± 0.03	0.75 ± 0.01	0.95 ± 0.02	0.48 ± 0.02
Ex vivo	1.51 ± 0.08	0.91 ± 0.07	1.30 ± 0.09	3.11 ± 0.19	--	--	--	--	--

^†(P < 0.05) and

^‡(P < 0.001) indicate significant differences in the shear wave velocity when comparing imaging to mechanical testing estimates.

Abbreviations are as follows: B = Backgrounds, A = Ablation (Ellipsoid), PAR = Partially Ablated Region, L = Left, R = Right. Ex vivo results are presented under "Ablation Only" side of Table 1.

The shear wave velocity reconstructions for FEA and ultrasound simulation from phantom 2 are shown in Fig. 5. The shear wave velocity artifact on the left side of the stiff ellipsoid contacting the partially ablated region was less pronounced than the artifact on the right side of the ellipsoid contacting the background. High shear wave velocity artifacts similar to those seen in phantom 1 were present above and below the bonding between the electrode and ellipsoid. The shear wave velocity in the partially ablated region was higher than that of the background to the right of the ellipsoid. Shear wave velocity estimates in the partially ablated region, listed in Table I, were higher than the background but lower than the Young’s Modulus defined in ANSYS for both FEA and ultrasound simulation. As with phantom 1, the ultrasound simulation shear wave velocity estimates were lower than FEA estimates.

Fig. 5.

Shear wave velocity reconstructions from phantom 2 using (a) FEA and (b) ultrasound simulation. Images show clear delineation between the stiff ellipsoid and softer surrounding background. The shear wave velocity was higher in the partially ablated region on the left side of the ellipsoid than in the background right of the ellipsoid, indicating a stiffer material.

B. Tissue Mimicking Phantoms

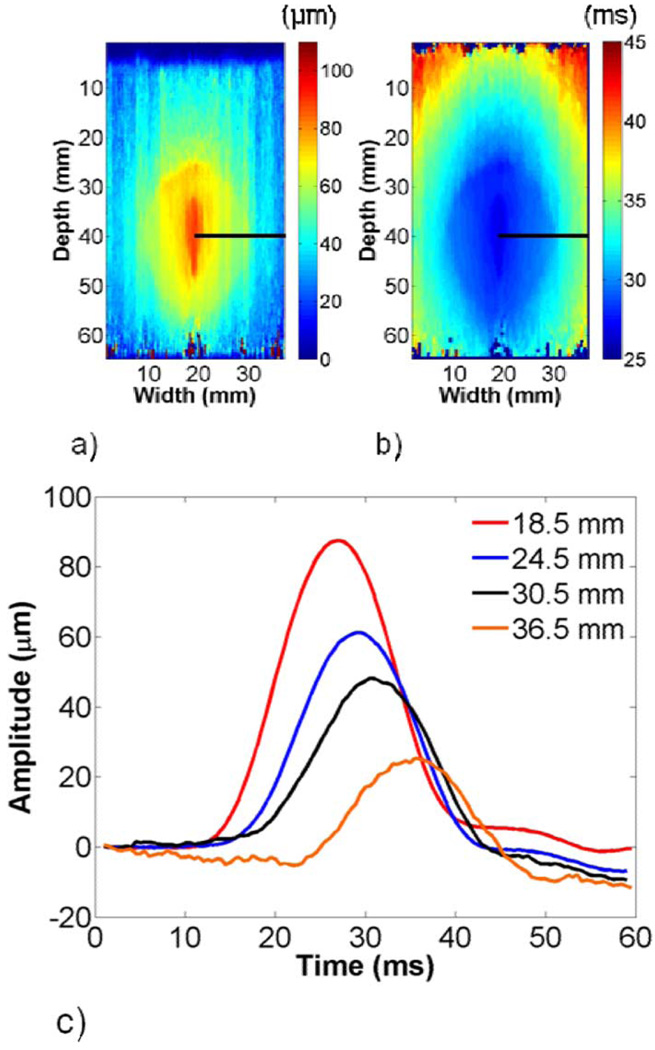
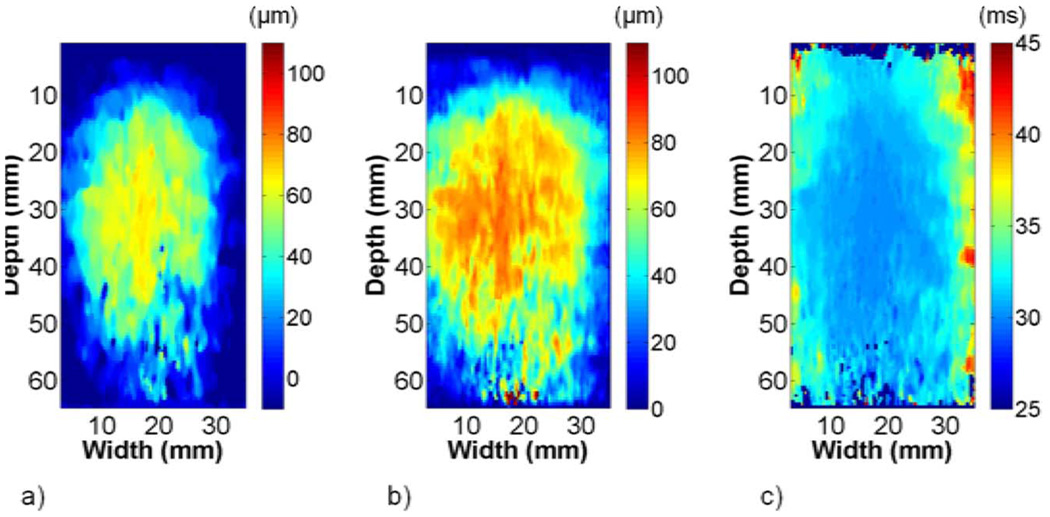
The maximum displacement and TTP images from phantom 1 were similar to images obtained from the FEA model data, as shown in Fig. 6. Shear wave propagation at different lateral offsets is illustrated in Fig. 6(c). The shear wave amplitude decayed to roughly 30 µm as the wave approached the edge of the transducer, which was slightly more than that obtained with the FEA model. TTP increased more slowly in the background than in the ellipsoid, as expected.

Fig. 6.

Representative (a) maximum displacement and (b) TTP images from phantom 1. The shear wave amplitude decays and TTP increases with increasing lateral offset from the perturbation, as shown in (c).

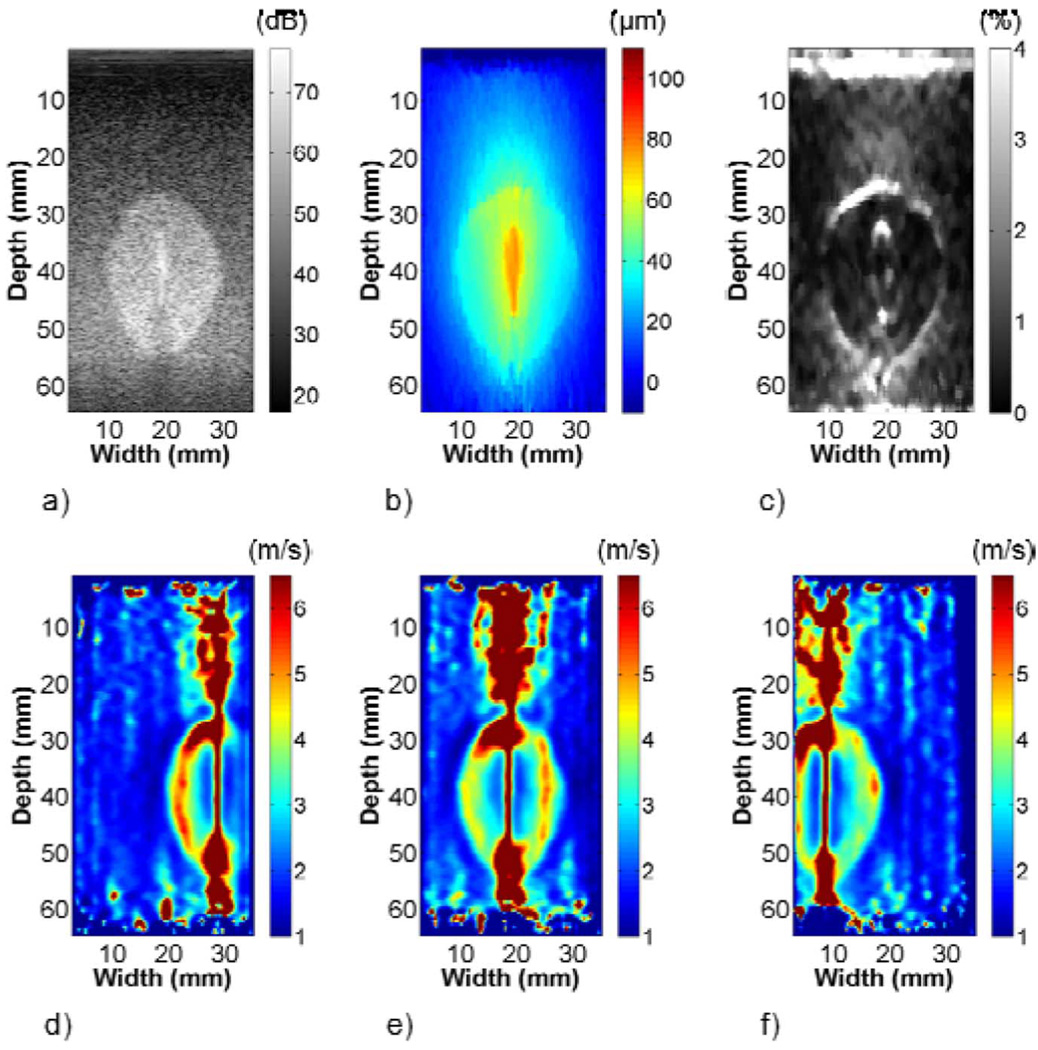
Fig. 7 highlights differences in ellipsoid representation on the B-mode, strain, and shear wave velocity images of phantom 1. Increased scatterer density in the ellipsoid clearly differentiated it from the background with traditional B-mode imaging. The EDE displacement image showed that displacement estimates in the vicinity of the electrode approached the 100 µm step and decayed with increasing lateral distance from the electrode. The decorrelation halo delineated the ellipsoid from the surrounding background and was most prominent on the top and bottom of the ellipsoid. Strain estimates inside the ellipsoid were approximately 0.55% compared to 0.25% in the background, as listed in Table I. The shear wave velocity images in Fig. 7(d)–(f) showed good boundary demarcation. Shear wave velocity artifacts were similar to FEA models, with regions of high shear wave velocity at the ellipsoid-background interface and above and below the ellipsoid-rod bonding. In Table I, the shear wave velocity estimate on the left side of the ellipsoid was significantly higher than mechanical testing results. Conversely, the left background estimate was significantly lower. All other shear wave velocity estimates were not statistically different.

Fig. 7.

Representative (a) B-mode, (b) EDE displacement, (c) strain, and (d)–(f) shear wave velocity images (left, center, and right of ellipsoid) from phantom 1. The stiff ellipsoid is visible on the B-mode image because of the increased scatterer density in the ellipsoid material. The boundary between the stiff ellipsoid and soft background in the strain image is demarcated by the characteristic decorrelation halo. Differences in the shear wave velocity clearly differentiate the stiff ellipsoid from the softer background in (d)–(f).

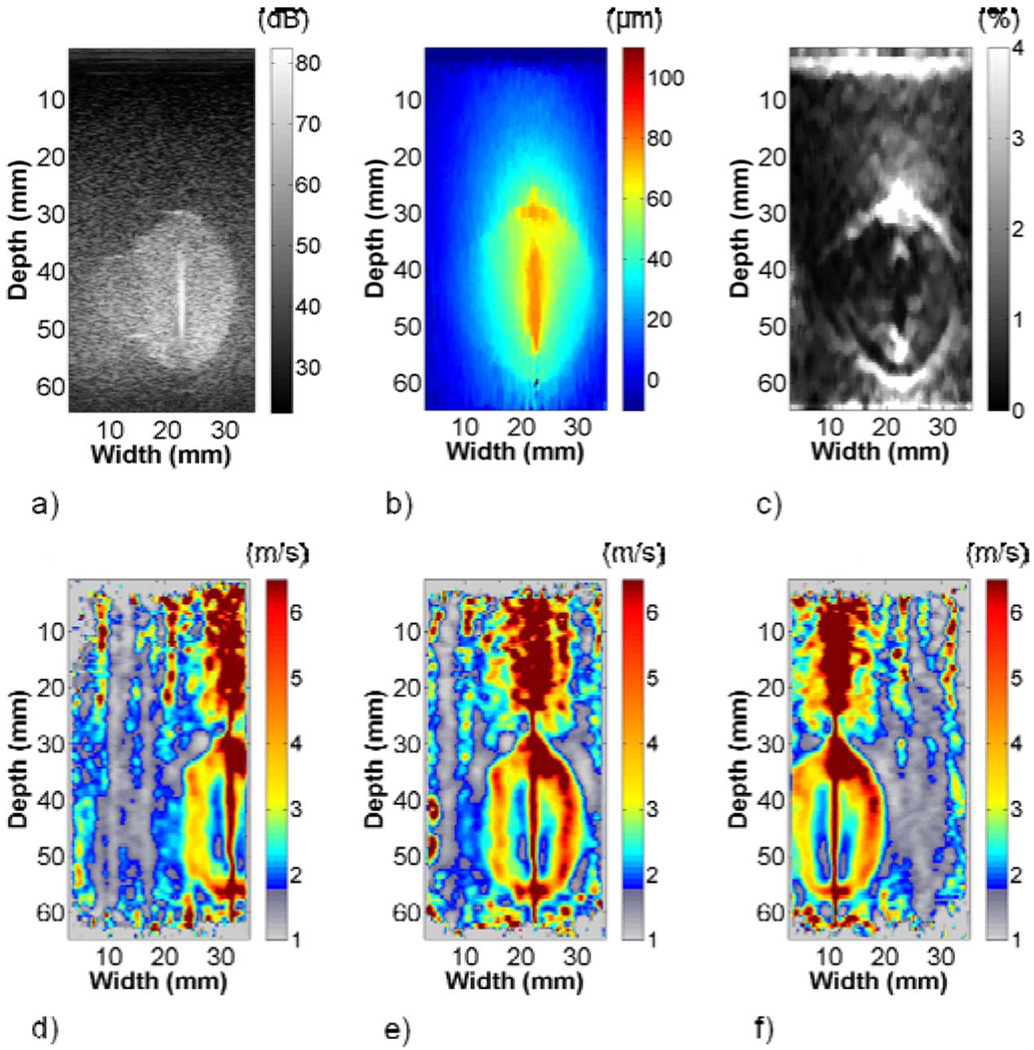
A comparison of B-mode, strain, and shear wave velocity images in phantom 2 is presented in Fig. 8. The ellipsoid, partially ablated region, and background were differentiable in the B-mode image. The step displacement produced a strain image with a decorrelation halo, which was more pronounced around the ellipsoid than around the partially ablated region. Strain estimates were 0.48% in the partially ablated region, 0.75% and 0.95% in the left and right sides of the ellipsoid, and 0.22% and 0.32% left and right of the ellipsoid in the background. Because the shear wave velocity contrast between the partially ablated region and background was only 1.3, the colormap was modified to display shear wave velocities less than or equal to the background velocity in grayscale to highlight differences among the partially ablated region, ellipsoid, and background. The images differentiate all three regions. A shear wave velocity artifact was present above the bonded region but not below. The shear wave velocity estimates in Table I were significantly lower in the partially ablated region, significantly higher in the right half of the ellipsoid, and significantly lower in the background right of the ellipsoid when compared to mechanical testing estimates.

Fig. 8.

Representative (a) B-mode, (b) EDE displacement, (c) strain, and (d)–(f) shear wave velocity images (left, center, and right of ellipsoid) from phantom 2. The B-mode image clearly shows the simulated ablated region and partially ablated region. The decorrelation halo in the strain image delineates the simulated ablated region and partially ablated region from the softer background. The partially ablated region appears stiffer than the ablated region because of the lateral decay of the focused compression provided by the steel rod. The shear wave velocity images show the partially ablated region to be stiffer than the surrounding background but softer than the fully ablated region. A modified colormap was used because of the low modulus contrast between the partially ablated region and background.

Table II lists area estimates for phantoms 1 and 2. The simulated ablations were manually segmented from the background. In phantom 1, the ellipsoid was delineated by tracing a boundary around the high shear wave velocity gradient bordering the relatively homogenous background. Delineation on the left, right, and top of the ellipsoid was fairly straightforward. Separating the ellipsoid from the artifact on the bottom was more subjective and was based on observer discretion. The ellipsoid border on the strain image was traced to lie inside the decorrelation halo [15]. There were no significant differences in area estimates for areas delineated from the shear wave velocity or strain images when compared to B-mode images. In phantom 2, the ellipsoid and partially ablated region were delineated from the background using the modified colormap to highlight these two regions. Boundaries were evident on the top, bottom, and right sides of the ablation but more subjective on the left side near the partially ablated region, particularly below it. The decorrelation halo provided boundary delineation on the strain images. Shear wave velocity and strain area estimates were significantly higher than the area estimates obtained from B-mode images.

TABLE II.

Comparison of Area Estimates

	Area (mm2)
Image Type	Phantom 1	Phantom 2	Ex vivo
Bmode	441.8 ± 7.6	489.2 ± 4.2	--
Gross Pathology	--	--	934.4
SWV	438.2 ± 7.0	501.1 ± 5.9**	928.4 ± 15.6
Strain	446.3 ± 5.3	512.3 ± 7.3**	849.0 ± 7.7

^*(p < 0.05) and

^**(p < 0.001) indicate significant differences in the area estimates from the shear wave velocity or strain images when compared to B-mode images (phantoms only).

Abbreviations are as follows: SWV = Shear Wave Velocity.

C. ex vivo Bovine Liver

The EDE displacement, EVE maximum displacement, and TTP images for the ex vivo RF ablation in bovine liver tissue are shown in Fig. 9. The EDE displacement estimates were approximately 70 µm near the electrode, which was lower than the 100 µm perturbation. The displacements inside the ablated region were fairly uniform compared to those in phantom 1. The EVE maximum displacements were closer to 100 µm and were relatively uniform throughout the ablation. TTP increased rapidly inside and more slowly outside the ablation.

Fig. 9.

(a) EDE displacement, (b) EVE maximum displacement, and (c) TTP from an ablation formed in bovine liver tissue. Maximum displacement is relatively uniform and TTP increases rapidly inside the ablation.

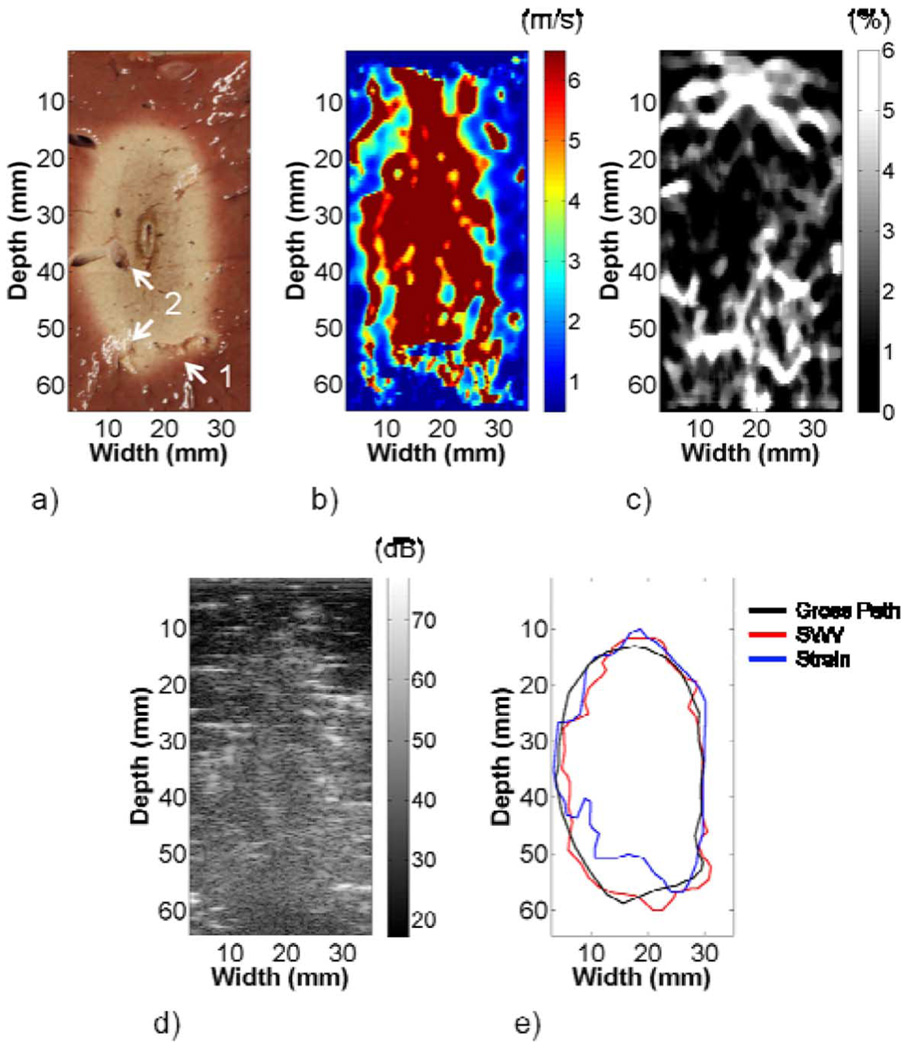
The gross pathology, shear wave velocity, strain, and B-mode images of the ablation are compared in Fig. 10. The white, necrotic tissue provided clear boundary delineation on the gross pathology image. Blood vessels present in the ablation are highlighted on the image. The ablation shape in the shear wave velocity image was similar to the gross pathology image, aside from a possible shear wave velocity artifact above the ablation. Artifacts were also present within the ablation. The strain image provided boundary demarcation where large axial gradients were present. No boundaries were discernable on the B-mode image. Table I shows the shear wave velocity estimates in the ablation and in the background left of the ablation were significantly higher than mechanical testing results. Strain values of 1.30% and 3.11% were estimated in the left and right halves of the ablation, and 1.51% and 0.91% in the background left and right of the ablation, respectively.

Fig. 10.

(a) Gross pathology, (b) shear wave velocity, and (c) strain images from an ablation formed in bovine liver tissue. Some artifacts in the shear wave velocity image may be a result of blood vessels highlighted in the imaging plane in (a). High shear wave velocity above the ablation may be an artifact, as was observed in the FEA and phantom images. The strain image shows good boundary demarcation where large gradients in the axial direction were present. No ablation boundaries were observed in the B-mode image in (d). A comparison of the boundary delineations in (e) shows good agreement between the gross pathology and shear wave velocity images. The strain image fails to detect the lower left corner of the ablation.

The gross pathology, shear wave velocity, and strain area estimates were 934.4 mm², 928.4 mm², and 849.0 mm², respectively. The ablation boundaries on shear wave velocity and strain images were determined similar to phantom 1. Delineations of the ablation on the shear wave velocity and gross pathology images were fairly consistent. However, the strain image failed to capture the lower left corner of the lesion, which was reflected in the area estimates in Table II.

IV. DISCUSSION

Shear wave velocity reconstructions from FEA data demonstrate the feasibility of EVE, as shown in Fig. 4. The shear wave amplitude in Fig. 4(a) decayed to approximately 40 µm at the edges of the imaging ROI. This result highlights the potential of electrode or needle perturbations as a method for shear wave generation because of the high shear wave amplitudes that are possible. Acoustic radiation force often does not generate 40 µm amplitude shear waves adjacent to the acoustic pulse, and displacements can reach the noise floor 10 mm lateral of the perturbation [26], [40]. High-amplitude shear waves provide greater lateral tracking distances and thus a greater “mechanical” field-of-view. Artifacts above and below the stiff ellipsoid in Fig. 4(c) were not surprising, as the shear wave is generated at the bonding between the steel rod and ellipsoid, and the TTP algorithm assumes lateral wave propagation. Artifacts at the interface of the ellipsoid and background and in the background may result from reflections at model boundaries and are similar to artifacts observed using other reconstruction techniques [41], [42]. Higher than expected shear wave velocity estimates inside and outside the inclusion were obtained, but these were consistent with previous FEA work modeling an electrode bonded to a spherical inclusion [32].

The shear wave velocity reconstructions on simulated radiofrequency data were consistent with the reconstructions from the FEA data, as depicted in Fig. 4(d)–(f). Prior work with this program modeling EDE has shown consistency with FEA simulation [13]. In phantom 1, artifacts were less pronounced and shear wave velocity estimates were lower when ultrasound simulations were compared to FEA reconstructions, which was likely a result of the smoothing applied to the TTP image. In phantom 2, shown in Fig. 5, the higher shear wave velocity left of the ellipsoid was indicative of a material that was stiffer than right of the ellipsoid, suggesting the presence of the partially ablated region. The artifact between the partially ablated region and ellipsoid was not as pronounced as that between the background and ellipsoid, which is likely a result of the lower modulus contrast between the partially ablated region and ellipsoid. Shear wave velocity estimates were higher than expected in the ellipsoid and background and lower than expected in the partially ablated region, perhaps a result of reflections in the irregular geometry.

The results from phantom experiments were in good agreement with FEA simulation, as shown in Fig. 6. Differences existing above the inclusion may be a result of the tilt of the transducer, i.e., the transducer cannot be centered on the needle as in FEA models. Because of this, FEA models and actual phantoms share a common plane only in the vicinity of the ellipsoid. A 3-D FEA model could be used to match imaging planes; however, node limitations prevented us from implementing this. The shear wave amplitude at the edges of the transducer was slightly lower in phantoms than in FEA models, which may be a result of either slight differences in material properties in the phantom or transducer tilt. The striping in the maximum displacement image likely occurs as a result of reflections from earlier perturbations in the EVE sequence.

A comparison of EDE and EVE in phantom 1 is presented in Fig. 7. The EDE displacement field in Fig. 7(b) decayed faster than the EVE maximum displacement field shown in Fig. 6(a), which may be a result of time-dependent relaxation. EDE displacements were estimated using frames near the beginning and end of the actuator waveform, a time period of approximately 1 s, whereas the EVE displacements were estimated within 60 ms, as illustrated in Fig. 2. The decorrelation halo was most prominent on the top and bottom of the ellipsoid and grew faint near the lateral edges, which is consistent with previous studies [13], [14]. The EVE images did not have artifacts in the background like the FEA models, which may have been due to the plane strain assumption or boundary conditions in the FEA models. Sharp transitions in shear wave velocity delineated the ellipsoid, but some border ambiguity existed on the top and bottom of the ellipsoid. The high shear wave velocity on the top and bottom of the ellipsoid might result from the super glue that was applied to the stainless steel rod to ensure bonding with the ellipsoid, which may have stiffened the TM material near the rod.

Shear wave velocity and strain estimates were compared in ROIs in the phantom 1 images. Prior work estimated strain in ROIs within the inclusion and above the inclusion because of the focused nature of the compression [13]. That is, because the compression is nonuniform, the strain is dependent on not only the modulus contrast but also the lateral position relative to the compressive focus, i.e., the electrode. As illustrated in Fig. 7, the compression is highly focused at the rod bonding site and decays moving laterally into the tissue. Because of this, strain estimates inside and outside of the ablation must lie along the same axial lines to make a meaningful comparison. In contrast, we compared strain estimates laterally to make a comparison to our shear wave velocity ROIs. The strain estimates in Table I had a contrast opposite of what we expected, confirming the importance of comparing strain estimates in regions with the same level of compression, i.e., axially. In contrast, the shear wave velocity estimates in phantom 1 provided the correct modulus contrast and were close to mechanical testing estimates. The ROIs in the left half of the ellipsoid and background were significantly higher and lower than mechanical testing estimates; however, the differences were only 7% higher and 5% lower, respectively.

A comparison of EDE and EVE in phantom 2 is shown in Fig. 8. The decorrelation halo in Fig. 8(c) only faintly outlines the partially ablated region, possibly because of the low modulus contrast with the background or nonuniform compression. The shape of the partially ablated region on the B-mode image was more similar to that on the shear wave velocity images than on the strain image. This shows that EVE may be a useful tool in detecting and delineating partially ablated regions with ultrasound following ablation therapy, where traditional B-mode imaging often fails because echogenicity has been shown to be a poor predictor of ablation boundaries or disease state [4], [5].

The strain and shear wave velocity estimates from phantom 2 are listed in Table I. The strain contrast determined laterally was opposite the actual contrast, as in phantom 1, whereas the shear wave velocity estimates followed the expected trend. A lower-than-expected shear wave velocity estimate in the partially ablated region followed the trends in the FEA model and ultrasound simulation. However, EVE only underestimates the mechanical testing estimate by 8.5%. Overestimation inside the ellipsoid with an underestimation in the adjacent background was observed on the right side of the ellipsoid, as was observed on the left side of the ellipsoid in phantom 1. This may be a result of a slightly unbalanced loading of the steel rod.

Area comparisons of the different imaging modalities are presented in Table II. No significant differences in ellipsoid area among shear wave velocity, strain, and B-mode area were observed in phantom 1. A small underestimation in strain area has been observed when performing EDE on a spherical inclusion phantom [14]. In that study, strain area was slightly lower than B-mode area for 50 µm and 100 µm deformations, but underestimation grew progressively worse for 150 µm and 200 µm deformations. In this study, only a 100 µm deformation was used; larger deformations could lead to area underestimation. In contrast, phantom 2 strain and shear wave velocity area estimates were significantly higher when compared to B-mode area. The discrepancies likely occurred at the sharp corners where the partially ablated region meets the stiffer ellipsoid. Area overestimation was only 2.4% on shear wave velocity images and 4.7% on strain images. The decorrelation halo appears to have a smoothing effect on the sharp boundaries in strain images, which may account for the higher area overestimation. An exhaustive study of the spatial resolution of EVE was not performed. This study investigated boundary delineation of relatively large inclusions. An interesting follow-up to this work would be to perform EVE on several smaller inclusions to determine the spatial resolution limits of this approach. Reconstructions were also inaccurate around the electrode. Increasing the electrode-to-inclusion diameter ratio therefore may result in poorer reconstructions.

Interesting similarities and differences between EDE and EVE were observed in the ex vivo RF ablation experiment. In Fig. 9, the TTP increased rapidly inside but much more slowly outside the ablated region because of the large mechanical contrast. Fig. 10 shows differences in the gross pathology, shear wave velocity, strain, and B-mode images. Low shear wave velocity regions inside the ablation may correlate with blood vessels. Vessel 1, shown in Fig. 10(a), may be represented by the blue horizontal line at the bottom of the ablation in the shear wave velocity image. Similarly, vessel 2, running vertical on the gross pathology image, lies close to the vertical blue-cyan region on the left side of the ablation. These regions were slightly shifted to the left in Fig. 10(b) when compared to gross pathology, which may indicate that they show a reflection on one side of the vessel. This could also indicate slight misregistration of the image. Echogenic differences did not provide boundary delineation of the ablation on the B-mode image in Fig. 10(d), which highlights the importance of both the EDE and EVE techniques.

The shear wave velocity and strain estimated in ROIs in the background left and right of the ablation (images not presented) are compared in Table I. The shear wave velocity estimates in the background were comparable to mechanical measurements from tissue excised near the ROIs, as well as to estimates made in beef liver in other studies by either mechanical testing or shear wave elasticity imaging (SWEI) [43], [44]. The shear wave velocity was significantly higher left of the ablation but within 20% of the mechanical testing estimate.

Estimates inside the ablation were much higher than the mechanical measurements. A possible explanation is the large modulus contrast between the ablation and the normal background. The large contrast appears to make the ablation move as a rigid body with the RF electrode in Fig. 9(b), which may prevent shear wave propagation within the ablation. Large contrasts would be less likely when treating an actual malignancy because of elevated background stiffness from an underlying condition such as cirrhosis or lower maximum ablation stiffness resulting from active perfusion and convective heat transfer [45]. Lower mechanical contrast would result in a lower reflection coefficient, coupling more shear energy into the background. However, in the case of cirrhosis, this perceived gain may be outweighed by shear amplitude decreases resulting from the increased stiffness in the background. The overestimation may also be a result of frequency- or strain-dependent effects. Dynamic compression tests performed at 30 Hz on the ablation following the 1 Hz tests estimated the Young’s Modulus to be 161.1±36 kPa. Neglecting the effects of viscosity or compression may make this more of a qualitative approach; however, boundary delineation is more crucial clinically, which EVE provides. The strain ROIs indicated that the ablation was stiffer than the background left of the electrode and softer right of the electrode, which may result from the presence of blood vessels inside the ablation.

A comparison of area estimates in Fig. 10 shows that the shear wave velocity image outperformed the strain image when compared to gross pathology. The shear wave velocity image provided well-defined borders on the left and right sides of the ablation. Some ambiguity existed on the top border, similar to phantom experiments. In contrast, the strain image had pronounced borders on the top and bottom of the ablation where large axial displacement gradients were present. There was minimal border on the right side of the lesion because the nearly vertical edge shown in Fig. 10(a) provided a small displacement gradient. The strain image failed to capture the bottom left corner of the ablation, resulting in the area underestimation listed in Table II. Area underestimation on strain images is consistent with prior ex vivo porcine experiments [46]. These results show the utility of both shear wave velocity and strain images, and the complementary boundary information that they can provide.

This study has shown the ability of EVE to quantify shear wave velocity in phantoms and in ex vivo bovine liver tissue. EVE benefits from high amplitude shear waves generated in deep abdominal organs, which can be tracked laterally further than the lower amplitude waves that are generated using ARFI. EVE provides quantitative information that EDE does not, as well as more defined ablation boundaries. Limitations do exist. The shear wave velocity reconstructions in ablations may be errant with high inclusion-to-background modulus contrast; however, good boundary delineation was still observed. Some shear wave velocity artifacts, particularly those below the ellipsoid in phantom experiments and above the ablation in the ex vivo experiment, made boundary delineation somewhat subjective. A more thorough investigation is necessary to determine the full utility of boundary delineation with this approach. However, this paper focuses on the EVE method. A multiple observer comparison of boundary delineation on shear wave velocity and strain images or an overlay of the two is beyond the scope of this study but will be investigated in future work. EVE currently requires multiple perturbations to generate an image because of the sequential scanning on the ultrasound scanner, which may not be suitable when holding the transducer freehand. This would be an issue clinically, but parallel channel acquisition devices may soon make this a moot point. The linear array transducer used in this study does not provide sufficient penetration for percutaneous in vivo applications. Future work will modify this technique for a more clinically relevant curvilinear array transducer. EVE has been demonstrated in simulations, phantom experiments, and ex vivo experiments in this study. With further development, EVE holds promise as a complementary imaging modality for monitoring ablative therapies and detecting partially ablated regions post-procedure.