Motor equivalence and self-motion induced by different movement speeds

Abstract

This study investigated pointing movements in 3D asking two questions: (1) Is goal-directed reaching accompanied by self-motion, a component of the joint velocity vector that leaves the hand’s movement unaffected? (2) Are differences in the terminal joint configurations among different speeds of reaching motor equivalent (i.e., terminal joint configurations differ more in directions of joint space that do not produce different pointer-tip positions than in directions that do) or non-motor equivalent (i.e., terminal joint configurations differ equally or more in directions of joint space that lead to different pointer-tip positions than in directions that do not affect the pointer-tip position). Subjects reached from an identical starting joint configuration and pointer-tip location to targets at slow, moderate, and fast speeds. Ten degrees of freedom of joint motion of the arm were recorded. The relationship between changes in the joint configuration and the three-dimensional pointer-tip position was expressed by a standard kinematic model, and the range- and null subspaces were computed from the associated Jacobian matrix. (1) The joint velocity vector and (2) the difference vector between terminal joint configurations from pairs of speed conditions were projected into the two subspaces. The relative length of the two components was used to quantify the amount of self-motion and the presence of motor equivalence, respectively. Results revealed that reaches were accompanied by a significant amount of self-motion at all reaching speeds. Self-motion scaled with movement speed. In addition, the difference in the terminal joint configuration between pairs of different reaching speeds revealed motor equivalence. The results are consistent with a control system that takes advantage of motor redundancy, allowing for flexibility in the face of perturbations, here induced by different movement speeds.

Introduction

A long-standing question in the study of motor control is what variables the central nervous system (CNS) uses to plan movements given that the motor system is kinematically and dynamically redundant for most functional tasks (Bernstein 1967). Some have suggested that planning of targeted reaching involves specifying a sequence of joint postures (Rosenbaum et al. 1999) or the terminal joint configuration (Tillery et al. 1995; Desmurget et al. 1998; Gréa et al. 2000). If so, relatively invariant terminal joint configurations could be expected when reaching repetitively from a fixed initial hand location and arm configuration to the same target location. Multivariate statistical procedures have been used previously to investigate this question (Tillery et al. 1995; Desmurget et al. 1998; Gréa et al. 2000). Those results were used to argue that a specific terminal joint configuration is planned for the reaching movement. However, results of other studies of reaching tasks provided equivocal evidence for movement planning based on terminal joint postures (Cruse et al. 1993). Pointing movements to the same targets from different starting positions lead to different terminal configurations (Soechting et al. 1995). On the other hand, investigations of arm movements at different speeds did not reveal differences in the resulting spatial 3D trajectories of the movement plane of the arm or 3D path curvature (Nishikawa et al. 1999). Similarly, monkeys learning an obstacle avoidance task varied movement speed, but kept their spatial trajectories relatively constant (Torres and Andersen 2006). Recent investigations that used a formal model to map joint variance across repetitive reaches onto end-effector variance suggest that a family of equivalent joint postures are used when reaching repetitively under identical task conditions (Scholz et al. 2000; Tseng et al. 2002, 2003; Tseng and Scholz 2005; Yang and Scholz 2005).

In this study, we vary the speed of pointing movements and ask whether either the terminal joint configuration or the terminal pointer-tip position or both are invariant across movement speeds. As with variance measures, judgements of differences in terminal joint configuration or pointer-tip position across conditions require a theoretical basis. For instance, differences in terminal pointer-tip position that lie within the size of the reaching target may be considered irrelevant for task success. On the other hand, the direct comparison of differences in pointer-tip position and differences in joint configuration is impossible as these differences have different units and dimensions. A theoretically grounded comparison of these two variables can be based on the concept of the uncontrolled manifold (Scholz and Schoner 1999). If the terminal joint configurations across different movement speeds differ significantly primarily in those directions in joint space that have no effect on the pointer-tip position (that is, along the null space of the pointer-tip Jacobian), then the terminal joint configurations may be considered motor equivalent solutions of the task. If, in contrast, the differences between the terminal joint configurations of pairs of speed conditions lie equally or more in directions of joint space that leads to different pointer-tip positions than in directions that do not affect the pointer-tip position, then the terminal joint configurations at different speeds cannot be considered motor equivalent: the differences do not reflect a particular pattern of coordination that preferentially keeps the task of pointing invariant across speeds of reaching. We apply this approach to determine whether different movement speeds lead to significantly different terminal joint configurations that are motor equivalent solutions to the pointing task.

Planning for the entire temporal sequence of joint configurations for a given desired hand trajectory could presumably simplify trajectory control. This is because differences in movement velocity could be achieved by simply scaling the transition time between the planned sequence of joint postures without significantly affecting the postures themselves (Hollerbach and Flash 1982; Rosenbaum et al. 1999). A three-dimensional reaching model based on the separation of planning for geometric features versus dynamic features of the movement has been suggested (Torres and Zipser 2002), and experimental evidence in support of that independence has been provided (Torres and Zipser 2004). Rosenbaum et al. (1999) proposed a formal model of reaching that hypothesized the planning of a predetermined sequence of joint postures to achieve the goal. The model weighs a variety of costs, depending on the movement context, to identify an optimal sequence of joint postures for a given task. Although not addressed by this model or its subsequent iterations (Rosenbaum et al. 2001a, b, 2009), one could expect that the joint velocity vector at each time point during a reach would contribute primarily to end-effector motion, with little or no self-motion. Self-motion refers to a component of the joint velocity vector that does not affect the end-effector’s motion (Murray et al. 1994). For example, if the arm is redundant, it is possible to raise the elbow to flick a light switch while transporting the hand forward in space without that motion affecting the hand’s motion. Joint motions contributing to flicking the light switch represent self-motion relative to hand motion. However, there is no a priori reason to expect a significant amount of self-motion when there is no explicit secondary task as in this study.

A second goal of this study, therefore, was to investigate how much of the joint velocity vector acts to transport the hand versus being a reflection of self-motion. According to the theories of Rosenbaum et al. (1999) and Hollerbach and Flash (1982), we could expect minimum amount of self-motion. Such a control strategy would presumably simplify control by making the same purported inverse-dynamics computation valid for all movements by a simple scaling of the required torques. Then, most of the joint velocity should be directed toward transporting the hand. In contrast, a recent study of Martin et al. (2009) proposed a process model of the control of a redundant motor system in which neural dynamics determines the time course of a vector of muscle–joint equilibrium positions (see “Discussion” for more detail). This model predicts a considerable amount of self-motion, a prediction that was confirmed with empirical data obtained when participants made planar reaches involving four kinematic degrees of freedom (DOFs). If confirmed here, this finding would raise doubts about planning for a fixed sequence of postural states. To our knowledge, the question of how much self-motion accompanies goal-directed movements has not been thoroughly addressed in the context of three-dimensional arm reaching tasks (See Scholz et al. 2007 for an example from a postural task).

In this study, subjects performed reaches at different speeds to induce perturbations by changing movement dynamics. Although invariance of kinematic features have been reported previously when reaching under different speed conditions (Soechting and Lacquaniti 1981; Atkeson and Hollerbach 1985; Nishikawa et al. 1999; Torres and Zipser 2004), conclusions from many of those studies were based on relatively qualitative analyses of movement trajectories (Soechting and Lacquaniti 1981; Atkeson and Hollerbach 1985; Nishikawa et al. 1999). Moreover, a study of targeted reaching at different speeds by Thomas et al. (2003) found that subjects had significantly larger excursions of the thigh, pelvis, humerus, and forearm during faster reaches compared to reaching at their comfortable speed. Thus, the segmental kinematics were not simply scaled in time.

Methods and materials

Subjects

Two male and four female right-handed, healthy volunteers (20.5 ± 1.26 years of age) were paid $25 each for their participation. A consent form approved by the Institutional Review Board at University of Delaware was completed and signed by all subjects. All subjects had normal or corrected to normal vision.

Experimental setup and procedures

Hardware and subject setup

Subjects sat in a height-adjustable chair so that their left forearm rested on a table top in 90° of elbow flexion with a vertical upper arm in the starting position. Trunk motion was eliminated by positioning the front of the torso tightly against the edge of the table and by strapping the trunk with harness to the chair back. Thus, reaching involved only motion of the clavicle–scapula complex and arm joints. Left arm and scapula movement was recorded at 120 Hz with a six-camera VICON™ motion capture system. The cameras formed a semicircle around the subjects, from slightly behind and to the left to slightly forward on the right side, to ensure that all markers could be observed by at least three cameras during performance. Reaching was performed with the non-dominant left arm because it was expected to be more influenced by the higher interaction torques generated by the higher speed reaches (Sainburg and Kalakanis 2000). Before each experiment, the cameras were calibrated to the measurement volume.

Spherical reflective markers were placed over the skin using hypoallergenic tape at the sternoclavicular (SC) joint, just inferior and lateral to the acromion process of the shoulder, on the lateral and medial epicondyles of the elbow (which defined the elbow axis), and on the ulna and radius styloid processes. Four rigid bodies made of plastic orthoplast™ shells were fitted to contour the superior part of the upper trunk (i.e., above the clavicle and scapula), the lateral part of the upper arm, the dorsum of the forearm and the posterior surface of the hand. Each shell had four reflective markers that formed rigid bodies used to compute 3D joint angles. The hand shell had an extended pointer with a reflective marker at its tip that subjects used to point to the targets. The position of the reflective marker was positioned at the tip of the index finger when in its fully extended position. The shells were kept in place by elastic wraps and double-sided tape (hand shell).

Two flat, circular targets (4.76 cm in diameter) were placed at 90% of the subjects’ arm length (defined as the distance from the lateral aspect of the acromion process of the shoulder to the proximal interphalangeal joint of the index finger), at a 30° angle to the right and left of an imaginary line pointing straight ahead from the acromion process. Target height was three inches above the height of the subjects’ left shoulder, measured while sitting at the table. The starting location of the pointer was marked on the table so that it could be aligned with this mark before each trial. The configuration of the joints was kept constant in the starting position of each trial by placing alignment marks on the table.

Movement time was measured directly with a Lafayette™ Instrument Timer. Microswitches were mounted on the table below the hand in the starting position and behind the center of each target. Lifting of the hand released the switch, starting the timer. Hitting the target depressed that switch and stopped the timer. The resulting movement time (MT) for each trial was shown on an LED display to provide subjects feedback about their MT after every trial. Trials that did not fall within ±50 ms of the fast and moderate velocity conditions or within ±100 ms of the slow condition were repeated.

Calibration of subject position

A static calibration of subjects’ upper extremity including the scapula was performed as a basis for later joint angle computations. In the calibration position, the arm was held at 90° of shoulder flexion with the elbow fully extended, the forearm in neutral pronation–supination, and the wrist in a neutral position between flexion–extension and abduction–adduction, thumb pointing upward (see Fig. 1 of Tseng et al. 2003). The reflective marker positions were captured in this position at the beginning of each experimental session. All joint angles were defined as zero degrees in this static calibration position.

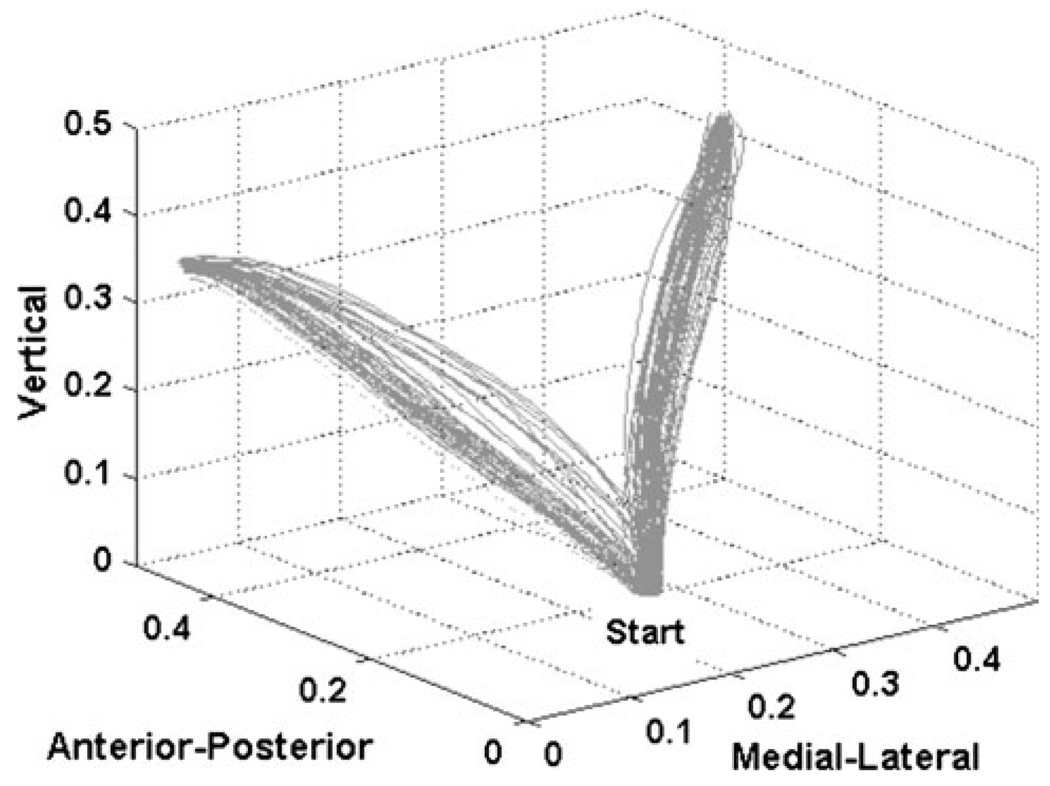
Fig. 1.

Sample hand paths for all trials of one representative subject for slow (solid), moderate, (dashed) and fast (dotted) reaching to the left and right targets

Instructions

Subjects were given several practice trials to ensure the consistency of their MT across trials. The number of trials depended on the subject’s ability to achieve a consistent MT. The investigator ensured that the subject attained the same starting joint configuration and pointer-tip position before each trial. The investigator started each trial with a “ready” command, at which point the start of data collection was initiated. This was followed by a “go” command that signaled to the subject to reach and depress the target switch with the pointer when they were ready. Pretrial instructions emphasized that this was not a reaction time task. Subjects were instructed to reach in one continuous motion and try to touch the center of the designated target within the required movement time. Once the target was reached, the subject was instructed to wait for the investigator’s “back” command to return to the starting position. A 1-s pause was provided between the “ready” and “go” command, and between reaching the target and the “back” command. Rest periods were given to subjects when needed throughout the experiment. No subject reported fatigue during or after the experiment.

Experimental conditions

Three different speed conditions were defined by movement time. (1) Fast: 400 ± 50-ms; (2) moderate: 700 ± 50-ms; and (3) slow: 1,100 ± 100 ms. Twenty-five acceptable trials were completed at each of the three speeds of reaching at each of the two target locations. The trials were randomized in blocks of five, first by target location and second by speed.

Data processing

Marker coordinates were filtered before all calculations using a recursive, 5-Hz lowpass Butterworth filter. Three-dimensional pointer-tip marker coordinates then were rotated into a local coordinate system, with origin at the pointer-tip’s starting position and the local x-axis pointing from the starting position to the calibrated target center. Thus, movement along the x-dimension represented movement extent, while movement along the y-axis and z-axis represented deviations from that path, or movement direction. The velocity of the pointer-tip was obtained using a central-difference algorithm in Matlab™. Movement onset and termination were determined as the sample values where the local × component of pointer-tip velocity rose above or returned to, respectively, values equal to 5% peak velocity.

Joint angle computation

Joint angles were derived using local coordinate systems defined at each joint based on the subject calibration position, where the local axes were aligned with the global system, except for the elbow axis (see Tseng et al. 2002). All joint angles were defined as zero degrees in the static calibration posture. The method of Soderkvist and Wedin (1993) was used to define the rotation matrices required to take a given rigid body from its position at each sample of the reaching trials to its position in the subject calibration trial. The product of rotation matrices for adjacent limb segments was then used to extract the joint angles in a Z–X–Y order. Details of the approach as well as our approach to modeling clavicular-scapula complex motions are described elsewhere (Scholz et al. 2000; Tseng et al. 2002). Joint angles measured during the pointing task were scapular (1) abduction–adduction (Z-axis); (2) elevation–depression (X-axis); (3) upward–downward rotation (Y-axis); glenohumeral (4) horizontal abduction–adduction (Z-axis); (5) flexion–extension (X-axis); (6) internal– external rotation (Y-axis); elbow (7) flexion–extension (about a skewed axis based on rotation to the axis formed by a line between the medial and lateral humeral epicondyle markers using Rodriquez formula; Belongie 1999); (8) forearm pronation–supination (Y-axis); wrist (9) flexion– extension (Z-axis); and (10) radial-ulnar deviation (X-axis). The data were then time-normalized to 100% based on movement onset and termination using a cubic spline algorithm in Matlab™.

Movement time

The mean, standard deviation (SD), and coefficient of variation (CV) of the movement times (MT) produced by subjects were computed to confirm that subjects followed the speed instruction and the existence of distinct velocities of movement.

Pointer-tip path deviation

To estimate path curvature, we computed the path deviation at each point in the movement from a straight line to the target (local x-coordinate). Path deviation was determined by computing the geometric mean of the pointer-tip’s local y- and z-coordinates (off-direction) at each sample value and then summed across samples. These coordinate values would be zero if the hand followed a perfectly straight path to the target along the local X-axis. We also computed the arithmetic mean of the y- and z-axis deviations.

Terminal pointer-tip position

The position of the pointer-tip after reaching the target was obtained from the filtered data on all trials of each condition, before time-normalization. It occurred when the target switch was fully depressed, when the resultant distance of the pointer-tip position from the calibrated target center was smallest. These coordinates were used to examine differences in the terminal pointer-tip position across the three velocities of reaching.

Self-motion analysis

The uncontrolled manifold (UCM) approach (Schöner 1995) provides a framework for investigating the extent to which motor abundance (Gelfand and Latash 1998) is used by the CNS in the control of multi-DOF tasks. Abundance, commonly referred to as redundancy, is the availability of more degrees of freedom than minimally required to achieve a particular kinematic goal. According to the theory underlying the UCM approach (Latash et al. 2007; Martin et al. 2009), control is organized around a subspace in the space of the motor elements, referred to as the UCM, within which variations of those elements have no effect on the values of variables most directly related to task success. In the context of controlling the hand’s spatial position during reaching, variations of the joint angles within the UCM subspace have no effect on the hand’s current position. Thus, in principle, the CNS only needs to restrict joint variation outside of the UCM subspace, but not within the UCM, depending on the presence of other task constraints. Previous studies based on this hypothesis have focused on how the variance of joint angles or muscle EMG patterns across repetitions of a given condition is structured to stabilize task-relevant variables, such as the hand’s path.

This same framework was used to investigate how the joint velocities contribute to the velocity of the pointer-tip along its path to a target. Self-motion refers to joint velocities that have no effect on motion of an end-effector, here the hand or the rigidly attached pointer-tip. It occurs within the null space of joint space, which is a linear approximation to the uncontrolled manifold (Scholz and Schoner 1999). The null-space vectors are estimated mathematically in Matlab™ from the Jacobian matrix, which can be used to relate small changes in joint velocities to changes in the end-effector velocity (Murray et al. 1994). During a reaching movement, the vector of joint velocities is related to the hand’s velocity through a geometric model such that the hand’s velocity is of the correct magnitude and direction. If the velocity of one or several joints point in the wrong direction or have an inappropriate magnitude, the hand’s movement course will be altered unless other joint velocities compensate. Such compensation should lead to an increase in the component of the joint velocity vector lying within the null space, or the UCM. In addition, self-motion can be used to accomplish other tasks simultaneously with the primary task.

The method of computing appropriate UCMs based on the geometric model has been described in detail elsewhere (Scholz and Schoner 1999; Scholz et al. 2000; Reisman and Scholz 2003). Self-motion was computed in this study as follows (see Appendix for a simple illustration): (1) the geometric model relating changes in the three-dimensional (3D) hand/pointer-tip position to changes in the 10 joint angles was computed; (2) the Jacobian matrix was determined as the partial derivatives of the three coordinates of the hand’s position with respect to each of the ten joint angles from the geometric model; (3) for each trial, numerical values of the Jacobian matrix were computed from the instantaneous joint configuration; (4) the null space of this Jacobian at each time point was obtained using the null function in Matlab™. The null space is defined by 7 basis vectors in the 10-DOF joint space (10–3 task dimensions) and linearly approximates the UCM; (5) the 10-dimensional vector of joint velocities at each time point was projected into the null space and into its complementary space, and the length of projection in each subspace was computed. The length of projection into the UCM represents the magnitude of the joint velocity vector (i.e., self-motion) that has no effect on the task variable, here 3D hand motion. The complementary projection represents the magnitude of the joint velocity vector that causes hand motion (i.e., range-space motion). Steps (4) and (5) were performed at each sample of the reach trajectory for each trial. The mean of the two components of the velocity vector was computed across four equal periods of each trial (1–25, 26–50, 51–75, and 76–100) and then averaged across trials for each target, speed condition, and subject for statistical analyses. Mathematical details of the method are available elsewhere (Scholz et al. 2000).

Because the goal of the task is to move the hand to the target, one can expect range-space motion to be larger than self-motion; that is, joint velocities should move the hand in the planned direction. Then, self-motion could be expected to be minimal from the standpoint of optimizing energy cost (this may be wasted motion) or minimizing joint excursions, especially because there was no explicit secondary task in this experiment. Because the subspace of the UCM within which self-motion occurs has seven dimensions while the dimension of the range space equals that of the task space (i.e., three dimensions), the lengths of projection of the velocity vector were normalized by the square root of the number of dimensions of their subspace. Also, because range-space motion is directly related to the planned movement (i.e. component of the joint velocity vector that moves the pointer-tip), it is expected to increase with speed. Self-motion, however, may or may not increase with speed because, by definition, it is unrelated to pointer-tip movement.

Motor equivalence

This analysis investigated whether differences found in the terminal joint configuration induced by different reaching speeds were structured to preferentially keep task-level performance (i.e., the pointer-tip position) invariant. Motor equivalence was detected when significant differences between terminal joint configurations lay significantly more within the null space of the pointer-tip Jacobian than within its range space. Non-motor equivalence was detected when significant differences between terminal joint configurations either lay equally in both subspaces or when these differences lay significantly more in the range space than the null space of the pointer-tip Jacobian.

In this analysis, the terminal joint configuration was estimated as the joint configuration obtained at the smallest resultant distance between the pointer-tip and the calibrated target position, which occurred when the target switch was completely depressed. At this terminal position, the following analysis steps were performed separately for each target location: (1) the mean, across reaches, terminal joint configuration was obtained for each speed condition; (2) the norm of the difference between each pair of mean terminal joint configurations was then computed as a joint difference vector, i.e.,

$${\text{nJDV}}_{i,j}=\sqrt{{\displaystyle {\sum }_{10}^{k=1}{({\underset{¯}{\overline{\theta }}}_{i,k}-{\underset{¯}{\overline{\theta }}}_{j,k})}^2}},$$

where nJDV_i,j is the normed difference of the 10 element (k = {1,…,10}) mean terminal joint configurations, ${\underset{¯}{\overline{\theta }}}_{i,k}$ and ${\underset{¯}{\overline{\theta }}}_{j,k}$ between pairs of speed conditions, i and j; i, j = {slow, moderate, fast}; (3) the norm of the vector of variances of terminal joint configurations across trials of reaching for each speed condition was computed, i.e.,

$${\sigma }_i^{\text{norm}}=\sqrt{{\displaystyle {\sum }_{10}^{k=1}\left({\sigma }_{{\theta }_{i,k}}^2\right)}.}$$

The latter measure represents naturally occurring differences in terminal joint configurations across trials of a given speed condition. (4) nJDV_i,j was then compared to ${\sigma }_{\mathrm{i}}^{\text{norm}}$ to determine whether the joint configurations of the two speed conditions were statistically different. For example, when comparing the slow and moderate speed conditions, if nJDV_s,m does not differ significantly from ${\sigma }_{\mathrm{s}}^{\text{norm}}$ or ${\sigma }_{\mathrm{m}}^{\text{norm}}$, then we would conclude that the terminal joint configurations for these two speeds were not different, i.e., that they lie within the natural variability of each individual speed condition. If, on the other hand, nJDV_s,m differed significantly from the σ measures, this would indicate that the joint configurations of the two speed conditions fall beyond the trial-to-trial variability of the terminal joint configuration of an individual speed condition, i.e., that the speed conditions are different.

Even if the terminal joint configurations for different speed conditions differed, however, this could be because of differences in the terminal pointer-tip positions of the two speed conditions. Assessing this possibility is not trivial because even though the mean terminal pointer-tip position might differ slightly between speed conditions, all (or even most) of the differences in joint configuration might not be the result of these differences in pointer-tip position. That is, some of the joint configuration difference might reflect motor equivalence, related to the motor system’s attempt to preserve a consistent terminal pointer position. This question was addressed by using a modification of the UCM approach (Scholz and Schoner 1999). The mean joint configurations for each speed condition were obtained at the terminal pointer-tip position as above. For each condition, the null space of its mean terminal configuration was obtained, which is a linear approximation of that subspace in joint space where all inclusive joint configurations are equivalent to the mean configuration and would produce the same pointer-tip position. The vector differences in the terminal joint configurations for each pair of speed conditions were then obtained (i.e.,${\underset{¯}{\overline{\theta }}}_i-{\underset{¯}{\overline{\theta }}}_j)$ and projected onto the null space estimated for each speed condition and into the orthogonal subspace (range space). If the length of projection was significantly larger within the null space, or UCM, for a given speed condition than in the range space, then we concluded that most of the difference in joint configurations between speed conditions was not due to a difference in terminal pointer-tip position.

Statistical analyses

The effects of the factors target location and speed of reaching on the values of most experimental variables were tested using repeated-measures analyses of variance (ANOVA). Analyses of the ratio of self-motion to range space motion or that included self-motion and range-space motion individually were performed separately for each of the four equal phases of reaching. The analysis of differences between the projection of the terminal joint configuration from pairs of speed conditions onto the null space and the range space also included subspace type as a factor in the ANOVA. For the comparison of the nJDV_i,j and ${\sigma }_i^{\text{norm}}$, t tests were performed. All analysis accepted P < 0.05 as the significance value.

Results

Movement time (MT)

The data reported in Table 1, which were averaged across target locations, indicate that the speed instruction was followed, on average. MT for the speed conditions differed significantly (F_2,10 = 2780.0, P < 0.01). There was no effect of target location (P = 0.55) or an interaction (P < 0.19) with target location. Moreover, MT of each speed condition was well beyond the 95% confidence interval of each other condition.

Table 1.

Movement time (MT) variables

Speed condition	Mean (s)	SEM	95% Confidence interval
			Lower bound	Upper bound
Slow	1.185	0.0097	1.16	1.21
Moderate	0.77	0.0059	0.754	0.785
Fast	0.474	0.0032	0.466	0.482
	SDMT	SEM	95% Confidence interval
			Lower bound	Upper bound
Slow	0.0678	0.0039	0.058	0.078
Moderate	0.037	0.0015	0.033	0.041
Fast	0.0256	0.0015	0.022	0.03
	CVMT	SEM	95% Confidence interval
			Lower bound	Upper bound
Slow	5.712	0.308	4.921	6.503
Moderate	4.811	0.195	4.309	5.313
Fast	5.413	0.353	4.506	6.32

The standard deviation of MT (SD_MT) was smaller for the faster movements, as expected (F_2,10 = 75.6, P < 0.01). The relative variability (coefficient of variation or CV_MT) did not differ among the speed conditions (F_2,10 = 2.6, P = 0.12), however. There was an effect of the target, however. Reaching away from the midline toward the left target resulted in slightly higher absolute (F_1,5 = 6.6, P < 0.05) and relative (F_1,5 = 11.2, P < 0.05) MT variability than did reaching to the right target.

Pointer-tip path deviation

Figure 1 presents the pointer-tip path for all trials of reaching of the three speed conditions for one representative subject. Although this subject appeared to have different trajectories for the fast (dashed line) compared to the other conditions, deviation of the pointer-tip path from a straight line for all subjects to the target was not affected significantly by either movement speed (P = 0.64) or the target location (P = 0.16) alone. There was, however, a significant interaction between speed and target location (F_2,10 = 6.1, P < 0.05). When reaching ipsilaterally, away from the body’s midline, the hand path deviation was largest for the slowest MT (slow: 0.031 ± 0.005-m; moderate: 0.024 ± 0.002-m; fast: 0.025 ± 0.003-m). In contrast, when reaching toward the body midline, hand path deviation increased with movement speed (slow: 0.015 ± 0.005-m; moderate: 0.017 ± 0.005-m; fast: 0.020 ± 0.008-m). Variability of hand path deviation did not differ between speed conditions (P = 0.54) or target locations (P = 0.59), and there were no interaction effects (P = 0.78).

Terminal pointer-tip position

Main effects of target were not of interest because they were expected to differ in the x-dimension, as they did (F_1,5 = 894.7, P < 0.01), but not in the y-dimension (P = 0.66) or the z-dimension (0.95). The medial–lateral pointer-tip position did not differ among the speed conditions (P = 0.94) nor was there an interaction between the target location and speed (P = 0.98). Speed also did not affect significantly the y-dimension (P = 0.07) nor was there a target by speed interaction (P = 0.85). However, the effect of speed was significant for the z-dimension (F_2,10 = 5.43, P < 0.05). There also was an interaction with target location (F_2,10 = 6.24, P < 0.05). These resulted from a tendency for the pointer-tip to end lower on the target for the faster velocity movements, although this difference was present for the slow and fast conditions only for the left (0.406 ± 0.002 → 0.401 ± 0.002 → 0.398 ± 0.002 m) but not the right target (0.407 ± 0.002 → 0.406 ± 0.002 → 0.397 ± 0.003 m).

Self-motion

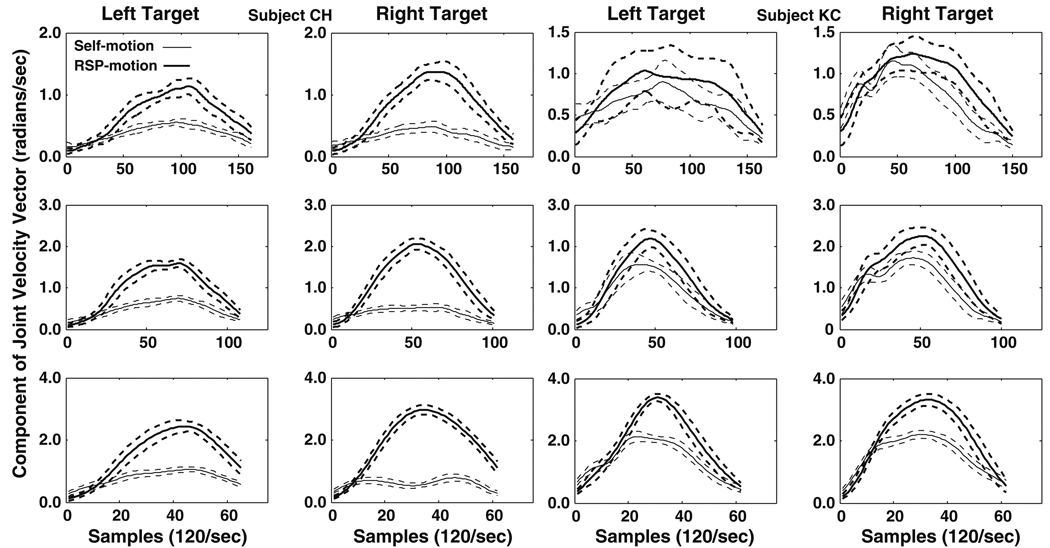
Figure 2 presents the average self-motion and range-space motion across trials for three speeds of reaching for two subjects. Subject CH exhibited the smallest amount of self-motion of all subjects. Self-motion typically was substantial for most subjects, generally amounting to over 50% of the amount of range-space motion (Fig. 3). Although an increased range-space motion is expected at faster movement speeds, the proportional increase in self-motion with increasing reaching speed observed in this experiment is not necessary because self-motion has no effect on the hand’s motion, by definition.

Fig. 2.

Self-motion (thin lines) and range-space motion (thick lines) per subspace dimension (see text) for slow, moderate, and fast reaching speeds (top to bottom) performed to two target locations. Dashed lines represent across trials standard deviation. Subject CH showed the smallest amount of self-motion of all subjects. Results were averaged across trials of relatively equal movement time for each subject

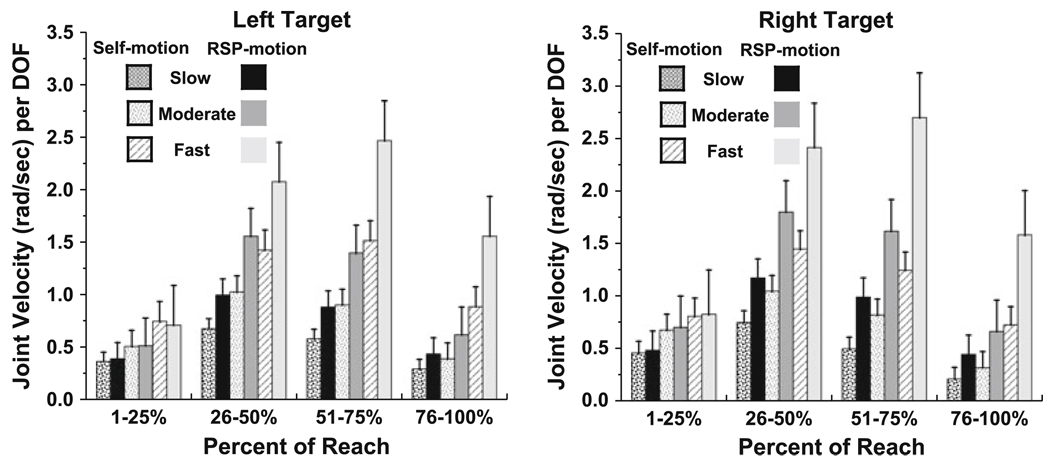
Fig. 3.

Self-motion (patterned bars) and range-space motion (solid bars) per dimension (see text) for three speeds of reaching at each of four phases of the reach trajectory (thick lines). Results for each phase were computed separately for each subject and then averaged across subjects. Results are presented for reaching to the left and right targets, with error bars indicating standard error of the means

Figure 3 presents the average across subjects self-motion and range-space motion, ± standard error of the means (SEM) for each target location. Both self-motion and range-space motion increased with movement speed, although not always proportionally as seen in the figure. Required movement speed affected significantly combined self-motion and range-space motion for all four phases of the reach (F_2,10 = 27.9, P < 0.0001; F_2,10 = 52.6, P < 0.0001; F_2,10 = 235.8, P < 0.0001; F_2,10 = 84.6, P < 0.0001), as expected. However, there was a significant interaction between speed and projection component of the joint velocity vector (i.e., self-motion and range-space motion components) for the last three phases of reaching (F_2,10 = 7.1, P < 0.01; F_2,10 = 49.5, P < 0.0001; F_2,10 = 34.4, P < 0.0001) but not for the first phase (P = 0.647), independent of the target location. This was because the increase in range-space motion was proportionally greater with increasing reaching speed than the increase in self-motion. We quantified this difference by computing the slope of the change in range-space motion or self-motion with required reaching speed (in seconds) for each subject and comparing the slopes with a repeated-measures ANOVA. A decrease in slope (K) of the change in the vector component with speed (negative because movement time decreases with speed) was greater for range-space motion compared to self-motion for the second (K_SM = − 1.02 ± 0.16 vs. K_RSP = −1.65 ± 0.25; F_1,5 = 7.97, P < 0.05), third (K_SM = −1.18 ± 0.15 vs. K_RSP = −2.30 ± 0.12; F_1,5 = 53.0, P < 0.001) and fourth phases (K_SM = −0.76 ±0.11 vs. K_RSP = −1.55 ± 0.17; F_1,5 = 37.1, P < 0.01) of the reach trajectory.

There were no significant interactions that involved both target location and required reaching speed for any of the phases of reaching. Target location did interact with the projection component for the third phase of reaching only (F_1,5 = 14.5, P < 0.01). This occurred because the amount of self-motion was slightly less when reaching to the right target (0.856 ± 0.11 rad/s) compared to the left target (1.00 ± 0.76 rad/s) while range-space motion was larger when reaching to the right target (1.77 ± 0.096 rad/s) versus the left target (1.58 ± 0.046 rad/s).

Motor equivalence

Comparisons of normalized joint difference vectors (nJDV) between pairs of speed conditions to ${\sigma }_{\mathrm{i}}^{\text{norm}}$ computed across trials of each individual speed condition are presented in Table 2. Results are provided separately for each target location.

Table 2.

Comparison of normed difference between terminal joint configurations for different speed conditions (nJDVij) versus the standard deviation of the joint configuration for each speed condition ${\sigma }_{\mathrm{i}}^{\text{norm}}$

Target	Speed	nJDVij (radians)	Qjnorm (radians)	t value (df = 11)	P-value
Left	Slow versus Mod	0.1405 ± 0.0578	0.1341 ± 0.0414	0.688	0.522
			0.1246 ± 0.0240	0.836	0.441
	Slow versus Fast	0.2147 ± 0.0628	0.1341 ± 0.0414	3.376	0.05
			0.1180 ± 0.0318	4.287	0.01
	Mod versus Fast	0.1565 ± 0.0566	0.1246 ± 0.0240	1.646	0.161
			0.1180 ± 0.0318	1.594	0.172
Right	Slow versus Mod	0.1240 ± 0.6437	0.1370 ± 0.3507	−0.679	0.527
			0.1268 ± 0.1405	−0.146	0.809
	Slow versus Fast	0.2000 ± 0.0602	0.1370 ± 0.3507	2.581	0.05
			0.1214 ± 0.0167	3.571	0.05
	Mod versus Fast	0.1874 ± 0.0548	0.1268 ± 0.1405	3.661	0.05
			0.1214 ± 0.0167	3.793	0.01

Bold values in this table highlight the comparisons that were significantly different, i.e., P < 0.05

For the left target, nJDV_s,m was not significantly different from ${\sigma }_{\mathrm{s}}^{\text{norm}}$ or ${\sigma }_{\mathrm{m}}^{\text{norm}}$; nJDV_m,f was also not significantly different from ${\sigma }_{\mathrm{m}}^{\text{norm}}$ or ${\sigma }_{\mathrm{f}}^{\text{norm}}$. However, nJDV_s,f was significantly different from both ${\sigma }_{\mathrm{s}}^{\text{norm}}$ and ${\sigma }_{\mathrm{f}}^{\text{norm}}$, indicating a significant difference between the joint configurations of the slow and fast speed conditions. For the right target, nJDV_s,m did not differ from ${\sigma }_{\mathrm{s}}^{\text{norm}}$ or ${\sigma }_{\mathrm{m}}^{\text{norm}}$, but nJDV_i,j did differ significantly from ${\sigma }_{\mathrm{i}}^{\text{norm}}$ and ${\sigma }_{\mathrm{j}}^{\text{norm}}$ when comparing slow-to-fast and moderate-to-fast speeds (Table 2). Thus, the terminal joint configuration for the fast condition differed from those for both the slow and moderate speed conditions.

The next step was to estimate how much of the identified differences in terminal joint configurations were related to differences in the terminal pointer-tip position, which differed slightly in the vertical dimension among speed conditions.

Figure 4 presents the results of the analysis that projected the difference in the terminal joint configurations from pairs of speed conditions onto UCMs that were estimated from the mean terminal joint configurations of individual speed conditions. All results were normalized for the dimension of each subspace. If the difference in terminal joint configurations from pairs of speed conditions was due primarily to differences in terminal pointer-tip position, then most of the projection length should lie in the range space and not in the subspace defined by the UCM.

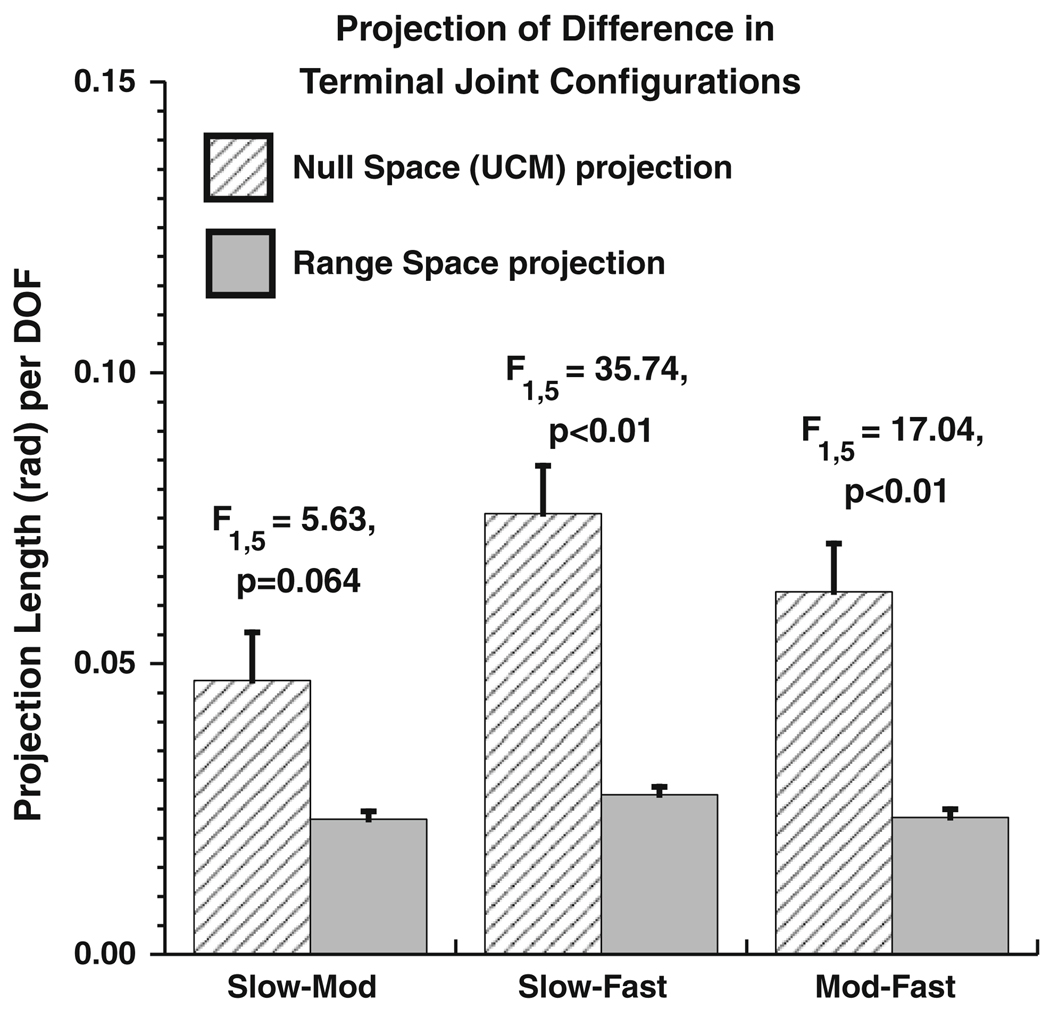
Fig. 4.

Projection of the difference in the terminal joint configurations for pairs of speed conditions (x-axis) onto the UCM, estimated from the terminal joint configuration of each individual speed condition, and the range space. Projections of the joint configuration differences onto the UCMs estimated from the terminal joint configuration of either speed making up that pair did not differ significantly. Therefore, the mean values are presented here

The only factor in the ANOVA that reached significance was the comparison between the null space (i.e., linear approximation of the UCM) and range-space projections. As can be seen from Fig. 4, the projection onto the UCM was significantly and substantially larger than the projection onto the range space (F_1,5 = 32.3, P < 0.01). There was no effect of the target location. The speed comparison was close to but did not reach significance (P = 0.062). The results of comparisons between the UCM and range-space projections for individual pairs of speed conditions are shown in the figure above each pair of bars.

Discussion

This study investigated two related questions about the control of multi-DOF movements. First, we were interested in determining whether the transport of the pointer-tip to the targets was accompanied by a significant amount of self-motion, that is, joint motion that did not propel the pointer-tip. Second, we investigated whether the terminal joint postures were invariant across reaches at different movement speeds (Desmurget et al. 1995; Desmurget and Prablanc 1997; Desmurget et al. 1998; Gréa et al. 2000), and if not, whether differences in terminal joint postures between speed conditions were associated with motor equivalence, that is, were structured to keep pointer-tip position more invariant across reaching speeds than to produce different pointer-tip position.

Regarding the first question, a significant amount of self-motion accompanied this redundant, three-dimensional reaching task. Except for one subject who showed a limited effect (Fig. 2, left panel), self-motion cannot be considered simply a residual effect because the absolute amount of self-motion scaled with the velocity of movement (Fig. 3). When accounting for differences in the number of dimensions of each subspace, self-motion was typically about half of the amount of range-space motion. That self-motion was smaller than range-space motion is not surprising. If anything, it is surprising that self-motion was as large as it was, given that there was no explicit secondary task constraint in these experiments. During the earliest portion of the reach, the amount of self-motion was equal to range-space motion. This result may reflect the effect of initial adjustments of the joint configuration during the transition from the fixed initial posture to transport of the hand toward the targets. Although the amount of self-motion and range-space motion were larger for higher speed reaches, these increases were relatively proportional except during the period including the initial deceleration of the reach (51–75%). Thus, when examining the relative amount of self-motion (i.e., its ratio to range-space motion), the results generally agree with previous studies showing little effect of reaching speed on kinematics (Soechting and Lacquaniti 1981; Nishikawa et al. 1999; Torres and Zipser 2004). The difference in the ratio for the fastest reaches during the deceleration phase is an exception, however. This result may be due to higher interaction torques during this phase for the fastest reaches, although we did not specifically measure torques in this study.

To our knowledge, this is the first study of human reaching that has investigated self-motion without artificially constraining joint motion, although similar issues have been addressed during natural movements by other investigators. A recent study of a throwing task, performed at a preferred movement speed and without a specified terminal hand position, also reported a significant amount of self-motion particularly early and late in the hand’s trajectory (Yang and Scholz 2005).

What accounts for this significant amount of self-motion without an additional task requirement? One possible interpretation is that this finding reflects the design of a control system that uses motor abundance to perform additional tasks without disturbing the primary task or when compensating for unexpected perturbations. The self-motion results are consistent with a recent model of the control of reaching in which a neuronal dynamics is used to generate a virtual joint trajectory (Martin et al. 2009). Within this dynamics, virtual joint velocity vectors that move the end-effector are dynamically decoupled from velocity vectors that have no effect on the end-effector. Because sensory information about the real joint configuration is coupled back into this neuronal dynamics, the virtual trajectory is updated by task-equivalent deviations from the dynamic movement plan. This back-coupling was found to be essential to correctly approximate empirically measured self-motion during planar reaching when motion was limited to four joints. Considered within the framework of this model, changes in the joint configuration with faster reaches in the current experiment would be resisted by the control system insofar as they would alter the pointer-tip path. In contrast, deviations of the joint configuration from the planned configuration that do not affect the hand’s path would not be resisted, but would result in updating the plan to the current joint configuration. The simulations of Martin et al. (2009) also showed that models in which an inverse dynamics cancels interaction torques predict too little self-motion and end-effector paths that were too straight compared to typical paths. Thus, the presence of self-motion provides an important constraint on models of motor tasks such as reaching.

The classical idea of the pseudo-inverse postulates that in a redundant effector system, a given end-effector velocity is achieved by minimizing the total amount of joint motion (Klein and Huang 1983; Mussa-Ivaldi and Hogan 1991). The principle of the pseudo-inverse predicts, therefore, zero self-motion. Imperfect control may lead to deviations of the real from the planned joint trajectory, which may partly lie in the null space of the end-effector Jacobian. The observation of non-negligible self-motion does not, therefore, categorically rule out the optimality principle of the pseudo-inverse. Quantitative modeling has suggested, however, that self-motion induced solely by imperfect control is not sufficient to account for the large proportion of self-motion observed here (see above; Martin et al. 2009). Other optimality principles such as minimum effort (Todorov 2004) or minimum torque change (Uno et al. 1989) do not exclude that movement plans may include self-motion. The amount of self-motion identified in the current experiments also question the posture-based model of Rosenbaum (Rosenbaum et al. 1999). The use of multiple cost factors to identify an optimal path of joint motion should, under identical initial posture and target conditions, lead to relatively little self-motion.

The second question investigated here was whether the CNS generally plans for a specific terminal joint configuration, not only a terminal end-effector position. The nervous system certainly is capable of specifying a particular joint configuration, for example, during artistic or athletic performances. However, is this typically the case for everyday activities such as reaching? It is possible that the self-motion measured during this experiment was a reflection of adjustments needed to achieve a specific terminal joint configuration. The question of whether the terminal joint configuration is specified in a redundant motor system has received considerable attention. We contribute to this discussion by asking whether the difference between joint configurations for pairs of speed conditions was greater than the variability of the joint configurations of the individual speed conditions. If the difference between joint configurations for two speed conditions was greater statistically than the joint configuration variability of a given speed condition, we concluded that the terminal arm postures achieved in the two speed conditions were different. The results indicate that the joint configuration for the fast condition was consistently different from those of either the moderate or slow reaching conditions. Could this difference be due primarily to differences in the terminal pointer-tip position between reaching speeds? Analysis of the terminal pointer-tip position revealed differences among the speed conditions along the vertical dimension of the target, so this account cannot be rejected off hand.

To investigate this question, we employed another modification of the UCM method (Scholz and Schoner 1999). The geometric model that describes how changes in the joint configuration affects the pointer-tip position first was used to define the Jacobian based on the average terminal joint configuration of a reference target speed condition. The null space or estimated UCM of that Jacobian was then computed. To review, the UCM represents the subspace of joint space within which deviations of the joint configuration away from the average joint configuration for the reference speed condition would still produce the same pointer-tip position obtained with the reference joint configuration. Then, deviations in the complementary subspace or range space would lead to different pointer-tip positions. Once the null space and complementary subspace of a given speed condition was obtained, the difference between the average terminal joint configuration of that speed and each of the other speed conditions was obtained and projected onto the null and range spaces of the reference joint configuration. If the difference in terminal joint configurations between pairs of speed conditions was due primarily to differences in the terminal pointer-tip position, then the length of projection should be substantially larger in the range space compared to the null space. Instead, the results showed that the projection into the null space was significantly larger regardless of which speed conditions were compared. This result indicates that the terminal pointer-tip position was affected less than the terminal joint configuration as the speed of reaching increased, with most of the change in joint configuration with speed lying in the null space of the reference condition’s joint configuration. Thus, differences in the terminal joint configuration across speed conditions cannot be attributed to systematic differences in terminal pointer-tip position. They instead reflect a substantial degree of motor equivalence.

In conclusion, the first question of this investigation was answered affirmatively. Significant differences existed among the speed conditions in the terminal joint configuration that were related to motor equivalence, i.e., disturbances induced by higher movement speeds were compensated by adjustments in joint coordination, tending to stabilize the pointer-tip position. Thus, a fixed terminal joint configuration does not appear to be planned by the CNS for typical movement tasks such as reaching and pointing, although the specification of particular patterns of joint configuration over time may be used by the nervous system when controlling other tasks, such as artistic endeavors or athletic performances. The answer to our second question was also affirmative. Reaching to targets in different parts of the arm’s workspace was accompanied by a significant amount of self-motion that scaled with movement speed. The results are consistent with a control system that takes advantage of available motor abundance, allowing for flexibility in the face of perturbations (Kelso et al. 1984; Cole and Abbs 1986, 1987), induced here by different speeds of reaching.

Appendix

Self-motion related to the three-dimensional movement of the hand refers to a component of the joint velocity vector that does not affect hand motion (Murray et al. 1994). Self-motion is only possible if joint motions are redundant. Although self-motion could be considered wasted motion with respect to movement efficiency, the ability to produce self-motion is crucial for the performance of multiple tasks simultaneously. For example, the redundancy of angular motion of arm joints allows one to flip a light switch with the elbow while carrying and stabilizing a tray of drinks, i.e., without negatively impacting the hand’s movement. Thus, the component of the joint velocities linked to flipping the switch is self-motion when viewed with respect to hand movement. In principle, without a specific secondary task as was the case in the current experiment, one could expect self-motion to be minimal, most of the joint velocity vector acting to move the hand in space.

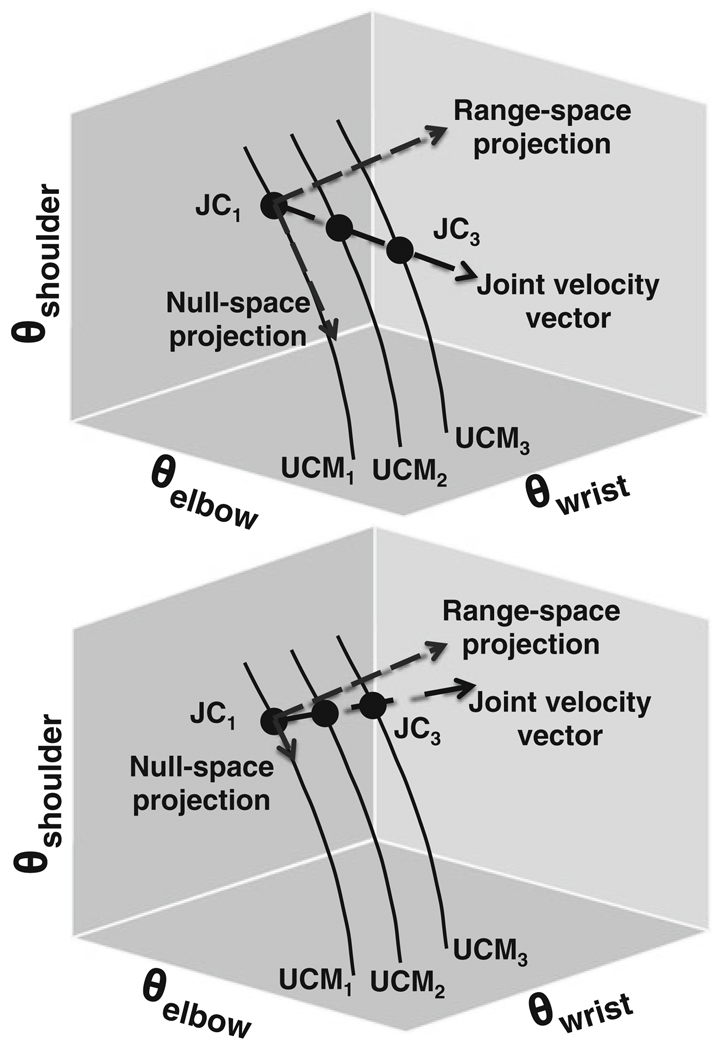
The conceptual framework of the method used here to differentiate between the component of the joint velocity vector that leads to hand movement, referred to by its technical term range-space motion (Murray et al. 1994), and the self-motion component is based on the uncontrolled manifold (UCM) variance analysis (Scholz and Schoner 1999). However, this analysis does not examine variances. The method can be illustrated by a simple example. Consider pointing with the hand in the horizontal plane where only three joint angles are available to transport the hand, shoulder horizontal flexion–extension, elbow flexion–extension, and wrist flexion–extension. To reach a target, at least two DOFs of joint motion are required, equivalent to the required two-dimensional hand position. Thus, there is one free joint DOF in this redundant system. That is, there exists a one-dimensional subspace (Fig. 5) within the space of the three arm joint motions within which a set of different combinations of shoulder, elbow, and wrist angles lead to an identical two-dimensional hand position. This subspace has been referred to as the uncontrolled manifold (UCM; Scholz and Schoner 1999) and a different UCM exists at each time point due to changing arm geometry. Thus, the first step in the self-motion analysis, like UCM analysis, was to estimate the UCM subspace at each data sample. First, the geometric model relating joint motion to hand motion is obtained as follows for the illustration:

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{l}_{\text{arm}}*\text{cos}({\theta }_{\text{shoulder}})+l_{\text{forearm}}*\text{cos}({\theta }_{\text{shoulder}}+{\theta }_{\text{elbow}})+l_{\text{hand}}*\text{cos}({\theta }_{\text{shoulder}}+{\theta }_{\text{elbow}}+{\theta }_{\text{wrist}})\hfill \\ l_{\text{arm}}*\text{sin}({\theta }_{\text{shoulder}})+l_{\text{forearm}}*\text{sin}({\theta }_{\text{shoulder}}+{\theta }_{\text{elbow}})+l_{\text{hand}}*\text{sin}({\theta }_{\text{shoulder}}+{\theta }_{\text{elbow}}+{\theta }_{\text{wrist}})\hfill \end{array}\right].$$

Fig. 5.

Cartoon examples of self-motion and range-space motion estimates from linear estimates of uncontrolled manifolds (UCMs). JC = joint configurations; Upper panel shows an example where there would be a relatively large amount of self-motion. The lower panel is an example of low self-motion. See “Appendix” for details

The Jacobian (J) of the geometric model is then computed using each instantaneous joint configuration ‘i’, ${[{\theta }_{\text{shoulder}}^{\mathrm{i}},{\theta }_{\text{elbow}}^{\mathrm{i}},{\theta }_{\text{wrist}}^{\mathrm{i}}]}^{\mathrm{T}}$, of each trial. The Jacobian is defined as the matrix of partial derivatives of the hand coordinates relative to the joint angles,

$$J(\theta )=\left[\begin{array}{c}\partial x/\partial {\theta }_{\text{shoulder}}\partial x/\partial {\theta }_{\text{elbow}}\partial x/\partial {\theta }_{\text{wrist}}\hfill \\ \partial y/\partial {\theta }_{\text{shoulder}}\partial y/\partial {\theta }_{\text{elbow}}\partial x/\partial {\theta }_{\text{wrist}}\hfill \end{array}\right]$$

The Jacobian is used to transform changes in joint angles or angular velocities into hand or more generally end-effector velocities, i.e., dr/dt = J(θ) * dθ/dt.

The null space of the Jacobian is then computed by singular value decomposition of the Jacobian in Matlab™, [u, s, v] = svd(J^T), where ‘T’ is the transpose of the Jacobian, ‘u’ is a matrix of eigenvectors, and ‘s’ is the diagonal matrix of eigenvalues. The first two columns of u are the range-space vectors, and the last column is the null-space vector in this 3D example.

The final step in the self-motion analysis is to project the instantaneous joint velocity vector ${[\mathrm{d}{\theta }_{\text{shoulder}}^{\mathrm{i}}/\text{dt},\mathrm{d}{\theta }_{\text{elbow}}^{\mathrm{i}}/\text{dt},\mathrm{d}{\theta }_{\text{wrist}}^{\mathrm{i}}/\text{dt}]}^{\mathrm{T}}$ into the range space and null space and then compute the lengths of projection.

Figure 5 provides a cartoon illustration of the results of this procedure. In the figure, three hypothetical one-dimensional UCMs representing three consecutive time points are illustrated. The solid filled circles lying on each UCM represent joint angle combinations, or joint configurations, for a given trial at each time point. Note that given the definition of the UCM, combinations of joints lying anywhere along each line would produce the same 2D hand position (but a different hand position for each UCM). Thus, movement of the hand can be conceived of as a transition among sequences of UCMs. The heavy dashed line in each panel represents the change in joint configuration, or the joint velocity vector. If most of the joint velocity vectors act to move the hand in space, then this vector should be relatively perpendicular to the UCMs. If, instead, there is a significant amount of self-motion, then the vector will form a more acute angle with the UCMs. The upper panel is an illustration of the later situation. The lower panel represents a hand movement accompanied by little self-motion. The different situations are estimated by the lengths of projection of the joint velocity vector into each subspace, i.e., the null space (self-motion) and its complement (range-space motion). These projection lengths are also illustrated in the figure.