Multi-Contrast Human Neonatal Brain Atlas: Application to Normal Neonate Development Analysis

Abstract

MRI is a sensitive method for detecting subtle anatomic abnormalities in the neonatal brain. To optimize the usefulness for neonatal and pediatric care, systematic research, based on quantitative image analysis and functional correlation, is required. Normalization-based image analysis is one of the most effective methods for image quantification and statistical comparison. However, the application of this methodology to neonatal brain MRI scans is rare. Some of the difficulties are the rapid changes in T1 and T2 contrasts and the lack of contrast between brain structures, which prohibits accurate cross-subject image registration. Diffusion tensor imaging (DTI), which provides rich and quantitative anatomical contrast in neonate brains, is an ideal technology for normalization–based neonatal brain analysis. In this paper, we report the development of neonatal brain atlases with detailed anatomic information derived from DTI and co-registered anatomical MRI. Combined with a diffeomorphic transformation, we were able to normalize neonatal brain images to the atlas space and three-dimensionally parcellate images into 122 regions. The accuracy of the normalization was comparable to the reliability of human raters. This method was then applied to babies of 37 to 53 post-conceptional weeks to characterize developmental changes of the white matter, which indicated a posterior-to-anterior and a central-to-peripheral direction of maturation. We expect that future applications of this atlas will include investigations of the effect of prenatal events and the effects of preterm birth or low birth weights, as well as clinical applications, such as determining imaging biomarkers for various neurological disorders.

Introduction

Recent advances in obstetrics and neonatology have led to a marked improvement in survival of babies with perinatal insults. However, the neurological and psychological morbidities associated with these problems still remain (D'Angio et al., 2002; Marlow, 2004; Vohr et al., 2000; Wilson-Costello et al., 2005). These resultant challenges are not restricted to obvious disabilities, such as cerebral palsy, epilepsy, and mental retardation, but also include impaired academic achievement and behavioral disorders that manifest after these children reach school-age (Hack and Fanaroff, 1999; Hack et al., 2000; Perlman, 2001). Despite the importance of treatment, there are currently a limited number of interventional options to reduce or prevent the neurologic morbidity suffered by babies with prenatal problems (Als et al., 2004; Blauw-Hospers and Hadders-Algra, 2005). One of the reasons such treatments have not been developed is that the diagnosis depends on the neurological evaluation, which can detect only substantial brain damage, while many neuro-cognitive symptoms are not easily detectable during the first year of life. To develop new treatments, methods are needed that can detect and quantify even subtle abnormalities of the neonatal brain.

Imaging modalities have played an important role in detecting damage to the neonatal brain. MRI, in particular, has advantages in showing subtle abnormalities, such as small hemorrhagic lesions, ischemic lesions, and signal abnormalities that cannot be appreciated by other modalities like CT or ultrasound. Previous studies have reported that there is a substantial correlation between several types of abnormalities and their prognosis (De Vries et al., 1999; Hayakawa et al., 1996; Inder et al., 2005; Roelants-van Rijn et al., 2001; Shah et al., 2006; Woodward et al., 2006). However, there are several reasons why MRI has not been routinely used to evaluate the neonatal brain. First, MR contrast in the neonate brain varies considerably with age, and it is difficult to understand what constitutes a normal appearance and what degree of variability constitutes a pathological condition. Second, the location and the extent of abnormalities may vary considerably. To make MRI truly applicable to evaluate abnormalities in the neonatal brain, a quantitative characterization of the entire normal brain anatomy is an essential first step. For MRI analysis of the adult brain, normalization-based quantitative analysis methods are widely used, which is an effective way to quantitatively characterize the brain anatomy. For pediatric brain analysis, attempts have been made to create age-specific brain templates (Fonov et al., 2010; Wilke et al., 2008; Wilke et al., 2003; Yoon et al., 2009). However, for the neonate population, there are only a small number of studies using image normalization (Kazemi et al., 2008; Kazemi et al., 2007; Shi et al., 2009). One of the major issues has been the lack of a reliable method for delineating neonatal brain structures, which is required for accurate normalization of one brain to another. This difficulty is due to a reduction in gray matter/white matter contrast in both T1- and T2-weighted images compared to the adult brain. There have been attempts to increase the accuracy of tissue segmentation, using a region-wise comparison approach and a multi-modal image set registration, which successfully increased the accuracy of the tissue classification (Shi et al., 2010). This method could increase the normalization accuracy, based on the T1- and T2-weighted images (Lorenzen et al., 2006; Shi et al., 2009). Accurate registration of intra-white matter structures is, on the other hand, still challenging due to the lack of contrasts.

Diffusion Tensor Imaging (DTI)–derived contrasts (diffusion anisotropy and fiber orientation) can provide rich anatomical information about the pre-myelinated neonatal brain (Huang et al., 2006); in fact, most of the white matter structures seen in the adult brain with DTI have already been established in the neonatal brain and can be visualized by DTI (Zhang et al., 2007). Therefore, DTI contrast has the potential to guide normalization of the neonatal brain more accurately than conventional relaxation-based MRI. In addition, DTI can provide quantitative measures related to water diffusivity, which is believed to reflect certain maturation processes, such as axonal growth and myelination (Beaulieu, 2002; Dubois et al., 2008; Mori and Zhang, 2006; Mukherjee et al., 2002; Ramenghi et al., 2009). These quantitative measures could be statistically analyzed in a tract-specific manner using normalization-based DTI analyses, even for the pre-myelinated neonatal brain (Anjari et al., 2007; Goodlett et al., 2009).

In this study, we created an MRI atlas for neonate brain analysis. This includes a group-averaged atlas and a single-subject-based atlas that includes T1- and T2-weighted contrasts and DTI-derived contrasts. One hundred and twenty-two brain structures were parcellated in the atlas. In the past, we have developed a multi-contrast (T1-, T2-weighted, and DTI) adult brain atlas (JHU -MNI atlas) and a normalization-based quantification analysis method for quantitative MRI analysis (Oishi et al., 2009; Oishi et al., 2008). Here, we extended this method to enable analysis of neonatal brains by combining the neonatal brain atlas and multi-contrast diffeomorphic warping. The method was applied to the DTIs from normal-term infants to measure the accuracy of atlas-based segmentation. In addition, the age dependency of DTI parameters was characterized using 33 neonatal images from infants who ranged in age from 37 to 53 post-conceptional weeks. Finally, the normal average values and standard deviations of diffusion parameters of 24 brain structures were characterized from normal-term neonates from 37 to 43 post-conceptional weeks to create a term-equivalent database of DTI parameters.

Methods

Creation of multi-contrast MRI atlases

We created group-averaged atlases and a single-subject atlas. The purpose of a group-averaged atlas is to determine the average shape and size of the neonate brain. This atlas can be used as a template for the brain normalization using linear transformations or nonlinear transformations with image “smoothing.” However, as a result of averaging, the sharpness of the image contrast can be lost. Therefore, a single-subject atlas with the size adjusted to that of the group-averaged atlas was created as well, providing a template for highly elastic nonlinear transformations, which require sharp image features (Oishi et al., 2009).

Subjects

The data used to create the atlas were based on a de-identified database of normal neonate brain MRI scans. The subjects recruited to create the database were born at the Johns Hopkins Hospital, which is a regional referral, subspecialty care center. The database contains 25 brain images from 0- to 4-day-old (38 to 41 post-conceptional weeks) healthy, full-term neonates, including 15 boys and 10 girls. For the database creation, permission was obtained from the Johns Hopkins Medicine Institutional Review Board and written, informed consent was provided by the infants’ parents.

MRI scans

The scans were performed without sedation with infants asleep. To ensure that neonates were sleeping during the scan, neonates were well fed before the scan and were well wrapped in a blanket with the ears covered with an ear muff. The subjects were then placed in cushions that occupied the space between the subject and the RF coil. Images were acquired using a 3.0 T Philips scanner equipped with gradients of up to 8.0 G/cm per direction. The RF was transmitted by a body coil and the receive coil was an 8-element SENSE coil, in which two of the coils were combined to be connected to a 6-channel receiver. After T₁-weighted scout imaging, Diffusion Tensor imaging (DTI), Double-echo fast spin-echo (DE-FSE), and Magnetization-Prepared Rapid Gradient Echo (MPRAGE) sequences were used to obtain images.

A single-shot EPI with SENSE acquisition was used for DTI (Bammer et al., 2001; Jaermann et al., 2004; Pruessmann et al., 1999). The imaging matrix was 80 × 80 with a field-of-view of 150 × 150 mm, which gave a nominal 1.88 mm isotropic in-plane resolution. These were zero-filled to 256 × 256 mm. The slice orientation was axial with a 1.9 mm thickness parallel to the anterior–posterior commissure (AC - PC) line. Forty to fifty slices covered the entire hemisphere and the brainstem. Echo time was 71 ms and repetition time was more than 3s. A SENSE reduction factor of 3 was used. Diffusion-weighting was applied along 30 independent axes (Jones et al., 1999) with b = 700 s/mm², in addition to 5 minimally diffusion -weighted images. The scanning time for one complete DTI dataset was approximately 5 min. Co-registered DE-FSE images were also acquired with a first echo time of 27.7 ms, a second echo time of 120 ms, and a repetition time of 4.5 sec. The imaging matrix was 80 × 70 with a field of view of 150 × 150 mm, zero-filled to 256 × 256, and an axial slice thickness of 1.9 mm. For MPRAGE, we used an echo time of 4.6 ms and a repetition time of 9.9 ms with an imaging matrix of 160 × 160 × 80 - 100 and a field of view of 150 × 150 × 72 – 90 mm, zero-filled to 256 × 256 × 80 - 100 matrix acquired parallel to the AC - PC line

DIT data processing

The raw diffusion-weighted images (DWIs) were first co-registered to one of the minimally diffusion-weighted images and corrected for participant motion and the linear portion of eddy current distortions using a 12-parameter affine transformation of Automated Image Registration (AIR) (Woods et al., 1998). The six elements of the diffusion tensor were calculated for each pixel with multivariate linear fitting using DtiStudio (H. Jiang and S. Mori, Johns Hopkins University, Kennedy Krieger Institute, lbam.med.jhmi.edu or www.MriStudio.org) (Jiang et al., 2006; Mori et al., 2008; Pierpaoli et al., 2001). After diagonalization, three eigenvalues and eigenvectors were obtained. For the anisotropy map, fractional anisotropy (FA) was used (Pierpaoli and Basser, 1996). The eigenvector (v1) associated with the largest eigenvalue was used as an indicator of fiber orientation. For the mean diffusivity (MD) map, the average of three eigenvalues of the tensor was used. A 24-bit, color-coded orientation map was created by assigning red, green, and blue channels to the x (right-left), y (anterior-posterior), and z (superior-inferior) components of the v1, where intensity was proportional to FA (Makris et al., 1997; Pajevic and Pierpaoli, 1999). DTIs were then re-sliced to 0.6 mm isotropic resolution (180 × 220 × 180 matrix). B0-susceptibility distortion was corrected using a previously published method (Huang et al., 2008). Briefly, the least diffusion-weighted image (b0) of the DTI was warped to the T2-weighted contrast of the DE-FSE image (echo time: 120 ms) that was resliced to 0.6 mm isotropic resolution (180 × 220 × 180 matrix), using a large deformation diffeomorphic metric mapping (LDDMM) (Beg et al., 2005; Miller et al., 2006), and the warping was applied to the tensor field. The tensor transformation was based on a method proposed by (Xu et al., 2003). MPRAGE was also resliced to the same image matrix and was linearly co-registered to the DE-FSE using a six-parameter rigid transformation of AIR. These procedures resulted in a co-registered set of MPRAGE, DE-FSE, and B0–distortion-corrected DTI, with a 0.6 mm isotropic resolution. All images were reviewed for artifacts, and twenty DTIs, twenty T2-weighted images, and fourteen T1-weighted images were selected out of 25 images as high quality images suitable for creating an atlas with the following procedure.

Atlas creation

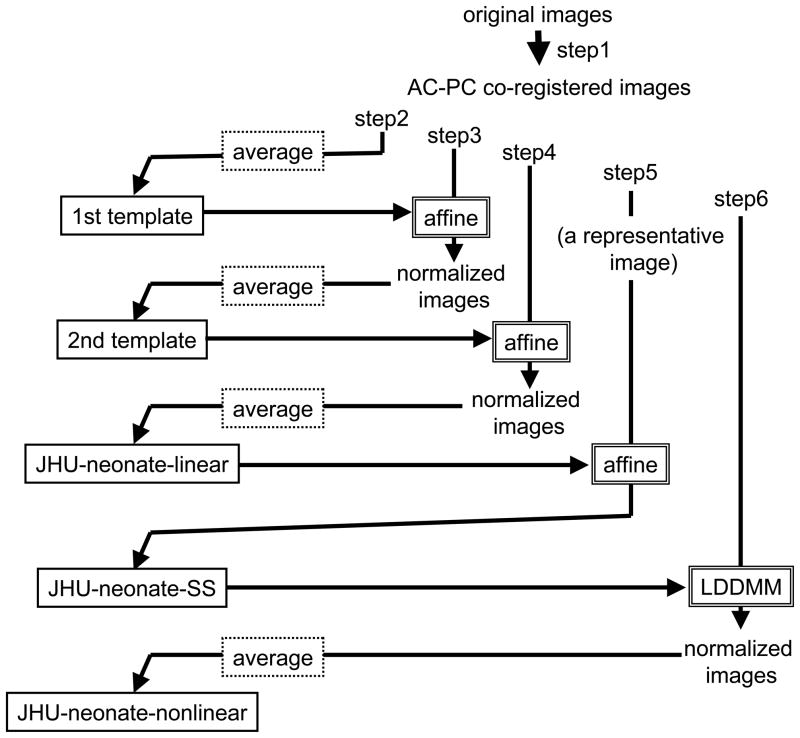
The procedure followed six steps (Fig. 1) similar to the concept for creating the adult group-averaged atlas (ICBM-152) (Mazziotta et al., 2001; Mazziotta et al., 1995) and the single-subject atlas (colin27)(Aubert -Broche et al., 2006; Collins et al., 1998; Holmes et al., 1998), all of which are commonly used in the neuroimaging community. The key is to align the anterior commissure-posterior commissure (AC–PC) line using a linear transformation. However, for the neonate brain, a single-subject atlas, like the Talairach atlas for adult brains, which can be used as a reference for the AC–PC line has not been established yet. Therefore, the common AC–PC line was set according to the shape and size of the averaged brain. First, the orientation of the midline and the AC–PC line of each T₂ weighted image were aligned along the Y-axis of the image by rigid rotation using two-point landmarks. Then, all images from the 20 subjects were aligned at the AC. The shift and rotation matrices used for the co-registration were also applied to the MPRAGE and the DTI. Second, an average image of the co-registered T₂-weighted images was created. This averaged image worked as a tentative template for the next step (1^st template). Third, each co -registered T₂-weighted image was normalized to the 1^st template using an affine transformation of AIR to create the average image (2^nd template). Fourth, each co -registered T₂-weighted image was normalized to the 2^nd template using an affine transformation to create the average image. The purpose of this step was to obtain a sharper edge of the averaged image than that of the 2^nd template. The linear transformation matrices derived from this step were also applied to the co-registered MPRAGE and DTI to create an averaged MPRAGE and DTI. The set of averaged T₂-weighted images, MPRAGE, and DTI were named the JHU-neonate-linear, since these images were created by averaging linearly normalized images. Fifth, a single-subject image with the brain shape best fitted to that of the JHU- neonate-linear was selected from the 20 images, and linearly normalized to the T₂-weighted image of the JHU-neonate-linear. The resultant transformation matrix was applied to the co-registered MPRAGE and DTI to create a single-subject atlas with a brain size and shape almost identical to that of the JHU-neonate-linear. These images were named the JHU-neonate-SS. Finally, co-registered DTI images were nonlinearly normalized to the single-subject atlas using dual-channel LDDMM (Ceritoglu et al., 2009), with MD and FA maps to drive the transformation. The resultant nonlinear transformation matrices were also applied to the co-registered MPRAGE and T₂-weighted image to create a set of averaged MPRAGE, T₂-weighted image, and DTI. This set was named the JHU-neonate-nonlinear, since these images were created by averaging nonlinearly normalized images. All normalization was performed using DiffeoMap (www.mristudio.org, Johns Hopkins University).

Figure 1.

Diagram showing the steps required to create group-averaged neonate atlases (JHU- neonate-linear and JHU-neonate-nonlinear) and a single-subject atlas (JHU-neonate-SS).

Parcellation of the MRI atlas

The deep white matter structures identified in our previous studies of adult brains (Mori et al., 2008; Mori et al., 2005; Oishi et al., 2009)were readily identified in the neonate brains using DTI contrasts. We manually parcellated these structures on the JHU-neonate-SS using a color-coded orientation map as a guide (Appendix fig.1). The parcellation followed the definition of our previous adult atlas as much as possible. As previously reported (Zhang et al., 2007), the superior longitudinal fasciculus of neonates was not necessarily clear for its entire length and had a fragmented appearance. Therefore, the approximate location was estimated by extrapolating the location from the adult atlas, and connecting the fragmented sections. After the core white matter regions were defined, we identified the cortical surface and the subcortical gray matter using the MPRAGE and T₂-weighted images. Between the brain surface and the deep white matter, we located the cerebral cortex and the superficial white matter adjacent to the cortex. We parcellated this area according to the gyral pattern. The nomenclature followed our previous adult MRI atlas (Oishi et al., 2009), based on Talairach’s atlas (Talairach and Tournoux, 1988). For these manual parcellation procedures, ROIEditor (www.Mristudio.org) was used with inspection of all three slice orientations. A total of 122 structures were parcellated, as shown in the Appendix.

Appendix figure.

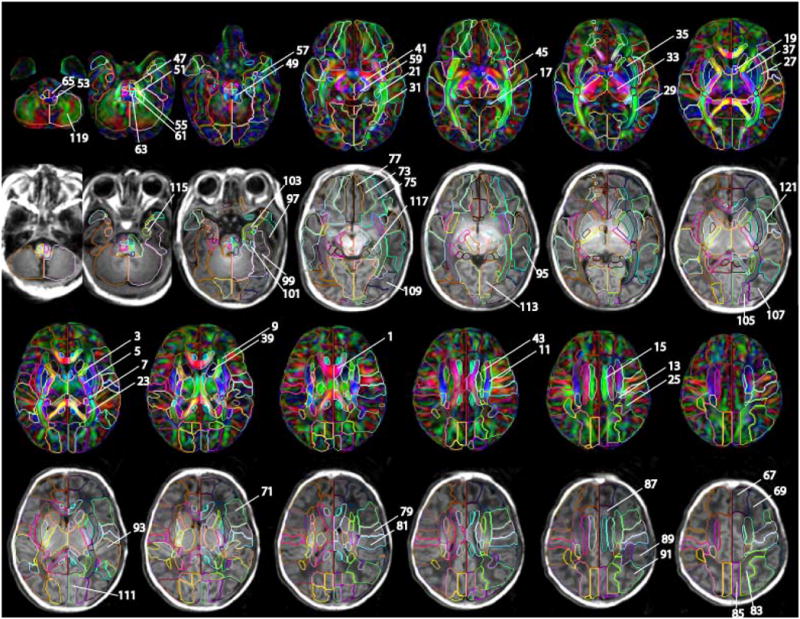
The detail of the parcellation map on the JHU-neonate-SS atlas. Numbers indicated in the figure are identical to the structure number listed in the appendix table. For the manual parcellation, we used the following criteria. The first criterion was the clear boundary defined by fiber orientation difference, which is obvious even in the color-coded orientation map of the group averaged atlas (JHU-neonate-nonlinear). This procedure allowed us to parcellate deep gray and white matter structures. The exceptions were between anterior/superior and superior/posterior subdivision of the corona radiata, and between posterior thalamic radiation and sagittal stratum, which were arbitrary defined. The second criterion was a pattern of gyrus/sulcus formation, which is obvious in T₁-weighted atlas of JHU-neonate-SS. Lastly, we extend the sulcus to the deep white matter structures as smooth as possible. Many boundaries in this paper were consistent with our three previous papers to establish the adult atlases (Mori et al., 2008; Oishi et al., 2009; Oishi et al., 2008)

Appendix.

Parcellated structures and abbreviations

	abbreviation	structure	left/right	volume (mm3)
1	CC	corpus callosum	left	3677
2	CC	corpus callosum	right	4194
3	ALIC	anterior limb of internal capsule	left	883
4	ALIC	anterior limb of internal capsule	right	889
5	PLIC	posterior limb of internal capsule	left	1181
6	PLIC	posterior limb of internal capsule	right	1146
7	RLIC	retrolenticular part of internal capsule	left	345
8	RLIC	retrolenticular part of internal capsule	right	337
9	ACR	anterior corona radiata	left	1031
10	ACR	anterior corona radiata	right	913
11	SCR	superior corona radiata	left	1692
12	SCR	superior corona radiata	right	1946
13	PCR	posterior corona radiata	left	545
14	PCR	posterior corona radiata	right	606
15	CGC	cingulum cingular part	left	1009
16	CGC	cingulum cingular part	right	1064
17	CGH	cingulum hippocampal part	left	632
18	CGH	cingulum hippocampal part	right	559
19	Fx	fornix	left	865
20	Fx	fornix	right	1139
21	ST	stria terminalis	left	785
22	ST	stria terminalis	right	754
23	TAP	tapetum	left	688
24	TAP	tapetum	right	670
25	SLF	superior longitudinal fasciculus	left	667
26	SLF	superior longitudinal fasciculus	right	738
27	EC	external capsule	left	1818
28	EC	external capsule	right	1696
29	PTR	posterior thalamic radiation	left	1695
30	PTR	posterior thalamic radiation	right	1687
31	SS	sagittal stratum	left	1048
32	SS	sagittal stratum	right	997
33	Thal	thalamus	left	3824
34	Thal	thalamus	right	4209
35	Put	putamen	left	1301
36	Put	putamen	right	1153
37	GP	globus pallidus	left	473
38	GP	globus pallidus	right	418
39	Cau	caudate nucleus	left	1181
40	Cau	caudate nucleus	right	1254
41	CP	cerebral peduncle	left	500
42	CP	cerebral peduncle	right	497
43	SFO	superior fronto-occipital fasciculus	left	217
44	SFO	superior fronto-occipital fasciculus	right	234
45	IFO	inferior fronto-occipital fasciculus	left	437
46	IFO	inferior fronto-occipital fasciculus	right	438
47	CST	corticospinal tract	left	157
48	CST	corticospinal tract	right	191
49	SCP	superior cerebellar peduncle	left	303
50	SCP	superior cerebellar peduncle	right	415
51	MCP	middle cerebellar peduncle	left	696
52	MCP	middle cerebellar peduncle	right	747
53	ICP	inferior cerebellar peduncle	left	171
54	ICP	inferior cerebellar peduncle	right	175
55	PCT	pontine crossing tract	left	149
56	PCT	pontine crossing tract	right	210
57	UNC	uncinate fasciculus	left	163
58	UNC	uncinate fasciculus	right	203
59	midbrain	midbrain	left	781
60	midbrain	midbrain	right	983
61	pons	pons	left	143
62	pons	pons	right	192
63	ML	medial lemniscus	left	112
64	ML	medial lemniscus	right	163
65	Medulla	medulla oblongata	left	211
66	Medulla	medulla oblongata	right	256
67	SFG	superior frontal gyrus	left	12457
68	SFG	superior frontal gyrus	right	13720
69	MFG	middle frontal gyrus	left	10497
70	MFG	middle frontal gyrus	right	11650
71	IFG	inferior frontal gyrus	left	6151
72	IFG	inferior frontal gyrus	right	5565
73	MFOG	medial fronto-orbaital gyrus	left	2706
74	MFOG	medial fronto-orbaital gyrus	right	1956
75	LFOG	lateral fronto-orbital gyrus	left	2912
76	LFOG	lateral fronto-orbital gyrus	right	2878
77	RG	gyrus rectus	left	2247
78	RG	gyrus rectus	right	2857
79	PrCG	precentral gyrus	left	7618
80	PrCG	precentral gyrus	right	5993
81	PoCG	postcentral gyrus	left	6930
82	PoCG	postcentral gyrus	right	5443
83	SPL	superior parietal lobule	left	7535
84	SPL	superior parietal lobule	right	7957
85	PrCu	precuneus	left	3289
86	PrCu	precuneus	right	3925
87	CingG	cingular gyrus	left	7963
88	CingG	cingular gyrus	right	9947
89	SMG	supramarginal gyrus	left	4200
90	SMG	supramarginal gyrus	right	4093
91	AG	angular gyrus	left	7268
92	AG	angular gyrus	right	6439
93	STG	superior temporal gyrus	left	7056
94	STG	superior temporal gyrus	right	7140
95	MTG	middle temporal gyrus	left	6565
96	MTG	middle temporal gyrus	right	5693
97	ITG	inferior temporal gyrus	left	4188
98	ITG	inferior temporal gyrus	right	4326
99	Fu	fusiform gyrus	left	5078
100	Fu	fusiform gyrus	right	5412
101	PHG	parahippocampal gyrus	left	531
102	PHG	parahippocampal gyrus	right	590
103	ENT	entrhinal cortex	left	887
104	ENT	entrhinal cortex	right	903
105	SOG	superior occipital gyrus	left	2293
106	SOG	superior occipital gyrus	right	2139
107	MOG	middle occipital gyrus	left	6702
108	MOG	middle occipital gyrus	right	6935
109	IOG	inferior occipital gyrus	left	3135
110	IOG	inferior occipital gyrus	right	2854
111	Cu	cuneus	left	3173
112	Cu	cuneus	right	2787
113	LG	lyngual gyrus	left	5004
114	LG	lyngual gyrus	right	5526
115	Amyg	amygdala	left	286
116	Amyg	amygdala	right	310
117	Hippo	hippocampus	left	936
118	Hippo	hippocampus	right	826
119	Cerebrellum	cerebellar hemisphere	left	11967
120	Cerebrellum	cerebellar hemisphere	right	12707
121	Ins	insular cortex	left	1662
122	Ins	insular cortex	right	1671

Application to DTI of normal-term infants

We applied the JHU-neonate-SS atlas and LDDMM to DTI datasets from healthy neonates to measure the size and DTI parameters of each segmented brain structure. The segmentation accuracy was also measured by comparing the automated results with manual segmentation for selected brain structures. We used a de-identified database of normal infant brain MRI scans who were born at the Queen’s Medical Center, Honolulu, Hawaii. The database contains 33 brain images from 22 healthy full-term babies (ranging from 37 to 53 post-conceptional weeks), including 9 boys and 13 girls. For the brain imaging, permission was obtained from the Co-operative Institutional Review Board of the Queen’s Medical Center and the University of Hawaii, and written informed consent was provided by the infants’ parents or legal guardians.

MRI scans and image processing

A setup that was similar to the scans performed to create the JHU-neonate templates was used to scan these infants without sedation. Infant motion was minimized by wrapping the infants in a vacuum immobilization mat (Noras MRI Products, Hoechberg, Germany) with earmuffs. Images were acquired using a 3.0 T Siemens TIM Trio scanner (Siemens Medical Solutions, Erlangen, Germany) equipped with a twelve-channel, phased-array RF coil for parallel imaging. A single-shot EPI with SENSE acquisition was used for DTI. The imaging matrix was 160 × 160 with a field-of-view of 160 × 160 mm, which resulted in a 1.0 mm isotropic in-plane resolution. The slice orientation was axial with 2.0 mm thickness. Forty to fifty slices covered the entire cerebral hemisphere. Echo time was 106 ms and repetition time was 7 to 9 sec, depending on the specific absorption rate limitations. Diffusion-weighting was applied along 12 independent axes with b = 1000 s/mm², in addition to a minimally diffusion-weighted image. The DTI processing followed exactly the method we used to create the JHU-neonate templates. The procedures resulted in DTI maps with a 0.6 mm isotropic resolution and a 180 × 220 × 180 matrix.

Normalization of the images

Data from each subject was first co-registered to the JHU-neonate-SS space and then linearly normalized to the JHU-neonate-SS using 12-parameter affine transformation. The resultant matrix was applied to the tensor field to create an affine-normalized tensor field as described in (Xu et al., 2003). FA and MD were calculated from the normalized tensor field and then nonlinearly normalized to the FA and MD map of the JHU-neonate-SS using LDDMM. The resultant matrix was applied to the affine-normalized tensor field to create an LDDMM-normalized tensor field. During this procedure, reverse-transformation, which can transform the JHU-neonate-SS atlas to each co-registered image, was also created. DiffeoMap was used to run LDDMM, as described elsewhere (Oishi et al., 2009).

Measurement of registration quality

To measure the accuracy of the white matter registration, we selected five images from neonates of 40 post-conceptional weeks and four images from infants of 49 - 52 post-conceptional weeks. Two types of accuracy measurements, Dice’s coefficient (Dice) and L1 error, were used. We first delineated ten brain structures on the normalized images manually (manual delineation), which worked as a benchmark for the registration accuracy measurement. Then, we overlaid the parcellation map onto the JHU-neonate-SS atlas to delineate the brain structures automatically (automated delineation), and see how accurately the overlap reflected the manual delineation.

Manual delineation

Ten brain structures were delineated manually on five pre-determined 2D slices of the normalized images. The criteria for structural delineation closely followed the method of parcellation in the JHU-neonate-SS atlas. Table 1 shows the list of these WM structures. The delineated set of structures was named the “standard ROI set.” To investigate inter-rater variability, two raters (K.O. and A.F., neurologist and neuroradiologist) performed the manual delineation.

Table 1.

List of seven brain structures and slice locations for manual delineation

Axial #	structures
z = 91	posterior limb of the internal capsule, the putamen, and the external capsule
z = 80	anterior limb of the internal capsule, thalamus
z = 111	cingulum
Sagittal #
x = 90	corpus callosum

Automated delineation

The “standard ROI set” was readily identified by superimposing the parcellation map of the JHU-neonate-SS atlas onto the normalized images.

Accuracy measurements

The various structures defined by automated and manual delineation were saved as binary maps, in which the structure of interest was defined as “1” and the rest of the pixels were “0.” By superimposing the binary maps from the automated and manual methods, each pixel could be categorized into one of three classes: (1) pixels that were outside the structures (“0”) in either method (nn); (2) pixels that were defined as the structure of interest (“1”) in only one of the two methods (pn, np); and (3) pixels that contained the structure in both methods (pp). After this categorization, reliability analyses were performed using the Dice metric, which evaluates overlap of the two areas defined as 2pp/(pn + 2pp + np), and the L1 error, which evaluates misclassification error defined as (1-pp/(pp+pn+np))/2 (Ratnanather et al., 2004). The Dice and L1 error metrics within the manual trials by two different raters provided the level of precision for manual delineation, which was treated as the gold standard. Then, the Dice and L1 error metrics comparing the automated and manual delineation were calculated for each ROI.

DTI measurement of the segmented brain structures

To test the feasibility of the atlas-based analysis to detect the diffusion properties of the infant brain using the JHU-neonate-SS and LDDMM, we measured FA and MD of 20 white matter structures and four deep gray structures of the 33 DTIs normalized to the JHU-neonate-SS. By using ROIEditor, the parcellation map was overlaid on the normalized FA and MD maps to calculate the mean and standard deviation for each structure. The cortical areas, brain stem, and the cerebellar areas were omitted because only DTI was available, and about half the images did not cover the entire brainstem or cerebellum.

Power analysis to detect FA and MD alterations

A power analysis was performed to test the ability to detect subtle abnormalities, such as a 10% alteration of FA and MD for each brain structure using the JHU-neonate-SS atlas and LDDMM. Past literature indicates that the DTI parameters for several white matter bundles change drastically during the month after birth (Dubois et al., 2008). Therefore, for the cross-sectional group analysis, we needed to select subjects from a narrow age range. Since we assumed that the JHU-neonate atlas would be used to normalize term-equivalent neonatal brains, we selected ten full-term neonates, scanned at 38–43 post-conceptional weeks, for the analysis. We investigated the required number of subjects to detect a 10% alteration in MD and FA of the target group, compared to the control group, with p < 0.05, using a t-test. The software G*power (Faul et al., 2007) was used for the analysis.

Results

Multi-contrast neonatal brain atlas

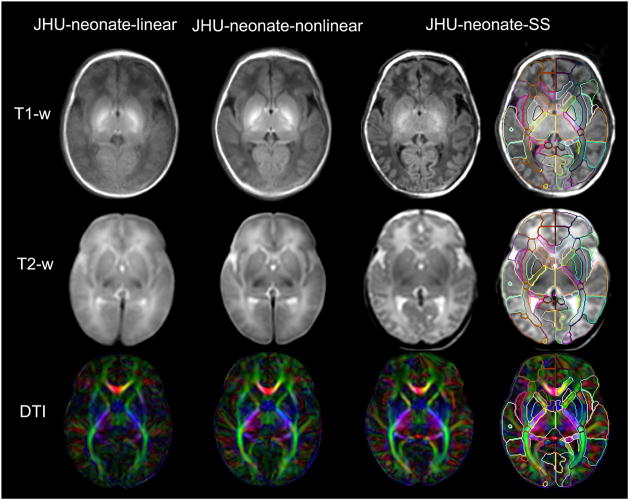
Fig. 2 shows the images from the JHU-neonate-linear, the JHU-neonate-nonlinear, and the JHU-neonate-SS. The gray matter/white matter contrasts of the T1- and T2-weighted images were opposite to those of adults, and had poor contrast inside the white matter area. Conversely, DTI provided superior contrast to reveal the white matter anatomy. The core white matter structures, in particular, such as the internal capsule, were easily identified even in the group-averaged images. The rightmost column shows the parcellation map overlaid on the JHU-neonate-SS. This parcellation map works as a set of pre-defined ROIs for automated brain parcellation after the normalization.

Figure 2.

Multi-contrast atlases created in this study. The upper row shows a T1-weighted atlas, the middle row shows a T2-weighted atlas, and the lower row shows a DTI atlas (color-coded orientation map of the diffusion anisotropy were used as the representative image). The JHU-neonate-linear atlas (the leftmost column) represents the average size and shape of the twenty images used to create the template. The sharpness of the edge of each brain structure seen in the JHU-neonate-nonlinear atlas (the column next to the linear template) indicates that the LDDMM transformation was fairly accurate. The JHU-neonate-SS atlas (the rightmost two columns; right column with the parcellation map) was used as a template for the normalization using LDDMM.

Measurement of registration quality

Fig. 3 shows the original neonate images and the images normalized to the JHU-neonate-SS atlas, overlaid by the parcellation map that can qualitatively demonstrate the registration accuracy. Structures that are grossly mis-registered are indicated by yellow arrows. After affine transformation, overall brain shapes were well-normalized to the JHU-neonate-SS space. However, registration accuracy of the inner structures was low, as can be appreciated from the mismatch between the superimposed parcellation map and underlying white matter structures. These registration errors were much improved after LDDMM transformation.

Figure 3.

Examples of the normalization using 12-parameter affine transformation of AIR and multi-channel LDDMM. The original neonate images from 40 post-conceptional weeks (left two images) and 50 post-conceptional weeks (right two images) are shown in the upper row. Note that the size of the brain is larger at 50 post-conceptional weeks. The images were normalized to the JHU-neonate-SS space and overlaid by the parcellation map that can qualitatively demonstrate the registration accuracy. The mis-registrations seen in the ALIC, PLIC, RLIC, CC, EC, and PTR after affine normalization were corrected after LDDMM. See the appendix for abbreviations.

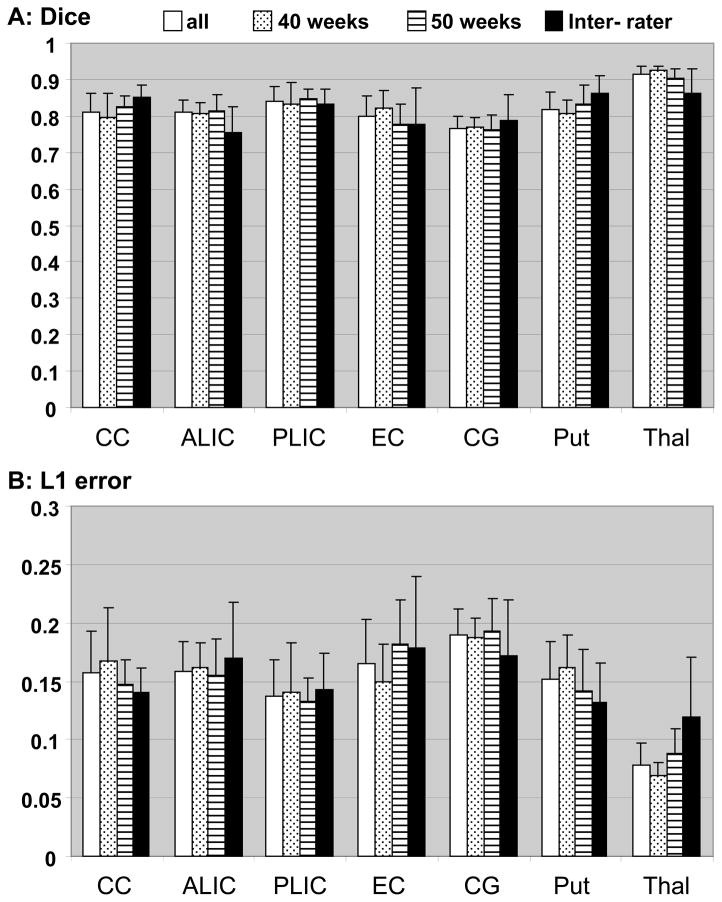
Fig. 4 shows the result of Dice and L1 error analyses. In most areas, the Dice scores between automated and manual delineation were over 0.8, which indicate almost perfect registration accuracy. Even in the thin, string-like structure of the cingulum, the Dice measure was more than 0.75, which indicates substantial registration accuracy. Misclassification measured by L1 error was comparable to that of the inter-rater comparison (Fig. 4B). There was no difference in the registration accuracy measured by Dice and L1 errorbetween brains from 40 post -conceptional weeks and 49–52 post-conceptional weeks. There was also no difference in the accuracy between manual–automated ROI registration and manual–manual ROI registration (inter-rater variability). Therefore, this method could successfully normalize the brain images ranging from 40 to 52 post-conceptional weeks, thus rivaling the reproducibility of the manual segmentation.

Figure 4.

The Dice (A) and L1 error (B) measures for each brain structure. The data are from averageof all ten infants (all: white bars), average of five 40 post-conceptional weeks (40 weeks: bars with dots), average of five 49 – 52 post-conceptional weeks(49 – 52 weeks: ho rizontal lines), and inter-rater comparison (Inter-rater: black bars). There was no difference in the Dice and L1 error measures between all and inter-rater, and between 40 weeks and 49 – 52 weeks of age.

Diffusion properties of the normal-term-birth neonate brain

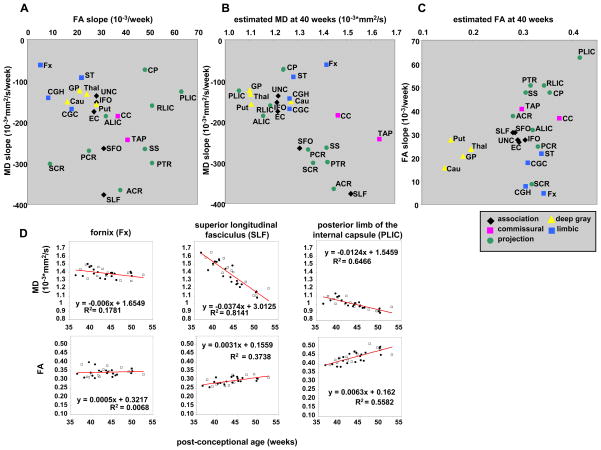
Overall, we found a general trend toward decreasing MD and increasing FA with age, which is interpreted as the maturation of the brain structures. In addition, there is a structure-specific maturation pattern. The slope and the intercept (40 post -conceptional week estimated value) of MD and FA against the age were calculated by linear regression. Fig. 5 shows a chart with scatter plots that indicate the relation between the MD slope and the FA slope (Fig. 5A), the estimated MD at 40 post-conceptional weeks and the MD slope (Fig. 5B), and the estimated FA at 40 post -conceptional weeks and the FA slope of the 24 structures (Fig. 5C). In Fig. 5D, three representative areas with markedly different slopes and intercepts are shown, which should provide an idea about the relationships between data variability and effect size. Generally, the gray matter, limbic fibers (the fornix, the stria terminalis, and the cingulum), and some of the association fibers (the uncinate, the external capsule, and the inferior fronto-occipital fasciculus) show relatively slow decreases in MD and slow increases in FA with age. There was a tendency of inverse relationship between the slope and the 40-week intercept for MD(Fig. 5B) but not for FA (Fig. 5C). Within projection fibers, fibers that are located distant from the brainstem (the corona radiata, posterior thalamic radiation, and the sagittal striatum) show a higher MD at 40 weeks and a faster MD decrease with age than those that are located close to the brainstem (the posterior limb of the internal capsule, the retrolenticular part of the internal capsule, and the cerebral peduncle). Areas with rich crossing fibers (the corona radiata and the anterior limb of the internal capsule) show a lower FA at 40 weeks and a slower FA increase with age than those with less crossing fibers (the posterior limb of the internal capsule, the retrolenticular part of the internal capsule, the cerebral peduncle, the posterior thalamic radiation, and the sagittal striatum). Within association fibers, the superiorly located structures (the superior longitudinal fasciculus and the superior fronto-occipital fasciculus) show a higher MD at 40 weeks and a faster MD decrease with age than inferiorly located structures (the external capsule, the inferior fronto-occipital fasciculus, and the uncinate), even though the FA at 40 weeks and the FA slopes were similar.

Figure 5.

The relationship between (A) the age-dependent MD decreasing slope and the age-dependent FA increasing slope, (B) the estimated MD at 40 post-conceptional weeks and the age-dependent MD decreasing slope, and (C) the estimated FA at 40 post-conceptional weeks and age-dependent FA increasing slope. The white matter structures were categorized to the association fibers (black dots: SLF, SFO, ILF, IFO, and UNC), the commissural fibers (pink dots: CC and TAP), the limbic fibers (blue dots: CGC, CGH, Fx, and ST), and the projection fibers (green dots: ALIC, PLIC, RLIC, CP, PTR, SS, ACR, SCR, and PCR). (D): Linear regression analysesof MD and FA from three representative areas. Open squares indicate data from boys, and black circles indicate data from girls. The MD and FA of each structure show time-dependent changes with markedly different slopes and intercepts. See the appendix for abbreviations.

Required number of subjects to detect a 10% alteration in FA and MD

To detect a 10% alteration in FA and MD, most of the 24 structures required fewer than 20 subjects, which was sensitive enough for the subsequent cross-sectional group analysis (Table 2). However, we anticipate that this method will not be suitable to detect FA differences less than 10% in the basal ganglia, such as in the caudate, the putamen, and the globus pallidus, since the standard deviation of the FA was too high.

Table 2.

Average and standard deviation (SD) of each structure with a required total number of subjects (total of diseased subjects and control subjects) needed to detect a 10% difference. See appendix for the abbreviations.

structures	average trace	SD of trace	sample size	average FA	SD of FA	sample size
ACR	4.27	0.216	16	0.274	0.010	10
ALIC	3.53	0.164	14	0.304	0.009	8
CC	4.15	0.135	10	0.359	0.013	10
CGC	3.74	0.151	12	0.299	0.010	10
CGH	3.78	0.162	12	0.296	0.016	18
CP	3.58	0.140	12	0.342	0.016	14
EC	3.66	0.143	12	0.290	0.015	16
Fx	3.96	0.135	10	0.331	0.028	41
IFO	3.69	0.137	10	0.298	0.011	10
PCR	3.94	0.178	14	0.325	0.012	10
PLIC	3.17	0.149	14	0.410	0.020	16
PTR	4.15	0.190	14	0.307	0.013	12
RLIC	3.57	0.189	18	0.336	0.020	20
SCR	3.99	0.233	20	0.311	0.010	8
SFO	3.93	0.226	20	0.273	0.010	10
SLF	4.39	0.166	10	0.278	0.016	20
SS	4.19	0.191	14	0.294	0.016	18
ST	3.74	0.117	8	0.325	0.016	16
TAP	4.56	0.097	6	0.290	0.016	18
UNC	3.65	0.158	14	0.283	0.014	16
Cau	3.76	0.135	10	0.142	0.025	192
GP	3.32	0.140	12	0.181	0.038	238
Put	3.35	0.127	10	0.158	0.030	190
Thal	3.3	0.133	12	0.195	0.014	30

Discussion

Multi-contrast-based atlas for neonatal brain normalization studies

The atlases created in this paper contain three types of MR contrasts: T₁-weighted; T₂- weighted; and DTI. This enabled us to perform not only the DTI-based studies described in this paper, but also T1- or T2- weighted image-based normalization studies. There are studies about the effects of the atlas sharpness and the elasticity of the transformation (warp regularization), which suggest that better normalization accuracy can be achieved by the proper choice of atlas sharpness and warp regularization(Van Leemput, 2009; Yeo et al., 2008) . To respond to the various transformation methods with various warp regularizations used in the neuroimaging studies, we created two types of the group-averaged atlases and a single-subject atlas.

JHU-neonate-linear

This atlas was created by linearly averaging MRI data from 20 neonates (DTI and T₂-weighted image) and 14 neonates (T₁-weighted image). Since this linear transformation is not based on a single representative template, the shape and size represent average features of neonate brains. A group-averaged MRI template based on linear transformation has been widely used as a template for both linear and nonlinear normalizations (Mazziotta et al., 2001; Mazziotta et al., 1995).

JHU-neonate-nonlinear

Researchers have attempted to create templates based on nonlinear transformation because such templates provide a sharper contrast for each brain structure than that of linear transformation-based templates. This may possibly improve the registration accuracy, even though the choice depends on the study design. Therefore, we also created a nonlinear transformation-based template so that researchers can use the template of their choice. This could be a valuable template if nonlinear transformation with isotropic spatial smoothing is used. A traditional pair-wise approach was used to create the JHU-neonate nonlinear atlas. This method is intuitive, and is commonly used for atlas creation. On the other hand, the shortcoming of using a pair-wise approach is that, even after averaging of the normalized images, the averaged image is still inevitably biased by the selected single-subject image that was used as the template. To avoid this bias, group-wise registration methods have been developed (Bhatia et al., 2004). However, we still adopted a pair-wise approach, because we needed to use the resultant JHU-neonate nonlinear atlas to guide the manual parcellation of the deep white matter structures, as mentioned in the next paragraph. In addition, we intended to keep the consistency between group averaged atlas and the single subject atlas.

JHU-neonate-SS

When using highly nonlinear normalizations without isotropic spatial smoothing, our experience has shown that the blurred anatomical definitions in the group-averaged template could confuse the transformation process (Oishi et al., 2009). This prompted us to construct the single-subject MRI atlas. Compared to the group-averaged atlases, the advantage of the single-subject atlas is that it contains sharp definitions of anatomical structures. In particular, the structures near brain surface cannot be appreciated in group-averaged atlases since those structures are highly variable across individuals. However, this can also be a disadvantage of the single-subject atlas since it contains anatomical features that exist only in the arbitrarily selected subject. Therefore, to create the parcellation map of the white matter, we selected only the structures with less variability that could be appreciated even in the JHU-neonate-nonlinear atlas. One idea about creating an unbiased atlas with the image sharpness comparable to the single-subject atlas is to create a Bayesian template (Ma et al., 2008) from a large number of neonatal images, which will be the focus of our future study.

Accuracy of the registration

It was essential to determine the accuracy of the atlas-based anatomical segmentation. We used the parcellation map of the JHU-neonate-SS and compared the segmentation results to manual-based delineation. The average Dice measure was 0.82 +/− 0.061 (40 post-conceptional weeks) and 0.82 +/− 0.058 (49–52 post-conceptional weeks), while the average Dice of the manual method was 0.82 +/− 0.075. The average L1 error was 0.15 +/- 0.045 (40 post-conceptional weeks) and 0.15 +/− 0.041 (49–52 post-conceptional weeks), while the average L1 error of the manual method was 0.15 +/− 0.051. Thus, the accuracy of the atlas-based anatomical segmentation achieved the same accuracy as manual segmentation. However, this level of accuracy was achieved for normal subjects and may not hold for pathological brains. If mis-registration occurs due to severe brain abnormality, the automated segmentation may report erroneous results for FA and MD measurements. Therefore, it is essentialto carefully interpret the results.

DTI measurements of normal neonate brain

Analysis of neonate brains is expected to have a significant value for future assessment of various abnormalities at birth. If we can establish a quantitative tool to evaluate the anatomies of these abnormalities, and compare them with normal values, it is expected to complement the routine, qualitative evaluation of the images.

Based on the MRI atlas developed in this study, we characterized DTI parameter changes during the normal brain development process within three months after birth. Myelination processes have been studied in postmortem tissue (Yakovlev and Lecours, 1967) and, recently, with MRI (Berman et al., 2005; Cascio et al., 2007; Dubois et al., 2008; Dubois et al., 2006; Gao et al., 2009; Huppi et al., 1998; Lobel et al., 2009; Neil et al., 1998; Partridge et al., 2005; Paus et al., 2001; Provenzale et al., 2007). The result of this study is congruent with these studies that indicate a basic pattern to the maturation process, such as an FA increase and an MD decrease with age, and a posterior-to-anterior and a central-to-peripheral direction of maturation. We also found several patterns of the relationship among the MD and FA at 40 post-conceptional weeks, age-dependent FA increasing slope, and the age-dependent MD decreasing slope. Namely, we observed that in the more superior locations, the MD was higher and decreased faster with age in the corticofugal pathway (i.e., the superior corona radiata > the posterior limb of internal capsule > the cerebral peduncle), and in the more anterior regions, the MD was higher and decreased faster with age in the corona radiata (the anterior portion > the superior portion > the posterior portion). These tendencies seen in MD were not observed in the FA analysis, especially for the structures with rich crossing fibers, such as the corona radiata. Our analysis suggested that the time-dependent FA changes may provide more information about the development of the crossing fibers, compared with the time-dependent MD change. However, this is outside the scope of this paper and requires further longitudinal investigations.

When interpreting the regional FA values based on the proposed method, care must be taken because FA is the primary contrast that drives the registration of the parcellation map. For example, if a white matter region has abnormally low FA, it could lead to a reduction in the size of the segmentation, while the FA value remains unchanged. Any changes in segmented volumes and FA values must be carefully interpreted.

Potential for future research and clinical applications

The novel aspect of this study is that our measurement is based on 3D regions-of-interest placed by a fully automated method to evaluate the entire brain. This is important for clinical and research application studies since manual drawing of 3D regions-of-interest is prohibitively labor-intensive and subjectivity is difficult to avoid. In addition, our atlas covers as many as 22 brainstem and cerebellar structures, 38 cerebral white matter structures, 10 deep gray matter structures, and 52 cerebral cortical structures, for a total of 122 structures bilaterally. The proposed method is, thus, suitable for quantitative screening of abnormal brain regions.

From the normal-term neonate dataset, we estimated the statistical power required to detect abnormalities using the combination of the JHU-neonate-SS and LDDMM. The required number was adequate to detect a subtle alteration in MD and FA in most of the core white matter areas. This is important for research planning since we can reduce the number of scans required to test research hypotheses. However, note that FA is not suitable to detect alterations of the basal ganglia, because approximately 200 subjects would be required to detect a 10% alteration. Instead, we recommend using MD, which requires only 10–12 subjects to test hypotheses.

Future applications of this atlas include scientific investigations, such as determining the effects of prenatal events (ischemia, infections, or exposure to toxic substances) and the effects of preterm birth or low birth weight. This method enables us to perform whole-brain analysis, which is important to visualize structural specificity, but was lacking in previous studies. These basic studies will lead to more clinical investigations, such as seeking imaging biomarkers for various neurological disorders. Another future direction is to optimize the normalization approach. The tensor based or vector based normalization could potentially improve the registration accuracy.

In summary, we developed neonatal brain atlases for atlas -based, whole-brain analysis. Combined with a highly elastic nonlinear transformation, the entire brain was three-dimensionally parcellated into122 regions. This automated approach is fast and avoids the subjectivity associated with manually drawn ROIs. The accuracy level of our approach was measured using normal subjects and was comparable to the reliability level of human raters. This tool is expected to be applied for whole-brain screening to detect developmental abnormalities. The atlases developed in this study are now available for downloading from our website (http://lbam.med.jhmi.edu/ or www.mri.kennedykrieger.org). The software programs used in this study are also available (www.MriStudio.orgor www.mri.kennedykrieger.org).