Guar Gum, Xanthan Gum, and HPMC Can Define Release Mechanisms and Sustain Release of Propranolol Hydrochloride

Abstract

The objectives were to characterize propranolol hydrochloride-loaded matrix tablets using guar gum, xanthan gum, and hydroxypropylmethylcellulose (HPMC) as rate-retarding polymers. Tablets were prepared by wet granulation using these polymers alone and in combination, and physical properties of the granules and tablets were studied. Drug release was evaluated in simulated gastric and intestinal media. Rugged tablets with appropriate physical properties were obtained. Empirical and semi-empirical models were fit to release data to elucidate release mechanisms. Guar gum alone was unable to control drug release until a 1:3 drug/gum ratio, where the release pattern matched a Higuchi profile. Matrix tablets incorporating HPMC provided near zero-order release over 12 h and erosion was a contributing mechanism. Combinations of HPMC with guar or xanthan gum resulted in a Higuchi release profile, revealing the dominance of the high viscosity gel formed by HPMC. As the single rate-retarding polymer, xanthan gum retarded release over 24 h and the Higuchi model best fit the data. When mixed with guar gum, at 10% or 20% xanthan levels, xanthan gum was unable to control release. However, tablets containing 30% guar gum and 30% xanthan gum behaved as if xanthan gum was the sole rate-retarding gum and drug was released by Fickian diffusion. Release profiles from certain tablets match 12-h literature profiles and the 24-h profile of Inderal^® LA. The results confirm that guar gum, xanthan gum, and HPMC can be used for the successful preparation of sustained release oral propranolol hydrochoride tablets.

INTRODUCTION

Propranolol hydrochloride is a non-selective beta adrenergic blocking drug commonly used in the prophylaxis of migraine (1,2) and in the treatment of a variety of cardiovascular disorders (3), such as angina, tachycardia, and hypertension. For hypertension, the usual daily 40 mg in three to four divided doses may be increased to 160–260 mg daily. Although its oral absorption is almost complete (3), it undergoes hepatic metabolism, resulting in a 3–4-h elimination half-life (4). Sustained release matrix tablets containing propranolol hydrochloride have been prepared (5–8), since oral sustained release formulations can provide a slower fall in plasma drug levels, maintaining plateau values between 8 and 14 ng/ml (9). In hypertensive patients, a constant therapeutic plasma drug level must be maintained to keep the blood pressure at adequate levels.

Natural and semi-synthetic gums or polymers, such as guar gum, xanthan gum, hydroxypropyl methylcellulose, ethylcellulose, hydroxypropylcellulose, and sodium carboxymethylcellulose, are being used as release retarding materials (10–12). Indeed, hydroxypropylmethylcellulose (HPMC) has received the most attention, likely due to its low toxicity and ease of manufacture (13). The desired near zero-order release profile, however, is not usually obtained with a single hydrophilic swellable polymer (14), and it has been recommended that combinations of these polymers are more likely to provide the desired release profile (14,15). Guar gum and xanthan gum were chosen for the present study since these natural polymers have proved to be effective in sustaining drug release from a matrix system, much as HPMC does (3,16,17).

Guar gum consists of a linear chain of β-(1→4)-linked d-mannose units with d-galactose attached by α-(1→6) linkages to every other mannose unit to form short side chains (18). Though not self-gelling, guar gum has a high low-shear viscosity. Because it is nonionic, it is not affected by ionic strength or pH (19). Guar gum has been used in the preparation of oral sustained release diltiazem hydrochloride tablets by wet granulation (18) and by roller compaction as a dry granulation method (20). It has also served as the release-modifying agent in tablets containing theophylline (21) and trimetazidine dihydrochloride (22).

Xanthan gum has a β-(1→4)-d-glucose backbone where every second glucose unit is attached to a trisaccharide consisting of mannose, glucuronic acid, and mannose. The negatively charged carboxylates from glucuronic acid allow it to form highly viscous fluids at appropriate pH. Although it is considered a nongelling gum, it generates a viscous medium due to its tenuous associations (16). Although it is highly swellable, it slows drug release in sustained release formulations (11,23).

HPMC is a nonionizable hydrophilic cellulose derivative containing methoxyl and hydroxypropyl groups that support its hydration properties. Higher molecular weight results in a more viscous gel and slower drug release from an HPMC matrix tablet (8,24,25). In sustained release dosage forms, it gives pH-independent drug release (5,26) due to its nonionic nature. Drug release is controlled by matrix swelling and polymer dissolution (25). The first mechanism allows the HPMC to form a viscous gel that slows dissolved drug diffusion from the matrix. The second causes a reduction in the diffusion pathlength and evidence of erosion, which increase the release rate. Interestingly, first-order kinetics is evident at HPMC levels greater than 10% w/w of the tablet (8,24,27,28); only at 5% w/w HPMC was erosion observed (25).

Drug release from hydrophilic polymer matrix tablets involves wetting, hydration, swelling, dissolution of the drug, diffusion of the dissolved drug, and dissolution or erosion of the matrix (25,29). Diffusion, erosion or a combination of these processes usually governs the release of drug from these systems (30,31), although polymer relaxation—representing the swelling and gelling behavior of these polymers (32)—was also to be considered as a potential release rate controlling mechanism in the present study.

The objectives of this study were to prepare and characterize matrix tablets of propranolol hydrochloride using guar gum, xanthan gum, and HPMC K100M. Since the drug/polymer ratio proved to be the principal release rate controlling factor with propranolol hydrochloride-containing HPMC matrix tablets (24), matrix tablets were prepared with different drug:polymer ratios with propranolol hydrochloride. Guar gum, xanthan gum, and HPMC were used alone and in combination in the formulations to investigate the release retarding efficiency of these polymers for this water soluble drug. The tablets were manufactured by a wet granulation method because guar gum has been shown to exhibit poor flow (18).

MATERIALS AND METHODS

Materials

Propranolol hydrochloride, guar gum, and xanthan gum were purchased from Sigma-Aldrich (St. Louis, MO, USA). Sodium chloride, hydrochloric acid, disodium hydrogen phosphate anhydrous, each of which was analytical reagent grade, were purchased from Merck Chemicals (Karachi, Pakistan). Lactose monohydrate was from DMV-Fonterra Excipients (Goch, Germany), magnesium stearate from Peter Greven Asia Sdn Bhd (Penang, Malaysia), and talc from Haicheng Ginghua Mineral Product Company Ltd. (Haicheng, China). Hydroxypropylmethylcellulose K100M and polyvinylpyrrolidone (PVP K30) were purchased from Sigma-Aldrich Chemie (Buchs, Germany). K100M, a high viscosity, high molecular weight version of HPMC, was chosen because lower viscosity grades of HPMC are more susceptible to erosion (27).

Methods

Matrix tablets were prepared by a wet granulation method according to the formulations given in Table I. The powder ingredients were passed through US Standard Sieve No. 80 before preparation of the granules. Lactose was chosen as the filler because lactose tablets are reported to possess low friability and low weight variation, with no sticking, binding, or capping (33). Because lactose is a water soluble filler (about 2 g/ml at 37°C) (34), there must be a sufficient increase in viscosity due to the presence of the hydrated and swollen polymer at the tablet interface with the release medium to resist erosion (27). Drug was mixed with lactose and release-modifying polymer for 5 min in a cone mixer and then granulated with 5% PVP K30 solution. Granules were dried in an oven at 60°C for 2 h, and then passed through sieve No. 8. The granules were further dried to a moisture content of 3–5%, measured by heating at 102°C with a model MX-50 moisture analyzer (A&D Co., Ltd., Tokyo, Japan) until a constant mass was achieved. These dried granules were passed through sieve No. 20. Magnesium stearate and talc each at 1% w/w were added and the product was mixed in the cone mixer for 5 min. Tablets were compressed using 12 mm standard concave punch and die sets and a Manesty ZP-19 tablet press (OYSTAR Manesty, Knowsley, UK).

Table I.

Formulations for the Matrix Tablets

Formulation code	Guar gum (mg)	Xanthan gum (mg)	HPMC K100M (mg)	Lactose (mg)
PG1	80	–	–	212
PG2	160	–	–	132
PG3	240	–	–	52
PX1	–	80	–	212
PX2	–	160	–	132
PX3	–	240	–	52
PK1	–	–	80	212
PK2	–	–	160	132
PK3	–	–	240	52
PGX1	40	40	–	212
PGX2	80	80	–	132
PGX3	120	120	–	52
PGK1	40	–	40	212
PGK2	80	–	80	132
PGK3	120	–	120	52
PXK1	–	40	40	212
PXK2	–	80	80	132
PXK3	–	120	120	52

Tablets of 400 mg mass also contained 80 mg of drug, 20 mg PVP K30, and 4 mg each of magnesium stearate and talc

P propranolol hydrochloride, G guar gum, X xanthan gum, K HPMC K100M, 1–3 drug/polymer ratio 1:1, 1:2, and 1:3, respectively

Characterization of Granules and Tablets

Tablet and granule mass and drug content analyses were performed in triplicate following the method described in USP 27. The angle of repose of the granules, θ, was measured in triplicate using the fixed funnel and freestanding cone method (35) and calculated using Eq. 1:

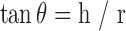1

where h and r are the height and radius of the granule cones, respectively. Bulk density (BD) and tapped density (TD) were determined by the graduated cylinder method (36) to calculate Carr’s compressibility index using Eq. 2 (36,37):

2

The hardness and thickness of the tablets were measured using six tablets and a Model PTB 311E Hardness Tester (Pharma Test Apparatebau AG, Hainburg, Germany) and a micrometer, respectively, and the tablet friability was determined in triplicate as described in USP 27 using a TA series 120 friabilator (Erweka, Heusenstamm, Germany).

Drug Release Studies

The release studies were performed with six replicates using USP dissolution apparatus II with the paddle stirring rate at 100 rpm. Release media included 0.1 N HCl buffer at pH 1.2 ± 0.2 for 2 h and then 0.05-M phosphate buffer at pH 6.8 ± 0.2 for subsequent time. Each medium was adjusted to 37 ± 0.5°C. Samples of 5 ml were collected at 0.5, 1, 2, 4, 6, 8, 12, 16, and 24 h and analyzed by UV spectrophotometry at 290 nm.

Mathematical Modeling of Drug Release Profiles

The existence of zero- or first-order release was tested by fitting mathematical models that describe zero-order kinetics:

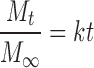3

and first-order kinetics:

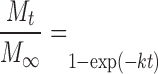4

to the release data (5). M_t/M_∞ is the fraction of drug released at time t in the release study. The coefficient k is a release rate constant. To begin to elucidate the mechanism(s) of drug release, the Korsmeyer model (38):

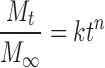5

was also fit to the data. The value of n can indicate likely mechanisms for drug release. For example, Ritger and Peppas (39) determined that n should be in the range 0.425–0.500 for disk-shaped devices if the release profile indicates that diffusion of dissolved drug through a matrix is the dominant release mechanism. An n value of about 1.0 indicates that polymer relaxation, polymer dissolution, or tablet erosion is the dominant mechanism. An intermediate value suggests a combination of mechanisms are effective, with so-called non-Fickian diffusion, anomalous release, or mixed transport.

The first model equation that acknowledges specific release mechanisms was based on the assumption of dissolution of drug in the entering release medium and then diffusion of dissolved drug through an essentially intact matrix. (The intact matrix could be an already hydrated and swollen polymer matrix.) Originally presented by Higuchi (40,41) to describe drug release from a slab, the equation has successfully described drug release from other geometries, including spheres and tablets (28,42):

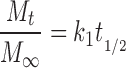6

Some suggest that this equation should be applied only up to 75% cumulative drug released (43) or even 60% drug released (44,45). In the present study, care was taken to limit the percent release if the fit of Eq. 6 was excellent with earlier data and application to data for greater than 75% cumulative percent released invalidates the fit.

Diffusion is seldom the only mechanism controlling drug release from hydrophilic matrix tablets (13). The next model equation was presented by Peppas and Sahlin (32) to acknowledge the additive contribution of polymer relaxation to the diffusion release mechanism, presented as k₂t in Eq. 7:

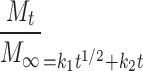7

The expression typically labeled the Weibull equation (Eq. 8) was used by Bidah and Vergnaud (46) to describe the release profiles in their studies. There are at least two mechanisms for drug release. The first is immediately evident when drug at the surface of the tablet dissolves and diffuses away. As the hydrophilic polymer takes up water, swelling might cause pieces of material to erode or dissolve away from the surface of the tablet (47). With erosion, more surfaces are created for ready drug dissolution and the resulting diffusion pathlength of the remaining tablet and its pieces becomes shorter with time. With tablet dissolution, the diffusion pathlength for dissolved drug becomes shorter with time, which results in an increased release rate at later times. These mechanisms result in a cube root relationship between the fraction of drug yet to be released, (1 − M_t/M_∞), and the release time (48):

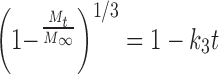8

This equation can be expanded and rearranged to give:

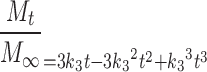9

The relationship of the coefficients to the release rate constant k₃ should be acknowledged in fitting this equation to release profile data.

Since additional release mechanisms appear as additional contributions to a release model equation (32), the dissolution/erosion contribution (Eq. 9) was combined with the equation describing drug diffusion and polymer relaxation (Eq. 7) to give:

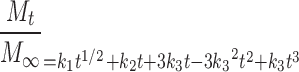10

Acknowledging these three release mechanisms provided a release model equation (Eq. 10) that could describe well drug release from ethylcellulose tablets intended to deliver indomethacin or theophylline (49) and from ethylcellulose tablets with silicon dioxide included as an erosion agent to deliver theophylline (50). If the polymer relaxation term proved to have a statistically insignificant coefficient (k₂), the model was fit to the data again without the k₂t term, limiting the mechanisms to drug diffusion and tablet dissolution or erosion.

The release data were analyzed using a SigmaStat 3.1 linear or nonlinear regression method (SyStat Software, Inc., Chicago, IL, USA) that presents estimates of the parameters found in the equation and their standard errors, as well as the p value associated with each estimated parameter. If these p values are greater than 0.05, the estimated parameter is considered statistically insignificant at the 95% confidence level (α = 0.05). A constant term, c, was added to equations, as necessary, to acknowledge a burst release of drug (c > 0) or a lag time before release of drug was evident (c < 0).

Selection of the model that best fits the release data is based on the validity of the estimated parameters and the use of the Akaike Information Criterion (AIC). A model equation is removed from consideration if a single estimated parameter proves invalid (p > 0.05). The AIC is calculated using:

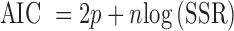11

where p is the number of parameters in the equation that are estimated, n is the number of data points that can be used in the calculation, and SSR is the sum of the squared residuals:

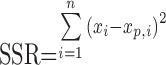12

where x_i is the mean observed fraction of drug released at a particular time in the release study and x_p,i is the corresponding predicted fraction of drug released based on the model equation and its estimated parameters (51). A lower SSR reflects a better fit to the data and results in a more negative AIC that indicates a better model equation. Model equations with a greater number of estimated parameters inherently fit the release data better, but including the 2p term in Eq. 11 gives a definite advantage to those equations with fewer estimated parameters that can still describe the data well. If two equations both fit the data well, the AIC will be more negative for the equation with fewer estimated parameters.

RESULTS

Physical Properties

The physical properties of granules and tablets of different formulations are reported in Table II.

Table II.

Physical Properties of Granules and Tablets, Presented as Mean ± Standard Deviation

Formulation code	Granules			Tablets
	Angle of reposea (°)	Carr’s indexa (%)	Drug contenta (%)	Friabilitya (%)	Thicknessb (mm)	Hardnessb (kg/cm2)	Massa (mg)	Drug contenta (%)
PG1	24.0 ± 0.03	22.50 ± 0.05	99.2 ± 0.9	0.10 ± 0.01	6.09 ± 0.04	5.29 ± 0.27	405.3 ± 15.3	95.2 ± 2.3
PG2	26.5 ± 0.02	21.13 ± 0.06	98.6 ± 1.5	0.33 ± 0.05	6.15 ± 0.01	5.34 ± 0.35	408.4 ± 23.6	95.3 ± 1.6
PG3	28.0 ± 0.04	21.13 ± 0.03	100.4 ± 1.4	0.12 ± 0.06	6.18 ± 0.02	5.45 ± 0.30	413.2 ± 12.7	100.1 ± 2.3
PX1	24.0 ± 0.06	22.02 ± 0.50	99.7 ± 0.8	0.64 ± 0.07	5.94 ± 0.13	5.24 ± 0.32	412.8 ± 11.9	99.1 ± 1.7
PX2	27.5 ± 0.03	20.21 ± 0.04	101.3 ± 1.7	0.25 ± 0.08	5.98 ± 0.15	5.38 ± 0.48	413.4 ± 15.6	101.0 ± 2.6
PX3	28.5 ± 0.03	21.36 ± 0.02	98.3 ± 1.9	0.30 ± 0.01	6.03 ± 0.23	5.36 ± 0.33	410.3 ± 8.8	97.5 ± 1.3
PK1	24.5 ± 0.04	21.75 ± 0.05	100.6 ± 2.1	0.29 ± 0.04	5.88 ± 0.07	5.62 ± 0.31	413.3 ± 14.4	99.3 ± 1.8
PK2	25.5 ± 0.01	20.23 ± 0.03	101.5 ± 1.6	0.11 ± 0.05	5.94 ± 0.16	5.66 ± 0.29	412.9 ± 13.3	100.2 ± 2.2
PK3	27.5 ± 0.03	22.82 ± 0.04	99.7 ± 2.3	0.42 ± 0.01	6.17 ± 0.18	5.58 ± 0.42	405.7 ± 7.4	101.2 ± 1.3
PGX1	25.0 ± 0.06	18.79 ± 0.07	98.0 ± 2.4	0.40 ± 0.06	5.94 ± 0.09	5.25 ± 0.46	413.3 ± 13.3	99.3 ± 2.2
PGX2	23.5 ± 0.07	19.06 ± 0.03	98.2 ± 1.2	0.45 ± 0.07	6.12 ± 0.21	5.36 ± 0.37	409.2 ± 8.6	99.5 ± 2.3
PGX3	28.0 ± 0.09	18.48 ± 0.04	99.2 ± 1.7	0.10 ± 0.03	6.20 ± 0.18	5.42 ± 0.21	411.8 ± 13.2	98.1 ± 2.0
PGK1	23.5 ± 0.03	16.60 ± 0.02	99.0 ± 1.5	0.21 ± 0.05	6.02 ± 0.41	5.48 ± 0.39	408.9 ± 9.8	98.7 ± 2.6
PGK2	24.5 ± 0.03	19.44 ± 0.02	97.6 ± 1.7	0.10 ± 0.05	6.11 ± 0.08	5.52 ± 0.23	412.5 ± 11.3	99.5 ± 1.9
PGK3	27.5 ± 0.05	19.36 ± 0.06	101.3 ± 1.1	0.51 ± 0.03	6.19 ± 0.26	5.44 ± 0.41	409.4 ± 8.6	100.1 ± 2.3
PXK1	21.5 ± 0.05	18.20 ± 0.03	98.7 ± 0.8	0.30 ± 0.08	5.85 ± 0.27	5.41 ± 0.40	411.7 ± 9.8	99.6 ± 2.0
PXK2	22.5 ± 0.02	16.32 ± 0.04	98.6 ± 2.3	0.27 ± 0.07	6.10 ± 0.25	5.49 ± 0.33	409.3 ± 12.3	98.1 ± 2.6
PXK3	24.0 ± 0.03	17.03 ± 0.03	99.6 ± 1.7	0.29 ± 0.09	6.20 ± 0.22	5.51 ± 0.43	407.2 ± 9.8	99.1 ± 1.3

P propranolol hydrochloride, G guar gum, X xanthan gum, K HPMC K100M, 1–3 drug/polymer ratio 1:1, 1:2, and 1:3, respectively

^a n = 3

^b n = 6

Drug Release

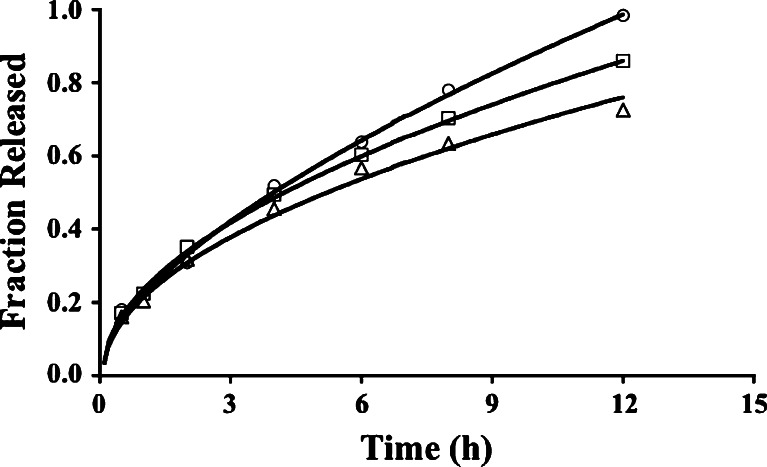
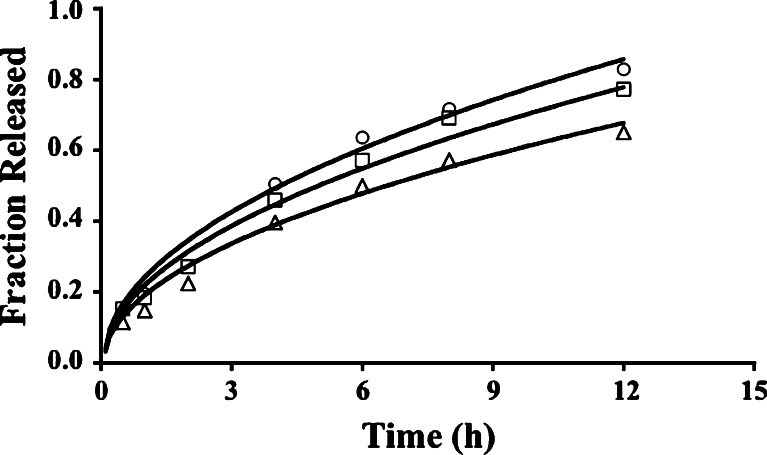
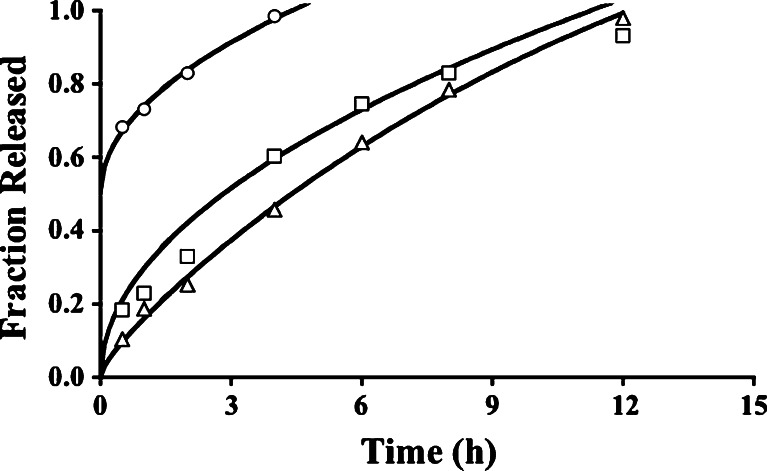
Guar gum in the drug:gum ratio of 1:1, 1:2, and 1:3, comparable to 20, 40, and 60% w/w guar gum in the tablet, retarded the release of propranolol HCl only for 4, 6, and 12 h, respectively (Fig. 1). At each of the three ratios, HPMC sustained the release of the drug with first-order kinetics for about 12 h (Fig. 2). Interestingly, the increase in the HPMC content in the formulation did not result in a marked difference in the drug release profile. First-order kinetics over 24 h describes the release data for tablets from batches PX1-PX3 (Fig. 3). First-order kinetics were also observed for tablets from PGK1, PGK2, and PGK3 (Fig. 4), PGX1, PGX2, and PGX3 (Fig. 5), and PXK1, PXK2, and PXK3 batches (Fig. 6).

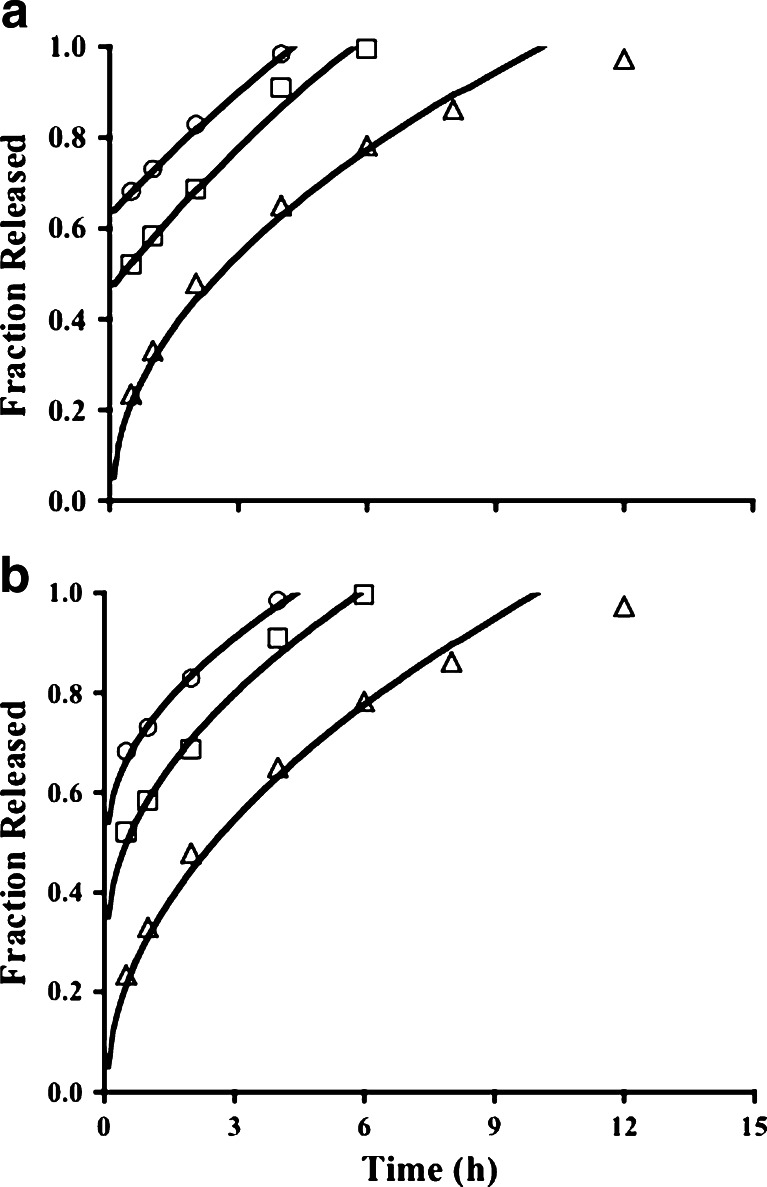
Fig. 1.

Release profiles for tablets with formulation codes PG1 (circles), PG2 (squares), and PG3 (triangles). In Fig. 1a, the curves are based on the fit of the Weibull equation (Eq. 9) to data for batches PG1 and PG2, each with a positive y-intercept acknowledging a burst release of drug, and the Higuchi model (Eq. 6) for PG3. The curves in Fig. 1b represent the fit of the Higuchi model (Eq. 6) to the release data for tablets from PG1, PG2 and PG3 batches. For PG1 and PG2 data, the fit required a positive constant term in the model equation; no constant term was necessary for PG3 data

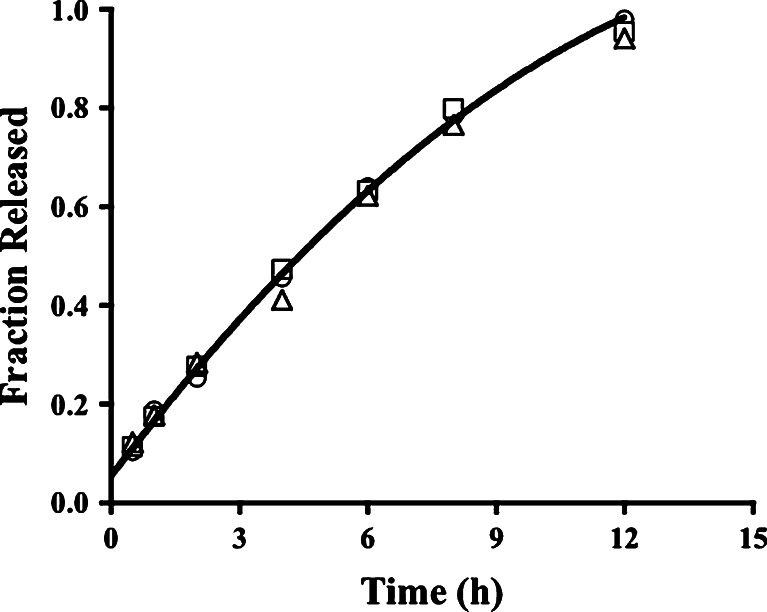
Fig. 2.

Near-zero-order propranolol release over 12 h from tablets with formulation codes PK1 (circles), PK2 (squares), and PK3 (triangles). The curve is the data predicted by the fit of the diffusion and erosion equation (modified Eq. 10 with the k ₂ t term eliminated) to PK1 data

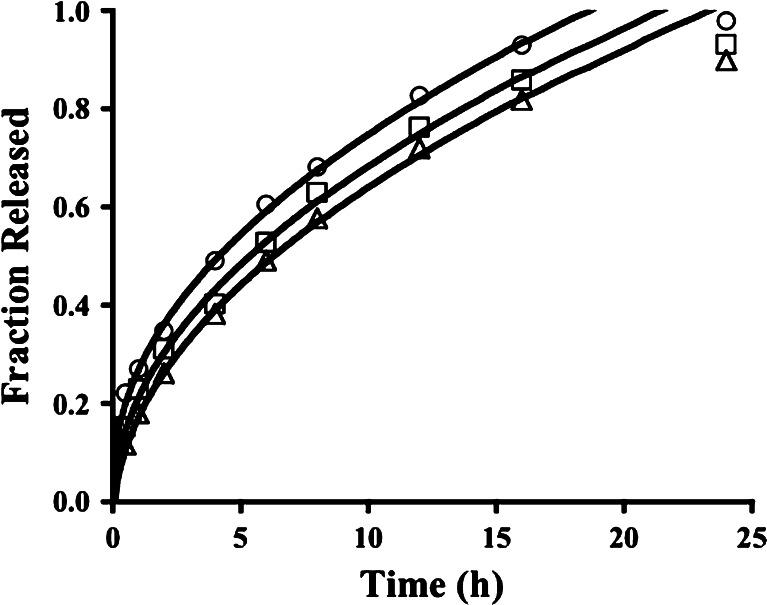
Fig. 3.

Release profiles over 24 h for tablets with formulation codes PX1 (circles), PX2 (squares), and PX3 (triangles). The curves are based on the fit of the Higuchi model (Eq. 6) and a nonzero y-intercept acknowledging a burst release from tablets from batch PX1 and a lag time for tablets from batch PX3

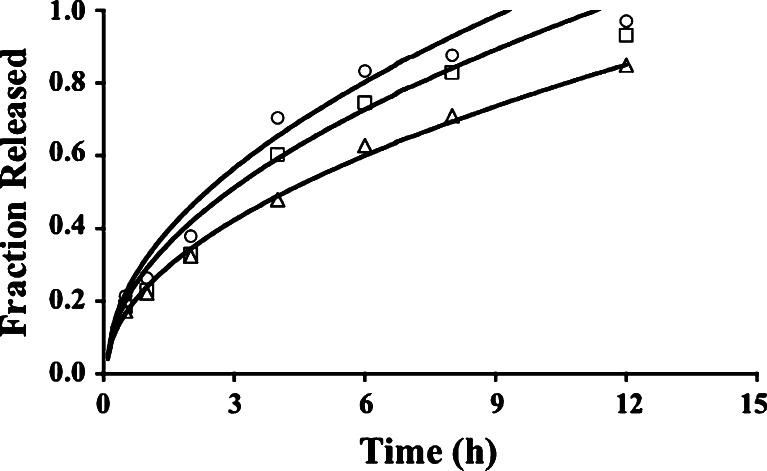
Fig. 4.

Release profiles for tablets from PGK1 (circles), PGK2 (squares), and PGK3 (triangles) batches. The curves present data generated by a fit of the Higuchi model with no constant term

Fig. 5.

Release profiles for tablets from PGX1 (circles), PGX2 (squares), and PGX3 (triangles) batches. The curves reveal the fit of the Diffusion and Erosion model to PGX1 data, the Peppas equation (Eq. 7) to PGX2 data, and the Higuchi model to PGX3 data

Fig. 6.

Release data for tablets from the PXK1 (circles), PXK2 (squares), and PXK3 (triangles) batches. The Higuchi model fit the release data best when a constant term was not included

DISCUSSION

Physical Properties

According to the literature, an angle of repose in the range 23.5–28.5^o indicates excellent flow, and a Carr’s Compressibility Index between 18.5 and 22.8% indicates fair to passable flow (16). Thus, the results for these two parameters (Table II) indicate poor flow for many of the batches of granules. Uniformity in drug content, however, confirmed excellent mixing and flow during wet granulation and compression, respectively. Clearly, addition of magnesium stearate and talc improved the flow of the granules. The low friability of the tablets, as observed earlier with tablets containing these polymers (26), ranged from 0.100% to 0.801%. The thickness of the tablets varied within the narrow range 6.2–6.4 mm, leading to consistent initial tablet surface area in the release studies. The weight variation was within the pharmacopoeial limits, again confirming good flow. The average tablet hardness of 5.43 kg/cm² agrees well with literature values for comparable tablets (18,52).

Drug Release

Drug pKa and solubility are important factors affecting drug release from a solid dosage form. Propranolol hydrochloride is a weakly basic drug (pKa 9.5) and thus is soluble in an acidic environment, >150 mg/ml (53). Its solubility should decrease when the pH is increased. However, since the pH is never higher than 6.8, this drug is ≥99.8% protonated and highly soluble in the two release media and there should be no hindrance to drug release due to low solubility.

Gum- or HPMC-containing tablets take up water on contact with the release medium (16,28,54), thus allowing dissolution of a certain percent of the drug found at and near the tablet surface prior to gel or viscous medium formation. This is followed by hydration and swelling of the polymer, creating porous pathways that could lead to an initial burst release (55). Tablet swelling was directly correlated with the level of the gum in different formulations (18). Increasing the level of polymer in the formulation can further sustain the release of the drug, apparently due to a thicker gel or a more viscous region (56). The gel or viscous aqueous region inhibits further entry of release medium due to its high water content. With time, the diffusion pathlength increases, resulting in slower drug release. With sufficient viscosity, the gel or viscous region can resist erosion.

Release data from tablets from PG1 and PG2 batches come close to following zero-order kinetics (Fig. 1a, Table III) if a burst drug release is acknowledged. For tablets from the PG3 batch, first-order kinetics are evident with no constant term. Initial drug release can be rapid because water uptake is higher and faster with guar gum than with other natural gums, such as xanthan gum (23). Similar initial rapid drug release has been reported with soluble drugs salbutamol sulfate (55) and tramadol HCl (23), although the initial release of diltiazem HCl could be controlled (20). Korsmeyer n values of 0.781, 0.554, and 0.425 were estimated for the PG1, PG2, and PG3 batches, respectively (see Table III), indicating essentially Fickian diffusion of the dissolved drug out of the hydrated and swollen tablet from the PG3 batch. This proved to be the broadest range for n values among the different batches of tablets, uniquely revealing a polymer content effect on the release mechanism.

Table III.

Fit of the Zero-Order (Eq. 3), First-Order (Eq. 4), and Korsmeyer (Eq. 5) Equations to the Release Data for Tablets Involving Only One Release Rate Determining Polymer

Batch	k	c	n	R 2
Zero order
PG1	0.0860 ± 0.00370a	0.646 ± 0.00852	–	0.996
PG2	0.0889 ± 0.00894	0.499 ± 0.0303	–	0.971
PG3	0.130 ± 0.0130	–	–	0.605
PK1	0.0921 ± 0.00521	–	–	0.941
PK2	0.0916 ± 0.00586	–	–	0.923
PK3	0.0890 ± 0.00544	–	–	0.929
PX1	0.483 ± 0.0707	–	–	0.483
PX2	0.0510 ± 0.00586	–	–	0.618
PX3	0.0484 ± 0.00508	–	–	0.701
First order
PG1	0.532 ± 0.124	−0.835 ± 0.131	–	0.959
PG2	0.425 ± 0.0757	−0.475 ± 0.0954	–	0.969
PG3	0.295 ± 0.0246	–	–	0.972
PK1	0.179 ± 0.0119	–	–	0.981
PK2	0.181 ± 0.00934	–		0.988
PK3	0.169 ± 0.0107	–	–	0.981
PX1	0.168 ± 0.0153	–	–	0.955
PX2	0.131 ± 0.00943	–	–	0.968
PX3	0.113 ± 0.00592	–	–	0.982
Korsmeyer
PG1	0.128 ± 0.0186	0.606 ± 0.0178	0.781 ± 0.0742	0.999
PG2	0.247 ± 0.153	0.343 ± 0.151	0.554 ± 0.232	0.989
PG3	0.351 ± 0.0136	–	0.425 ± 0.0196	0.995
PK1	0.176 ± 0.0104	–	0.700 ± 0.0279	0.996
PK2	0.187 ± 0.0120	–	0.669 ± 0.0303	0.995
PK3	0.178 ± 0.0123	–	0.678 ± 0.0327	0.994
PX1	0.288 ± 0.0157	–	0.404 ± 0.0214	0.990
PX2	0.234 ± 0.0145	–	0.452 ± 0.0240	0.990
PX3	0.200 ± 0.0134	–	0.492 ± 0.0258	0.990

^aData in the tables are presented as the mean ± standard error

Acknowledging the initial burst release, the data for PG1 and PG2 batches were described well by the Higuchi model or the Weibull equation (Fig. 1a, b; Table IV), indicating diffusion or dissolution/erosion as the release mechanism. The levels of guar gum in the PG1 and PG2 batches are probably too low to resist erosion. Nevertheless, it has been reported that guar gum matrix tablets experienced minimal mass loss over the drug release period (23). Data for PG3 tablets are described well by the Higuchi model, suggesting that guar gum at 60% of the tablet mass can resist erosion. The Peppas model proved invalid because the estimated coefficients were not statistically significant at α = 0.05 (p > 0.2). The DRE model cannot be fit to the PG1 and PG2 data because there are only three data points with <0.9 fraction released, thus insufficient data to allow the degrees of freedom to fit a model equation with three estimated parameters. An increase in the gum level or its molecular weight is expected to slow the drug release rate (18). This was evident in the slower drug release when the guar gum content was increased, with the Higuchi model still describing the drug release pattern well (Fig. 1b). Formulation PG3 represents tablets with 60% guar gum, and yet a biphasic release profile was not observed, as was reported when guar gum was 64–65% of the tablet to deliver diltiazem HCl (18) or tramadol HCl (23).

Table IV.

Fit of Various Model Equations (Eqs. 6, 7, 9, and 10) to Release Data for Tablets with a Single Release-Modifying Polymer

Batch	k 1	k 2	k 3	c	AIC
Higuchi
PG1	0.237 ± 0.0138	–	–	0.503 ± 0.0190	−27.70
PG2	0.287 ± 0.0174	–	–	0.305 ± 0.0286	−21.53
PG3	0.318 ± 0.00501	–	–	–	−33.49
PK1	0.260 ± 0.0127	–	–	–	−20.98
PK2	0.260 ± 0.0112	–	–	–	−22.62
PK3	0.252 ± 0.0113	–	–	–	−22.56
PX1	0.221 ± 0.00365	–	–	0.0524 ± 0.00908	−55.29
PX2	0.217 ± 0.00218	–	–	–	−56.50
PX3	0.216 ± 0.00237	–	–	−0.0397 ± 0.00590	−60.22
Peppas and Sahlin
PG1	0.0991 ± 0.0394a	0.0504 ± 0.0143a	–	0.585 ± 0.0244	−36.03
PG2	0.268 ± 0.144a	0.00601 ± 0.0451a	–	0.318 ± 0.100a	−19.73
PG3	0.318 ± 0.0229	1.71 × 10−10 ± 0.00964a		–	−31.49
PK1	0.143 ± 0.0190	0.0431 ± 0.00676	–	–	−33.32
PK2	0.161 ± 0.0216	0.0365 ± 0.00767	–	–	−31.54
PK3	0.150 ± 0.0194	0.0376 ± 0.00688	–	–	−33.06
PX1	0.221 ± 0.0201	3.093 × 10−12 ± 0.00424a	–	0.0524 ± 0.0203	−51.33
PX2	0.208 ± 0.0169	8.56 × 10−11 ± 0.00436a	–	–	−37.48
PX3	0.214 ± 0.0130	0.000467 ± 0.00275a	–	−0.0378 ± 0.0131	−26.20
Weibull
PG1	0.0337 ± 0.00809	–	–	0.634 ± 0.00439	−36.11
PG2	0.0393 ± 0.00361	–	–	0.470 ± 0.0239	−22.07
PG3	0.0784 ± 0.00989	–	–	–	−16.31
PK1	0.0498 ± 0.00182	–	–	–	−33.25
PK2	0.0502 ± 0.00143	–	–	–	−36.73
PK3	0.0472 ± 0.00203	–	–	–	−30.91
PX1	0.0234 ± 0.00136	–	–	0.209 ± 0.0171	−42.05
PX2	0.0360 ± 0.00307	–	–	–	−33.00
PX3	0.0224 ± 0.00130	–	–	0.116 ± 0.0168	−40.77
Diffusion, relaxation, and erosion
PG1	0.0682 ± 0.0527a	–	0.0228 ± 0.00796a	0.599 ± 0.00287	−37.14
PG2	0.264 ± 0.161a	–	0.00240 ± 0.0162a	0.320 ± 0.103a	−19.66
PG3	0.318 ± 0.0229	–	5.700 × 10−11 ± 0.00321a	–	−31.49
PK1	0.0733 ± 0.0269	–	0.00591	–	−40.37
PK2	0.0326 ± 0.0194a	–	0.0403 ± 0.00542	–	−37.80
PK3	0.114 ± 0.0289	–	0.0202 ± 0.00517	–	−35.20
PX1	0.221 ± 0.0201	–	1.031 × 10−12 ± 0.00141a	0.0524 ± 0.0203	−51.33
PX2	0.208 ± 0.0180	–	2.862 × 10−11 ± 0.00156a	–	−30.69
PX3	0.214 ± 0.0131	–	0.000161 ± 0.000927a	−0.0377 ± 0.0132	−58.32

^a p > 0.05 and this coefficient is statistically insignificant. Therefore this model was not considered a candidate for the model that best fits the data

HPMC sustained the release of the drug with first-order kinetics (Table III), as seen in an earlier report even with a lower molecular weight HPMC (5). It has been reported that, even for the lower viscosity grades of HPMC, a maximum release retarding influence of HPMC is reached in tablets containing 20–50% HPMC, with lower viscosity grades reaching the maximum at higher HPMC levels (25). Thus, the 20% HPMC in batch PK1 could be sufficient to already see the maximum release retarding effect of HPMC K100M, a high viscosity grade of HPMC. The exponent n in the Korsmeyer model was 0.700, 0.669, and 0.678 for formulations PK1, PK2, and PK3, respectively, indicating an anomalous release mechanism. Drug release profiles from a matrix tablet containing HPMC can provide evidence of a lag time, albeit a small one (28), and it was not necessary to acknowledge a lag time in the present study. During release studies, particles of the tablet were observed in each vessel, providing visual confirmation of an erosion mechanism. It is not surprising then that the release of propranolol HCl from tablets from PK1 and PK3 batches was best described by the model that includes diffusion, relaxation, and erosion. However, the relaxation contribution proved to be insignificant and its term was eliminated from the equation when the final fit to the data was made (Table IV). Drug release from PK2 tablets was best described by the Weibull equation and erosion is likely the principal release mechanism. Erosion is a mechanism not often seen with guar gum (23) and only seen at low levels (<15% w/w) of xanthan gum (17,54,57), leading to the formation of new surfaces, allowing dissolution of drug at those new surfaces, and shortening the diffusion pathlength, each of which increases the drug release rate with time. Erosion was evident at HPMC levels ≤10% with lower viscosity grades of HPMC (25) because, although a viscous region was formed, it was not continuous and the pockets of swollen HPMC allow localized disruption of the tablet integrity either by erosion or by HPMC dissolution allowing the pocket to be released into the medium. Hydration of higher levels of polymer can lead to regions of higher viscosity that are more resistant to erosion (17). This was not evident in the present results since each of the best fit models involved dissolution/erosion as a release mechanism.

The value of exponent n in the Korsmeyer model was 0.404, 0.452, and 0.492 for PX1, PX2, and PX3, respectively, indicating Fickian diffusion as the principal mechanism, as noted in earlier reports (13,23). It is interesting to note that xanthan gum matrix tablets swelled in both axial and radial directions in a manner that followed Fickian kinetics (13), which should lead to a profile described by the Higuchi model if drug dissolution is not slow. The Higuchi model fit the PX1–PX3 release data best, although a slight nonzero y-intercept, amounting to 5% drug released, must be acknowledged with batch PX1 (Table IV). An initial burst release was observed in earlier reports of xanthan gum matrix tablets (54), which is not surprising since xanthan gum can hydrate rapidly even in cold water (16). The Peppas model and the DRE model revealed negligible contributions from polymer relaxation and dissolution/erosion (Table IV), each collapsing to the Higuchi model.

Xanthan gum prolonged the release for a longer time than either guar gum or HPMC, and drug release across essentially 24 h was observed with each of the three drug/gum ratios (Fig. 3). This could be due to cationic propranolol relating well to the carboxylate groups of xanthan gum even as carboxylates from crosslinked polyacrylic acid can sustain chlorpheniramine maleate release (58). This ionic interaction is not available with nonionic guar gum and HPMC. Varshosaz et al. (23) reported first-order profiles and Fickian diffusion for each batch of tablets containing a combination of guar gum and HPMC. First-order kinetics were observed in the present study also (Fig. 4; Table V), with Korsmeyer n values of 0.478, 0.526, and 0.526 for tablets from PGK1, PGK2, and PGK3 batches, respectively. In each case in the present study, the Higuchi model fit best when no constant term was included (Table VI; Fig. 4). Using the data for tablets from batches that contained 20% of each polymer alone (PG1 and PK1), the batch involving both 20% guar gum and 20% HPMC (PGK2) exhibited a release profile intermediate to those for tablets containing 20% of a single polymer. The influence of guar gum is of little consequence in comparison to that of HPMC (Fig. 7).

Table V.

Fit of the Zero-Order (Eq. 3), First-Order (Eq. 4), and Korsmeyer (Eq. 5) Equations to the Release Data for Tablets Involving Two Release-Modifying Polymers

Batch	k	n	R 2
Zero order
PGK1	0.104 ± 0.0124	–	0.686
PGK2	0.0968 ± 0.00996	–	0.774
PGK3	0.0848 ± 0.00812	–	0.796
PGX1	0.0938 ± 0.00717	–	0.878
PGX2	0.0849 ± 0.00827	–	0.786
PGX3	0.0751 ± 0.00836	–	0.713
PXK1	0.0842 ± 0.00792	–	0.814
PXK2	0.0786 ± 0.00737	–	0.813
PXK3	0.0665 ± 0.00622	–	0.819
First order
PGK1	0.287 ± 0.0169	–	0.988
PGK2	0.228 ± 0.0109	–	0.990
PGK3	0.169 ± 0.0110	–	0.974
PGX1	0.195 ± 0.0141	–	0.975
PGX2	0.170 ± 0.0123	–	0.967
PGX3	0.139 ± 0.0124	–	0.935
PXK1	0.167 ± 0.00839	–	0.985
PXK2	0.146 ± 0.00855	–	0.976
PXK3	0.109 ± 0.00715	–	0.962
Korsmeyer–Peppas
PGK1	0.319 ± 0.0352	0.478 ± 0.0551	0.970
PGK2	0.268 ± 0.0252	0.526 ± 0.0461	0.982
PGK3	0.234 ± 0.00817	0.526 ± 0.0171	0.997
PGX1	0.222 ± 0.00921	0.598 ± 0.0199	0.997
PGX2	0.239 ± 0.00401	0.516 ± 0.00825	0.999
PGX3	0.230 ± 0.0105	0.477 ± 0.0229	0.995
PXK1	0.220 ± 0.0183	0.552 ± 0.0405	0.987
PXK2	0.208 ± 0.0152	0.548 ± 0.0358	0.990
PXK3	0.172 ± 0.0145	0.557 ± 0.0411	0.987

Table VI.

Fit of Various Model Equations (Eqs. 6, 7, 9, and 10) to Release Data for Tablets with Two Release-Modifying Polymers

Batch	k 1	k 2	k 3	AIC
Higuchi
PGK1	0.329 ± 0.0105	–	–	−22.10
PGK2	0.298 ± 0.00464	–	–	−23.63
PGK3	0.246 ± 0.00304	–	–	−40.95
PGX1	0.269 ± 0.00699	–	–	−29.28
PGX2	0.247 ± 0.00160	–	–	−49.94
PGX3	0.220 ± 0.00351	–	–	−38.94
PXK1	0.248 ± 0.00448	–	–	−29.50
PXK2	0.225 ± 0.00494	–	–	−32.25
PXK3	0.196 ± 0.00419	–	–	−32.35
Peppas and Sahlin
PGK1	0.329 ± 0.0747	2.11 × 10−10 ± 0.0298a	–	−20.10
PGK2	0.289 ± 0.0323	0.00351 ± 0.0129a	–	−22.32
PGK3	0.233 ± 0.0114	0.00494 ± 0.00404a	–	−40.49
PGX1	0.205 ± 0.0117	0.0234 ± 0.00416	–	−40.11
PGX2	0.238 ± 0.00565	0.00311 ± 0.00201a	–	−50.26
PGX3	0.220 ± 0.0147	6.954 × 10−11 ± 0.00522a	–	−36.94
PXK1	0.248 ± 0.0255	7.107 × 10−11 ± 0.00875a	–	−27.50
PXK2	0.218 ± 0.0210	0.00253 ± 0.00724a	–	−30.80
PXK3	0.196 ± 0.0239	4.574 × 10−11 ± 0.00819a	–	−30.35
Weibull
PGK1	0.0778 ± 0.00869	–	–	−21.76
PGK2	0.0621 ± 0.00532	–	–	−19.20
PGK3	0.0466 ± 0.00364	–	–	−22.57
PGX1	0.0532 ± 0.00342	–	–	−25.47
PGX2	0.0467 ± 0.00395	–	–	−21.46
PGX3	0.0386 ± 0.00393	–	–	−18.99
PXK1	0.0452 ± 0.00377	–	–	−23.78
PXK2	0.0400 ± 0.00459	–	–	−23.45
PXK3	0.0305 ± 0.00289	–	–	−23.24
Diffusion, relaxation, and erosion
PGK1	0.329 ± 0.0747	–	7.028 × 10−11 ± 0.00993a	−20.10
PGK2	0.288 ± 0.0329	–	0.00127 ± 0.00444a	−19.20
PGK3	0.232 ± 0.0117	–	0.00176 ± 0.00144a	−40.56
PGX1	0.198 ± 0.0142	–	0.00944 ± 0.00203	−40.39
PGX2	0.238 ± 0.00576	–	0.00107 ± 0.000696a	−50.33
PGX3	0.220 ± 0.0141	–	2.318 × 10−11 ± 0.00174a	−36.94
PXK1	0.248 ± 0.0255	–	2.369 × 10−11 ± 0.00292a	−27.50
PXK2	0.217 ± 0.0213	–	0.000893 ± 0.00250a	−30.75
PXK3	0.196 ± 0.0454	–	1.525 × 10−11 ± 0.00273a	−30.35

^a p > 0.05 and this coefficient is statistically insignificant. Therefore this model was not considered a candidate for the model that best fits the data

Fig. 7.

Guar gum has little influence on the release from PGK2 tablets. The circles present release data for PG1 (20% guar gum) tablets, the squares for PGK2 (20% guar gum and 20% HPMC) tablets, and the triangles for PK1 (20% HPMC) tablets

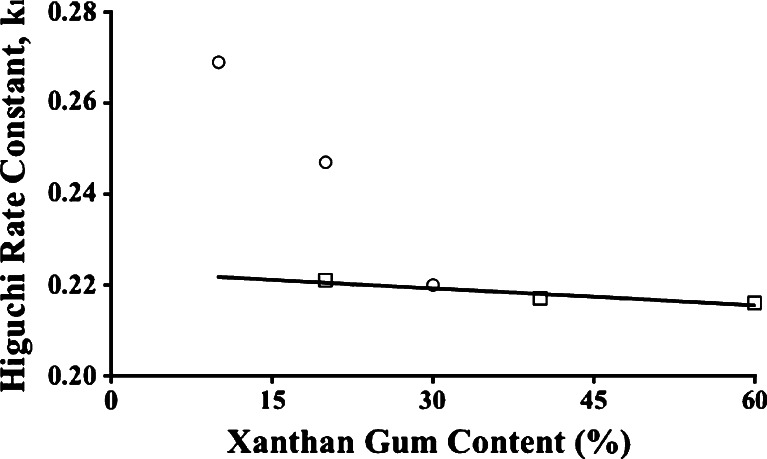
For tablets from PGX1, PGX2, and PGX3 batches, the Korsmeyer n values were 0.598, 0.516, 0.477, respectively, first-order kinetics applies (Table V), and the Higuchi model fits the data best (Table VI; Fig. 5). There have been reports of a synergistic effect when guar and xanthan gums were used in combination (56,59). Due to this synergy, the viscosity of the medium was higher than the viscosity expected if one assumes no interaction between the two gums. The data in Fig. 8 reveal that not only is a synergistic effect absent, but the presence of 30% guar gum cannot influence the release mechanism for tablets when 30% xanthan gum is also included (PGX3). Indeed the tablets from PGX3 behaved as if from a PX batch with 30% xanthan gum alone, their average Higuchi rate constant meeting the line crossing through the PX1–PX3 Higuchi rate constants, suggesting that Fickian diffusion is the mechanism for drug release because of a sufficient xanthan gum content. At the lowest gum level with PGX1, guar gum apparently disrupts the formation of the viscous gel by xanthan gum and dissolution/erosion participates in the release mechanisms (Table VI), even as dissolution/erosion was evident with PG1 and PG2 (Table IV).

Fig. 8.

Higuchi rate constants for tablets from PGX1, PGX2, and PGX3 batches (circles) lead to agreement with rate constants from PX1, PX2, and PX3 tablets (squares) when the xanthan gum level is increased to 30% (PGX3)

With formulations PXK1, PXK2, and PXK3, the values of exponent n were 0.552, 0.548, and 0.557, respectively, implying that the release mechanism is predominantly Fickian diffusion (Table V). The Higuchi model without a constant term best describes the data for PXK1, PXK2, and PXK3 tablets (Table VI; Fig. 6), although dissolution/erosion was evident with PK1, PK2 and PK3 tablets. Once again, the presence of xanthan gum leads to Fickian diffusion as the release mechanism and xanthan gum can dominate the influence of the second polymer, eliminating the dissolution/erosion contribution from HPMC. No synergistic effect was observed.

Sustained release direct compression propranolol hydrochloride matrix tablets prepared with a 1:1.25 drug/HPMC ratio were reported to provide drug release over 12 h described best by a first-order model (R² = 0.9987) and the Higuchi model (5). To determine if the release profiles in the present study agree with their release profile, the dissimilarity factor, f₁:

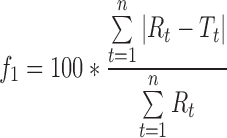13

and the similarity factor, f₂, can be calculated:

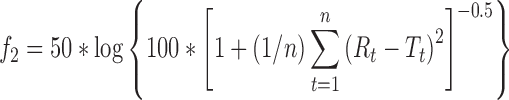14

where R_t is the reference average percent released at time t, T_t is the test sample mean percent released at time t, and n is the number of time points used for comparison of the two profiles (60). An f₁ value less than 15 and an f₂ value greater than 50 indicates similarity of the two release profiles. The f₁ values are 11, 10, and 14, and the f₂ values are 59, 60, and 54 for PK1, PK2, and PK3 results as the test data, respectively, indicating that a sustained release 12-h profile comparable to that in literature can be achieved. This is surprising because the use of wet granulation instead of direct compression can result in faster drug release due to pore formation when the granulating liquid is evaporated. However, Sahoo et al. (5) used a lower molecular weight HPMC that is expected to result in faster drug release.

Dabbagh et al. (6) reported 14-h release profiles for propranolol hydrochloride-containing direct compression matrix tablets with 64% w/w HPMC levels. First-order release was evident with the Higuchi model describing the data best. Interestingly, the release data for these tablets is similar to that of PX2 and PX3, with f₁ values of 8 and 5, and f₂ values equal to 74 and 83, respectively, demonstrating excellent similarity. Note that none of the HPMC-containing tablets could match their profile, yet xanthan gum at a comparable level could provide similarity. Indeed a 40% xanthan gum matrix tablet could release drug in a manner similar to their profile, providing evidence of a reduction in the level of release rate determining polymer, and also the successful use of a natural material that is less expensive than HPMC.

If seeking near zero-order release with a 12-h profile, several formulations would satisfy these requirements. Any of the three formulations with HPMC alone, PK1, PK2, or PK3, provide nearly zero-order release over 12 h. From the formulations with a combination of polymers, tablets from batch PGX1 comply with these stipulations.

The release profile for Inderal^® LA, the 80 mg propranolol hydrochloride capsules containing coated beads providing sustained release over 24 h, has been presented (61). Although a condition for pharmaceutical equivalence is not met (tablets are being compared to the reference material that is a capsule with coated beads), several batches of tablets can provide drug release that matches the release profile of the long acting commercial product. Tablets from PX2, PX3, PGX3, PXK2, and PXK3 batches each have similar profiles, evidenced by f₁ values of 12, 9, 11, 11, and 8, and f₂ values of 56, 63, 54, 59, and 64, respectively. Thus, if a 24-h release profile is desired, there are several formulations that would satisfy that requirement.

CONCLUSIONS

When guar gum, xanthan gum, and HPMC, alone or in combination, were used as release retarding agents, rugged propranolol hydrochloride-containing granules that demonstrated good flow could be produced, and sustained release matrix tablets with good physical properties could be obtained from compression of these granules. Xanthan gum was best able to retard propranolol release and exerted its influence on the release mechanism even in the presence of a second release rate modifying polymer. Fickian diffusion is the release mechanism that can define the release profile with most formulations, although dissolution/erosion is introduced when HPMC is the sole release-modifying polymer. These polymers can be used to formulate successful sustained release propranolol hydrochloride matrix tablets that have desirable characteristics.