Controlling the False Discovery Rate for Feature Selection in High-resolution NMR Spectra

Abstract

Successful implementation of feature selection in nuclear magnetic resonance (NMR) spectra not only improves classification ability, but also simplifies the entire modeling process and, thus, reduces computational and analytical efforts. Principal component analysis (PCA) and partial least squares (PLS) have been widely used for feature selection in NMR spectra. However, extracting meaningful metabolite features from the reduced dimensions obtained through PCA or PLS is complicated because these reduced dimensions are linear combinations of a large number of the original features. In this paper, we propose a multiple testing procedure controlling false discovery rate (FDR) as an efficient method for feature selection in NMR spectra. The procedure clearly compensates for the limitation of PCA and PLS and identifies individual metabolite features necessary for classification. In addition, we present orthogonal signal correction to improve classification and visualization by removing unnecessary variations in NMR spectra. Our experimental results with real NMR spectra showed that classification models constructed with the features selected by our proposed procedure yielded smaller misclassification rates than those with all features.

1. INTRODUCTION

Metabolomics approaches that use proton nuclear magnetic resonance (¹H-NMR) have been developed in recent years as a way to study the dynamic and time-dependent profiles of metabolic responses that occur in response to pathophysiological stimuli or to genetic modifications in integrated biological systems [1]. A metabolomics approach enables the investigation of hundreds of metabolites simultaneously. In biofluids, metabolites are maintained in dynamic balance with those that are inside cells and tissues, and consequently, abnormal perturbations after toxic insult or disease progression will be reflected in disturbances in the ratios and concentrations of biofluid metabolites. The introduction of ¹H-NMR spectroscopic techniques makes it possible to investigate changes in metabolic composition and to quantify them without complex preparation of samples.

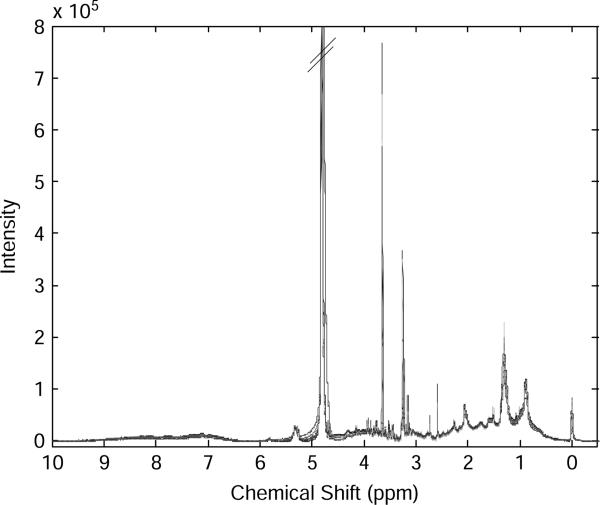
¹H-NMR depends upon the characteristic spin of the atomic nucleus of hydrogen, which exists in two spin states in the presence of a strong external magnetic field. The lower energy spin state is aligned with the external field, but the higher energy spin state is opposed to the external field. Irradiation of a sample with radio frequency energy corresponding exactly to the spin state separation will cause excitation of those nuclei in the lower spin state to the higher spin state. This radio frequency energy is reflected in the ppm (parts per million) value of the x-axis shown in Fig. 1, which displays an example of multiple NMR spectra of human plasma. In different biological molecules, the energy required for this transition, often referred to as the chemical shift, is a characteristic for different hydrogens in specific chemicals. Traditionally, chemical shifts along the x-axis are listed from largest to smallest. The y-axis is proportional to the concentration of the hydrogen nucleus absorbing energy so that the spectrum provides information on the chemicals, which are present and also the concentrations of those chemicals.

Fig. 1.

An example of multiple NMR spectra of human plasma obtained by a 600 MHz NMR spectroscopy.

A major limitation in NMR spectroscopic evaluation of tissues and body fluids lies in the complexity of the signals generated by the presence of multiple chemical species, which often have signals that overlap. Because of this overlap, we refer to the amplitude at specific ppm (chemical shift) values as features. To search for chemical species that are useful for classification and prediction, we separate two components, the first being an effort to identify metabolite features linked to potential risk factors (i.e., feature extraction/selection) and the second being a study to explicitly test whether these metabolite features predict disease (i.e., prediction or classification).

The main purpose of feature extraction/selection is to simplify the entire modeling process and to reduce computational and analytical efforts by identifying the important features from the high-dimensional original dataset. There is a distinction between feature extraction and feature selection, although much of the literature fails to make a clear distinction. Feature extraction techniques attempt to create new features based on transformations of the original features to extract the useful information for the model, while feature selection techniques attempt to pick the subset of original features that leads to the best prediction or classification [2, 3]. Despite numerous studies of feature extraction/selection that have been conducted in the field of signal and image processing, feature extraction/selection methods have not been thoroughly studied for the application of NMR spectra.

The most widely used method in NMR applications includes a combination of principal component analysis (PCA) and classification models [4, 5]. Although PCA has been successfully used to facilitate visualization of the complicated spectra and, thus, provide an initial idea to guide subsequent statistical analyses [6–8], PCA is not an efficient method for the interpretation of the features selected. The reduced dimensions, called principal components (PC) from PCA are each a linear combination of the original features, where the number of original features in the NMR spectra is usually hundreds to thousands. Thus, interpretation of the PCs cannot readily be made, and the extraction of meaningful information is cumbersome. Another major drawback of PCA is that the PCs may not always produce maximum discrimination between classes because the transformation process of PCA relies solely upon the input variables, and does not take into account class information.

Partial least squares (PLS) is another popular method that utilizes class information to help select a transformation better suited for classification [9, 10]. However, the reduced dimensions from PLS also do not provide a clear interpretation with respect to the original features due to the same reason described for PCA. Recently, a two-stage genetic programming (GP) method was developed for identifying important metabolite features for the classification of genetically modified barley [11]. GP is also known as a hierarchical genetic algorithm, introduced by Koza [12]. The first stage of this method searches a whole spectrum to identify the significant features for classification using standard GP. In the second stage, additional GP is employed to find significant features from the features selected in the first stage. This method apparently overcomes the interpretation problem of PCA and PLS since the method does not utilize any transformations to find the significant features. However, GP is known to be vulnerable to overfitting when the features are noisy or the dimension of the features is high [13]. Furthermore, GP is a purely numerical optimization technique, and it may be hard to interpret the feature selection results statistically.

In this paper, we formulate a feature selection problem in NMR spectra as a multiple hypothesis testing problem controlling false discovery rate (FDR). More precisely, we propose a procedure to determine, which metabolite features discriminate spectra among the experimental conditions based on a multiple testing framework. It is well known that applying a single testing procedure to the multiple testing problems leads to an exponential increase of the probability that at least one of the tests leads to rejection of a null hypothesis when the null hypothesis holds. To compensate for this problem, the procedures controlling the family-wise error (FWE) rate that control all the tests were developed simultaneously [14]. However, these procedures are too stringent to detect true significant features. In other words, the procedures that control FWE lead to low power, where the power is the proportion of false null hypotheses, which are correctly rejected [14]. The FDR is the error rate in multiple hypothesis tests and is defined as the expected proportion of false positives among all the hypotheses rejected [15]. The advantage of an FDR procedure is to identify as many significant hypotheses as possible while keeping a relatively small number of false positives [15–17].

The FDR-based procedure overcomes a limitation posed by the reduced dimensions in PCA or PLS and can identify the metabolite features necessary for classification without losing any information in the original features. Moreover, the FDR-based procedure is a statistical approach that enables us to control FDR of the features identified, thus providing the logical interpretation of feature selection results. FDR-based procedures have recently been used in microarray analysis to find co-expressed genes [18] and applied to neuroimaging analysis to identify active voxels in the image data [19]. In microarray/neuroimaging studies, a hypothesis test was performed in each gene/voxel to determine whether the gene/voxel contributes to classification between the different experimental conditions.

It is known that high-resolution ¹H-NMR spectra obtained from multiple samples may contain variability from a variety of sources (e.g. instrumental, environmental, and physiological), which deteriorate classification ability [20]. To improve visualization and discrimination in spectra, we applied orthogonal signal correction (OSC) that enhanced the separability of the different classes by removing variability that did not contribute to prediction or discrimination [21]. The OSC technique for NMR spectra has been shown to minimize physical and biological variation, thus, improving the interpretation of statistical results [20, 22].

Throughout the paper, the effectiveness of our procedures is demonstrated with ¹H-NMR spectra of human plasma, where the goal is to examine metabolic perturbation in response to sulfur amino acids (SAA) intake. SAA are highly variable in human food, and either the deficiency or the excess of SAA may lead to potential risk in human health. They are required for physiologic processes in addition to their role in the maintenance of protein synthesis and nitrogen balance.

2. EXPERIMENTAL DATA

2.1. Collection of NMR Spectra and Experimental Data Structure

We conducted the study within two phases during which plasma samples were obtained from four healthy subjects under controlled metabolic conditions in the Emory General Clinical Research Center (GCRC). The subjects signed an informed consent approved by the Emory Institutional Review Board. During the 12-day GCRC admission, the subjects consumed defined diets at standardized intervals. During the 48-hour equilibration period, the subjects consumed a balanced meal plan with foods selected to ensure adequate energy, protein and SAA intake. The subjects were then placed on constant semipurified diets designed to alter SAA intake, a 5-day zero-sulfur amino acid phase (zero-SAA phase) immediately followed by a 5-day SAA supplementation phase (supplemented-SAA phase). In other words, during the initial 17 time points (first 5 days), blood was collected when the subjects were consuming diets providing zero SAA, and during the latter 17 time points (next 5 days), blood was collected when the subjects were consuming diets providing 117 mg/kg/day SAA, or approximately 10 times the recommended daily/dietary allowance for SAA. ¹H-NMR spectra of human plasma (drawn from blood) were then obtained by a Varian INOVA 600 MHz instrument.

In our experiment, 34 NMR spectra were collected from each subject. The 34 spectra were analyzed in each individual, where half of them (17 spectra) were collected from the zero-SAA phase (class label = 0) and the other half were collected from the supplemented-SAA phase (class label = 1). Because there are four subjects, the total number of spectra are 136 (= 4 subjects × 34 spectra), where again, half of them (68 spectra) were collected from the zero-SSA phase (class 0) and the other half (68 spectra) were collected from the supplemented-SAA phase (class 1).

2.2. Preprocessing of NMR Spectra

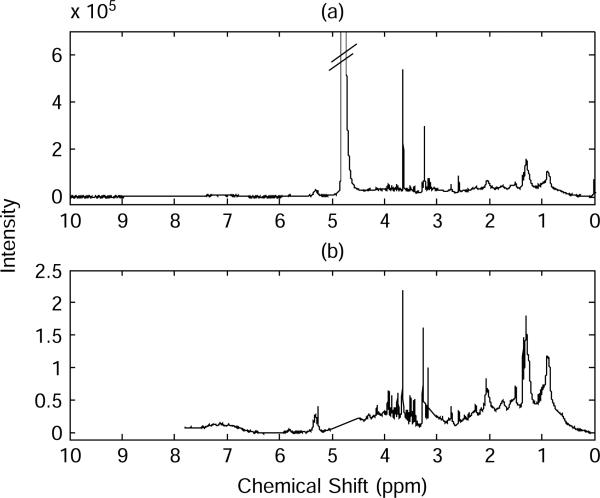
NMR spectra require preprocessing steps before conducting statistical analysis to detect subtle variations from metabolic profiles. In general, the steps involve phase and baseline correction, spectral alignment, elimination of noninformative spectral regions, and normalization. Phase and baseline corrections using NUTS software (Acorn NMR Inc., Livermore, CA) achieved accurate computing of integration of peak regions. Spectral alignment enables direct comparison across different spectra. We utilized a beam search algorithm [23], which by maximizing their correlation determines the best alignment between the reference spectrum and the sample spectra that require alignment. Because they can mask signals from low metabolites, we removed the spectral regions containing signals from water (4.5–5 ppm) and artificial signals caused by endogenous plasma calcium and magnesium (in ppm: 2.573616–2.589738, 2.721409–2.726783, 3.020354–3.156727, 3.22189–3.260854, and 3.62429–3.649818). Further, the spectral regions in 5.4–6.7 ppm and 7.8–10 ppm were not considered in subsequent statistical analyses because they contained no significant metabolite signal. To ensure comparability between spectra, spectra were normalized to the area of the internal standard. An example of original spectrum is displayed in Fig. 2(a). A spectrum after preprocessing and removal of the redundant regions is shown in Fig. 2(b).

Fig. 2.

The 600 MHz ¹H-NMR spectra of human plasma: (a) original spectrum, and (b) spectrum after preprocessing and removal of redundant regions.

3. ANALYTICAL METHODS

3.1. A Multiple Testing Procedure Controlling False Discovery Rate

A multiple testing procedure controlling FDR is proposed to identify the metabolite features that play a significant role in discriminating time points in the zero-SAA phase from those in the supplemented-SAA phase. FDR is a convenient definition of an error rate, which is defined as the expected proportion of false positives among the entire hypothesis rejected [15]. Furthermore, Benjamini and Hochberg introduced an ordered p-value procedure and proved that the procedure controls the specified FDR (or α) [15]. A multiple testing procedure identifies the metabolite features that are central to discriminating time points by their amount of SAA intake. More precisely, each null hypothesis states that the average intensities of the ith metabolite features are equal between the time points from the zero-SAA phase and the supplemented-SAA phase, and the alternative hypothesis is that they differ. Because we have 8444 metabolite features of interest, we can construct multiple hypotheses as follows:

$$\begin{array}{cc}\hfill H_1:m_{1,g1}& =m_{1,g2}\hfill \\ \hfill H_2:m_{2,g1}& =m_{2,g2}\hfill \\ \hfill & ⋮\hfill \\ \hfill H_{8444}:m_{8444,g1}& =m_{8444,g2},\hfill \end{array}$$

where g1 and g2 are the time groups with the zero-SAA phase and the supplemented-SAA phase, respectively. The metabolite features corresponding to the rejected hypotheses imply strong discrimination between the two SAA phases. Now we can employ a two-sample t test for each metabolite feature using test statistics as follows:

$$t_i=\frac{{\stackrel{‒}{y}}_{i,g1}-{\stackrel{‒}{y}}_{i,g2}}{\sqrt{\frac{s_{i,g1}^2}{n_{g1}}+\frac{s_{i,g2}^2}{n_{g2}}}}$$

for i = 1, 2, . . . , 8444. ȳ_{i, g1} and $s_{i,g1}^2$ are the sample mean and variance of metabolite feature i among the time points taken from g1. Likewise, ȳ_{i, g2} and $s_{i,g2}^2$ are obtained from g2. We compute t_i for i = 1, 2, . . . , 8444 assuming that the null hypothesis is true. We next calculate p-values using a permutation method due to repeated measurements and thus we cannot clearly assume that each t_i follows a t distribution. Under the assumption that there is no differential spectral intensity between the two classes (two SAA phases), the t statistic should have the same distribution regardless of how we make the permutation of spectra. Therefore, we can permute (shuffle) the labels of the 136 spectra and re-compute a set of t-statistics for each individual metabolite feature based on the permuted dataset. If this procedure is repeated M times, we can obtain M sets of t-statistics as follows: $t_1^m,t_2^m,\dots t_{8444}^m$, m = 1, 2, . . . , M. The p-value for metabolite feature i for i = 1, 2, . . . , 8444 and M = 200 is obtained by

$$p_i=\sum _{m=1}^{200}\frac{\#\{k:\mid t_k^m\mid \ge \mid t_i\mid ,k=1,2,\dots ,8444\}}{8444\cdot 200}$$

Finally, we used the FDR procedure [15] that used ordered p-values (p(1) ≤ p(2) ≤ . . . ≤ p (8444)) to select the significant metabolite features to discriminate the time points in the zero-SAA phase from those in the supplemented-SAA phase. The summary of the procedure is as follows:

• Select a desired FDR level (= α) between 0 and 1

• Find the largest i denoted as w

$$w=\text{max}\left[i:p\left(i\right)\le \frac{i}{m}\frac{\alpha }{\delta }\right],$$

where m is the total number of hypothesis (here m = 8444) and δ denotes the proportion of true null hypothesis. Several studies discuss the assignment of δ. We used δ = 1, the most conservative choice.

• Let the p-value threshold be p_(w), and declare the metabolite feature t_i significant if and only if p_i ≤ p_(w).

The original FDR procedure [15] assumes that the hypotheses tests are all independent. Later work revealed that the conclusion still holds even if the hypothesis tests are positively correlated [24]. Furthermore, Benjamini and Yekutieli [24] provided a procedure that can handle general dependency of the hypothesis tests through a simple modification of the original FDR procedure. It should be noted that metabolite features in an NMR spectrum are correlated with each other.

3.2. Orthogonal Signal Correction

To determine whether visualization and classification could be improved by removal of unwanted spectral variations, an OSC method was used. In a seminal paper, Wold et al., [21] introduced OSC, a PLS-based solution that can selectively remove from X (i.e., predictor) the unwanted largest variation orthogonal (or unrelated) to Y (response). The first step of OSC is to calculate the PC score vector t from X. The score vector t is then orthogonalized with respect to Y through the following equation:

$${\mathbf{t}}^{\ast }=\mathbf{t}-\mathbf{Y}{\left({\mathbf{Y}}^{\mathrm{T}}\mathbf{Y}\right)}^{-1}{\mathbf{Y}}^{\mathrm{T}}\mathbf{t}.$$

It is not difficult to show thatt* is orthogonal to Y [21]. In the next step, a weight vector, w is calculated such that Xw = t*, followed by the calculation of a new score vector from X and w, t = Xw. The above steps are repeated until the difference between the new score vector and the previous score vector is less than a predefined threshold. Finally, a loading vector, p is calculated, and the correction is performed by subtracting tp^T from X giving a residual vector (E = X – tp^T). The subsequent components can be computed using E as a replacement of X.

Since the introduction of OSC by [21], a number of OSC algorithms have been proposed in the literature. These include modified versions of the original OSC [25, 26], a direct orthogonal signal correction (DOSC; [27]), and orthogonal projections to latent structures [28]. A comprehensive summary of OSC algorithms can be found in Ref. [29].

In the present study a DOSC algorithm was used and implemented using MATLAB codes available from Ref. [27]. DOSC was applied to raw spectra for the purposes of classification or discrimination, as in PLS-discrimination analysis. Thus, the response matrix Y, as categorical variables, contains information about class memberships of spectra (e.g. zero-SAA phase and supplemented-SAA phase).

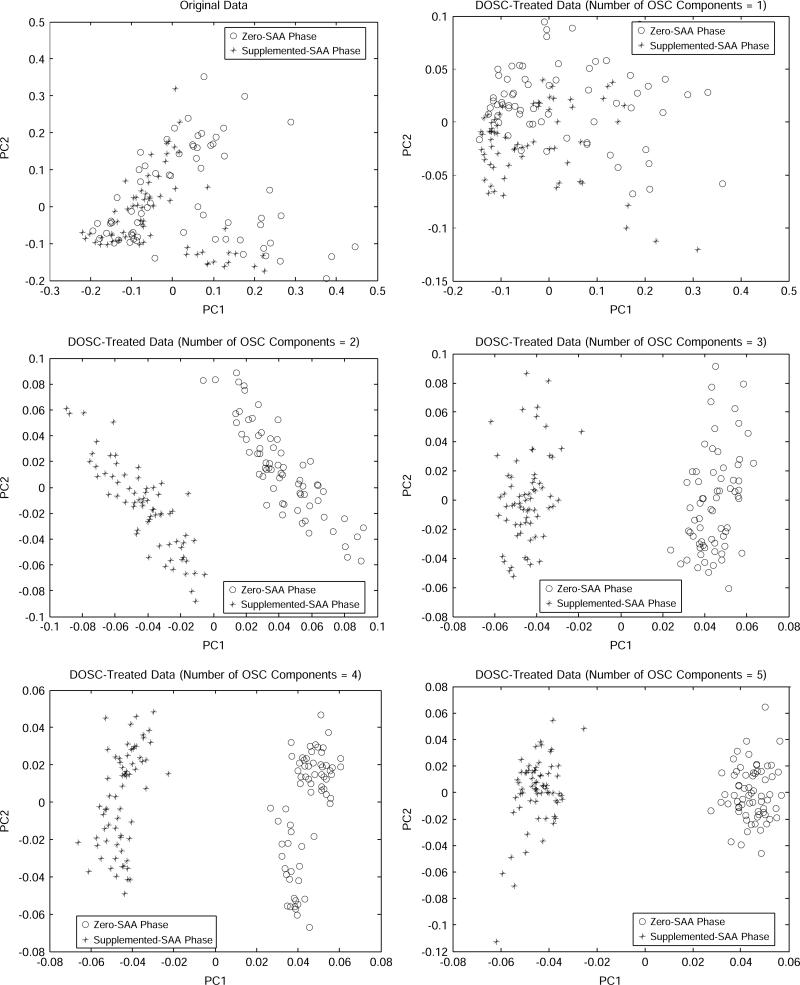
It is important to determine the proper number of OSC components in a given application because there is a risk of overfitting when too many components are used. Thus, OSC results were cross validated using the classification tree method [9]. A brief overview of the classification tree method is given in Section 3.3. To obtain cross-validated error rates, the experimental datasets were split into four groups corresponding to four subjects. Three subjects were used for training, and the one remaining subject was used for testing. This process was repeated three more times. The final classification results from the four different testing samples were then averaged to obtain the cross-validated error rates of the models. It can be seen from Table 1 that the classification tree model, processed by one OSC component yielded higher cross-validated error rates than other classification tree models, processed by more than two OSC components. A comparison of models with more than two OSC components showed that they are all comparable in terms of their cross-validated errors. Thus, we used two-component OSC models in this paper. Previous studies also indicated that one or two OSC components are usually sufficient [21, 27].

Table 1.

Misclassification rates of classification tree models obtained from fourfold cross validation for the DOSC-processed data with different number (#) of OSC components.

	No. of components (#) = 1	No. of components (#) = 2	No. of components (#) = 3	No. of components (#) = 4	No of components (#) = 5
Classification of trees	0.10	0.04	0.08	0.06	0.08

3.3. Classification Methods and Validation

Classification was performed to obtain the models for separating distinct classes and classifying new spectra into previously defined classes. We used k-nearest neighbors (kNNs), classification trees, and support vector machines (SVMs) for evaluation of the FDR-based feature selection method and DOSC. Classification trees partition the feature space into disjoint hyper-rectangular regions according to performance measures (e.g. misclassification errors, Gini index, and cross-entropy) and then fit a constant model in each disjoint region [30]. We used the Gini index as a performance measure. The number of disjoint regions (or the number of terminal nodes in a tree) should be determined appropriately because a very large tree overfits the training set, while a small tree cannot capture important information in the data. A common approach to determine the right size of a tree is tree pruning that removes the leaves and branches of a full-grown tree to find the right size of the tree [31]. A cost-complexity pruning algorithm was used for tree pruning [30]. SVMs use geometric properties to obtain the separating hyperplane by solving a convex optimization problem that simultaneously minimizes the generalization error and maximizes the geometric margin between the points for different classes (two SAA groups in our case) [32, 33]. Nonlinear SVM models can be constructed from kernel functions that include linear, polynomial, radial basis functions. In our experiment, we used polynomial (with degrees of two) kernel functions. kNN classifier is a type of lazy-learning (instance-based learning) technique [34]. kNNs do not require a trained model. Given a query point, we find the kclosest points. A variety of distance measures can be applied to calculate how close each point is to the query point. We then examine the k-nearest points and find which of the most categories belong to the k-nearest points. Finally, we assign this category to the query point being examined. This procedure is repeated for all the points that we wish to classify [34]. Here we used Euclidean distance to determine the neighborhoods and tested different values of k (k = 2ⁱ for i = 1, 2, . . . , 6). Classification trees, SVMs, and kNNs were performed using MATLAB (The MathWorks Inc., Natick, MA).

Classification models are frequently evaluated based on their misclassification rate. Fourfold cross validation was used to estimate of the true misclassification rate. As discussed in Section 2 for determining the number of OSC components, we divided the experimental datasets into four groups corresponding to four subjects. In each of four iterations, three subjects were used for training the models, and the one remaining subject was used for testing. This process was repeated three times more. The final classification results from the four different testing samples were then averaged to obtain the cross-validated error rates (or misclassification rates) of the classification tree and SVMs models.

4. RESULTS AND DISCUSSIONS

4.1. Metabolite Feature Selection

A multiple testing procedure controlling FDR at 0.01 was performed to find the potentially significant metabolite features that differentiate spectra from time points in the zero-SAA phase to those in the supplemented-SAA phase. The procedure identified the region containing 1458 chemical shifts as potentially significant metabolite features, demonstrating significant dimension reduction. In order to confirm the assignment of these chemical shifts to specific metabolites, an experimental validation is needed using, for example, two-dimensional NMR spectroscopy. In the present study, we focus on a computational evaluation of features selected. Interpretation of results in the context of FDR implies that there are on average 15 (15 ≈ 1458 × 0.01) false discoveries out of the 1458 features discovered from the FDR-based procedure. Higher levels of FDR (e.g. FDR level = 0.05 or 0.1) increase the number of significant features, which yields larger power but produces more false significant features (or false discoveries).

4.2. Direct Orthogonal Signal Correction Processing

The effect of DOSC preprocessing of original data in terms of discrimination can be found from the PCA score plots (Fig. 3). PCA was performed after normalization of spectra using MATLAB. PCA identifies a lower dimensional space called PCs through orthogonal transformations of the original features [35]. The PCs are uncorrelated to each other and generally, the first few PCs are sufficient to account for most of the variability in the original high-dimensional space. Figure 3 displays two-dimensional PCA score plots of the first two PCs (PC1 vs. PC2) for the DOSC processed spectra with different numbers of OSC components. Compared to the top panel of Fig. 3 (obtained from original spectra), the middle and bottom panels of Fig. 3 (obtain from DOSC-processed spectra) show a well-defined discrimination of the two classes. It can be seen that the PCA score plots with large numbers of OSC components showed that metabolic variation, because of dietary SAA intake, is largely described by PC1. Different numbers of OSC components were plotted to see their effect on the PCA score plots (Fig. 3). Although using one OSC component improves the separation of the group somewhat compared to original spectra, the score plot using more than two OSC components clearly visualizes groupings between the time points from the zero-SAA phase and the supplemented SAA phase. Generally, as the number of OSC components increase, the score plots provided a slightly better separation in that the groups appeared more compact but not to a significant degree. This graphical analysis from the PCA score plots further justified that two OSC components are sufficient to discriminate two classes.

Fig. 3.

PCA score plots (PC1 vs. PC2) of the original data and the DOSC-processed data with different number of OSC components from ¹H-NMR spectra of human plasma for time points from the zero-SAA phase and those from the supplemented-SAA phase.

4.3. Development of Classification Rules and Validation

Classification methods construct the decision rules that maximize the mathematical separation between different classes with knowledge of predefined class labels. To see the potential advantage of FDR and DOSC, the datasets with the different numbers of metabolite features indicated in parentheses were used for the classification methods.

1. Dataset 1: All metabolite features (8444).

2. Dataset 2: Metabolite features selected by FDR with level = 0.01 (1458).

3. Dataset 3: DOSC-processed dataset 1 (8444).

4. Dataset 4: DOSC-processed dataset 2 (1458).

5. Dataset 5: Metabolite features selected by FDR at α = 0.01 after DOSC (5810).

Dataset 1 is the full dataset containing all metabolite features. Dataset 2 contains 1458 features selected by the FDR procedure (FDR level = 0.01). Datasets 3–5 were preprocessed by DOSC with two OSC components. Dataset 3 consists of all metabolite features (dataset 1) processed by DOSC. Dataset 4 consists of the features selected from FDR (dataset 2) processed by DOSC. Dataset 5 applies FDR to Dataset 3 (post-DOSC), resulting in the selection of 5810 features. The FDR procedure selected more features after DOSC because the reduced variation in the dataset enabled FDR to distinguish more potentially important features.

Misclassification rates obtained from fourfold cross validation are shown to evaluate the accuracy of classification trees, SVMs and kNNs for each dataset (Table 2). For kNN, six different values of k(k = 2ⁱ for i = 1, 2, . . . , 6) were run with Euclidean distance to find the appropriate model. For classification trees, SVMs, and kNNs, the performance of classification using DOSC-processed datasets (Datasets 3, 4, 5) was significantly better than datasets without DOSC (Datasets 1 and 2). More importantly, the FDR-based feature selection method identified 1458 features among 8444 features, and classification trees and SVMs constructed with the features selected by FDR (Dataset 2) yielded smaller misclassification rates than those with all features (Dataset 1). Among kNNs, different values of k affected model performance. kNN models constructed with Dataset 1 produced the minimum error rate (0.35) at k = 8, 32, 64, while kNN models with Dataset 2 produced the minimum error rate (0.35) at k = 4, 8. The classification results from Dataset 1 and Dataset 2 suggested that the FDR-based feature selection method achieved a huge dimensionality reduction by eliminating noninformative features for classification, and yielded classification accuracy that is at least as good as using all features. Classification modeling with these reduced features reduces computational and analytic efforts. For the DOSC-processed datasets (Datasets 3, 4, 5), the application of DOSC post-FDR (Dataset 4) takes advantage of the dimensionality reduction (from 8444 to 1458) while achieving nearly as good misclassification rates as using all features (Dataset 3), and the application of FDR post-DOSC (Dataset 5) achieves dimensionality reduction (from 8444 to 5810) and equivalent misclassification rates compared with all features. The results also indicated that kNNs perform better than classification trees and SVMs in our experimental data. Overall, the FDR-based feature selection method reduced the dimensionality of the original data without degrading classification accuracy.

Table 2.

Misclassification rates obtained from fourfold cross validation of classification trees, SVMs, and kNNs (k = 2ⁱ for i = 1, 2,. . ., 6) for the datasets with the different number of features. Boldface values indicate the kNN models with minimum error rates within Dataset 1 and Dataset 2.

	Dataset 1	Dataset 2	Dataset 3	Dataset 4	Dataset 5
Classification trees	0.49	0.41	0.04	0.04	0.07
SVMs	0.48	0.46	0.00	0.00	0.00
kNN (k = 2)	0.38	0.36	0.00	0.00	0.00
kNN (k = 4)	0.37	0.35	0.00	0.00	0.00
kNN (k = 8)	0.35	0.35	0.00	0.00	0.00
kNN (k = 16)	0.43	0.39	0.00	0.00	0.00
kNN (k = 32)	0.35	0.37	0.00	0.00	0.00
kNN (k = 64)	0.35	0.44	0.00	0.00	0.00

5. CONCLUSION

¹H-NMR spectroscopy measures extract a considerable amount of the structural information available from a profile of a metabolite signal. Analysis of NMR spectra, accompanied by appropriate multivariate statistical techniques, has the potential to provide the tools necessary to facilitate visualization of inherent patterns by reducing the complexity of such information-rich data and discerning metabolic changes reflective of physiological variation, disease states, toxic stress, and nutrition intake.

In this paper, we proposed use of a multiple testing procedure controlling FDR to compensate for the limitations of PCA and PLS by achieving better interpretation of the feature selection results. The advantage of using the FDR-based feature selection method is fourfold. First, the identified features are not linear combination of a large number of original features; thus, the interpretation of results is straightforward. Second, the procedure utilizes class information to help select features better suited for classification. Third, the ability of the procedure to control FDR allows us to interpret the results efficiently. Four, the effect of correlated features can be automatically accommodated. In addition, the present study utilized a DOSC technique to enhance visualization, which leads to more accurate classification results.

The experimental results from real NMR spectra from human plasma demonstrate the effectiveness of FDR-based feature selection and DOSC to achieve better feature selection and classification. The overall results show that classification accuracy was improved by FDR and DOSC, while keeping only relevant features.

It should be noted that because our procedures are purely statistical methods based upon the available data, the metabolite features selected in the procedure may not be generally applicable to samples collected under other conditions. Further, in the experimental design, giving 10 times more RDA of SAA to one of two subject groups might be a lot in reality. Finally, the relatively small number of samples used in the present study may not allow the biological implications of our application to be generalized for practical applications. Nevertheless, we have shown that the procedures used here are potentially useful for the understanding of implicit metabolic patterns in biological systems and stimulate further investigation in the development of better analytic tools for the study of complex high-resolution NMR spectra.