The Hippocampal Rate Code: Anatomy, Physiology and Theory

Abstract

Since the days of Cajal, the CA1 pyramidal cell has arguably received more attention than any other neuron in the mammalian brain. Hippocampal CA1 pyramidal cells fire spikes with remarkable spatial and temporal precision, giving rise to the hippocampal rate and temporal codes. However, little is known about how different inputs interact during spatial behavior to generate such robust firing patterns. Here, we review the properties of the rodent hippocampal rate code, and synthesize work from several disciplines to understand the functional anatomy and excitation-inhibition balance that can produce the rate coded outputs of the CA1 pyramidal cell. We argue that both CA3 and entorhinal inputs are crucial for the formation of sharp, sparse CA1 place fields and that precisely timed and dominant inhibition is an equally important factor.

Introduction

A CA1 pyramidal cell in the hippocampus only fires when an animal is at a selective spatial location and hence is called a place cell [1]. The region of space where a place cell has a high probability of firing is called the cell's place field. This spatially selective increase in firing rate is the hippocampal rate code: the number of spikes fired by the cell encodes information about the rat's position. Although there are over 400,000 pyramidal cells in the rat CA1, it is possible to accurately estimate the rat's position in space by observing the rate coded output of just 50 simultaneously recorded place cells [2], potentially indicating a tremendous redundancy in the rate code.

Embedded within the rate coded output of a CA1 cell is the hippocampal temporal code. When a rat runs, the local field potential (LFP) from the CA1 region reveals an approximately 8 Hz theta oscillation. As a rat enters the place field of a CA1 place cell, the first spikes fired by the cell occur late in a theta cycle. In subsequent cycles, the spikes occur earlier and earlier in each cycle. By the last theta cycle within the same place field, the spikes precess almost to the beginning of the cycle. This advancement of spike times with respect to theta is called phase precession. By observing the precise phase of spikes within a single theta cycle, the percentage of the cell's place field traversed by the rat can be estimated [3-8]. The theta-phase as a function of the rat's position is called a temporal code because information about space is encoded in the spike-timing and not the number of spikes.

To fully understand the origin of the temporal code it is instructive to first understand the hippocampal rate code. Here, we synthesize research ranging from electron microscopy to behavioral electrophysiology to try to answer the question of how these rate coded outputs come to be. What is the functional anatomy of the inputs to a CA1 cell? Which of these inputs are necessary to turn the cell into a place cell? How do inhibitory and excitatory inputs interact to ensure that a CA1 pyramidal neuron fires in a given location? We discuss the implications of recent papers [9-11] that attempt to assess the relative contributions of the entorhinal cortex and CA3 in determining the output of a CA1 cell.

A majority of CA1 pyramidal cells are silent cells

As many hippocampal electrophysiologists will attest to, CA1 cells can be notoriously reluctant to fire on a track. More than two-thirds of all CA1 pyramidal cells that are active under anesthesia or during slow-wave sleep do not have place fields in a given environment [12]. These cells are often called silent cells, and they rarely fire more than a handful of spikes in an hour long recording session on a track [12]. Some silent cells have place fields in other tested environments, but most do not [12]. The small proportion of cells active at any given point in time suggests that the hippocampal rate code is also a sparse code (Box 1).

Box 1. Sparse Codes: Population Sparseness versus Single-Cell Sparseness.

The phrase “sparse code” appears often in sensory-coding literature. However, this term is used to describe two slightly different phenomena: the sparseness of the activity of a brain region (population sparseness) and the sparseness of the activity of a single neuron (single-cell sparseness). This box attempts to clarify the uses of these two terms in the context of the hippocampus.

In this review, we state that the hippocampal rate code is sparse. More accurately, the hippocampal rate code shows population sparseness [66]. Population sparseness means that a very small percentage of the CA1 pyramidal cell population is active at any location in a given environment.

Population sparseness in dorsal CA1 can arise because of two independent reasons:

1. A large proportion of CA1 pyramidal cells are silent cells. These silent cells do not fire anywhere in the environment.

2. Dorsal CA1 place cells have very small place fields, ensuring that each cell is active over a small region of space.

Individual CA1 cells whose firing rate is sharply elevated in a small region of space are also said to display sparseness. We call this single-cell sparseness, although it has also been called “lifetime sparseness” [66]. Single-cell sparseness can be quantified using the sparsity index [67]:

$$S=\frac{{(\frac{1}{n}{\sum }_i{r}_i)}^2}{\frac{1}{n}{\sum }_i(r_i^2)}$$

Where i is a spatial bin and r_i is the firing rate of the cell in bin i of an environment containing a total or n spatial bins. A sparsity value of 1 implies no single-cell sparseness. A sparsity value approaching 0 is indicative of maximal single-cell sparseness, and implies a greater amount of spatial information in each spike emitted by that cell. However, the sparsity index provides no direct information about population sparseness.

At this point, it is instructive to consider the results of Jung et al. [19]. They compared the firing properties of dorsal and ventral CA1 pyramidal cells. Ventral place fields were almost four times larger than dorsal place fields. The sparsity values were 0.32 (dorsal) and 0.59 (ventral). Thus, as expected, dorsal place cells showed more single-cell sparseness. However, 54% of dorsal cells were silent in this study, whereas 82% of ventral cells were silent cells. Thus it is possible that, in ventral CA1, the opposing influences of decreased single-cell sparseness and increased number of silent cells might cancel out and the population sparseness might be identical in dorsal versus ventral CA1, albeit due to very different reasons.

Here, we suggest that one simple formula for the population-sparsity index may be:

$$p=\langle s\rangle \times \left(\frac{\alpha }{n}\right)$$

where 〈s〉 is the mean single-cell sparsity index of all active cells, a is the number of cells active in a given environment, and n is the total number of cells isolated during the sleep and track sessions combined. The closer the population-sparsity index is to 0, the sparser the population activity is.

It should be noted that a sparse code resulting from high population sparseness (population-sparsity index approaching 0) is not necessarily better than a distributed code (but see ref [67, 68, 69, 70]). However, it is commonly thought that a CA1 pyramidal cell showing a high degree of single-cell sparseness (small, sharply tuned place fields) is of more use for spatial navigation and spatial learning than a broadly tuned cell. This is an implicit assumption of the lesion and inactivation studies discussed in this review. If the removal of CA3 or entorhinal inputs decreases single-cell sparseness in CA1 (indicated by increased values of the sparsity index) then those inputs can be considered important for sharply tuned CA1 place cells. However, additional behavioral tests are crucial to test if a decrease in single-cell sparseness necessarily translates into behavioral or memory deficits.

It is important that an understanding of the inputs to a CA1 pyramidal cell explain the existence of both place cells and silent cells. Silent cells will be discussed at numerous points in this review, and although they are silent, they reveal a lot about the mechanisms underlying the emergence of the hippocampal rate code. We begin by looking at the anatomical roadmap of the hippocampal-entorhinal system.

Functional anatomy of the entorhinal-hippocampal network

More than 400 years ago, the Italian anatomist, Arantius, was the first to use the term ‘hippocampus’ in reference to the human dentate gyrus (DG) in 1587 [13, 14]. The literal translation of this Greek word is ‘horse-caterpillar’, and it refers both to a sea-horse and to a mythical Greek creature resembling a horse-mermaid [13]. Arantius is thought to have had the sea-horse in mind when he used the term, although the curvature of the structure also reminded him of a ‘white silk-worm’ [13, 14]. In 1732, Winslow described the hippocampus as resembling a ram's horns, and in 1742 de Garengeot coined the term Cornu Ammonis (Ammon's horn), in reference to the Egyptian god often depicted as having the head of a ram [13]. The acronym for this Latin phrase (CA) is the root of the names assigned to the hippocampal subfields (CA1, CA2 [15, 16] and CA3) by Lorenté de Nó in 1934 [17].

The hippocampus starts at a dorsal and septal (medial) part of the brain. Arching in the shape of a ram's horn, it ends up at a ventral and temporal (lateral) location. This is the long axis of the hippocampus. It is also sometimes called the septo-temporal or dorso-ventral axis [18]. Most place cell recordings are made in the dorsal-most part. However, ventral CA1 pyramidal cells also show spatial modulation, but have place fields that are 4-5 times larger than their dorsal counterparts [19, 20]. Indeed, recent recordings on an 18 meter linear track have shown that place field size increases 10 fold along the entire dorso-ventral axis of CA3 [21], ranging from 1 meter at the dorsal most part to 10 meters at the ventral most tip of the hippocampus. It should be pointed out that the absolute size of place fields can also scale with the size of the environment [22, 23]. This can potentially explain why most studies on shorter tracks report dorsal place fields that are about 20 cm long, whereas 1 meter long place fields were seen in the dorsal hippocampus on the 18 meter track [21]. Unlike receptive fields in the sensory cortices, hippocampal pyramidal cells do not show fine-grained topographic organization: anatomically contiguous cells in CA1 can fire at very different locations on the track [24].

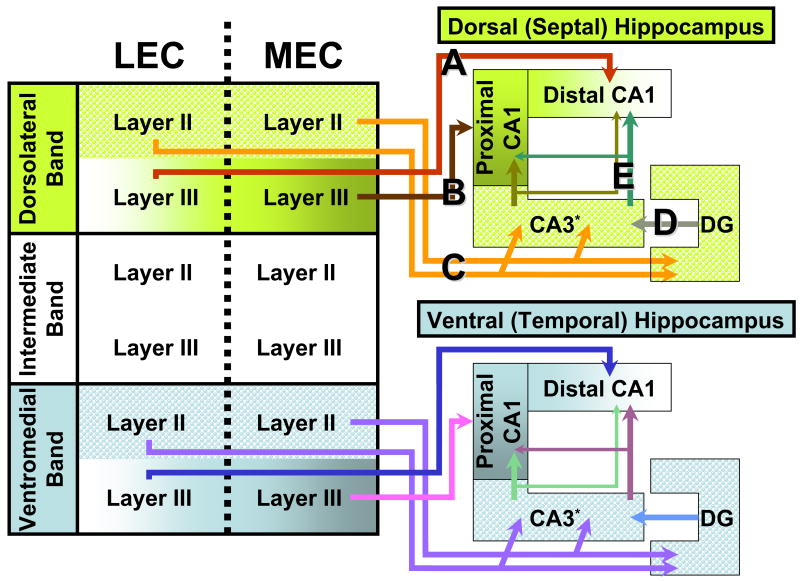
The main source of cortical input to the hippocampus is the entorhinal cortex (EC). The EC is usually divided into the medial entorhinal cortex (MEC) and lateral entorhinal cortex (LEC) [25]. Further, three bands cut across the MEC/LEC divide: the dorsolateral, intermediate and ventromedial bands [26] (Figure 1). Multi-peaked, spatially periodic place cells, also known as grid cells, are found in layer II of all bands of MEC [27, 28]. The grid field size increases with increasing depth along the dorso-ventral axis of the MEC [29].

Figure 1. Entorhinal projections to the hippocampus in the rat.

The entorhinal cortex (EC) has traditionally been divided into 2 major subdivisions: the lateral entorhinal cortex (LEC) and the medial entorhinal cortex (MEC). However, there are also three bands that run perpendicular to the MEC/LEC divide: the dorsolateral, intermediate and ventromedial bands. The hippocampus has a septo-temporal axis (also called its long axis): it starts off at a septal, medial and dorsal location in each hemisphere and then arches backwards and outwards in a C-shape, ending up at a temporal, lateral and ventral location [18, 25]. The pathway projecting from the EC to the hippocampus is called the perforant path. This projection has a number of key organizing principles. There are topographic projections from the bands of the EC to the septo-temporal axis of the hippocampus. The dorsolateral band (encompassing parts of both the MEC and LEC) projects to the septal half of the hippocampus. The intermediate band projects to the third quarter of the hippocampus (projections not shown for sake of clarity). The ventromedial band goes to the most temporal quarter of the hippocampus [26].

A) Layer III pyramidal neurons in the LEC component of each band project to the distal portion of CA1 (cells distant from CA3) [25]. LEC layer III cells show poor spatial modulation [33].

B) Layer III pyramidal neurons in the MEC project to the proximal part of CA1 (cells closer to CA3) [25]. MEC layer III cells are spatially modulated: about half are head-direction cells, a quarter are grid cells and the rest are mixed [32].

C) In each of the three bands, layer II stellate cells of both the MEC and LEC project to the DG and CA3* [25]. This means that an individual DG or CA3 cell can be innervated by axons from both MEC and LEC.

D) Granule cells in DG provide intra-hippocampal projections to CA3 [25, 80].

E) CA3 pyramidal cells provide input to CA1 via the Schaffer Collaterals. There is some topography in this projection: at each transverse level of the hippocampus, CA3 close to DG primarily project to distal CA1 cells, whereas CA3 cells closer to CA1 project to proximal CA1 cells [25].

* This figure shows projections from the EC to the hippocampus in the rat. In the mouse, however, CA3 does not receive its inputs from layer II of the EC. Instead, most projections to the mouse CA3 originate in layer III of both the MEC and LEC [73] (Table 2 and Box 2.4).

The topography of projections from the MEC bands to the long axis of the hippocampus suggests that the increases in place and grid field size are related. The dorsolateral band of the MEC projects to the dorsal half of the hippocampus, the intermediate band to the next quarter, and the ventromedial band to the most ventral quarter of the hippocampus [26] (Figure 1). Thus, there exists a clear anatomical pathway for grid cell inputs to shape the output of hippocampal place cells.

A theoretical study [30] suggests that the linear summation of less than 50 grid fields of varying sizes can give rise to place fields in hippocampal pyramidal cells. This study is ideally suited to understanding CA3, not CA1, place fields [30]: in the rat, layer II of EC projects almost exclusively to the DG and to CA3 (Figure 1C, but see Table 2 and Box 2.4 for a discussion of mouse anatomy). CA1, on the other hand, receives its inputs from layer III of the EC [25, 31]. To further complicate matters, the proximal (close to CA3; Figure 1) half of the CA1 region, receives inputs primarily from layer III MEC cells [25] (Figure 1B). The distal half (distant from CA3) of CA1 receives its inputs from layer III of the LEC [25] (Figure 1A). There is a significant difference between the firing patterns of layer III MEC and LEC cells. MEC layer III cells show a multitude of spatially modulated firing: some of these cells are grid cells, others are head-direction cells, whereas another subgroup conjunctively encodes both grid and head-direction information [32]. LEC cells, on the other hand, show extremely weak spatial modulation [33], which might reflect the different inputs they receive [34].

Table 2.

Comparative hippocampal anatomy of rats and mice.

	Rat	Mouse
Main source of cortical inputs to CA3	EC layer II [25]	EC layer III [73]
Density of pyramidal (excitatory) neurons in CA1 (1000s of neurons/mm3)	270 [75, 76]	1600 [75, 77].
Density of GABAergic (inhibitory) neurons in CA1 (1000s of neurons/mm3)	13.3 [75, 78]	13.5 [75, 79].
Ratio of CA1 excitatory:inhibitory neuron density	20:1	120:1

Footnotes:

EC = Entorhinal Cortex

Box 2. Hypotheses and Outstanding Questions.

2.1 Does proximal CA1 have place cells that are sparser and more spatially informative than those in distal CA1?

The anatomy and physiology reviewed here (Figures 1,2) predict the predominance of sparse, spatially informative place cells in proximal CA1, whereas cells showing poor spatial modulation are expected in distal CA1. This dichotomy would be expected to occur at every transverse section along the dorso-ventral axis of the hippocampus. Thus lesions of proximal CA1 might be expected to impair performance on spatial tasks more than lesions of distal CA1. Anatomically precise quantification of the sparseness and spatial information ratios across the distal and proximal CA1 regions can test this hypothesis.

2.2 Is inhibition onto a single CA1 pyramidal cell far stronger than excitation?

Our review of the literature provides indirect evidence for this hypothesis (Figure 2M-O). In vivo whole cell recordings, ideally from behaving rats [71], can test this hypothesis directly.

2.3 Does plasticity play an important role in generating similar CA1 place cells after EC or CA3 lesions?

To remove any potential plastic or meta-plastic [60] consequences of lesions or slow-acting transgenic inactivation, optogenetic inactivation of EC or CA3 using halorhodopsin [72] can be combined with CA1 tetrode recordings. This will help to further understand the relative, instantaneous contributions of EC and CA3 inputs in giving rise to a CA1 place field.

2.4 Are there any anatomical differences between rat and mouse hippocampus?

CA3 receives the majority of its cortical inputs from EC layer II in rats [25] and from EC layer III in mice [73]. Grid field dynamics are similar in the MEC of both rats and mice [74]. This suggests that CA3 neurons in mice receive inputs from less spatially selective MEC layer III head-direction cells, whereas rat CA3 neurons are primarily driven by more spatially selective grid cells in layer II of MEC. Thus, CA3 neurons might be more spatially informative in rats than in mice. Consistently, the removal of CA3 inputs in rats impairs spatial recall on a Morris water maze in rats [9] but not in mice [11], although methodological differences (lesion versus transgenic inactivation) might account for this discrepancy. Additionally, as shown in Table 2, the ratio of excitation-to-inhibition is much larger in mice (120:1) than in rats (20:1) [75]. The lower inhibition in mouse CA1 can potentially explain why CA1 place fields in mice are larger, more diffuse (Figure 3A) and less spatially informative than in rats (figure 3B, Table 1) [9, 11]. It is worth exploring if interneurons in mice fire at higher rates or have more axonal collaterals to balance the excitation-inhibition ratios across species.

In summary, cells in DG and CA3 receive a mixture of inputs from the parts of EC that have abundant grid cells (MEC layer II) as well as parts that show poor spatial modulation (LEC layer II; Figure 1C). Proximal CA1 cells receive inputs from parts of EC with a combination of grid and head-direction cells (MEC layer III; Figure 1B) and distal CA1 cells receive inputs from parts of EC with poor spatial tuning (LEC layer III; Figure 1A). A careful delineation of sparseness and spatial information ratios across the distal and proximal CA1 regions would help decipher the functional anatomy of this circuit (Box 2.1).

In addition to the spatially modulated inputs from layer III of MEC, proximal CA1 cells receive intrahippocampal inputs from CA3 pyramidal cells [18] (Figure 1E). Since CA3 inputs are also spatially modulated [35], it is not clear who is primarily responsible for the spatial output of these CA1 cells. Is it MEC or CA3? We next discuss recent lesion and inactivation experiments that have investigated this question.

The relative contribution of CA3 versus MEC in governing CA1 place fields

To study the importance of CA3 in shaping the output of CA1 place cells, Brun et al. [9] bilaterally lesioned CA3 inputs to CA1. Almost all the CA3 inputs to CA1 were successfully removed. CA1 pyramidal cells continued to have place fields in the absence of CA3 inputs, suggesting that MEC inputs are sufficient to drive the spatial output of the CA1 cell. CA1 cells did not turn into grid cells since they still receive inputs from multiple MEC grid cells with different spatial tuning, as well as from head-direction and conjunctive cells [25, 32]. A sum of such inputs is expected to give rise to place fields [30]. However, there were significant differences between the rate codes produced by CA1 cells in the CA3 lesioned versus control rats. Most importantly, compared to the sharp place fields in control rats, CA1 place cells in lesioned animals fired more diffusely, had larger place fields, and had a lower peak firing rate within their place fields (Table 1). Lesioned rats had impaired spatial recall, suggesting that the combination of CA3 and EC inputs is necessary for spatial learning and memory.

Table 1.

Place field statistics suggest that CA3 and EC are both required for generating sharp, sparse place fields.

Manipulation:	Chemically Lesion CA3			Chemically Lesion EC Layer III			Transgenically Silence CA3
Recording Site:	Dorsal CA1			Ventral CA1			Dorsal CA1
Species:		Rat			Rat			Mouse
Reference:		[9]			[10]			[11]
Metric	Control	- CA3	Signif	Control	- EC III	Signif	Control	- CA3	Signif
Place Field Size Novel (Day 1) Environment	N/A	N/A	N/A	0.46 m2 Fig 6Da	0.55 m2 Fig 6Da	+20% Z=1.19 N.S	52.2% of box	69.3% of box	+33% p<0.001
Place Field Size Familiar Environment	18.9% of box	28.2% of box	+49% Z=1.7 N.S	0.25 m2	0.36 m2	+44% Z=2.22* p<0.05	44.3% of box	56.3% of box	+27% p<0.001
Peak Firing Rate Novel (Day 1) Environment (Hz)	N/A	N/A	N/A	N/A	N/A	N/A	13.34	13.26	-1% N.S
Peak Firing Rate Familiar Environment (Hz)	10.3	7.0	-32% Z=2.2* p<0.05	11.32	8.66	-23% Z=1.69 N.S	17.14	11.32	-34% N/A
Mean Firing Rate Novel (Day1) Environment (Hz)	N/A	N/A	N/A	1.45 Fig 6Fa	1.85 Fig 6Fa	N/A	1.85	2.64	+43% p<0.001
Mean Firing Rate Familiar Environment (Hz)	1.00	0.91	-9% Z=0.2 N.S	1.34	1.20	-10% Z=0.12 N.S	2.27	1.77	-22% N.S.
Spatial Information Novel (Day 1) Environment (bits)	N/A	N/A	N/A	0.40 Fig 6Ca	0.28 Fig 6Ca	-30% Z=2.25* p<0.05	0.8	0.4	-50% p<0.001
Spatial Information Familiar Environment (bits)	N/A	N/A	N/A	0.71	0.47	-34% Z=2.81* p<0.005	1.1	0.7	-36% p<0.001
Sparsity Index (see Box 1), Familiar Environment	0.30	0.46	+53% Z=2.9* p<0.005	0.45	0.56	+24% Z=2.92* p<0.005	N/A	N/A	N/A

Footnotes:

^aValues represent the mean activity during minutes 10-20 in a novel environment

^bN.S: Not Significant.

^cN/A: Not Available.

Recently, Nakashiba et al. [11] have used transgenic techniques to reversibly inactivate CA3 inputs to CA1 in mice. They, too, found that the loss of CA3 lead to larger, diffuse CA1 place fields with decreased peak firing rates (Table 1). However, contrary to the Brun et al. study [9], they found no deficits in recall on the Morris water maze in these mice. This behavioral difference between the two studies could be due to species specific anatomical differences between rats and CB57L/6 mice (Table 2 and Box 2.4).

To understand the contribution of EC inputs to the hippocampus, a recent study [10] used chemical lesions of EC layer III to see if CA3 inputs alone can sustain CA1 place fields. Since the chemical lesions preferentially targeted the ventromedial and intermediate bands of the MEC, and these regions project to the ventral and intermediate hippocampus, their recordings were restricted to cells at an intermediate location along the dorso-ventral axis of CA1. As discussed earlier, place fields are larger and hence less sparse in this region (Table 1). Surprisingly, the removal of EC inputs had the same effects: CA1 place fields became larger and had a decreased peak firing rate. The detailed statistical results of all three studies are compared in Table 1, and suggest that the main physiological results from all three studies are similar in nature.

These findings indicate that CA3 inputs alone or EC inputs alone can give rise to spatial selectivity in a CA1 cell, although this selectivity is impaired in both cases when compared to controls. The decrease in peak rate in both lesion conditions makes sense: the net excitatory input to CA1 is decreased by the removal of either set of inputs. But why does the absence of CA3 or EC inputs lead to more diffuse, less sparse place fields? To answer this question, and to understand how EC inputs alone can possibly drive a CA1 cell's firing, we now discuss the organization of synaptic inputs to a single CA1 pyramidal cell.

Synaptic inputs to a single CA1 cell: source, number, strength and rate

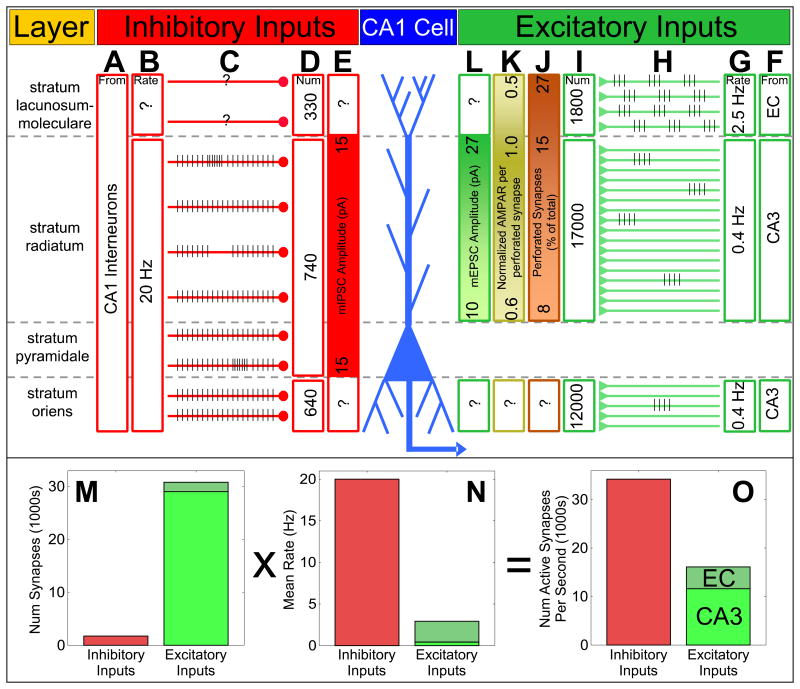
The cell bodies of CA1 pyramidal cells are restricted to a single layer, the stratum pyramidale (S-P). The basal dendrites of these cells extend into the stratum oriens (S-O), with the apical dendrites occupying the stratum radiatum (S-R) and stratum lacunosum-moleculare (S-LM). Note the distinction between the proximal CA1 region and proximal CA1 dendrites. The proximal CA1 region refers to CA1 cells that are close to CA3 and DG in a transverse slice of the hippocampus. CA1 proximal dendrites are the dendrites of a single CA1 cell that are closest to the cell body. Dendrites in S-LM are the most distal (Figure 2).

Figure 2. Synaptic organization of inputs to a single CA1 cell: source, number, strength and rate.

A) Most inhibitory GABAergic inputs onto a single CA1 cell are from CA1 interneurons [48, 49].

B) Fast spiking putative interneurons corresponding to basket and axo-axonic cells project primarily to the proximal dendrites of the CA1 cell and to the cell body and axon. These cells fire at rates of at least 20 Hz in vivo during exploration [50-52]. However, few in vivo recordings have been made from interneurons with broad spikes such as O-LM neurons and other cells that project more heavily to the distal CA1 dendrites. Thus, the in vivo firing rate of these cells is unknown.

C) Schematic showing representative spatial firing profiles of interneurons. Most of these cells fire at high rates and normally show little spatial modulation. However, recent studies have shown that some interneurons can also increase or decrease their firing rates in restricted regions of space [50-52].

D) The number of GABAergic synapses found across the CA1 cell body and dendrites [36].

E) The miniature inhibitory postsynaptic current (mIPSC) is relatively constant across the cell body and proximal dendrites of the CA1 cell [81]. The mIPSC magnitude at distal S-LM and basal S-O dendrites is unknown, as it is difficult to patch onto these very thin dendrites.

F) The source of excitatory inputs to different dendritic regions of a CA1 cell [25].

G) The mean rate of excitatory inputs to a CA1 cell during exploration [32, 47].

H) Schematic showing representative spatial firing profiles of entorhinal and CA3 cell during exploration. Two-thirds of CA3 cells are silent, and the rest have sparse place fields. Entorhinal cells, on the other hand, encode space in a repeating grid pattern or encode head direction information [32].

I) The number of excitatory synaptic inputs onto dendritic spines at all locations along the dendritic tree of a CA1 cell. Note the larger number of putative CA3 inputs [36]. It should be pointed out that a small proportion of the excitatory synaptic inputs to a CA1 cell are from regions other than CA3 or EC [25].

J) The proportion of large, perforated synapses increases along the apical dendrite, peaking at the most distal synapses [39].

K) The number of AMPA receptors per perforated synapse peaks at the distal S-R dendrites, but then falls rapidly at the most distal dendrites in S-LM [38, 39].

L) As expected from the numbers in (I) and (J), the size of the miniature excitatory postsynaptic current (mEPSC) increases from proximal to distal S-R [42, 81]. However, no direct evidence exists for the value of this current in the most distal dendrites in S-LM as these dendrites are far too thin to patch on to. It is estimated that due to the decreased AMPA receptor count at these most distal synapses, the mEPSC would decrease in these distal dendrites [39].

M) The total number of inhibitory synapses on a CA1 neuron is far less than the number of excitatory synapses [36].

N) The mean firing rate of the inhibitory neurons is far greater than that of excitatory neurons [50-52]. Furthermore, entorhinal firing rates are much greater than CA3 rates [32, 47].

O) A product of the number of synapses times the firing rates yields an estimate of the net inhibitory and excitatory drive onto a CA1 cell. Conservative estimates suggest that the inhibitory drive may be at least twice as large as the excitatory drive. Note that this calculation does not factor in the efficacy, strength or short term dynamics of the synapses.

CA3 represents the largest source of excitatory synapses onto a CA1 pyramidal cell, forming about 30000 synapses onto the spines of dendrites in S-R and S-O, although some of these may come from other sources such as the medial septum [36] (Figure 2I). EC makes far fewer synapses: at most 1800, all of them restricted to the distal dendrites in S-LM [36]. There are also about 1700 GABAergic, inhibitory inputs distributed over the CA1 cell body and dendritic tree [36] (Figure 2D). The functional significance of these inhibitory inputs will be addressed shortly.

Glutamatergic synapses onto a CA1 pyramidal neuron are of two types: perforated and non-perforated. Perforated synapses express more AMPA receptors and generate larger EPSPs than non-perforated synapses [37]. EC inputs onto distal CA1 dendrites have a higher percentage of perforated synapses (Figure 2J). However, this is not as advantageous as it may seem. The number of AMPA receptors per perforated synapse, indicative of the synaptic strength, peaks at the distal S-R dendrites [38, 39] (Figure 2K). Electron microscopy studies have shown that this number then falls dramatically at S-LM synapses [39] (Figure 2K). Thus, EPSPs generated at an EC synapse are expected to be smaller than those at CA3 synapses [39, 40]. To make matters worse for EC inputs, dendritic filtering causes the amplitude of distal dendritic EPSPs to be significantly reduced by the time the signal reaches the soma [41]. The increased AMPA receptor numbers in distal S-R is a synaptic scaling method that compensates for dendritic filtering [42]. However, as evidenced by the decrease in AMPA receptors in S-LM, synaptic scaling might not apply to the EC inputs.

Given their fewer number, more distal location and lower AMPA receptor count, the synaptic inputs from EC would appear to be far less likely to make a CA1 cell fire, compared to the more numerous, and more proximal, CA3 inputs. But the lesion studies discussed above [9, 11] suggest otherwise. There may be three complementary solutions to this apparent impasse: dendritic spikes, gating of EC inputs by CA3 inputs, and the firing properties of EC in vivo.

Synchronous activation of nearby synapses can lead to a large dendritic depolarization and a resulting dendritic spike [43-45]. This mechanism is thought to be especially efficacious for the thin, high input resistance distal dendrites in the S-LM [39, 40]. However, a dendritic spike does not necessarily translate into a somatic spike [43]. Two groups have recently shown that the chances of an EC-induced dendritic spike eliciting a somatic spike are increased by a modest coactivation of CA3 inputs [40, 46]. The depolarization provided by such CA3 inputs prevents the EC-generated dendritic spike from falling victim to inhibitory inputs and dendritic filtering. In this scenario, inputs from CA3 act as a “gate” that permits the passage of an EC-induced distal dendritic spike to the soma, where it can then trigger a somatic action potential.

The third piece of the puzzle comes from the in vivo firing properties of EC and CA3 cells. CA3 pyramidal cells, like CA1 cells, can be either place cells or silent cells. In fact, 67% of CA3 cells are silent cells [47] (Figure 2H). Including the silent cells, the mean firing rate of all recorded CA3 cells is around 0.4 Hz [47] (Figure 2G). In contrast, MEC has very few silent cells and the active cells have a six-fold higher mean firing rate: around 2.5 Hz [32] (Figure 2G). The firing of all types of MEC layer III cells (head-direction, grid, and conjunctive [32]) is less sparse than that of CA3 place cells [32, 47]. Grid cells fire in a regular, repeating pattern over the entire environment and do so in all environments [28, 32]. These factors increase the chances of synchronous MEC inputs from overlapping grid and head direction cells. This synchronous input can result in a dendritic spike in the distal S-LM dendrites. When accompanied by simultaneous inputs from even a very small number of CA3 place cells, the aforementioned “gate” would open, and the CA1 cell would be able to output a spatially-modulated rate code. When CA3 is lesioned, the gate would close and the CA1 cell would be expected to fire less often. Experiments show that this is only partially true: although the peak firing rate of the CA1 cell is lower in CA3 lesioned animals, the cell fires more diffusely and has larger place fields. To explain what could underlie this diffuse firing, we finally turn our focus to CA1 interneurons.

CA1 interneurons are anything but silent

Interneurons local to the CA1 region are the main source of inhibitory inputs onto a CA1 pyramidal cell [48, 49]. Basket, bistratified and axo-axonic interneurons have their cell bodies in S-P and form synapses on the proximal dendrites and cell body of the CA1 pyramidal cell, exerting a powerful control over its output. O-LM, LM-R and several other types of interneurons inhibit the distal dendrites of the CA1 cell. The cell bodies of these interneurons are located in S-O or near the border between S-R and S-LM [48, 49]. Over the last few years, there has been a surge in the number of studies analyzing the spatial firing properties of CA1 interneurons [50-52].

Fast-spiking S-P interneurons fire at high rates (greater than 20 Hz) and are active on almost all parts of the track [50-52] (Figure 2B,C). Some interneurons have ON place fields, where they further increase their firing rate, and others have OFF place fields, where they decrease their rate [50-52] (Figure 2C). The existence of OFF interneuron place fields suggests the possibility that some CA1 pyramidal cells may fire on the track due to a release-from-inhibition effect (Figure 3D).

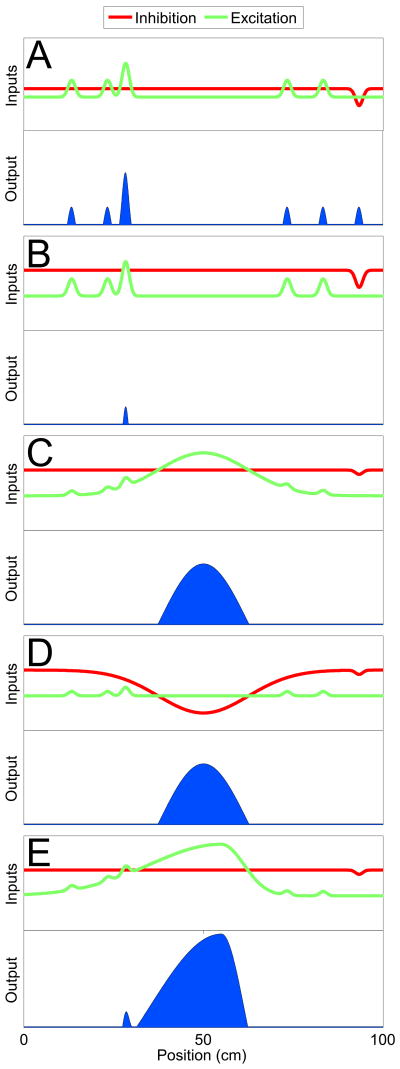
Figure 3. Excitation-inhibition balance onto a single CA1 pyramidal cell.

Schematic representation of the relative influence of excitation and inhibition on the spatial selectivity of a place cell. The x-axis in all plots represents distance along a linear track.

A) Perfectly balanced excitation and inhibition would lead to spikes at several points on the track due to random increases in excitation or decreases in inhibition. However, silent cells do not fire many spikes on the track [12].

B) Dominant inhibition would prevent random fluctuations in excitatory and inhibitory inputs from resulting in spikes. This could explain the observed, very rare firing of silent cells [12].

C) A synchronous increase in excitation at a particular point on the track can lead to excitation overcoming inhibition and the CA1 cell firing in a place-dependent manner [30].

D) A synchronous decrease in inhibition in a given region of space can also lead to the spatially modulated firing of a CA1 cell [50-52].

E) Experience-dependent changes in the excitatory inputs can lead to asymmetric place fields with higher firing rates [56-58].

The high firing rates and sustained activation of CA1 interneurons, coupled with the relative sparseness of CA3 and EC inputs suggests that inhibition onto CA1 pyramidal cells far outweighs excitation. In fact, using the most conservative estimates, the total number of inhibitory spikes arriving at a CA1 pyramidal neuron may be at least twice the number of excitatory inputs during spatial navigation (Figure 2M-O). This has a number of important consequences. Consider the case of perfectly balanced excitation and inhibition onto a CA1 pyramidal cell. In this scenario, any small, random increases in excitation or decreases in inhibition would make the CA1 cell fire. This would give rise to numerous spikes on a track at randomly distributed locations, something that is rarely seen in vivo [12] (Figure 3A). Instead, if inhibition was the dominant force, minor fluctuations in excitatory or inhibitory inputs would rarely make the CA1 pyramidal cell spike. Thus, an inhibition-dominated regime can help explain the numerous silent cells seen in CA1 and the almost complete absence of spiking of place cells outside their place fields (Figure 3B). In such a regime, a large number of synchronous excitatory inputs would be required to make the CA1 cell fire, as discussed in the previous section (Figure 3C).

This dominant inhibition can also explain the more diffuse firing in CA3-lesioned rats. CA3 activation directly excites CA1 pyramidal cells. However, it also generates strong, feedforward inhibition by activating CA1 interneurons. Rapid disynaptic inhibition of the proximal dendrites and soma of the CA1 pyramidal cell follows [53]. This gives excitatory CA3 inputs a very short time window in which to bring the CA1 cell to threshold and make it spike. It also gives any EC driven dendritic spikes generated in the distal dendrites a very short time window to propagate to the soma and cause a somatic spike. This combination of strong and rapid feedforward inhibition could be responsible for the sparsity of CA1 place cells: only strongly synchronized EC and CA3 inputs can make the cell fire. When CA3 is lesioned, much of the precisely timed feedforward inhibition is also lost. This gives the EC generated dendritic spikes a larger time window to travel down to the soma and make the CA1 cell fire over wider regions of space. This would give rise to the more diffuse rate code that is seen in CA3-lesioned animals, and suggests an easily testable hypothesis: in CA3-lesioned animals, the firing rates of interneurons recorded from S-P should be significantly lower than in controls.

Similar arguments may apply to the effects of EC lesions on CA1 place fields. EC inputs to CA1 terminate on the distal dendrites of CA1 pyramids, but also excite LM-R and other interneurons in the S-LM layer [31, 48, 49], as evidenced by recent in vivo studies showing that LM-R cells are phase locked to entorhinal inputs during slow-wave sleep [54]. The dominant effect of this disynaptic inhibition is well documented [55]. Although LM-R neurons are primarily driven by EC inputs, their axons project to both the proximal and distal dendrites of CA1 pyramidal cells [48, 49], inhibiting the feedforward excitatory inputs from both EC and CA3. When EC is lesioned, this source of dominant inhibition is also lost and CA3 inputs alone can cause a CA1 cell to spike more diffusely [10].

Accounting for plasticity

While a detailed understanding of the excitation-inhibition balance can help explain certain facets of the hippocampal code, it cannot explain changes in the rate code over different time-scales. For example, the place field size decreases across the first 3 days of exposure to a novel environment [10, 11] (Table 1). Other prominent changes occur on an even faster timescale – the firing rate of CA1 place cells almost doubles within the first few traversals of a familiar environment [56-59]. In lesion [9, 10] and slow-acting transgenic inactivation studies [11], there is a delay of many days between the lesion/inactivation and the CA1 recordings. Thus it is possible that several plasticity-dependent or metaplastic [60] changes have already taken place during this time period (Box 2.3).

Conclusions

The hippocampal rate code can best be understood in terms of the anatomical inputs to the hippocampus and the excitation-inhibition balance within the hippocampus. There appear to be a few key factors that play a role in generating the spatially-precise firing of a CA1 pyramidal cell. First, strong input from spatially overlapping MEC layer III cells can generate a large EPSP or a dendritic spike in the distal dendrites of the CA1 cell [30, 39, 40, 43-45]. Once the dendritic spike is generated, the strong feed-forward inhibition would prevent it from propagating to the soma [43, 53]. However, additional synchronous inputs from CA3 can help overcome the inhibition and lead to somatic spikes [40, 46]. It is possible that the converse is also true: strong depolarization from overlapping CA3 place fields can lead to an EPSP that would normally be counteracted by the stronger feed-forward inhibition. However, the synchronous arrival of MEC inputs, together with the CA3 inputs can help overcome the inhibition and lead to a somatic spike.

This makes sense given the anatomical inputs to a CA1 cell and the in vivo firing rates of the input cells. There are relatively few inputs from MEC, but these input cells fire at higher mean rates and their grid and head-direction fields are more likely to overlap [30, 32, 36]. CA3 cells are sparser and fire at much lower rates than MEC cells [47], but CA3 synaptic inputs onto a CA1 cell outnumber EC inputs by an order of magnitude – 30,000 versus 2,000 [36] – increasing the chances of temporally overlapping inputs from CA3. Thus, synchronous inputs from both EC and CA3 seem to be necessary to give rise to small, sparse, sharply peaked place fields in CA1. When either CA3 or EC inputs are removed, not only is the synchronous input removed (resulting in lower peak firing rates [9-11]), but the strong feed-forward inhibition (caused by either CA3 or MEC inputs) is also removed. This allows relatively weaker EPSPs and dendritic spikes (that would have otherwise been shunted by the strong inhibition) to lead to somatic spikes, resulting in larger and more diffuse place fields [9-11]. In fact, since inhibition seems to outweigh excitation onto a CA1 pyramidal neuron, precisely timed synchronous excitatory inputs are needed to output the spatially precise CA1 rate code [53].

This approach leads to an intriguing conclusion: the hippocampal rate code is strongly dependent on the temporal pattern of inputs. The goal of future experiments will be to provide a unified explanation of how the rate and temporally coded outputs of the CA1 cell can arise from a set of excitatory and inhibitory inputs and to understand how these CA1 outputs are interpreted by neurons in downstream brain regions [61-65]. Exactly seventy-five years after being christened by Lorenté de Nó [17], the CA1 pyramidal neuron promises to be the focus of both basic and clinical research for many decades to come.