Predicting In Vitro Antibacterial Efficacy across Experimental Designs with a Semimechanistic Pharmacokinetic-Pharmacodynamic Model

Abstract

We have previously described a general semimechanistic pharmacokinetic-pharmacodynamic (PKPD) model that successfully characterized the time course of antibacterial effects seen in bacterial cultures when exposed to static concentrations of five antibacterial agents of different classes. In this PKPD model, the total bacterial population was divided into two subpopulations, one growing drug-susceptible population and one resting drug-insensitive population. The drug effect was included as an increase in the killing rate of the drug-susceptible bacteria with a maximum-effect (E_max) model. The aim of the present study was to evaluate the ability of this PKPD model to describe and predict data from in vitro experiments with dynamic concentration-time profiles. Dynamic time-kill curve experiments were performed by using an in vitro kinetic system, where cultures of Streptococcus pyogenes were exposed to benzylpenicillin, cefuroxime, erythromycin, moxifloxacin, or vancomycin using different starting concentrations (2 and 16 times the MIC) and elimination conditions (human half-life, reduced half-life, and constant concentrations). The PKPD model was applied, and the observations for the static as well as dynamic experiments were compared to model predictions based on parameter estimation using (i) static data, (ii) dynamic data, and (iii) combined static and dynamic data. Differences in experimental settings between static and dynamic experiments did not affect the growth kinetics of the bacteria significantly. With parameter reestimation, the structure of our previously proposed PKPD model could well characterize the bacterial growth and killing kinetics when exposed to dynamic concentrations with different elimination rates of all five investigated antibiotics. Furthermore, the model with parameter estimates based on data from only the static time-kill curve experiments could predict the majority of the time-kill curves from the dynamic experiments reasonably well. Adding data from dynamic experiments in the estimation improved the model fit for cefuroxime and vancomycin, indicating some differences in sensitivity to experimental conditions among the antibiotics studied.

In vitro time-kill curve experiments are commonly used to characterize the pharmacodynamic (PD) interaction between bacteria and antibacterial agents (11). Compared to animal studies, in vitro studies are easy to perform, provide a large range of concentrations to be studied, and allow human pharmacokinetics (PK) to be fairly easily simulated. In vitro studies are also unaffected by several factors that may cause great variability when measuring the antibacterial effect in vivo, e.g., variability in drug disposition, the host's immune response, and underlying diseases. In time-kill curve experiments changes in the bacterial count are monitored over time during antibacterial exposure, and data are most efficiently characterized by using a mechanistic modeling approach (10). Besides allowing a good summarization and description of the data, this approach offers the possibility to make predictions and simulation of untested scenarios, which is useful for the design of new studies as well as in the search for more optimized dosing schedules (26, 27).

We previously developed a general semimechanistic pharmacokinetic-pharmacodynamic (PKPD) model describing the events seen in an in vitro bacterial culture when exposed to antibacterial agents (31). One of the strengths of this model is that it was shown to perform well when data from five antibacterial drugs belonging to different classes were analyzed simultaneously. In this PKPD model, the total bacterial population is divided into two subpopulations, one proliferating and drug-susceptible population and one resting and drug-insensitive population (Fig. 1). A large total bacterial population in the system is assumed to stimulate the transfer of bacteria from the susceptible stage into the resting stage. With this structure the model captures the low bacterial net growth and the low antibacterial effect when the system is reaching the stationary phase. The model also describes the early rapid killing effect and the presence of persisting cells often seen following antibiotic exposure (3, 19, 40).

FIG. 1.

Semimechanistic PKPD model describing the time course of bacterial growth and killing after antibacterial treatment. C, drug compartment; Ce, drug effect compartment; S, proliferating and drug-sensitive bacteria; R, resting and drug-insensitive bacteria; k_e, drug elimination rate constant; k_deg, degradation rate constant; k_e0, rate constant for effect delay; k_growth and k_death, rate constants for multiplication and degradation of bacteria, respectively; k_SR, rate constant for transformation from the growing, sensitive stage into the resting stage.

This model was found to successfully describe the bacterial growth and killing kinetics of Streptococcus pyogenes both without drug exposure and following exposure to a wide range of static concentrations of the antibiotics benzylpenicillin, cefuroxime, erythromycin, moxifloxacin, and vancomycin (31). However, when using intermittent dosing, the concentration of the antibiotic in the body will not be static but rather will gradually decrease during the dosing interval. For the PKPD model to be useful in predicting clinical effects, it is important that the model is able to characterize the effects after drug exposures that mimic those observed in vivo as closely as possible.

The aim of this study was to evaluate the performance of the previously developed PKPD model (31) in predicting the time course of antibacterial effects seen for bacterial cultures when the concentration of the antibiotic decreases over time, with half-lives similar to those observed for patients. Dynamic time-kill curve experiments were performed by using an in vitro kinetic model (24) where S. pyogenes was exposed to the same five antibiotics as those used to develop the model. The PKPD model was applied to the new data both with and without a reestimation of the model parameters.

MATERIALS AND METHODS

Bacterial strain and media.

S. pyogenes group A strain M12 NCTC P1800 (National Culture Type Collection) was used as the test strain throughout the study. The bacteria were stored at −80°C and kept on blood agar plates between experiments. Before experiments the bacteria were grown in Todd-Hewitt broth at 35°C for 6 h, resulting in a starting inoculum of approximately 5 × 10⁸ CFU/ml.

Antibiotics.

Five drugs were evaluated: benzylpenicillin (Bensylpenicillin; AstraZeneca), cefuroxime (Zinacef; GlaxoSmithKline), erythromycin (Abboticin; Abbott), moxifloxacin (Bayer), and vancomycin (Vancomycin Abbott; Electra-Box Pharma). Fresh stock solutions were prepared on the day of the experiments by dissolving the antibiotic in sterile distilled water (benzylpenicillin, cefuroxime, erythromycin, and moxifloxacin) or sterile phosphate-buffered saline (vancomycin) to a concentration of 10 mg/ml. The stock solutions were further diluted in Todd-Hewitt broth to obtain the desired concentrations.

In vitro kinetic system.

The dynamic time-kill curve experiments were performed with an in vitro kinetic system described previously (13, 24). This system is based on the dilution of the medium in the culture vessel by connecting it to a pump that removes the medium at a constant rate. This creates negative pressure in the vessel, and fresh medium is sucked into the culture vessel, resulting in a first-order elimination rate of the antibiotic. The culture vessel consists of an open-bottom spinner flask (110 ml) with a modified base. The base includes an outlet connected to the pump and a perforated metal support onto which a filter membrane and a prefilter are placed to prevent the dilution of the bacteria. One side arm of the spinner flask is connected to a vessel containing the fresh medium that is drawn into the flask. In the other side arm, a silicon membrane is inserted to enable repeated sampling. A magnetic stirrer is placed above the membrane to ensure homogenous mixing and to prevent membrane blockage. The concentration-time profiles simulated in this in vitro kinetic system were previously shown to be as expected, with little variance for a number of antibiotic and pathogen combinations (24, 25, 33).

Time-kill curve experiments.

The culture vessel was filled with Todd-Hewitt broth, and bacteria from the 6-h logarithmic-growth-phase culture were added to reach a starting inoculum of 10⁶ CFU/ml. Antibiotics were added to the vessel to achieve the desired initial concentrations. The mixtures were incubated at 35°C for 24 or 48 h, during which frequent samples were taken for measurements of viable count. The samples were serially diluted in sterile phosphate-buffered saline and plated onto two to four blood agar plates. After incubation at 35°C in 5% CO₂ for 18 to 24 h, the numbers of CFU were manually calculated. The limit of detection (LOD) was 10 CFU/ml, and drug carryover was assessed by a visual inspection of the distribution of colonies on the plates. Each time-kill experiment was carried out in at least duplicate on separate occasions.

(i) Growth control experiments.

To study whether there is a difference in the growth kinetics of the bacteria between different environments (static and dynamic), growth control experiments (i.e., experiments without the addition of antibiotics) were performed with test tubes as well as with the in vitro kinetic system. In the kinetic system, fresh medium was supplied at a flow rate corresponding to a half-life of 4 h. For the growth control experiments, a range of starting inocula of between 10³ and 10⁶ CFU/ml were used.

(ii) Static time-kill curve experiments.

Data from the static time-kill curve experiments were reported previously (31). In short, these experiments were performed by using 10-ml test tubes with a total Todd-Hewitt broth volume of 4 ml. The tubes were placed into sand to minimize fluctuations in the temperature during the experiments. A total of 135 static time-kill curve experiments were performed, and for each of the five antibiotics, the starting inocula were exposed to a wide range of static antibiotic concentrations (Table 1).

TABLE 1.

MIC values, initial concentrations used in time-kill curve experiments (as multiples of the MIC), simulated half-lives in the dynamic experiments, and numbers of observations per type of experiment

Drug	MIC (mg/liter)	Type of exposure	Initial concn as multiple of MIC	Simulated t1/2 (h)a	No. of observations
Growth control		Static	0		273
		Dynamic	0	4.0	88
Benzylpenicillin	0.012	Static	0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 16, 64		455
		Dynamic	2, 16	0, 1.0, 3.0	138
		Repeated	2, 13, 16	1.0, 1.1	306
Cefuroxime	0.0313	Static	0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 16, 64		427
		Dynamic	2, 16	0, 1.7, 5.1	161
Erythromycin	0.125	Static	0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 16, 64		455
		Dynamic	2, 16	0, 1.7, 5.1	161
Moxifloxacin	0.125	Static	0.25, 0.5, 1, 2, 4, 16, 64		376
		Dynamic	2, 16	0, 12.7, 38.1	138
Vancomycin	0.25	Static	0.25, 0.5, 1, 1.5, 2, 4, 16, 64		409
		Dynamic	2, 16	0, 5.1, 15.2	171

^aSee reference 14.

(iii) Dynamic time-kill curve experiments.

In the in vitro kinetic system the starting inocula were exposed to initial concentrations of 2 and 16 times the MIC, with a simulated half-life corresponding to the human half-life reported previously for each of the drugs (14) (Table 1). In addition, experiments with a starting concentration of 2 times the MIC and a simulated reduced half-life (one-third of the human half-life) were also performed. To study the influence of different experimental settings on the killing kinetics, experiments with a constant concentration in the in vitro kinetic system were also performed by adding antibiotics to the incoming medium. In these experiments the concentrations were 16 times the MIC throughout the experiment, and the flow rate used corresponded to the human half-life of the respective drug.

(iv) Experiments with repeated dosing.

The pharmacodynamic effect of repeated dosing was studied by using benzylpenicillin as the test substance. In the in vitro kinetic system, cultures of S. pyogenes were exposed to repeated doses of benzylpenicillin corresponding to a starting concentration of 2 or 16 times the MIC with dosing intervals of 4 or 11 h, respectively, using a simulated half-life of 1.0 h (human half-life). The dosing intervals were selected so that the bacterial count at the time of the additional doses would approximate the starting inoculum of 10⁶ CFU/ml. Data from previously reported experiments with a repeated dosing of benzylpenicillin were also included in this study (24). In these experiments the same bacterial strain was exposed to a starting benzylpenicillin concentration of 13 times the MIC with a second dose of either 13 or 1.3 times the MIC administered after 8 h. The simulated half-life in these experiments was 1.1 h (24). Data for the experiments with repeated dosing were used as external validation data only and were thus not included in model parameter estimations.

Semimechanistic PKPD model.

The PK model includes the drug compartment (with drug concentration C) with a first-order degradation rate constant (k_deg) and also, for the dynamic experiments, a first-order elimination rate constant (k_e) set to the elimination rate (flow rate/volume) used in the in vitro kinetic system (Fig. 1 and equation 1). Benzylpenicillin and cefuroxime previously showed degradation during 24-h incubation experiments (31), and for these drugs the k_deg values were fixed to 0.020 and 0.026 h⁻¹, respectively. For the other drugs, the k_deg was set to zero. An effect compartment (37), with drug concentration Ce, was introduced to allow for a possible time delay between the drug concentration in the central compartment and the observed effect on bacterial killing (equation 2). This effect delay was characterized by a first-order rate constant (k_e0), and the effect compartment was introduced without affecting the mass balance of the concentration in the kinetic compartment (C) (37).

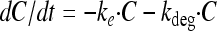(1)

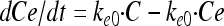(2)

To account for the biphasic killing behavior seen for the time-kill curve experiments as well as the reduced growth rate and reduced drug sensitivity at high bacterial concentrations, two bacterial stages were specified in the PD part of the model: one proliferating and drug-sensitive stage (S) and one nongrowing and drug-insensitive stage (R) (3) (Fig. 1 and equations 3 and 4). In the starting inoculum, with the bacteria being in the early logarithmic growth phase, the majority of the bacteria are assumed to be in the growing stage (S), with a net growth rate determined by a rate constant for the multiplication of bacteria (k_growth) and a rate constant for the natural death of bacteria (k_death). In the resting stage, the bacteria show no growth, although they are still assumed to have the same natural death rate (k_death) as bacteria in the growing stage. The total bacterial content (S + R) stimulates bacteria to transfer from the sensitive to the resting stage (i.e., k_SR) by a linear function. Instead of estimating the proportionality factor, the equation was reparameterized by estimating the maximum number of bacteria reached in the system (B_max), according to equation 5. The transfer from the resting stage to the sensitive stage was considered to be negligible in these experiments, and k_RS was set to 0. The drug effect was assumed to increase the death of bacteria being in the sensitive stage according to a sigmoidal E_max function (equation 6), where E_max is the maximum achievable effect in terms of an increased killing rate of the bacteria being in the susceptible stage, EC₅₀ is the effect compartment concentration (Ce) of the antibiotic that produces 50% of the E_max, and γ is the sigmoidicity factor characterizing the steepness of the concentration-effect relationship. The PKPD model was described using the following equations:

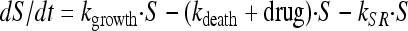(3)

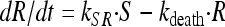(4)

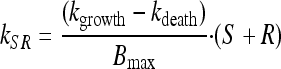(5)

(6)

The mixture module within NONMEM was used to allow for variability between experiments in the proportions of bacteria being in the resting stage in the starting inoculum. Two subpopulations were allowed. In the first subpopulation no resting bacteria were present in the starting inoculum. In the second subpopulation the fraction of bacteria being in the resting stage in the starting inoculum was estimated as a parameter (f_pers). The proportion of the total number of experiments belonging to the first subpopulation was estimated (f_Mix1), and each experiment was allocated by NONMEM to belong to one of the two subpopulations.

Data analysis and model evaluation.

Modeling and simulations were performed by using the Laplacian method in NONMEM, version VI (4), together with Pearl-Speaks-NONMEM (PsN), version 3.1 (22). The modeling was guided based on mechanistic plausibility, the precision of parameter estimates, the objective function value (OFV) supplied by NONMEM, and graphical diagnostics using R-based Xpose software, version 4.0 (15). When discriminating between nested models, the more complex model was chosen if the reduction in the OFV was at least 10.83 (P < 0.001, 1 degree of freedom).

All data were included and analyzed simultaneously. The viable count measurements were transformed into natural logarithms, and an additive residual error on the logarithmic scale was used. Since several measurements (with different dilutions) were made at each sampling time point, the residual error was divided into a replicate-specific error (ɛ_repl) and a common residual error (ɛ). The level 2 (L2) data item in NONMEM was used to group together the replicate measurements. In a previously reported analysis of the data from static time-kill curve experiments (31), only a small fraction of the observations were below the LOD, and these were handled according to the M6 method, i.e., entering the first value in a consecutive series as LOD/2 and omitting all other values below the LOD (1). The experiments run in the dynamic setting resulted in a higher proportion of data below the LOD. Therefore, for this analysis all observed values below the LOD (obtained in the static as well as the dynamic settings) were retained in the analysis and handled by using a likelihood-based approach according to the M3 method (1, 5). With this method, data above the LOD are treated as continuous data, while data below the LOD are treated as categorical data. The F_FLAG option in NONMEM VI was used to indicate values below the LOD. For these data the likelihood is obtained by integrating the density function from minus infinity to the LOD and thereby estimating the probability that the observed data are in fact below the LOD.

The observed bacterial counts in the static and dynamic time-kill experiments were compared to simulations from the semimechanistic PKPD model, where the parameter estimates were obtained based on three different sets of data: data from (i) static experiments, (ii) dynamic experiments, and (iii) combined static and dynamic experiments. In the simulations, the combined data set (data set 3) was used as a template (i.e., using the same antibiotic concentration-time profile and sampling design as those used for the real experiments), and 1,000 simulated data sets were generated for each of the three scenarios where parameters were estimated using data sets 1 to 3. The variability observed in the simulated data reflects differences in the fractions of persister cells being present in the starting inoculum (as estimated using the mixture module) in combination with the magnitude of the residual error (including for instance measurement error and model misspecification). The real observed data were compared with the distribution (median and 95% prediction interval) of the simulated data and presented graphically as visual predictive checks (16). To assess the ability of the models to accurately predict the observed data in the dynamic time-kill curve experiments, bias and precision were calculated as the mean prediction error (MPE) and mean absolute prediction error (MAPE) (36). The prediction error used was calculated as the residuals between observations and predictions on the natural logarithmic scale, and both the MPE and MAPE were normalized to the median of the observations.

To further evaluate the impact of differences in experimental setup between the static and dynamic experiments, experimental setup was regarded as a categorical covariate and introduced into each estimated parameter in the model. This was performed by using the stepwise covariate model (SCM) building tool implemented in PsN (21). For including a covariate effect in the forward step of the SCM, a significance level of a P value of <0.01 was used, corresponding to a reduction in the OFV of at least 6.63 for 1 degree of freedom. In the backward step, a significance level of a P value of <0.001 was used, corresponding to a reduction in the OFV of at least 10.83 for 1 degree of freedom. Experimental setup was introduced as a potential categorical covariate according to the following equation:

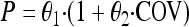(7)

where θ₁ is the value of the parameter (P) for the experiments with static concentrations and θ₂ is the fractional change in P for the dynamic experiments.

RESULTS

Growth control experiments.

No difference in growth characteristics was seen when growth control experiments performed with test tubes (i.e., static setting) and with the in vitro kinetic system (i.e., dynamic setting) were compared (Fig. 2). No statistical improvement in the model fit was observed by allowing a separate estimation of the bacterium-specific parameters depending on the experimental type (static or dynamic) when only data from the growth control experiments were used.

FIG. 2.

Growth curves of S. pyogenes performed in static (gray dotted) and dynamic (black dotted) environments for starting inocula aimed at 10³ to 10⁶ CFU/ml. Included are model predicted growth curves for a start inoculum of 5 × 10⁴ CFU/ml where parameters were estimated using all data simultaneously (with and without antibiotics) from experiments run in a static (black dashed line) or in a dynamic (black solid line) setting.

Prediction of dynamic time-kill curve experiments.

For the majority of the dynamic time-kill curve experiments, the observed bacterial counts were reasonably well predicted when applying the PKPD model with parameter estimates based on only data from the static experiments (Fig. 3a). For vancomycin, the killing effect in the dynamic experiments with the lower initial concentration (2× the MIC) persisted for a longer time period than anticipated based on the analyses of data from only the static experiments. However, this prolonged killing effect was not observed when the bacteria were exposed to a higher initial concentration of 16 times the MIC. In contrast to the finding for vancomycin, a somewhat faster regrowth than predicted based on the static experiments was seen for cefuroxime.

FIG. 3.

Observed time-kill curves for the dynamic experiments with model predictions (as medians and 95% prediction intervals) using parameter estimates based on data from only static experiments (A), only dynamic experiments (B), or combined static and dynamic experiments (C). Bacterial counts below the LOD are plotted as 5 CFU/ml. PEN, benzylpenicillin; CXM, cefuroxime; ERY, erythromycin; MXF, moxifloxacin; VAN, vancomycin. Numbers in panel strips indicate types of PK profiles: 2:n, initial concentration 2× the MIC with simulated human half-life; 2:r, initial concentration 2× the MIC with simulated one-third of the human half-life; 16:n, initial concentration 16× the MIC with simulated human half-life; 16:c, initial concentration 16× the MIC with a constant concentration.

The structure of the PKPD model was shown to also be applicable to data derived from experiments with a dynamic concentration-time profile, as the observed dynamic time-kill curve experiments were very well predicted for all simulated concentration-time profiles of all five studied antibiotics when allowing parameter reestimation based on the dynamic data (Fig. 3b). A simultaneous analysis of static and dynamic experiments improved predictive performances for cefuroxime and vancomycin compared to when the parameter estimates used for simulation were based only on static experiments (Fig. 3c).

The bias (MPE) and precision (MAPE) of the dynamic experiments for the three sets of model parameter estimates are presented in Table 2. Overall, the parameter estimates based on the static experiments underpredicted the antibacterial efficacy for vancomycin and erythromycin (MPE of 16% and MPE of 8%, respectively), while the efficacy was overpredicted for cefuroxime (MPE of −9%). Compared to using parameters from the static experiments only, both bias and precision improved when the combined data set was used.

TABLE 2.

Bias and precision in terms of MPE (%) and MAPE (%) for the dynamic experiments with model predictions using parameter estimates based on data from static experiments, dynamic experiments, and combined static and dynamic experiments

Drug	Static		Dynamic		Static and dynamic
	MPE	MAPE	MPE	MAPE	MPE	MAPE
Benzylpenicillin	−4.0	14.5	−1.4	6.6	0.6	10.1
Cefuroxime	−9.4	31.8	3.9	14.6	1.1	20.8
Erythromycin	8.2	14.4	−0.1	13.2	0.7	11.8
Moxifloxacin	−0.1	14.8	−2.5	10.4	−1.3	14.7
Vancomycin	15.9	17.1	3.1	8.6	10.8	12.8

Using the parameter estimates from the simultaneous analysis of static and dynamic time-kill curve experiments, the PKPD model could also predict reasonably well the time-kill curves following exposure to repeated doses of benzylpenicillin (Fig. 4).

FIG. 4.

Observed time-kill curves of S. pyogenes exposed to repeated doses of benzylpenicillin. Included are model predictions (as medians and 95% prediction intervals) using parameter estimates based on combined data from static and dynamic experiments. PEN, benzylpenicillin. Numbers in panel strips indicate the concentrations of the antibiotic used as multiples of the MIC.

Prediction of static time-kill curve experiments.

When all data were used in the parameter estimation (static and dynamic), the PKPD model still performed very well in predicting the data from the static experiments (Fig. 5a and c). The model with parameter estimates based on only the dynamic experiments resulted in relatively poor predictions of the static experiments when the concentration of the antibiotic was close to the EC₅₀ (Fig. 5b). This indicates poor predictability across experimental designs when the parameter estimates are based on a limited amount of dynamic data. Higher and lower drug levels used in the static experiments were generally well predicted for all three simulation settings (data not shown).

FIG. 5.

Observed time-kill curves for a selection of the static experiments with model predictions (as medians and 95% prediction intervals) using parameter estimates based on data from only static experiments (A), only dynamic experiments (B), and combined static and dynamic experiments (C). Bacterial counts below the LOD are plotted as 5 CFU/ml. PEN, benzylpenicillin; CXM, cefuroxime; ERY, erythromycin; MXF, moxifloxacin; VAN, vancomycin. Numbers in panel strips indicate the concentrations of the antibiotic used as a multiple of the MIC.

Impact of differences in experimental settings on parameter estimates.

In general, there was a good agreement between the parameter estimates of the PKPD model based on the static and the dynamic time-kill curve experiments (Table 3). However, the sparseness of the dynamic data resulted in a larger parameter uncertainty (RSE) for most model parameters. There was a trend for lower values of γ when the combined data set was used. When only the dynamic data were used or when allowing separate estimations for static and dynamic data, γ was estimated to be high (>20) for the dynamic experiments for all drugs except erythromycin and was therefore fixed to 20 to increase model stability. When allowing separate parameter estimates based on the type of experiment (results from SCM), a slightly higher growth rate (1.8 versus 1.3 h⁻¹) and a higher rate of natural death (0.41 versus 0.17 h⁻¹) was found for the dynamic experiments (Table 3). No general trend was found for the drug-specific parameters; however, for three out of five studied drugs a slight but statistically significantly higher E_max (benzylpenicillin, erythromycin, and vancomycin) and a steeper concentration effect relationship (benzylpenicillin, cefuroxime, and moxifloxacin) were found for the dynamic experiments. The model predictions based on the final model from the covariate analysis were close to those obtained when the data from the static or dynamic experiments were estimated separately (data not shown). For the majority of the data there were no major differences in the goodness-of-fit plots for the analysis with common parameter estimates (Fig. 6a) and when separate parameter estimates were allowed (Fig. 6b) for the static and dynamic experiments. However, the model with common parameter estimates overpredicted the antibacterial efficacy (Fig. 6a) in the dynamic experiments with bacteria exposed to the lower initial concentration of cefuroxime using a reduced half-life (Fig. 3c).

TABLE 3.

Parameter estimates with typical values and relative standard errors (RSE%) of the PKPD model as estimated using data from static experiments, dynamic experiments, and combined static and dynamic experiments^a

Parameter	Staticb	Dynamic	Static and dynamic	Static and dynamic/covariate analysis
				Typical value	Fractional change	OFV drop
kgrowth (h−1)	1.35 (5.1)	1.61 (6.2)	1.46 (4.1)	1.34 (4.4)	0.344 (21)	63.4
kdeath (h−1)	0.182 (6.8)	0.342 (12)	0.187 (6.2)	0.165 (6.2)	1.50 (12)	117
Bmax (CFU/ml)	4.13 × 108 (8.4)	7.24 × 108 (32)	5.00 × 108 (8.7)	4.37 × 108 (10)
fpersd	0.0547 (48)	0.00810 (54)	0.0652 (49)	0.0374 (43)
fMix1d	0.747 (16)	0.698 (21)	0.880 (7.5)	0.800 (10)
Emax PEN (h−1)	2.44 (8.4)	3.08 (5.2)	2.70 (7.4)	2.42 (5.1)	0.264 (25)	14.8
Emax CXM (h−1)	3.32 (6.6)	2.73 (5.4)	2.72 (5.1)	3.81 (8.3)	−0.262 (22)	26.4
Emax ERY (h−1)	2.03 (6.2)	3.24 (26)	2.46 (13)	2.36 (12)	0.170 (49)	16.4
Emax MXF (h−1)	3.21 (4.5)	3.34 (8.0)	3.40 (4.6)	3.39 (4.6)
Emax VAN (h−1)	1.36 (5.1)	1.64 (5.3)	1.52 (5.3)	1.36 (4.5)	0.292 (26)	47.3
EC50 PEN (mg/liter)	0.00436 (8.0)	0.00768 (8.9)	0.00531 (25)	0.00445 (4.3)	0.743 (9.9)	22.7
EC50 CXM (mg/liter)	0.00832 (7.8)	0.0124 (15)	0.00787 (8.3)	0.0130 (12)
EC50 ERY (mg/liter)	0.0275 (14)	0.0953 (119)	0.0336 (44)	0.0387 (40)
EC50 MXF (mg/liter)	0.0745 (2.8)	0.145 (3.3)	0.0750 (6.9)	0.0851 (10)	0.646 (24)	122
EC50 VAN (mg/liter)	0.384 (0.9)	0.298 (2.9)	0.304 (13)	0.383 (0.8)	−0.23 (9.6)	143
γ PENd	1.29 (11)	20 FIX	1.06 (24)	1.25 (3.7)	20 FIXc	37.4
γ CXMd	1.69 (8.3)	20 FIX	1.35 (14)	1.08 (11)	20 FIXc	88.5
γ ERYd	0.770 (19)	0.461 (21)	0.652 (20)	0.635 (18)
γ MXFd	1.59 (6.8)	20 FIX	1.42 (7.6)	1.40 (9.1)	20 FIXc	49.5
γ VANd	20 FIX	20 FIX	4.99 (24)	20 FIX
ke0 PEN (h−1)	0.990 (9.6)	100 FIX	100 FIX	1.71 (2.5)
ke0 CXM (h−1)	0.848 (19)	100 FIX	100 FIX	1.73 (16)
ke0 ERY (h−1)	100 FIX	100 FIX	1.02 (21)	1.05 (29)
ke0 MXF (h−1)	0.635 (20)	0.893 (4.5)	0.627 (18)	0.827 (7.6)
ke0 VAN (h−1)	100 FIX	100 FIX	100 FIX	100 FIX
ε (%)	98.6 (10)	144 (9.4)	140 (7.4)	112 (7.0)
εrepl (%)	46.5 (4.7)	47.5 (5.2)	46.8 (3.7)	46.8 (3.7)

^aPEN, benzylpenicillin; CXM, cefuroxime; ERY, erythromycin; MXF, moxifloxacin; VAN, vancomycin; k_growth, growth rate; k_death, rate of natural cell death; B_max, maximum bacterial count; f_pers, fraction of bacteria being in the resting stage in the starting inoculum for the second subpopulation; f_Mix1, fraction of experiments belonging to the first subpopulation; E_max, maximum effect; EC₅₀, concentration producing 50% of the E_max; γ, sigmoidicity factor; k_e0, rate constant for effect delay; ε, residual error; ε_rep, replicate residual error; FIX, parameter not estimated.

^bThe data in reference 31 were reanalyzed using the M3 method (including all LOD observations) with only marginal changes in parameter estimates (<3.4%).

^cParameter fixed to 20 for dynamic-type experiments.

^dParameter has no unit.

FIG. 6.

Goodness-of-fit plots with observed and model-predicted bacterial counts with all data used in the parameter estimation. (A) No separate parameters were estimated for static and dynamic experiments. (B) Results from the final model in the SCM allowing separate estimates for experimental type if statistically significant. Bacterial counts below the LOD are plotted as 5 CFU/ml. ○, static experiments; +, dynamic experiments. Included are lines of identity.

DISCUSSION

We have shown that the structure of our previously developed semimechanistic PKPD model based on data from static experiments using five antibiotics of different classes could also describe the bacterial growth and killing kinetics derived under different elimination rates as well as after repeated dosing. Despite its fairly simple structure, the PKPD model was found to show good predictive performance for experiments with both static and dynamic concentration-time exposures (Fig. 3 to 5). Furthermore, it was shown that the experiments with static concentrations were informative in terms of predicting the time-kill curves following dynamic concentration-time profiles. Therefore, the need to perform the more time-consuming and labor-intensive dynamic experiments is limited, as the antibacterial effect following dynamic concentration exposures can be simulated by including the PK model describing the change in the drug concentration over time.

The in vitro time course of the antibiotic effect has previously been modeled mainly using either data from experiments with static concentrations (see, e.g., references 7, 23, 31, 34, 38, 39, and 41) or data from experiments with dynamic concentrations (see, e.g., references 8, 9, 12, 18, 23, 28, and 30). In only a couple of examples have data from static and dynamic experiments been simultaneously analyzed, and in these examples, common parameter estimates were generally used for the two experimental settings (6, 35). In the present study we evaluated potential differences between in vitro systems using a modeling approach. The differences in experimental settings between the static and dynamic time-kill curve experiments did not have a significant effect on the growth kinetics of the control experiments (i.e., without antibiotics) for the experimental conditions used in this study. This is in agreement with what was previously observed experimentally (18, 24) and implies that the net bacterial growth rate is not limited by nutrition and that entry into stationary phase is due primarily to reasons other than a lack of nutrition. However, significant differences in drug-specific parameter estimates were found when all data were used in the estimation.

Even though the effect of exposures to concentrations below the MIC (sub-MICs) was generally well characterized by the PKPD model, the sustained suppression of bacterial growth for vancomycin at an initial concentration of 2× the MIC was not well predicted by the model for either a simulated normal human half-life or a reduced half-life (5.1 and 15 h, respectively). In a previous study, differences in antibacterial efficacy between exposure to sub-MICs alone and sub-MICs following concentrations exceeding the MIC (postantibiotic sub-MIC effect [PA SME]) were shown (25). The presence of a long PA SME compared to the sub-MIC effect alone could indicate expected differences between the static and dynamic exposures, since the bacteria in the dynamic setting have always been exposed to higher concentrations (32). With a more thorough understanding of the underlying mechanism of these phenomena, this may be incorporated into the model to enhance the predictive capacity of the model. The killing of vancomycin has also been shown to be more efficient under aerobic conditions (20), which could be one of the reasons for the higher efficacy seen for the dynamic experiments. For cefuroxime a faster regrowth was observed than what was predicted based on the parameter estimates from the static experiments only (Fig. 3a). The predictions improved significantly when both static- and dynamic-type data were used in the parameter estimations (Fig. 3c). This improvement was seen without a detrimental effect on the model fit of the static time-kill curve experiments (Fig. 5a and c). However, even after parameter estimations using the combined data set, the model overpredicted the antibacterial effect at the end of the experiments with the lower starting concentration of cefuroxime.

In this study a single S. pyogenes strain was exposed to five different antibiotics. The static experiments performed with this stain and these antibiotics did not show bacterial regrowth, and therefore, the PKPD model applied here was not developed to capture the presence or emergence of resistance. The semimechanistic structure of the model, however, allows the addition of additional complexity to characterize, for example, drug resistance (29). A limitation with the performed model validation is that most experiments were performed during a period of 24 h. Even though the first 24 h is critical in the management of infections, it would be of interest to also evaluate model performance using experiments beyond this relatively limited study period.

In vitro experiments allow the investigation of a wide range of different drug concentrations, and here we have shown that in combination with a modeling approach, the whole time course of the antibacterial effect can be predicted based on a limited number of experiments with dynamic concentrations. It was previously demonstrated that the magnitudes of exposure associated with efficacy as determined with both animal and in vitro infection models are in accordance with those required for efficacy in humans (2, 17, 18). Computer simulations, where the model is predictive of effects observed for in vitro experiments, may therefore be a powerful tool in the optimization of dosing regimens for antibiotics. In addition, a wide range of dosing regimens can be evaluated in the simulations, taking factors such as protein binding, tissue distribution, and interindividual variability in PK and PD into account.

In conclusion, the growth characteristics of S. pyogenes did not differ significantly between experiments run in the static and the dynamic environments used in this study. The structure of the previously proposed semimechanistic PKPD model could well describe bacterial growth and killing when exposed to dynamic concentrations of the five investigated antibiotics. The majority of the time-kill curves from experiments run in the dynamic system with different initial concentrations and half-lives were reasonably well predicted by the model and parameter estimates from time-kill experiments with constant drug concentrations. The PKPD model may therefore limit the need for labor-intensive experiments with dynamic drug concentrations and provide a useful tool for optimizing the dosing regimens and design of future preclinical and clinical studies of antibacterial efficacy.