Effect of Half-Life on the Pharmacodynamic Index of Zanamivir against Influenza Virus Delineated by a Mathematical Model

Abstract

Intravenous zanamivir is recommended for the treatment of hospitalized patients with complicated oseltamivir-resistant influenza virus infections. In a companion paper, we show that the time above the 50% effective concentration (time>EC₅₀) is the pharmacodynamic (PD) index predicting the inhibition of viral replication by intravenous zanamivir. However, for other neuraminidase inhibitors, the ratio of the area under the concentration-time curve to the EC₅₀ (AUC/EC₅₀) is the most predictive index. Our objectives are (i) to explain the dynamically linked variable of intravenous zanamivir by using different half-lives and (ii) to develop a new, mechanism-based population pharmacokinetic (PK)/PD model for the time course of viral load. We conducted dose fractionation studies in the hollow-fiber infection model (HFIM) system with zanamivir against an oseltamivir-resistant influenza virus. A clinical 2.5-h half-life and an artificially prolonged 8-h half-life were simulated for zanamivir. The values for the AUC from 0 to 24 h (AUC_0-24) of zanamivir were equivalent for the two half-lives. Viral loads and zanamivir pharmacokinetics were comodeled using data from the present study and a previous dose range experiment via population PK/PD modeling in S-ADAPT. Dosing every 8 h (Q8h) suppressed the viral load better than dosing Q12h or Q24h at the 2.5-h half-life, whereas all regimens suppressed viral growth similarly at the 8-h half-life. The model provided unbiased and precise individual (Bayesian) (r², >0.96) and population (pre-Bayesian) (r², >0.87) fits for log₁₀ viral load. Zanamivir inhibited viral release (50% inhibitory concentration [IC₅₀], 0.0168 mg/liter; maximum extent of inhibition, 0.990). We identified AUC/EC₅₀ as the pharmacodynamic index for zanamivir at the 8-h half-life, whereas time>EC₅₀ best predicted viral suppression at the 2.5-h half-life, since the trough concentrations approached the IC₅₀ for the 2.5-h but not for the 8-h half-life. The model explained data at both half-lives and holds promise for optimizing clinical zanamivir dosage regimens.

In April 2009, a novel swine origin influenza A (H1N1) virus was identified in California (14, 17, 20, 21, 23). This virus spread rapidly throughout the population, causing the World Health Organization to declare a pandemic in July 2009. Initial drug susceptibility assays indicated that clinical isolates of pandemic H1N1 (pH1N1) influenza virus were completely resistant to amantadine and rimantadine but remained generally susceptible to the neuraminidase (NA) inhibitors oseltamivir and zanamivir (12). However, as the pandemic progressed, the detection of oseltamivir-resistant pH1N1 viruses became more frequent (9-13). The spread of dually resistant pH1N1 viruses would likely jeopardize successful therapy and spur a public health crisis. Thus, there is an urgent need to design innovative dosing strategies with alternative antiviral compounds that will be effective against influenza viruses resistant to oseltamivir.

Although zanamivir and oseltamivir belong to the same drug class, zanamivir interacts with the neuraminidase active site in a manner very different from that of oseltamivir (24). As a result, mutations in the neuraminidase gene that cause resistance to oseltamivir do not affect viral susceptibility to zanamivir. Therefore, zanamivir is a viable therapeutic option for the treatment of oseltamivir-resistant influenza. In order to use zanamivir effectively, the pharmacodynamics (PD) of the compound must be understood. In a companion paper, we have shown that for intravenous (i.v.) zanamivir, the pharmacodynamic index linked with the suppression of viral replication is the time for which the level of drug is above the 50% effective concentration (time>EC₅₀) (5). This parameter is different from that for other neuraminidase inhibitors, as demonstrated by our previous findings that the ratio of the area under the concentration-time curve (AUC) to the EC₅₀ (AUC/EC₅₀) is the pharmacodynamic index for oseltamivir and peramivir (16, 22). Our first objective was to assess whether the dynamically linked index for zanamivir changes from time>EC₅₀ to AUC/EC₅₀ in the hollow-fiber infection model (HFIM) if zanamivir is eliminated with an oseltamivir-like half-life of 8 h instead of the 2.5-h half-life reported for i.v. zanamivir (7). As our second objective, we sought to develop a new, mechanism-based population pharmacokinetic (PK)/PD model that describes the time course of viral load.

(This work was presented in part at the 2010 Interscience Conference on Antimicrobial Agents and Chemotherapy, Boston, MA.)

MATERIALS AND METHODS

Viruses and cells.

The oseltamivir-resistant pandemic 2009 H1N1 influenza A/Hong Kong/2369/2009 [A/Hong Kong (H275Y)] virus was provided by the U.S. Centers for Disease Control and Prevention (Atlanta, GA). Viral stocks were propagated in Madin-Darby canine kidney (MDCK) cells as described previously (6), aliquoted, and stored at −80°C. MDCK cells (ATCC CCL-34) were obtained from the American Type Culture Collection (Manassas, VA) and were grown in minimal essential medium (MEM) supplemented with 10% fetal bovine serum (FBS), nonessential amino acids, 2 mM l-glutamine, 1 mM sodium pyruvate, 100 U/ml of penicillin, 100 μg/ml of streptomycin, and 1.5 g/liter sodium bicarbonate at 37°C under 5% CO₂.

Compound.

Zanamivir was provided by GlaxoSmithKline (Philadelphia, PA). The drug was reconstituted in sterile distilled water to a final concentration of 10 mg/ml and was filter sterilized through a 0.2-μm-pore-size filter, and aliquots were stored at −80°C.

Plaque assay.

Plaque assays were performed as described previously (19) and were used to titrate viral stocks and to assess viral burdens in experimental samples. Briefly, serial 10-fold dilutions were performed on viral samples in virus growth medium (VGM) [MEM, 0.2% (final concentration) bovine serum albumin (BSA; Sigma-Aldrich, Inc.), 2 μg/ml of l-1-(tosyl-amido-2-phenyl)ethyl chloromethyl ketone (TPCK)-treated trypsin (Sigma-Aldrich, Inc.), 100 U/ml of penicillin, and 100 μg/ml of streptomycin]. Confluent MDCK cell monolayers in 6-well culture plates were washed twice with VGM and were inoculated with 100 μl of diluted virus. Each dilution was tested in duplicate. Plates were incubated for 2 h at 36°C under 5% CO₂ and were rocked every 15 min. The inoculum was removed, and a primary overlay (MEM, 0.5% agar, 1% DEAE-dextran, 0.2% BSA, 2 μg/ml TPCK-treated trypsin, 100 U/ml of penicillin, and 100 μg/ml of streptomycin) was added to each well (4 ml/well) and was incubated for 2 to 3 days at 36°C under 5% CO₂. Following the incubation period, the virus was inactivated by fixing each well with 10% formaldehyde for at least 2 h at room temperature. The agar overlay was removed from all wells, and cell monolayers were stained with a crystal violet solution (70% ethanol and 0.8% crystal violet). Visible plaques were counted with the naked eye.

Drug susceptibility assays.

Two different methods were used to determine the susceptibility of A/Hong Kong to zanamivir: the plaque inhibition assay and the neuraminidase (NA) inhibition assay. The plaque inhibition assay was performed as described previously (19, 22). In brief, confluent MDCK cell monolayers were washed twice with VGM, and the virus was inoculated onto cell monolayers at a multiplicity of infection (MOI) of 0.0001. Following a 2-h absorption period at 36°C under 5% CO₂, the viral inoculum was removed, and cells were overlaid with VGM containing various concentrations of zanamivir. Cells were observed daily for cytopathic effect (CPE). Cell supernatants were harvested at 24 h postinoculation, clarified by high-speed centrifugation (21,130 × g for 5 min), and frozen at −80°C until further use. The effective zanamivir concentration required to reduce the number of plaques by 50% (EC₅₀) from that in untreated controls was determined by a plaque assay of harvested supernatants. The EC₅₀s were calculated using GraphPad Prism software (GraphPad, La Jolla, CA).

NA inhibition assays were performed as described by Gubareva et al. (18). Briefly, the NA activity of the virus was determined prior to NA inhibition assays. Twofold dilutions of virus were placed in a black opaque 96-well plate and were incubated with the fluorigenic substrate 2′-(4-methylumbelliferyl)-α-d-N-acetylneuraminic acid, sodium salt (MUNANA; Sigma, St. Louis, MO) for 30 min on an orbital shaker (75 to 100 rpm) at 37°C in the dark. After 30 min, the reaction was stopped by the addition of stop solution (80% ethanol and 20% NaOH) to all wells. NA activity was evaluated using a Synergy HT multidetection microplate reader (BioTek, Winooski, VT) at an excitation wavelength of 365 nm and an emission wavelength of 460 nm.

For NA inhibition assays, various concentrations of zanamivir were incubated with the appropriate concentration of virus, as determined from the NA activity assay, in a black opaque 96-well plate on an orbital shaker for 30 min at 37°C in the dark. The MUNANA substrate was then added to the plates, which were incubated for an additional hour under the same conditions. The NA activity of the virus in the presence of zanamivir was evaluated following the addition of stop solution. The EC₅₀, or the concentration of zanamivir that reduced the NA activity of A/Hong Kong to 50% of the NA activity of untreated controls, was calculated using GraphPad Prism software.

HFIM system.

We used the hollow-fiber infection model (HIFM) system to study the response of the oseltamivir-resistant pandemic H1N1 influenza A virus, A/Hong Kong (H275Y), to zanamivir exposure. The use of the HFIM system for influenza A viruses has been described previously (6, 22). Briefly, 10² MDCK cells infected with H1N1 A/Hong Kong influenza virus were mixed with 10⁸ uninfected MDCK cells in 25 ml of VGM and were inoculated into the extracapillary space (ECS) of several hollow-fiber (HF) cartridges (FiberCell Systems, Frederick, MD). The 24-h area under the concentration-time curve (AUC) for exposure to zanamivir at 1,200 mg per day was delivered into HF units as either the total 24-h AUC exposure once a day (Q24h), one-half the 24-h AUC exposure twice a day (Q12h), or one-third the 24-h AUC exposure three times a day (Q8h). One cartridge did not receive zanamivir and served as a no-treatment control. Each dose was infused into the system over 1 h via programmable syringe pumps. In this study, two different half-lives of 2.5 h and 8 h were simulated for zanamivir in order to determine if the PK/PD index varied with the duration of the half-life. The 2.5-h half-life was chosen based on PK data reported for i.v. zanamivir in healthy human volunteers (7). A half-life of approximately 8 h has been described for oseltamivir (15); thus, we selected this value to represent the artificially prolonged half-life of zanamivir. PK samples were harvested from the central reservoir at various time points during the first 48 h and were quantified by high-pressure liquid chromatography-tandem mass spectrometry (HPLC-MS-MS) to ensure that the desired concentration-time profiles for zanamivir were achieved. During the 5-day study, the ECS from each HF unit was sampled daily from the left and right sampling ports in order to elucidate the effect of zanamivir on the viral burden over time. All ECS samples were harvested, centrifuged for 5 min at 10,000 × g to remove any cellular debris, and frozen at −80°C until the end of the study. The amount of virus in each sample was determined by a plaque assay on MDCK cells.

Determination of zanamivir concentrations.

Medium samples were diluted with HPLC water (0.050 ml of sample diluted in 1.0 ml of water) and were analyzed by HPLC-MS-MS for zanamivir concentrations. The LC-MS-MS system comprised a Shimadzu Prominence HPLC system and an Applied Biosystems/MDS Sciex API5000 LC-MS-MS.

Chromatographic separation was performed using a Thermo Scientific Hypersil Gold C₁₈ column (length, 150 mm; inner diameter, 4.6 mm; particle size, 5 μm) and a mobile phase consisting of 90% 10 mM ammonium acetate and 10% acetonitrile, at a flow rate of 0.75 ml/min.

Zanamivir concentrations were obtained by using LC-MS-MS and monitoring the MS-MS transition m/z 333 → m/z 60. The analysis run time was 3.5 min. The assay was linear over a range of 0.05 to 20.0 μg/ml (r², >0.997). The interday coefficients of variation (CVs) for the quality control samples analyzed in replicates of three at three concentrations on each analysis day (0.100, 1.00, and 10.0 μg/ml) were 7.12% or less, with accuracies (% recovery) ranging from 95.2% to 107%.

Mathematical modeling.

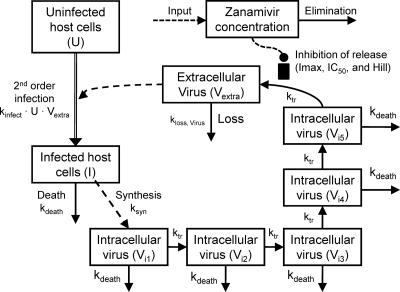
We developed a new mechanism-based population PK/PD model to simultaneously describe host cell dynamics, viral replication, and the PK of zanamivir (Fig. 1). The model contained compartments for uninfected host cells, infected host cells, intracellular virus, extracellular virus, and the amount of zanamivir.

FIG. 1.

Mechanism-based model for zanamivir against the oseltamivir-resistant pH1N1 influenza virus A/Hong Kong (H275Y). The model describes the inhibitory effect of zanamivir on the release of extracellular influenza virus over time.

Host cell dynamics.

Uninfected host cells (U) were assumed to be infected by extracellular virus (V_extra) via a second-order process with an infection rate constant (k_infect). Models with a saturable rate of infection described by a Michaelis-Menten function were considered. Both uninfected and infected (I) host cells were assumed not to replicate under the experimental conditions chosen. Infected host cells were assumed to die with a first-order death rate constant (k_death). Initial conditions (IC) were fixed to the targeted initial inocula of 10⁸ for the total hollow-fiber cartridge for uninfected host cells (equation 1) and 10² for infected host cells (equation 2). Differential equations were as follows:

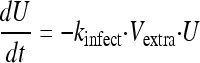(1)

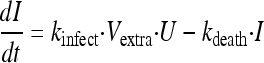(2)

Viral replication.

New intracellular virus (V_i) was generated by infected host cells with a first-order synthesis rate constant (k_syn). Viral replication involves multiple steps, including the uncoating of RNA, its translocation into the nucleus, RNA replication, the transcription of RNA to mRNA, the translocation of mRNA into the cytoplasm, the translation of mRNA into proteins, virion synthesis, and the egress of the synthesized virus from the cell. We did not measure intermediates involved in these intracellular processes. To empirically describe the time delay between the infection of host cells and the release of virus due to the various stages of intracellular replication, we included a series of transit compartments linked by a transit rate constant (k_tr). Models with zero to 15 transit compartments were explored. Depending on the number of transit compartments, the time “delay” between the entry of a virus into a host cell and the egress of the virus takes different shapes.

In the final model, the five stages are called intracellular virus 1 to 5 (V_i1, V_i2, V_i3, V_i4, and V_i5). Since the number of infected host cells was negligible compared to the number of uninfected cells (10² versus 10⁸ cells), and since extracellular virus and infected host cells were undetectable at 0 h, the initial conditions of V_i1 to V_i5 were set at 0 PFU/ml. The differential equations for intracellular virus are as follows:

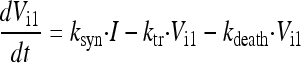(3)

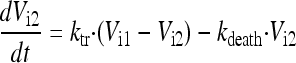(4)

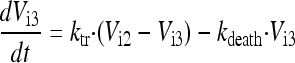(5)

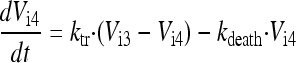(6)

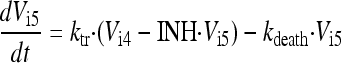(7)

We assumed that the death of an infected host cell also causes the loss of the respective intracellular virus components, since the intracellular viral components were assumed to be incomplete. A first-order death rate constant (k_death) for intracellular virus was included for V_i1 to V_i5. The inhibition (INH) term in the equation for V_i5 represents the effect of zanamivir. We considered alternative models without the death of intracellular virus.

Extracellular virus (V_extra) is the result of the egress of intracellular virus from the last intracellular virus compartment (V_i5) and was assumed to be subject to a first-order loss rate constant (k_loss,Vextra). The latter represents the degradation of virus in medium due to temperature sensitivity (6). The initial condition for extracellular virus was set to 0 PFU/ml, because the inoculum was free of intracellular virus. The initial condition for extracellular virus was estimated for alternative models.

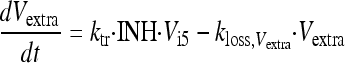(8)

Drug effect.

Zanamivir inhibits the release of virions from infected host cells. Drug effect was modeled as inhibition of the release of mature virions from compartment V_i5 by an inhibitory Hill equation with the maximum extent of inhibition (Imax) and the zanamivir concentration causing 50% of Imax (IC₅₀):

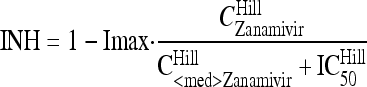(9)

where C_Zanamivir stands for the zanamivir concentration. The differential equation for the amount of zanamivir (A_Zanamivir), with the initial condition set at 0 mg, was as follows:

(10)

The zanamivir concentration is calculated as A_Zanamivir/V, where V represents the volume of medium in the central reservoir. Because the hollow-fiber system has rapid intercompartmental clearance between the central reservoir and the hollow-fiber cartridge, and because the surface area (approximately 0.3 m²) available for equilibration between the two compartments is large, we used a simplified one-compartment model instead of a two-compartment model to describe the PK of zanamivir. Figure 1 summarizes the structure of the full model.

System outputs and residual error model.

The model contained the log₁₀ (PFU/ml) and the zanamivir concentration as dependent variables. In the plaque assay, each extracellular virus forms 1 plaque, and plaques are counted as described above. To account for samples below the quantification limit for the plaque assay at time zero, we employed the Beal M3 method (2) in the population PK/PD modeling. We used an additive residual error on a log₁₀ scale for the PFU/ml data and an additive plus proportional residual error for zanamivir concentrations.

Parameter variability model.

An exponential parameter variability model was employed. A logistic transformation was employed to constrain the individual Imax estimates between zero and 1, and Imax was assumed to be normally distributed on the transformed scale. Parameters estimated on a log₁₀ scale were assumed to be normally distributed.

Model qualification.

Individual curve fits, individual- and population-fitted versus observed plots, and normalized prediction distribution error (NPDE) plots (4) were used to assess the goodness of curve fits and predictive performance. Models were compared based on these diagnostic plots, the objective function (−2·log likelihood), and the plausibility of parameter estimates.

Software and algorithm.

For nonlinear mixed-effect modeling, we employed the Monte Carlo parametric expectation maximization method (MC-PEM) with the pmethod = 4 option for importance sampling in S-ADAPT (version 1.56). Normalized prediction distribution errors were computed in S-ADAPT (version 1.57 beta). An automated translator, debugging, and plotting tool (SADAPT-TRAN) was utilized for efficient model coding and development.

RESULTS

Susceptibility to zanamivir.

We evaluated the antiviral activity of zanamivir against the A/Hong Kong (H275Y) virus, an oseltamivir-resistant 2009 pandemic H1N1 influenza virus strain, by measuring the inhibitory effect of the compound on (i) the yield of infectious virus in MDCK cell culture and (ii) the neuraminidase activity of the virus. The EC₅₀ for zanamivir was 0.418 ± 0.065 ng/ml (1.254 ± 0.196 nM) by the plaque inhibition assay and 0.1 ± 0.03 ng/ml (0.3 ± 0.09 nM) by the NA inhibition assay. These results were similar to those reported for other susceptible viruses, indicating that the A/Hong Kong (H275Y) virus is susceptible to zanamivir, despite its resistance to oseltamivir.

HFIM studies with the A/Hong Kong (H275Y) virus and zanamivir.

In a companion paper, we showed that zanamivir is an effective treatment for oseltamivir-resistant influenza virus and that the pharmacodynamic index for this compound is time>EC₅₀ (5). Since the pharmacodynamically linked index previously described for the neuraminidase inhibitors oseltamivir and peramivir is AUC/EC₅₀ (16, 22), we determined if AUC/EC₅₀ is the most predictive PK/PD index for zanamivir at a longer half-life (8 h) that is similar to the half-lives of other neuraminidase inhibitors, such as oseltamivir.

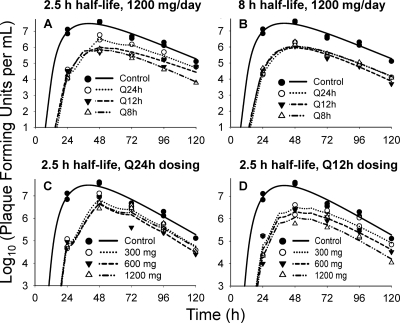
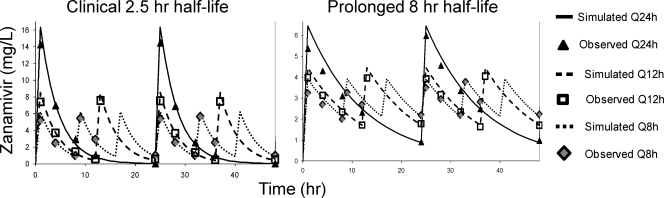
The A/Hong Kong (H275Y) virus replicated well in the system in the absence of drug. All dosage regimens suppressed viral replication relative to the no-treatment control (Fig. 2). For the 2.5-h half-life, the Q8h administration yielded the greatest inhibition of viral burden throughout the course of the study, followed by the Q12h regimen. The Q24h regimen suppressed viral burden the least (Fig. 2). In contrast, all dosage regimens with an 8-h simulated half-life achieved similar extents of viral inhibition (Fig. 2). Simulated and observed zanamivir concentrations for both half-lives (Fig. 3) show that the target 24-h AUCs were attained for all dosage regimens.

FIG. 2.

Individual-fitted viral loads for zanamivir against oseltamivir-resistant H1N1 influenza virus in the hollow-fiber infection model. (A and B) Graphs based on the dose fractionation study described in Materials and Methods. A 1,200-mg/day dose of zanamivir was fractionated at Q24h, Q12h, and Q8h dosing intervals with a simulated 2.5-h (A) or 8-h (B) half-life for zanamivir. (C and D) Graphs based on the dose range study described in the companion paper (5). In this study, a total daily dose of 300 mg, 600 mg, or 1,200 mg of zanamivir was administered Q24h (C) or Q12h (D). A half-life of 2.5 h was simulated for zanamivir in this study.

FIG. 3.

Pharmacokinetic analysis of zanamivir with a simulated half-life of 2.5 h (left) or 8 h (right). Samples were harvested from the dose fractionation study with oseltamivir-resistant H1N1 virus. Zanamivir concentrations were measured by LC-MS-MS. Note the difference in scale between the y axes.

Mechanism-based population PK/PD model.

We developed a novel mechanism-based population PK/PD model to describe the relationship between zanamivir concentrations and the extracellular viral concentration over time. The mathematical model (Fig. 1) was simultaneously fit to all viral burden and PK data generated in the HFIM system in the present study and in a dose fractionation study reported in the companion paper (5). We comodeled the two studies to obtain more-robust estimates. Viral load and PK data from the present study are depicted in Fig. 2 (top) and Fig. 3, respectively, and are described above. Figure 2 (bottom) shows the viral burden data described in the companion paper. Briefly, these results demonstrate that the Q12h regimens inhibited viral replication better than the corresponding Q24h regimens at all doses of zanamivir, indicating that time>EC₅₀ is the pharmacodynamic parameter predictive of viral suppression. Measured zanamivir concentrations from our companion study were within 10% of the targeted values (5; data not shown).

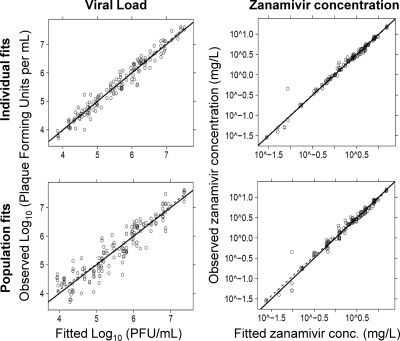
The proposed model showed precise and unbiased curve fits, as shown by the predicted-versus-observed plots for viral load and zanamivir concentration (Fig. 4). Linear regression of observed versus fitted log₁₀ (PFU/ml) yielded a slope of 1.014, an intercept of −0.074, and an r² value of 0.96 for individual fits (Bayesian) and a slope of 0.972, an intercept of 0.163, and an r² value of 0.87 for population fits (pre-Bayesian) (Fig. 4). For zanamivir concentrations, both the individual fits and the population fits had a slope of 1.0 (r², 0.99).

FIG. 4.

Individual (Bayesian)- and population (pre-Bayesian)-fitted viral loads and pharmacokinetics for zanamivir against oseltamivir-resistant H1N1 influenza virus in the hollow-fiber infection model system.

Parameter estimates (Table 1) were precise, with coefficients of variation for uncertainty below 20% for all population means except IC₅₀, which had a CV of 26.1%. The between-curve variability of PK and PD parameters was small, with apparent coefficients of variation (calculated as the square roots of the variances shown in Table 1) below 20% for most parameters.

TABLE 1.

Parameter estimates for the population PK/PD model of zanamivir against oseltamivir-resistant H1N1 influenza virus in the hollow-fiber infection model

Parameter	Symbol (unit)	Population mean estimates		Estimate for between-curve variability
		Mean	% CV (uncertainty)	Variance	% CV (uncertainty)
PK/PD parameters
Log10 of 2nd-order infection rate constant	Log10kinfect	−2.49	6.1	0.0834	90
Synthesis rate constant of virus	ksyn (1/h)	3.49	19.8	0.0045	145
Mean delay time until release of virus in the absence of drug	TDelay = 5/ktr (h)	37.6	2.6	0.0067	82
Mean survival time of infected cells	MSTInfected = 1/kdeath (h)	7.4	5.3	0.0054	74
Mean survival time for extracellular virus	MSTVirus = 1/kloss,virus (h)	12.4	6.9	0.0183	87
Maximum extent of inhibition	Imax (normal scale)	0.990
Maximum extent of inhibition (on transformed scale)	Imax (transformed scale)	4.62a,b	9.6	0.133a,b	140
Zanamivir concn causing 50% of Imax	IC50 (mg/liter)	0.0168	26.1	0.0114	285
Hill coefficient	Hill	0.885	9.7	0.0017	136
Clearance	CL (liters/h)	16.0	2.1	0.0041	51
Volume of distribution for 8.0-h half-life	V18h half-life (liters)	170	15.0	0.0399	282
Volume of distribution for 2.5-h half-life	V12.5h half-life (liters)	69.8	0.4	<0.0001	872
Log10 of initial no. of uninfected cells	LogU	8	0 (fixed)
Log10 of initial no. of infected cells	LogI	2	0 (fixed)
Residual error parameters
Additive error for viral load on log10 scale	SDin	0.224	6.9
Additive error for zanamivir concn	PKin (mg/liter)	0.092	20.6
Proportional error for zanamivir concn	PKsl	0.071	14.8

^aImax was assumed to be normally distributed on the transformed scale (Imax_Transformed). The following logistic transformation was used to constrain Imax between 0 and 1: Imax = 1/[1 + exp(−Imax_Transformed)].

^bIndividual Imax estimates (on the normal scale) ranged from 0.988 to 0.991 for all curves.

The maximum extent of inhibition of viral release was 0.990 (Imax on normal scale), and the IC₅₀ was 0.0168 mg/liter. This modeled IC₅₀ estimate is part of the model component describing the inhibition of viral release from the last intracellular virus compartment. The IC₅₀ parameter needs to be distinguished from the EC₅₀ estimate, which relates the drug concentration to the overall measured effect in the plaque or NA inhibition assay. The extent of inhibition at the end of the dosing interval (i.e., caused by the trough concentration) was 0.962 for Q24h, 0.974 for Q12h, and 0.977 for Q8h dosing at the 8-h half-life. These high extents of inhibition indicate near-maximal inhibition of viral release during the entire dosing interval. This was achieved at the 8-h but not at the 2.5-h half-life, with which the extents of inhibition were 0.718 for Q24h, 0.940 for Q12h, and 0.963 for Q8h dosing.

Alternative models.

A model with no compartments for intracellular virus yielded an objective function (−2·log likelihood) worse by 34.4 than the final model and had notably less-precise population fits. Compared to that for the final model with 5 transit compartments, representing stages of intracellular virus, the objective function was worse by 15.7 for a model with 1, worse by 9.6 for a model with 2, worse by 5.3 for a model with 3, worse by 2.1 for a model with 4, and worse by 6.3 for a model with 15 transit compartments. Models with 5 to 10 transit compartments yielded objective functions within 1.9 points. Since the performance of these nonnested models was indistinguishable, we chose the model with 5 transit compartments as the final model by following the rule of parsimony, since it is simplest of these models. Interested readers may contact the authors for details on the alternative models explored.

Exclusion of the first-order death process of intracellular virus for all transit compartments or only for the last transit compartment caused an objective function worse by 20 (P, <0.001 by the likelihood ratio test) and yielded notably less-precise population fits. Therefore, the death of intracellular virus due to the death of infected host cells was included as a significant and useful model feature. The inclusion of a saturable infection rate instead of the second-order infection process yielded a high Michaelis-Menten constant and had no effect on the objective function. Estimating the initial condition of extracellular virus improved the objective function insignificantly by 1.6 and yielded a very small initial condition of 10^−0.13 PFU/ml. Therefore, these two features were not included in the final model.

Predictive performance.

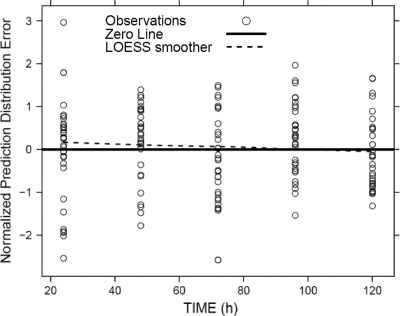
Due to the large number of different dosage regimens, the present data set is not amenable to a classic visual predictive check. Instead, we employed a state-of-the-art and statistically rigorous method for assessing predictive performance. The NPDE spanned the ideal range from approximately −2 to +2 for a standard normally distributed variable at essentially every observation time (Fig. 5). A Shapiro-Wilk test did not reject the null hypothesis (P, 0.40) that all samples originate from the same distribution as the predictions by the final model. Since this test result is known to be very difficult to achieve, the NPDE statistic supports the excellent predictive performance of the final model.

FIG. 5.

Normalized prediction distribution error (NPDE) for viral load. Ideally, the NPDE should have a standard normal distribution, with approximately 95% of the points falling between −2 and +2 at each observation time.

DISCUSSION

Antiviral agents are paramount for the control of infections caused by influenza. Unfortunately, influenza A viruses resistant to most commercially available antiviral compounds are becoming more prevalent, posing a significant threat to public health. This threat was recently observed during the 2009 influenza A (H1N1) pandemic, in which several pH1N1 viral isolates were determined to be resistant to amantadine, rimantadine, and oseltamivir (9-12). The potential for spread of these dually resistant viruses causes great concern that our current anti-influenza drugs will be rendered ineffective. Thus, there is an urgent need to design innovative dosing strategies with alternative antivirals. In this study we focused on the neuraminidase inhibitor zanamivir.

Elsewhere, we demonstrate that time>EC₅₀ is the predictive PK/PD index for the intravenous administration of zanamivir (5). This finding contrasts with those for other neuraminidase inhibitors (oseltamivir and peramivir), for which AUC/EC₅₀ is the PK/PD index predictive of viral suppression (16, 22). For the present study, we hypothesized that the pharmacodynamically linked parameter for zanamivir is different from that for the other neuraminidase inhibitors due to its short clinical half-life (2.5 h) in humans; the half-lives for oseltamivir and peramivir are 8 h and 21 h, respectively (15, 27). To test this hypothesis, a dose fractionation study was performed with a 2.5-h half-life or an 8-h half-life at a zanamivir dose of 1,200 mg/day, with all regimens generating the same AUC from 0 to 24 h (AUC_0-24). The results demonstrated that for the 2.5-h half-life, more-frequent dosing intervals provided greater inhibition of viral replication. In contrast, the extents of viral inhibition were similar for all dosage regimens with a simulated 8-h half-life. This suggests that time>EC₅₀ best predicted the suppression of viral burden for the 2.5-h half-life, whereas AUC/EC₅₀ best predicted the suppression of viral burden for the 8-h half-life. These data confirmed the hypothesis.

These findings have important implications for the clinical use of intravenous zanamivir in patients, since a single PK/PD index may not be sufficient to describe optimal therapeutic regimens for all patient groups. Cass et al. (8) have shown that individuals with renal impairment have PK profiles significantly altered from those of healthy volunteers following an intravenous zanamivir dose. Because zanamivir is eliminated almost exclusively via renal excretion (7), zanamivir clearance was markedly decreased in individuals with renal impairment, resulting in higher serum AUCs and longer zanamivir half-lives. Therefore, it is likely that patients with renal disease would have a PK/PD index of AUC/EC₅₀ and healthy individuals would have a PK/PD index of time>EC₅₀.

The different most-predictive PK/PD indices for zanamivir at the 2.5-h and 8-h half-lives were explained by our mechanism-based mathematical model. This model is capable of describing viral burden for any half-life that may be relevant for patients with different degrees of renal impairment. The model showed a mean IC₅₀ of 0.0168 mg/liter and a mean Imax of 0.990 (Table 1). Identification of an Imax of 0.990 indicates that it is possible to shut down virtually all rounds (99%) of viral replication if enough zanamivir reaches the infection site. Q24h dosing with the 2.5-h half-life had a trough concentration of 0.05 mg/liter, which resulted in a suboptimal extent of inhibition of 72%. In contrast, the trough concentrations at Q12h and Q8h dosing had extents of inhibition of 93% and 96%. These estimates explain why the low trough concentrations for the longer dosing intervals (Q24h) with the 2.5-h half-life provided suboptimal viral suppression and why shorter dosing intervals are necessary for successful therapy at the 2.5-h half-life. Thus, time>EC₅₀ is the PK/PD index best predicting the inhibition of viral replication for the 2.5-h half-life. On the other hand, all dosage regimens with the 8-h half-life had trough concentrations at or above 0.9 mg/liter, resulting in extents of inhibition of viral release in excess of 96% for the entire dosing interval. This is how the model explained AUC/EC₅₀ to be the most predictive PK/PD index for the 8-h half-life.

Our newly developed mechanism-based model is a powerful tool for predicting the viral load over time for any zanamivir dosage regimen. Such predictions cannot be achieved using traditional PK/PD experimental approaches, because these methods do not account for the entire time course of infection. This mathematical model can also be used to predict therapeutic success for special population groups. For example, patients with medical impairments, such as renal dysfunction, often exhibit PK profiles markedly different from those of healthy volunteers. Our model can predict optimal zanamivir dosage regimens that maximize viral inhibition throughout the course of infection for such patients.

Others have instituted mathematical models to describe the growth kinetics of influenza A virus and the effect of amantadine on viral growth kinetics (1, 3). The models described in these reports are different from our mechanism-based model. Baccam et al. and Beauchemin et al. (1, 3) modeled the infection state of target cells using a single delay compartment for infected cells. In contrast, we modeled the intracellular stages of the virus replication cycle employing a transit compartment model and optimized the number of transit compartments. Both approaches can describe the delay between the infection of a host cell and the egress of infectious virus. We included compartments for different stages of intracellular virus to specify the mechanism of action for zanamivir that inhibits the egress of infectious virus. Importantly, inclusion of the first-order death process for intracellular virus improved the predictive performance of the model. Therefore, inhibition of viral egress also reduces the total number of infectious viruses released in our model, since zanamivir therapy reduces the fraction of intracellular virus that is released as infectious virus.

The emergence and spread of influenza viruses resistant to the available treatments have pushed combination chemotherapy to the forefront of antiviral research. Currently, there are several studies investigating the efficacy of antiviral agents when used in combination against influenza viruses (25, 26, 28). To use combination chemotherapy efficaciously, dosage regimens for antiviral combinations must be optimized. Our new mechanism-based mathematical model offers an advantage over traditional PK/PD index approaches in that the model is amenable to describing the effects of combination chemotherapy with two agents. Such combination regimens may be most efficacious if two antivirals, such as zanamivir and amantadine, affect different stages of the viral life cycle (Fig. 1). Therefore, our model could be a very useful tool for optimizing dosage regimens with multiple antiviral compounds.

This study showed that the dynamically linked PK/PD index for the suppression of the A/Hong Kong (H275Y) virus, an oseltamivir-resistant pH1N1 influenza virus, by zanamivir was time>EC₅₀ for the clinical 2.5-h half-life, whereas AUC/EC₅₀ was most predictive for the artificial 8-h half-life. This change in the most predictive PK/PD index was explained by a new mechanism-based mathematical model that described all viral load profiles well and had excellent predictive performance. The model showed that the trough concentrations for Q24h (and Q12 h) dosing provided worse viral suppression than Q8h dosing for the 2.5-h half-life. In contrast, all dosage regimens yielded similar extents of inhibition of viral release for the 8-h half-life. This proposed model may be used as a predictive tool for determining the viral load over time with any dosage regimen of zanamivir and can be adapted for estimation of the viral load for combination chemotherapy. Overall, these studies offer a better understanding of the time course of the pharmacodynamics of i.v. zanamivir and hold great promise for optimizing dosage regimens for patients.