Latent transition models with latent class predictors: attention deficit hyperactivity disorder subtypes and high school marijuana use

Summary

Attention deficit hyperactivity disorder (ADHD) is a neurodevelopmental disorder which is most often diagnosed in childhood with symptoms often persisting into adulthood. Elevated rates of substance use disorders have been evidenced among those with ADHD, but recent research focusing on the relationship between subtypes of ADHD and specific drugs is inconsistent. We propose a latent transition model (LTM) to guide our understanding of how drug use progresses, in particular marijuana use, while accounting for the measurement error that is often found in self-reported substance use data. We extend the LTM to include a latent class predictor to represent empirically derived ADHD subtypes that do not rely on meeting specific diagnostic criteria. We begin by fitting two separate latent class analysis (LCA) models by using second-order estimating equations: a longitudinal LCA model to define stages of marijuana use, and a cross-sectional LCA model to define ADHD subtypes. The LTM model parameters describing the probability of transitioning between the LCA-defined stages of marijuana use and the influence of the LCA-defined ADHD subtypes on these transition rates are then estimated by using a set of first-order estimating equations given the LCA parameter estimates. A robust estimate of the LTM parameter variance that accounts for the variation due to the estimation of the two sets of LCA parameters is proposed. Solving three sets of estimating equations enables us to determine the underlying latent class structures independently of the model for the transition rates and simplifying assumptions about the correlation structure at each stage reduces the computational complexity.

1. Introduction

Attention deficit hyperactivity disorder (ADHD) is a neurodevelopmental disorder which is most often diagnosed in childhood and characterized by symptoms of inattention, hyperactivity and impulsiveness. It is estimated that 3–7% of school-aged youth in the USA have ADHD (American Psychiatric Association, 2000) and 1–5% in Europe (Swanson et al., 1998; Polanczyk et al., 2007). Many children with ADHD experience behavioural and psychosocial difficulties. In particular, high rates of substance use disorders have been evidenced in studies of adolescents who were diagnosed with ADHD in childhood (Barkley et al., 1990; Levin and Kleber, 1995). Whereas early studies focused on global assessments of substance use, more recent work suggests that individuals with ADHD might be at risk for using specific drugs; however, the results are not consistent. Molina and Pelham (2003) found that, although ADHD adolescents were more likely than controls to report alcohol-related problems, they were not more likely to use alcohol, cigarettes or marijuana. In contrast, others have found increased rates of nicotine dependence, regular cannabis smoking and daily smoking but not alcohol use or dependence among adolescents with ADHD (Galera et al., 2005, 2008; Biederman et al., 2006). Just as there has been an increased focus on specific drugs and ADHD, researchers are beginning to look at the relationship between specific symptoms or subtypes of ADHD and substance use. Currently three ADHD subtypes are recognized in American Psychiatric Association (2000); predominantly inattentive, predominantly hyperactive–impulsive and a combined subtype. Inattentiveness symptoms have been shown to be associated with marijuana and nicotine dependence (Abrantes et al., 2005), tobacco use (Burke, et al., 2001) and frequency of alcohol, marijuana and tobacco use (Molina and Pelham, 2003). Symptoms of hyperactivity and impulsiveness have been shown to be associated with alcohol use (Burke et al., 2001), illicit drug use (Molina and Pelham, 2003), earlier age of initiation of substance use (Molina and Pelham, 2003; Elkins et al., 2007) and marijuana and nicotine dependence (Elkins et al., 2007).

In this paper, we propose to use a latent transition model (LTM) to study stage sequential transitions in use of marijuana through the high school years and to examine the influence of ADHD subtypes on these transitions. The transition concept, which was introduced in the 1990s, depicts drug involvement as a sequence of transitions from earliest opportunities to use a drug, to first use and consequences, followed by the drug dependence syndrome (Stenbacka et al., 1993; Anthony and Helzer, 1995). Within this framework it has been suggested that determinants of transitions across stages of drug involvement may be different (Clayton, 1992; Anthony and Helzer, 1995). This may explain the inconsistent findings regarding the relationship between drug use and ADHD. For example, ADHD may influence drug use initiation differently from how it does for more serious drug involvement. In addition to positing drug use as a stage sequential process with the potential for different influences at each stage, LTMs offer two additional advantages. First, LTMs are an empirically based procedure that allows the data to guide our understanding of how drug use progresses by creating homogeneous groups of individuals with similar drug use profiles. Secondly, LTMs account for the measurement error that is often found in self-reported substance use data (Harrison and Hughes, 1997; Golub et al., 2000) by assuming that each response is an imperfect measure of drug use.

The current study extends the LTM of Reboussin et al. (1999) by incorporating a latent class predictor to represent ADHD subtypes. This is appealing because data that are based on clinic-based samples have demonstrated higher rates of the combined subtype (Lahey et al., 1994; Faraone et al., 1998) whereas population-based studies have had mixed results with some suggesting that the inattentive subtype is the most prevalent (Gaub and Carlson, 1997; Froehlich et al., 2007) and others the combined type (Angold et al., 2002; Ford et al., 2003). In addition, we know that using different diagnostic criteria (e.g. those of American Psychiatric Association (2000) and version 10 of the international classification of diseases) results in different ADHD prevalence estimates (Swanson et al., 1997; Polanczyk et al., 2007). Therefore, rather than rely on specific diagnostic criteria to define ADHD subtypes, we use latent class analysis (LCA) to identify empirically subgroups of individuals in an urban sample of high school students with similar profiles of inattentive, hyperactive and impulsive behaviours. Parameter estimation involves an estimating equations analogue of the pseudolikelihood method for estimation of the parameters of interest, namely the transition model parameters. We begin by fitting two separate LCA models by using second-order estimating equations:

1. a longitudinal LCA model to define stages of marijuana use, which is hereafter referred to as the latent stage model, and

2. a cross-sectional LCA model to define the ADHD subtypes.

The LTM model parameters describing the probability of transitioning between the LCA-defined stages of marijuana use and the influence of the LCA-defined ADHD subtypes on these transition rates are then estimated by using a set of first-order estimating equations given the LCA model parameter estimates. A robust estimate of the LTM parameter variance that accounts for the variation due to the estimation of the two sets of LCA parameters is proposed. By solving three separate estimating equations that only require specification of first and second moments and that allow us to make simplifying assumptions about the correlation structure at each stage, computational complexity is significantly reduced.

2. Latent transition model with latent class predictor

2.1. The latent stage model of drug use

Let y_it = (y_i1t, …, y_ipt), t = 1, …, T, be a vector of binary responses regarding drug use behaviours for individual i at time t where y_ijt = 1 if the response to behaviour j at time t is ‘yes’ and y_ijt = 0 otherwise. We refer to y_it as the drug use behaviour profile at time t. We assume that the co-occurrence of the behaviours comprising the drug use profile y_it can be explained by an underlying classification of individuals into subgroups (classes) with similar drug use profiles representing stages of drug use. In a statistical sense this means that, within a stage of drug use, behaviours are independent. This is the axiom of local independence that forms the basis for LCA. Since latent class membership is not observed without error, this assumption is not verifiable; however, its adequacy under various class assumptions will be discussed later. For estimation purposes, we assume there are D latent stages indexed by 1, …, D. The latent stage of drug use for individual i at time t is denoted by D_it.

Information about the latent stages of drug use are conveyed through two sets of parameters; the probability of reporting behaviour j at time t within stage m of drug use,

$$p_{\mathit{jmt}}=P(y_{\mathit{ijt}}=1\mid D_{it}=m),$$

and the proportion of individuals in stage of m of drug use at time t, or the latent class prevalence,

$${\pi }_{mt}=P(D_{it}=m).$$

We shall refer to θ_1t = (p_t, π_t) as the latent stage parameters for time t where θ₁ = (θ₁₁, …, θ_1T). The conditional response probabilities p_jmt aid in the interpretation of the stages of drug use by characterizing the behaviour of individuals within a particular stage. Although in principle it is possible to allow the conditional response probabilities to vary over time, this implies that the definition of drug use stages is changing, which would substantially complicate interpretation of the longitudinal model. Therefore, we constrain the conditional response probabilities to be constant over time, i.e. p_jmt = p_jm ∀t = 1, …, T. This is analogous to constraining the factor loadings to be equal over time in a longitudinal factor analysis model (which is sometimes referred to as factor invariance). To restrict the conditional response probabilities to the admissible interval, a logistic representation was used, p_jm = exp(ζ_jm)/{1 + exp(ζ_jm)}. Consistent with the longitudinal framework, the proportion of individuals in each drug use stage π_mt is allowed to vary over time.

2.2. The latent class attention deficit hyperactivity disorder predictor model

Let z_i = (z_i1, …, z_ir) be a vector of responses regarding ADHD symptoms measured before the drug use behaviours for individual i where z_iu = 1 if ADHD symptom u is present and z_iu = 0 otherwise. We refer to z_i as the ADHD symptom profile for individual i. We assume that the co-occurrence of the ADHD symptoms can be explained by an underlying classification of individuals into subgroups (classes) with similar symptom profiles representing ADHD subtypes. For estimation purposes, we assume that there are A subtypes indexed by 1, …, A. The latent ADHD subtype for individual i is denoted by A_i. Similarly to the latent stage model, information about ADHD subtypes is conveyed through two sets of parameters; the probability of reporting ADHD symptom u for individuals with ADHD subtype l,

$$p_{ul}^{\ast }=P(z_{iu}=1\mid A_i=l),$$

and the proportion of individuals with ADHD subtype l,

$${\pi }_l^{\ast }=P(A_i=l).$$

We refer to θ₂ = (p*, π*) as the ADHD measurement parameters. Similarly to the latent stage model in Section 2.1, to restrict the conditional response probabilities to the admissible interval, a logistic representation was used, $p_{ul}^{\ast }=exp({\zeta }_{ul}^{\ast })/\{1+exp({\zeta }_{ul}^{\ast })\}$.

2.3. The latent transition model

Scientific interest focuses on changes in stages of drug use over time and the influence of ADHD subtypes on these transitions. This makes the modelling of transition probabilities τ_it (k, m) = P(D_it = m|D_i,t−1 = k) as a function of predictors natural. We begin by considering the first-order transition model of Reboussin et al. (1999) where the transition probabilities are modelled as a function of observed covariates x_it, discrete or continuous and possibly time dependent:

$$log\left\{\frac{{\tau }_{it}(k,m;{\mathbf{x}}_{it})}{{\tau }_{it}(k,1;{\mathbf{x}}_{it})}\right\}={\alpha }_m+{\beta }_{km}+{\mathbf{\Upsilon }}_m{\mathbf{x}}_{it}+{\mathbf{\Psi }}_{km}{\mathbf{x}}_{it}$$ (1)

where t = 2, …, T, m = 2, …, D, k = 1, …, D, β_1m = 0 and Ψ_1m = 0. Model (1) is a multinomial logistic regression model. The probability that an individual transitions from stage D_i,t−1 = k at time t − 1 to stage D_it = m at time t given covariates x_it is represented by the logistic function:

$${\tau }_{it}(k,m;{\mathbf{x}}_{it})=\frac{exp({\alpha }_m+{\beta }_{km}+{\mathrm{\Upsilon }}_m{\mathbf{x}}_{it}+{\mathrm{\Psi }}_{km}{\mathbf{x}}_{it})}{1+{\displaystyle \sum _{l=2}^D}exp({\alpha }_l+{\beta }_{kl}+{\mathrm{\Upsilon }}_l{\mathbf{x}}_{it}+{\mathrm{\Psi }}_{kl}{\mathbf{x}}_{it})}.$$ (2)

The parameter α_m in model (1) is the log-odds of transitioning from stage D_i,t−1 = 1 (e.g. no drug use) at time t − 1 to stage D_it = m at time t relative to remaining in stage 1 at time t given x_it = 0. The log-odds of transitioning from stage D_i,t−1 = k at time t − 1 to stage D_it = m at time t relative to remaining in stage k at time t when k ≠ 1 and m > k is given by α_m − α_k + β_km − β_kk when x_it = 0. If we assume for illustration that there is a single binary variable x_it, then υ_m is the log-odds-ratio comparing the odds of transitioning from stage 1 to stage m for x_it = 1 versus x_it = 0. Similarly, υ_lm − υ_lk + ψ_km − ψ_kk is the log-odds-ratio comparing the odds of transitioning from stage k to stage m for x_it = 1 versus x_it = 0 when k ≠ 1 and k > m.

We extend model (1) to examine how transition probabilities depend on latent ADHD subtypes by including an interaction between an individual’s prior latent stage of drug use D_i,t−1 and latent ADHD subtype A_i as shown below:

$$log\left\{\frac{{\tau }_{it}(k,m;{\mathbf{x}}_{it},A_i=l)}{{\tau }_{it}(k,1;{\mathbf{x}}_{it},A_i=l)}\right\}={\alpha }_m+{\beta }_{km}+{\mathrm{\Upsilon }}_m{\mathbf{x}}_{it}+{\mathrm{\Psi }}_{km}{\mathbf{x}}_{it}+{\delta }_{lm}+{\mathrm{\Gamma }}_{\mathit{lkm}}$$ (3)

where m = 2, …, D, k = 1, …, D, l = 1, …, A, δ_1m = 0 and Γ_lkm = 0 if k = 1 or l = 1. We shall refer to θ₃ = (α, β, ϒ, Ψ, δ, Γ) as the latent transition parameters. The parameter δ_lm is the log-odds-ratio comparing the odds of transitioning from stage 1 to stage m for a youth of ADHD subtype l compared with a youth of ADHD subtype 1. The log-odds-ratio that compares the odds of transitioning from stage k to stage m where k ≠ 1 and m > k for a youth of ADHD subtype l compared with a youth of ADHD subtype 1 is given by δ_lm − δ_lk + γ_lkm − γ_lkk. This model can be extended further to allow the effect of ADHD subtype on the transition probabilities to depend on observed covariates x_it, e.g. age and gender, by including an interaction between ADHD subtype and x_it and a three-way interaction between prior stage of drug use, ADHD subtype and x_it.

3. Estimation

3.1. Estimation of θ₁

Similarly to Reboussin et al. (1999), we propose first to solve a set of estimating equations U_1t (θ_1t) for estimating the latent stage parameters θ_1t at time t that incorporate information from both the first- and the second-order moments of the observed drug use profile y_it. This is unlike estimating equations for generalized linear models which only use information in the first-order moments (Zeger and Liang, 1986). Information in the second-order moments is necessary for identification of the latent stage model parameters in which the covariance between responses is of scientific interest.

The estimating equations are formed by equating the observed responses y_it and w_it = {(y_ijt − μ_ijt)(y_iht − μ_iht); j < h = 1, …, p} to their expected values μ_it = E[y_it] and σ_it = E[w_it]. The first-order moments are given by ${\mu }_{\mathit{ijt}}=E[y_{\mathit{ijt}}]={\mathrm{\sum }}_{m=1}^D{p}_{\mathit{jmt}}{\pi }_{mt}$. Under the assumption of conditional independence, the second-order moments are now

$${\sigma }_{\mathit{ijht}}=E[(y_{\mathit{ijt}}-{\mu }_{\mathit{ijt}})(y_{\mathit{iht}}-{\mu }_{\mathit{iht}})]=\sum _{m=1}^D{p}_{\mathit{jmt}}{p}_{\mathit{hmt}}{\pi }_{mt}-{\mu }_{\mathit{ijt}}{\mu }_{\mathit{iht}}.$$

The estimating equations are weighted by the matrix C_it of first-order derivatives of the first two moments with respect to the set of parameters θ_1t and a working p(p + 1)/2 × p(p + 1)/2 covariance matrix R_it of y_it and w_it. The covariance matrix is referred to as working because, as demonstrated by Liang et al. (1992), parameter estimates and standard errors remain consistent even if the covariance is misspecified.

The proposed second-order estimating equations are then

$$U_{1t}({\mathit{\theta }}_{1t})=\sum _{i=1}^N{\mathbf{C}}_{it}^{\prime }{\mathbf{R}}_{it}{({\mathit{\theta }}_{1t})}^{-1}\left(\begin{array}{c}{\mathbf{y}}_{it}-{\mathit{\mu }}_{it}({\mathit{\theta }}_{1t})\\ {\mathbf{w}}_{it}({\mathit{\theta }}_{1t})-{\mathit{\sigma }}_{it}({\mathit{\theta }}_{1t})\end{array}\right)=0.$$ (4)

The solution of the estimating equations (4) can occur simultaneously for all t, t = 1, …, T, assuming independence between time periods. The cross-products of indicators at adjacent time points, e.g. y_ijt y_ih,t−1, are not included since they contain the same information as the first moments in the estimating equations for θ₃. Cross-products of indicators that are more than 1 unit apart in time are also not incorporated owing to the computational burden. It is reasonable to assume that the indicators at time t provide most of the information about the latent stage variable D_it. Failure to incorporate cross-products of indicators that are more than 1 unit apart in time results in potential loss of efficiency in parameter estimation but no risk of bias. To avoid higher order moment specifications, we assume that cov(y_it w_it) = 0 and cov(w_it) is diagonal. These estimating equations are solved simultaneously for θ_1t, t = 1, …, T, by using a Newton–Raphson iterative procedure. A robust variance estimator of θ̂₁ that is consistent even when the working covariance matrix of y_i and w_i is misspecified is given in Appendix A.

3.2. Estimation of θ₂

The ADHD measurement parameters θ₂ are estimated by solving a set of estimating equations U₂(θ₂) similar to the estimating equations (4) that incorporate information from both the first- and the second-order moments of the observed ADHD symptom profile z_i. Unlike equations (4), we consider the ADHD symptom profile at a single time point. The estimating equations are formed by equating the observed responses z_i and ${\mathbf{w}}_i^{\ast }=\{(z_{ij}-{\mu }_{ij}^{\ast })(z_{ih}-{\mu }_{ih}^{\ast });j<h=1,\dots ,r\}$ to their expected values ${\mathit{\mu }}_i^{\ast }=E[{\mathbf{z}}_i]$ and ${\mathit{\sigma }}_i^{\ast }=E[{\mathbf{w}}_i^{\ast }]$. The first-order moments are given by ${\mu }_{ij}^{\ast }=E[z_{ij}]={\sum }_{l=1}^A{p}_{jl}^{\ast }{\pi }_l^{\ast }$. Under the assumption of conditional independence, the second-order moments are given by

$${\sigma }_{\mathit{ijh}}^{\ast }=E[(Z_{ij}-{\mu }_{ij}^{\ast })(Z_{ih}-{\mu }_{ih}^{\ast })]=\sum _{l=1}^A{p}_{jl}^{\ast }{p}_{hl}^{\ast }{\pi }_l^{\ast }-{\mu }_{ij}^{\ast }{\mu }_{ih}^{\ast }.$$

The estimating equations are weighted by the matrix E_i of first-order derivatives of the first two moments with respect to the set of parameters θ₂ and a working r(r + 1)/2 × r(r + 1)/2 covariance matrix ${\mathbf{R}}_i^{\ast }$ of z_i and ${\mathbf{w}}_i^{\ast }$. The proposed second-order estimating equations

$$U_2({\theta }_2)=\sum _{i=1}^N{\mathbf{E}}_i^{\prime }{\mathbf{R}}_i^{\ast }{({\theta }_2)}^{-1}\left(\begin{array}{c}{\mathbf{z}}_i-{\mathit{\mu }}_i^{\ast }({\theta }_2)\\ {\mathbf{w}}_i^{\ast }({\theta }_2)-{\mathit{\sigma }}_{it}^{\ast }({\theta }_2)\end{array}\right)=0$$ (5)

are solved for θ₂ by using a Newton–Raphson iterative procedure. Similarly to the estimation of θ₁, we avoid higher order moment specifications by assuming that $cov({\mathbf{z}}_i{\mathbf{w}}_i^{\ast })=0$ and $cov({\mathbf{w}}_i^{\ast })$ is diagonal. A robust variance estimator of θ̂₂ that is consistent even when the working covariance matrix of z_i and ${\mathbf{w}}_i^{\ast }$ is misspecified is given in Appendix B.

3.3. Estimation of θ₃

We propose to solve the following set of first-order estimating equations (Liang and Zeger, 1986; Zeger and Liang, 1986) for the latent transition parameters θ₃ similarly to Reboussin et al. (1999),

$$U_3({\theta }_3,{\widehat{\theta }}_1,{\widehat{\theta }}_2)=\sum _{i=1}^N{B}_i{V}_i^{-1}({\theta }_3,{\widehat{\theta }}_1,{\widehat{\theta }}_2)\{{\mathbf{y}}_i^{\ast }-{\mathit{\eta }}_i({\theta }_3,{\widehat{\theta }}_1,{\widehat{\theta }}_2)\}=0$$ (6)

where ${\mathbf{y}}_i^{\ast }=({\mathbf{y}}_{i2},\dots ,{\mathbf{y}}_{iT})$, η_i = (η_i2, …, η_iT), η_it = E[y_it|y_i,t−1, x_it, z_i; θ₃, θ̂₁, θ̂₂], θ̂₁ is a √N-consistent estimator of the latent stage parameters θ₁ discussed in Section 3.1 and θ̂₂ is a √N-consistent estimator of the ADHD measurement parameters θ₂ discussed in Section 3.2. The matrix B_i is a matrix of first-order derivatives of the first conditional moments with respect to θ₃.

Assuming that the covariates x_it and ADHD symptom profile z_i are only included because of their expected association with the transition probabilities, the first conditional moment of y_ijt given y_i,t−1, x_it and z_i can be expressed as

$${\eta }_{\mathit{ijt}}=\sum _{m=1}^D\sum _{k=1}^D\sum _{l=1}^A{p}_{\mathit{jmt}}{\tau }_{it}(k,m;{\mathbf{x}}_{it},A_i=l)P(D_{i,t-1}=k\mid {\mathbf{y}}_{i,t-1})P(A_i=l\mid {\mathbf{z}}_i)$$

where

$$P(D_{i,t-1}=k\mid {\mathbf{y}}_{i,t-1})=\frac{{\displaystyle \prod _{s=1}^p}{p_{sk,t-1}}^{y_{is,t-1}}{(1-p_{sk,t-1})}^{1-y_{is,t-1}}{\pi }_{k,t-1}}{{\displaystyle \sum _{f=1}^D}{\displaystyle \prod _{q=1}^p}{p_{qf,t-1}}^{y_{iq,t-1}}{(1-p_{qf,t-1})}^{1-y_{iq,t-1}}{\pi }_{f,t-1}}$$

and

$$P(A_i=l\mid {\mathbf{z}}_i)=\frac{{\displaystyle \prod _{s=1}^r}{p}_{sl}^{\ast z_{is}}{(1-p_{sl}^{\ast })}^{1-z_{is}}{\pi }_l^{\ast }}{{\displaystyle \sum _{f=1}^A}{\displaystyle \prod _{q=1}^r}{p}_{qf}^{\ast z_{iq}}{(1-p_{qf}^{\ast })}^{1-z_{iq}}{\pi }_f^{\ast }}.$$

We refer to the matrix V_i as a working covariance matrix. Let V_it = cov(y_it|y_i,t−1, x_it, z_i) be the working covariance matrix for the indicators at the tth time point. To simplify calculations, we assume that V_i = diag(V_i2, …, V_iT) so that cov(y_it, y_it′|y_i,t−1, y_i,t′−1, x_it, x_it′, z_i) = 0 ∀t ≠ t′. If the random process {y_it, t = 1, …, T} is a first-order Markov chain this assumption is met. The (j, h)-element of V_it is given by V_it (j, h) = E[y_ijt y_iht|y_i,t−1, x_it, z_i] − η_ijt η_iht where

$$E[y_{\mathit{ijt}}{y}_{\mathit{iht}}\mid {\mathbf{y}}_{i,t-1},{\mathbf{x}}_{it},{\mathbf{z}}_i]=\sum _{m=1}^D\sum _{k=1}^D\sum _{l=1}^A{p}_{\mathit{jmt}}{p}_{\mathit{hmt}}{\tau }_{it}(k,m;{\mathbf{x}}_{it},A_i=l)P(D_{i,t-1}=k\mid {\mathbf{y}}_{i,t-1})P(A_i=l\mid {\mathbf{z}}_i).$$

The generalized estimating equations (GEEs) (6) are not explicitly solvable for θ̂₃ so an iterative approach is necessary for parameter estimation. Starting with an initial estimate ${\widehat{\theta }}_3^0$, equation (6) can be solved by using the following Newton–Raphson iterative scheme:

$${\widehat{\theta }}_3^f={\widehat{\theta }}_3^{f-1}+{\left(\sum _{i=1}^N{\widehat{B}}_i^{\prime }{\widehat{V}}_i^{-1}{\widehat{B}}_i\right)}^{-1}\sum _{i=1}^N{\widehat{B}}_i^{\prime }{\widehat{V}}_i^{-1}({\mathbf{y}}_i^{\ast }-{\widehat{\mathit{\eta }}}_i),f=1,2,\dots ,$$

where ${\widehat{B}}_i={\widehat{B}}_i({\widehat{\theta }}_3^{f-1},{\widehat{\theta }}_1,{\widehat{\theta }}_2),{\widehat{V}}_i=V_i({\widehat{\theta }}_3^{f-1},{\widehat{\theta }}_1,{\widehat{\theta }}_2),{\widehat{\eta }}_i={\eta }_i({\widehat{\theta }}_3^{f-1},{\widehat{\theta }}_1,{\widehat{\theta }}_2)$ and f denotes the estimate at the f th iteration.

Following the work of Zeger and Liang (1986) and Liang and Zeger (1986), the GEEs (6) yield consistent and asymptotically multivariate normal estimates of θ₃ as long as the first conditional moment η_i is correctly specified. The covariance of $y_i^{\ast }$ need not be correctly specified. If θ̂₁ and θ̂₂ are √N-consistent estimators of θ₁ and θ₂ respectively, this approach can be considered an estimating function analogue of the pseudolikelihood method for the parameters of interest θ₃ (Gong and Samaniego, 1981). If the covariance of $y_i^{\ast }$ is correctly specified and θ₁ and θ₂ are known, a model-based consistent estimator of the asymptotic covariance of θ̂₃ is

$${\widehat{var({\widehat{\theta }}_3)}}_{mod}={\left(\sum _{i=1}^N{B}_i^{\prime }{V}_i^{-1}{B}_i^{-1}\right)}^{-1}/N$$ (7)

where θ₃ is replaced by θ̂₃. A robust estimator of the variance of θ̂₃ which accounts for the variation due to the estimation of θ₁ and θ₂ and which remains consistent even when the covariance of $y_i^{\ast }$ is misspecified is given in Appendix C.

4. Use of marijuana and attention deficit hyperactivity disorder subtype example

Our application concerns a sample of 495 high school students who participated in a randomized school-based, preventive intervention trial which targeted early learning and aggressive or disruptive behaviour in the first grade in nine schools in Baltimore, Maryland, USA (Ialongo et al., 1999). In 1993, 799 urban first-graders were recruited from 27 classrooms in nine Baltimore city public elementary schools. Students and their families were interviewed annually, although no assessments were conducted in the fourth and fifth grades. Beginning in the sixth grade, parental consent was obtained to participate in middle and high school assessments in which youths would be asked about their experiences with drugs. Of the original 799 adolescents who were recruited in the first grade, 495 (85%) completed face-to-face interviews in the eighth grade that included questions about inattentive, hyperactive and impulsive behaviours and questions about use of marijuana in the ninth and 10th grades. These 495 youths comprised the sample of interest for studying transitions in high school use of marijuana. Approximately 55% of the sample were male and 87% were African American. Because data on use of marijuana were not collected until the sixth grade, we could not compare the 495 youths participating in this study and the 304 youths from the original sample who were not included in this study on the response variables. However, t-tests revealed no differences between these groups in terms of the first-grade behavioural measures of self-reported anxious and depressive symptoms or teacher ratings of concentration problems, hyperactivity and impulsiveness. The 304 youths who were not participating in this study had slightly higher scores on the teacher-rated aggressive–disruptive behaviour scale. The sample of 495 youths with data available in the ninth and 10th grade decreased to 432 youths in the 11th grade and 415 youths in the 12th grade. χ²-tests revealed no differences in terms of measures of marijuana use in the ninth and 10th grades between the 415 youths with complete data and the 80 youths with missing assessments. These youths also did not differ on first-grade behavioural measures.

We characterized use of marijuana in high school by considering responses to five questions that were asked in the spring of the ninth, 10th, 11th and 12th grades.

1. Have you used marijuana since this time last year?

2. Did you use marijuana in the last month?

3. How many times have you used marijuana in the past month?

4. Have you ever used marijuana every day or almost every day for 2 or more weeks?

5. During the past 12 months, have you gotten into trouble at home, at school or with the police because you used marijuana?

For analysis, we dichotomized the third question as three or more times in the past month versus two or fewer to represent someone who has used marijuana more than just a couple of times in the past month. The last question combined responses to three individual questions that were asked during the assessments into a single indicator of social problems. This was done because of the low individual prevalences and their lack of discriminatory power.

We first applied the latent stage model of drug use that was described in Section 2.1 to examine the structure underlying the five behaviours comprising the marijuana use profile. We started with the most parsimonious one-stage model (‘all marijuana use the same’) with progression to a less parsimonious model with three stages of marijuana use. Because models with different numbers of stages (classes) are not nested, precluding the use of a difference likelihood ratio test, we must rely on measures of fit such as Akaike’s information criterion (AIC), which is a global fit index which combines goodness of fit and parsimony. In comparing different sets of models with the same set of data, models with lower values are preferred. Because the AIC requires a likelihood for model comparison and estimating equations approaches are non-likelihood based, we used a modified version of the AIC (Pan, 2001; Reboussin et al., 2006, 2008). The AIC suggested a best fitting model based on two stages of use of marijuana (AIC1=111811; AIC2 =110810; AIC3 =175981). However, rather than rely solely on global indices of fit like the AIC, we also examined the validity of the latent stage model assumption of local independence more directly. Specifically, we use a modified version of Garrett and Zeger’s (2000) log-odds-ratio check that was suggested by Uebersax (2000). This method involved calculating the log-odds-ratio in both the observed and the expected two-way tables for all pairs of marijuana use behaviours. The observed data log-odds-ratio is then expressed as a z-score relative to the expected data log-odds-ratio. This z-value is then used as a guide to detect items that are locally dependent. Uebersax (2000) suggested that the p-values should not be interpreted literally but rather that the focus should be on the relative magnitude of the z-values. A threshold of ±1.5 was conservatively chosen as suggestive of local dependence. Under the two-stage model of use of marijuana, z-values exceeding the threshold provided evidence for violation of the local independence assumption. The addition of a third stage removed all local dependences.

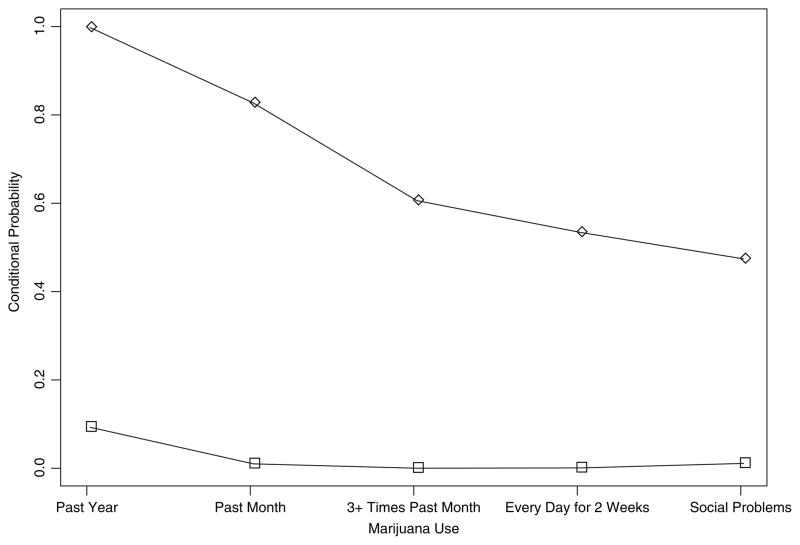
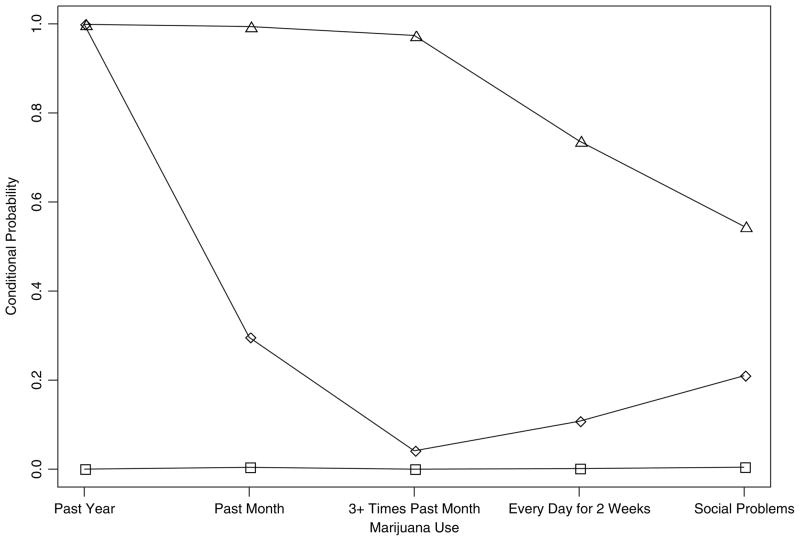
Although we can always achieve local independence by increasing the number of latent classes (Suppes and Zanotti, 1981), doing so may yield spurious classes that are not immediately interpretable to experts in the field. For this reason, we examined the resultant latent structures to evaluate their interpretability. As displayed in Fig. 1, the two-stage model divided use of marijuana into ‘no use’ (stage 1) and ‘use’ (stage 2). However, the second stage is predominantly characterized by past-month users with moderate levels of use (approximately 80% report past-month use and 60% report using three or more times in the past month). In contrast, the three-stage model (Fig. 2) creates a stage of use of marijuana that is characterized by less frequent use. Under the two-stage model infrequent use is difficult to classify with 15% of those in the ‘no-use’ stage reporting past year use and 20% of those in the ‘current use’ stage not reporting past-month use. With the three-stage model, infrequent use becomes an intermediary stage of use of marijuana between no use (stage 1) and current, more frequent and problematic marijuana use (stage 3). The three-stage model is consistent with Anthony and Helzer’s (1995) transition concept where an individual might experiment with a drug once or twice and then over time proceed to a more frequent and problematic pattern of drug use as opposed to going directly from no use to frequent use. Since the two-stage model provided the best overall fit on the basis of the AIC but did not fully explain the heterogeneity in the marijuana use profiles as evidenced by residual local dependences and because the three-stage model provided a substantively meaningful description of the progression of use of marijuana, we present results for both the two-stage and the three-stage models when examining associations with ADHD subtypes. We note that our stepwise approach has the advantage that the latent structures of marijuana use and ADHD are determined separately. Hence, the acceptance of a two- or three-stage model of marijuana use does not influence the choice of the appropriate number of ADHD classes.

Fig. 1.

Estimated stages of use of marijuana among 9th–12th-grade students on the basis of a latent two-stage model of use: □, no use, grade-specific latent stage prevalences (92%, 86%, 82%, 86%); ⋄, use, grade-specific latent stage prevalences (8%, 14%, 18%, 14%)

Fig. 2.

Estimated stages of use of marijuana among 9th–12th-grade students on the basis of a latent three-stage model of use: □, no use, grade-specific latent stage prevalences (88%, 77%, 75%, 75%); ⋄, infrequent use, grade-specific latent stage prevalences (7%, 16%, 15%, 17%); ▵, frequent use, grade-specific latent stage prevalences (4%, 7%, 10%, 7%)

Before examining associations with ADHD, we were interested in estimating the overall probability of transitioning between stages of use of marijuana during the high school years. Given the estimates of the latent stage parameters from the two- and three-stage models just described, we fit the LTM (1) where the observed covariate vector x_it = (x_it1, x_it2) contained two binary indicator variables representing the 10th–11th- and 11th–12th-grade transitions relative to the 9th–10th-grade transition respectively. Presented in Tables 1 and 2 are the estimated probabilities of transitioning from one stage of use of marijuana at the current grade to another stage of use of marijuana in the following grade for the two- and three-stage models respectively. Both models suggest that there is a greater risk of transitioning out of the no-use stage during the first 2 years of high school, i.e. 9th–10th grade and 10th–11th grade compared with 11th–12th grade. The rate of advance based on the two-stage model was 7.9% from ninth to 10th grade, 6.8% from 10th to 11th grade and 3.3% from 11th to 12th grade. On the basis of the estimated two-stage LTM, youths were significantly more likely to transition from no use to use during the 9th–10th-grade transition compared with the 11th–12th-grade transition (odds ratio OR = 4.14; 95% confidence interval CI = (2.15, 7.96)). Similarly, under the three-stage model, the rate of advance was 16.7% from ninth to 10th grade, 13.6% from 10th to 11th grade and 10.5% from 11th to 12th grade. The likelihood of transitioning from no use to infrequent use (stage 2) was 54% greater from ninth to 10th grade compared with from 11th to 12th grade (OR = 1.54; 95% CI = (0.98, 2.44)). This difference was marginally significant (p = 0.058). Although much less common, the risk of transitioning from no use to frequent use (stage 3) was almost five times greater from 10th to 11th grade compared with 11th to 12th grade (OR = 4.72; 95% CI = (1.08, 20.64)). The 9th–10th-grade transition posed the greatest risk for movement from infrequent (stage 2) to frequent (stage 3) use of marijuana but these differences were not statistically significant.

Table 1.

Estimated transition rates between stages of use of marijuana from ninth to 12th grade based on a latent two-stage model of use

Prior stage	Transition rates for the following transitions:
	9th–10th grade		10th–11th grade		11th–12th grade
	No use	Use	No use	Use	No use	Use
No use	0.921	0.079	0.932	0.068	0.967	0.033
Use	0.149	0.851	0.339	0.661	0.258	0.742

Table 2.

Estimated transition rates between stages of use of marijuana from ninth to 12th grade based on a latent three-stage model of use

Prior stage	Transition rates for the following transitions:
	9th–10th grade			10th–11th grade			11th–12th grade
	No use	Infrequent use	Frequent use	No use	Infrequent use	Frequent use	No use	Infrequent use	Frequent use
No use	0.832	0.138	0.029	0.864	0.101	0.035	0.895	0.097	0.008
Infrequent use	0.331	0.414	0.255	0.476	0.412	0.111	0.401	0.544	0.054
Frequent use	0.119	0.215	0.666	0.234	0.095	0.671	0.143	0.248	0.609

Next, we were interested in the influence of LCA-derived ADHD subtypes on these transitions in use of marijuana. We considered 11 items from three subscales of the ‘Teacher observation for classroom adaptation’ interview measuring symptoms of inattention, hyperactivity and impulsivity in the eighth grade. This is a structured interview with the teacher administered by a trained assessor (Werthamer-Larsson et al., 1991). Items were rated on a six-point frequency scale where 1 is almost never, 2 rarely, 3 sometimes, 4 often, 5 very often and 6 always. We dichotomized items so that an individual symptom was considered present if the teacher reported that it was present often, very often or always and absent if it was observed sometimes, rarely or almost never. We characterized ADHD symptom profiles in the eighth grade by considering teachers’ responses to the following items where items 1–5 are associated with inattention problems, items 6–8 with hyperactivity and items 9–11 with impulsiveness:

1. trouble completing assignments;

2. difficulty concentrating;

3. easily distracted;

4. cannot stay on task;

5. has difficulty organizing tasks;

6. cannot sit still;

7. is always on the go or acts as if driven by a motor;

8. fidgeted and/or squirmed a lot;

9. cannot wait for turn;

10. interrupts or intrudes on others;

11. blurts out answers before the question is complete.

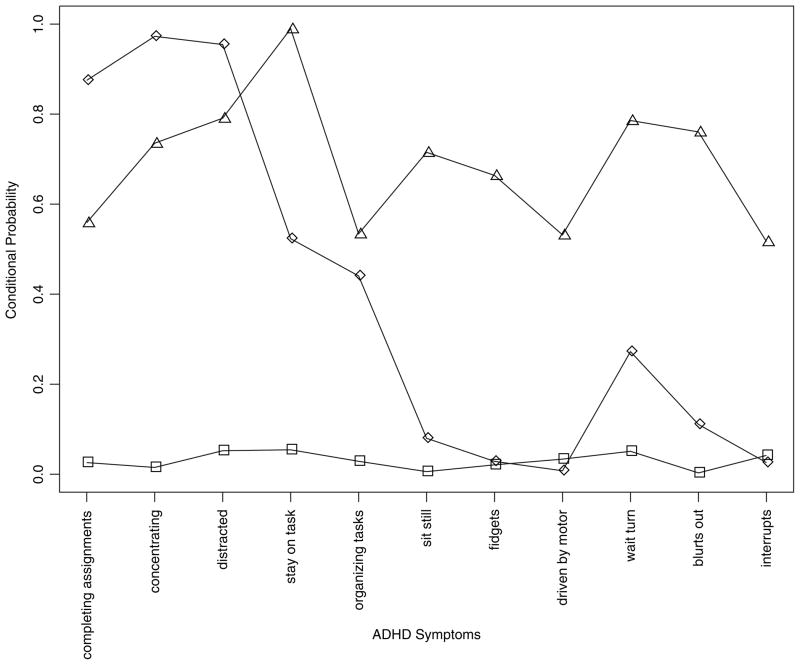
We applied the latent class ADHD predictor model in Section 2.2 to examine the structure underlying the ADHD symptom profile that was just described. We started with the most parsimonious one-class model with progression to a four-class model of ADHD. The AIC suggested a best-fitting model based on the three classes of ADHD (AIC1 = 63962; AIC2 = 60154; AIC3 = 58902; AIC4 = 59124). A check of the local independence assumption via the log-odds-ratio residuals for the three-class model indicated that there were no residual dependences. As stated previously, because statistical analysis may yield models that are not substantively meaningful despite their optimality based on goodness-of-fit statistics, we also examined the resultant three-class latent structure of ADHD to evaluate its interpretability. Under the three-class model that is displayed in Fig. 3, 65% of youths do not have ADHD on the basis of teacher reports. Approximately a quarter of youths were reported by teachers to exhibit only symptoms of inattention. The third class of youths, representing 12% of the sample, were reported to exhibit symptoms of inattention, hyperactivity and impulsiveness. We refer to this as the combined subtype. Although there was no evidence for a hyperactive–impulsive subtype in our sample of youth, the inattentive and combined subtypes were consistent with the diagnostic subtypes that are defined in American Psychiatric Association (2000).

Fig. 3.

Estimated subtypes of ADHD among eighth-grade students on the basis of a latent three-class model of ADHD: □, no ADHD (65%); ⋄, inattentive subtype (23%); ▵, combined subtype

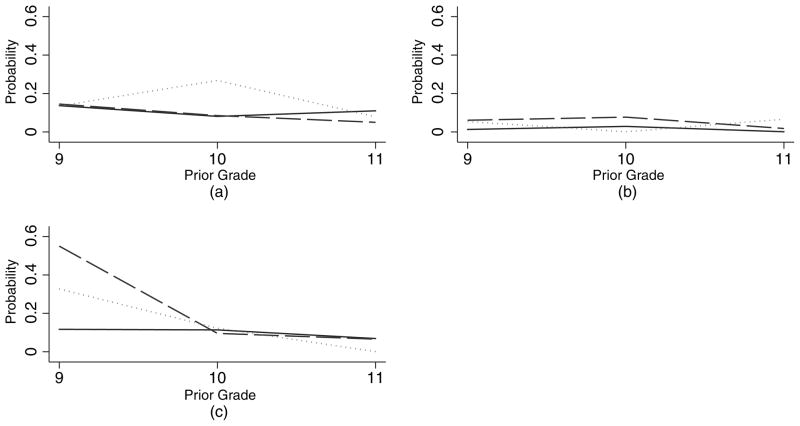
On the basis of the three-class model of ADHD, we then examined the influence of the ADHD subtypes on the probability of transitioning between stages of use of marijuana. We did this by fitting model (3) but included an interaction between grade and the ADHD subtype and a three-way interaction between prior latent stage, grade and ADHD subtype. This allowed us to estimate grade-specific influences of ADHD subtypes on transitions. On the basis of the two-stage model of marijuana use, youths with the inattentive and combined ADHD subtypes were more likely than youths without ADHD to transition from no use of marijuana (stage 1) to use of marijuana (stage 2) during high school. These differences were statistically significant for the inattentive subtype during the 9th–10th- (OR = 2.50; 95% CI = (1.17, 5.36)) and 10th–11th- (OR = 1.89; 95% CI = (1.07, 3.33)) grade transitions and for the combined subtype during the 10th–11th- (OR = 2.26; 95% CI = (1.11, 4.57)) and 11th–12th- (OR = 4.72; 95% CI = (1.35, 16.52)) grade transitions. As indicated by the three-stage model, this increased risk of transitioning for the ADHD subtypes relative to youths without ADHD was stage specific. Youths with the combined ADHD subtype were four times more likely to transition from no use of marijuana to infrequent use during the 10th–11th-grade transition relative to youths without ADHD (OR = 4.01; 95% CI = (1.57, 10.26)) as seen in Fig. 4(a). Youths with the inattentive subtype were five times more likely to transition from no use of marijuana to frequent use (Fig. 4(b)) from 9th to 10th grade compared with youths without ADHD (OR = 4.90; 95% CI = (1.17, 20.50)). Youths with the inattentive subtype were also marginally more likely to transition from infrequent to frequent use of marijuana (Fig. 4(c)) during this same time period compared with youths without ADHD (OR = 8.24; 95% CI = (0.86, 79.06)).

Fig. 4.

Estimated probability of transitioning from (a) no use of marijuana to infrequent use, (b) no use of marijuana to frequent use and (c) infrequent use of marijuana to frequent use: ———, no ADHD; — —, inattentive subtype; ·······, combined subtype

5. Discussion

We presented both an alternative model and a method for examining the relationship between ADHD and drug use. First, the LTM model of Reboussin et al. (1999) was extended to incorporate a latent class predictor. Using a multinomial logistic regression model, the odds to be in the current latent stage of drug use were modelled as a function of the prior stage, the latent class predictor and their interaction. This allowed us to examine the effect of empirically derived ADHD subtypes on stage sequential transitions in use of marijuana over time. The flexibility of this modelling approach also afforded us the ability to include observed covariates like grade in the model so that transition probabilities could be different over the course of high school. In addition to the innovative modelling of the transition probabilities, model development of the underlying latent structures and estimation occurred in a stepwise fashion. In the first step, the latent stage model of marijuana use that was described in Section 2.1 was used to create homogeneous groups of individuals with similar marijuana use profiles. This approach allowed us to examine empirically the progression of use of marijuana while accounting for the measurement error that occurs in self-reported substance use data. Although the two-stage model provided the best overall fit on the basis of global indices of fit, the three-stage model provided a better explanation of the heterogeneity in the profiles by delineating marijuana use further into infrequent and frequent use. On the basis of both the two- and the three-stage models of marijuana use, we then examined the rates of transitioning between stages over time as a function of grade by using the multinomial logistic regression model (1). Not only could we estimate the transition probabilities by using this model, but we could also perform inference on the log-odds-ratios by comparing the odds of transitioning between stages of use of marijuana relative to remaining in the same stage for different high school transitions (e.g. ninth to 10th versus 10th to 11th). Interestingly, we found that the movement from ninth to 10th grade and 10th to 11th grade posed the greatest risk of transitioning out of no use of marijuana compared with 11th to 12th grade.

Next, using the cross-sectional LCA model in Section 2.2, we could derive the ADHD subtypes independently from the derivation of the marijuana use stages. Rather than rely on diagnostic criteria for ADHD derived from clinic-based samples, we could explore profiles of inattentive, hyperactive and impulsive behaviours in our community-based sample of youth that might be associated with use of marijuana regardless of whether diagnostic criteria were met. Using this approach, we found evidence for two subtypes of ADHD that corresponded well to the diagnostic subgroups: both an inattentive and a combined subtype. There was not evidence in our sample for a strictly hyperactive–impulsive subtype. Given the estimates of the latent stage parameters described in Section 2.1 and the ADHD measurement parameters in Section 2.2, we could estimate the influence of the latent ADHD subtypes on the rates of transitioning by using the LTM model (3). Although the two-stage model of use of marijuana found that the two ADHD subtypes had a greater likelihood of transitioning to use of marijuana compared with youth without ADHD, it could not delineate between the type of transition, i.e. no use to infrequent use (initiation) and no use or infrequent use to frequent use (escalation or progression). The richer three-class model provided evidence that different subtypes had influences at different stages of use of marijuana. Using this approach, we found that the combined ADHD subtype had a significantly greater risk of transitioning from no use of marijuana to infrequent (initiation) use during the 10th–11th-grade transition relative to youths without ADHD. Although our combined subtype includes symptoms of inattention in addition to symptoms of hyperactivity and impulsiveness, this finding is generally consistent with Elkins et al. (2007) who found that the hyperactive–impulsive subtype was associated with initiation of use of marijuana. Youths with the inattentive subtype were significantly more likely to transition directly from no use of marijuana to frequent use and marginally more likely to transition from infrequent to frequent use during the 9th–10th-grade transition relative to those without ADHD (escalation or progression). These findings were similar to Abrantes et al. (2005), who found that the inattentive subtype was associated with an increased risk of dependence on marijuana.

This particular example of high school use of marijuana collected from a sample of students participating in a randomized school-based intervention trial demonstrated the usefulness of the LTM approach for modelling stage sequential transitions in behaviour while accounting for the measurement error that often occurs in self-reported substance use data. The flexibility of the multinomial logistic regression model for the latent transition parameters allowed us to incorporate both observed and latent class predictors easily. By including both grade and latent-class-derived ADHD subtypes, we could fit a combined and more sensitive model of progression of drug use that did not rely on clinical criteria and was consistent with the transition concept of Anthony and Helzer (1995) allowing for different influences at each stage of drug use. We should note, however, that the small sample size and relatively low prevalence of use of marijuana in our example resulted in some insignificant findings despite the magnitude of the odds ratios relating the transition probabilities. The results of simulation studies for the LTM of Reboussin et al. (1999) indicate that the estimating equations approach has good finite sample properties even with samples as small as 400. This suggests that the low prevalence of the underlying stages of use of marijuana in our example in combination with the small sample size may have resulted in an underpowered study.

Limitations of the study should be noted. As in most longitudinal studies, some of the original study population was lost to follow-up, i.e. participated in the first-grade assessments but not the middle and high school assessments. GEE-type estimation approaches were developed for the analysis of multivariate categorical data when non-response is classified as missing completely at random. When the missingness depends only on the observed covariates (which is termed covariate-dependent missingness), GEEs provide consistent regression parameter estimates (Lipsitz et al., 2000; Preisser et al., 2002). However, when missingness depends on the observed outcomes as well as covariates (which is termed missingness at random), GEEs may provide biased results. Although those who were lost to follow-up for the middle and high school assessments scored slightly higher on teacher-rated aggressive–disruptive behaviour, they did not differ on first-grade behavioural measures of anxiety, depression, concentration problems, hyperactivity or impulsiveness. In addition, attrition in our sample of 495 in the 11th and 12th grades was not related to use of marijuana in the ninth and 10th grades or the first-grade behavioural measures.

We also recognize that identifiability is a well-known problem in latent class modelling. For simple cases, the conditions for latent class parameters to be identified are known. In the absence of any restrictions, three classes become identifiable when there are four dichotomous variables (Lazarsfeld and Henry, 1968; McHugh, 1956). Conditions for model identifiability become more complex with covariate effects on underlying and measured variables (see Huang and Bandeen-Roche (2004)). However, an advantage of our three-stage estimating equations approach is that the latent class structures are determined without covariates in the first two stages. The latent transition regression model is then fitted given the latent class model parameters. For the latent stage model of use of marijuana, we have five binary indicators and fit two- and three-stage models. Although we have longitudinal data, we constrain the conditional response probabilities to be the same over time. Hence, within each time point, the latent class model is theoretically identifiable. The cross-sectional latent class predictor model for ADHD with three classes and 13 indicators is also theoretically identifiable. Despite the theoretical identifiability of our models, the model may not be empirically identifiable given our data. A drawback of the semiparametric GEE approach is that we cannot check the empirical identifiability of our fitted model by examining the matrix of second-order partial derivatives of the log-likelihood. We did check the condition of the matrix of the second-order derivatives of the quasi-score function and it was non-singular for the three-class models. However, methods for diagnosing model identifiability for latent class models estimated by using GEEs are needed and should be the focus of future research.

Perhaps the most important strength of our approach is that it enabled us to determine the underlying stages of use of marijuana and ADHD subtypes independently of the multinomial logistic regression model for the transition rates. Separate estimation of the model parameters by using three sets of estimating equations reduced the complexity that was introduced by the longitudinal nature of the data and the extension to the incorporation of a latent class predictor. Compared with a full likelihood approach, estimation of model parameters and standard errors was made less problematic by virtue of simplifying assumptions to the working covariance matrix at each stage of estimation. Although a possible loss of efficiency associated with making these simplifying assumptions (and possibly an explanation for some of the insignificant findings) warrants further exploration, a robust estimate of the LTM parameter variance that accounted for the variation due to the estimation of the latent stage and latent class parameter estimates was easily obtained. This made inference on the latent transition odds ratios possible under the stagewise estimating equation approach whereas estimation of standard errors in likelihood-based approaches is problematic, so standard errors are often not reported.

Finally, latent transition analysis is an attractive approach for modelling the evolution of stage sequential developmental processes. Not only does it allow the data to guide our understanding of how these processes unfold but also it accounts for the measurement error that is often found in self-report data. Although much of the application of latent transition modelling has occurred in the context of substance use, methods for modelling transitions between health states are important more broadly as are methods allowing for multiple indicators of health. It is increasingly difficult to quantify health with a single measure leading to widespread use in public health studies of questionnaires and surveys involving a series of self-report questions. Although each question on its own is an imperfect measure, together the questions may describe variation in a health profile. The extension of these multiple indicator methods to the predictor variable in the form of a latent class variable is also important for identifying subgroups of individuals with homogeneous risk profiles. These combined models have the potential to inform our understanding of the aetiology of stage sequential developmental processes and to aid in the development of targeted intervention and prevention programmes that are stage and subgroup specific.

Appendix A

Consider a first-order Taylor series approximation of U₁(θ₁) about θ₁ = θ̂₁ which results in

$$\surd N({\widehat{\theta }}_1-{\theta }_1)\approx -\frac{1}{\surd N}\text{diag}{(K_1,\dots ,K_T)}_{{\mid }_{{\theta }_1={\widehat{\theta }}_1}}^{-1}{U}_1({\theta }_1)$$

where

$$K_t={\left(\sum _{i=1}^N{\widehat{C}}_{it}^{\prime }{\widehat{R}}_{it}^{-1}{\widehat{C}}_{it}\right)}^{-1},t=1,\dots ,T,$$

and U₁(θ₁) is defined in Section 3.1. Then

$$\surd N({\widehat{\theta }}_1-{\theta }_1)\to N(0,V_{11}=M^{-1}{SM}^{-1^{\prime }})$$

where

1. M = diag(K₁, …, K_T),

2. $S={\mathrm{\sum }}_{i=1}^N{C}_i{R_i}^{-1}{F}_i{F}_i^{\prime }{{R_i}^{\prime }}^{-1}{C}_i$ where C_i and R_i are block diagonal matrices with elements C_it and R_it, t = 1, …, T, and

3. F_i is a vector with elements

   $$F_{it}=\left(\begin{array}{c}{y}_{it}-{\mu }_{it}({\theta }_{1t})\\ y_{it}-{\sigma }_{it}({\theta }_{1t})\end{array}\right),t=1,\dots ,T.$$

A consistent estimator of the asymptotic covariance of θ̂₁ that is robust to misspecification of the covariance of y_i and w_i is obtained by replacing θ₁ by θ̂₁, and the covariance of y_i and w_i by its empirical estimate $F_i{F}_i^{\prime }$.

Appendix B

Consider a first-order Taylor series approximation of U₂(θ₂) about θ₂ = θ̂₂ which results in

$$\surd N({\widehat{\theta }}_2-{\theta }_2)\approx -\frac{1}{\surd N}{\left(\sum _{i=1}^N{\widehat{E}}_i^{\prime }{{\widehat{R}}_i^{\ast }}^{-1}{\widehat{E}}_i\right)}_{{\mid }_{{\theta }_2={\widehat{\theta }}_2}}^{-1}{U}_2({\theta }_2)$$

where U₂(θ₂) is defined in Section 3.2. Then,

$$\surd N({\widehat{\theta }}_2-{\theta }_2)\to N(0,V_{22}={M^{\ast }}^{-1}{S}^{\ast }{M^{\ast }}^{-1\prime })$$

where

1. $M^{\ast }={({\mathrm{\sum }}_{i=1}^N{\widehat{E}}_i^{\prime }{{\widehat{R}}_i^{\ast }}^{-1}{\widehat{E}}_i)}^{-1}$,

2. $S={\mathrm{\sum }}_{i=1}^N{E}_i{R_i^{\ast }}^{-1}{F}_i^{\ast }{F}_i^{\ast \prime }{R_i^{\ast \prime }}^{-1}{E}_i$ and

3. $$F_i^{\ast }=\left(\begin{array}{c}{z}_i-{\mu }_i^{\ast }({\theta }_2)\\ w_i^{\ast }-{\sigma }_i^{\ast }({\theta }_2)\end{array}\right).$$

A consistent estimator of the asymptotic covariance of θ̂₂ that is robust to misspecification of the covariance of z_i and $w_i^{\ast }$ is obtained by replacing θ₂ by θ̂₂, and the covariance of z_i and $w_i^{\ast }$ by its empirical estimate $F_i^{\ast }{F}_i^{\ast \prime }$.

Appendix C

The variance of the estimate of θ₃ is constructed by using two first-order Taylor series approximations of U₃(θ₃, θ̂₁, θ̂₂)/√N about

1. θ̂₁= θ₁ and θ̂₂= θ₂, and

2. θ₃ = θ̂₃

given by

$$\frac{U_3({\theta }_3,{\widehat{\theta }}_1,{\widehat{\theta }}_2)}{\surd N}+\frac{\partial U_3({\theta }_3,{\widehat{\theta }}_1,{\widehat{\theta }}_2)/\partial {\widehat{\theta }}_1{\mid }_{{\widehat{\theta }}_1={\theta }_1,{\widehat{\theta }}_2={\theta }_2}}{N}{L}_1+\frac{\partial U_3({\theta }_3,{\widehat{\theta }}_1,{\widehat{\theta }}_2)/\partial {\widehat{\theta }}_2{\mid }_{{\widehat{\theta }}_1={\theta }_1,{\widehat{\theta }}_2={\theta }_2}}{N}{L}_2,$$ (8)

$$\frac{\partial U_3({\theta }_3,{\widehat{\theta }}_1,{\widehat{\theta }}_2)/\partial {\theta }_3{\mid }_{{\theta }_3={\widehat{\theta }}_3}}{N}\surd N({\widehat{\theta }}_3-{\theta }_3)$$ (9)

where L₁ = √N(θ̂₁ − θ₁) and L₂ = √N(θ̂₂ − θ₂). On the basis of the approximation in model (1) and applying the weak law of large numbers, we have that U₃(θ₃, θ̂₁, θ̂₂)/√N is asymptotically normally distributed with mean 0 and variance equal to

$$V=V_{33}+{GV}_{11}{G}^{\prime }+{HV}_{22}{H}^{\prime }+2Gcov(L_1,L_3)+2Gcov(L_1,L_2)H+2cov(L_3,L_2)H^{\prime }$$

where

$$\begin{array}{c}G=\sum _{i=1}^N\frac{E[\partial U_{3i}({\theta }_3,{\theta }_1,{\theta }_2)/\partial {\theta }_1^{\prime }]}{N},\\ H=\sum _{i=1}^N\frac{E[\partial U_{3i}({\theta }_3,{\theta }_1,{\theta }_2)/\partial {\theta }_2^{\prime }]}{N},\\ V_{33}=\sum _{i=1}^N\frac{E[U_{3i}({\theta }_3,{\theta }_1,{\theta }_2)U_{3i}{({\theta }_3,{\theta }_2,{\theta }_1)}^{\prime }]}{N}\end{array}$$

and U_3i(θ₃, θ₁, θ₂) is the contribution of individual i to the estimating equation for θ₃. The covariances of L₁, L₂ and L₃ with each other are based on their first-order Taylor series approximations so that

$$\begin{array}{l}cov(L_1,L_3)={\left\{\sum _{i=1}^N\frac{E[\partial U_{1i}({\theta }_1)/\partial {\theta }_1]}{N}\right\}}^{-1}\sum _{i=1}^{N}E[U_{1i}({\theta }_1)U_{3i}{({\theta }_3,{\theta }_1,{\theta }_2)}^{\prime }],\\ cov(L_3,L_2)=\sum _{i=1}^{N}E[U_{3i}({\theta }_3,{\theta }_1,{\theta }_2)U_{2i}{({\theta }_2)}^{\prime }]{\left\{\sum _{i=1}^N\frac{E[\partial U_{2i}({\theta }_2)/\partial {\theta }_2]}{N}\right\}}^{-1}\end{array}$$

where U_1i is the contribution of individual i to the estimating equation for θ₁ and U_2i is the contribution of individual i to the estimating equation for θ₂. Because the estimating equations for θ₁ and θ₂ are orthogonal, cov(L₁, L₂) = 0. Rearranging equation (2), √N(θ̂₃ − θ₃) is asymptotically normally distributed with mean 0 and variance equal to $V_{33}^{\ast }=A^{-1}{V}_{33}{A^{-1}}^{\prime }$

where A = −E[∂U₃(θ₃, θ₁, θ₂)/∂θ₃]/N. If we replace the expected by the observed information and θ₃, θ₁ and θ₂ by their √N-consistent estimates we obtain a consistent estimate of $V_{33}^{\ast }$ after adjusting for the estimation of θ₁ and θ₂.