Reconstructing population exposures to environmental chemicals from biomarkers: Challenges and opportunities

Abstract

A conceptual/computational framework for exposure reconstruction from biomarker data combined with auxiliary exposure-related data is presented, evaluated with example applications, and examined in the context of future needs and opportunities. This framework employs physiologically based toxicokinetic (PBTK) modeling in conjunction with numerical “inversion” techniques. To quantify the value of different types of exposure data “accompanying” biomarker data, a study was conducted focusing on reconstructing exposures to chlorpyrifos, from measurements of its metabolite levels in urine. The study employed biomarker data as well as supporting exposure-related information from the National Human Exposure Assessment Survey (NHEXAS), Maryland, while the MENTOR-3P system (Modeling ENvironment for TOtal Risk with Physiologically based Pharmacokinetic modeling for Populations) was used for PBTK modeling. Recently proposed, simple numerical reconstruction methods were applied in this study, in conjunction with PBTK models. Two types of reconstructions were studied using (a) just the available biomarker and supporting exposure data and (b) synthetic data developed via augmenting available observations. Reconstruction using only available data resulted in a wide range of variation in estimated exposures. Reconstruction using synthetic data facilitated evaluation of numerical inversion methods and characterization of the value of additional information, such as study-specific data that can be collected in conjunction with the biomarker data. Although the NHEXAS data set provides a significant amount of supporting exposure-related information, especially when compared to national studies such as the National Health and Nutrition Examination Survey (NHANES), this information is still not adequate for detailed reconstruction of exposures under several conditions, as demonstrated here. The analysis presented here provides a starting point for introducing improved designs for future biomonitoring studies, from the perspective of exposure reconstruction; identifies specific limitations in existing exposure reconstruction methods that can be applied to population biomarker data; and suggests potential approaches for addressing exposure reconstruction from such data.

Introduction

It has been recently acknowledged that the “ability to generate new biomonitoring data often exceeds the ability to evaluate whether and how a chemical measured in an individual or population may cause a health risk or to evaluate its sources and pathways for exposure” (NRC, 2006). It is in fact now widely recognized that these biomonitoring data can be used not only as early indicators of a biological effect for assessing health risks but that, under certain circumstances, they may also be used to identify contributors to exposures, thus allowing for rational health risk management planning. However, the use of biomonitoring data to date has been limited to assessing the effectiveness of pollution controls for relatively straightforward exposure scenarios, such as those involving inert and persistent chemicals with relatively long biological half-lives and well-defined sources and pathways of exposure. For example, a well-known successful use of biomonitoring data has been in relation to lead exposures (Pirkle et al., 1995; Needham et al., 2007), which are easily attributable to relatively few source–route combinations (e.g., ingestion and inhalation.) For complex exposure scenarios, involving multiple routes of entry into the body the use of biomonitoring data in designing and evaluating exposure reduction strategies may require significant amounts of supporting or complementary exposure information (e.g. variability in source activities and in background concentrations, and multimedia dynamics of the chemicals). Table 1 lists examples of available population biomarker databases and the extent of supporting exposure-related information they provide in each case, from the perspective of interpreting biomonitoring data. It is clear that the available complementary or supporting exposure information is quite variable. Thus, source or contact inferences would be difficult in most cases. Selected data sets from the National Human Exposure Assessment Survey (NHEXAS) and National Health and Nutrition Examination Survey (NHANES) studies are in fact examined in demonstration applications within the present analysis.

Table 1.

Biomarker databases for population exposure reconstruction. Databases that include complementary exposure data can be used to evaluate exposure reconstruction approaches.

	Organophosphate Pesticides			Pyrethroid Pesticides			Metals
Program/study	Chlorpyrifos	Diazinon	Malathion	Permethrins	Cyfluthrin	Cypermethrin	As	Cd	Cr	Hg/MeHg	Pb	Location; number of subjects
CHAMACOS (1999–2000) (Castorina et al., 2003)	bd	bd	bd									CA; 600 pregnant women
CTEPP (2000–2001) (Wilson et al., 2004)	ac	ac		ad	ad							NC, OH; 257 children (1.5–5 yrs)
MNCPES (1997) (Quackenboss et al., 2000)	ac	ac	ac									MN; 102 children (3–12 years)
NHANES-III (1988–94) (Hill et al., 1995)	c							c			bc	US; 1000 adults (20–59 yrs)
NHANES (1999–2000) (CDC, 2005)	cd	cd	cd					c		c	bc	US; 9,282 subjects (all ages)
NHANES 2001–2002 (CDC, 2005)	cd	cd	cd	c	cd	c		c		c	bc	US; 10,477 subjects (all ages)
NHANES 2003–2004	cd	cd	cd	c	cd	c	c	c		c	bc	US; 9,643 subjects (all ages)
NHEXAS-AZ (1995–97) (Robertson et al., 1999)	ac	ac	ac				ac	ac	ac		ac	AZ; 179 subjects (all ages)
NHEXAS-MD (1995–96)	ac		ac				ac	ac	ac		ac	MD; 80 subjects (above 10 yrs)
NHEXAS-V (1995–1997) (Whitmore et al., 1999)							ac	ac	ac	c	ac	EPA Region V; 251 subj. (all ages)

^ameasurements of multimedia concentrations (indoor, outdoor, and personal air; drinking water; duplicate diet; dust; and soil);

^bpartial measurements of environmental concentrations (e.g. outdoor air concentrations, pesticide use, etc.);

^cspecific metabolites;

^dnonspecific metabolites.

Assessing biological doses and their effects using exposure measurements constitutes a “forward” mode of analysis, while estimating or reconstructing exposures from biomarkers requires an “inverse” mode of analysis. The forward analysis can be accomplished through the direct application of environmental (microenvironmental) exposure, toxicokinetic and toxicodynamic models, either empirical or mechanistic (i.e. physically and biologically based), whereas the reconstruction analysis requires application of numerical model inversion techniques applied in conjunction with the toxicokinetic and/or toxicodynamic models, and with available complementary data for interpretation. The magnitude of error and uncertainty introduced by simplifying assumptions in the “forward” modeling process can be substantial, in relation to the objectives of particular applications (see e.g. Isukapalli et al., 2008).

A computational framework that can address both the forward and inverse modeling aspects of exposures to multiple chemicals is essential for enhanced interpretation of biomarkers and their sources and routes of exposure. Physiologically based toxicokinetic (PBTK) and biologically based dose–response (BBDR) models in conjunction with numerical inversion techniques and optimization methods should form major components of such a framework, as shown in Figure 1. The figure shows how available supporting or complementary exposure data can be used to develop prior estimates of exposures for individuals and populations. These estimates can then be improved by using PBTK modeling and inversion techniques along with corresponding biomarker data. The approach presented in Figure 1 involves straightforward application of inversion via brute-force sampling, with significant computational requirements and consequent needs for performance improvements, as discussed in the following sections. A prerequisite for implementing such a computational framework is a systematic evaluation of available methods and computational tools that can be used to “merge” existing forward models and biomarker data for exposure reconstruction. This will allow for the identification and recommendation of appropriate methods and development needs for different types of biomarker and exposure timescales and chemical characteristics. This study examines these tools and provides demonstration applications. Eventually, a comprehensive exposure reconstruction framework should address reconstructions involving aggregate (i.e. from multiple exposure routes) and cumulative (i.e. for multiple chemicals) exposures, and provide user-friendly computational tools for use by the exposure/risk assessment and management communities.

Figure 1.

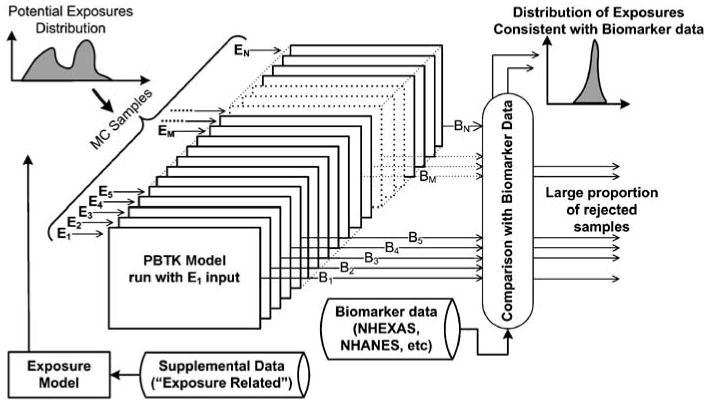
A simplified schematic of a computational framework for exposure reconstruction showing major components and processes. Available exposure-related data can provide “prior estimates” of exposures, which in turn can be used in conjunction with biomarkers and PBTK modeling to obtain improved estimates of exposures and doses.

Background

Various computational techniques have been employed in the literature for numerical model inversion in general and for exposure reconstruction from biomarkers in particular. Georgopoulos et al. (1994) used the maximum likelihood estimation (MLE) method in conjunction with PBTK modeling for reconstructing short-term (30 min) exposure to chloroform, and to resolve the total dose between two routes of uptake (i.e. inhalation and dermal absorption). Furthermore, Roy and Georgopoulos (1998) used the combined MLE–PBTK modeling approach with synthetic biomarker data and demonstrated that it is mathematically feasible to reconstruct longer term exposures to VOCs. The synthetic data were comprised of outputs from a PBTK model with known parameters and were used to represent exhaled breath concentration data while additional random “noise” was added to represent measurement error, with the rationale being that it is easier to evaluate the inversion method with synthetic data, because all the exposure and PBTK model parameters are already known. Rigas et al. (2001) used urinary biomarker data and the inverse solution of a simple, two-compartment toxicokinetic (PK) model for chlorpyrifos (CPF) to estimate the magnitude and timing of doses, based on the Minnesota Children's Pesticide Exposure Study (MNCPES) (Quackenboss et al., 2000; see Table 1). Some recent studies on population-level exposure reconstruction focused on data sampled from distributions of biomonitoring studies such as NHANES using direct deconvolution of biomarker distributions assuming a linear response (Tan et al., 2006), or a brute-force Monte Carlo sampling approach (Sohn et al., 2004; Tan et al., 2007). However, simplifying assumptions such as linearity are known to produce erroneous exposure characterizations in the forward mode of analysis and therefore they should be considered with great caution in the inverse mode of analysis. An “interim” step in interpreting biomonitoring data is provided by biomonitoring equivalents, which employ forward modeling to determine exposure levels that correspond to the reference doses of the chemicals of concern (Hays et al., 2007). This indeed can provide useful insight in relating biomarker levels to regulatory requirements under the simplifying assumption of chronic, steady exposures. However, as Hays et al. (2007) also implicitly recognize, these techniques are not applicable to reconstructing real-world exposure scenarios, because such scenarios typically involve non-steady, transient exposures with variable frequencies, durations, and magnitudes.

Computational inversion can be formulated as a problem where the objective is to identify the specific input combinations or distributions that best explain the observed outputs while minimizing an “error metric.” In the case of exposure and dose models, the inputs involve spatial and temporal information on microenvironmental media concentrations of contaminants as well as corresponding information on human activities that result in intakes of these contaminants, whereas the outputs are observed biomarkers, and the error metric can be defined in terms of population variation, random error, etc.

Computational inversion/optimization techniques can be broadly classified into “deterministic” and “stochastic” (see e.g. Moles et al., 2003). These methods in general utilize a systematic exploration of the input space to identify the “global” minimum of the error metric and the corresponding values of inputs. Stochastic methods randomly sample the input space and do not necessarily guarantee convergence to the best solution to the inversion problem. Deterministic methods can, in principle, guarantee the convergence to a global minimum, though not necessarily in a finite time, but they often lead to a prohibitive “exponential” increase in computational resources as the number of inputs increases. In contrast, stochastic methods can provide a reasonable solution with relative efficiency; this solution is in practice often the best available for modest computation times (Moles et al., 2003). Furthermore, these methods are usually quite simple to implement and use, especially for “black box” models. Many specialized monographs are available covering a wide range of both deterministic and stochastic inversion techniques (Vogel, 2002; Aster et al., 2005; Tarantola, 2005). A selective list of representative deterministic and stochastic inversion methods, that can be used for exposure reconstruction, is presented in Tables 2 and 3.

Table 2.

Representative “deterministic” inversion methods, example environmental and biological applications and software.

Method/technique	Example application area	Example available software
Regression methods
Non-linear least squares (Dennis et al., 1981; Yano et al., 1989; Kaltenbach and Vistelle, 1994; Bender and Heinemann, 1995)	Estimation of PK parameters (Kaltenbach and Vistelle, 1994; Muzic and Christian, 2006)	MOT (Mathworks, 2006c); NIST (NIST, 2006); Boomer (Bourne, 1989); MultiFilt (Yano et al., 1989)
Singular value decomposition (SVD) (Paige, 1986; Anderson, 1999)	Spectrum reconstruction from dose (Armbruster et al., 2004); pathway analysis of gene expression (Tomfohr et al., 2005)	Numerical recipes (NR) (Press, 2002); Netlib-TOMS (ACM, 2006)
Extreme (LeBlanc et al., 2006)/logistic Projection pursuit (PPR) (Friedman and Stuetzle, 1981; Lingjaerde and Liestol, 1998)	Survival analysis (LeBlanc et al., 2006) Phenol toxicity mechanism (Ren and Kim, 2003)	Matlab toolboxes R (RFSC, 2006); XTAL (Cherkassky and Gehring, 1996)
Multivariate adaptive (MARS) (Friedman and Roosen, 1995); Bayesian MARS (Denison et al., 1998; Holmes and Denison, 2003; Nott et al., 2005)	Phenol toxicity mechanisms (Ren and Kim, 2003); GI absorption (Deconinck et al., 2005); subgroup disease–risk relationships (York et al., 2006)	Netlib-Misc (Netlib, 2006)
Gradient methods
Automatic differentiation (Hovland et al., 2005; Ringrose and Forth, 2005)	Uncertainty in PBPKs (Isukapalli et al., 2000)	ADIFOR (Bischof et al., 1996); ADIC (Bischof et al., 1997); MAD (Kharche and Forth, 2006)
Steepest descent (Marquardt, 1963; Conway et al., 1970)	Inverse treatment planning (Hristov et al., 2002)	NR (Press, 2002); TOMS (ACM, 2006)
Likelihood methods
Maximum (MLE); restricted MLE (Elzo, 1994; Jamshidian, 2004); approximate likelihood (Albertini et al., 2006); NONMEM (Overgaard et al., 2005; Tornoe et al., 2005)	Short- and long-term exposure reconstruction using PBPK for chloroform (Georgopoulos et al., 1994; Roy et al., 1996)	Matlab (MathWorks Inc., 2006); NR (Press, 2002); TOMS (ACM, 2006); NONMEM (Beal, 2002)

Table 3.

Representative “stochastic” inversion methods and statistical pattern methods, along with example environmental and biological applications and software.

Method/technique	Example application area	Example available software
Evolutionary methods
Tabu search (Glover, 1994; Glover et al., 1995; Youssef et al., 2001) Genetic algorithms (Kazarlis et al., 2001; Youssef et al., 2001; Coello and Pulido, 2005)	Cancer classification (Tahir et al., 2005); protein structure prediction (Blazewicz et al., 2005); ordering microarray data (Moscato et al., 2006); PBPK parameter estimation (Holmes et al., 2000); outlier detection (Vankeerberghen et al., 1995)	OpenTS (Abramov et al., 2005); OptQuest (OptTek Systems, 2006); Matlab toolbox (Mathworks, 2006a); GEATbx (Pohlheim, 2005)
Artificial neural networks (Gobburu and Chen, 1996; Chow et al., 1997; Hashemi and Young, 2003; Winkler, 2004)	PK parameters (Opara et al., 1999); QSPK relationships (Nestorov et al., 1999); ADME prediction (Balakin et al., 2005); in silico CYP 450 estimation (Yap et al., 2006)	Matlab NN toolbox (Mathworks, 2006b); NeuroSolutions (NeuroDimension, 2006)
Bayesian methods
Bayesian MCMC (Metropolis–Hastings–Gibbs) (Gelman, 2004)	Reconstruction of intakes with PBPK (Gosselin et al., 2006); population pharmacokinetics (Dokoumetzidis and Aarons, 2005)	MCSIM (Bois, 2000); PKBUGS (Lunn et al., 2002); Matlab toolboxes
Bayesian model averaging	Benchmark dose estimation for As (Morales et al., 2006)	Matlab toolboxes
Surrogate/FEOM modeling
SRSM (Isukapalli et al., 1998)+MCMC	Groundwater contamination (Balakrishnan et al., 2003)	MENTOR (Georgopoulos and Lioy, 2006)
Regularization (Morozov and Stessin, 1993; Engl et al., 1996; Tenorio, 2001; Farquharson and Oldenburg, 2004)	Mass spectrometry (Mohammad-Djafari et al., 2002); reconstruction of membrane potentials (Messnarz et al., 2004)	RegTools (Hansen, 1994); ORBIT (Johansen and Foss, 1998); NLCSmoothReg (Wendlandt et al., 2005)
Deconvolution	PBPK reconstruction (Sparacino et al., 2002); estimation of metabolism (Yamashita et al., 1995); transport parameters (Nair and Gratzl, 2005)	WinStoDec (Sparacino et al., 2002)
Maximum entropy (Clarke and Janday, 1989; Gamboa and Gassiat, 1997)	Biomagnetic inversion (Clarke and Janday, 1989); absorption kinetic rates (Ablonczy et al., 2003)	BMElib (Christakos et al., 2001; Serre, 2006)
Statistical pattern recognition methods
CART (Breiman, 1984; Hastie et al., 2001; Venables and Ripley, 1999); MART (Friedman and Meulman, 2003); C4.5 method (Quinlan, 1993; Treenet (Jitnah and Nicholson, 1997; Flouris and Duffy, 2006)	Biomarkers–demographics correlation (Balakrishnan et al., 2003); oral absorption (Bai et al., 2004); biomarkers from mass spectrometric data (Liu and Li, 2005); cervical neoplasia (Friedman and Meulman, 2003)	S-Plus (Venables and Ripley, 1999); Matlab (Mathworks, 2006d); DTREG (Sherrod, 2006); ENTOOL (Merkwirth, 2006); R (CRAN, 2006); Treenet/MART (Salford Systems, 2006)

Deterministic Inversion

The exposure reconstruction problem can be formulated as a global minimization problem that involves finding possible exposures x by minimizing a “cost function” J, based on observed biomarker data b′(t_i) at each time point t_i (a total of N_meas measurements), and a forward model for estimating biomarkers: b = m(x,t_i). Additionally, constraints can be included in the form of

• bounds on possible exposures (x^L≤x≤x^U),

• equality constraints on the model (f(x,b,t) = 0), and

• inequality constraints (g(x,b,t≤0).

Typical examples of J include

$$J=\sum _{i=1}^{N_{\text{means}}}{(\mathbf{b}\prime (t_i)-\mathbf{m}(\mathbf{x},t_i))}^T(\mathbf{b}\prime (t_i)-m(\mathbf{x},t_i))$$ (1)

(least square minimization)

and

$$J=-\mathbf{L}(\mathbf{m},\mathbf{x},\mathbf{b}\prime )=-\prod _{i=1}^{N_{\text{meas}}}{f}_{\mathbf{x}}(\mathbf{b}\prime (t_i)\mid \mathbf{x},\mathbf{m}(\mathbf{x},t_i))$$ (2)

(maximum likelihood estimation)

where the likelihood L is expressed as a product of likelihood of the data at each point through function f_x, which depends on the assumptions regarding the distribution of “errors” (i.e. the differences between observations and model estimates).

Stochastic Inversion/Bayesian Approach

A general probabilistic framework for inverse problem solution is provided by the Bayesian approach, which is based on Bayes' Theorem

$$p(\mathbf{x}\mid \mathbf{b})=\frac{p(\mathbf{b}\mid \mathbf{x})p(\mathbf{x})}{\int p(\mathbf{b}\mid \mathbf{x})p(\mathbf{x})\text{d}\mathbf{x}}$$ (3)

where x and b are defined as in the previous subsection and the probability densities p(.) are interpreted as representing available knowledge/information rather than as representing intrinsic properties of the variables.

If prior knowledge information on exposure attributes is represented by p_prior(x), and the theoretical (“model”) knowledge of the relation between x and b is represented by p_theory(x∣b′),

$$\begin{array}{l}{p}_{\text{theory}}(\mathbf{b}\mid \mathbf{x})=p_{\mathrm{model}}(\mathbf{b}\mid \mathbf{x})\\ p(\mathbf{x},\mathbf{b})=p_{\mathrm{theory}}(\mathbf{b}\mid \mathbf{x})p_{\mathrm{prior}}(\mathbf{x})\end{array}$$ (4)

For a specific set of biomarker measurements b′, the posterior (inferred) distribution of exposure attributes will be p_inferred(x∣b′) and

$$p_{\mathbf{\text{prior}}}(\mathbf{x},\mathbf{b}\prime )=p_{\text{inferred}}(\mathbf{x}\mid \mathbf{b}\prime )p_{\text{prior}}(\mathbf{b}\prime );\text{for fixed}\mathbf{b}\prime$$ (5)

Overall,

$$p_{\text{prior}}(\mathbf{x})=\int p_{\text{prior}}(\mathbf{x},\mathbf{b})\text{d}\mathbf{b}=p_{\text{prior}}(\mathbf{x})\int p_{\text{theory}}(\mathbf{b}\mid \mathbf{x})\text{d}\mathbf{b}$$ (6)

Therefore,

$$\underset{\text{Posterior distribution}}{\underbrace{p_{\text{inferred}}(\mathbf{x}\mid \mathbf{b}\prime )}}=\frac{p_{\text{theory}}(\mathbf{b}\prime \mid \mathbf{x})p_{\text{prior}}(\mathbf{x})}{\int p_{\text{theory}}(\mathbf{b}\prime \mid \mathbf{x})p_{\text{prior}}(\mathbf{x})\text{d}\mathbf{x}}$$ (7)

If p_model(m,x) denotes the probability density of the “true” model output being m for inputs x,

$$p_{\text{theory}}(\mathbf{b}\mid \mathbf{x})=p_{\text{error}}(\mathbf{b}\mid \mathbf{m})p_{\text{model}}(\mathbf{m}\mid \mathbf{x})\text{d}\mathbf{m}$$ (8)

where p_error(b∣m) is the probability of measuring b when the true value is m; i.e. it is the distribution of “measurement error” and not “model error.” Therefore

$$p(\mathbf{x},\mathbf{b})=\frac{p(\mathbf{x})\int p_{\text{error}}(\mathbf{b}\mid \mathbf{m})p_{\text{model}}(\mathbf{m}\mid \mathbf{x})\text{d}\mathbf{m}}{\int p(\mathbf{x})\int p_{\text{error}}(\mathbf{b}\mid \mathbf{m})p_{\text{model}}(\mathbf{m}\mid \mathbf{x})\text{d}\mathbf{m}\text{d}\mathbf{x}}$$ (9)

• For a “deterministic” model, p_model(m∣x) is a delta function centered on m(x).

• For a “deterministic” model with “model error” (or uncertainty), p_model(m∣x) represents the distribution of uncertainty in m(x).

• For a “stochastic” model, p_model(m∣x) represents the distribution of predictions that can be obtained for a specific (fixed) set of inputs x.

Methods for Exposure Reconstruction from Population Biomonitoring Studies

There are several Bayesian and non-Bayesian approaches for inversion of biomarker data for obtaining exposures and PBTK model parameters. Georgopoulos et al. (2008) discuss the relative advantages of Bayesian and non-Bayesian approaches for population parameter estimation using PBTK models and biomarker data. Some of the recently proposed methods for exposure reconstruction are discussed next.

Exposure Conversion Factor Approach

The exposure conversion factor (ECF) method, proposed by Tan et al. (2006), assumes that the relationship between biomarker and dose can be approximated by a linear function for exposure reconstruction purposes. This approach involves three steps: (1) generating samples for forward model runs from distributions of possible exposure, physiological, and biochemical parameters, (2) running the forward model using a set of input samples from these distributions, and (3) inverting the distribution of output (i.e. simulated biomarker levels) to obtain an “ECF.” Using the ECF and the distribution of observed biomarkers, the possible exposures for that particular biomarker distribution can then be estimated through a straightforward convolution (Tan et al., 2006).

In a typical application of this simple method, the PBTK model can be run using a unit dose or concentration value, and various samples from the possible distributions of parameters such as activities, physiological parameters, biochemical parameters, biomarker sample times, etc., to generate a set of biomarker levels. These levels then provide the distribution of biomarkers for a unit exposure metric, which can be inverted to obtain an ECF in units of the exposure metric divided by biomarker level units. The ECF can then be multiplied by the values of available biomonitoring data (e.g. from biomarker databases such as NHEXAS or NHANES) to produce an estimate of dose distributions for the corresponding population. This convolution is performed by multiplying samples from the biomarker distribution with samples from the ECF distribution. The aggregate samples then provide the distribution of reconstructed exposures. Though this method is conceptually simple and straightforward to use, as it involves direct generation of samples of the corresponding statistics from these samples, the ECF can be highly sensitive to the assumptions of the prior distributions. Furthermore, the assumption of linearity can sometimes produce unreasonably large tails in the distribution of reconstructed exposure metrics, especially when exposures occur infrequently, and the sampling time relative to the last exposure is unknown. The section titled Impact of Biochemical Properties and Sampling Characteristics on Reconstruction in the following provides further details on the impact of exposure and sampling times on the outcomes of exposure reconstruction.

Discretized Bayesian Approach

This approach, which was used, for example, by Sohn et al. (2004) and Tan et al. (2007), employs a simplified, discrete Bayesian scheme to estimate the posterior probability of exposures from the biomarker data and prior exposure distributions. Posterior probabilities of exposures/doses are computed using biomarker data and forward modeling results at regularly spaced samples (“bins”) or random samples, spanning the range described by prior probabilities. The forward model results are then divided into a set of regular intervals or bins, and the posterior probability is estimated from the samples that agree most closely with the biomarker data (e.g. those that belong to the same bin) (Tan et al., 2007). Like the ECF method, it requires strong informative prior probability distributions of exposure-related activities to produce a realistic reconstruction. Furthermore, as the number of dimensions increases, the corresponding sampling space becomes “vastly empty” (Tarantola, 2005), in the sense that the number of points required to adequately sample from this space increases exponentially as the number of dimensions increases. This approach, therefore, necessitates trade-offs with respect to sample size, the resolution of the sampling, and the accuracy of the results.

Bayesian Markov Chain Monte Carlo

The Markov Chain Monte Carlo (MCMC) approach provides a means for sampling from the “posterior probability distribution” without having to sample the entire range of the prior distribution. The method requires defining the prior distributions, available biomarker data, and a likelihood function defining the likelihood of the data given a set of forward model parameters; then the MCMC approach involves marching in the sample space based on acceptance criteria that consider the likelihood of the data given the parameters. MCMC techniques (Gilks et al., 1998; Gamerman and Lopes, 2006) have been coupled with PBTK models for forward modeling of population health risk assessment (Covington et al., 2007), and inverse modeling for parameter estimation (Bois, 2000; Yokley et al., 2006; Bois et al., 2007; Yang et al., 2008). In practice, with adequate data and prior information on exposure metrics and population toxicokinetic parameters, it is possible to directly apply MCMC techniques to estimate individual and population exposure parameters. For example, Allen et al. (2007) applied the MCMC technique to the reconstruction of long-term exposures to MeHg using steady-state approximations, basing this approach on the fact that the half-life of MeHg is very large, and assuming that time-varying exposures were unimportant. However, for many real-life exposure scenarios, the time-varying exposures cannot be assumed to be negligible, and, in general, would have to be explicitly incorporated into the reconstruction process, thus leading to intensive data requirements (including multiple biomarker measurements for each individual during each measurement period) and non-steady-state models. When sufficient information is not available for estimating individual parameters, the estimation of population parameters using MCMC and PBTK models becomes impractical, as there would be limited data for the hierarchical modeling needed to estimate these parameters. This is typically the case, as for example with studies such as NHEXAS and NHANES, which include relatively few biomarker measurements (often just one measurement) for different individual–chemical combinations.

Even though the estimation of population parameters without the estimation of the parameters for individuals may appear feasible using the MCMC approach, it is in fact impractical. The estimation of population parameters, when one distribution is assumed to be representative of “all” individuals, quite often results in an artificial fit of a single parameter and thus results in a large “error term.” These errors will be substantial when there are large inter-individual variabilities with regard to exposure patterns.

Major Factors Influencing Exposure Reconstruction

Several major factors influence the feasibility and efficacy of exposure reconstruction from biomarkers. The specificity and the sensitivity of the biomarker with respect to the exposure metric of interest (e.g. concentration of the agent of concern) are two of the most important such factors. Lack of specificity can lead to the problem of identifiability, whereas the lack of sensitivity may result in large uncertainties in the reconstruction results. Biochemical properties of absorption, distribution, metabolism, and elimination (ADME) impact the types of exposures that can be estimated from the biomarker data (Hays et al., 2007). Variability in ADME characteristics also results in a significant variation in the biological half-lives of different groups of environmental pollutants, such as volatile organics, organophosphate pesticides, and toxic metals. Some of these properties are also highly variable for a given contaminant within a population, reflecting inter-individual physiological and biochemical variabilities, which may result in significant uncertainties in the use of biomarkers for exposure reconstruction.

Various exposure characteristics, such as the frequency, magnitude, and duration of exposures, provide supplemental information that is valuable and often necessary for reconstructing exposures from biomarkers. Because biologically relevant exposures can occur through multiple pathways and mechanisms (e.g. direct exposure to a metabolite versus exposure to the parent compound), supplemental exposure information such as data on mouthing behavior, activities, macro- and micro-environmental source locations and personal concentration levels monitoring, also provide realistic constraints on possible exposures from specific pathways. Additionally, the adequacy of the biomarker data can be characterized in terms of the specificity of the available supplementary information such as the time of collection of biomarkers in relation to other relevant parameters (e.g. amount of urine collected, total urinary void volume, last time of urination, etc.). Other characteristics of the data sets, such as the detection limits of contaminants of concern, can also significantly impact the reconstruction process. However, while all of the above should be considered, in practice, two other factors impact the inversion process significantly: the applicability and adequacy of the forward model (e.g. toxicokinetic/toxicodynamic model) and the efficacy of the computational inversion technique employed for the reconstruction.

Impact of Biochemical Properties and Sampling Characteristics on Reconstruction

The “residence time” or “age” of an “observed” (i.e. measured) biomarker molecule can be defined as the time elapsed since it entered (or was generated in) the organ or organism studied. The observed biomarker levels (molecules of either a chemical or its metabolites, potentially involving multiple exposures across multiple timescales) represent an “integration” over molecules of different “ages,” dependent on the time each molecule entered or was generated in the system, and on elimination kinetics. As an example, for chemicals and metabolites with relatively short half-lives, only the exposure history of the previous days or weeks can be estimated. For those with longer half-lives, larger timescales of exposure history have to be considered, and the influence of confounding sources creates additional uncertainties.

In general, the age or residence time distribution can be defined as $R(t)=b(t)/{\int }_0^{\infty }b(t)\text{d}t$, where b(t) is the concentration of a chemical in the system (i.e. a single biomarker concentration in blood, tissue, or urine) at time t. Furthermore, R(t)dt represents the fraction of the molecules that have spent a time between t and t + dt in the system. The corresponding cumulative distribution function, F(t) is the fraction of the molecules that have spent time t or less in the system, and is given by $F(t)={\int }_0^{t}R(t)\text{d}t$.

In the simplest case of a steady, continuous exposure, and of toxicokinetics that can be described adequately by a single-compartment PK model, b(t) = x′e^−kt, R(t) = ke^−kt, and F(t) = 1−e^−kt, where x′ is a known exposure concentration, and the elimination rate k is related to half-life t_1/2 as k = log₂/t_1/2. These equations for age distribution also represent the output versus time function from a bolus input.

In the case of discrete repeated (“cyclical”) exposures of time period Δt, assuming that the biomarkers are collected at a time λΔt after the end of the last exposure (0<λ≤1), and that all exposure concentrations are equal to x′, the relative contribution of exposures that occurred at different times can be expressed in terms of “cycles” of exposure, as follows:

$$\begin{array}{lll}b(n)\hfill & =\hfill & \sum _{i=0}^{n}x\prime e^{-k(i+\gamma )\Delta t}\text{and}\hfill \\ F(n)\hfill & =\hfill & \sum _{i=0}^n{e}^{-ik\Delta t}/\sum _{j=0}^{\infty }{e}^{-\mathit{\text{jk}}\Delta t}\hfill \end{array}$$ (10)

Figure 2 shows, as a function of different half-lives, the relative contributions of different timescales of continuous, steady exposures to observed chemical biomarker levels in a single-compartment system. These calculations are an extension of the approach presented in NRC (2006). Figure 3 shows the relative contributions of prior exposures (discrete bolus doses) to observed chemical biomarker levels, as a function of different sampling times and exposure frequencies. When Δt is significantly larger than the exposure timescale of interest (β), λΔt becomes an important variable. When λΔt≤β, the biomarker captures exposures occurring within the past time period β. Otherwise, exposures occurring within β are not captured. It must be noted that the relative contributions are independent of the time of sampling within a “cycle,” whereas the relationship between the magnitude of the observed biomarker concentration and the exposure concentration is highly dependent on the time of sampling within a cycle.

Figure 2.

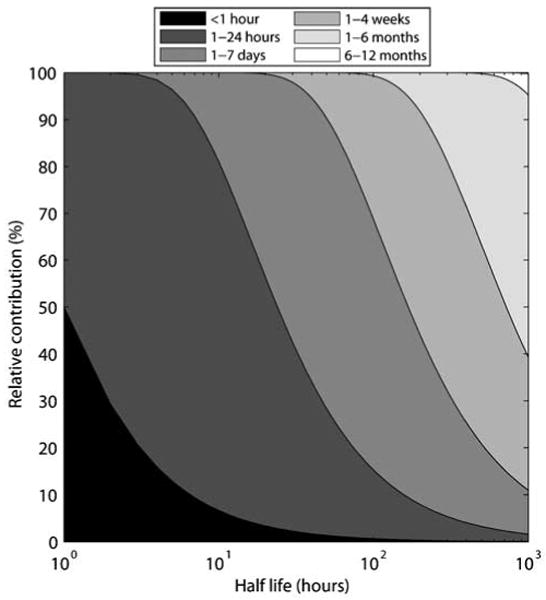
Impact of half-life on the relative contributions of different timescales of exposures to observed chemical biomarker levels. The example shown above is based on a one-compartment PK model (linear decay); the biomarker represents the level of chemical in the compartment.

Figure 3.

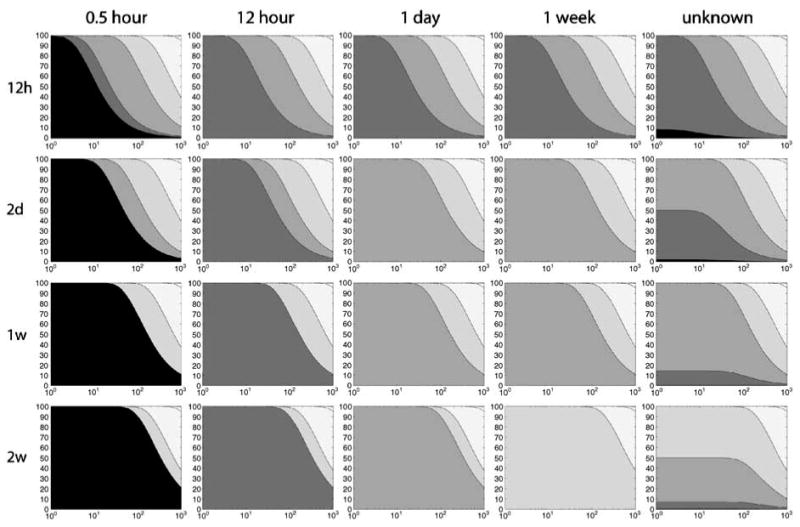
Contribution of prior exposures to observed biomarker levels as a function of intake frequency, sampling time, and biochemical properties. The rows represent the time period of exposure (e.g. every 12 h, every 2 days, etc), the columns represent the time of sampling after the last exposure. For cases when sampling time is unknown, the mean values of the contributions are shown, assuming a uniformly random sampling time. The legend for the scales of gray is the same as in Figure 2.

As an example, consider a scenario where exposures occur once per month (Δt = 1 month), and the biomarker contribution due to exposure within the past 1 day (β = 1 day) is known. If a sample is taken 12 h after the last exposure (λΔt = 12 h), the biomarker will incorporate contributions that originate from exposure occurring within the past 24 h. If the sample is taken 30 h after the last exposure, there is zero mass contribution due to exposures within the past 24 h. Figure 3 illustrates the effect of λΔt and Δt on the half-life and exposure timescale relationship previously shown for the steady-state case in Figure 2.

As the length of time between biomarker sampling and the last exposure increases, the contribution to biomarker levels from recent exposures diminishes. As the frequency of cyclic exposure decreases, relative contributions become more sensitive to biomarker sampling time. If exposures occur with high frequency, the system approaches a pseudo steady state and relative contributions are less sensitive to sampling time. In general, the residence time analysis approach can be readily expanded to include realistic PBTK models instead of half-life parameterizations, and estimates such as those shown in Figure 3, can be generated for different types of exposure and sampling profiles for different classes of compounds. Screening level estimates from the residence time analysis can provide help in identifying of the types of reconstruction that are feasible and realistic for a given chemical, biomonitoring characteristics, and possible exposure profiles.

A Simple Toxicokinetic Model for CPF Exposure

The case studies used for evaluation of reconstruction approaches in the following sections utilize a simple toxicokinetic model for CPF exposures. This model, formulated for demonstration purposes, is adapted from a two-compartment PK model for CPF and 3,5,6-trichloro-2-pyridinol (TCPy) used by Rigas et al. (2001). The rapid transformation of CPF to TCPy, and the fact that currently available CPF PBTK models (Timchalk et al., 2002a, b) describe TCPy using one-compartment kinetics, provide the justification for employing this assumption in this simple demonstration. This simple toxicokinetic model can be described by the following equations:

$$\begin{array}{l}\frac{\text{d}{C}_{\text{a}}}{\text{d}t}=-k_{\text{a}}{C}_{\text{a}}\\ \frac{\text{d}{C}_{\text{b}}}{\text{d}t}=k_{\text{a}}{C}_{\text{a}}-k_{\text{e}}{C}_{\text{b}}\\ \frac{\text{d}{U}_{\text{TCP}}}{\text{d}t}=k_{\text{e}}{C}_{\text{b}}{V}_{\text{d}}\\ C_{\text{a}}=C_{\text{a}}(t_0)+\frac{SRF{D}_{\text{CPF}}}{V_{\text{d}}}\left(\frac{M_{\text{TCP}}}{M_{\text{CPF}}}\right)\end{array}$$ (11)

where M_TCP is the molecular weight of TCPy; M_CPF, molecular weight of CPF; D_CPF, bolus dose of CPF (μg; the dose here refers to the total amount instead of being scaled by the bodyweight); C_a, concentration of TCPy in absorption reservoir (μg/l); C_a(t_o), concentration of TCPy in absorption reservoir before bolus event at time t_o (μg/l); C_b, concentration of TCPy in body (μg/l); F, absorption factor for ingested dose; R, stoichiometric ratio of CPF to TCPy conversion; S, selectivity (which refers to the amount on molar basis of the absorbed material that can be collected as metabolite of interest; Rigas et al., 2001); V_d, volume of distribution (L); k_e, elimination rate constant (1/h); and k_a, absorption rate constant (1/h).

Since the focus of the case studies is on method evaluation and on highlighting data gaps, the demonstration case studies employ significant simplifications. For example, the entire absorbed CPF is assumed to be directly converted to TCPy, and variability in fractional absorption is neglected; thus, the reconstruction focuses only on the absorbed amount of CPF. These simplifications do not significantly affect the evaluation process here. In fact, more detailed PBTK models, which incorporate additional information about bioavailability, can be used directly for exposure reconstruction employing the approaches evaluated here; however, the approach adopted here aims to help the reader focus on the reconstruction process and methodology rather than on the details of comprehensive PBTK modeling that can be employed in the reconstruction process.

Case study 1: CPF dose reconstruction from available NHEXAS-MD data

The NHEXAS Maryland (NHEXAS-MD) data set is longitudinal, and contains multiple biomarker and environmental measurements for households over a period of time. With respect to CPF, the available biomarker data are urinary TCPy measurements corresponding to the first void of the day. These biomarkers represent statistically weighted probability samples, with each biomarker associated with a statistical weight. For the purposes of the evaluation of reconstruction methodologies, these weights are assumed to be equal for simplification purposes, and only the adult population (over 18 years of age) was modeled. The concentrations of CPF in food, air (at home), dust, etc., are also available in the NHEXAS-MD dataset. The corresponding TCPy concentrations in food, however, were not measured. The food intake can be estimated through the 4-day duplicate plate, but the actual amount of food consumed was not readily available. The urinary void volume, the time of earlier urination, and the last food intake time, are also not available, thus introducing significant uncertainties into the process of exposure reconstruction.

Two exposure scenarios are examined here:

1. Steady-state, continuous exposure, which neglects potential issues in temporal variability in both exposure timing and biomarker sampling (referred to in the following as scenario 1).

2. Time-varying dose and biomarker collection, assuming “reasonable” distributions for the frequency of intake and for the timing of the biomarker collection. An analysis of three separate time-varying exposure scenarios is performed, where each scenario employs different constraints on the exposure profile (referred to in the following as scenarios 2a–c):

   1. Bolus dose frequency is modeled as a complex time–activity profile. An individual may consume zero, one, two, or three meals containing CPF in a given day. An exposure may occur randomly on any, all, or none of the days in a week. More details on this scenario are given in Case Study 2.

   2. Bolus dose frequency is fixed at certain values (i.e. once per day, once per week).

   3. Modifications and combinations of scenarios 2a and 2b. These include scenarios where a background CPF inhalation dose occurs (sampled from summary distributions presented by Pang et al., 2002), and/or dietary exposure to the metabolite TCPy occurs.

The NHEXAS-MD data set contains multiple samples per individual. However, for any given individual, the sampling intervals are separated by at least a month. Since the biomarker half-life is approximately 1 day (ATSDR, 1997), it was assumed that the measurements for the same individual at different sampling intervals are independent, and the correlations between them are assumed to be negligible.

There are significant differences in the types of uncertainties associated with scenarios 1 and 2. For scenario 1, the average daily dose (ADD) is distributed evenly throughout the day, and therefore dynamic uncertainties do not exist. For scenarios 2a–c, the ADD is apportioned differently throughout time: t. The ADD is not known, the apportionment is not known, and the modeled “biomarker collection time” is randomly assigned to a time before the first meal of the day. Since the half-life of TCPy is 1 day, there is the potential that a sampled individual receives a high ADD, which occurs infrequently. Depending on the sampling time, the biomarker concentrations can vary from extremely high to non-detectable levels. The less frequent the exposure, the more likely the biomarker measurement will be a non-detect, regardless of the exposure magnitude. Some simulated individuals may receive a moderate dose once per day, and the biomarker profile approaches the steady-state condition. A more detailed discussion of exposure frequency and ADD in relation to biomonitoring can be found in Hays et al. (2007).

In this case study, uncertainties in PK parameters are assumed to be negligible and so these parameters are set to the mean values derived from an original toxicokinetics study by Nolan et al. (1984). For both the steady-state and time-variant biomarker dose reconstructions, only the total dose absorbed was considered because the absorption fraction and intake amount are coupled, and hence, individually unidentifiable. There is also a factor-of-two difference in the fraction absorbed that has been found across different studies (e.g. Nolan et al., 1984; Timchalk et al., 2002a).

The simple toxicokinetic model is used to predict cumulative amount of TCPy excreted in urine. The biomarker is estimated from the model calculations of cumulative TCPy excreted over a 6- to 10-h period (according to a uniform random distribution), resulting in an average TCPy excretion rate. NHEXAS biomarkers are assumed to represent morning void samples, with overnight bladder TCPy accumulation occurring over approximately 8 h. Converting model output (in mass TCPy/day) to biomarker measurement units (mass TCPy/volume urine, and mass TCPy/mass creatinine) introduces additional uncertainties, since urinary liquid or creatinine excretion rates must be known. The NRC biomonitoring report (NRC, 2006) notes that inter- and intra-individual variation in urinary water and creatinine content can be a source of biomarker misinterpretation (specific discussion on CPF exposure and TCPy biomarkers is also contained in the above report). The following three methods for converting the units are considered here:

• For data from the Minnesota study, Rigas et al. (2001) converted measured urinary TCPy concentrations to urinary TCPy excretion rates. TCPy concentration in urine is multiplied by urine void volume, and divided by the length of time urine accumulated in the bladder (estimated from the Minnesota study questionnaire). However, the NHEXAS-MD study does not provide urine void volume amounts, so this approach is not used here.

• An assumption of a mean daily liquid urine output of 22 ml/kg body weight is used to convert TCPy rates to mass TCPy/volume urine (Wilson et al., 2003; Morgan et al., 2005).

• Age, gender, body weight, and body height relationships are used to estimate creatinine excretion rates (Mage et al., 2004). This converts TCPy rate to mass TCPy/mass creatinine (which is reported in NHEXAS-MD). Advantages of this method over the previous two methods listed above for population exposure assessment purposes have been previously discussed in Barr et al. (2005).

Analysis of the Linked PK/Biomarker Approach Using Forward Modeling

A CPF exposure/dose model for the NHEXAS-MD population was coded based on the approach of Pang et al. (2002) and evaluated for its use as a “prior” estimate of CPF dose. It was found that by using the exposure estimates from Pang et al. (2002) as inputs to the PK model (using both steady-state and time-variant assumptions) the TCPy biomarker levels are significantly under-predicted (Figure 4). This under-prediction is likely to be even more severe when the variability in the CPF absorption, which can be as low as 18% (Timchalk et al., 2002b), is taken into account. This leads to the conclusion that the NHEXAS-MD-derived exposure estimates are inadequate for use as “prior” exposure information in this particular case. This limitation can be attributed to one or more of the following possible reasons:

Figure 4.

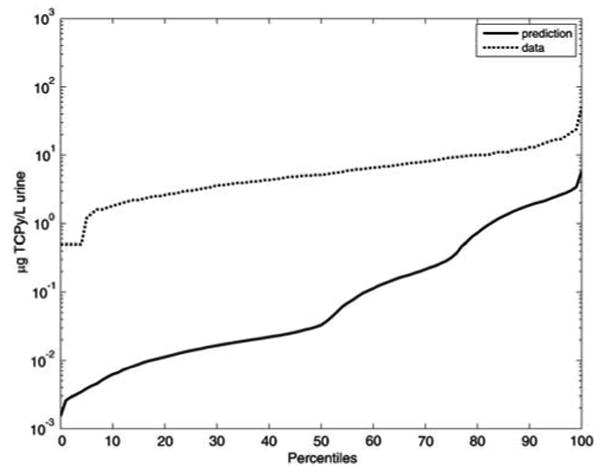
Comparison of urinary TCPy biomarker levels predicted using exposure estimates of Pang et al. (2002) for the NHEXAS-MD population with the toxicokinetic model, and actual NHEXAS-MD biomarker measurements.

• The exposure model is not appropriate, as the available environmental and biomarker measurements correspond to spot samples;

• Food and air concentrations change with time, and more of an exposure history is needed to reduce exposure/dose uncertainty;

• The NHEXAS-MD population also experienced direct TCPy exposure, or exposure to CPF-methyl, a grain fumigant, which metabolizes to TCPy; and

• Uncertainties in both TCPy exposure and in CPF exposure/dose modeling exist.

Previous studies mentioned in the NRC biomarkers report have found that levels of TCPy in multimedia situations are generally comparable to CPF, and TCPy levels in solid food are an order of magnitude higher than CPF (Wilson et al., 2003; Morgan et al., 2005; NRC, 2006). It has also been noted that only a small percentage of dietary CPF exposure correlates with the TCPy levels seen in urine for the NHEXAS-MD data set (MacIntosh et al., 2001; Egeghy et al., 2005), further supporting the strong possibility that neglecting TCPy exposure in dose reconstruction overpredicts CPF exposure (Barr and Angerer, 2006).

In Case Study 1, it was assumed that the CPF exposure is the primary source of the TCPy biomarker. However, given the apparent inconsistency of NHEXAS exposure and biomarkers data, an additional biomarker inversion was performed to estimate population CPF exposure that considers direct TCPy exposures (see Case study 2). This inversion also used the estimates of NHEXAS-MD population CPF exposures developed by Pang et al. (2002). The PK model was modified to allow for both CPF and TCPy exposure contributions to urinary TCPy biomarkers, and was used in subsequent exposure reconstruction. However, without CPF exposure data, the decoupling of TCPy and CPF exposure contributions to biomarker levels is not possible.

Computational Inversion Techniques used for Evaluation

Steady-State Approximation

Assuming intake and excretion rates on a molar basis are equal, the following equations relate TCPy biomarker and CPF dose:

$$D_{\text{CPF}}=C_{\text{TCP}-\text{adj}}{E}_{\text{cre}}\text{(}{M}_{\text{CPF}}/M_{\text{TCP}})$$ (12)

$$D_{\text{CPF}}=C_{\text{TCP}-\text{liq}}{E}_{\text{liq}}\text{(}{M}_{\text{CPF}}/M_{\text{TCP}})$$ (13)

where D_CPF in the bolus dose of CPF (μg); E_liq in the urinary excretion rate (l/day); E_cre in the creatinine excretion rate (g/day); C_TCP-liq in the urinary TCPy biomarker (μg/l urine); C_TCP-adj in the urinary TCPy biomarker adjusted for creatinine concentration (μg/g creatinine); M_TCP in the molecular weight of TCPy; and M_CPF in the molecular weight of CPF.

Equation (12) is applicable when TCPy urinary biomarker measurements are specified in terms of mass TCPy/mass creatinine, and Eq. (13) is applicable when biomarker measurements are specified in terms of mass TCPy/volume urine. An estimation of either liquid urinary production or urinary creatinine elimination is needed (as this is a source of potential biomarker misinterpretation stated earlier (NRC, 2006)). Both approaches have been previously used in the context of CPF exposure: Mage et al. (2004) used creatinine-adjusted biomarkers to estimate CPF exposures of the NHANES population; and Morgan et al. (2005) used absolute liquid concentrations and excretion rates in assessing CPF and TCPy exposures.

Time-Varying Approaches

When incorporating temporal uncertainties in dose and biomarker collection, an algebraic solution is usually not possible. Dose and sample time uncertainties, and uncertainties in PK model parameters affecting dynamics and TCPy half-life need to be accounted for. The discretized Bayesian approach and the ECF approach were used in this study, as they have been developed relatively recently and have been applied for population dose reconstruction of short half-life chemicals (Tan et al., 2006, 2007). The Bayesian approach employed here used 40,000 model simulations, while the ECF approach used 5000 simulations. These TCPy biomarker data from NHEXAS-MD represent statistically weighted probability samples, with each biomarker associated with a statistical weight. In the case studies presented here, these weights are assumed to be equal; however, it should be pointed out that the incorporation of any statistical weights into the reconstruction process is relatively straightforward because, in the reconstruction process, random samples generated for inversion can use the weighted data instead of unweighted sampling from the available biomarker data.

Results for Case Study 1

Figure 5 compares CPF exposures estimated via a steady-state assumption, using either liquid urinary biomarkers, or creatinine-adjusted urinary biomarkers. Both methods appear to agree, with creatinine-adjusted predictions of daily CPF doses being slightly lower than the absolute liquid concentration predictions. At the tails of the distribution, however, there is a difference by about a factor of 5 in the lower tail of the distribution and about a factor of 2.5 in the higher tail, with the urinary concentration-based method predicting systematically higher intakes.

Figure 5.

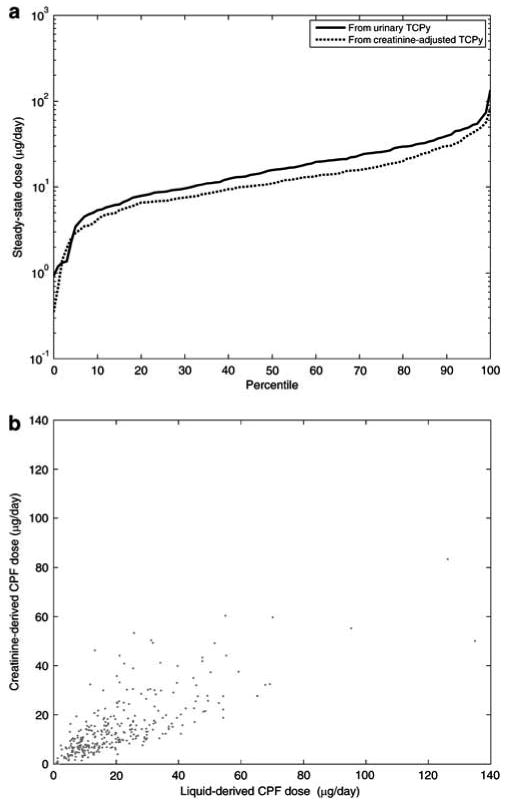
Comparison of predicted steady-state doses using creatinine-adjusted urinary TCPy biomarkers, and using liquid urinary concentration TCPy biomarkers: (a) cumulative distributions, and (b) scatter plot.

The inversion results appear to be sensitive to the dose profile assumption, as shown in Figures 6 and 7. The results also indicate that apportioning “ADD” randomly to once a week resulted in greater uncertainty (evident in the upper tails), when compared to constraining doses to once per day. Incorporating the more complex time–activity assumption (scenario 2a) resulted in estimated doses similar to the once-per-day case (results not shown). This may be due to the fact that both scenarios approach steady-state conditions, due to the high frequency of exposures. As the exposures become less frequent, there are more cases of low simulated biomarker levels implying a high exposure, since the biomarkers from any magnitude exposure have likely reduced to low levels by the time a hypothetical sample is taken. As previously noted, inversion becomes more sensitive to uncertainties in biomarker sampling time for less frequent exposures.

Figure 6.

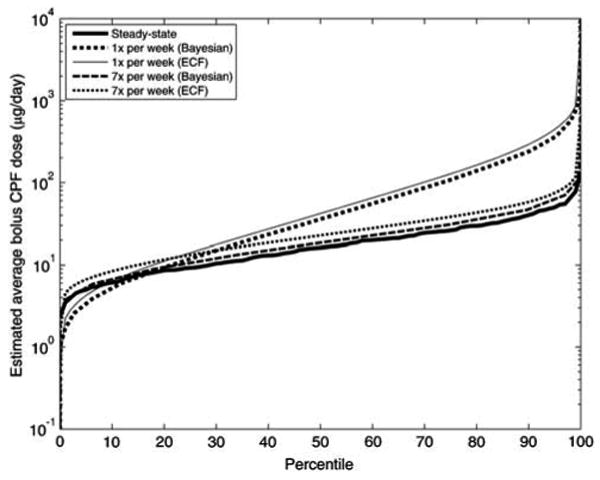
Cumulative distribution functions of dietary CPF uptakes for the NHEXAS-MD population estimated by the ECF and Bayesian methods, using three different dose assumptions. Results only show population for which the biomarkers were above the detection limit (which comprised 95% of the samples).

Figure 7.

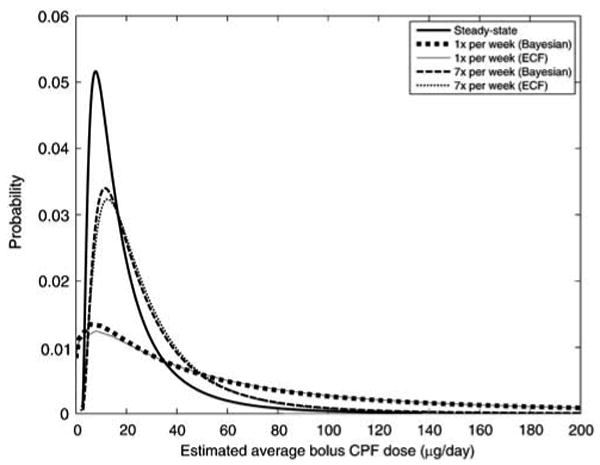
Probability density functions of dietary CPF uptakes for the NHEXAS-MD population estimated by the ECF and Bayesian methods, corresponding to results in Figure 6.

Additionally, there was only a slight difference between the results from the ECF and the discretized Bayesian methods. Because of the uncertainties involved, none of these three methods considered can be conclusively termed superior when examining a short half-life biomarker, such as TCPy. As shown in Figure 6, for higher frequency exposures (once a day or seven per week), all the three methods considered showed similar results. For the lower frequency exposures (once a week) case, the steady-state approximation is not valid, while there was only a slight difference between the results from the ECF and the discretized Bayesian methods. Theoretically, the simple Bayesian method should produce more realistic results than the ECF method, since it does not involve the assumption of a linear relationship of biomarker to dose. The Bayesian method can be further improved by including better prior information of population doses or activities. However, this was not possible for the NHEXAS-MD data used here, due to the apparent non-specificity of the TCPy biomarker to low-dose CPF exposure, and the difficulty in adequately characterizing exposure time profile and biomarker collection times.

Value of Additional Information

From the preceding, it is clear that more detailed information on exposure parameters reduces uncertainty in back-calculating doses from biomarker information. Many “data-intensive” methods to collect more data are relatively impractical for large-scale studies (e.g. urine collection through an entire day, blood collection, and longitudinal dietary and multimedia concentration measure ments). While more detailed dietary recall and exposure information has previously been shown to aid in exposure assessment and biomarker interpretation for chemicals such as CPF (Wilson et al., 2003; Meeker et al., 2005; Morgan et al., 2005), it is likely that the short biomarker half-life prohibits practical reconstruction of exposures via toxicokinetic modeling inversion for large population studies. However, sub-population studies that collect detailed measurements can produce complementary data needed to reduce uncertainties in exposure reconstruction.

For example, in the case of a long half-life chemical such as methylmercury, it has been illustrated that by merging fish consumption surveys, dietary intake models, and national fish methylmercury data, reasonable agreement between biomarkers and data can be reached (Carrington and Bolger, 2002).

Case study 2: CPF dose reconstruction from “synthetically augmented” NHEXAS-MD data

This case study presents an evaluation of inversion methods using “augmented” biomarker data, so as to assess the uncertainties associated with gaps in actual data. The data set used is thus a “synthetically augmented” version of the NHEXAS-MD database that was developed by filling in missing information via randomly sampling distributions derived from estimates available in the literature (e.g. Pang et al., 2002). This data set, referred here also as “synthetic data,” was then used to evaluate approaches for estimating population parameters. The advantage of this approach is that since all the relevant parameter values were known for the new data set, the performance of various inversion methods could be directly assessed. Table 4 presents the distributions used for filling in missing information and to synthetically augment the biomarker data.

Table 4.

Ranges of supporting exposure parameters used in augmenting the NHEXAS-MD data.

Parameter (and distribution)	Values/ranges	Description
Meal time ranges (U)	7–9 (breakfast); 11–14 (lunch); 17.5–20.5 (dinner)	Hours of the day a meal may be consumed
Sample time ranges (U)	6.5–8	Hour of the day a sample is collected
Prior urination time (U)	21–24	Hour of previous day the bladder is emptied, before biomarker collection
Meal probabilities (C)	0.3 (breakfast); 0.3 (lunch); 0.4 (dinner)	Probability of CPF being in a given meal
Background CPF concentrations (CDF)	From Pang et al. (2002)	Percentiles of background CPF concentrations
Daily ingested CPF (dietary) (CDF)	From Pang et al. (2002)	Percentiles of daily CPF intake dose
Ratio of TCPy to CPF in diet (CDF)	10:1 assumed for simplicity	Amount of TCPy ingested (synthetic)
Biomarker	PBTK model output	PBTK model run with corresponding sampled inputs

It was assumed there are only two routes of CPF exposure: (a) continuous background inhalation exposure, and (b) bolus doses due to dietary ingestion. It was also assumed that dietary CPF exposure was directly correlated with dietary TCPy exposure, based on studies showing that TCPy may exist in food at levels higher than CPF (Wilson et al., 2003; Morgan et al., 2005; NRC, 2006). For simplicity, a 10:1 ratio of TCPy:CPF dietary exposure was initially assumed for the generation of synthetic data.

While the synthetic dietary and background exposures were based on the summary exposure distributions from Pang et al. (2002), they were not reassigned to specific individuals as the corresponding data on intake amounts are not available. For the purpose of this case study, the impact of this assignment is not significant, as the aim is simply to obtain augmented data that are similar to NHEXAS-MD, but with the ability to specify all exposure-relevant parameters for each individual. Only the total doses absorbed are considered because the absorption fraction and intake amount are coupled, and, hence, individually unidentifiable.

The assignment of synthetic data for each of the 339 entries in the NHEXAS-MD database was performed through the following procedure:

• Individuals were randomly drawn from the NHEXAS-MD population (relevant physiological parameters were age, gender, body weight, and body height).

• Parameters, such as daily liquid urination rate, daily creatinine elimination rate, and inhalation rate, were calculated based on physiological parameter distributions for populations from available sources such as NHANES, the data of the International Commission on Radiological Protection (ICRP — ICRP, 2003), and the Physiological Parameters for PBPK Modeling (P3M –– Lifeline Group, 2004) database/model.

• An average daily background CPF dose, average daily dietary CPF dose, and average daily TCPy dose (10 times the CPF dose) were drawn randomly from distributions available in Pang et al. (2002), and randomly assigned to individuals of the population.

• A week-long exposure profile was generated, randomly assigning bolus doses to three meals per day. Each day was a separate random assignment of both meal times, and distribution of CPF dose among the three meals (consumption of CPF during one, two, or three meals was possible, with uneven distribution). The problem was constrained so that the total bolus weekly dose was consistent with the individual's assigned ADD.

• The week-long exposure profile was used as an input to the CPF/TCPy PK model, and repeated until a quasi-steady state was reached (a little over a month).

• A biomarker collection day was randomly chosen within the quasi-steady-state region. A biomarker collection time was simulated to occur some time in the morning before the first meal of the day.

• The biomarker simulated was the total amount of TCPy which had accumulated in the bladder since the previous urinary excretion time (dependent on the sample time and prior urination time). This is assumed to be the total urinary void, even though a residual volume of urine remains from the previous void that mixes in with the next quantity of urine that the kidney sends to the bladder.

Results for Case Study 2

Different inversion approaches were applied to the “synthetically augmented” data, with varying degrees of augmentation being introduced. It was assumed that the population-level exposure parameters are known to the same degree as the initial biomarker generation (i.e. the inversion method utilized the same probability distributions for meal times and sample times for the population). The physiological parameters were drawn from the adult NHANES population. The inversion was carried out employing different assumptions: (a) assuming no TCPy exposure; (b) assuming a 10:1 TCPy/CPF bolus dose exposure ratio (consistent with the approach used in the generation scenario), (c) assuming no background CPF exposure, and (d) assuming increased randomness/uncertainty in PK parameters (i.e. PK parameters and meal time parameters). As in case study 1, the Bayesian approach used 40,000 model simulations, while the ECF used 5000 simulations. Neglecting background CPF exposure, or increasing PK parameter or exposure uncertainty resulted in only minor differences in predicted doses (not shown). This is likely due to an overall high frequency of bolus doses, and a quasi-steady state is reached in biomarker measurement.

Analyzing the synthetic biomarker data with different constraints on bolus dose affected the results in a manner similar to Case Study 1. Constraining doses to once per day gave results nearly identical to the steady-state and “base-case” assumptions, and constraining doses to once per week gave a wider distribution (results are not shown).

As shown in Figures 8 and 9, the ECF and the simplified Bayesian techniques do not adequately reconstruct the exposures, despite using the same sampling time assumptions. This limitation arises from the fact that these methods, as used currently, cannot utilize the correlations between the exposure and supporting biomarker data at the “actual” individual level. Instead, in the current usage of these methods, information on the exposure–biomarker relationship for specific individuals is “lumped” to obtain statistical distributions for the population, thus “losing information” in the process. While population-level probability distributions in exposure, sampling, and TCPy exposure remained the same for both forward and inverse modeling, the inability to match individual-level exposure information prevents a more accurate analysis of the biomarker data. This is evident in Figures 8 and 9 where, despite neglecting or incorporating TCPy exposure, predicted dose levels remain between the levels of apparent and actual CPF doses.

Figure 8.

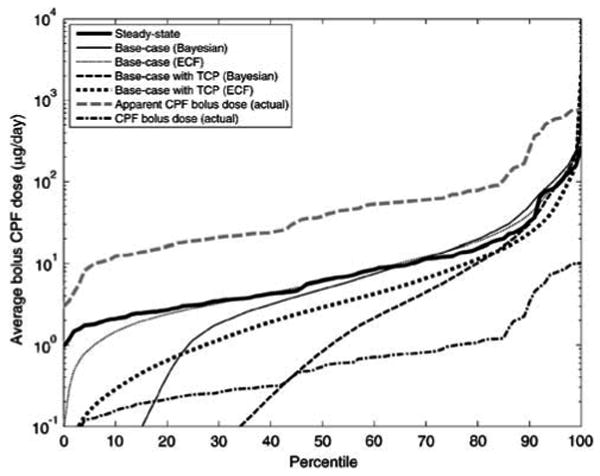
Cumulative distribution functions of dietary CPF uptakes for the synthetic population estimated by the ECF and Bayesian methods, using different dose assumptions. Results only show the synthetic individuals with detectible biomarker levels (which comprised 42% of the samples). “Apparent” CPF dose denotes the sum of the actual CPF and TCPy bolus doses (corrected for molecular weight), which may be misinterpreted as a CPF dose if TCPy exposure is neglected. “Base-case” results denote those results obtained using the random time–activity assumption with three potential CPF doses per day, 0–7 days per week.

Figure 9.

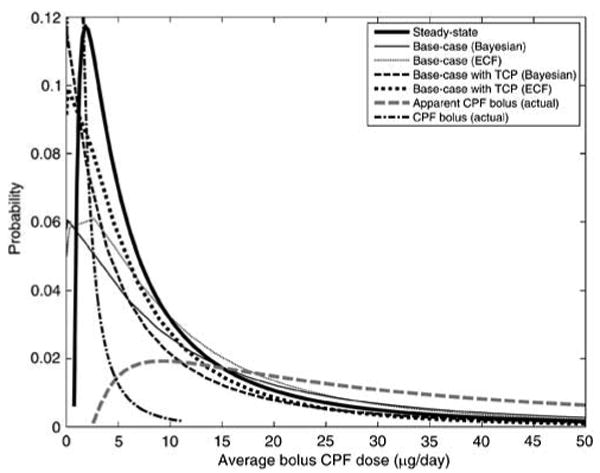
Probability density functions of dietary CPF uptakes for the synthetic population estimated by the ECF and Bayesian methods, using different dose assumptions, corresponding to results in Figure 8.

Discussion

A comparison of general characteristics of the NHEXAS and NHANES databases vis a vis exposure and dose reconstruction is shown in Table 5. Although the NHEXAS data set provides a significant amount of more detailed supporting or complementary exposure-related information, when compared to NHANES, this information is still not adequate for detailed reconstruction of exposures under the various types of conditions considered in the case studies. The analysis presented here provides a starting point for developing improved designs for future biomonitoring studies from the perspective of exposure reconstruction. Furthermore, the analysis here identifies specific limitations in existing exposure reconstruction methods that can be applied to population biomarker data, and suggests potential approaches for addressing exposure reconstruction from population biomarker data based on the supporting or complementary exposure data available. Such information needs to be incorporated in the development of future biomonitoring study designs. For example, simply recording the last urinary void time along with urinary biomarker samples can significantly aid in the interpretation of the urinary biomarker data.

Table 5.

Comparison of NHEXAS and NHANES data sets vis a vis needs for detailed exposure reconstruction. “X” represents available, “–” represents not available, and “o” represents available for some chemicals.

Attribute	NHANES	NHEXAS	Requirement*
Baseline parameters (individual characteristics)
Smoking and tobacco use	X	X	Chemical dependent
Dietary recall	X	X	Required
Pesticide use	X	X	Chemical dependent
Demographic background/occupation	X	X	Dependent on model complexity and biomarker
Recent activity diary	—	X	Dependent on model complexity
Housing characteristics	X	X	Dependent on model complexity
Physiological characteristics (at individual level)
Age	X	X	Required
Gender	X	X	Required
Body weight	X	X	Required
Body height	X	X	Required
Cardiac output	—	—	Required (population distributions)
Urinary excretion rate	—	—	Required for urinary biomarkers
Urinary creatinine excretion rate	—	—	Required
Environmental concentrations
Food residues	—	X	Required
Personal air	o (VOCs)	X	Required
Indoor/outdoor air	—	X	Required
Dust	o (lead)	X	Required
Soil	—	X	Required
Tap water	—	X	Required
Behavioral/health
Diet behavior and nutrition	X	X	Dependent on the chemical of interest
Baseline health condition	X	—	Dependent on the biomarker
Biochemical parameters	—	—	Required (from other studies)
Biomarker data characteristics
Actual sampling time	—	—	For short half-life chemicals
Time of last void	—	—	Required for urinary biomarkers
Time of last meal before void	—	—	Urinary biomarkers
Multiple biomarkers	o	o	Chemical and pathway dependent

One component of the problem of reconstructing exposures from biomarkers can be addressed through the development or use of more sophisticated numerical inversion techniques. The techniques used in the evaluation presented in this study (i.e. the ECF and the discrete Bayesian approach) are not fully capable of utilizing all available biomarker and supporting exposure-related data (e.g. data for specific individuals). For example, when partial individual-level exposure information is available, the data can be potentially used in reconstructing population exposures. However, such data cannot be used in reconstructing exposures at an individual level. This implies that when sparse, individual level exposure data are available, the traditional techniques such as MLE cannot be applied (as the data are too sparse), whereas, on the other hand, methods such as ECF and the discrete Bayesian approaches cannot utilize all the available information. Clearly there is a need to improve inversion approaches for the purpose of characterizing real world exposures. One major goal for a useful exposure reconstruction framework should be the development or identification of methods that can fully utilize “incomplete” exposure-related data in exposure reconstruction.

Two other areas for potential improvement in exposure reconstruction involve reconstruction of route- or pathway-specific exposures (i.e. simultaneous reconstruction/estimation of multiple inputs/parameters), and the ability to provide a gradual convergence process. The simplified approaches evaluated here, ECF and discretized Bayesian, require performing a number of model simulations at a time, and then estimating the exposures. Successive refinement of exposure estimates, therefore, requires running a pre-set number of simulations. Several time-marching techniques such as the Bayesian MCMC can be used to achieve a more gradual iterative process. The methods evaluated here are applicable in their current form to the reconstruction/estimation of a single input/parameter. Furthermore, the discretized Bayesian method requires a large set of simulations at a fixed discretization to assure that all the discretized “bins” contain adequate number of samples for reconstruction. Refinement of resolution, therefore, requires a substantially large number of additional simulations. So, development or use of new methods that utilize a “time-stepping” type of algorithm (e.g. similar to the Bayesian MCMC approach) will clearly aid the exposure reconstruction process.

There is also a need for “optimal” exposure reconstruction using PBTK models, based on the rationale that incorporating optimization approaches in the inverse modeling process can result in faster convergence and more robust solutions. Though typical PBTK/PK models can be run quickly on modern computers (of the order of seconds to tens of seconds per simulation), the computational demands can become challenging when hundreds of thousands of simulations are used in the inverse modeling on desktop computers. Likewise, complex PBTK modeling scenarios (e.g. mixtures of metals or pesticides with large half-lives) may need significantly more computational time for a single simulation. Thus, use of fast equivalent operational models (FEOMs) (e.g. see Li et al., 2002; Balakrishnan et al., 2003; Wang et al., 2005; and Table 3) may be necessary to achieve reasonable computational performance. Figure 10 presents the conceptual framework depicting the steps involved in using optimization techniques in conjunction with inverse modeling for faster convergence that incorporates the use of FEOMs for faster simulation times. The framework shown in Figures 1 and 10 is not limited to exposure reconstruction. It can also be used for estimating distributions of physiological and biochemical PBTK model parameters for individuals and populations that are consistent with available biomarker data (typically study-specific data where exposures are adequately characterized) by combining the data with prior estimates of the parameters. Furthermore, the framework can be used to select appropriate PBTK model structures when alternative formulations are available.

Figure 10.

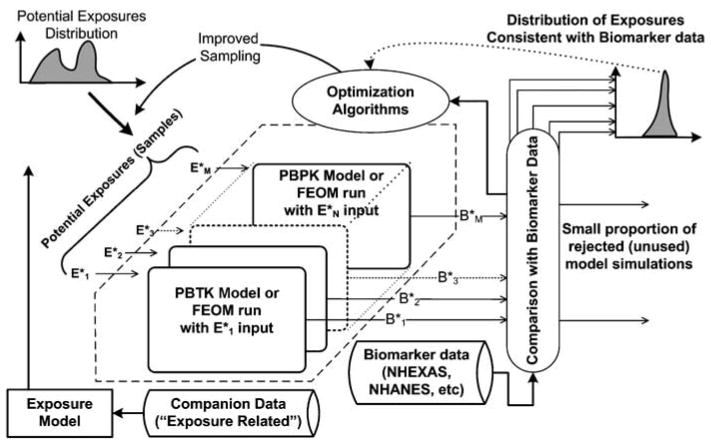
Exposure reconstruction process using optimization-aided approach with the original PBTK model or fast equivalent operational models (FEOMs). The coupling with optimization techniques reduces the number of simulations significantly, and the use of FEOMs reduces the time required for each run.

One of the issues not considered in this analysis was the uncertainty associated with genetic polymorphisms. A genetic polymorphism affecting the metabolism of an intermediate metabolite (CPF-oxon) exists in the population, and has been previously incorporated into a CPF PBTK model (Timchalk et al., 2002b). However, the metabolism of CPF-oxon to TCPy is rapid in relation to overall TCPy formation and elimination. The polymorphism alters toxicodynamics, but does not significantly alter the TCPy biomarker. For chemicals besides CPF, genetic polymorphisms may, however, affect the biomarker level distributions within the populations considered (e.g. arsenic metabolites and the AS3MT polymorphism; Thomas et al., 2007). For short half-life chemicals, the uncertainties in exposure and biomarker assumptions overshadow any effect that polymorphisms may have. For long half-life chemicals, where the biomarker levels are at a quasi-steady state, it may be more practical to analyze the effect of polymorphisms in the context of dose reconstruction. Table 6 lists examples of major underlying biochemical and genetic factors that can contribute to the variability in the metabolism and biological transport of organophosphates, VOCs, and metals in humans and animals. When sufficient biomarker and exposure data are available, numerical inversion exposure methods can also be applied in a hierarchical manner to estimate parameters for populations of interest. The results of such analysis would allow one to elicit differences in the toxicokinetic characteristics due to genetic polymorphisms. However, this is a significantly data-intensive exercise, and the availability of databases from population studies that explicitly incorporate genetic variability is presently very limited. Likewise, when the impacts of specific genetic polymorphisms are known, data on these impacts could provide relevant information for parameterizing the underlying PBTK models to improve the exposure reconstruction process.

Table 6.

Selected information available on underlying mechanisms for inter-individual variability due to genetic factors that affect the transport and transformation of organophosphates, VOCs, and metals in humans and animals.

Species class	Metabolism and transport	Notes
Organophosphates	Liver microsomes, CYP-1A2, 2B6, 2C8, 2C9, 2C19, 2D6, 2E1, 3A4, and 3A5 (Hodgson, 2003)	Organophosphates share P450s for metabolism (Tang et al., 2001; Rose and Hodgson, 2005). Chlorpyrifos-oxonase (PON1) polymorphism is incorporated into chlorpyrifos PBPK model (Timchalk et al., 2002a)
Metals/metalloids	Glutathione, cystein (Quig, 1998; Patrick, 2003), arsenic methyltransferase (arsenic) (Drobna et al., 2004; Meza et al., 2005; Wood et al., 2006; Thomas et al., 2007), metallothionein (Nordberg and Nordberg, 2000), divalent metal transporter-1 (DMT1) (Garrick et al., 2003; Bressler et al., 2004), bone mineral exchange (lead)	Interactions with essential elements (Goyer, 1997; Ballatori, 2002). Arsenic metabolism affected by CYT19, hNP, and hGSTO1-1 genotypes (Drobna et al., 2004; Meza et al., 2005). Cadmium and lead can alter P450 levels and activities (Moore, 2004; Baker et al., 2005). Metal speciation significantly alters toxicity (Yokel et al., 2006)
VOCs	Glutathione, glutathione-S-transferase, CYP-2E1, 2C6, 2C11, 1A1, and 1A2 (Reddy et al., 2005)	GST genotypes effect metabolism and toxicity (Haber et al., 2002; Qu et al., 2003; Dirksen et al., 2004; Silva Mdo et al., 2004; Reddy et al., 2005)

Conclusion

The analyses and discussion presented in this study provide a foundation for developing new and improved approaches for exposure reconstruction. Clearly, there is a strong incentive to implement more biomonitoring tools into the field of exposure science. However, it must be recognized that exposure reconstruction requires not only a sound set of information from monitoring tools but also a well-defined set of modeling tools that can be used within an integrative analytical framework to reduce uncertainties about the origins of exposure. Thus, exposure measurement and modeling professionals must work together to improve the accuracy of reconstruction methods and applications. This is essential for risk assessment and, more importantly, risk management.

The case studies presented here highlighted the gaps in existing biomonitoring studies with respect to supplemental or complementary data needed on exposure, contaminant sources, and human activities. These gaps need to be seriously considered when developing improved designs for future biomonitoring studies if there is a desire to complete realistic exposure modeling simulations. The analyses here identified specific limitations in existing exposure reconstruction methods, which have been applied to population biomarker data, and suggested potential approaches for addressing exposure reconstruction from population biomarker data based on the availability of supporting exposure data. Included are state-of-the-art numerical inversion techniques, customized approaches for reconstruction of route- or pathway-specific exposures, and optimization tools for more effective use of PBTK models.