Cellular Decision-Making and Biological Noise: From Microbes to Mammals

Abstract

Cellular decision-making is the process wherein cells assume different, functionally important and heritable fates without an associated genetic or environmental difference. Such stochastic cell-fate decisions generate non-genetic cellular diversity, which may be critical for metazoan development as well as optimized microbial resource utilization and survival in a fluctuating, frequently stressful environment. Here we review several examples of cellular decision-making from viruses, bacteria, yeast, lower metazoans and mammals, highlighting the role of regulatory network structure and molecular noise. We propose that cellular decision-making is one of at least three key processes underlying development at various scales of biological organization.

INTRODUCTION

If we, humans want to control living cells, two strategies are typically available: modifying their genome or changing the environment in which they reside. Does this mean that cells with identical genomes exposed to the same (possibly time-dependent) environment will necessarily have identical phenotypes? Not at all, for reasons that are still not entirely clear. When cells assume different, functionally important and heritable fates without an associated genetic or environmental difference, cellular decision-making occurs. This includes asymmetric cell divisions as well as spontaneous differentiation of isogenic cells exposed to the same environment. Specific environmental or genetic cues may bias the process causing certain cellular fates to be more frequently chosen (as when tossing identically biased coins). Still, the outcome of cellular decision-making for individual cells is a priori unknown.

A growing number of cell types are being described as capable of decision-making under various circumstances, suggesting that such cellular choices are widespread in all organisms. What are the molecular mechanisms underlying the decisions of various cell types and why are such decisions so common? We hope to suggest answers to these questions here by considering examples at increasing levels of biological complexity, from viruses to mammals. Such a comparative overview may reveal common themes across different domains of life and may offer clues about the significance of cellular decision-making at increasing levels of biological complexity (Maynard Smith and Szathmáry, 1995).

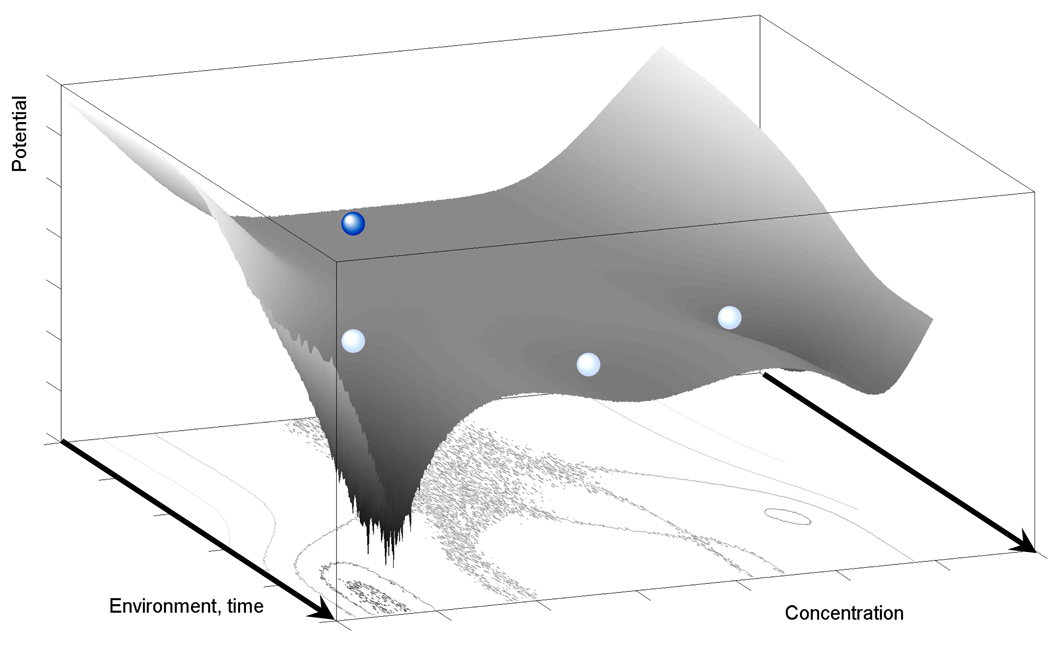
Balls rolling down a slanted landscape with bifurcating valleys (Waddington and Kacser, 1957) have been widely and repeatedly used for several decades as a pictorial illustration of differentiation in multicellular development. Despite its suggestive qualities and repeated use, it has been largely unclear what the valleys and peaks represent in the illustration called “Waddington’s epigenetic landscape”. Nowadays, based on the increasingly quantitative characterization of gene regulation at the single-cell level, it is becoming possible to actually compute Waddington’s landscape (Fig. 1), which can serve as a general illustration of an emerging theoretical framework for cellular decision-making. Assuming for a moment that cellular states can be represented by the concentration of a single molecule, the horizontal axes in Fig. 1 will correspond to the concentration of this molecule and a time-dependent environmental factor, while the vertical dimension corresponds to a potential that governs cellular dynamics. Cells illustrated as spheres will tend to slide down along the concentration axis (pointing from left to right) towards local minima (stable cell states) on this landscape, while they also progress towards the observer in time as a time-dependent environmental factor continuously reshapes the geography of the landscape. Based solely on these considerations, identical cells released from the same point on Waddington’s landscape will follow indistinguishable trajectories, precluding cellular decision-making and differentiation. On the other hand, cells released from distinct, but nearby points can move to different minima as the bifurcating valleys amplify pre-existing positional differences. According to this deterministic interpretation, cellular decision-making and differentiation are completely explained by pre-existing phenotypic differences within isogenic cell populations.

Figure 1. Illustration of cellular decision-making on a molecular landscape.

The landscape (projected onto the concentration of a specific molecule) is reshaped as the environment changes in time. The blue ball represents a cell that under the influence of a changing environment can assume three different fates at the proximal edge of the landscape (white balls at the end of the time course). Even in a constant environment, cells can transition between local minima due to random perturbations to the landscape (intrinsic molecular noise).

Extensive theoretical and experimental work has started to seriously challenge this simplistic deterministic view, as it is becoming clear that at least four critical revisions to Waddington’s picture are needed to properly describe cellular dynamics. First, in reality the landscape is high-dimensional, defined by all intracellular molecular concentrations and multiple relevant environmental factors, and is not a potential in the usual sense. For this reason, cyclic flows (eddies) may exist that move cells around on closed trajectories in concentration space, even if the local geography is completely even (Wang et al., 2008). Second, the landscape is under the constant influence of omnipresent molecular noise (Kaern et al., 2005; Maheshri and O'Shea, 2007; Rao et al., 2002) – stochastic “seismic vibrations” of varying amplitudes and spectra, specific to each location on the landscape (Fig. 1). Third, the landscape is not rigid: cells themselves may reshape the geography due to cell-cell interactions (Waters and Bassler, 2005) and the growth-rate dependence of protein concentrations (Klumpp et al., 2009; Tan et al., 2009). Last, but not the least, growth rate differences between various cellular states reshape the landscape, lowering locations of high fitness and elevating points with reduced fitness as fast growth “overpopulates” certain locations and thereby deepens the landscape. Therefore, Waddington’s landscape must be integrated with a non-genetic version of Sewall Wright’s fitness landscape for genetically identical individuals (Pál and Miklós, 1999).

For the purposes of this review, intrinsic gene expression noise (Blake et al., 2003; Elowitz et al., 2002; Ozbudak et al., 2002) is the most critical component missing from Waddington’s picture. The reason is that even identical cells released from the same location in Fig. 1 will feel the perturbing effects of omnipresent random fluctuations at every point on their way. Random noise will shake them apart, modifying their trajectories and forcing them to cross barriers, diffuse along plateaus and find new local minima. Thus, intrinsic noise enables the phenotypic diversification of completely identical cells exposed to the same environment, and further facilitates cellular decision-making for cells already slightly different when released onto Waddington’s landscape. Moreover, according to the concepts of escape-rate theory (Hänggi et al., 1984; Mehta et al., 2008; Walczak et al., 2005), even cells maintained in a constant environment will have limited residence time around each local minimum (valley) on the landscape, as noise can induce repeated transitions between various cellular states.

Why is cellular decision-making so wide-spread, and when could it confer advantages compared to more deterministic cell-fate scenarios? Considering that noise is unavoidable whenever a few copies of a certain molecule react with others inside small volumes (as is the case of DNA inside cells), non-genetic diversity should be very common in the cellular world. Since noise reduction requires high intracellular concentrations or costly negative feedback loops, it should be more surprising if a cellular process is not noisy than if it is. However, not all phenotypic diversity is functionally important and heritable, and may therefore not classify as cellular decision-making. Still, some cellular processes are noisier than expected based on Poissonian protein synthesis and degradation (Newman et al., 2006), or the resulting cellular states are heritable across several cell cycles (see below), arguing for functionality as the reason for their existence.

The need for stochastic differentiation appears when individual cells are unable to fully adapt to their environment. For example photosynthesis and nitrogen fixation are essential, but mutually exclusive functions in many cell types. To resolve this dilemma, many cyanobacteria dedicate a subpopulation of cells entirely to nitrogen fixation, while the rest of the cells remain photosynthetic (Wolk, 1996), thereby ensuring that the cell population can simultaneously fix carbon and nitrogen. The segregation of somatic cells from germ cells is another classic example where the tasks of locomotion and replication are allocated to different subpopulations (Kirk, 2005). Stochastic differentiation into a growth-arrested, but stress-resistant state (such as a spore) may optimize survival in an uncertain, frequently stressful environment by segregating two essential tasks: growth in the absence of stress, and survival in the presence of stress. Theoretical work has demonstrated the advantage of phenotypic specialization in a cell population when the added benefits from two vital tasks are smaller than the cost for one cell to perform both tasks (Wahl, 2002). Theory has also shown that a population of cells capable of random phenotypic switching can have advantage in a fluctuating environment (Kussell and Leibler, 2005; Thattai and van Oudenaarden, 2004; Wolf et al., 2005). Recent experiments confirmed these predictions, showing that noise can aid survival in severe stress (Blake et al., 2006), can optimize the efficiency of resource uptake during starvation (Çağatay et al., 2009) and can optimize survival in specific fluctuating environments (Acar et al., 2008).

Still, the optimality of stochastic cellular decision-making in a well-defined environment does not guarantee that this behavior can evolve. This is because usually one of the stochastically chosen cellular states has low direct fitness (West et al., 2007), rendering the switching strategy vulnerable to invasion by mutants that never switch into the less fit state, but nevertheless reap the benefits of cohabitation with faithful switchers. This can be prevented by cheater control (West et al., 2006) or by the regular recurrence of detrimental environmental conditions that suppress or eliminate such mutants. Once stochastic switching became an evolutionarily stable strategy, such task-sharing decisions in microbial populations (Bonner, 2003; Veening et al., 2008a) may have formed the bases of multicellular development. Therefore, the need for optimal resource utilization and survival in a changing environment may have been important driving forces behind the evolution and maintenance of cellular decision-making across various domains of life, as suggested by the recent laboratory evolution of bet-hedging (Beaumont et al., 2009).

In the following, we will describe how approaches from molecular biology, nonlinear dynamics and synthetic biology have been used to gain insight into the role of biological noise in cellular decision-making, effectuated by a variety of molecular network structures in organisms of increasing biological complexity, including viruses, bacteria, yeast, lower metazoans and mammals.

VIRUSES

One of the earliest molecular choices made during the evolution of life on Earth may have been the environment-dependent decision to replicate. As the first replicators appeared in the primordial soup (Dawkins, 2006), it may have been advantageous to copy themselves only when conditions were favorable – including an appropriate level of basic building blocks, temperature, acidity, radiation, and preferably no fellow competitors. Moreover, symbiosis between replicators and sensor molecules may have evolved to ensure that replication occurred primarily under the appropriate circumstances.

While we may never be certain about the specific events that took place as life began on our planet, viral infections probably offer some clues (Koonin et al., 2006). Viruses are among the simplest nucleic acid-based replicating entities, which presently can only multiply inside the cells they parasitize, and thus are usually considered non-living. Nevertheless, viral decisions taking place in host cells are in every aspect similar to the bacterial, fungal, and metazoan cellular-fate choices described in the subsequent sections, indicating that cellular decision-making is a misnomer. In fact, “cellular” decisions are taken by more or less autonomous replicating systems that reside inside and manipulate the behavior of carrier cells to maximize the chance of their own propagation (Dawkins, 2006).

A particularly well-studied virus is bacteriophage lambda (Ptashne, 2004), which preys on the bacterium Escherichia coli and has served as a model for virology for more than half a century. The infection cycle of this “coliphage” virus begins with attachment to the bacterial cell wall, followed by the injection of viral DNA into the host, and the initiation of transcript synthesis. From this point, two outcomes are possible. The infection either culminates with replication and virus assembly that causes host lysis, or it concludes with the integration of viral DNA into the bacterial chromosome followed by a prolonged period of lysogeny. This is a typical example of decision-making at the subcellular level – since viruses with identical genomes infecting isogenic cells can either become lytic or lysogenic. Despite the apparent simplicity of the viral genome, the story of lambda phage decision-making is still not completely written, and may hold many surprises.

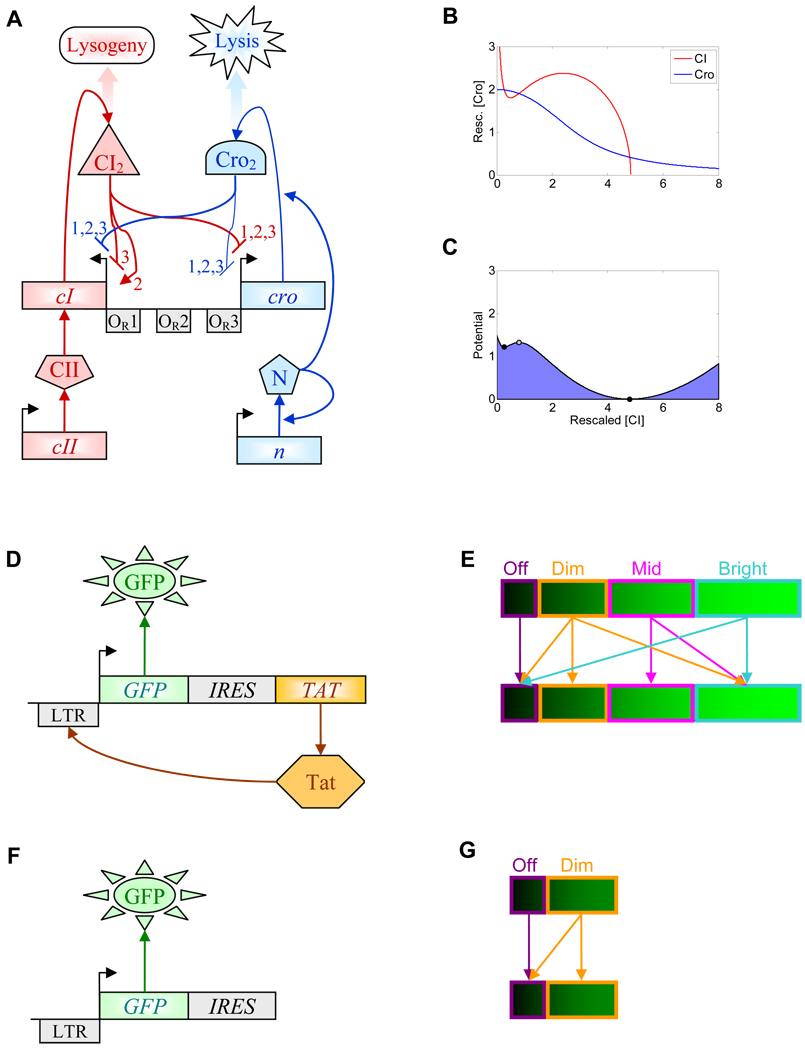
In a series of papers starting in the 1960s (Ptashne, 1967), Mark Ptashne described two repressors (CI and Cro) that proved to be essential for the lysis-lysogeny decision of phage lambda (Fig. 2A). CI and Cro are encoded from two divergent promoters (P_RM and P_R, respectively) and controlled by three shared operator sites (O_R1, O_R2, O_R3) to which either CI or Cro dimers can bind, but with different affinities (O_R1 > O_R2 > O_R3 for CI, and O_R3 > O_R2 > O_R1 for Cro). CI repressor binding to O_R1 has negligible effect on cI transcription, while CI binding to O_R2 activates, and CI binding to O_R3 represses cI transcription. CI binding to any operator site represses cro transcription (Fig. 2A). Cro represses both its own and cI expression, but has a stronger effect on cI. Consequently, CI and Cro mutually repress each other, operating as a natural toggle switch (Gardner et al., 2000) with bistable dynamics (Fig. 2B,C), augmented with autoregulatory loops. This regulatory structure inspired the first mathematical models of the lambda switch (Shea and Ackers, 1985).

Figure 2. Viral decision-making.

(A) Gene regulatory network controlling the lambda phage lysis/lysogeny decision consists of the core repressor pair CI and Cro, and a number of additional regulators, such as N and CII. Cro and CI mutually repress each other, and CI also activates itself from the O_R2 operator site, which results in a structure of nested positive and negative feedback loops. The mutual regulatory effects of CI and Cro are annotated with the number of the O_R site corresponding to each particular interaction.

(B) Nullclines for CI and Cro, based on the model from Weitz and colleagues (Weitz et al., 2008) at a multiplicity of infection MOI=2. Along the CI nullcline there is no change in CI and along the Cro nullcline there is no change in Cro. Neither CI nor Cro changes in the points where the nullclines intersect, which represent steady states. The nullclines intersect in three distinct points, indicating that there are three steady states.

(C) Potential calculated along the Cro nullcline, based on the Fokker-Planck approximation: $\phi =2{\displaystyle \int \frac{f-g}{f+g}}d[\text{CI}]$, where f and g represent CI synthesis and degradation along the Cro nullcline, respectively. Filled circles indicate stable nodes. The gray circle indicates that the middle state is a saddle (unstable along the Cro nullcline, but stable along the CI nullcline). Molecular noise will force the system to transition between the two valleys, especially in the beginning of infection when transcripts and proteins are rare and noise is high.

(D) The autoregulation of the TatA transcription factor from HIV was reconstituted by expressing both GFP and TatA from the LTR promoter, which is naturally activated by TatA. The internal ribosomal entry site (IRES) (Pelletier and Sonenberg, 1988) between the two coding regions ensures that GFP and TatA are co-translated from the same mRNA template.

(E) After being sorted based on their expression level as Off, Dim, Mid and Bright, the cells followed different relaxation patterns: Off remained Off; Dim first trifurcated into Off, Dim and Bright, and then the Dim peak gradually disappeared; Mid relaxed to Bright, and most of Bright remained Bright, with a small subpopulation relaxing to Low.

(F) Control synthetic gene circuit without feedback.

(G) After sorting, the control gene circuit had a much simpler relaxation pattern. Most cells were Low, which remained Low after sorting; while Dim cells mostly remained Dim, with a few of them relaxing to Off. These patterns were interpreted as the hallmarks of excitable dynamics.

While the CI-Cro module is most commonly known as the core of the “lambda switch”, it is only the tip of the iceberg of regulatory interactions involved in the lysis/lysogeny decision (Oppenheim et al., 2005; Ptashne, 2004). Additional mechanisms include DNA loop formation that reinforces Cro repression, regulation of CI expression by CII and CIII, and antitermination of cro transcript synthesis (Fig. 2A). These components were included into a comprehensive stochastic model of the lambda switch (Arkin et al., 1998), which was also the first study to apply the Gillespie algorithm (Gillespie, 1977) for modeling a natural gene network. This seminal work pointed out how stochastic molecular events, originating from the random movement of cellular contents can trigger decisions on a much larger scale, leading to divergent cellular phenotypes.

Stochastic decision-making starts as soon as the first viral gene products appear in the cytoplasm. Cro gets a head start, but CI catches up soon, and both fluctuate due to random transcription-regulatory events. The race continues until the abundance of one of these molecules overwhelms the other, terminally flipping the lambda switch into one of two possible stable states (Cro-on/CI-off or CI-on/Cro-off). In addition to early stochastic events, many environmental factors can bias stochastic decision-making and influence the outcome of infection, including the nutritional state and DNA damage response of the host cell, as well as the number of phages coinfecting the host cell (multiplicity of infection). Therefore, the lambda phage has a stochastic switch capable of hedging bets in a “smart”, environment-dependent manner, investing in both immediate and future expansions.

The importance of intrinsic noise in the lambda switch was recently questioned by a number of research groups. First, it was shown that the host cell volume plays an important role in the lambda decision, with larger cells being more likely to lyse (St-Pierre and Endy, 2008). This pointed to the concentration of infecting phages (rather than their absolute number) as the critical factor in the outcome of infection. Following theoretical predictions by Weitz et al. (Weitz et al., 2008), Zeng and colleagues explained away even more stochasticity (Zeng et al., 2010), showing that the predictability of infection outcome improves if each phage is assumed to cast its own lysis/lysogeny vote, with a unanimous vote being necessary for lysogeny. Importantly, stochasticity was reduced, but not eliminated in this study, suggesting that while further details of the phage-host system may be discovered that make the outcome of infection more predictable, intrinsic stochasticity stemming from the random nature of gene expression will remain an important factor to consider.

So, is noise a general factor in viral choices between lysis and dormancy? This seems to be the case as suggested by recent work on the latency of Human Immunodeficiency Virus (HIV) in CD4+ T-cells (Weinberger et al., 2005). After HIV integrates into the host genome, active HIV infections almost always culminate in lysis. However, the site of HIV integration is highly variable and has a strong effect on the resulting expression dynamics. In rare occasions the integrated virus becomes latent, creating an incurable reservoir that is the main obstacle preventing the elimination of the disease (Han et al., 2007). To determine the mechanism of HIV latency, Weinberger and colleagues focused on the positive autoregulatory loop of the Tat transcription factor as the key component in HIV decision-making (Weinberger et al., 2005). The authors built two synthetic gene constructs, the first of which co-expressed the Green Fluorescent Protein (GFP) with Tat from the Long Terminal Repeat (LTR) promoter (positive feedback, Fig. 2D), while the second consisted of GFP alone transcribed from the same promoter (no feedback, Fig. 2F). After integrating these constructs into the genome, the authors monitored the dynamics of GFP expression over several weeks after sorting CD4+ T cells by their fluorescence as either Off, Dim, Mid or Bright. The relaxation of these sorted cell populations over time (Fig. 2E,G) was interpreted as a signature of excitable dynamics, when cells perturbed from the stable Off state undergo transient excursions into the Bright regime from which they return to the Off state. Remarkably, this behavior depended on the site of HIV integration (since most clonal populations initiated from a Bright cell remained Bright, and all Off clones remained Off). Only a small subset of clones exhibited excitable dynamics, suggesting that excitability requires weak basal LTR promoter activity. These findings were in agreement with a simple mathematical model that captured the experimentally observed behavior of these constructs, and identified pre-integration transcription as the stochastic perturbation that causes the spikes in Tat expression. Further work showed a lack of cooperativity in the response of the LTR promoter to Tat and a rightward shift in the autocorrelation function of GFP expression due to positive feedback (Weinberger et al., 2008), confirming the earlier conclusions that Tat autoregulation does not induce bistability (Weinberger et al., 2005). Instead, futile cycles of acetylation/deacetylation of Tat en route to the LTR promoter act as a dissipative “resistor”, weakening autoregulation and reducing Tat expression to basal levels. The fact that excitable HIV integration clones readily respond to a number of immune response-related external factors suggests that these exceptional integrants may provide the pool of latent HIV infection in resting memory T-cells. When highly active antiretroviral therapy eliminates the productive HIV pool, these latent but excitable viruses wait for their chance to reappear as a new infection.

In conclusion, these studies on lambda phage and HIV suggest that viral choices between replication and latency may in general be stochastic, driven by random molecular noise within networks characterized by bistable or excitable dynamics. This hints at the possibility that some of the most studied cellular processes such as DNA replication may be based on stochastic decision-making inherited from ancient biomolecular circuits, e.g., that autonomously dictate the length of the G1 phase before cell cycle Start (Di Talia et al., 2007). Moreover, these studies on viruses support the idea that “cellular” decisions actually occur at the level of intracellular molecular networks. The outcome of these stochastic decisions is an environment-dependent balance between lysis and lysogeny within viral populations, faithfully encoded by the viral genome and the host environment. Therefore, cellular decision-making constitutes a very simple mechanism for pattern formation that does not require cell-cell interactions or inter-cell communication and can therefore operate from the lowest to the highest levels of biological complexity (from viruses to multicellular eukaryotes), as discussed below.

BACTERIA

Bacillus subtilis would probably win a microbial tournament for the role of model organism in unicellular development. Besides its easy genetic manipulation, the main reason for the popularity of this soil bacterium is the variety of developmental choices that it assumes during starvation (Lopez et al., 2009). As nutrients become limiting, B. subtilis gears up to differentiate into spores – non-growing capsules highly resistant to a variety of stresses and starvation – but without a rush. In fact, these bacteria take every possible opportunity to delay their sporulation by exploring a number of alternative options, including extracellular matrix production, motility, cannibalism, nutrient release through cell lysis, cell growth arrest and DNA uptake (competence). The cells stop the sporulation program and start growing as soon as one of these alternative strategies enables them to do so, or as soon as nutrients become available.

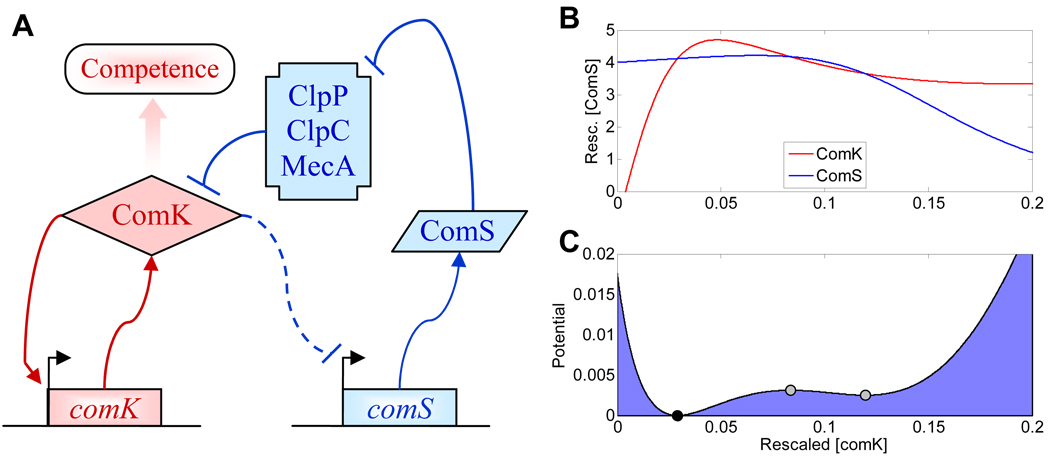
One particular B. subtilis cell-fate decision that has attracted much attention recently is the transition to competence, when cells take up extracellular DNA and use it as food – or perhaps integrate it into the genome, as a mechanism of increased evolvability under stress (Galhardo et al., 2007). During starvation only a limited percent of the bacterial population becomes competent, a decision dictated by the master regulator ComK that activates the genes involved in this developmental program, including itself (Fig. 3A). ComK levels are controlled by the protease complex MecA/ClpC/ClpP, which also binds ComS, a factor capable of preventing ComK degradation through competitive binding to the protease. Since ComS is repressed during competence, these interactions form a negative feedback loop around comK.

Figure 3. Competence initiation in B. subtilis.

(A) The gene regulatory network controlling entry into competence consists of the master regulator ComK and its indirect activator, ComS. ComK activates its own expression, and ComS is downregulated during competence, which results in a structure of nested positive and negative feedback loops. Regulatory interactions mediating positive and negative feedback are shown in red and blue, respectively. Arrowheads indicate activation; blunt arrows indicate repression.

(B) Nullclines for ComK and ComS, based on the model from (Süel et al., 2006). The nullclines intersect in three distinct points, indicating that there are three steady states.

(C) Potential calculated along the nullcline d[comS]/dt=0, based on the Fokker-Planck approximation: $\phi =2{\displaystyle \int \frac{f-g}{f+g}}d[\text{comK}]$, where f and g represent comK synthesis and degradation, respectively, along the ComS nullcline. The filled circle on the left indicates a stable steady state. The gray circles in the middle and on the right indicate saddle points: the middle one is unstable along the ComS nullcline (it is sitting on a “crest“ in the potential), while the one on the right is unstable along the ComK nullcline. A small perturbation (due to molecular noise) will drive ComK expression from the stable steady state near the other two steady states, initiating transient differentiation into competence, after which the system returns to the steady state on the left.

Süel and colleagues were the first to develop a mathematical model and show that the nested positive and negative feedback loops enable excitable dynamics (Fig. 3B,C), generating pulses of ComK expression and episodes of competence (Süel et al., 2006). Each of these episodes starts with a transient increase in ComK levels that is amplified through autoregulation, leading to a quick rise to maximal ComK expression and transition to competence. This in turn leads to ComS repression, enabling the protease complex to degrade ComK, terminating the ComK pulse and the episode of competence.

If ComK controls entry into and ComS controls exit from competence, then they should affect different aspects of these transient differentiation events. This was indeed the case, as found by controlled ComK and ComS overexpression (Süel et al., 2007). High basal ComK expression increased the frequency of competence epochs, until the point where the cells remained permanently competent. On the other hand, high ComS basal expression prolonged the time spent in competence. To further establish the mechanism of competence initiation, the authors ingeniously inhibited cell division while DNA replication continued unaltered. This caused the cell volume to increase, leaving the average ComK concentrations unaffected while lowering the noise in ComK expression. Examining the rate of competence initiation in cells of increasing length (and consequently, decreasing ComK noise), the rate of competence initiation dropped substantially. Consequently, ComK noise plays a crucial role in competence initiation, by elevating subthreshold levels of ComK towards a critical point where positive feedback takes effect to initiate periods of competence, in a manner similar to stochastic resonance (Wiesenfeld and Moss, 1995). Likewise, ComS expression noise was found crucial for controlling not just the length, but also the variability of competence episodes. A synthetic gene circuit with equivalent average dynamics to the natural one had much lower variability of competence episodes, which severely compromised the DNA uptake capacity of the cell population (Çağatay et al., 2009). The crucial role of noise in competence initiation was independently confirmed by another group (Maamar et al., 2007) after successfully decoupling ComK gene expression noise and mean. Although they studied ComK dynamics over a shorter time, Maamar et al. found that entry into competence occurred predominantly during a transient rise in ComK expression around the time of entry into stationary phase.

Competence is a bacterial attempt to avoid sporulation. However, if no cells decide to sporulate while the environment continues to worsen, the population will have a decreased chance of survival. Therefore, bacteria must eventually sporulate, which they do, but only gradually over several days. A recent account of cell-fate decision in sporulation conditions reported on cell population size and individual cell length in growing B. subtilis microcolonies (Veening et al., 2008b). After the initial exponential phase, the authors observed a period of slow bacterial growth (diauxic shift), later followed by complete growth arrest for approximately half a day. By measuring the growth rate and morphology of individual cells, three distinct cell fates were identified: spores, vegetative cells, and lysing cells. Interestingly, only the vegetative cells grew during the diauxic phase, accounting alone for all the growth observed during this period. Cells that later formed spores or lysed did not grow, indicating that their cellular fates bifurcated much before their terminal phenotypes could be determined. This phenotypic bifurcation was independent of cell age (measured for the first time for B. subtilis), but was consistent within “cell families” defined as a cell and all its descendants, implying “transgenerational epigenetic inheritance” (Jablonka and Raz, 2009) of this decision. These heritable cell-fate decisions correlated with SpoIIA promoter activity and were eliminated when the phosphorelay feedback through Sad67 was disrupted, demonstrating the importance of post-translational (rather than transcriptional) positive feedback in the inheritance of cellular fate.

Quorum sensing is the ability of bacteria to detect their density and thereby orchestrate population-level behaviors such as luminescence or virulence. Quorum sensing brings up an interesting question: is there a role for cellular decision-making as bacteria join forces in a population-level effort? This question is currently being addressed using Vibrio harveyi as a model organism. As V. harveyi cells divide and their density exceeds a threshold, they undergo a remarkable transition and become bioluminescent, which is made possible by their ability to synthesize and detect specific small signaling molecules (autoinducers) through quorum sensing (Waters and Bassler, 2005). Growing cell populations produce more and more autoinducer, which becomes concentrated and turns on bioluminescence, in addition to a number of other functions related to multicellularity. Whether all or only some individual cells undergo the decision triggered by quorum-sensing remains an important open question that will soon be answered thanks to recent efforts to measure quorum sensing-related gene expression at the single cell level in newly engineered V. harveyi strains. So far, gene expression measurements for the master quorum-sensing regulator LuxR (Teng et al., 2010) and a small RNA controlling LuxR expression revealed relatively low, but autoinducer-dependent noise (Long et al., 2009), which may imply that the V. harveyi quorum-sensing circuit has evolved to reduce noise and bacterial individuality while transitioning to multicellular, population-level behavior. Indeed, multiple nested negative feedback loops have been identified along the signaling cascade connecting autoinducer receptors to LuxR (Tu et al., 2010), which are network structures capable of noise reduction (Becskei and Serrano, 2000; Nevozhay et al., 2009).

Other examples of cellular decision-making in bacteria are the activation of the lactose operon in E. coli and bacterial persistence (phenotypic switching of bacteria to an antibiotic-tolerant state). The first of these has a history of more than five decades (Novick and Weiner, 1957), and will not be discussed here. Regarding bacterial persistence, some critical information is still missing. Persistence of E. coli cells has been observed at the single-cell level (Balaban et al., 2004), but the underlying network and molecular mechanisms may be highly complex and are currently unknown. Conversely, a bistable stress response network has been proposed to underlie persistence in Mycobacteria (Sureka et al., 2008; Tiwari et al., 2010), but the measurements to observe persistent cells and link them to this network have yet to be performed.

In summary, bacteria are masters of cellular decision-making, which enables them to hedge bets in a fluctuating, often stressful environment. This may explain their presence in the most extreme and unpredictable environments. Unlike viruses, which typically decide between lysis and lysogeny, bacteria can select their fates randomly from a spectrum of multiple options. Fates with lowest direct fitness (such as the spore state) are entered gradually, with a delay, while a variety of alternative options are explored. Bacterial cell decisions involve noisy networks with feedback loops, capable of bistable or excitable dynamics. Unlike viruses, bacteria can combine cellular decision-making with other mechanisms (such as cell-cell communication). Cellular decision-making appears suppressed when cell-cell communication becomes prominent (as in quorum sensing), suggesting that microbial individuality is undesired when bacteria assume multicellular behaviors. The above examples, taken together with the reproducible phenotypic diversification and pattern formation in bacterial colonies (Lopez et al., 2009) or differentiation in suspension (Novick and Weiner, 1957) indicate that many bacterial species are capable of primitive multicellular development. Which of the observed patterns have a functional role remains to be discovered. Still, these examples suggest that the simplest forms of multicellular behavior do not require physical contact or communication between cells.

YEAST

The budding yeast Saccharomyces cerevisiae was the first organism for which the noise of thousands of fluorescently tagged proteins expressed from their native promoters was measured (Bar-Even et al., 2006; Newman et al., 2006). Many yeast genes were found to be significantly noisier than expected based on Poissonian protein synthesis and degradation, suggesting that gene expression bursts may cause the elevated noise of certain genes, which may be beneficial and under selection. These noisy genes had a tendency to be associated with stress responses (Gasch et al., 2000) and often contained a TATA box in their core promoter. Accordingly, TATA box mutations were found to diminish gene expression noise, which lowered the chance of survival in severe stress from which the gene’s protein product offered protection (Blake et al., 2006). Taken together, these results suggested that yeast cells carry an arsenal of genes with unexpectedly noisy expression, supplying the noise needed for phenotypic diversification, which can benefit the population in a fluctuating, often stressful environment.

The galactose uptake system is a relatively well-studied example of a noisy environmental response network. Yeast cells show bimodal expression of galactose uptake (GAL) genes when exposed to a mixture of low glucose and high galactose, indicating that cells decide stochastically between utilizing either the limited amount of glucose or growing on galactose (Biggar and Crabtree, 2001). On the other hand, the expression of GAL genes is in general more uniform in the absence of glucose, when grown on galactose alone, or galactose mixed with raffinose and glycerol. How is it possible for a gene network to generate uniform or bimodal (noisy) expression across the cell population, depending on the stimulus?

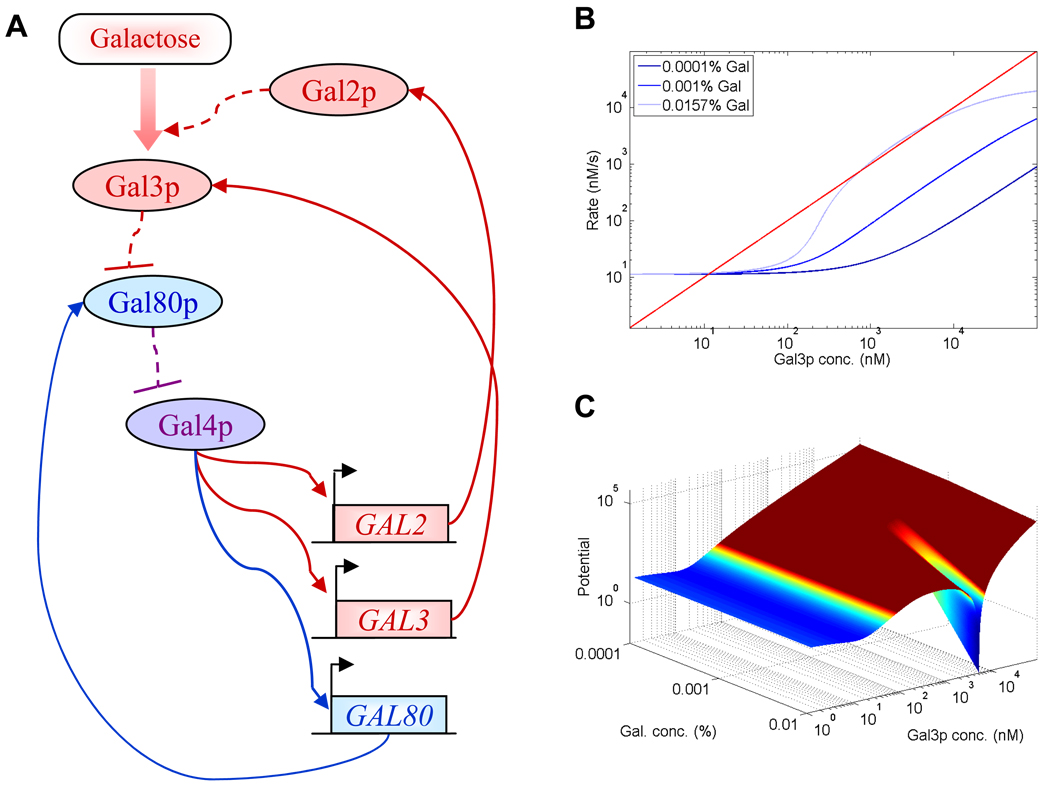
Essentially, the GAL molecular circuitry consists of three feedback loops. Two of these feedback loops are positive and involve the galactose permease Gal2p and the signaling protein Gal3p. The third feedback loop is negative, and involves the inhibitor Gal80p. All three molecules (Gal2p, Gal3p and Gal80p) are under the control of the activator Gal4p, while they also regulate Gal4p activity and galactose uptake (Fig. 4). To understand how network structure affects cellular decision-making, each of these feedback loops was individually disrupted (Acar et al., 2005), and the pattern of GAL gene expression across the cell population was examined after transferring the cells from no galactose- or high galactose-containing medium to various intermediate galactose concentrations.

Figure 4. The galactose uptake network in S. cerevisiae.

(A) Regulatory network controlling galactose uptake. Regulatory interactions mediating positive and negative feedback are shown in red and blue, respectively, while the regulatory interaction that participates in both positive and negative feedback loops is shown in purple. Solid lines indicate transcriptional regulation; dashed lines indicate non-transcriptional regulation (for example, Gal80p binds to Gal4p and represses Gal4p activator function on GAL promoters). Arrowheads indicate activation; blunt arrows indicate repression.

(B) Gal3p synthesis (blue lines) and degradation (red line) rates as functions of Gal3p concentration, for three different galactose concentrations.

(C) Potential based on the Fokker-Planck approximation: $\phi =2{\displaystyle \int \frac{f-g}{f+g}}d[\text{Gal3p}]$, where f and g represent Gal3p synthesis and degradation, respectively. There is a stable steady state on the left side of the surface at all galactose concentrations. At sufficiently high galactose concentrations, an additional steady state appears (deep well on the right). As galactose concentration is slowly increased, cells can end up in either potential well (cellular decision-making). Moreover, molecular noise can move cells from one potential well to the other even in constant galactose concentration.

The wild-type strain, with all three feedback loops intact, had history-dependent gene expression one day after transfer, depending on the original growth condition. Specifically, wild-type cells transferred from high galactose had unimodal GAL expression tracking the galactose concentration, whereas those transferred from low galactose had bimodal expression, indicating that only a subpopulation of cells made the choice to take up galactose. GAL2 deletion had minimal effect on the GAL expression pattern compared to wild-type cells. On the other hand, disruption of the Gal3p-based positive feedback loop resulted in unimodal GAL gene expression regardless of the conditions prior to transfer, indicating that the cells lost their capacity of decision-making. Finally, disruption of the Gal80p-based negative feedback loop resulted in unimodal, low GAL expression for cells transferred from no galactose, while cells transferred from high galactose had a bimodal distribution. Overall, these results indicate that the Gal3p- and Gal80p-based feedback loops play critical roles in cellular decision-making and history-dependence of GAL expression.

The gene expression patterns observed by Acar and colleagues (Acar et al., 2005) bring up an important concept: cellular memory. Considering that cells make stochastic decisions, how long do they stick to their choices? This question can be reformulated in terms of escape rates, and addressed theoretically, as follows: given that a cell resides in a potential well on Waddington’s landscape (Fig. 1), how long does it take for it to escape under the influence of noise to a nearby well? Theory predicts that the chance of escape depends on two factors: noise strength and the height of the barrier that needs to be surpassed in order to escape (Hänggi et al., 1984) (noise facilitates, while a tall barrier hinders escape). Based on the noise strength and the “geography” of the potential shown in Fig. 4, the authors predicted that by controlling GAL80 expression they could prolong or shorten the maintenance of high and low GAL expression states in cells with disrupted negative feedback. This was then confirmed experimentally (Acar et al., 2005).

Another remarkable case of yeast cell decision-making was described by Paliwal and colleagues, who used clever microfluidic chip design to study the response of individual a mating-type yeast cells to the α pheromone (Paliwal et al., 2007). Pheromone was supplied artificially so as to establish a spatial gradient, in which a high number of cells exposed to various pheromone concentrations could be observed. Normally, the pheromone serves as a cue to direct a cell elongation (shmooing) towards a mating partner of opposite type (α). Cells exposed to no pheromone or high pheromone behaved in a uniform fashion (all cells budding and shmooing, respectively). However, a very different scenario emerged for cells exposed to identical intermediate pheromone concentrations: a mixture of budding, cell cycle arrested, and shmooing phenotypes were observed, demonstrating cellular decision-making. Shmooing cells had significantly higher expression of the transcription factor Fus1p, indicating that at least one observed phenotype was attributable to bimodal gene expression. The network responsible for Fus1p activation consists of a Mitogen-Activated Protein Kinase (MAPK) pathway that encompasses multiple positive feedback loops, prime candidates for inducing bimodal FUS1 expression. Indeed, disruption of these feedback loops made FUS1 expression and the response to pheromone more uniform across yeast cell colonies, supporting the idea that positive autoregulation can induce cellular decision-making.

These examples indicate that cellular decision-making is widely utilized by yeast cells to maximize the propagation of their genome in a changing environment. A prominent role of feedback regulation in cellular decision-making is emerging from these examples, although other regulatory mechanisms (such as epigenetic regulation) can also play a role (Octavio et al., 2009). While many genes are noisy when yeast cells grow in suspension, it is interesting to ask how noise and cellular decision-making are regulated and exploited during the transition to population-level behaviors such as flocculation due to quorum sensing in yeast cell populations (Smukalla et al., 2008). Yeast cells carry a primitive version of the molecular arsenal utilized during metazoan development, such as homeodomain proteins, morphogens, and the apoptosis pathway. Is noise in these pathways suppressed or elevated in yeast compared to higher eukaryotes? Answering these questions may yield important insights into the regulation of cellular decision-making in metazoan development.

LOWER METAZOANS

Animals are compact multicellular organisms that grow out from a single zygote cell following a complex embryonic developmental program. During development, increasingly differentiated cell types emerge through sequential rounds of cell division, giving rise from about one thousand (Caenorhabditis elegans) to millions (Drosophila melanogaster) or tens of trillions (humans) of isogenic cells in a fully developed animal. Moreover, these expanding and diversifying cell subpopulations perform remarkably well-defined movements in space and time, such that they arrive to appropriate locations relative to each other, ready to perform their function in the adult animal (Goldstein and Nagy, 2008). Importantly, a few cells embed themselves into specific niches and remain partially undifferentiated, thereby becoming adult stem cells capable of replacing differentiated cells that are lost during adult life.

The tremendous population expansion that cells undergo during embryonic development poses a serious danger of error amplification, implying that stochastic cellular decision-making should be less common than in unicellular organisms, and control mechanisms should exist to suppress it during development (Arias and Hayward, 2006). Without proper control, a random switch to an incorrect cell fate in the wrong place or at the wrong time could have detrimental consequences for the adult. For this reason, highly stochastic cell-fate choices may be restricted to specific cell types and developmental stages, such as the differentiation of adult and embryonic stem cells, or the differentiation of cells whose precise location is unimportant (such as retinal patterning and hematopoiesis).

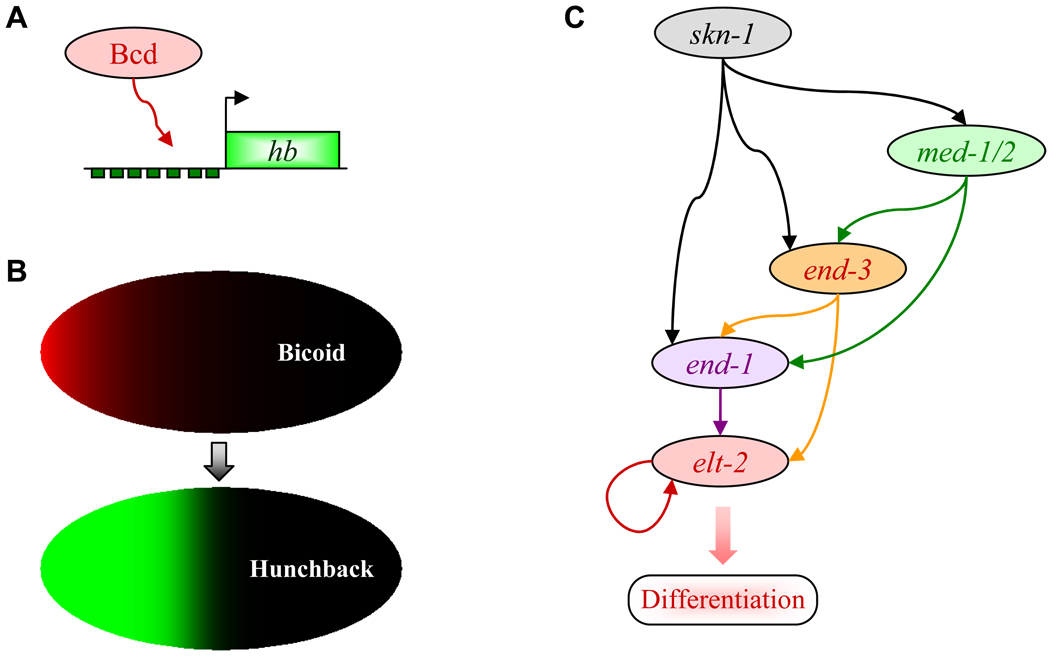
So, given the omnipresence of noise, how precise can animal development be, and what noise control mechanisms are utilized? These questions were addressed recently by monitoring the spatial expression pattern of the gap gene hunchback in single D. melanogaster nuclei in response to the morphogen Bicoid (Fig. 5A,B), which is asymmetrically deposited by the mother to the anterior pole of the egg (Gregor et al., 2007). The fertilized fruit fly zygote initially does not separate into individual cells, allowing Bicoid to freely diffuse away from this pole and create an exponential anterior-posterior gradient along the dividing nuclei. Consequently, single nucleus-wide sections perpendicular to the anterior-posterior axis in the developing embryo will have practically identical, exponentially decreasing morphogen concentrations (Fig. 5B), with a 10% drop between neighboring sections, regardless of their location in the embryo (Gregor et al., 2007). This concentration change is successfully and reliably detected by neighboring nuclei, as indicated by their gene expression pattern (Holloway et al., 2006). How is it possible to achieve this precision?

Figure 5. Cell-fate specification during lower metazoan development.

(A) The morphogen Bicoid regulates hunchback expression during fruit fly development, setting up the scene for subsequent patterning of the embryo.

(B) Bicoid and Hunchback concentrations along the anterior-posterior axis of the fruit fly embryo (length: ~500 µm), according to the measurements by Gregor and colleagues (Gregor et al., 2007). The Bicoid concentration (red color) is exponentially decreasing towards the posterior end, with a length constant of 500 µm, and is “read out” by Hunchback (green color) with a 10% relative error rate according to the average dose-response relationship Hb/Hb_max=(Bcd/Bcd_1/2)⁵/[1+(Bcd/Bcd_1/2)⁵].

(C) Gene regulatory network controlling intestinal cell-fate specification during Caenorhabditis elegans development.

Among other genes, hunchback expression represents a critical readout of Bicoid concentration (Fig. 5A), restricting future segments in the larva, and later the adult fly to their appropriate locations. Hunchback expression levels showed sigmoidal morphogen dependence, indicating highly cooperative activation by Bicoid (Fig. 5B). More importantly, Hunchback had remarkably low noise levels in sets of nuclei exposed to identical morphogen concentrations, with a noise peak corresponding to the steepest region of the Hunchback dose response, where the coefficient of variation was about 20%. Assuming that hunchback expression noise was originating from Bicoid fluctuations, the authors used the Bicoid-Hunchback dose-response data to infer the noise in Bicoid concentration as perceived by individual nuclei, and found a U-shaped error profile along the anterior-posterior axis, with a minimum coefficient of variation of 10%, consistent with earlier work (Holloway et al., 2006). This indicates that cellular decision-making is strongly suppressed while setting up hunchback expression along the embryo in response to Bicoid. Individual nuclei have merely 10% autonomy in deciding what Bicoid concentration is in their surroundings, and setting up the appropriate response.

Seeking to understand how neighboring nuclei could reliably detect a 10% drop in Bicoid concentration, Gregor and co-workers estimated the averaging time necessary to reduce the error that individual nuclei make in estimating Bicoid concentrations, relying solely on stochastic Bicoid binding/dissociation events to/from its DNA binding sites. The results were strikingly inconsistent with the temporal averaging hypothesis, requiring nearly two hours of averaging to reach 10% relative error. Looking for alternatives, the authors asked if spatial averaging could also contribute to noise reduction. Measuring the spatial autocorrelation of Hunchback concentration fluctuations around the mean revealed that nuclear communication indeed occurs over approximately five nuclear distances, reducing the averaging time to a single nuclear cycle (approximately three minutes). In summary, sets of neighboring nuclei talk to each other and jointly accomplish quick and accurate estimates of the local Bicoid gradient. The identity of the mediator for this nuclear communication remains elusive.

To study spatiotemporal patterns of expression for several genes during a later developmental stage (mesodermal patterning), another group applied quantitative in situ hybridization followed by automated image processing in hundreds of fruit fly embryos (Boettiger and Levine, 2009). Contrary to the high precision of Hunchback response to Bicoid (Gregor et al., 2007), several genes had variable, “dotted” expression across the developing pre-mesodermal surface, indicating that gene expression can be noisy even during multicellular development. This noise was, however, transient, since by the end of the mesodermal patterning phase all cells expressed these genes at maximal level, indicating that cells can choose autonomously the time of their activation during mesodermal patterning, but have no freedom to choose their final expression level at the end of this period. Importantly, another subset of genes behaved differently from their noisy peers, and reached their full expression in concert, over a relatively short time scale. Seeking to identify mechanisms underlying this type of “synchrony” for this second subclass of genes, the authors found that their expression was typically regulated through a stalled polymerase. Moreover, one of the low-noise genes, dorsal, had to be present in two copies for maintaining the synchrony and low noise of other genes from the second subclass. The few genes that still maintained low noise after deleting one dorsal copy were found to have shadow enhancers – distal sequences involved in gene activation, which apparently ensure the robustness and reliability of expression for a few highly critical developmental genes. These findings indicate that noisy gene expression and stochastic cell-fate decisions would be the default even during metazoan development, if intricate regulatory mechanisms did not exist to suppress these variations, ensuring reliable patterning.

One developmental process that fully exploits cellular decision-making is the patterning of the fly’s eye. Compound fly eyes consist of hundreds of ommatidia, each of which harbor eight photoreceptors, two of which (R7 and R8) are responsible for color vision. Based on rhodopsin (Rh) expression in these photoreceptors, the corresponding ommatidia can become pale or yellow. The pale/yellow choice occurs in the photoreceptor R7 of each ommatidium: if R7 expresses Rh3 then the ommatidium becomes pale, while if it expresses Rh4, the ommatidium becomes yellow. R7’s choice is then transferred to R8 and stabilized through a positive feedback loop between the regulators warts and melted. Pale and yellow ommatidia are randomly localized and make up 30% and 70% of the fly eye, respectively, suggesting that their positioning results from stochastic cell-fate choices. This random patterning can be abolished by the deletion or overexpression of the transcription factor spineless, which changes the retinal mosaic into uniformly pale and yellow, respectively (Wernet et al., 2006).

Fruit fly development suggests that gene expression noise and stochastic cell-fate choices are carefully controlled and often suppressed, except when they are not disruptive for developmental patterning (Boettiger and Levine, 2009), or when they are exploited to assign random cell fates with desired probabilities (Wernet et al., 2006). What happens if noise suppression fails and fluctuations escape from control? This was examined by monitoring mRNA expression in single cells during C. elegans development (Raj et al., 2010) in a regulatory cascade composed of multiple feed-forward loops controlling the expression of elt-2, a self-activating transcription factor critical for intestinal cell-fate specification (Fig. 5C). After the 65-cell stage, elt-2 expression was high in all cells of all wild-type worm embryos. However, this uniform expression pattern became variable from embryo to embryo and bimodal within individual embryos after mutation of the transcription factor skn-1, which sits at the top of the regulatory hierarchy in Fig. 5C, and caused lack of intestinal cells in some, but not all, embryos. Similar phenomena, when genetically identical individuals carrying the same mutation show either disrupted or wild-type phenotype, are called partial penetrance.

Counting individual mRNAs in all cells of hundreds of embryos, Raj et al. observed sequential activation of the genes in Fig. 5C during development from the top towards the bottom of the hierarchy, with med-1/2 exhibiting an early spike of expression, accompanied by a wider end-3 spike, and a prolonged, but still transient high expression period of end-1. The outcome of these gene expression events was high and stable elt-2 expression and proper intestinal cell-fate specification. By contrast, in the skn-1 mutant the expression of all genes was diminished or absent, and the majority of embryos had practically no elt-2 expression. Moreover, end-1 expression was highly variable within individual embryos, indicating that skn-1 mutations relieve pre-existing noise suppression, thereby allowing stochastic cell-fate decisions to occur. Downregulation of the histone deacetylase hda-1 partially rescued the skn-1 mutant phenotype, indicating that chromatin remodeling was one source of end-1 noise unveiled in skn-1 mutant embryos. However, deletion of upstream transcription factors other than skn-1 (i.e., med-1/2, end-3) did not cause a comparably detrimental reduction of end-1 levels. Taken together, these data suggest that these intermediate transcription factors act in a redundant fashion, buffering noise in the system and ensuring sufficiently high end-1 expression, which can then switch the elt-2 positive feedback loop to the high expression state, ensuring reliable intestinal cell-fate specification.

These examples together indicate that the noise of certain genes is suppressed and buffered by a variety of mechanisms (such as spatial and temporal averaging, stalled polymerases, and redundant regulation) during the development of lower metazoans. Consequently, cellular decision-making is generally suppressed unless specifically required for developmental patterning (as for the ommatidia of the composite fly eye) or unless it is harmless (does not interfere with the execution of the overall developmental program). Disruption of the noise control mechanisms unmasks noise and can have detrimental effects on the development of the organism. Noise control during development may resemble the apparent suppression of cellular individuality during quorum-sensing, which triggers population-wide behavior in microbes. These and similar open questions can be properly addressed in the context of social evolution theory (West et al., 2006). On the experimental side, much remains to be discovered about the consequences of “letting noise loose” during development. For example, once the factor responsible for spatial averaging across fruit fly nuclei (Gregor et al., 2007) is identified, it would be interesting to examine how fly development tolerates the inhibition of this inter-nuclear communication.

MAMMALS

Embryonic development is highly conserved among mammals: after a few divisions of the fertilized egg, the resulting cells quickly advance to the blastocyst stage, which manifests as a spherical trophectoderm surrounding the inner cell mass. The inner cell mass consists of pluripotent embryonic stem (ES) cells capable of differentiating into any cell type in the future organism. Therefore, efficiently isolating and maintaining ES cells in laboratory conditions holds exceptional potential for future medical applications.

However, to truly exploit the pluripotency of stem cells, it is essential to understand and control the processes underlying their differentiation into various tissues. Moreover, the recent success of reverting differentiated cells into induced pluripotent stem (iPS) cells (Takahashi and Yamanaka, 2006) poses further questions about the efficiency and stability of this reversal. Is differentiation into specific cell types solely the result of cellular decision-making or is it somewhat controllable? To what degree is differentiation reversible, and can the rate of induced pluripotency be increased? And what is the role of noise in pluripotency?

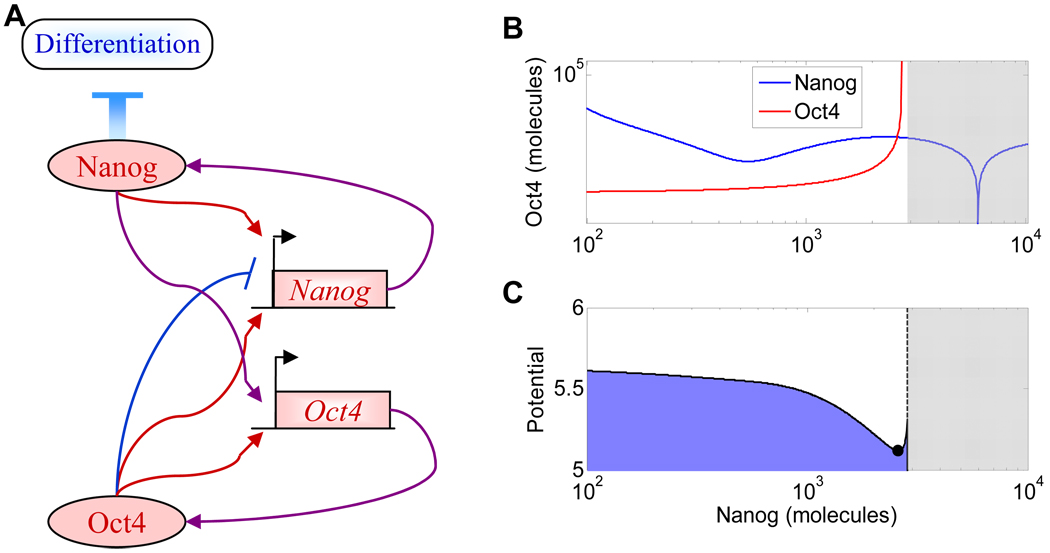
Nanog is a critical pluripotency marker whose expression is lost during ES cell differentiation, and it is maintained at a high level only in pluripotent cells. Following in the footsteps of Chambers et al. who first showed stochastic Nanog expression corresponding to attempts of ES cell differentiation (Chambers et al., 2007), Kalmar et al. monitored single ES cells and embryonal carcinoma (EC) cells to better understand Nanog dynamics (Kalmar et al., 2009). Both cell lines had a surprisingly strong, bimodal heterogeneity of Nanog expression that involved transitions between the high and low expression states. Consistent with Nanog’s function, cells with low expression responded better to differentiation signals. Analyzing the dynamics of the gene regulatory network controlling Nanog expression (Fig. 6A), the authors suggested that the system was excitable rather than bistable, giving rise to a small ES cell subpopulation with low Nanog expression through occasional random excursions from the high to the low expression state (Fig. 6B,C). While this expression pattern is opposite to ComK dynamics during competence initiation in B. subtilis, it relies on a gene regulatory network of similar structure, involving nested positive and negative feedback loops, namely: mutual Oct4 and Nanog activation, Oct4 and Nanog autoregulation and Nanog repression by Oct4. However, since the network underlying ES cell pluripotency is not completely known, it cannot yet be excluded that the high- and low-Nanog subpopulations result from noise-induced transitions in a bistable system (Chickarmane et al., 2006; Glauche et al., 2010; Kalmar et al., 2009). Indeed, the source of noise driving Nanog excursions into the low expression state remains elusive, especially considering that high molecular levels are often associated with low noise. Gene expression bursts (Raj et al., 2006) may offer a solution, since highly expressed proteins can be noisy provided they are expressed in bursts (Newman et al., 2006).

Figure 6. Embryonic stem cell (ESC) decision-making in mammals.

(A) The Nanog-Oct4 gene regulatory network primes ESC differentiation. Regulatory interactions mediating positive and negative feedback are shown in red and blue, respectively. Regulatory interactions that participate in both positive and negative feedback loops are shown in purple. Arrowheads indicate activation; blunt arrows indicate repression.

(B) Nullclines for Nanog and Oct4, based on the model from Kalmar et al. (Kalmar et al., 2009). The nullclines intersect only once, corresponding to a single stable steady state.

(C) Potential calculated along the nullcline d[Nanog]/dt=0, based on the Fokker-Planck approximation. The filled circle on the right indicates the only stable steady state. The gray shaded area is inaccessible since it corresponds to non-physical solutions. The system undergoes transient excursions to the left (low Nanog concentrations) under the influence of molecular noise. This will prime the ESCs for differentiation if appropriate signals are present.

Differentiation is accompanied by loss of Nanog expression, in addition to downregulation of Oct4, and Sox2, the other transcription factors responsible for the maintenance of Nanog expression and pluripotency. Contrary to the early belief that differentiated cells cannot return to the pluripotent state, Takahasi and Yamanaka (Takahashi and Yamanaka, 2006) found that controlled upregulation of Oct4, Sox2, Klf4 or c-Myc can convert fully differentiated cells into induced pluripotent stem (iPS) cells. However, such iPS cells were remarkably difficult to obtain, and appeared as only a minuscule percentage in large differentiated cell populations exposed to identical genetic and environmental perturbations. Trying to understand the enigmatic source of iPS cells, two possible scenarios for their generation were proposed (Yamanaka, 2009): the elite model assumed pre-existing differences responsible for reversal to the iPS cell state, while the stochastic model assumed that reversal occurred by random chance, even without any pre-existing differences. The dichotomy of these models is analogous to the contrasting views of deterministic versus stochastic dynamics on Waddington’s landscape, as well as the recent controversy on the predictability of the lambda switch (St-Pierre and Endy, 2008; Zeng et al., 2010).

A recent study set out to test experimentally the validity of the elite versus the stochastic model in iPS cell induction (Hanna et al., 2009). Differentiated murine B-cells were identically prepared to harbor inducible copies of Oct4, Sox2, Klf4 and c-Myc and to express Nanog-GFP once reversal to the iPS state occurred. A large number of clonal populations established from such B cells were maintained in constant conditions continuously for several months, and the appearance of iPS cells was monitored over time. The first iPS cells appeared after 2–3 weeks, followed by other iPS reversals as time progressed. Towards the end of the experiment, nearly every clonal population (93%) had a significant number of iPS cells, demonstrating that obtaining the iPS state is just a matter of time and patience, since some descendants of every B cell were capable of returning to the pluripotent state (also confirmed by their ability to generate teratomas and chimaeras). These findings strongly support the stochastic model of induced pluripotency. The authors also studied the influence of overexpressing either p53, p21, Lin28, or Nanog (in combination with all of the iPS inducing factors Oct4, Sox2, Klf4 and c-Myc) on the speed of reversal to the iPS state. All of these additional perturbations were found to increase the rate of reversals to the iPS state, but for different reasons. Whereas p53, p21, and Lin28 increased the cell division rate, and had an effect by raising the B cell population size while leaving the reversal rate per individual B cell unaffected, Nanog overexpression had a significant effect even after adjusting for growth rate differences.

Considering these studies demonstrating the role of noise in ES cell differentiation and the induction of pluripotency, it is intriguing to ask if there is a role for cellular decision-making in adult mammals. One of the first studies to address this question focused on adult progenitor cells (a multipotent hematopoietic stem cell line) (Chang et al., 2008), observing that the expression of the stem cell marker Sca-1 varied over three orders of magnitude across this cell population. Sorting the cells into distinct subpopulations based on their expression revealed that the variability in Sca-1 levels was dynamic: all sorted populations relaxed to the original distribution in approximately 9 days. The variability was found to reflect predisposition for certain cell fates, since cells with low Sca-1 expression had relatively high expression of the erythroid differentiation factor Gata1, and lower expression of the myeloid differentiation factor PU.1. Accordingly, upon stimulation with erythropoietin, low Sca-1-expressing cells differentiated much faster into erythrocytes than their peers with high Sca-1 expression. Moreover, the differences among the original pluripotent stem cells were not restricted to these two differentiation factors: microarray analysis revealed additional genome-wide differences in gene expression between three subpopulations sorted by their Sca-1 expression (Sca-1^low, Sca-1^mid, and Sca-1^high).

Besides cell differentiation, one of the most important processes recently shown to rely on cellular decision-making is apoptosis (Spencer et al., 2009). These authors followed by microscopy the fate of sister cell lineages exposed to a “mortal” agent: tumor necrosis factor-related apoptosis inducing ligand (TRAIL) in two clonal cell lines (HeLa and MCF10A). A striking heterogeneity in cell fate was observed. Some cells never died; and those that died showed a highly variable time between TRAIL exposure and commitment to programmed cell death (indicated by caspase activation or mitochondrial outer membrane permeabilization). Moreover, sister cells that died soon after TRAIL exposure showed synchronous commitment to apoptosis, while those that died later showed gradually decreasing correlation between their time of death, indicating that these suicidal decisions depend on factors inherited from the mother cell that gradually and stochastically diverge as daughter cells divide over time. Measuring the concentrations of five apoptosis-related proteins in single cells, together with a mathematical model of TRAIL-induced apoptosis allowed the authors to conclude that most stochastic variation in the commitment to cell death was due to initiator pro-caspase activity that cleaves the apoptotic regulator BID (BH3 interacting domain death agonist) into the truncated form tBID. When tBID hits a threshold, this sets off an irreversible avalanche of molecular interactions that culminate in apoptosis.

In summary, these examples from mammalian cells indicate that cellular decision-making underlies the most basic cellular processes in some of the most complex organisms, relying on regulatory networks with dynamics similar to those found in lower metazoans and microbes. However, the exact structure of the regulatory networks controlling mammalian cell decisions are much less understood than for lower organisms. Moreover, these studies were conducted in cell lines, and not actual mammals, and very little is known about mammalian cell-fate choices in vivo. To start overcoming this gap, it will be important compare and analyze cellular decision-making from microbes and lower metazoans from an evolutionary perspective, hoping to learn lessons applicable to mammals.

CONCLUSIONS, CHALLENGES AND OPEN QUESTIONS

Here we reviewed several examples of cellular decision-making at multiple levels of biological organization. The generality of this phenomenon suggests that we are dealing with a fundamental biological property, which many organisms evolved to utilize due to the benefits of task allocation in isogenic cell populations. Cellular decision-making combined with environmental sensing and cell-cell communication are three key processes underlying pattern formation and development from microbes to mammals. Moreover, viral decision-making suggests that some form of random diversification may have been present even before cells existed. In fact, the phrase “cellular decision-making” is an oxymoron, since these decisions actually occur at the level of gene regulatory networks such as the ones highlighted in this review. Cells only provide microscopic meeting places for the real key players: genes connected into regulatory networks (Dawkins, 2006).

Several conclusions can be drawn from the examples discussed above. First, cellular decision-making is frequently based on networks with multiple nested feedback loops, at least one of which is positive. The role of these feedback loops in various decision-making circuits remains to be determined, but it appears that positive feedback makes cellular decisions stable, while negative feedback makes them more easily reversible. Studying the dynamics of multiple feedback loops and their role in differentiation and development has much insight to offer (Brandman et al., 2005; Ray and Igoshin, 2010; Tiwari et al., 2010). Second, these networks appear to operate in parameter regimes enabling either bistable or excitable dynamics. Third, cellular decision-making relies on intrinsic molecular noise, which induces transitions between steady states in bistable systems and transient excursions of gene expression in excitable systems. Fourth, as a consequence of the above, all cellular decisions are reversible from a theoretical point of view – although in practice this may not occur, due to the irreversibility of secondary effects triggered by cellular decision-making (such as cell lysis or apoptosis).

The importance of intrinsic noise in cellular decision-making has been questioned in a number of recent papers, which found that pre-existing differences in cell size, virus copy number, etc., explain to a significant degree cell-fate decisions (St-Pierre and Endy, 2008; Weitz et al., 2008). However, while the variability in cell-fate choices was somewhat reduced after accounting for certain newly identified factors, viral decisions were by far not entirely deterministic (Zeng et al., 2010). While it may be tempting to expect that increasingly detailed measurements of the structure and properties of single cells may enable the exact prediction of cell fate, this hope is unlikely to be fully realized. Imagine for a moment that we could find two cells of exactly the same size and molecular composition, and place them into the same environment. These cells could then theoretically have the same fate if all of their corresponding molecules would be in identical positions and would have identical velocities at a given time. However, this condition can never be satisfied in practice, since the probability of finding all of the molecules in the same state (position, velocity, etc.) is infinitesimally small. Noise is inherent to gene networks confined to small compartments, such as cells or artificial microscopic compartments (Doktycz and Simpson, 2007) and cannot be eliminated.

Instead, researchers should strive to understand and control noise increasingly better in order to control cell-fate decisions. While noise makes individual cells somewhat uncontrollable, the same may not be the case for large cell populations, which can develop reliable patterns from unreliable elements due to the sheer power of statistics. For example, repeatedly tossing 100 fair coins will very likely result in nearly-equal numbers of heads and tails, even though the fate of the individual coins is unpredictable. The same way, the fly eye will reliably consist of 30% pale and 70% yellow ommatidia, even though the fate of individual ommatidia prior to patterning is uncertain. Synthetic gene networks capable of controlling gene expression noise (Murphy et al., 2010), the rate of random phenotypic switching (Acar et al., 2005), or the duration variability of transient differentiation episodes (Çağatay et al., 2009) may be useful in the future for adjusting the rate and outcome of cellular differentiation.

Finally, a major challenge is to understand how cellular decision-making evolves under well-defined conditions. As discussed above, stochastic cellular-fate choices lead to cell population diversity, the simplest possible developmental pattern within isogenic cell populations. Such population-level characteristics are, however, conferred by gene networks carried by every individual cell in these populations, and stochastic diversification may ultimately serve the propagation of their constituent genes (Dawkins, 2006). Phenotypic diversity implies that some individual phenotypic variants will have low direct fitness and will be at a disadvantage without stress, while others will perish when the environment becomes stressful. However, in specific cases this type of sacrifice can be justified by Hamilton’s rule (Hamilton, 1964), considering that the relatedness between clonal individual cells is maximal, and the survival of any individual will propagate the same genome. This may allow for kin selection, as suggested by recent theoretical work (Gardner et al., 2007). On the experimental side, laboratory evolution of microbes in fluctuating environments may offer exciting opportunities to address these questions (Cooper and Lenski, 2010), as exemplified by the recent experimental evolution of random phenotypic switching (Beaumont et al., 2009).

More generally, it will be interesting to examine from the perspective of social evolution (West et al., 2006) the formation of more complex biological patterns, which may involve altruism (Lee et al., 2010), selfishness, spite and other forms of mutual benefit in addition to stochastic cell-fate choices. Observation of patterns in growing microbial colonies (Ben-Jacob et al., 1998) has lead to the proposal of considering microbes as multicellular organisms (Shapiro, 1998). While criticized by researchers from the field of social evolution (West et al., 2006), this proposal brings up an interesting question: which microbial patterns are functional, and when can patterns evolve? Since patterns readily form in non-living systems due to purely physical reasons, it will be interesting to examine in the context of sociobiology (West et al., 2007) whether specific biological patterns have biological function and whether they can evolve.