Abstract
We propose a novel framework for the automatic propagation of a set of manually labeled brain atlases to a diverse set of images of a population of subjects. A manifold is learned from a coordinate system embedding that allows the identification of neighborhoods which contain images that are similar based on a chosen criterion. Within the new coordinate system, the initial set of atlases is propagated to all images through a succession of multi-atlas segmentation steps. This breaks the problem of registering images that are very “dissimilar” down into a problem of registering a series of images that are “similar”. At the same time, it allows the potentially large deformation between the images to be modeled as a sequence of several smaller deformations. We applied the proposed method to an exemplar region centered around the hippocampus from a set of 30 atlases based on images from young healthy subjects and a dataset of 796 images from elderly dementia patients and age-matched controls enrolled in the Alzheimer’s Disease Neuroimaging Initiative (ADNI). We demonstrate an increasing gain in accuracy of the new method, compared to standard multi-atlas segmentation, with increasing distance between the target image and the initial set of atlases in the coordinate embedding, i.e., with a greater difference between atlas and image. For the segmentation of the hippocampus on 182 images for which a manual segmentation is available, we achieved an average overlap (Dice coefficient) of 0.85 with the manual reference.
Keywords: Structural MR images, Atlas-based segmentation, Coordinate system embedding, Manifold learning, Spectral analysis
Introduction
The automated extraction of features from magnetic resonance images (MRI) of the brain is an increasingly important step in neuroimaging. Since the brain anatomy varies significantly across subjects and can undergo significant change, either during aging or through disease progression, finding an appropriate way of dealing with anatomical differences during feature extraction has gained increasing attention in recent years.
Among the most popular methods for dealing with this variability are atlas-based approaches. These approaches assume that the atlases can encode the anatomical variability either in a probabilistic or statistical fashion. When building representative atlases, it is important to register all images to a template that is unbiased towards any particular subgroup of the population (Thompson et al., 2000). Two approaches using the large deformation diffeomorphic setting for shape averaging and atlas construction have been proposed by Avants and Gee (2004) and Joshi et al. (2004), respectively. Template-free methods for co-registering images form an established framework for spatial image normalization (Studholme and Cardenas, 2004; Avants and Gee, 2004; Zöllei et al., 2005; Lorenzen et al., 2006; Bhatia et al., 2007). In a departure from approaches that seek a single representative average atlas, two more recent methods describe ways of identifying the modes of different populations in an image dataset (Blezek and Miller, 2007; Sabuncu et al., 2008). To design variable atlases dependent on subject information, a variety of approaches have been applied in recent years to the problem of characterizing anatomical changes in brain shape over time and during disease progression. Davis et al. (2007) describe a method for population shape regression in which kernel regression is adapted to the manifold of diffeomorphisms and is used to obtain an age-dependent atlas. Ericsson et al. (2008) propose a method for the construction of a patient-specific atlas where different average brain atlases are built in a small deformation setting according to meta-information such as sex, age, or clinical factors.
Methods for extracting features or biomarkers from MR brain image data often begin by automatically segmenting regions of interest. A very popular segmentation technique is to use label propagation, which transforms labels from an atlas image to an unseen target image by bringing both images into alignment. Atlases are typically, but not necessarily, manually labeled. Early work using this approach was proposed by Bajcsy et al. (1983) as well as more recently by Gee et al. (1993) and Collins et al. (1995). The accuracy of label propagation strongly depends on the accuracy of the underlying image alignment. To overcome the reliance on a single segmentation, Warfield et al. (2004) proposed STAPLE, a method that computes for a collection of segmentations a probabilistic estimate of the true segmentation. Rohlfing et al. (2004) demonstrated the improved robustness and accuracy of a multi-classifier framework where the labels propagated from multiple atlases are combined in a decision fusion step to obtain a final segmentation of the target image. Label propagation in combination with decision fusion was successfully used to segment a large number of structures in brain MR images by Heckemann et al. (2006).
Due to the wide range of anatomical variation, the selection of atlases becomes an important issue in multi-atlas segmentation. The selection of suitable atlases for a given target helps to ensure that the atlas-target registrations and the subsequent segmentation are as accurate as possible. Wu et al. (2007) describe different methods for improving segmentation results in the single atlas case by incorporating atlas selection. Aljabar et al. (2009) investigate different similarity measures for optimal atlas selection during multi-atlas segmentation. van Rikxoort et al. (2008) propose a method where atlas combination is carried out separately in different sub-windows of an image until a convergence criterion is met. These approaches show that it is meaningful to select suitable atlases for each target image individually. Although an increasing number of MR brain images are available, the generation of high-quality manual atlases is a labor-intensive and expensive task (see, e.g., Hammers et al., 2003). This means that atlases are often relatively limited in number and, in most cases, restricted to a particular population (e.g., young, healthy subjects). This can limit the applicability of the atlas database even if a selection approach is used. To overcome this, Tang et al. (2009) seek to produce a variety of atlas images by utilizing a PCA model of deformations learned from transformations between a single template image and training images. Potential atlases are generated by transforming the initial template with a number of transformations sampled from the model. The assumption is that, by finding a suitable atlas for an unseen image, a fast and accurate registration to this template may be readily obtained. Test data with a greater level of variation than the training data would, however, represent a significant challenge to this approach. Additionally, the use of a highly variable training dataset may lead to an unrepresentative PCA model as the likelihood of registration errors between the diverse images and the single template is increased. This restriction makes this approach only applicable in cases were a good registration from all training images to the single initial template can be easily obtained.
The approach we follow in this work aims to propagate a relatively small number of atlases through to a large and diverse set of MR brain images exhibiting a significant amount of anatomical variability. The initial atlases may only represent a specific subgroup of target image population, and the method is designed to address this challenge. As previously shown, atlas-based segmentation benefits from the selection of atlases similar to the target image (Wu et al., 2007; Aljabar et al., 2009). We propose a framework where this is ensured by first embedding all images in a low-dimensional coordinate system that provides a distance metric between images and allows neighborhoods of images to be identified. In the manifold learned from coordinate system embedding, a propagation framework can be identified and labeled atlases can be propagated in a stepwise fashion, starting with the initial atlases, until the whole population is segmented. Each image is segmented using atlases that are within its neighborhood, meaning that deformations between dissimilar images are broken down to several small deformations between comparatively similar images and registration errors are reduced. To further minimize an accumulation of registration errors, an intensity-based refinement of the segmentation is done after each label propagation step. Once segmented, an image can in turn be used as an atlas in subsequent segmentation steps. After all images in the population are segmented, they represent a large atlas database from which suitable subsets can be selected for the segmentation of unseen images. The coordinate system into which the images are embedded is obtained by applying a spectral analysis step (Chung, 1997) to their pairwise similarities. As labeled atlases are propagated and fused for a particular target image, the information they provide is combined with a model based on the target image intensities to generate the final segmentation (van der Lijn et al., 2008; Wolz et al., 2009).
Prior work where automatically labeled brain images were used to label unseen images did not result in an improvement of segmentation accuracy over direct multi-atlas propagation. In Heckemann et al. (2006), when multiple relatively homogenous atlases were propagated to randomly selected intermediate images that were used as single atlases for the segmentation of unseen images, the resulting average Dice overlaps with manual delineations were 0.80, compared with 0.84 for direct multi-atlas propagation and fusion. In a second experiment, single atlases were propagated to randomly selected intermediate subjects that were then further used for multi-atlas segmentation, resulting in Dice overlaps with manual delineations of 0.78 at best. In this article, however, we use multi-atlas segmentation to systematically label intermediate atlases that are then used for multi-atlas segmentation of target images that are selected according to their similarity with the previously labeled atlas images. Compared to previous work, we are dealing with a very diverse set of images. In such a scenario, the gain from only registering similar images is more likely to outweigh the accumulation of registration errors.
Our initial set of atlases consists of 30 MR images from young and healthy subjects together with manual label maps defining 83 anatomical structures of interest. We used the proposed method to propagate this initial set of atlases to a dataset of 796 MR images acquired from patients with Alzheimer’s disease (AD) and mild cognitive impairment (MCI) as well as age-matched controls from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (Table 1). We show that this approach provides more accurate segmentations due, at least in part, to the associated reductions in inter-subject registration error.
Table 1.
Information relating to the subjects whose images were used in this study.
| N | M/F | Age | MMSE | |
|---|---|---|---|---|
| Normal | 222 | 106/216 | 76.00±5.08 [60–90] | 29.11±0.99 [25–30] |
| MCI | 392 | 138/254 | 74.68±7.39 [55–90] | 27.02±1.79 [23–30] |
| AD | 182 | 91/91 | 75.84±7.63 [55–91] | 23.35±2.00 [18–27] |
Materials and methods
Subjects
Images were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (www.loni.ucla.edu/ADNI) (Mueller et al., 2005). In the ADNI study, brain MR images are acquired at baseline and regular intervals from approximately 200 cognitively normal older subjects, 400 subjects with MCI, and 200 subjects with early AD. A more detailed description of the ADNI study is given in Appendix A.
In this work, we used the 796 available baseline images. An overview on the subjects is given in Table 1. For each subject group, the number of subjects, the male/female distribution, the average age, and the average result of the mini-mental state examination (MMSE) (Folstein et al., 1975) are shown.
Image acquisition was carried out at multiple sites based on a standardized MRI protocol (Jack et al., 2008) using 1.5T scanners manufactured by General Electric Healthcare (GE), Siemens Medical Solutions, and Philips Medical Systems. Out of two available 1.5T T1-weighted MR images based on a 3D MPRAGE sequence, we used the image that has been designated as “best” by the ADNI quality assurance team (Jack et al., 2008). Acquisition parameters on the SIEMENS scanner (parameters for other manufacturers differ slightly) are echo time (TE) of 3.924 ms, repetition time (TR) of 8.916 ms, inversion time (TI) of 1000 ms, flip angle 8°, to obtain 166 slices of 1.2-mm thickness with a 256×256 matrix.
All images were preprocessed by the ADNI consortium using the following pipeline:
GradWarp: a system-specific correction of image geometry distortion due to gradient non-linearity (Jovicich et al., 2006).
B1 non-uniformity correction: correction for image intensity nonuniformity (Jack et al., 2008).
N3: a histogram peak sharpening algorithm for bias field correction (Sled et al., 1998).
Since the Philips systems used in the study were equipped with B1 correction and their gradient systems tend to be linear (Jack et al., 2008), preprocessing steps 1 and 2 were applied by ADNI only to images acquired with GE and Siemens scanners.
For a subset of 182 of the 796 images, a manual delineation for the hippocampus was provided by the ADNI consortium.
Atlases
The initial set of manually labeled atlases used in this work consists of 30 MR images acquired from young healthy subjects (age range, 20–54; median age, 30.5 years). The T1-weighted MR images were acquired with a GE MR scanner using an inversion recovery-prepared fast spoiled gradient recall sequence with the following parameters: TE/TR 4.2 ms (fat and water in phase)/15.5 ms, time of inversion (TI) 450 ms, flip angle 20°, to obtain 124 slices of 1.5-mm thickness with a field of view of 18×24 cm with a 192×256 image matrix.
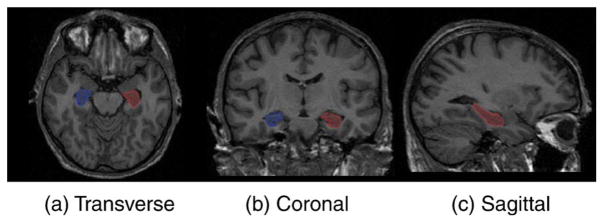
This set of atlases was chosen because manual labels maps for 83 anatomical structures were available. These have been shown to be useful for many neurological tasks (Hammers et al., 2003; Gousias et al., 2008; Heckemann et al., 2008)3 and could be used in extensions of the present work. Since no manual segmentations based on this protocol exist for the ADNI images used for evaluation in this work, the definition of the hippocampus in the initial atlas was changed to make it consistent with manual hippocampus label maps provided by ADNI. An example of the delineation of the hippocampus is given in Fig. 1.
Fig. 1.
Hippocampus outline on a brain atlas.
Overview of the method
To propagate an initial set of atlases through a dataset of images with a high level of inter-subject variance, a manifold representation of the dataset is learned where images within a local neighborhood are similar to each other. The manifold is represented by a coordinate embedding of all images. This embedding is obtained by applying a spectral analysis step (Chung, 1997) to the complete graph in which each vertex represents an image and all pairwise similarities between images are used to define the edge weights in the graph. Pairwise similarities can be measured as the intensity similarity between the images or the amount of deformation between the images or as a combination of the two.
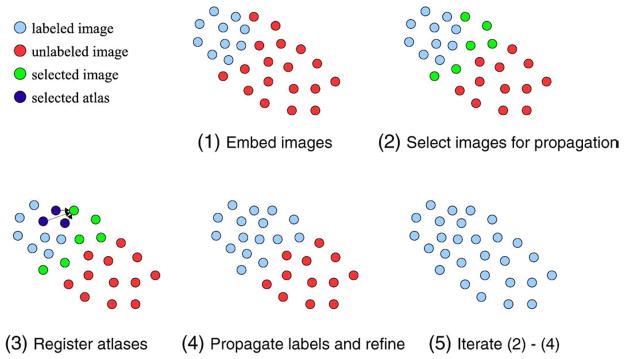
In successive steps, atlases are propagated within the newly defined coordinate system. In the first step, the initial set of atlases are propagated to a number of images in their local neighborhood and used to label them. Images labeled in this way become atlases themselves and are, in subsequent steps, further propagated throughout the whole dataset. In this way, each image is labeled using a number of atlases in its close vicinity, which has the benefit of decreasing registration error. An overview on the segmentation process with the LEAP (Learning Embeddings for Atlas Propagation) framework is depicted in Fig. 2.
Fig. 2.
Process of atlas propagation with the proposed framework. All labeled (atlases) and unlabeled images are embedded into a low-dimensional manifold (1). The N closest unlabeled images to the labeled images are selected for segmentation (2). The M closest labeled images are registered to each of the selected images (an example for one image is shown in panel 3). Intensity refinement is used to obtain label maps for each of the selected images (4). Steps 2 to 4 are iterated until all images are labeled.
Graph construction and manifold embedding
In order to determine the intermediate atlas propagation steps, all images are embedded in a manifold represented by a coordinate system, which is obtained by applying a spectral analysis step (Chung, 1997). Spectral analytic techniques have the advantage of generating feature coordinates based on measures of pairwise similarity between data items such as images. This is in contrast to methods that require distance metrics between data items such as multidimensional scaling (MDS) (Cox and Cox, 1994). After a spectral analysis step, the distance between two images in the learned coordinate system is dependent not only upon the original pairwise similarity between them but also upon all the pairwise similarities that each image has with the remainder of the population. This makes the distances in the coordinate system embedding a more robust measure of proximity than individual pairwise measures of similarity which can be susceptible to noise. A good introduction to spectral analytic methods can be found in von Luxburg (2007), and further details are available in Chung (1997).
The spectral analysis step is applied to the complete, weighted, and undirected graph G=(V,E) with each image in the dataset being represented by one vertex vi. The non-negative weights wij between two vertices vi and vj are defined by the similarity sij between the respective images. In this work, intensity-based similarities are used (see section 5). A weights matrix W for G is obtained by collecting the edge weights wij = sij for every image pair and a diagonal matrix T contains the degree sums for each vertex dii = Σjwij. The normalized graph Laplacian 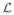 is then defined by (Chung, 1997)
is then defined by (Chung, 1997)
| (1) |
The Laplacian 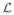 encodes information relating to all pairwise relations between the vertices and the eigen decomposition of
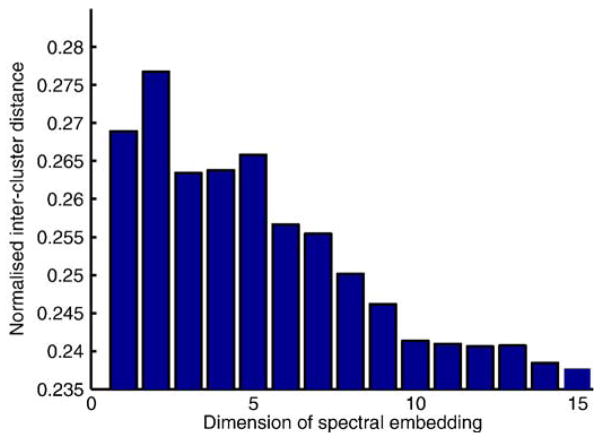
encodes information relating to all pairwise relations between the vertices and the eigen decomposition of 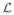 provides a feature vector for each vertex. The dimension of the feature data derived from a spectral analysis step can be chosen by the user. In our work, we tested each dimension for the feature data in turn and assessed the ability to discriminate between the four subject groups (young, AD, MCI, and older control subjects). The discrimination ability was measured using the average inter-cluster distance based on the centroids of each cluster for each feature dimension. For the groups studied, it was maximal when using two-dimensional features and reduced thereafter (see Fig. 3). We therefore chose to use the 2D spectral features as a coordinate space in which to embed the data.
provides a feature vector for each vertex. The dimension of the feature data derived from a spectral analysis step can be chosen by the user. In our work, we tested each dimension for the feature data in turn and assessed the ability to discriminate between the four subject groups (young, AD, MCI, and older control subjects). The discrimination ability was measured using the average inter-cluster distance based on the centroids of each cluster for each feature dimension. For the groups studied, it was maximal when using two-dimensional features and reduced thereafter (see Fig. 3). We therefore chose to use the 2D spectral features as a coordinate space in which to embed the data.
Fig. 3.
The discrimination ability for different chosen feature dimensions among the four subject groups (healthy young, elderly controls, MCI, AD). The best discrimination was achieved using two-dimensional features therefore a 2D embedding was used to define the distances between images.
Image similarities
In this article, we use an intensity-based similarity between a pair of images Ii and Ij. This similarity is based on normalized mutual information (NMI) (Studholme et al., 1999), which is with the entropy H(I) of an image I and the joint entropy H(Ii,Ij) of two images defined as
| (2) |
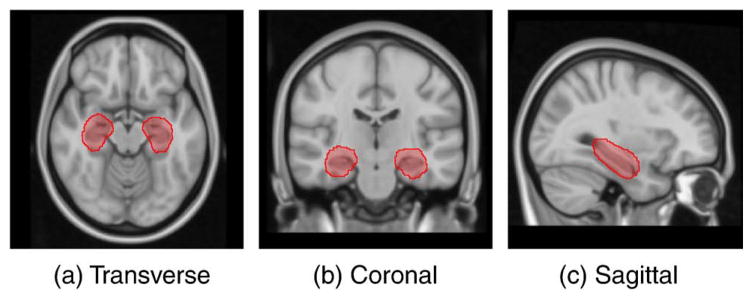
In this work, we are primarily interested in segmenting the hippocampus; we therefore compute the similarity measure between a pair of images as the NMI over a region of interest (ROI) around the hippocampus. The framework is, however, general and a user can choose the similarity measure and region of interest appropriate to the region or structure being segmented. To define the ROI, all training images were automatically segmented using standard multi-atlas segmentation (Heckemann et al., 2006). The resulting hippocampal labels were then aligned to the MNI152 brain T1 atlas (Mazziotta et al., 1995) using a coarse non-rigid registration modeled by free-form deformations (FFDs) with a 10 mm B-spline control point spacing (Rueckert et al., 1999) between the corresponding image and the atlas. The hippocampal ROI was then defined through the dilation of the region defined by all voxels, which were labeled as hippocampus by at least 2% of the segmentations. To evaluate the pairwise similarities, all images were aligned to the MNI152 brain atlas using the same registrations used for the mask building. Fig. 4 shows the ROI around the hippocampus superimposed on the brain atlas used for image normalization.
Fig. 4.
The MNI152 brain atlas showing the region of interest around the hippocampus that was used for the evaluation of pairwise image similarities.
Segmentation propagation in the learned manifold
In order to propagate the atlas segmentations through the dataset using the learned manifold, all images I ∈  are separated into two groups, containing the labeled and unlabeled images. These groups are indexed by the sets
are separated into two groups, containing the labeled and unlabeled images. These groups are indexed by the sets 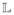 and
and 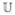 , respectively. Initially,
, respectively. Initially, 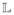 represents the initial atlas images and
represents the initial atlas images and 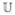 represents all other images. Let d(Ii,Ij) represent the Euclidean distance between images Ii and Ij in the manifold, the average distance from an unlabeled image Iu to all labeled images is:
represents all other images. Let d(Ii,Ij) represent the Euclidean distance between images Ii and Ij in the manifold, the average distance from an unlabeled image Iu to all labeled images is:
| (3) |
At each iteration, the images Iu, u∈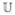 with the N smallest average distances d̄ (Iu) are chosen as targets for propagation. For each of these images, the M closest images drawn from Il, l∈
with the N smallest average distances d̄ (Iu) are chosen as targets for propagation. For each of these images, the M closest images drawn from Il, l∈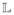 are selected as atlases to be propagated. Subsequently, the index sets
are selected as atlases to be propagated. Subsequently, the index sets 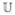 and
and 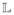 are updated to indicate that the target images in the current iteration have been labeled. Stepwise propagation is performed in this way until all images in the dataset are labeled.
are updated to indicate that the target images in the current iteration have been labeled. Stepwise propagation is performed in this way until all images in the dataset are labeled.
N is a crucial parameter as it determines the number of images labeled during each iteration and therefore it strongly affects the expected number of intermediate steps that are taken before a target image is segmented. M defines the number of atlas images used for each application of multi-atlas segmentation. A natural choice is to set M to the number of initial atlases. Independent of the choice of N, the number of registrations needed to segment K images is M×K. The process of segmentation propagation in the learned manifold is summarized in algorithm 1.
Algorithm 1.
Segmentation propagation in the learned manifold
Set 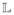 to represent the initial set of atlases to represent the initial set of atlases |
Set 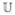 to represent all remaining images to represent all remaining images |
while |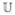 | > 0 do | > 0 do
|
for all Iu ∈ 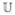 do do
|
calculate d̄ (Iu, 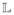 ) ) |
| end for |
Reorder index set 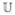 to match the order of d̄ (Iu, to match the order of d̄ (Iu, 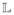 ) ) |
| for i = 1 to N do |
Select M images from Il, l ∈ 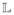 that closest to Iui that closest to Iui
|
| Registered the selected atlases to Iui |
| generate a multi-atlas segmentation estimate of Iui |
| end for |
Transfer the indices {u1, …, uN} from 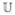 to to 
|
| end while |
Multi-atlas propagation and segmentation refinement
Each label propagation is carried out by applying a modified version of the method for hippocampus segmentation described in van der Lijn et al. (2008). In this method, the segmentations f j, j=1, …, M obtained from registering M atlases are not fused to hard segmentation as in Heckemann et al. (2006) but are instead used to form a probabilistic atlas in the coordinate system of the target image I. For each voxel p∈I, the probability of its label being fi is
| (4) |
In the original work, this subject-specific atlas is combined with previously learned intensity models for foreground and background to give an energy function that is optimized by graph cuts. We previously extended this method in a way that directly estimates the intensity models from the unseen image and that generalizes the approach to more than one structure (Wolz et al., 2009). A Gaussian distribution for a particular structure is estimated from all voxels which at least 95% of the atlases assign to this particular structure. The background distribution for a particular structure i with label fi is estimated from the Gaussian intensity distributions of all other structures with label fj, j ≠ i and of Gaussian distributions for the tissue classes Tk, k =1, …, 3 in areas where no particular structure is defined. Spatial priors γj = PA(fj) for defined structures and for the tissue classes γk (obtained from previously generated an non-rigidly aligned probabilistic atlases) are used to formulate a mixture of Gaussians (MOG) model for the probability of a voxel being in the background with respect to structure i:
| (5) |
with γstruct = Σj =1, …,N,j ≠ iγj defines the weighting between the distributions of defined structures and the general distributions of the tissue classes. The intensity and spatial contributions are combined to give the data term Dp(fp) of a Markov random field (MRF) (Li, 1994):
| (6) |
The smoothness constraint Vp,q (fp,fq) between two voxels p and q in a local image neighborhood is based on intensities and gradient (Song et al., 2006). In a graph defined on I, each voxel is represented by a vertex. Edges in this graph between neighboring vertices as well as between individual vertices and two terminal vertices s and t are defined by Vp,q (fp,fq) and Dp (fp), respectively. By determining an s−t cut on this graph, the final segmentation into foreground and background is obtained (Boykov et al., 2001).
By incorporating intensity information from the unseen image into the segmentation process, errors done with conventional multi-atlas segmentation can be overcome (van der Lijn et al., 2008; Wolz et al., 2009).
Each registration used to build the subject-specific probabilistic atlas in Eq. (4) is carried out in three steps: rigid, affine, and non-rigid. Rigid and affine registrations are carried out to correct for global differences between the images. In the third step, two images are non-rigidly aligned using a free-form deformation model in which a regular lattice of control point vectors are weighted using B-spline basis functions to provide displacements at each location in the image (Rueckert et al., 1999). The deformation is driven by the normalized mutual information (Studholme et al., 1999) of the pair of images. The spacing of B-spline control points defines the local flexibility of the non-rigid registration. A sequence of control point spacings was used in a multi-resolution fashion (20, 10, 5, and 2.5 mm).
Experiments and results
Coordinate system embedding
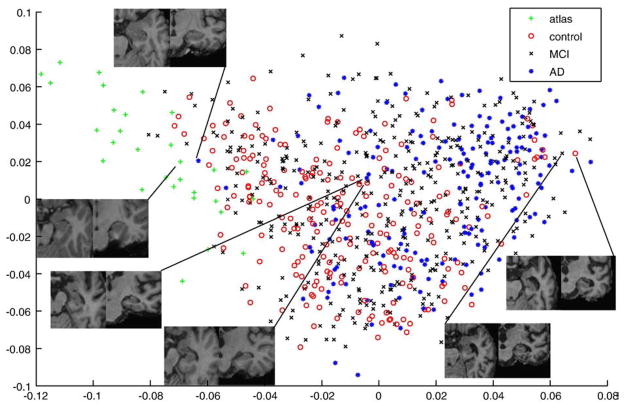
We applied the method for coordinate system embedding described in section 4 to a set of images containing the 30 initial atlases and the 796 ADNI images. We used the first two features from spectral graph analysis to embed all images into a 2D coordinate system. The results of coordinate system embedding are displayed in Fig. 5. The original atlases form a distinct cluster on the left hand side of the graph at low values for the first feature. Furthermore, it can be seen that control subjects are mainly positioned at lower values, whereas the majority of AD subjects is positioned at higher values. The hippocampal area for chosen example subjects is displayed in Fig. 5. These types of observations support the impression that neighborhoods in the coordinate system embedding represent images that are similar in terms of hippocampal appearance.
Fig. 5.
Coordinate embedding of 30 atlases based on healthy subjects and 796 images from elderly dementia patients and age-matched control subjects. Looking at the hippocampal areas for chosen example subjects support the impression that neighborhoods in the coordinate system embedding represent images that are similar in terms of hippocampal appearance.
All 796 images were segmented using five different approaches:
Direct segmentation using standard multi-atlas segmentation (Heckemann et al., 2006).
Direct segmentation using multi-atlas segmentation in combination with an intensity refinement based on graph cuts (van der Lijn et al., 2008; Wolz et al., 2009) (see also section 7).
LEAP with M=30 and N=300 and no intensity refinement after multi-atlas segmentation.
LEAP (see section 2) with M=30 and N=1.
LEAP with M=30 and N=300.
Evaluation of segmentations
For evaluation, we compared the automatic segmentation of the ADNI images with a manual hippocampus segmentation. This comparison was carried out for all of the images for which ADNI provides a manual segmentation (182 out of 796). Comparing these 182 subjects (Table 2) with the entire population of 796 subjects (Table 1) shows that the subgroup is characteristic of the entire population in terms of age, sex, MMSE, and pathology.
Table 2.
Characteristics of the subjects used for comparison between manual and automatic segmentation.
| N | M/F | Age | MMSE | |
|---|---|---|---|---|
| Normal | 57 | 27/30 | 77.1±4.60 [70–89] | 29.29±0.76 [26–30] |
| MCI | 84 | 66/18 | 76.05±6.77 [60–89] | 27.29±3.22 [24–30] |
| AD | 41 | 21/20 | 76.08±12.80 [57–88] | 23.12±1.79 [20–26] |
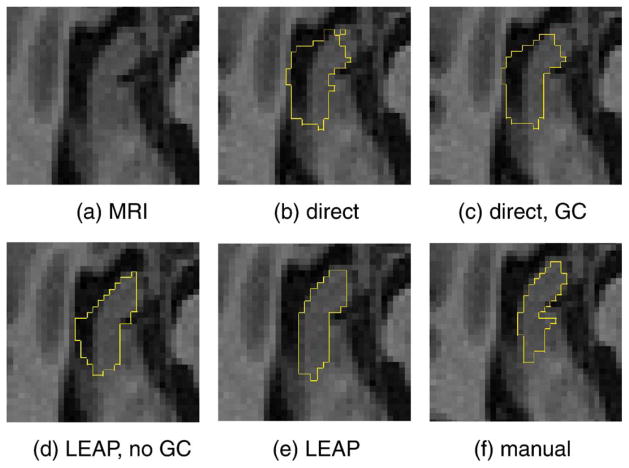
An example for the segmentation of the right hippocampus of an AD subject is shown in Fig. 6. A clear over-segmentation into CSF space and especially an under-segmentation in the anterior part of the hippocampus can be observed, both in the case of multi-atlas segmentation with and without intensity-based refinement (methods I and II). The fact that the intensity-based refinement cannot compensate for this error is due to the high spatial prior in this area that is caused by a significant misalignment of the majority of atlases in this area. The resulting high spatial prior cannot be overcome by the intensity-based correction scheme. When using the proposed framework without intensity-refinement (method III), the topological errors can be avoided, but the over-segmentation into CSF space is still present. The figure also shows that all observed problems can be avoided by using the proposed framework.
Fig. 6.
Comparison of segmentation results for the right hippocampus on a transverse slice. Panels b, c, d, and e correspond to methods I, II, III, and V, respectively.
The average overlaps as measured by the Dice coefficient or similarity index (SI) (Dice, 1945) for the segmentation of left and right hippocampus on the 182 images used for evaluation are shown in Table 3. The difference between all pairs of the five methods is statistically significant with p<0.001 on Student’s two-tailed paired t-test.
Table 3.
Dice overlaps for hippocampus segmentation.
| Left hippocampus | Right hippocampus | |
|---|---|---|
| Direct | 0.775±0.087 [0.470–0.904] | 0.790±0.080 [0.440–0.900] |
| Direct, GC | 0.820±0.064 [0.461–0.903] | 0.825±0.065 [0.477–0.901] |
| LEAP, N=300, no GC | 0.808±0.054 [0.626–0.904] | 0.814±0.053 [0.626–0.900] |
| LEAP, N=1 | 0.838±0.023 [0.774–0.888] | 0.830±0.024 [0.753–0.882] |
| LEAP, N=300 | 0.848±0.033 [0.676–0.903] | 0.848±0.030 [0.729–0.905] |
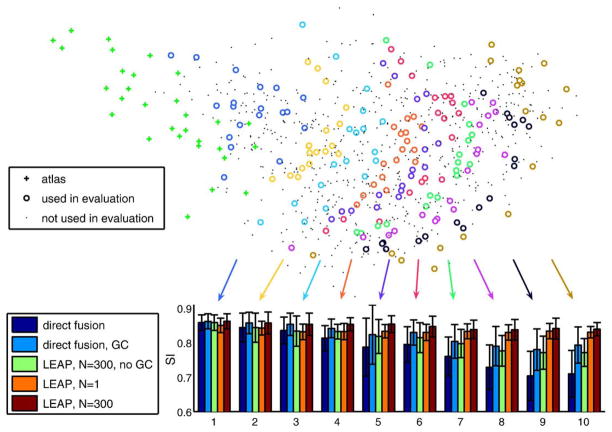
These results clearly show an improved segmentation accuracy and robustness for the proposed method. Our hypothesis is that by avoiding the direct registration of images whose distance in the embedded space is too large but instead registering the images via multiple intermediate images improves significantly the segmentation accuracy and robustness of multi-atlas segmentation. To test this hypothesis, we have investigated the development of the segmentation accuracy as a function of distances in the coordinate system embedding as well as the number of intermediate steps. Fig. 7 shows this for the five segmentation methods in the form of ten bar plots. Each bar plot corresponds to the average SI overlap of 18 images (20 in the last plot). The first plot represents the 18 images closest to the original atlases, the next plot represents images slightly further from the original atlases and so on. These results show the superiority of the proposed method over direct multi-atlas segmentation approaches in segmenting images that are different from the original atlas set.
Fig. 7.
Development of segmentation accuracy with increasing distance from the original set of atlases. Each subset of images used for evaluation is represented by one bar plot.
With increasing distance from the original atlases in the learned manifold, the accuracy of direct multi-atlas segmentation (method I) as well as multi-atlas segmentation with intensity-based refinement (method II) steadily decreases. By contrast, LEAP with both parameter settings shows a steady level of segmentation accuracy. It is interesting to see that our method with a step width of N=1 (method IV) leads to worse results than the direct multi-atlas methods up to a certain distance from the original atlases. This can be explained by registration errors accumulated through many registration steps. With increasing distance from the atlases, however, the gain from using intermediate templates outweighs this registration error. Furthermore, the accumulated registration errors do not seem to increase dramatically after a certain number of registrations. This is partly due to the intensity-based correction in every multi-atlas segmentation step which corrects for small registration errors. Segmenting the300 closest images with LEAP before doing the next intermediate step (N=300, method V) leads to results at least as good as and often better than those given by the direct methods for images at all distances from the initial atlases. The importance of an intensity-based refinement step after multi-atlas segmentation is also underlined by the results of method III. When applying LEAP without this step, the gain compared to method I gets more and more significant with more intermediate steps, but the accuracy still declines significantly, which can be explained by a deterioration of the propagated atlases (note that for the first 300 images, method II and method V are identical, as are methods I and III). The influence of N on the segmentation accuracy is governed by the trade-off between using atlases that are as close as possible to the target image (small N) and using a design where a minimum number of intermediate steps are used to avoid the accumulation of registration errors (large N). Due to the computational complexity of evaluating the framework, we restricted the evaluation in this article to two values.
Volume measurements
A reduction in hippocampal volume is a well-known factor associated with cognitive impairment (e.g., Jack et al., 1999; Reiman et al., 1998). To measure the ability of our method to discriminate clinical groups by hippocampal volume, we compared the volumes measured on the 182 manually labeled images to the ones obtained from our automatic method (method V, LEAP with M=30 and N=300). Box plots showing these volumes for the left and right hippocampus are displayed in Fig. 8. The discriminative power for the volume of left and right hippocampus between all pairs of clinical groups is statistically significant with p<0.05 on a Student’s t-test but is slightly less significant than the manual discrimination.
Fig. 8.
Average hippocampal volumes for manual and automatic segmentation using method V.
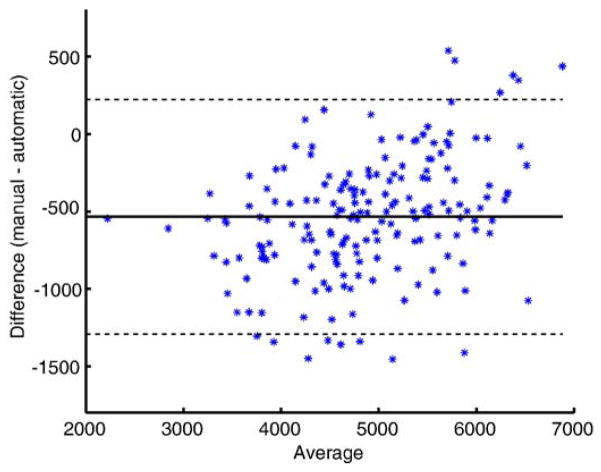
A Bland–Altman plot of the agreement of the two volume measurements is shown in Fig. 9. This plot supports the impression of the volume measures in Fig. 9 that the automated method tends to slightly overestimate the hippocampal volumes. This over-segmentation is more significant for small hippocampi. The same phenomenon has been described for an automatic segmentation method before by Hammers et al. (2007). The intraclass correlation coefficient (ICC) between the volume measurements based on the manual and automatic segmentation is 0.898 (ICC (3,1) Shrout-Fleiss reliability (Shrout and Fleiss, 1979)). This value is comparable to the value of 0.929 reported in Niemann et al. (2000) for inter-rater reliability.
Fig. 9.
A Bland–Altman plot showing the agreement between volume measurement based on manual and automatic segmentation of the hippocampus (method V). The solid line represents the mean and the dashed lines represent ±1.96 standard deviations.
Discussion and conclusion
In this work, we have described the LEAP framework for propagating an initial set of brain atlases to a diverse population of unseen images via multi-atlas segmentation. We begin by embedding all atlas and target images in a coordinate system where similar images according to a chosen measure are close. The initial set of atlases is then propagated in several steps through the manifold represented by this coordinate system. This avoids the need to estimate large deformations between images with significantly different anatomy and the correspondence between them is broken down into a sequence of comparatively small deformations. The formulation of the framework is general and is not tied to a particular similarity measure, coordinate embedding, or registration algorithm.
We applied LEAP to a target dataset of 796 images acquired from elderly dementia patients and age-matched controls using a set of 30 atlases of healthy young subjects. In this first application of the method, we have applied it to the task of hippocampal segmentation even though the proposed framework can be applied to other anatomical structures as well. The proposed method shows consistently improved segmentation results compared to standard multi-atlas segmentation. We have also demonstrated a consistent level of accuracy for the proposed approach with increasing distance from the initial set of atlases and therefore with more intermediate registration steps. The accuracy of standard multi-atlas segmentation, on the other hand, steadily decreases. This observation suggests three main conclusions: (1) the decreasing accuracy of the standard multi-atlas segmentation suggests that the coordinate system embedding used is meaningful. The initial atlases get less and less suitable for segmentation with increasing distance. (2) The almost constant accuracy of the proposed method suggests that, by using several small deformations, it is possible to indirectly deform an atlas appropriately to a target in a way that is not matched by a direct deformation within the multi-atlas segmentation framework used. (3) The gain from restricting registrations to similar images counters the accumulation of errors when using successive small deformations.
Our results indicate that, if many intermediate registrations are used, the segmentation accuracy initially declines quickly but then remains relatively constant with increasing distance from the initial atlases. The initial decline can be explained by an accumulation of registration errors, which results from many intermediate registration steps. The reason why the accuracy does not monotonically decline is likely to be due to the incorporation of the intensity model during each multi-atlas segmentation step. By automatically correcting the propagated segmentation based on the image intensities, the quality of the atlas can be preserved to a certain level.
Apart from the obvious application of segmenting a dataset of diverse images with a set of atlases based on a subpopulation, the proposed method can be seen as an automatic method for generating a large repository of atlases for subsequent multi-atlas segmentation with atlas selection (Aljabar et al., 2009). Since the manual generation of large atlas databases is expensive, time-consuming, and in many cases unfeasible, the proposed method could potentially be used to automatically generate such a database.
Notwithstanding the challenge represented by variability due to image acquisition protocols and inter-subject variability in a dataset as large and as diverse as the one in the ADNI study, the results achieved with our method compare well to state of the art methods applied to more restricted datasets (van der Lijn et al., 2008; Morra et al., 2008; Chupin et al., 2009; Hammers et al., 2007) in terms of accuracy and robustness.
In future work, we plan to evaluate other approaches for the coordinate system embedding of brain images. The main methodological choices to consider in this context are the pairwise image similarities where we are planning to investigate the use of an energy based on image deformation (e.g., Beg et al., 2005) and the embedding method itself. Using a direct metric based on pairwise diffeomorphic registration to describe the distances between images would allow for the use of manifold learning techniques such as MDS (Cox and Cox, 1994) or Isomap (Tenenbaum et al., 2000). An alternative is to use the Euclidean distance derived from spectral analysis as data for a subsequent learning step using these techniques. The resulting geodesic distance of such an embedding could lead to an improved description of a complex manifold covering a large variety of images.
The ultimate goal is to apply the proposed method to all 83 structures in our atlas set. In its current form, the LEAP framework would need to be applied to each structure separately. Future work will therefore need to be carried out to adapt the method to segment multiple structures in a computationally efficient manner. In this work, we chose the number of dimensions for the embedded coordinates based on the resulting discrimination between the subject groups. The optimal number of dimensions can vary according to the data studied. Other methods for selecting the dimension of embedding coordinates are possible and represent a potentially useful area of future study.
Another area of future research will be the extension of this framework to 4D datasets so that atrophy rates can be accurately determined. One approach would be to align follow-up scans with their baseline and then use the same label maps as for the baseline image to segment the follow-up scan using an intensity model as described in Wolz et al. (2009).
Acknowledgments
This project is partially funded under the 7th Framework Programme by the European Commission (http://cordis.europa.eu/ist/).
Data collection and sharing for this project were funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI; Principal Investigator: Michael Weiner; NIH grant U01 AG024904). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering (NIBIB), and through generous contributions from the following: Pfizer Inc., Wyeth Research, Bristol-Myers Squibb, Eli Lilly and Company, GlaxoSmithKline, Merck & Co. Inc., AstraZeneca AB, Novartis Pharmaceuticals Corporation, Alzheimer’s Association, Eisai Global Clinical Development, Elan Corporation plc, Forest Laboratories, and the Institute for the Study of Aging, with participation from the US Food and Drug Administration. Industry partnerships are coordinated through the Foundation for the National Institutes of Health. The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory of Neuroimaging at the University of California, Los Angeles.
Appendix A. The Alzheimer’s Disease Neuroimaging Initiative
The Alzheimer’s Disease Neuroimaging Initiative (ADNI) was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The principle investigator of this initiative is Michael W. Weiner, M.D., VA Medical Center and University of California–San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the United States and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55 to 90 years, to participate in the research—approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years, and 200 people with early AD to be followed for 2 years. For up-to-date information, see www.adni-info.org.
Footnotes
References
- Aljabar P, Heckemann R, Hammers A, Hajnal J, Rueckert D. Multi-atlas based segmentation of brain images: atlas selection and its effect on accuracy. Neuro Image. 2009;46 (3):726–738. doi: 10.1016/j.neuroimage.2009.02.018. [DOI] [PubMed] [Google Scholar]
- Avants B, Gee JC. Geodesic estimation for large deformation anatomical shape averaging and interpolation. Neuro Image. 2004;23(Suppl 1):S139–S150. doi: 10.1016/j.neuroimage.2004.07.010. mathematics in Brain Imaging. [DOI] [PubMed] [Google Scholar]
- Bajcsy R, Lieberson R, Reivich M. A computerized system for the elastic matching of deformed radiographic images to idealized atlas images. J Comput Assisted Tomogr. 1983 Aug;7:618–625. doi: 10.1097/00004728-198308000-00008. [DOI] [PubMed] [Google Scholar]
- Beg MF, Miller MI, Trouve A, Younes L. Computing large deformation metric mappings via geodesic OWS of diffeomorphisms. International Journal of Computer Vision. 2005 Feb61(2):139–157. [Google Scholar]
- Bhatia KK, Aljabar P, Boardman JP, Srinivasan L, Murgasova M, Counsell SJ, Rutherford MA, Hajnal JV, Edwards AD, Rueckert D. Groupwise combined segmentation and registration for atlas construction. In: Ayache N, Ourselin S, Maeder AJ, editors. MICCAI (1) Vol 4791 of Lecture Notes in Computer Science. Springer; 2007. pp. 532–540. [DOI] [PubMed] [Google Scholar]
- Blezek DJ, Miller JV. Atlas stratification. Medical Image Analysis. 2007;11 (5):443–457. doi: 10.1016/j.media.2007.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. IEEE Transactions on PAMI. 2001 Nov23(11):1222–1239. [Google Scholar]
- Chung FRK. Spectral graph theory. Regional Conference Series in Mathematics, American Mathematical Society. 1997;92:1–212. [Google Scholar]
- Chupin M, Hammers A, Liu R, Colliot O, Burdett J, Bardinet E, Duncan J, Garnero L, Lemieux L. Automatic segmentation of the hippocampus and the amygdala driven by hybrid constraints: method and validation. Neuro Image. 2009;46 (3):749–761. doi: 10.1016/j.neuroimage.2009.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins DL, Holmes CJ, Peters TM, Evans AC. Automatic 3-D model-based neuroanatomical segmentation. Hum Brain Mapp. 1995;3 (3):190–208. [Google Scholar]
- Cox TF, Cox MAA. Multidimensional Scaling. Chapman & Hall; London: 1994. [Google Scholar]
- Davis BC, Fletcher PT, Bullitt E, Joshi S. Population shape regression from random design data. ICCV. 2007:1–7. [Google Scholar]
- Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26 (3):297–302. [Google Scholar]
- Ericsson A, Aljabar P, Rueckert D. Construction of a patient-specific atlas of the brain: application to normal aging. ISBI IEEE. 2008:480–483. [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. Mini-mental state: a practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12 (3):189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Gee JC, Reivich M, Bajcsy R. Elastically deforming 3D atlas to match anatomical brain images. Journal of Computer Assisted Tomography. 1993 Mar.–Apr;17(2):225–236. doi: 10.1097/00004728-199303000-00011. [DOI] [PubMed] [Google Scholar]
- Gousias IS, Rueckert D, Heckemann RA, Dyet LE, Boardman JP, Edwards AD, Hammers A. Automatic segmentation of brain MRIs of 2-year-olds into 83 regions of interest. Neuro Image. 2008;40 (2):672–684. doi: 10.1016/j.neuroimage.2007.11.034. [DOI] [PubMed] [Google Scholar]
- Hammers A, Allom R, Koepp MJ, et al. Three-dimensional maximum probability atlas of the human brain, with particular reference to the temporal lobe. Hum Brain Mapp. 2003 Aug;19(4):224–247. doi: 10.1002/hbm.10123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammers A, Heckemann R, Koepp MJ, Duncan JS, Hajnal JV, Rueckert D, Aljabar P. Automatic detection and quantification of hippocampal atrophy on mri in temporal lobe epilepsy: a proof-of-principle study. Neuro Image. 2007;36 (1):38–47. doi: 10.1016/j.neuroimage.2007.02.031. [DOI] [PubMed] [Google Scholar]
- Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. Neuro Image. 2006;33 (1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- Heckemann RA, Hammers A, Rueckert D, Aviv R, Harvey C, Hajnal J. Automatic volumetry on MR brain images can support diagnostic decision making. BMC Medical Imaging. 2008;8(9):8, 9. doi: 10.1186/1471-2342-8-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CRJ, Petersen RC, Xu YC, O’Brien PC, Smith GE, Ivnik RJ, Boeve BF, Waring SC, Tangalos EG, Kokmen E. Prediction of AD with MRI-based hippocampal volume in mild cognitive impairment. Neurology. 1999;52 (7):1397–1407. doi: 10.1212/wnl.52.7.1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Bernstein MA, Fox NC, Thompson P, Alexander G, Harvey D, Borowski B, Britson PJ, Whitwell JL, Ward C, Dale AM, Felmlee JP, Gunter JL, Hill DL, Killiany R, Schuff N, Fox-Bosetti S, Lin C, Studholme C, DeCarli CS, Krueger G, Ward HA, Metzger GJ, Scott KT, Mallozzi R, Blezek D, Levy J, Debbins JP, Fleisher AS, Albert M, Green R, Bartzokis G, Glover G, Mugler J, Weiner MW. The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods. J Magn Reson Imag. 2008;27 (4):685–691. doi: 10.1002/jmri.21049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. Neuro Image. 2004;23(Supplement 1):151–160. doi: 10.1016/j.neuroimage.2004.07.068. mathematics in Brain Imaging. [DOI] [PubMed] [Google Scholar]
- Jovicich J, Czanner S, Greve D, Haley E, van der Kouwe A, Gollub R, Kennedy D, Schmitt F, Brown G, MacFall J, Fischl B, Dale A. Reliability in multi-site structural MRI studies: effects of gradient non-linearity correction onphantom and human data. Neuro Image. 2006;30 (2):436–443. doi: 10.1016/j.neuroimage.2005.09.046. [DOI] [PubMed] [Google Scholar]
- Li SZ. Markov random field models in computer vision. ECCV. 1994:B:361–370. [Google Scholar]
- Lorenzen P, Prastawa M, Davis B, Gerig G, Bullitt E, Joshi S. Multi-modal image set registration and atlas formation. Med Imag Anal. 2006;10(3):440–451. doi: 10.1016/j.media.2005.03.002. special Issue on The Second International Workshop on Biomedical Image Registration (WBIR’03) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans AC, Fox PT, Lancaster JL. A probabilistic atlas of the human brain: theory and rationale for its development. the international consortium for brain mapping (ICBM) Neuro Image. 1995 Jun;2(2a):89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- Morra JH, Tu Z, Apostolova LG, Green AE, Avedissian C, Madsen SK, Parikshak N, Hua X, Toga AW, Jr, Jack CR, Jr, Weiner MW, Thompson PM. Validation of a fully automated 3D hippocampal segmentation method using subjects with Alzheimer’s disease mild cognitive impairment, and elderly controls. Neuro Image. 2008;43 (1):59–68. doi: 10.1016/j.neuroimage.2008.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller SG, Weiner MW, LJT, et al. The Alzheimer’s disease neuroimaging initiative. Neuroimaging Clinics of North America. 2005;15(4):869–877. doi: 10.1016/j.nic.2005.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niemann K, Hammers A, Coenen VA, Thron A, Klosterktter J. Evidence of a smaller left hippocampus and left temporal horn in both patients with first episode schizophrenia and normal control subjects. Psychiatry Research: Neuroimaging. 2000;99 (2):93–110. doi: 10.1016/s0925-4927(00)00059-7. [DOI] [PubMed] [Google Scholar]
- Reiman EM, Uecker A, Caselli RJ, Lewis S, Bandy D, de Leon MJ, Santi SD, Convit A, Osborne D, Weaver A, Thibodeau SN. Hippocampal volumes in cognitively normal persons at genetic risk for Alzheimer’s disease. Ann Neurol. 1998 Aug;44(2):288–291. doi: 10.1002/ana.410440226. [DOI] [PubMed] [Google Scholar]
- Rohlfing T, Russakoff DB, Jr, CRM Performance-based classifier combination in atlas-based image segmentation using expectation maximization parameter estimation. IEEE Trans Med Imaging. 2004;23 (8):983–994. doi: 10.1109/TMI.2004.830803. [DOI] [PubMed] [Google Scholar]
- Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans Medical Imaging. 1999 Aug;18(8):712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- Sabuncu MR, Balci SK, Golland P. MICCAI (2) Vol 5242 of Lecture Notes in Computer Science. Springer; 2008. Discovering modes of an image population through mixture modeling; pp. 381–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrout P, Fleiss J. Intraclass correlation: uses in assessing rater reliability. Psychological Bulletin. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Medical Imaging. 1998 Feb;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Song Z, Tustison NJ, Avants BB, Gee JC. Integrated graph cuts for brain MRI segmentation. In: Larsen R, Nielsen M, Sporring J, editors. MICCAI (2) Vol 4191 of Lecture Notes in Computer Science. Springer; 2006. pp. 831–838. [DOI] [PubMed] [Google Scholar]
- Studholme C, Cardenas V. A template free approach to volumetric spatial normalization of brain anatomy. Pattern Recogn Lett. 2004 Jul25(10):1191–1202. [Google Scholar]
- Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recogn. 1999 Jan32(1):71–86. [Google Scholar]
- Tang S, Fan Y, Kim M, Shen D. RABBIT: rapid alignment of brains by building intermediate templates. SPIE. 2009 Feb;7259 doi: 10.1016/j.neuroimage.2009.02.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenenbaum JB, de Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. 2000 Dec;290(5500):2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- Thompson PM, Woods RP, Mega MS, Toga AW. Mathematical/computational challenges in creating deformable and probabilistic atlases of the human brain. 2000 doi: 10.1002/(SICI)1097-0193(200002)9:2<81::AID-HBM3>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Lijn F, den Heijer T, Breteler MM, Niessen WJ. Hippocampus segmentation in MR images using atlas registration, voxel classification, and graph cuts. Neuro Image. 2008;43 (4):708–720. doi: 10.1016/j.neuroimage.2008.07.058. [DOI] [PubMed] [Google Scholar]
- van Rikxoort EM, Isgum I, Staring M, Klein S, van Ginneken B. Adaptive local multi-atlas segmentation: application to heart segmentation in chest CT scans. SPIE Vol. 2008;6914:691407. doi: 10.1016/j.media.2009.10.001. [DOI] [PubMed] [Google Scholar]
- von Luxburg U. A tutorial on spectral clustering. Statistics and Computing. 2007;17 (4):395–416. [Google Scholar]
- Warfield SK, Zou KH, Wells WM., III Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans Med Imaging. 2004;23 (7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolz R, Aljabar P, Heckemann RA, Hammers A, Rueckert D. Segmentation of subcortical structures and the hippocampus in brain MRI using graph-cuts and subject-specific a-priori information. IEEE International Symposium on Biomedical Imaging - ISBI; 2009.2009. [Google Scholar]
- Wu M, Rosano C, Lopez-Garcia P, Carter CS, Aizenstein HJ. Optimum template selection for atlas-based segmentation. Neuro Image. 2007;34 (4):1612–1618. doi: 10.1016/j.neuroimage.2006.07.050. [DOI] [PubMed] [Google Scholar]
- Zöllei L, Learned-Miller EG, Grimson WEL, Wells WM., III . Efficient population registration of 3D data. In: Liu Y, Jiang T, Zhang C, editors. CVBIA Vol 3765 of Lecture Notes in Computer Science. Springer; 2005. pp. 291–301. [Google Scholar]