Do Over 200 Million Healthy Altitude Residents Really Suffer from Chronic Acid–Base Disorders?

Abstract

As the oxygen tension of inspired air falls with increasing altitude in normal subjects, hyperventilation ensues. This acute respiratory alkalosis, induces increased renal excretion of bicarbonate, returning the pH back to normal, giving rise to compensated respiratory alkalosis or chronic hypocapnia. It seems a contradiction that so many normal people at high altitude should permanently live as chronic acid–base patients. Blood gas analyses of 1,865 subjects at 3,510 m, reported a P_aCO₂ (arterial carbon dioxide tension ± SEM) = 29.4 ± 0.16 mmHg and pH = 7.40 ± 0.005. Base excess, calculated with the Van Slyke sea level equation, is −5 mM (milliMolar or mmol/l) as an average, suggesting chronic hypocapnia. THID, a new term replacing “Base Excess” is determined by titration to a pH of 7.40 at a P_aCO₂ of 5.33 kPa (40 mmHg) at sea level, oxygen saturated and at 37°C blood temperature. Since our new modified Van Slyke equations operate with normal values for P_aCO₂ at the actual altitude, a calculation of THID will always result in normal values—that is, zero.

Introduction

We have previously published the following calculations in another context [1] except for some minor corrections. However, the question formulated in the title still remains to be answered.

As the oxygen tension in the inspired air (P_IO₂) falls with increasing altitude in normal subjects, the oxygen tension in the arterial blood (P_aO₂) eventually falls below the ventilation threshold 55 mmHg, which stimulates the arterial chemoreceptors to elicit CO₂ washout. Hyperventilation is a classical reaction to life at high altitude [2–7]. Upon arrival, this acute respiratory alkalosis is compensated by increased renal excretion of bicarbonate, which is the result of decreased tubular H⁺ secretion. This happens because the low P_aCO₂ reduces the tubular H⁺ secretion, and alkalosis inhibits formation and secretion of ammonium ion (NH₄⁺). Renal compensation of the respiratory alkalosis is complete after some days, and pH is back to normal. The status is called totally compensated respiratory alkalosis or chronic hypocapnia. More than 200 million people live at altitudes above 2,500 m around the world. It seems to be a contradiction that so many normal people should live their whole lives as patients with acid–base disorders.

Materials and Methods

High Altitude Blood Gas Measurements and “Base Excess”

We have found this contradiction by looking at a large database from the city of La Paz in Bolivia.

A population of 1,865 persons breathing ambient air was examined at the High Altitude Pathology Institute in La Paz at 3,510 m above sea level. Arterial blood samples were analyzed with a Radiometer pHMK2 calibrated following the manufacturer recommendations. This population sample was mainly healthy female and male altitude residents of all ages. We have found no difference between the natives and lowlanders in the P_aCO₂ levels. Upon arriving to the high altitude in La Paz, the arterial blood gases of the lowlanders, initially show an acute respiratory alkalosis, where the pH is alkaline, above 7.45 and the P_aCO₂ tends to be lower than 28 mmHg. However, this condition is normalized following acute adaptation where the P_aCO₂ becomes normocapnic (for the corresponding altitude). For example at 3,600 m, P_aCO₂ is at 30 mmHg ± 2 mmHg.

Results

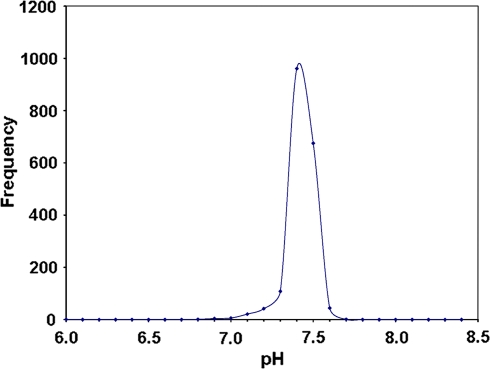
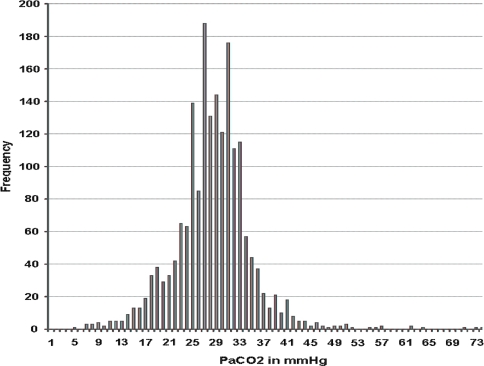
The average P_aCO₂ (arterial carbon dioxide tension) SEM was 29.4 ± 0.16 mmHg, normal for an altitude of 3,500 m. The body always compensates the pH and the mean pH in the arterial blood is always 7.40 ± 0.005, identical to sea level normal values. The third essential variable in the Radiometer methodology is called Base excess [2, 8–10], and this value was calculated by means of the Van Slyke sea level equation to be −5 mM (milliMolar or mmol/l) as an average at 3,510 m, suggesting chronic hypocapnia (Figs. 1 and 2).

Fig. 1.

The high kurtosis curve shows that most patients had a normal pH of 7.4. This is because many were suffering from disease that did not compromise the acid–base status of blood. However, the incidence of a pH of 7.5 is also important since at high altitude hyperventilation is one of the fundamental compensation mechanisms for acute hypoxia. Metabolic (or rarely respiratory) acidosis is present and a result of disease that is of the same characteristics as at sea level

Fig. 2.

Above 90% of the patients have a P_aCO₂ below 40 Torr (5.33 kPa). The average P_aCO₂ at 3,510 m is 29.4 Torr. This implies that although the average P_aO₂ can be lower at high altitude during disease, the average P_aCO₂ remains within the normal limits. It also shows that the highest values reached are around 57 and in some extreme but very isolated and serious cases up to 73 Torr (9.73 kPa). At high altitude it is not possible to tolerate a high P_aCO₂

This base excess calculation implies that the population group in La Paz is diagnosed as suffering from chronic hypocapnia. However, this is not chronic hypocapnia, but just the normal P_aCO₂ of 29.5 mmHg in La Paz. Obviously, since P_aCO₂ is normal and pH is 7.40 the third essential variable—which is calculated on the basis of the 2 first values—must be normal, which is zero. Consequently, the Van Slyke sea level equation for the calculation of base excess must be adapted to altitude, since it results in a false value namely an average base excess of −5 mM, instead of zero.

Base excess is identical with the actual buffer base (BB) minus the normal BB. However, the name base excess is misleading, since the essential variable is not a base and in reality not always an excess (i.e., neither excess or deficit). The essential concept is the titratable hydrogen ion.

Discussion

The Titratable Hydrogen Ion Concentration Difference (THID)

In 1971 Siggaard-Andersen published his precise acid–base chart [9]. Blood plus interstitial fluid work as one buffer compartment, which Siggaard-Andersen called “the extended ExtraCellular Fluid” or eECF. A generally accepted model for the eECF corresponds to an arterial blood sample diluted threefold in its own plasma [11]. In a 2004 publication [12] Siggaard-Andersen changed the scale of the base excess of his chart to a titratable hydrogen ion concentration scale, which we have shortened to THID.

The THID in the eECF is calculated from the Van Slyke equation [10] based on the measurements of pH and PCO₂. The Van Slyke sea level equation reads as follows:

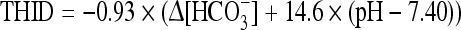where ∆[HCO₃⁻] = [actual bicarbonate] − 24.5 mM, for a hemoglobin concentration of 3 mM in eECF. The factors 0.93 and 14.6 depend upon the hemoglobin concentration [2, 8].

We have therefore looked after a better name, and actually Siggaard-Andersen himself introduced the term “concentration of titratable hydrogen ion” as an alternative [11]. Since the total concept is “Titratable Hydrogen Ion concentration Difference from normal”, we have suggested the short term: THID. The concept THID is equal to base excess but with opposite signs.

From now on THID is used instead of Base Excess. The THID is ideally determined by titration to a pH of 7.40 at a P_aCO₂ of 5.33 kPa (40 mmHg) at sea level, oxygen saturated and at a blood temperature of 37°C. The THID in vivo is independent of P_aCO₂, since any change of P_aCO₂ implies opposite molar changes of the bicarbonate and the non-carbonic buffer concentrations. Consequently, there is no change in THID, so the value is constant (normally equal to zero) during acute changes in P_aCO₂ by hyper- or hypoventilation. The buffer capacity of the carbon dioxide–bicarbonate buffer is high, since respiratory elimination of CO₂ and bicarbonate excretion of the kidneys rapidly maintains P_aCO₂.

Since the average P_aCO₂ for healthy altitude residents is reduced with increasing altitude, we have calculated mean values for three relevant altitudes: 2500, 3500 and 4500 m. The following formula fits the known data quite well up to 5,000 m, so we have used:

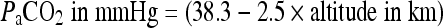to calculate P_aCO₂ at these altitudes. The mean P_aCO₂ values for the three relevant altitude are: 32.5, 29.5 and 27.5 mmHg, respectively.

The Van Slyke Equation Modified for High Altitude

Since the Van Slyke sea level equation [10] applied to the La Paz population group provides us with false values for the third variable, we had to modify the equation for use at high altitude. For healthy altitude residents a correction for acid–base disorders to a THID of zero is therefore performed:

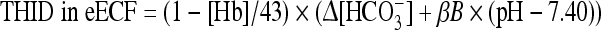where ∆[HCO₃⁻] = [actual bicarbonate] − [Altitude bicarbonate], [Hb] = hemoglobin concentration in mM/3 in eECF, [Altitude bicarbonate] = −1.8 × (altitude in km) + 24.32.

The calculated mean [Altitude bicarbonate] for the three chosen altitudes are 19.8, 18 and 16.2 mM, respectively. Additionally, the buffering capacity of a normally increased hemoglobin concentration at altitude must be included. The first term in the Van Slyke equation ([Hb]) is calculated based on data from the La Paz laboratory: [Altitude Hb] = [Hb] + 0.2 × (altitude in km), which results in 0.93, 0.92 and 0.91 in mM/3 at the three altitudes, respectively. The buffer value of non-bicarbonate buffers in blood (βB) is calculated using these altitude hemoglobin values and the formula: βB = 2.3 × [Hb] + 7.7 mM, being 15.8, 16.2 and 16.7 mM at the three altitudes, respectively.

• At sea level:

  

  where Δ(HCO₃⁻) = (actual bicarbonate) − 24.5 mM.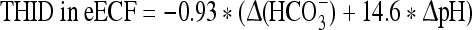

• At 2,500 m:

  

  where Δ(HCO₃⁻) = (actual bicarbonate) − 19.8 mM.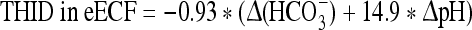

• At 3,500 m:

  

  where Δ(HCO₃⁻) = (actual bicarbonate) − 18.0 mM.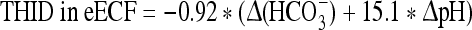

• At 4,500 m:

  

  where Δ(HCO₃⁻) = (actual bicarbonate) − 16.2 mM.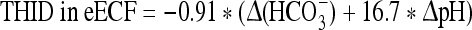

Based on these equations, acid–base charts have been developed for the three altitudes to aid clinicians at the sites of high altitude residence [1]. THID is equal to zero in healthy subjects, positive in primary (bicarbonate treatable) metabolic acidosis and negative in primary metabolic alkalosis. The pH balance is crucial also at altitude, and the body maintains a pH of 7.40 ± 0.04 at any altitude. Since our Van Slyke equations operate with normal mean values for P_aCO₂ at the actual altitude, a calculation of THID will always result in normal values—that is—zero.

Conclusions

The contradiction formulated in the title is still open for discussion, but we feel it preferable to introduce normal high altitude P_aCO₂ values in the Van Slyke equation. Hereby we avoid false diagnoses on 200 million healthy persons around the world living 2500 m above sea level. These concepts are transcendental during acid–base correction in continuously increasing high altitude intensive care units all over the world and are bound to be crucial in saving lives.