Abstract
Takens' theorem (1981) shows how lagged variables of a single time series can be used as proxy variables to reconstruct an attractor for an underlying dynamic process. State space reconstruction (SSR) from single time series has been a powerful approach for the analysis of the complex, non-linear systems that appear ubiquitous in the natural and human world. The main shortcoming of these methods is the phenomenological nature of attractor reconstructions. Moreover, applied studies show that these single time series reconstructions can often be improved ad hoc by including multiple dynamically coupled time series in the reconstructions, to provide a more mechanistic model. Here we provide three analytical proofs that add to the growing literature to generalize Takens' work and that demonstrate how multiple time series can be used in attractor reconstructions. These expanded results (Takens' theorem is a special case) apply to a wide variety of natural systems having parallel time series observations for variables believed to be related to the same dynamic manifold. The potential information leverage provided by multiple embeddings created from different combinations of variables (and their lags) can pave the way for new applied techniques to exploit the time-limited, but parallel observations of natural systems, such as coupled ecological systems, geophysical systems, and financial systems. This paper aims to justify and help open this potential growth area for SSR applications in the natural sciences.
Introduction
A growing realization in many natural sciences is that simple idealized notions of linearly decomposable, fixed equilibrium systems often do not accord with reality. Rather, empirical measurements on ecosystems, metabolic systems, financial networks, and the like suggest a more complex, but potentially more information-rich paradigm at work [1]–[14]. Despite a long history of linear methods development in the engineering sciences, natural systems are generally not well described as sums of independent frequencies that can be sensibly decomposed, analyzed as non-interacting, and reassembled (e.g. Fourier or spectral analysis) in the style of traditional reductionism [15], [16]. Rather, quantitative measurements show many systems to be fundamentally non-equilibrium and unstable, in a manner more consistent with nonlinear (state dependent) dynamics occurring on a strange attractor manifold  , where relationships between state variables cannot be studied independently of the overall system state [17]–[27]. This emergent comprehensive view may help explain why many natural systems, such a those mentioned above, appear so difficult to understand and predict. Mirage correlations are commonplace in nonlinear systems where the manifold may contain trajectories that can temporarily exhibit positive correlations between variables for surprisingly long time periods (and in some regions of the state space) and can subsequently and rapidly exhibit negative correlations or no relationship in other time periods (and other regions of
, where relationships between state variables cannot be studied independently of the overall system state [17]–[27]. This emergent comprehensive view may help explain why many natural systems, such a those mentioned above, appear so difficult to understand and predict. Mirage correlations are commonplace in nonlinear systems where the manifold may contain trajectories that can temporarily exhibit positive correlations between variables for surprisingly long time periods (and in some regions of the state space) and can subsequently and rapidly exhibit negative correlations or no relationship in other time periods (and other regions of 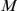 ). This transient property of apparent non-stationarity in correlations is one of the confounding phenomena faced by traditional linear models that require continual refitting and exhibit little or no predictive power.
). This transient property of apparent non-stationarity in correlations is one of the confounding phenomena faced by traditional linear models that require continual refitting and exhibit little or no predictive power.
In this paper, we present two general theorems that addresses the problem of characterizing the coupled dynamics of nonlinear systems using time series observations on a manifold  . A special case of this theorem, attributed originally to Takens [12], provided the first sketch of a mathematical proof for reconstructing a diffeomorphic shadow manifold
. A special case of this theorem, attributed originally to Takens [12], provided the first sketch of a mathematical proof for reconstructing a diffeomorphic shadow manifold 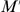 using lags of a single time series as coordinate axes. The basic idea, that was earlier demonstrated by Packard, Crutchfield, Farmer, and Shaw [28] and Crutchfield [2], is that under generic conditions, a shadow manifold
using lags of a single time series as coordinate axes. The basic idea, that was earlier demonstrated by Packard, Crutchfield, Farmer, and Shaw [28] and Crutchfield [2], is that under generic conditions, a shadow manifold 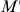 can be created using time-lagged observations of
can be created using time-lagged observations of 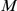 based on a single observation function (Cartesian coordinate variable) that is a smooth and smoothly invertible
based on a single observation function (Cartesian coordinate variable) that is a smooth and smoothly invertible 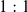 mapping with
mapping with 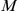 . Subsequently, Sauer, Yorke, and Casdagli [29] provided a definitive proof and an explicit extension of Takens' theorem to fractal sets; their theorems are also more powerful than the original theorem, as they show embeddings are not just generic in the sense of being open and dense in the set of all mappings, but in fact almost every mapping in the sense of prevalence [30] is an embedding (see [30] for an in-depth explanation of the advantages of “prevalence” over “generic”). The theorem was also extended by Stark, Broomhead, Davies, and Huke [31], [32] and Stark [33] to include certain classes of stochastic systems. Practical methods for reconstruction have also been explored, particularly to address the presence of noise in real data (e.g. [29], [34]). Casdagli et al. [35] give a thorough treatment of such techniques based on transformations of univariate maps, showing how optimal noise reduction can be achieved. These very important prior results all focused on reconstruction from a single time series; however, as proven below, they can be extended to the more practically significant case where multiple observation functions are used to generate
. Subsequently, Sauer, Yorke, and Casdagli [29] provided a definitive proof and an explicit extension of Takens' theorem to fractal sets; their theorems are also more powerful than the original theorem, as they show embeddings are not just generic in the sense of being open and dense in the set of all mappings, but in fact almost every mapping in the sense of prevalence [30] is an embedding (see [30] for an in-depth explanation of the advantages of “prevalence” over “generic”). The theorem was also extended by Stark, Broomhead, Davies, and Huke [31], [32] and Stark [33] to include certain classes of stochastic systems. Practical methods for reconstruction have also been explored, particularly to address the presence of noise in real data (e.g. [29], [34]). Casdagli et al. [35] give a thorough treatment of such techniques based on transformations of univariate maps, showing how optimal noise reduction can be achieved. These very important prior results all focused on reconstruction from a single time series; however, as proven below, they can be extended to the more practically significant case where multiple observation functions are used to generate 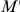 .
.
Here we prove the more general case of multivariate embeddings (embeddings using multiple time series and lags thereof), and show how time series information can be leveraged if multiple time series and their lags are used to construct embeddings of 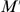 . These theorems pave the way for more extensive use of state space reconstruction methods in practical applications where long time series may not be available, so that multiple diffeomorphic embeddings may be created in factorial fashion to more fully exploit the coupled non-redundant information that can be extracted from multiple time series (multiple observation functions of dynamics on a manifold) to create predictive shadow manifolds [36]. The use of multiple time series allows the possibility of noise reduction that exceeds the limitations of univariate reconstructions in the presence of noise [35].
. These theorems pave the way for more extensive use of state space reconstruction methods in practical applications where long time series may not be available, so that multiple diffeomorphic embeddings may be created in factorial fashion to more fully exploit the coupled non-redundant information that can be extracted from multiple time series (multiple observation functions of dynamics on a manifold) to create predictive shadow manifolds [36]. The use of multiple time series allows the possibility of noise reduction that exceeds the limitations of univariate reconstructions in the presence of noise [35].
The possibility of extending Takens' theorem to allow lags of multiple observation functions was mentioned in Remark 2.9 from [29], but was not explicitly proven. The remark was also restricted to mappings strictly formed from consecutive lags, which is not the only possibility that needs to be considered in the multivariate case. Given the potential importance of multivariate reconstructions, we believe a full proof is required—in particular, one that extends the generalization to non-consecutive lags. We show how Takens' theorem is a special case of our more general Theorem 2 (below) and by following the structure of Takens' original proof we clarify the logic and highlight the restrictions and special cases (non-generic cases) that can arise in its application to real world systems. We then give explicit proof of a stronger version of Remark 2.9 from Sauer et al. [29] that allows non-consecutive lags. This third theorem is stronger than the first two in the sense that it shows embeddings are prevalent and not just generic. For those less familiar, we begin with a brief overview of some basic terms and concepts used in our proofs.
Some Basic Concepts of Embedding Theory
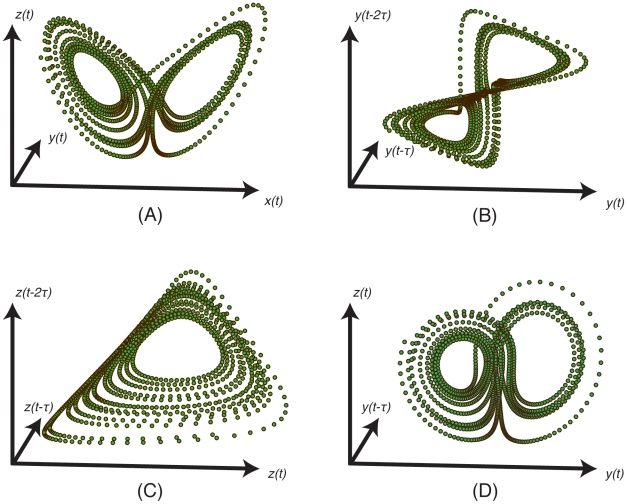
Consider the classic Lorenz attractor [37] shown in Figure 1(a), consisting of trajectories in three-dimensional space that together define a butterfly shaped surface or manifold. For simplicity, a manifold can be thought of as a generalized, n-dimensional surface embedded in some higher dimensional space, where the dimension of the manifold may be fractal (as is the case for the Lorenz attractor). More generally, an embedding is a multivariate transformation of a manifold that resolves all trajectories on the original manifold without crossings. That is, an embedding is globally 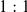 in that it resolves all singularities in trajectories that define the manifold (singularities are points on the manifold where trajectories cross so that future paths are not uniquely determined).
in that it resolves all singularities in trajectories that define the manifold (singularities are points on the manifold where trajectories cross so that future paths are not uniquely determined).
Figure 1. Lorenz attractor with three shadow manifolds.
The Lorenz attractor [37] is shown with three shadow manifolds created from lag-coordinate transformations. The typical parameters were used:  ,
, 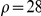 , and
, and 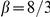 , giving the three coupled equations as
, giving the three coupled equations as  ,
, 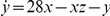 , and
, and  . The solution was computed using a fourth order Runge-Kutta method with a time step of
. The solution was computed using a fourth order Runge-Kutta method with a time step of 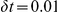 , and the time lag used to create the shadow manifolds was
, and the time lag used to create the shadow manifolds was  . (A) The trajectory shown in the
. (A) The trajectory shown in the  ,
, 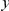 , and
, and  coordinates of the original system reveals a two-lobed manifold. (B) A univariate transformation using time lags of the
coordinates of the original system reveals a two-lobed manifold. (B) A univariate transformation using time lags of the 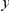 -coordinate,
-coordinate, 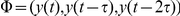 , preserves this two-lobed structure (and other topological properties), verifying Takens' theorem. (C) A univariate transformation using time lags of the
, preserves this two-lobed structure (and other topological properties), verifying Takens' theorem. (C) A univariate transformation using time lags of the  -coordinate,
-coordinate, 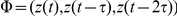 , does not preserve the two-lobed structure. Local neighborhoods of the original attractor are, however, preserved. Thus, though this mapping violates a genericity assumption of the original theorem and is not an embedding, it is an immersion of the original manifold. (D) A multivariate transformation using both the
, does not preserve the two-lobed structure. Local neighborhoods of the original attractor are, however, preserved. Thus, though this mapping violates a genericity assumption of the original theorem and is not an embedding, it is an immersion of the original manifold. (D) A multivariate transformation using both the  - and
- and  -coordinates,
-coordinates, 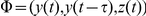 , fulfills the assumptions of Theorems 2 and 7. As predicted, it also preserves the two-lobed structure of the Lorenz and is a valid embedding.
, fulfills the assumptions of Theorems 2 and 7. As predicted, it also preserves the two-lobed structure of the Lorenz and is a valid embedding.
An immersion is a local embedding that may not preserve the global topology of a manifold. Rather an immersion preserves the topology of every local neighborhood of the original manifold, so that each point of the tangent space of the immersed manifold has the same dimensionality as the true manifold. Thus, an immersion is a mapping that is 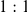 between any given “piece” of the true manifold and the immersed manifold. However, this condition does not guarantee that the global topology is preserved. This is illustrated in Figure 1(c), where two different pieces of the original manifold are mapped to the same piece of the immersed manifold, producing an immersion that is not an embedding. Immersions are nonetheless a useful conceptual stepping stone for constructing proofs about embeddings, since all embeddings are necessarily immersions.
between any given “piece” of the true manifold and the immersed manifold. However, this condition does not guarantee that the global topology is preserved. This is illustrated in Figure 1(c), where two different pieces of the original manifold are mapped to the same piece of the immersed manifold, producing an immersion that is not an embedding. Immersions are nonetheless a useful conceptual stepping stone for constructing proofs about embeddings, since all embeddings are necessarily immersions.
The Lorenz attractor, Figure 1(a), provides an excellent example to illustrate both of these concepts. Consider two different multivariate functions that transform the original manifold,  and
and 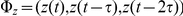 where
where  is a small time lag as in Takens' theorem. Both of these functions map points on the true manifold to points on a shadow manifold, shown in Figures 1(b) and 1(c). Examining these shadow manifolds, it is evident that both are immersions of the Lorenz attractor, because zooming in on a particular piece of either will reveal that the tangent spaces have the same dimensionality as the original. However, only Figure 1(b) is an embedding that successfully reproduces the two lobes of the butterfly. The reconstruction in Figure 1(c), based on lags of the
is a small time lag as in Takens' theorem. Both of these functions map points on the true manifold to points on a shadow manifold, shown in Figures 1(b) and 1(c). Examining these shadow manifolds, it is evident that both are immersions of the Lorenz attractor, because zooming in on a particular piece of either will reveal that the tangent spaces have the same dimensionality as the original. However, only Figure 1(b) is an embedding that successfully reproduces the two lobes of the butterfly. The reconstruction in Figure 1(c), based on lags of the  -coordinate, fails to do so, because the two fixed points of the original attractor have the same
-coordinate, fails to do so, because the two fixed points of the original attractor have the same  -coordinate; they are mapped to the same point on the shadow manifold, so the two lobes are stacked on top of each other. This singularity is a consequence of a special, non-generic symmetry in the Lorenz system that violates an assumption of Takens' theorem. Figure 1(d) shows an embedding based on lags of both
-coordinate; they are mapped to the same point on the shadow manifold, so the two lobes are stacked on top of each other. This singularity is a consequence of a special, non-generic symmetry in the Lorenz system that violates an assumption of Takens' theorem. Figure 1(d) shows an embedding based on lags of both 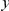 - and
- and  -coordinates and is an example of the generalized mappings addressed in this paper.
-coordinates and is an example of the generalized mappings addressed in this paper.
Results
Two Theorems in the Style of Takens: The Generic Case
Let 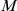 be a compact manifold of dimension
be a compact manifold of dimension  . A dynamical system is a diffeophorism
. A dynamical system is a diffeophorism 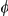 defining the trajectories or “flow” on
defining the trajectories or “flow” on 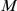 for discrete time or a vector field
for discrete time or a vector field  on
on 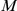 for continuous time. Takens [12] proved generically that given
for continuous time. Takens [12] proved generically that given 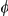 and
and 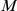 , a smooth observation function
, a smooth observation function  can be used to construct an embedding of
can be used to construct an embedding of 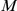 in
in 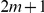 dimensions under the transformation
dimensions under the transformation  where
where 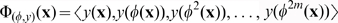 . Here the components
. Here the components 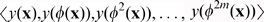 correspond to time-lagged observations of the dynamics on
correspond to time-lagged observations of the dynamics on 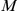 defined by
defined by 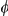 . Notice that such mappings involve a single distinct observation function (i.e. a single time series), and represent a small subset in the larger set
. Notice that such mappings involve a single distinct observation function (i.e. a single time series), and represent a small subset in the larger set 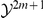 of all possible mappings
of all possible mappings 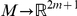 that could, for example, involve multiple time series and their lags.
that could, for example, involve multiple time series and their lags.
Takens explicitly refers only to the unlagged 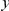 as an observation function, but in its most general sense an observation function is any
as an observation function, but in its most general sense an observation function is any 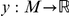 . Thus, the functions
. Thus, the functions  , corresponding to the lags of the time series are technically observation functions as well. This bears mention, because in the more general case of mappings
, corresponding to the lags of the time series are technically observation functions as well. This bears mention, because in the more general case of mappings 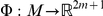 , the observation functions making up the components of
, the observation functions making up the components of 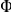 are not all derived from a single time series, but can be various lags of multiple time-series. To treat these cases, it is necessary to acknowledge that these are all observation functions, and we will refer to distinct time series as “unlagged” observation functions.
are not all derived from a single time series, but can be various lags of multiple time-series. To treat these cases, it is necessary to acknowledge that these are all observation functions, and we will refer to distinct time series as “unlagged” observation functions.
For a mapping  in the larger set
in the larger set 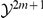 of all mappings
of all mappings 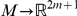 , consider the case with
, consider the case with 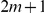 component functions
component functions 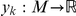 which are multiple unlagged observation functions of
which are multiple unlagged observation functions of  (i.e. multiple time series). Again, an observation function is any function
(i.e. multiple time series). Again, an observation function is any function 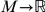 that assigns a real number to each point on the manifold
that assigns a real number to each point on the manifold  . For a mapping
. For a mapping 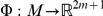 , we can think of
, we can think of 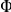 in terms of its
in terms of its 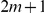 component functions, which correspond to the coordinates in
component functions, which correspond to the coordinates in 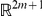 . These component functions may all be lags of a single distinct observation function tracking a dynamical system, as in the case of Takens, or they may be multiple observation functions, as in the case of Whitney, or they may be lags of multiple observation functions, as in Theorems 2 and 7 below.
. These component functions may all be lags of a single distinct observation function tracking a dynamical system, as in the case of Takens, or they may be multiple observation functions, as in the case of Whitney, or they may be lags of multiple observation functions, as in Theorems 2 and 7 below.
The question arises whether general multivariate mappings  form legitimate embeddings. Here we present two theorems: one that demonstrates that maps created from
form legitimate embeddings. Here we present two theorems: one that demonstrates that maps created from 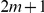 distinct observation functions are generically embeddings and another that shows that maps created from lags of multiple observation functions are also generically embeddings. Both of these theorems generalize Takens' theorem for which the component functions only involve a single observation function.
distinct observation functions are generically embeddings and another that shows that maps created from lags of multiple observation functions are also generically embeddings. Both of these theorems generalize Takens' theorem for which the component functions only involve a single observation function.
It follows from Whitney [38] that generically 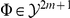 is an embedding. Note, however, that Whitney's work does not apply to the specific subsets of
is an embedding. Note, however, that Whitney's work does not apply to the specific subsets of 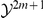 involving fixed lagged relationships as discussed by Takens for reconstructing attractor manifolds
involving fixed lagged relationships as discussed by Takens for reconstructing attractor manifolds 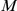 for dynamic systems. That is, Whitney's theorem is generic and does not address these specific subsets of
for dynamic systems. That is, Whitney's theorem is generic and does not address these specific subsets of 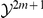 which have “measure zero” (e.g. in the sense of “shy” defined in [30]). To tackle this problem, we look to the proof of Takens and see that it can be readily generalized to the other subsets of
which have “measure zero” (e.g. in the sense of “shy” defined in [30]). To tackle this problem, we look to the proof of Takens and see that it can be readily generalized to the other subsets of 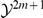 , including the case of generic
, including the case of generic 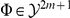 .
.
Recall that, for a compact manifold, a mapping that is an immersion and injective is also necessarily an embedding. Thus, Takens' general approach was to first show that (i) immersions are dense in the set of mappings 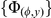 , then that (ii) there is a dense set of
, then that (ii) there is a dense set of 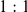 mappings within this set of immersions. Since the set of embeddings is open in the set of all possible mappings, Takens concludes that mappings in
mappings within this set of immersions. Since the set of embeddings is open in the set of all possible mappings, Takens concludes that mappings in 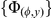 are generically embeddings. The critical word here is “generically,” meaning there can be exceptions (and as explained in [30], the set of such exceptions doesn't necessarily have zero measure).
are generically embeddings. The critical word here is “generically,” meaning there can be exceptions (and as explained in [30], the set of such exceptions doesn't necessarily have zero measure).
To demonstrate both (i) and (ii), Takens argues that even when the property of interest (e.g. the 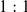 property) does not hold for some particular mapping, by making an arbitrarily small perturbation, it is possible to find a nearby mapping for which that property holds. The key to the theorem and also to adapting it to other sets of mappings is finding how to make these perturbations. The proof is most straightforward for the general case involving
property) does not hold for some particular mapping, by making an arbitrarily small perturbation, it is possible to find a nearby mapping for which that property holds. The key to the theorem and also to adapting it to other sets of mappings is finding how to make these perturbations. The proof is most straightforward for the general case involving  distinct observation functions (each a distinct time series) because it is possible to perturb the component functions of
distinct observation functions (each a distinct time series) because it is possible to perturb the component functions of 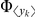 independently. Thus we begin with this proof to add clarity to the more powerful main theorem 2 involving lags of multiple observation functions.
independently. Thus we begin with this proof to add clarity to the more powerful main theorem 2 involving lags of multiple observation functions.
Theorem 1
Consider a compact,
 -dimensional manifold
-dimensional manifold
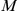 and a set of
and a set of
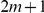 observation functions
observation functions
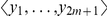 , where
, where
 smoothly; by “smooth” we mean at least
smoothly; by “smooth” we mean at least
 . Then it is a generic property of all possible
. Then it is a generic property of all possible
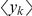 that the mapping
that the mapping
 defined as
defined as
is an embedding.
Proof
Consider an arbitrary set of  observation functions
observation functions 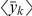 on
on 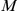 . We define a corresponding mapping
. We define a corresponding mapping 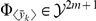 by letting each of these
by letting each of these 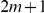 observation functions be one of the component functions of
observation functions be one of the component functions of 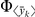 . Now, recall that an immersion is a map with a derivative that is globally injective, i.e.
. Now, recall that an immersion is a map with a derivative that is globally injective, i.e. 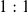 . We denote the total derivative of a function
. We denote the total derivative of a function 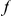 as
as 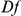 . If the derivative is evaluated at a particular point
. If the derivative is evaluated at a particular point  in the domain of
in the domain of 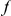 , we will write
, we will write 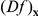 , and if
, and if 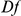 is a matrix, then we denote the derivative at a particular point and along a particular tangent vector
is a matrix, then we denote the derivative at a particular point and along a particular tangent vector  as
as 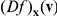 .
.
For any point 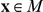 , we can perturb the co-vectors
, we can perturb the co-vectors 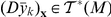 independently by perturbing individual
independently by perturbing individual 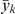 . By making infinitesimal perturbations at points
. By making infinitesimal perturbations at points 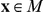 for which
for which 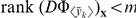 , we can get a set of observables
, we can get a set of observables 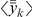 arbitrarily close to
arbitrarily close to 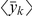 such that
such that  for all
for all 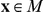 —i.e.,
—i.e., 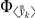 is an immersion. Since the set of immersions is open in the set of all mappings, there is a neighborhood
is an immersion. Since the set of immersions is open in the set of all mappings, there is a neighborhood 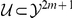 around this
around this 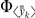 such that every
such that every 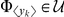 is an immersion.
is an immersion.
Since immersions are local embeddings, we can find a 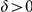 such that on the manifold,
such that on the manifold, 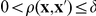 implies
implies  . Here we depart from Takens' notation and let
. Here we depart from Takens' notation and let 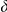 denote infinitesimal separations between two points on the manifold
denote infinitesimal separations between two points on the manifold 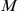 to avoid confusion with the later defined
to avoid confusion with the later defined  which is used to perturb the observable;
which is used to perturb the observable; 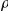 is any fixed metric on
is any fixed metric on 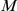 . In fact for this fixed
. In fact for this fixed 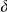 , there is a subset
, there is a subset 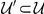 such that for any
such that for any 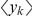 in
in 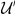 , the associated map
, the associated map  is an immersion, and
is an immersion, and 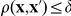 implies that
implies that  .
.
Next, we show that we can find a globally 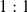
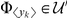 arbitrarily close to
arbitrarily close to 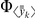 . To do this, we construct a finite collection of subsets
. To do this, we construct a finite collection of subsets 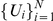 such that the
such that the 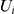 are open subsets of
are open subsets of 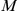 , the collection covers
, the collection covers 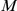 , and
, and 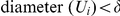 for every
for every  . Then, we take a partition of unity
. Then, we take a partition of unity  corresponding to these
corresponding to these 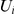 , so that we can vary the value of any
, so that we can vary the value of any 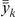 by an infinitesimal amount
by an infinitesimal amount 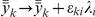 without altering the value of
without altering the value of 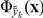 for
for 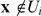 .
.
We now consider the mapping 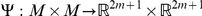 defined as
defined as 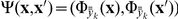 . We define the set
. We define the set 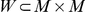 as
as 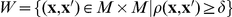 , so that (by our choice of
, so that (by our choice of 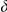 ), the mapping
), the mapping 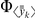 is necessarily injective on the complement of
is necessarily injective on the complement of 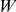 in
in 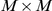 . Furthermore, note that the intersection of
. Furthermore, note that the intersection of 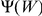 with the diagonal of
with the diagonal of 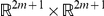 gives the set of points
gives the set of points 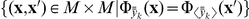 , and therefore
, and therefore 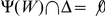 is equivalent to
is equivalent to 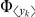 injective. Our task, then, is to perturb the manifold
injective. Our task, then, is to perturb the manifold 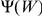 using the
using the  and
and 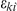 so that it does not intersect the diagonal manifold
so that it does not intersect the diagonal manifold 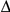 .
.
At each 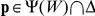 we know that
we know that 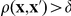 , so
, so  and
and 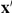 cannot belong to the same
cannot belong to the same 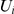 . Consequently, varying an
. Consequently, varying an 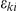 or
or  only alters the value of
only alters the value of 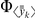 at either
at either  or
or 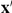 (respectively). In the tangent space
(respectively). In the tangent space  , then, the direction of the
, then, the direction of the 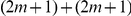 infinitesimal changes given by the
infinitesimal changes given by the 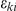 and
and 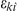 are all linearly independent (indeed orthogonal) and as such span
are all linearly independent (indeed orthogonal) and as such span 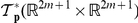 . Since the tangent spaces of
. Since the tangent spaces of 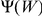 and
and  are at most
are at most  and
and  dimensional, respectively, we can construct a vector from a linear combination of
dimensional, respectively, we can construct a vector from a linear combination of 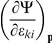 and
and 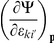 that lies outside of both
that lies outside of both 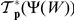 and
and 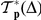 . Therefore, an infinitesimal perturbation corresponding to this linear combination will move the sub-manifolds
. Therefore, an infinitesimal perturbation corresponding to this linear combination will move the sub-manifolds 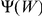 and
and 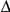 away from each other at the point
away from each other at the point 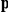 without creating a new intersection at another point. By keeping the size of these perturbations sufficiently small, we ensure that we stay confined to
without creating a new intersection at another point. By keeping the size of these perturbations sufficiently small, we ensure that we stay confined to 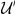 , so that
, so that 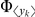 is still an immersion. This is a more transparent statement of the transversality argument used in the Takens proof (1981).
is still an immersion. This is a more transparent statement of the transversality argument used in the Takens proof (1981).
Thus, we have shown that for any arbitrary set of 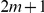 observables
observables 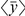 , we can find a set of observables
, we can find a set of observables  arbitrarily close to
arbitrarily close to  such that
such that 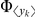 is an embedding—i.e., there is a dense set of observables
is an embedding—i.e., there is a dense set of observables 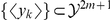 such that
such that 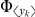 is an embedding. The set of embeddings is open in the set of all mappings, so this set is dense and open, meaning that the embedding property is generic over all mappings.
is an embedding. The set of embeddings is open in the set of all mappings, so this set is dense and open, meaning that the embedding property is generic over all mappings.
When mappings are confined to fixed lag relationships, Takens showed it is valid to independently perturb each component of  at a given point of the domain by perturbing the unlagged observation function,
at a given point of the domain by perturbing the unlagged observation function, 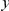 , in the other parts of the domain corresponding to neighborhoods of the lagged states
, in the other parts of the domain corresponding to neighborhoods of the lagged states  ,
,  , etc. This ensures that the perturbations to
, etc. This ensures that the perturbations to 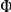 maintain the structure of the lag relationships and that we have not inadvertently left the subset of interest. As we now show, this allows the above result to be easily extended to families of maps having component functions that are the lags of multiple observation functions. This is the relevant case for many practical examples where lags of multiple time series (multiple variables or observation functions) are required to achieve a mechanistic reconstruction of
maintain the structure of the lag relationships and that we have not inadvertently left the subset of interest. As we now show, this allows the above result to be easily extended to families of maps having component functions that are the lags of multiple observation functions. This is the relevant case for many practical examples where lags of multiple time series (multiple variables or observation functions) are required to achieve a mechanistic reconstruction of 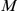 (e.g. [20]). It also allows information on
(e.g. [20]). It also allows information on 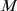 to be leveraged when the time series are short, as is the case in many physical and biological problems [22], [36].
to be leveraged when the time series are short, as is the case in many physical and biological problems [22], [36].
Before starting the proof, however, we must clarify exactly what the “subsets of interest” are. We define these sets as follows. First, we say 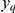 is a lag of the observable
is a lag of the observable 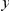 if we can write
if we can write  for positive
for positive  . We consider the lags in the positive time direction only to simplify notation in the proof, noting that the results apply equally to negative lags. Let
. We consider the lags in the positive time direction only to simplify notation in the proof, noting that the results apply equally to negative lags. Let 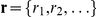 be the subset of
be the subset of  for which
for which  ,
,  is an unlagged observable, i.e.
is an unlagged observable, i.e. 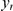 is not a lag of another
is not a lag of another 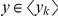 . We begin with the “unlagged” observation functions,
. We begin with the “unlagged” observation functions, 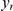 , or observation functions that are not a lag of another observable in
, or observation functions that are not a lag of another observable in  . Now define a set
. Now define a set 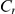 for each
for each  that contains
that contains 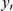 and any other observation function in
and any other observation function in 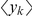 which is a lag of it. That is,
which is a lag of it. That is, 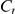 is the set of
is the set of  that are lags of
that are lags of 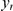 given as
given as 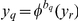 , where the lags
, where the lags 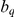 are distinct for fixed
are distinct for fixed  . This choice of
. This choice of 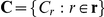 and
and 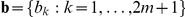 determine a subset
determine a subset 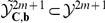 containing all choices of
containing all choices of 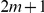 observables
observables 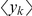 which obey the correct lag relationships under a dynamical system
which obey the correct lag relationships under a dynamical system 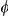 . Note that each element of
. Note that each element of 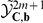 can be identified by the dynamical system and the
can be identified by the dynamical system and the 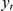 . We denote such an element, then, as
. We denote such an element, then, as 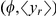 .
.
Theorem 2
Consider a diffeomorphism
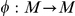 on some compact manifold
on some compact manifold
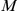 of dimension
of dimension
 , along with
, along with
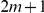 observation functions
observation functions
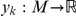 , smoothly; by “smooth” we mean at least
, smoothly; by “smooth” we mean at least
 . Restrict the
. Restrict the
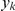 to have the lag relationships corresponding to a collection of sets
to have the lag relationships corresponding to a collection of sets
 and lags
and lags
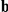 under the dynamical system
under the dynamical system
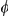 , and impose the following generic
[12], [39]
properties on
, and impose the following generic
[12], [39]
properties on
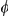 :
:
The set
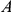 of periodic points with period
of periodic points with period
 has finitely many points,
has finitely many points,
The eigenvalues of
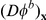 at each
at each
 in a compact neighborhood
in a compact neighborhood
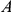 are distinct and not equal to 1.
are distinct and not equal to 1.
Then, for generic
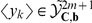 , the mapping described by
, the mapping described by
is an embedding.
Proof
The proof of this theorem closely follows the logic of the previous proof and the original argument of Takens [12]. As noted above, any perturbations to 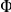 via its component functions
via its component functions 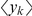 must remain within
must remain within 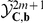 (the set of observables having the desired lag relationships under
(the set of observables having the desired lag relationships under 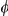 prescribed by the
prescribed by the 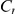 and the
and the  ). Here we must also deal with points of
). Here we must also deal with points of 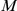 that are fixed points or periodic under the dynamical system
that are fixed points or periodic under the dynamical system  , i.e. the points for which there exists a
, i.e. the points for which there exists a 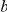 such that
such that 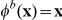 (including the fixed point case,
(including the fixed point case,  ). The above proof shows that the mapping
). The above proof shows that the mapping 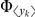 is generically an immersion because the co-vectors
is generically an immersion because the co-vectors 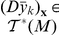 can be independently perturbed. This is also true for non-periodic points where there are fixed lag relationships between some observables, as we can perturb
can be independently perturbed. This is also true for non-periodic points where there are fixed lag relationships between some observables, as we can perturb 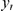 in the neighborhood of
in the neighborhood of  and thus perturb
and thus perturb  without affecting
without affecting 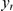 in the neighborhood of
in the neighborhood of  .
.
Note that periodic points  can exist such that the period
can exist such that the period 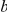 or some integer multiple of it,
or some integer multiple of it, 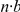 , is the fixed time lag between two observables
, is the fixed time lag between two observables 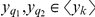 belonging to the same
belonging to the same 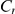 . Let
. Let 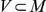 be a compact neighborhood of all such points. For
be a compact neighborhood of all such points. For 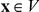 , the vectors
, the vectors  and
and 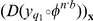 cannot necessarily be perturbed independently. Nonetheless, while
cannot necessarily be perturbed independently. Nonetheless, while 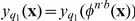 for such a point, it is not generally true that
for such a point, it is not generally true that 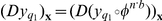 . By assumption, for each
. By assumption, for each 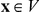 , the eigenvalues of the
, the eigenvalues of the 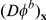 are distinct and not equal to 1. Thus, by the chain rule, it is clear that
are distinct and not equal to 1. Thus, by the chain rule, it is clear that 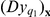 and
and 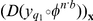 are linearly independent. As noted above, all the other
are linearly independent. As noted above, all the other 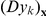 can be perturbed independently, so we can find a set of observables
can be perturbed independently, so we can find a set of observables 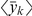 arbitrarily near
arbitrarily near  in
in 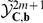 for which
for which  is an immersion on
is an immersion on 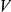 . Note that because the set of immersions is open, there is an open neighborhood in
. Note that because the set of immersions is open, there is an open neighborhood in 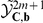 around this
around this  for which every set of observables in that neighborhood gives an immersion.
for which every set of observables in that neighborhood gives an immersion.
We must also satisfy 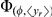 injective. The proof above relied on the ability to independently perturb the manifold
injective. The proof above relied on the ability to independently perturb the manifold 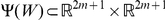 at any point
at any point 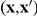 by an infinitesimal amount in any coordinate direction. For a periodic point on
by an infinitesimal amount in any coordinate direction. For a periodic point on 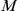 with perioid
with perioid 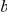 and two observables related as
and two observables related as 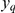 and
and 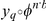 , it is impossible to independently perturb
, it is impossible to independently perturb 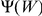 locally in the coordinate
locally in the coordinate 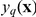 or
or 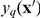 , as you also perturb
, as you also perturb 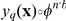 or
or 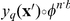 . By assumption, the set
. By assumption, the set  has a finite number of elements. For such a generic
has a finite number of elements. For such a generic 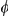 and any set
and any set 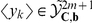 , any neighborhood of the
, any neighborhood of the  will contain a set of observables
will contain a set of observables 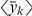 for which the unlagged observation functions
for which the unlagged observation functions 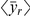 take distinct values at each point in
take distinct values at each point in 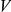 .
.
We first perturb the 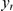 to find an open neighborhood of observables which give immersions when restricted to the set
to find an open neighborhood of observables which give immersions when restricted to the set 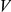 . We then further perturb the observables to find within this neighborhood a set of observables
. We then further perturb the observables to find within this neighborhood a set of observables  for which
for which 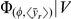 is also injective and therefore an embedding (on
is also injective and therefore an embedding (on 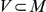 ). Since embeddings are dense in the space of all mappings, there is a neighborhood
). Since embeddings are dense in the space of all mappings, there is a neighborhood 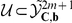 such that for all
such that for all 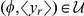 , the map
, the map 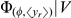 is an embedding.
is an embedding.
We now show that we can find a 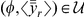 such that
such that  is an embedding on all of
is an embedding on all of 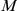 . We first note that at points
. We first note that at points 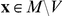 , the vectors
, the vectors 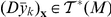 can be perturbed independently, so we can find
can be perturbed independently, so we can find 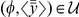 for which
for which 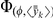 is an immersion. Because an immersion is a local embedding, there is a
is an immersion. Because an immersion is a local embedding, there is a 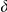 such that for
such that for 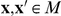 ,
, 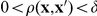 implies that
implies that  . Since the set of immersions is open in the set of possible mappings, there is a neighborhood
. Since the set of immersions is open in the set of possible mappings, there is a neighborhood 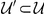 such that for any
such that for any 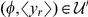 , the corresponding mapping
, the corresponding mapping 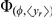 is an immersion. Thus, for the same
is an immersion. Thus, for the same 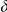 as above,
as above, 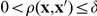 implies
implies 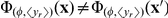 .
.
Now we need to show that there is a 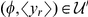 such that
such that 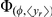 is also injective on
is also injective on  . As noted in the first proof, this is equivalent to
. As noted in the first proof, this is equivalent to 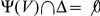 for the mapping
for the mapping 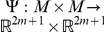 defined as
defined as 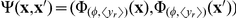 . If
. If  and
and 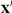 are both in
are both in 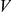 or
or  , we already know that
, we already know that  . Thus we restrict ourselves to the set
. Thus we restrict ourselves to the set 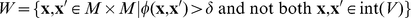 .
.
To perturb the manifold  away from
away from 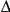 at points of intersection,
at points of intersection, 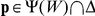 , we must be able to find variations for which the tangent vector
, we must be able to find variations for which the tangent vector 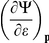 is linearly independent from the
is linearly independent from the  tangent vectors
tangent vectors 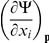 and
and 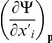 and lies outside of
and lies outside of  . In the first proof, it was obvious that each component of
. In the first proof, it was obvious that each component of  could be perturbed independently. Now we must be more careful. We do this by first creating a collection of
could be perturbed independently. Now we must be more careful. We do this by first creating a collection of  open subsets of
open subsets of  ,
, 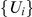 , with the following properties:
, with the following properties:
The
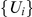 cover the closure of
cover the closure of 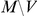 .
.For each
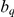 and
and  , the diameter of
, the diameter of 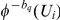 is less than
is less than 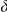 .
.For all choices of
 , the set
, the set 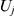 intersects with
intersects with 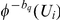 for at most one
for at most one 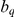 .
.For
 and
and 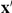 such that
such that 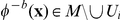 for some
for some  ,
, 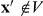 , and
, and 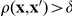 , no two of
, no two of 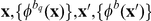 belong to the same
belong to the same 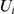 .
.
Take a partition of unity  corresponding to this
corresponding to this 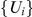 . Because of the way we constructed the
. Because of the way we constructed the 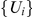 , we can vary the value of each
, we can vary the value of each 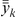 at any point
at any point 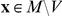 by an infinitesimal amount without altering the value of the other
by an infinitesimal amount without altering the value of the other 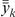 in the neighborhood of
in the neighborhood of  . We make this explicit as follows. To perturb the
. We make this explicit as follows. To perturb the 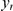 , we take
, we take 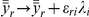 for
for  corresponding to
corresponding to 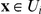 . To perturb the other
. To perturb the other 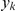 (
(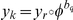 for some
for some  ), we perturb
), we perturb 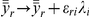 for
for  corresponding to
corresponding to 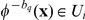 . Consider the
. Consider the 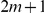 perturbations,
perturbations, 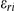 , which are independent shifts at
, which are independent shifts at  in distinct
in distinct 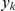 . In
. In 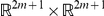 , we note that each corresponding tangent vector
, we note that each corresponding tangent vector 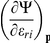 lies outside of
lies outside of 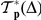 . Note the
. Note the 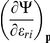 together with any basis of
together with any basis of 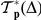 form a linearly independent set of vectors. Since the dimension of
form a linearly independent set of vectors. Since the dimension of 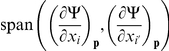 is at most
is at most  , there must be a linear combination of the
, there must be a linear combination of the 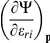 that lies outside of both
that lies outside of both 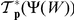 and
and 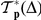 , which can be used to perturb
, which can be used to perturb 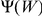 away from
away from 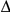 . By keeping variations in the
. By keeping variations in the 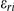 sufficiently small, we can find a set of
sufficiently small, we can find a set of 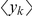 such that
such that 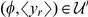 and
and 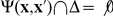 (where
(where 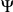 now corresponds to the
now corresponds to the 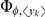 map). This pair gives a mapping
map). This pair gives a mapping 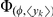 that is both an immersion and injective, and thus is an embedding. Because
that is both an immersion and injective, and thus is an embedding. Because  was an arbitrarily small neighborhood of any point in
was an arbitrarily small neighborhood of any point in  , this means embeddings are dense in
, this means embeddings are dense in 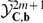 , and the set of embeddings is open in the set of mappings. Thus, the map
, and the set of embeddings is open in the set of mappings. Thus, the map 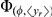 given by
given by 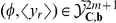 is generically an embedding.
is generically an embedding.
Just as Takens extends the original result for discrete time to dynamical systems in continuous time, we can extend our result as follows:
Corollary 3
Consider a smooth vector field
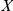 on some compact manifold
on some compact manifold
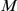 along with
along with
 observables
observables
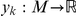 , smoothly; by “smooth” we mean at least
, smoothly; by “smooth” we mean at least
 . Define
. Define
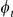 as the flow on
as the flow on
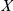 . Suppose we restrict the
. Suppose we restrict the
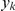 to have the lag relationships corresponding to a collection of sets
to have the lag relationships corresponding to a collection of sets
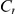 and lags
and lags
 under the discrete dynamical system
under the discrete dynamical system
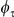 , where
, where
 is a constant. We impose the following generic properties on
is a constant. We impose the following generic properties on
 :
:
For points
 such that
such that
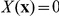 , the eigenvalues of
, the eigenvalues of
 are distinct and not equal to 1.
are distinct and not equal to 1.
No periodic integral curve of
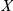 has integer period
has integer period
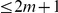 .
.
Then, for generic
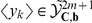 , the mapping described by
, the mapping described by
is an embedding.
Proof
In this case, 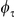 is a discrete time dynamical system on
is a discrete time dynamical system on 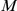 satisfying the conditions imposed in the theorem above, and this corollary follows directly.
satisfying the conditions imposed in the theorem above, and this corollary follows directly.
A Theorem in the Style of Sauer et al.: The Prevalent Case
We now give an explicit proof of Remark 2.9 from [29] using the framework constructed in their original paper, but we extend the language to cover reconstructions using non-consecutive lags (from multiple time series). The proof uses Lemma 4.1, 4.6, and 4.11 from [29] to show that 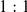 mappings and immersions are prevalent in the space
mappings and immersions are prevalent in the space 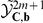 , just as Sauer et al. use Lemma 4.6 to prove Theorem 3.3, and Lemmas 4.1 and 4.11 to prove Theorem 3.5. These lemmas are now stated (for the proofs, see their original paper).
, just as Sauer et al. use Lemma 4.6 to prove Theorem 3.3, and Lemmas 4.1 and 4.11 to prove Theorem 3.5. These lemmas are now stated (for the proofs, see their original paper).
Lemma 4
(Originally part 2 of 4.1) Let
 and
and
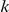 be positive integers,
be positive integers,
 distinct points in
distinct points in
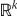 ,
,
 in
in
 , and
, and
 in
in
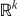 . Then there exists a polynomial
. Then there exists a polynomial
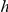 in
in
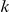 variables of degree at most
variables of degree at most
 such that for
such that for
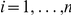 ,
,
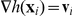 .
.
Lemma 5
(Originally 4.6) Let
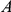 be a compact subset of
be a compact subset of
 . Let
. Let
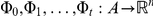 be Lipschitz maps. For each integer
be Lipschitz maps. For each integer
 , let
, let
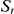 be the set of pairs
be the set of pairs
 in
in
 for which the
for which the
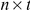 matrix
matrix
has rank
 , and let
, and let
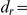 lower boxdim
lower boxdim
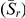 . Define
. Define
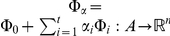 . If
. If
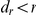 for all integers
for all integers
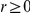 , then for
, then for
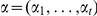 outside a measure zero subset of
outside a measure zero subset of
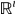 , the map
, the map
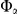 is
is
 .
.
Lemma 6
(Originally 4.11) Let
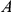 be a compact subset of a smooth manifold embedding in
be a compact subset of a smooth manifold embedding in
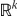 . Let
. Let
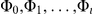 be a set of smooth maps from an open neighborhood
be a set of smooth maps from an open neighborhood
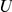 of
of
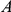 to
to
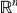 . For each positive integer
. For each positive integer
 , let
, let
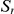 be the subset of the unit tangent bundle
be the subset of the unit tangent bundle
 such that the
such that the
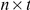 matrix
matrix
has rank
 , and let
, and let
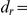 lower boxdim
lower boxdim
 . Define
. Define
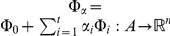 . If
. If
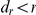 for all integers
for all integers
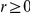 , then for almost every
, then for almost every
 , the map
, the map
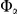 is an immersion on
is an immersion on
 .
.
To apply these lemmas, it is necessary to restrict the dimension of the sets of periodic orbits—that is, the sets 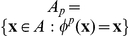 for
for 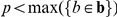 . For the case of consecutive lags, Sauer et al. state sufficient conditions to be boxdim
. For the case of consecutive lags, Sauer et al. state sufficient conditions to be boxdim 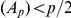 . A sufficient condition for non-consecutive lags is a bit more complicated. Define the constants
. A sufficient condition for non-consecutive lags is a bit more complicated. Define the constants 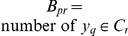 such that
such that 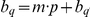 for at least one
for at least one 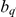 and
and 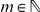 . Also, define
. Also, define 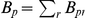 . A sufficient condition on the
. A sufficient condition on the  is
is 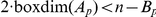 .
.
Theorem 7
Let
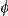 be a diffeomorphism on an open subset
be a diffeomorphism on an open subset
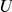 of
of
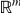 , and let
, and let
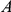 be a compact subset of
be a compact subset of
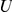 ,
,
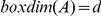 . Let
. Let
 be a collection of sets and
be a collection of sets and
 a set of lag relationships as above, such that
a set of lag relationships as above, such that
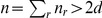 . Assume that for every positive integer
. Assume that for every positive integer
 , the set
, the set
 of periodic points of period
of periodic points of period
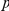 satisfies
satisfies
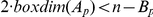 , and that for each point of
, and that for each point of
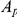 , the Jacobian
, the Jacobian
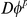 has distinct eigenvalues. Then, for almost every set of
has distinct eigenvalues. Then, for almost every set of
 observation functions
observation functions
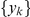 satisfying the given lag relationships, the map
satisfying the given lag relationships, the map
is an embedding on
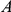 .
.
Proof
Without loss of generality, assume we have ordered the components of 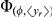 with
with 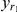 and all its lags first, then
and all its lags first, then 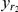 and its lags, etc. That is,
and its lags, etc. That is,
To show prevalence, we find a suitable probe space (see [29]). The infinite dimensional space for the univariate theorem is the observation functions 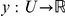 , smoothly. For maps constructed from multiple lags, this becomes the sets of
, smoothly. For maps constructed from multiple lags, this becomes the sets of 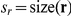 unlagged observation functions. Sauer et al. take the probe space for the univariate theorem to be any set
unlagged observation functions. Sauer et al. take the probe space for the univariate theorem to be any set  of polynomials in
of polynomials in  variables which include all such polynomials up to degree
variables which include all such polynomials up to degree 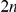 . It is now necessary to have a set of polynomials for each of the
. It is now necessary to have a set of polynomials for each of the 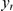 . Thus, we take the probe space for this theorem to be the Cartesian product of
. Thus, we take the probe space for this theorem to be the Cartesian product of 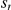 copies of
copies of 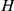 .
.
Let  be a basis for
be a basis for 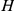 . We want to show that for almost all choices of
. We want to show that for almost all choices of 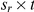 coefficients
coefficients 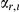 , the map
, the map 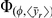 defined by the observation functions
defined by the observation functions 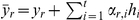 is an embedding. We first demonstrate that almost every
is an embedding. We first demonstrate that almost every 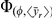 is
is  , proceeding as in the proof of Theorem 4.3 in [29].
, proceeding as in the proof of Theorem 4.3 in [29].
To sensibly apply Lemma 5, we adopt the following convention: think of 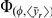 as a perturbation of
as a perturbation of 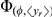 , which is the summed effect of perturbations on each
, which is the summed effect of perturbations on each 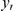 separately. For each pair
separately. For each pair 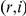 ,
,  and
and 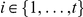 , there is a map
, there is a map 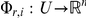 which is
which is 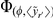 for
for 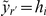 if
if 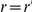 and
and 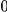 otherwise. The components of
otherwise. The components of 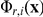 are either
are either 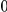 or of the form
or of the form 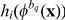 . Consequently,
. Consequently, 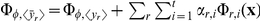 , which matches the structure Lemma 5.
, which matches the structure Lemma 5.
We now check that the rank of the matrix  satisfies the conditions of Lemma 5 for each pair of distinct
satisfies the conditions of Lemma 5 for each pair of distinct 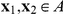 . Note that to avoid confusion with the previous section of this paper and Takens' original work, we continue to use row vectors to describe the transformations
. Note that to avoid confusion with the previous section of this paper and Takens' original work, we continue to use row vectors to describe the transformations  . However, Sauer et al. [29] prefer column vectors, so it is necessary to use of transposes in several instances. Thus, we have
. However, Sauer et al. [29] prefer column vectors, so it is necessary to use of transposes in several instances. Thus, we have
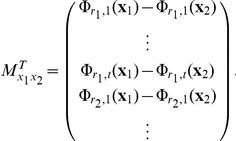 |
Note that 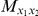 is a block diagonal matrix, and so it has rank equal to the sum of the rank of the blocks. Each of the
is a block diagonal matrix, and so it has rank equal to the sum of the rank of the blocks. Each of the 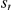 blocks can be rewritten as the product of two matrices,
blocks can be rewritten as the product of two matrices,  and
and 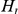 , where the entries of
, where the entries of  are values of a single polynomial
are values of a single polynomial 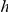 and the entries of
and the entries of 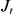 are each one of
are each one of 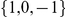 . Note, there are multiple possible choices for
. Note, there are multiple possible choices for 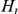 and
and 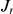 that give the same
that give the same 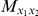 .
.
Case 1: First consider 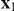 and
and 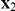 that do not both lie in a periodic orbit of integer period less than
that do not both lie in a periodic orbit of integer period less than 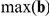 . We specify
. We specify 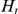 so that the first
so that the first 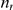 rows, where
rows, where 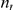 is the size of the set
is the size of the set 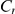 , correspond to the
, correspond to the 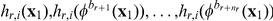 , and the next
, and the next 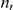 correspond to the
correspond to the 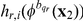 .
. 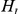 is onto, so the rank of
is onto, so the rank of 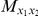 is just the sum of the ranks of the
is just the sum of the ranks of the 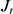 . For this case,
. For this case, 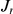 contains a copy of
contains a copy of 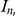 , and thus will have rank
, and thus will have rank 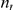 . The entire matrix
. The entire matrix 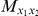 will thus have rank
will thus have rank 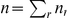 , which satisfies the conditions of Lemma 5.
, which satisfies the conditions of Lemma 5.
Case 2: Now consider 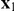 and
and 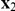 in separate periodic orbits with periods
in separate periodic orbits with periods 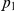 and
and 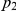 such that
such that 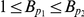 and
and 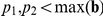 .
. 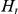 will have
will have 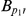 fewer rows corresponding to the
fewer rows corresponding to the 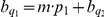 for some
for some 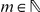 (there will also be a reduction in the number of rows associated with
(there will also be a reduction in the number of rows associated with  ). In this case,
). In this case, 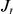 will still contain the column space of
will still contain the column space of 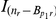 and thus
and thus 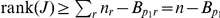 . Again the
. Again the 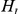 are onto, and so the rank of
are onto, and so the rank of 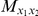 is the rank of
is the rank of 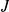 .
.
The dimension of the set 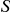 of all pairs
of all pairs 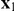 and
and 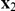 is
is 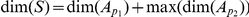 . By the conditions placed on the size of the
. By the conditions placed on the size of the 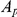 , we can conclude that
, we can conclude that 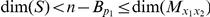 , and thus that Lemma 5 applies to this case as well.
, and thus that Lemma 5 applies to this case as well.
Case 3: Finally we consider 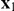 and
and 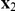 in the same
in the same 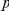 -periodic orbit,
-periodic orbit, 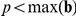 . Now the matrix
. Now the matrix 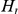 becomes more complicated, since some of the
becomes more complicated, since some of the  pertaining to
pertaining to 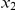 may be equal to
may be equal to 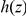 pertaining to
pertaining to 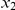 . Consequently, the
. Consequently, the  are no longer guaranteed to contain the column space of the identity. Each
are no longer guaranteed to contain the column space of the identity. Each 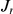 does contain the column space of an
does contain the column space of an 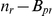 dimensional matrix with
dimensional matrix with  along the upper diagonal and a single
along the upper diagonal and a single  off the diagonal in each column. Using elementary operations, it is possible to make the first
off the diagonal in each column. Using elementary operations, it is possible to make the first  columns of
columns of 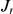 upper diagonal for some integer
upper diagonal for some integer 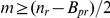 . Thus, the rank of each
. Thus, the rank of each 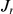 is at least
is at least 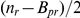 and the entire matrix has
and the entire matrix has 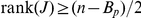 .
.
The dimension of the set 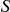 of all such
of all such 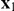 and
and 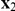 is just
is just  . By the imposed conditions,
. By the imposed conditions, 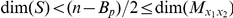 , and Lemma 5 applies.
, and Lemma 5 applies.
Now we want show that almost every 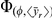 is an immersion. We check that the matrix
is an immersion. We check that the matrix
has full rank and thus satisfies the conditions of Lemma 6 for each 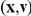 in the tangent bundle
in the tangent bundle 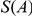 . Note that this is a block diagonal matrix with
. Note that this is a block diagonal matrix with 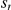 blocks, so it is sufficient to show that the columns of the
blocks, so it is sufficient to show that the columns of the  th block span the subspace
th block span the subspace 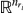 for
for 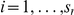 . We consider two cases.
. We consider two cases.
Case 1: Consider first the subset 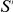 of
of  that are not periodic with period
that are not periodic with period 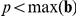 . The entries of each block are of the form
. The entries of each block are of the form 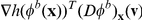 . Since
. Since 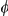 is a diffeomorphism and
is a diffeomorphism and 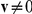 , we know that
, we know that 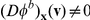 . Furthermore, the
. Furthermore, the 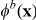 are distinct points. Examining Lemma 4, it is clear that the columns span
are distinct points. Examining Lemma 4, it is clear that the columns span  . The dimension of
. The dimension of  is at most
is at most 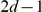 , so we may apply Lemma 6.
, so we may apply Lemma 6.
Case 2: Now consider the subset 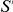 of
of  that are periodic with period
that are periodic with period 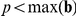 . By the conditions of the theorem,
. By the conditions of the theorem, 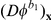 has distinct eigenvalues from
has distinct eigenvalues from 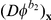 . Therefore,
. Therefore, 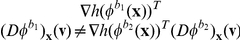 . Furthermore, the relationship depends on
. Furthermore, the relationship depends on 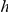 , and again referencing Lemma 4, it is clear that the columns span
, and again referencing Lemma 4, it is clear that the columns span 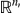 . The dimension of
. The dimension of 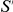 is certainly less than
is certainly less than 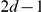 , so we can safely apply Lemma 6.
, so we can safely apply Lemma 6.
Theorem 7 can be extended to continuous dynamical systems (smooth vector fields on a manifold) by letting the flow 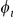 of
of 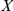 be
be 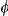 in the statement of the theorem.
in the statement of the theorem.
Discussion
Theorem 1 and the more general result presented in Theorem 2 (and its corollary) were given proofs intended to follow those presented by Takens. The original “transversality” argument, however, has been replaced with what we reckon is a simpler and more direct argument. These clarify how perturbations to the observation functions can be constructed and highlight why 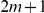 dimensions are necessary to have mappings that are generically embeddings. Theorem 7 is similar to Theorem 2, but takes advantage of the more powerful framework, built around the notion of prevalence, established by Sauer et al. [29]. It also provides more specific conditions on the periodic orbits than Theorem 2 and thus can be applied to certain non-generic situations that Takens' original framework would exclude. Namely, the set of periodic points need not be finite (as required in Takens' original theorem and Theorem 2), so long as the dimensionality does not exceed the bounds stated in Theorem 7. Theorem 7 is an extension of Remark 2.9 in [29], which we explicitly proved by determining a sufficient restriction for the periodic orbits when the lags composing
dimensions are necessary to have mappings that are generically embeddings. Theorem 7 is similar to Theorem 2, but takes advantage of the more powerful framework, built around the notion of prevalence, established by Sauer et al. [29]. It also provides more specific conditions on the periodic orbits than Theorem 2 and thus can be applied to certain non-generic situations that Takens' original framework would exclude. Namely, the set of periodic points need not be finite (as required in Takens' original theorem and Theorem 2), so long as the dimensionality does not exceed the bounds stated in Theorem 7. Theorem 7 is an extension of Remark 2.9 in [29], which we explicitly proved by determining a sufficient restriction for the periodic orbits when the lags composing 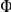 aren't necessarily consecutive.
aren't necessarily consecutive.
This work also develops a language to describe a wider family of cases for reconstructing state space manifolds from multiple observational time series to encourage wider applicability of SSR in the natural sciences. For example, these results can be extended to another special case of interest for reconstructions using time derivatives [40], when multiple observation functions are available. The argument for this case is analogous to that used by Takens [12] for the case when all the derivatives are from a single observation function. Furthermore, these theorems validate heuristic work using spatial lag reconstructions and mixed spatial and temporal lag reconstructions to study spatially coupled dynamics [41].
More importantly, in terms of future applications, Theorems 2 and 7 set the stage for practical reconstruction of state space manifolds from multiple observation functions. This is significant in answering objections to single variable state space reconstruction (SSR) concerning the excessive phenomenology of lagged-coordinate embeddings [26]. These two theorems provide proof of principle for modeling attempts of nonlinear dynamics in the natural sciences involving multiple time series (e.g. [20]), and lays bare the rather non-restrictive assumptions required in such applications for building mechanistic models from multiple time series variables. Moreover, it gives support to the notion of using multiple embeddings as a potentially efficient way of extracting information from time series data of limited length, but where there are potentially many simultaneous observations of dynamics on the same attractor manifold. By reducing correlations in noise between the reconstructed coordinates, these techniques should allow reconstructions to exceed the limitations placed on univariate methods [35], as heuristic examples have already suggested [20]. The potential information leverage provided by multiple embeddings possible from novel combinations of variables (and their lags) can pave the way for a plethora of new applied techniques to exploit the time-limited, but parallel observations of nature [36]. This paper is intended to complement the existing literature on SSR and help promote this potential growth area in the natural sciences.
Acknowledgments
We wish to thank Hao Ye, James Crutchfield, John Melack, Donald DeAngelis, Simon Levin, J. Doyne Farmer, Martin Casdagli, Tim Sauer, Sarah Glaser, Chih-hao Hsieh, Stephen Munch and Charles Peretti, Michael Fogarty, Alec MacCall, Andrew Rosenberg, Les Kaufman, and Irit Altman for helpful comments and editorial advice.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was supported by National Science Foundation (NSF) DEB1020372, NSF-NOAA CAMEO program (a partnership between the NSF and NOAA) NA08OAR4320894/CAMEO, EPA-STAR Fellowship, Sugihara Family Trust, Deutsche Bank-Jameson Complexity Studies Fund, and the McQuown Chair in Natural Sciences, University of California San Diego. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Casdagli M. Nonlinear prediction of chaotic time series. Physica D. 1989;35:335–356. [Google Scholar]
- 2.Crutchfield JP. Prediction and stability in classical mechanics. 1979. Senior thesis in physics and mathematics, University of California, Santa Cruz.
- 3.Farmer JD, Sidorowich JJ. Predicting chaotic time series. Physical Review Letters. 1987;59:845–848. doi: 10.1103/PhysRevLett.59.845. [DOI] [PubMed] [Google Scholar]
- 4.Jenouvrier S, Weimerskirch H, Barbraud C, Park YH, Cazelles B. Evidence of a shift in the cyclicity of antarctic seabird dynamics linked to climate. Proceedings of the Royal Society of London, Series B. 2005;272:887–895. doi: 10.1098/rspb.2004.2978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lo TT, Hsu HH. Change in the dominant decadal patterns and the late 1980s abrupt warming in the extratropical northern hemisphere. Atmospheric Science Letters. 2010;11:210–215. [Google Scholar]
- 6.Planque B, Batten SD. Calanus finmarchicus in the north atlantic: the year of Calanus in the context of interdecadal change. ICES Journal of Marine Science. 2000;57:1528–1535. [Google Scholar]
- 7.Ramanathan A, Wang C, Schreiber SL. Perturbational profiling of a cell-line model of tumorigenesis by using metabolic measurements. Proceedings of the National Academy of Sciences of the United States of America. 2002;102:5992–5997. doi: 10.1073/pnas.0502267102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ruelle D. Chaotic evolution and strange attractors: the statistical analysis of time series for deterministic nonlinear systems. 1989. Cambridge University Press, Cambridge.
- 9.Scheffer M, Carpenter SR. Catastrophic regime shifts in ecosystems: linking theory to observation. Trends in Ecology & Evolution. 2003;18:648–656. [Google Scholar]
- 10.Seth AK, Izhikevich E, Reeke GN, Edelman GM. Theories and measures of consciousness: an extended framework. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:10799–10804. doi: 10.1073/pnas.0604347103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Soramaki K, Bech ML, Arnold J, Glass RJ, Beyeler WE. The topology of interbank payment flows. Physica A. 2007;379:317–333. [Google Scholar]
- 12.Takens F. Detecting strange attractors in turbulence. In: Rand DA, Young LS, editors. Symposium on Dynamical Systems and Turbulence. Berlin: Springer-Verlag; 1981. pp. 366–381. , volume 898 of Lecture Notes in Mathematics. [Google Scholar]
- 13.Wagner BK, Kitami T, Gilbert TJ, Peck D, Ramanathan A, et al. Large-scale chemical dissection of mitochondrial function. Nature Biotechnology. 2008;26:343–351. doi: 10.1038/nbt1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.May RM, Levin SA, Sugihara G. Complex systems: Ecology for bankers. Nature. 2008;451:893–895. doi: 10.1038/451893a. [DOI] [PubMed] [Google Scholar]
- 15.Sugihara G. On early warning signs. 2010. Seed Magazine Global Reset 2010.
- 16.Sugihara G. Nature is nonlinear. Kyoto Journal. 2010;75:56–57. [Google Scholar]
- 17.Brock WA, Sayers CL. Is the business cycle characterized by deterministic chaos? Journal of Monetary Economics. 1988;22:71–90. [Google Scholar]
- 18.Brock WA, Malliaris AG. Differential Equations, Stability and Chaos in Dynamic Economics, volume 27 of Advanced Textbooks in Economics. North-Holland 1989 [Google Scholar]
- 19.Brock WA, Hsieh DA, LeBaron BD. Nonlinear Dynamics, Chaos, and Instability: Statistical Theory and Economic Evidence. 1991. MIT Press, Cambridge, Massachusettes.
- 20.Dixon PA, Milicich MJ, Sugihara G. Episodic fluctuations in larval supply. Science. 1999;283:1528–1530. doi: 10.1126/science.283.5407.1528. [DOI] [PubMed] [Google Scholar]
- 21.Hsieh CH, Glaser SM, Lucas AJ, Sugihara G. Distinguishing random environmental fluctuations from ecological catastrophes for the North Pacific Ocean. Nature. 2005;435:336–340. doi: 10.1038/nature03553. [DOI] [PubMed] [Google Scholar]
- 22.Hsieh CH, Anderson C, Sugihara G. Extending nonlinear analysis to short ecological time series. American Naturalist. 2008;171:71–80. doi: 10.1086/524202. [DOI] [PubMed] [Google Scholar]
- 23.Rodo X, Pascual M, Fuchs G, Faruque ASG. ENSO and cholera: a nonstationary link related to climate change? Proceedings of the National Academy of Sciences of the United States of America. 2002;99:12901–12906. doi: 10.1073/pnas.182203999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schaffer WM. Stretching and folding in lynx fur returns: evidence for a strange attractor in nature? American Naturalist. 1984;124:789–820. [Google Scholar]
- 25.Sugihara G, Grenfell B, May RM. Distinguishing error from chaos in ecological time series. Philosophical Transactions of the Royal Society of London, Series B: Biological Science. 1990;330:235–250. doi: 10.1098/rstb.1990.0195. [DOI] [PubMed] [Google Scholar]
- 26.Sugihara G, May RM. Nonlinear forecasting as a way of distinguishing chaos from measurement error in a data series. Nature. 1990;344:734–741. doi: 10.1038/344734a0. [DOI] [PubMed] [Google Scholar]
- 27.Sugihara G. Nonlinear forecasting for the classification of natural time series. Philosophical Transactions of the Royal Society of London, Series A. 1994;348:477–495. [Google Scholar]
- 28.Packard NH, Crutchfield JP, Farmer JD, Shaw RS. Geomtery from a time series. Physical Review Letters. 1980;45:712–716. [Google Scholar]
- 29.Sauer T, Yorke JA, Casdagli M. Embedology. Journal of Statistical Physics. 1991;65:579–616. [Google Scholar]
- 30.Hunt BR, Sauer T, Yorke JA. Prevalence: a translation-invariant “almost every” on infinite-dimensional spaces. Bulletin of the American Mathematical Society. 1992;27:217–238. [Google Scholar]
- 31.Stark J, Broomhead DS, Davies ME, Huke JP. Takens embedding theorems for forced and stochastic systems. Nonlinear Analysis: Theory, Methods, and Applications. 1997;30:5303–5314. [Google Scholar]
- 32.Stark J, Broomhead DS, Davies ME, Huke JP. Delay embeddings for forced systems: II. Stochastic forcing. Journal of Nonlinear Science. 2003;13:519–577. [Google Scholar]
- 33.Stark J. Delay embeddings for forced systems: I. Deterministic forcing. Journal of Nonlinear Science. 1999;9:255–332. [Google Scholar]
- 34.Gibson J, Farmer JD, Casdagli M, Eubank S. An analytic approach to practical state space reconstruction. Physica D. 1992;57:1–30. [Google Scholar]
- 35.Casdagli M, Eubank S, Farmer JD, Gibson J. State space reconstruction in the presence of noise. Physica D. 1991;41:52–98. [Google Scholar]
- 36.Ye H, Sugihara G, Deyle ER. Leverging information from multiple time series with ensemble state space reconstructions. 2011. In preparation.
- 37.Lorenz EN. Deterministic nonperiodic flow. Journal of Atmospheric Science. 1963;20:130–141. [Google Scholar]
- 38.Whitney H. Differentiable manifolds. Annals of Mathematics. 1936;37:645–680. [Google Scholar]
- 39.Huke JP. Embedding nonlinear dynamical systems, a guide to Takens' theorem. 1993. Internal report, DRA, Malvern, UK.
- 40.Crutchfield JP, McNamara BS. Equations of motion from a data series. Complex Systems. 1987;1:417. [Google Scholar]
- 41.Ørstavik S, Stark J. Reconstruction and cross-prediction in coupled map lattices using spatio-temporal embedding techniques. Physics Letters A. 1998;247:145–160. [Google Scholar]