Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2011 Mar 14;108(13):5266–5271. doi: 10.1073/pnas.1017604108

Interdomain communication revealed in the diabetes drug target mitoNEET

Elizabeth L Baxter a,b,✉, Patricia A Jennings a,1, José N Onuchic b,✉
PMCID: PMC3069162  PMID: 21402934

Abstract

MitoNEET is a recently identified drug target for a commonly prescribed diabetes drug, Pioglitazone. It belongs to a previously uncharacterized ancient family of proteins for which the hallmark is the presence of a unique 39 amino acid CDGSH domain. In order to characterize the folding landscape of this novel fold, we performed thermodynamic simulations on MitoNEET using a structure-based model. Additionally, we implement a method of contact map clustering to partition out alternate pathways in folding. This cluster analysis reveals a detour late in folding and enables us to carefully examine the folding mechanism of each pathway rather than the macroscopic average. We observe that tightness in a region distal to the iron–sulfur cluster creates a constraint in folding and additionally appears to mediate communication in folding between the two domains of the protein. We demonstrate that by making changes at this site we are able to tweak the order of folding events in the cluster binding domain as well as decrease the barrier to folding.

Keywords: protein folding, Thiazolidinedione, CISD1, aging, multiple routes

MitoNEET is a recently identified outer mitochondrial membrane protein that unexpectedly binds the commonly prescribed type II diabetes drug Pioglitazone (1–3). It is now recognized as a new drug target in diabetes therapy as opposed to the traditional PPARg therapeutics (4). Mis-splicing of Miner1, the structural homolog of mitoNEET, results in the rare disease Wolfram syndrome that initially presents with diabetes and rapidly progresses to blindness and early death (5). In addition, Miner1 appears to play a significant role in aging and associated diseases. MitoNEET and Miner1 possess a unique homodimeric fold with a CDGSH iron–sulfur cluster binding domain and a strand swapped beta cap (3, 6–10). Because regulating the activity of this new drug target is an area of high interest, investigation of the folding and possible allosteric modulation of function in this family is now a major research focus.

Energy landscape theory indicates that proteins have evolved to fold in a funneled fashion with minimal frustration (11–13). Because energetic frustration is sufficiently small, much of the heterogeneity in folding is dominated by the geometric constraints of the native structure. As a result, structure-based models are capable of capturing the main features of the transition state and intermediates formed during folding for many proteins (14–19). In addition, our analysis of the bottlenecks in folding have led to a deeper understanding of regulatory mechanisms operating in specific proteins. This led us to the hypothesis that functional regions in proteins may add roughness to the landscape because they are under separate evolutionary pressure than areas used for efficient folding. For example, structure-based simulations with adenylate kinase demonstrated that the introduction of frustration induced conformational transitions associated with enzymatic catalyisis through specific unfolding, or cracking (20, 21). Folding simulations with Csk and IL-1β successfully captured long range communication to functional sites (22, 23). Therefore folding studies provide a unique approach to explore the functional landscape of biomolecules.

As a first step toward defining not only the folding but also potential points of regulation in the NEET family, we initiated theoretical structure-based folding studies. A common approach to analyzing large quantities of data from structure-based simulations is to examine macroscopic averages at a point along a reaction coordinate, such as Q. However, many proteins can access multiple routes to folding (24–28). In these systems, this approach can become problematic because averaging over multiple pathways can obscure the actual folding events in each route. In these cases it is useful to examine reaction coordinates transverse to Q, but because the folding funnel is highly multidimensional, it is difficult to know which reaction coordinates to examine. We implement a scheme to investigate the dimeric transition state in structure-based models by clustering contact maps. Clustering provides us with an efficient way of compacting and visualizing this high-dimensional space in two dimensions, enabling us to efficiently sort data and identify alternate folding routes that make up this ensemble. It also proves especially effective for handling averaging over duplicate pathways that result from symmetry in multimeric systems. We show that in mitoNEET, the average transition state ensemble is misleading when compared with the transition state ensemble after clustering. Additionally, clustering reveals the presence of a detour late in folding.

Clustering enables us to carefully examine the folding mechanism of mitoNEET. We observe that a helical turn in the top of the beta cap domain introduces frustration in folding. Additionally, we see communication between the beta cap domain and the cluster binding domain. Rigidity in the beta cap domain creates a constraint for how the rest of the protein folds, and this results in backtracking in loop 1 in the cluster binding domain. We demonstrate that we can modulate the behavior of the cluster binding domain by making changes at the top of the beta cap domain. By destabilizing a set of contacts in loop 2 at the top of the beta cap domain, we can relieve backtracking in the cluster binding domain. Additionally, this drops the barrier to folding, suggesting that this structural feature introduces frustration in folding.

Results

Structure of MitoNEET and Nomenclature.

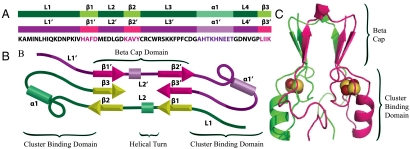
MitoNEET is a homodimeric Fe-S protein with a novel fold (6, 8, 9). Each protomer consists of three β-strands (β1, β2, and β3), an alpha helix (α1), and four loops (L1, L2, L3, and L4). Moving from the N to C terminus they are ordered L1, β1, L2, β2, L3, α1, L4, β3. Together the two protomers intertwine to form two domains, a beta cap domain and a cluster binding domain (Fig. 1). The cluster binding domain coordinates two redox active 2Fe–2S cluster (3, 29, 30). Each of the two cluster cradles is formed from loop 3 and helix 1 of a single protomer. The coordination is unusual in that each of the clusters are coordinated by three cysteines and one histidine. The beta cap domain consists of two beta sheets. Each beta sheet is composed of β2 and β3 from one protomer and β1′ from the other protomer, arranged in the order β1′ β3 β2. This strand swap of β1′ intertwines the two protomers and creates a helical turn across the top of the beta cap domain in loop 2 (Fig. 1). In an effort to understand the functional implications of the strand swap we now explore the mechanism of assembly of this protein.

Fig. 1.

Fig. 1.

Open in a new tab

Structural organization and domain topology of mitoNEET. (A) Protomers aligned with the sequence. Highlighted regions correspond to the loops, helices, and beta strands in mitoNEET. (B) Splay diagram showing the location of the helical turn in the beta cap domain. (C) Ribbon diagram of mitoNEET colored by chain. The beta cap domain consists of a beta sandwich composed of two three-stranded beta sheets. Each beta sheet is composed of two strands from one protomer and a third strand from a second protomer.

Mechanism of Assembly—Coupled Folding and Dimerization.

Structure-based models have proven to be informative in the mechanism of assembly of a number of proteins (17, 31, 32). For example, we explain the rop dimer switch between syn and anti structures as a dual basin landscape that corresponds to distinct but related structures (33, 34). The unusual strand swap in mitoNEET creates a large interface surface between the two protomers. This led us to ask: Does the strand swap introduce constraints into the mechanism of assembly? In order to determine the mechanism of assembly of mitoNEET, we performed molecular dynamics simulations using a structure-based model.

The free energy surface of assembly for the mitoNEET dimer is projected onto three reaction coordinates; two corresponding to the folding of each protomer, and the third corresponding to protomer association (Fig. 2A). QA represents the number of contacts formed in monomer A, QA′ represents contact formation in monomer A′, and QI represents the number of interface contacts formed. Moving along the reaction coordinate QA (or QA′) we see that when QI is low, only a subset of QA or QA′ contacts can be formed. It is only when a significant number of interface contacts are formed that an increase in the number of monomer contacts can be seen. The dimerization transition is broad, suggesting that there may be more than one population of structures in the transition state. It may be that multiple pathways to dimerization are present but are unable to be resolved using this particular set of reaction coordinates. This will be investigated in the next section. Analysis of the free energy barrier to folding (Fig. 2B) indicates that folding and dimerization are highly cooperative with no obvious populated intermediates. Taken together this initial analysis suggests that the folding and assembly of mitoNEET is coupled and dimerization is obligatory. That is, the formation of individual protomers A and A′ is only allowed upon binding. In addition, the 8 kt barrier is high for a protein of this size and suggests that traps along folding routes exist.

Fig. 2.

Fig. 2.

Open in a new tab

(A) Free energy surface for the assembly of mitoNEET. The free energy is projected on the reaction coordinates Q protomer A, Q protomer A′ and Q interface. A contour of the free energy as a function of QA and QA′ is plotted at eight different values of Q interface. (B) Free energy is plotted as a function of Q at Tf.

Clustering Uncovers The Folding Route.

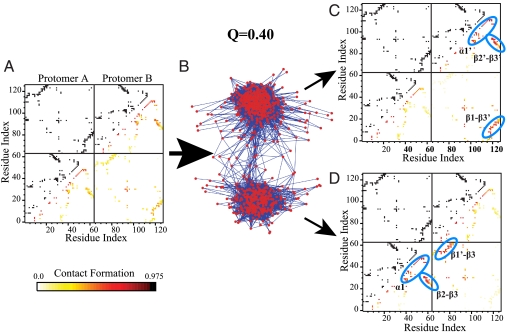
The presence of traps during folding and assembly was investigated by performing a detailed analysis of the transition state ensemble. The probability of specific native contact formation in the transition state (Q = 0.4) is shown Fig. 3A. This ensemble average view suggests that the transition state is diffuse and unstructured. However, examination of individual trajectories between the folded and unfolded basins indicates that transitions appear to choose between one of two pathways, and the averaging over these two pathways is responsible for the appearance of an unstructured transition state.

Fig. 3.

Fig. 3.

Open in a new tab

Cluster analysis of mitoNEET at Q = 0.4. (A) Probability of specific contact formation at Q = 0.4, represented with color on a contact map. White and yellow represent a lower probability of contact formation, and orange and dark red represent a higher probability of contact formation. All native contacts are plotted in black across the diagonal for reference. (B) Similarity network for Q = 0.4. Red nodes represent contact maps for individual snapshots in completed transitions at Q = 0.4. Blue edges represent similarity between nodes. Shorter edges represent higher similarity between snapshots. (C) Probability of specific contact formation for each cluster. Structural features are circled in blue. In the top cluster, a1′, B2′–B3′, and B1–B3′ form. (D) In the bottom cluster, a1, B2–B3, and B1′–B3 form.

An accurate description of the folding process requires efficient separation of alternative routes. To this end, we implement a method for clustering structures in the transition state by their associated contact maps (described in detail in Methods). The resulting similarity network for Q = 0.4 is shown in Fig. 3B. Two distinct clusters are observed, suggesting that two different ensembles are populated in the transition state. The probability of native contact formation for these two clusters at Q = 0.4 are provided in Fig. 3 C and D. In contrast to the initial contact map generated for the ensemble where the two alpha helices appeared to form together and all beta sheets appeared relatively unstructured, clustering reveals contact formation between β2′ and β3′, β1 and β3′, as well as contacts within helix α1′. In the second cluster, the same contacts are formed but in the complementary protomer (β2 and β3, β1′ and β3, and α1). In fact, at Q = 0.4 only a single dominant route is present; however, the symmetry of the multimeric system creates a duplicate pathway distinguishable only through naming of the individual protomers. A structural representation of the fraction of native contact formation by residue at Q = 0.4 is plotted in Fig. 4. After clustering the transition state is composed of one sheet from the beta sandwich and one half of the cluster binding domain. Half of the protein forms by the transition state and structural elements from both protomers are involved in the nucleation step. At Q = 0.6 (Fig. 5) a third cluster appears that represents an alternate folding route. Here residue contact formation between the two protomers is symmetric. L1 and L1′ within the cluster binding domain are disordered, while the entire beta cap domain is well formed (β2 and β3, β1′ and β3, β2′ and β3′, β1 and β3′, L2, and L2′).

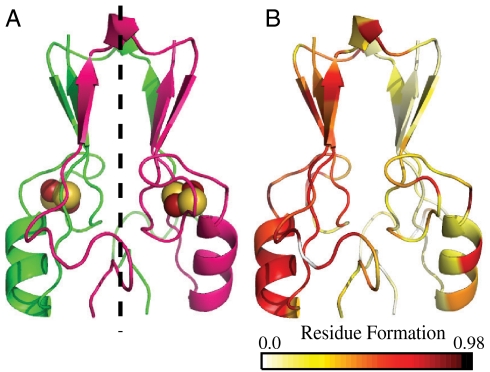
Fig. 4.

Fig. 4.

Open in a new tab

Transition state structure of mitoNEET. (A) MitoNEET colored by chain for reference. (B) Residue contact formation for mitoNEET at Q = 0.4. P(Qi,Qca) is the probability that the set of contacts involving residue i, Qi, are formed at a given Qca. P(Qi,Qca) was calculated for each cluster and represented with a color scale on the structure of mitoNEET. White and yellow residues represent decreased residue formation, and red and black represent higher residue formation. In the transition state half the beta sandwich forms (B1, B3′, and B2′) and one half of the cluster binding domain are formed.

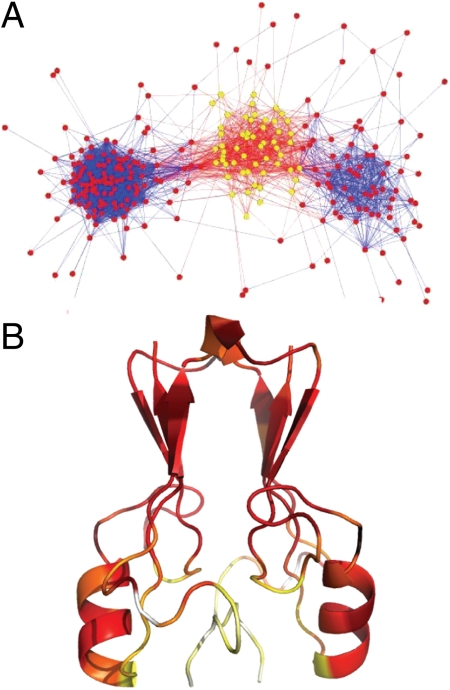
Fig. 5.

Fig. 5.

Open in a new tab

(A) Similarity network at Q = 0.6. The presence of a third cluster highlighted in yellow represents a detour in folding. (B) Residue contact formation for middle cluster at Q = 0.6.

Rigidity in the Beta Cap Domain Forces Backtracking in Distal Sites.

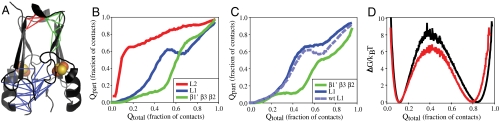
The formation of native contacts within the protein is not uniform across the molecule. We therefore partitioned and analyzed the behavior of specific subsets of contacts (Fig. 6A) within the protein as it folds to more carefully examine the order of events. We then plot the progression of these subsets of contacts (Qpart) as a function of the total number of contacts in the native fold (Qtotal) (Fig. 6 B and C). We observed that formation of contacts in a helical turn in L2, L1, and the late-forming beta sheet (β2 and β3, β1′ and β3) are interdependent. That is, contacts found in the helical turn (plotted in red) form early in the folding process, while contacts found in L1 (plotted in blue) form in a nonmonotonic manner, and those within the beta sheet (plotted in green) begin to populate after contact formation in L1 peak. These latter contacts (blue) exhibit a behavior called backtracking, a signal of frustration in folding. Backtracking is the forming, breaking, and reforming of native contacts as the protein proceeds to the folded state. The formation of contacts in the late forming beta sheet appears to be coupled to backtracking. As L1 contacts begin to break, the formation of these contacts begins, and then plateaus just as contacts in L1 begin to form again. In the similarity network at Q = 0.6 (Fig. 5) we see a third cluster appear that represents an alternate folding route present in 29% of complete folding/unfolding transitions. This detour in folding is the backtracking route. The second beta sheet comes together so that both beta sheets in the beta cap domain and the helical turns are well formed; however, in this process loop 1 twists away from the helix and cluster-binding region, breaking contacts that had formed earlier in folding.

Fig. 6.

Fig. 6.

Open in a new tab

Dynamic coupling between the beta cap domain and cluster binding domain. (A) Contacts to be examined are drawn on to the structure and grouped by color. Red lines represent contacts within and near the helix in loop 2, green lines represent contacts in the beta sheet (B1, B3′, B2′), and blue lines represent contacts between loop 1 and the cluster binding domain. (B) The average fraction of these subsets of contacts formed as a function of Qtotal. Contacts in and near the helix in the turn form early. Contacts between L1 and the cluster binding domain begin to form but backtrack. Contacts in L2 and the beta sheet are dynamically coupled to contacts in L1 and begin to form as L1 begins to reform contacts after backtracking. (C) The average fraction of groups of contacts formed as a function of Q after destabilization of contacts in L2. Contacts between L1 and the cluster binding domain begin to form but backtrack. For reference, contacts between L1 and the cluster binding domain are plotted before destabilization as a light blue dotted line. Contacts in the beta sheet are still coupled to contacts in L1 and begin to form as contacts in L1 plateau. (D) Overlay of the free energy barriers for mitoNEET (in black) and mitoNEET with contacts (shown in red in A) and dihedrals relaxed (in red).

To test if early formation of the helical part of loop 2 creates a constraint for how the second half of the protein folds, we performed a second set of simulations in which we destabilized this structural feature by removing three contacts in the helical turn and relaxing five dihedral angles. Relaxing this helical turn reduces the barrier to folding (Fig. 6D). We looked for changes in the folding mechanism by again plotting Qpart vs Qtotal for the same groups of contacts in this new set of simulations. Formation of Loop 1 plateaus at Q = 0.45, at which point beta sheet 2 begins to form. However, the backtracking observed in WT mitoNEET is abolished. Taken together, these data indicate that stabilization of the helical turn (beta cap domain) impedes final formation of the native homodimer.

Discussion

Cluster Analysis of the Transition State.

Often the approach to analysis of the transition state in molecular dynamics simulations is examination of the average transition state ensemble. Although useful for comparing to experiments, this approach can obscure the presence of multiple routes and the actual order of folding events. This is not only problematic for proteins that can access multiple pathways but also for symmetric multimeric systems. In addition, the amount of data generated for adequate sampling of transition states and intermediates during folding requires an efficient method for categorizing the multiple states sampled over hundreds of trajectories. To tackle this problem we implemented a method for clustering snapshots of populated states by scoring the similarity of associated contact maps. This method results in an efficient and robust way of visualizing and understanding complex folding landscapes. In our current study clustering revealed heterogeneity in the transition state and population of multiple routes in the folding of mitoNEET. This complexity in folding is obscured by the standard analysis. Thus, this methodology is not only superior for folding studies but also will be highly useful in characterizing local cracking and functional dynamics associated with regulation of activity in biomolecules.

Synchronization in Folding, Backtracking, and Frustration.

Despite being a symmetric homodimer, folding is asymmetric with each protomer contributing to early formation of one structural half. That is, when viewing the protein with a plane bisecting the beta sandwich, this plane crosses a loop (L2) with a helical turn that creates a swapped loop (L1) and strand (β1) between the two beta sheets. This swap tethers together the two protomers within each structural half, coupling folding and dimerization. An unswapped structure would necessarily have more intra-vs inter beta strand contacts within each sheet, allowing for more independent folding of each monomer. The swap forces contacts between residues that are on different protomers, therefore not close in sequence, to be part of the transition state for folding. This leads to increased cooperativity. It may be that the geometry and short length of loop 2 helps to enforce this strand swap by preventing the association of strand β1 with β3, and β1′ with β3′, thus preventing the monomers from forming independently.

Immediately following the transition state, as the downhill process initiates, rearrangement of the remaining structural features occurs. Sometimes these pieces pack in the wrong order and require backtracking as they search for the final structure. Interestingly, we observe that the swapped loops are involved in trapping and repacking during backtracking. That is, early formation of contacts in loop 1 and loop 2 result in a trap in folding where it is geometrically difficult for the remainder of contacts to form. In order for the second half of the beta cap domain to finish folding, the cluster binding domain must partially open up, and the swapped loop must break contacts with the cluster-binding domain. Weakening contacts in loop 2 relaxes some of the tightness of the beta cap domain. We see in these simulations that the barrier to folding drops and backtracking in the cluster-binding domain is relieved. This suggests that loop 2 is responsible for frustration in folding and that changes there can translate to the cluster-binding domain. The rop in barrier height is not a result of a decrease in backtracking, both are a result of decreased trapping. Thus, the swapped strands and associated loops contribute to both the nucleation process (transition state) and subsequent backtracking during final packing.

Allosteric Coupling of the Beta Cap Domain and Cluster-Binding Domain.

While evolution selects for robust folders, it must do this while conserving and selecting for function. This competition between selection for efficient folders and function can introduce frustration and prevent a landscape from becoming perfectly funneled (35, 36). It’s been observed that functional regions of many proteins do not aid in folding and may in fact interfere with it. For example, functional loop mutations in WW domain proteins speed up folding at the expense of function, and in some cases they remove the barrier to folding completely (37, 38). It is possible, then, that frustration in the folding landscape can give us important clues about which structural features are important for function. Previous work done with the beta trefoil family of proteins demonstrated that a functionally important beta bulge was involved in backtracking and responsible for the slow folding of the IL-1B family of proteins (19, 22, 39). It is possible that in mitoNEET evolution has kept this frustration in loop 2 because this structural feature is functionally important. We observe that rigidity in the beta cap domain forces backtracking of the swapped loop in the cluster binding domain, demonstrating that there is communication between the two domains. The beta cap domain could function as an allosteric control site, modulating cluster insertion, assembly, or electron transfer. It would be interesting to determine experimentally if this element of geometric frustration in loop 2 is linked to functional regulatory properties of mitoNEET.

Conclusion

We used a structure-based model to characterize the folding landscape of mitoNEET. The folding mechanism uncovered in this landscape reveals communication between distal regions of the protein. We see that because of the strand swap, folding and assembly is cooperative and dimerization precedes final folding. The individual monomers cannot independently fold then associate. We partition alternate routes in folding by clustering transition state contact maps. This efficiently separates out duplicate pathways caused by the symmetry of the dimeric system, and it reveals an alternate route late in folding. A careful examination of the folding mechanism reveals a region of frustration in loop 2 at the top of the beta cap domain, and that folding of the beta cap domain is dynamically coupled to the cluster binding domain. Tightness in the beta cap domain creates a constraint for how the rest of the protein folds, which results in backtracking in loop 1 in the cluster-binding domain. We demonstrate that by destabilizing a set of contacts in loop 2 at the top of the beta cap domain, we can relieve backtracking in the cluster-binding domain and drop the barrier to folding by a few kT.

Methods

The contact map gives all possible interactions between a given residue and the other residues in a given structure. Contacts are identified using the Contacts of Structural Units software package (CSU) (40) on the crystal structure of mitoNEET stored in PDB ID 2QH7 (6). Because of slight asymmetries in the crystal structure, 14 contacts were generated that were not symmetrical between the two monomers. To simplify the model we remove these 14 unsymmetrical contacts. The resulting contact map consisted of 98 intramonomer contacts for each of the two monomers and 132 interface contacts for a total of 324 contacts.

A coarse grained structure-based model is used to represent the protein as described previously (14). In this model, each residue is represented by its Ca atom, and only interactions present in the contact map (between residues in the native state) are considered. Nonnative interactions are not considered, and so energetic frustration is not included in this model. In our coarse grained folding studies the iron–sulfur cluster is implicitly included in the contacts present between cluster binding residues. Simulations were performed using Version 3.3.3 of the GROMACS software package (41). The integrator used was stochastic dynamics. The Berendsen algorithm was used with the coupling constant of 2. The time step τ was 0.0005. Each monomer was temperature coupled separately. Simulations were performed at folding temperature. Half of the simulations were started from the folded dimeric conformation, and half were started from unfolded and unbound monomers. A harmonic potential with an offset of 17 Å was applied to the center of mass of each monomer to hold the two monomers together.

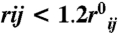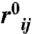We use the fraction of native contacts formed in a given snapshot of the protein as the reaction coordinate. (QCα is the fraction of natively interacting residue pairs whose ca atoms are within 1.2 times their native distance.) A contact is formed between Cα atoms I and j if Inline graphic where Inline graphic is the pair distance in the native state. QA represents the contacts formed in protomer A, QA′ represents contacts formed in protomer A′, and QI represents interface contacts between the two monomers. Qpart is calculated as the fraction of contacts formed within a specific subset of contacts at a given value of Qtotal.

Cluster analysis was performed as follows. All snapshots in the transition state at Q = 0.4 were represented with a contact map. Each representative contact map was internally compared using the logic gate xnor. If two structures had the same native contact formed or the same native contact not formed, a point was added to the similarity score between the two structures. If one structure had a contact formed that the other did not, this was considered dissimilar and no point was added to the score. Higher scores indicate higher similarity between contact maps, and therefore higher similarity between snapshots of the transition state. The highest possible score was 324, one point for each possible contact in the native state. A threshold value of 200 was set, meaning that in order for two structures to be considered similar, they must have 200 out of 324 native contacts in common. Similarity networks were created for different values of Q near the transition state and were visualized using the edge weighted spring embedded layout algorithm in Cytoscape (42, 43).

All structures were visualized using Pymol.

Acknowledgments.

E.L.B. thanks Jeffery Noel for helpful discussions. This work was supported in part by the Center for Theoretical Biological Physics sponsored by the National Science Foundation (NSF; Grant PHY-0822283) and NSF Grant MCB-1051438, and National Institutes of Health Grant GM-54038. E.L.B. was also supported by a San Diego Fellowship.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

References

  • 1.Wiley SE, Murphy AN, Ross SA, van der Geer P, Dixon JE. MitoNEET is an iron-containing outer mitochondrial membrane protein that regulates oxidative capacity. Proc Natl Acad Sci USA. 2007;104:5318–5323. doi: 10.1073/pnas.0701078104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Colca JR, et al. Identification of a novel mitochondrial protein (“mitoNEET”) cross-linked specifically by a thiazolidinedione photoprobe. Am J Physiol-Endoc M. 2004;286:E252–260. doi: 10.1152/ajpendo.00424.2003. [DOI] [PubMed] [Google Scholar]
  • 3.Wiley SE, et al. The outer mitochondrial membrane protein mitoNEET contains a novel redox-active 2Fe-2S cluster. J Biol Chem. 2007;282:23745–23749. doi: 10.1074/jbc.C700107200. [DOI] [PubMed] [Google Scholar]
  • 4.Geldenhuys WJ, Funk MO, Barnes KF, Carroll RT. Structure-based design of a thiazolidinedione which targets the mitochondrial protein mitoNEET. Bioorg Med Chem Lett. 2010;20:819–823. doi: 10.1016/j.bmcl.2009.12.088. [DOI] [PubMed] [Google Scholar]
  • 5.Amr S, et al. A homozygous mutation in a novel zinc-finger protein, ERIS, is responsible for Wolfram syndrome 2. Am J Hum Genet. 2007;81:673–683. doi: 10.1086/520961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Paddock ML, et al. MitoNEET is a uniquely folded 2Fe–2S outer mitochondrial membrane protein stabilized by pioglitazone. Proc Natl Acad Sci USA. 2007;104:14342–14347. doi: 10.1073/pnas.0707189104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Conlan AR, et al. Crystal structure of Miner1: The redox-active 2Fe-2S protein causative in Wolfram syndrome 2. J Mol Biol. 2009;392:143–153. doi: 10.1016/j.jmb.2009.06.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Hou X, et al. Crystallographic studies of human mitoNEET. J Biol Chem. 2007;282:33242–33246. doi: 10.1074/jbc.C700172200. [DOI] [PubMed] [Google Scholar]
  • 9.Lin J, Zhou T, Ye K, Wang J. Crystal structure of human mitoNEET reveals distinct groups of iron–sulfur proteins. Proc Natl Acad Sci USA. 2007;104:14640–14645. doi: 10.1073/pnas.0702426104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Conlan AR, et al. Structural comparison of a diabetes drug target, mitoneet a 2Fe-2S cluster protein to its more stable mutant, H87C. Biophys J. 2009;96(Suppl 1):67a–67a. [Google Scholar]
  • 11.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
  • 12.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci USA. 1992;89:8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Clementi C, Nymeyer H, Onuchic JN. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J Mol Biol. 2000;298:937–953. doi: 10.1006/jmbi.2000.3693. [DOI] [PubMed] [Google Scholar]
  • 15.Finke JM, Onuchic JN. Equilibrium and kinetic folding pathways of a TIM barrel with a funneled energy landscape. Biophys J. 2005;89:488–505. doi: 10.1529/biophysj.105.059147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Ding F, Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Molecular dynamics simulation of the SH3 domain aggregation suggests a generic amyloidogenesis mechanism. J Mol Biol. 2002;324:851–857. doi: 10.1016/s0022-2836(02)01112-9. [DOI] [PubMed] [Google Scholar]
  • 17.Levy Y, Wolynes PG, Onuchic JN. Protein topology determines binding mechanism. Proc Natl Acad Sci USA. 2004;101:511–516. doi: 10.1073/pnas.2534828100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Yang S, et al. Domain swapping is a consequence of minimal frustration. Proc Natl Acad Sci USA. 2004;101:13786–13791. doi: 10.1073/pnas.0403724101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Capraro DT, Roy M, Onuchic JN, Jennings PA. Backtracking on the folding landscape of the β-trefoil protein interleukin-1β? Proc Natl Acad Sci USA. 2008;105:14844–14848. doi: 10.1073/pnas.0807812105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Whitford PC, Gosavi S, Onuchic JN. Conformational transitions in adenylate kinase. J Biol Chem. 2008;283:2042–2048. doi: 10.1074/jbc.M707632200. [DOI] [PubMed] [Google Scholar]
  • 21.Whitford PC, Miyashita O, Levy Y, Onuchic JN. Conformational transitions of adenylate kinase: Switching by cracking. J Mol Biol. 2007;366:1661–1671. doi: 10.1016/j.jmb.2006.11.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Gosavi S, Whitford PC, Jennings PA, Onuchic JN. Extracting function from a β-trefoil folding motif. Proc Natl Acad Sci USA. 2008;105:10384–10389. doi: 10.1073/pnas.0801343105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Mills JE, et al. A novel disulfide bond in the SH2 domain of the C-terminal Src kinase controls catalytic activity. J Mol Biol. 2007;365:1460–1468. doi: 10.1016/j.jmb.2006.10.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Lindberg MO, Haglund E, Hubner IA, Shakhnovich EI, Oliveberg M. Identification of the minimal protein-folding nucleus through loop-entropy perturbations. Proc Natl Acad Sci USA. 2006;103:4083–4088. doi: 10.1073/pnas.0508863103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Chavez LL, Gosavi S, Jennings PA, Onuchic JN. Multiple routes lead to the native state in the energy landscape of the Inline graphic-trefoil family. Proc Natl Acad Sci USA. 2006;103:10254–10258. doi: 10.1073/pnas.0510110103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Shimada J, Shakhnovich EI. The ensemble folding kinetics of protein G from an all-atom Monte Carlo simulation. Proc Natl Acad Sci USA. 2002;99:11175–11180. doi: 10.1073/pnas.162268099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Wright CF, Lindorff-Larsen K, Randles LG, Clarke J. Parallel protein-unfolding pathways revealed and mapped. Nat Struct Mol Biol. 2003;10:658–662. doi: 10.1038/nsb947. [DOI] [PubMed] [Google Scholar]
  • 28.Lindberg M, Tangrot J, Oliveberg M. Complete change of the protein folding transition state upon circular permutation. Nat Struct Mol Biol. 2002;9:818–822. doi: 10.1038/nsb847. [DOI] [PubMed] [Google Scholar]
  • 29.Bak DW, Zuris JA, Paddock ML, Jennings PA, Elliott SJ. Redox characterization of the FeS protein mitoNEET and impact of thiazolidinedione drug binding. Biochemistry. 2009;48:10193–10195. doi: 10.1021/bi9016445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Zuris JA, et al. Engineering the redox potential over a wide range within a new class of FeS Proteins. J Am Chem Soc. 2010;132:13120–13122. doi: 10.1021/ja103920k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Levy Y, Caflisch A, Onuchic JN, Wolynes PG. The folding and dimerization of HIV-1 protease: Evidence for a stable monomer from simulations. J Mol Biol. 2004;340:67–79. doi: 10.1016/j.jmb.2004.04.028. [DOI] [PubMed] [Google Scholar]
  • 32.Levy Y, Cho SS, Onuchic JN, Wolynes PG. A survey of flexible protein binding mechanisms and their transition states using native topology based energy landscapes. J Mol Biol. 2005;346:1121–1145. doi: 10.1016/j.jmb.2004.12.021. [DOI] [PubMed] [Google Scholar]
  • 33.Gambin Y, et al. Direct single-molecule observation of a protein living in two opposed native structures. Proc Natl Acad Sci USA. 2009;106:10153–10158. doi: 10.1073/pnas.0904461106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Schug A, Whitford PC, Levy Y, Onuchic JN. Mutations as trapdoors to two competing native conformations of the rop-dimer. Proc Natl Acad Sci USA. 2007;104:17674–17679. doi: 10.1073/pnas.0706077104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Schreiber G, Buckle AM, Fersht AR. Stability and function: Two constraints in the evolution of barstar and other proteins. 1994;2:945–951. doi: 10.1016/s0969-2126(94)00096-4. [DOI] [PubMed] [Google Scholar]
  • 36.Zhang X-j, Baase WA, Shoichet BK, Wilson KP, Matthews BW. Enhancement of protein stability by the combination of point mutations in T4 lysozyme is additive. Protein Eng. 1995;8:1017–1022. doi: 10.1093/protein/8.10.1017. [DOI] [PubMed] [Google Scholar]
  • 37.Jäger M, et al. Structure–function–folding relationship in a WW domain. Proc Natl Acad Sci USA. 2006;103:10648–10653. doi: 10.1073/pnas.0600511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Karanicolas J, Brooks CL. Integrating folding kinetics and protein function: Biphasic kinetics and dual binding specificity in a WW domain. Proc Natl Acad Sci USA. 2004;101:3432–3437. doi: 10.1073/pnas.0304825101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Gosavi S, Chavez LL, Jennings PA, Onuchic JN. Topological frustration and the folding of interleukin-1[beta] J Mol Biol. 2006;357:986–996. doi: 10.1016/j.jmb.2005.11.074. [DOI] [PubMed] [Google Scholar]
  • 40.Sobolev V, Sorokine A, Prilusky J, Abola EE, Edelman M. Automated analysis of interatomic contacts in proteins. Bioinformatics. 1999;15:327–332. doi: 10.1093/bioinformatics/15.4.327. [DOI] [PubMed] [Google Scholar]
  • 41.Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. (Translated from English) J Chem Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. (in English) [DOI] [PubMed] [Google Scholar]
  • 42.Shannon P, et al. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Kamada T, Kawai S. An algorithm for drawing general undirected graphs. Inform Process Lett. 1989;31:7–15. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES