New host for carbon in the deep Earth

Abstract

The global geochemical carbon cycle involves exchanges between the Earth’s interior and the surface. Carbon is recycled into the mantle via subduction mainly as carbonates and is released to the atmosphere via volcanism mostly as CO₂. The stability of carbonates versus decarbonation and melting is therefore of great interest for understanding the global carbon cycle. For all these reasons, the thermodynamic properties and phase diagrams of these minerals are needed up to core mantle boundary conditions. However, the nature of C-bearing minerals at these conditions remains unclear. Here we show the existence of a new Mg-Fe carbon-bearing compound at depths greater than 1,800 km. Its structure, based on three-membered rings of corner-sharing (CO₄)^4- tetrahedra, is in close agreement with predictions by first principles quantum calculations [Oganov AR, et al. (2008) Novel high-pressure structures of MgCO₃, CaCO₃ and CO₂ and their role in Earth’s lower mantle. Earth Planet Sci Lett 273:38–47]. This high-pressure polymorph of carbonates concentrates a large amount of Fe^(III) as a result of intracrystalline reaction between Fe^(II) and (CO₃)^2- groups schematically written as 4FeO + CO₂ → 2Fe₂O₃ + C. This results in an assemblage of the new high-pressure phase, magnetite and nanodiamonds.

Carbonates are the main form of carbon-bearing minerals that can be transported deep in the Earth’s mantle via subduction of the oceanic lithosphere (1). This subducted component is considered to contribute significantly to the lower mantle carbon (C) reservoir along with primordial C (2, 3). Because of its very low solubility in deep Earth’s minerals (4, 5), C is likely to be present as a separate phase, either as carbonates or as diamonds. Several studies have suggested that magnesium carbonate (magnesite) could become the main host for C at depth at the expense of calcite and dolomite (6–8). Other models proposed that carbonates in equilibrium with peridotite would become reduced into diamonds at lower mantle conditions (9). However, as observed in the upper mantle, heterogeneities of the lower mantle redox state probably exist: For instance, subduction zones are made of more oxidized materials (10) that could survive on long time scales. Coexistence of both reduced and oxidized species in the deep Earth is also suggested by examples such as CO₂-rich kimberlitic magmas that have transported diamonds to the surface (11, 12), and some carbonate inclusions that were found in diamonds from the lower mantle (13, 14). Results of high-pressure experiments on carbonate stability suggest that the rhombohedral structure of MgCO₃ magnesite is stable up to 115 GPa at 2,000–3,000 K, but that it adopts a new structure at higher pressures (8). However, first-principle calculations predicted magnesite transformations into phases built with (CO₄)^4- tetrahedral groups at 82 GPa, and a transformation into pyroxene-like structures is expected at 160 GPa (15–17). Considering the average Fe/Mg molar ratio of 0.12 in the Earth’s mantle, the composition of carbonates is likely to lie between those of magnesite and the iron end member FeCO₃ siderite, the two phases being known to form a continuous solid solution. So far, transformations of iron-bearing carbonates have rarely been examined. Siderite is known to be stable up to at least 47 GPa and 2,000 K (18), and up to 90 GPa at ambient temperature (19). Overall, the structural behavior of siderite and magnesite end members is thought to be similar because the effect of size mismatch between Fe^(II) and Mg atoms is compensated by a spin transition in Fe^(II) (19, 20).

Results

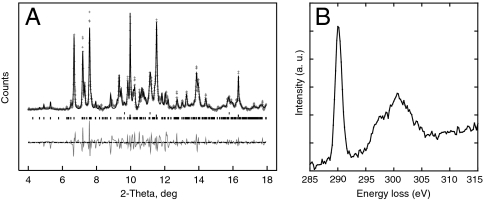
Consistent conclusions about the stability of a high-pressure carbon-bearing compound can be drawn for both MgCO₃ and the assemblage MgO + CO₂. In the two cases, X-ray diffraction (XRD) patterns collected at comparable pressure (P) and temperature (T) (about 80 GPa–2,400 K) show several new peaks that cannot be attributed to the known structures of MgO and CO₂ oxides nor to magnesite. Rather, they indicate that a new structure is stabilized in this pressure range. A typical XRD pattern of the assemblage of MgO + CO₂ obtained at 82 GPa and 2,350 ± 150 K is shown in Fig 1A. Upon quenching to room temperature, the high-pressure phase is back-transformed to the low-pressure magnesite structure. Electron energy loss spectroscopy (EELS) analyses performed on the recovered samples are consistent with in situ observations. Fig. 1B shows an EELS spectrum collected at the C K-edge on the recovered sample made from the assemblage MgO + CO₂. The sharp peak located at 290.3 eV is characteristic of (CO₃)^2- carbonate groups (21). In addition, the measured stoichiometry deduced by EELS analysis indicates an MgCO₃ composition. Therefore, the high-pressure phase is an isochemical polymorph of magnesite.

Fig. 1.

(A) X-ray diffraction pattern of a sample obtained from the transformation of periclase in CO₂ confining medium at 82 GPa and 2,350 ± 150 K. Crosses represent observed data after subtraction of the background and the solid line represents the profile refinement. For this refinement we used an assemblage of untransformed periclase (Upper), platinum (Middle), and the new high-pressure phase (Lower). Residual between observations and fit is shown below the spectrum. (B) C K-edge EELS spectrum done on the recovered sample.

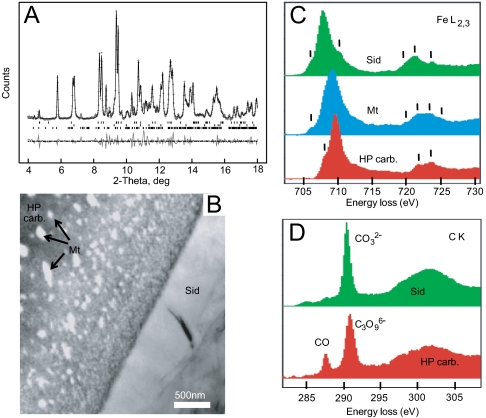
Above 80 GPa, natural siderite-rich samples transformed at 1,850–2,300 K yield XRD reflections similar to those obtained in the MgCO₃ samples described above, together with reflections of an iron oxide (Fig. 2A). This suggests the formation of a high-pressure carbon-bearing phase on the Mg-Fe join. In contrast with the MgCO₃ end member, this high-pressure Fe-bearing structure is quenchable. Subsequent transmission electron microscopy (TEM) analyses made on the recovered sample show the presence of three different phases: a relic of untransformed (Fe_0.75Mg_0.25)CO₃ siderite, the high-pressure phase, and an iron oxide (Fig. 2B). EELS spectra obtained at iron L_2,3 edges are presented in Fig. 2C; some spectra match well with a remnant siderite crystal, with features similar to Fe^(II) bearing phase’s spectra obtained with the same energy resolution (22). The presence of magnetite is also confirmed with our EELS analysis. The fine structure of the Fe L_2,3-edges of the high-pressure phase shows unambiguously fine structures expected in Fe^(III)-bearing minerals (22, 23) and quantification according to ref. 24 shows that at least about ¾ of iron is present under the Fe^(III) oxidation state. EELS data from the C K-edge (Fig. 2D) confirm the presence of a remnant siderite and show a spectroscopic signature for the transformed carbonate with a main peak shifted at 290.7 eV. The smaller peak at 287.5 eV corresponds to the presence of carbon monoxide (CO) (25) probably present as inclusions/nanobubbles that give the particular microstructure of this high-pressure phase (Fig. 2B). As discussed below, these inclusions are produced during the formation of the high-pressure polymorph of carbonate. EELS measurements indicate element ratios that are different from the initial carbonate: Fe/C ∼ 0.61 ± 0.07 and Fe/O ∼ 0.22 ± 0.02.

Fig. 2.

(A) X-ray diffraction pattern collected at 80 GPa and room temperature of siderite transformed at 1,850–2,300 K. Crosses represent observed diffraction data after subtraction of the background and solid line the profile refinement. For the refinement we used an assemblage of high-pressure polymorph of magnetite (37) (Upper), untransformed siderite (space group R-3c) (Middle), and the new high-pressure phase (Lower). Residual between observations and fit is shown below the spectrum. (B) STEM high-angle annular dark field showing the untransformed siderite (Sid), the iron oxide (Mt for magnetite), and the transformed carbonate (HP carb.) appearing as a dark gray uniform matrix in the left side of the image. (C) EELS spectra collected on the recovered sample. These spectra provide qualitative information on the 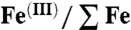ratio of each phase (23, 24) and noticeable features have been indicated by small bars and can be compared with reference siderite, magnetite, and Fe^(III) oxide (22). Spectrum collected on the untransformed carbonate shows a high intensity peak of 707.7 eV that indicates the main iron speciation to be Fe^(II). In the case of the iron oxide, the broad L₃ peak at 707–709 eV with no splitting is characteristic of magnetite, whereas the L₂ shows many subsplitting and an intermediate energy position between pure ferric and ferrous iron that is typical of a mixed valence of magnetite (23). The spectrum collected in the new phase shows a L₃ line at higher energy loss than in carbonate groups with a fine structure indicating the main iron speciation to be Fe^(III). (D) C K-edge spectra collected in the untransformed and transformed carbonate phases. In the case of siderite relic, the peak at 290.3 eV corresponds to planar (CO₃)^2- carbonate groups. In the spectrum collected in the transformed carbonate, the slightly broader peak at 290.7 eV is attributed to the tetrahedral (CO₄)^4- forming rings of (C₃O₉)^6-. Presence of CO can also be detected in intimate association with the new phase.

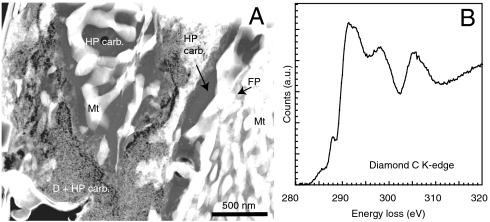
Transformation of (Mg_0.6,Fe_0.4)O + CO₂ at 105 GPa and ∼2,850 K led to the formation of the assemblage of a relic of unreacted material (M_0.6,Fe_0.4)O, a high-pressure phase of magnetite and the same new high-pressure phase. This assemblage was observed by X-ray diffraction (XRD) and further confirmed by analytical transmission electron microscopy (Fig. 3A). Nanodiamonds were also identified by electron diffraction and EELS spectroscopy performed at the C K-edge (Fig. 3B).

Fig. 3.

(A) TEM image of the recovered sample from the ferropericlase + CO₂ experiment. Magnetite (Mt), high-pressure carbon-bearing phase (HP carb.), ferropericlase (FP), and nanodiamonds (D) are present. (B) C K-edge EELS spectrum of nanodiamonds observed in the recovered sample. The spectrum presents the absorption edge at 289 eV and the dip at 303 eV is characteristic of diamond C K-edge (38, 39).

Discussion

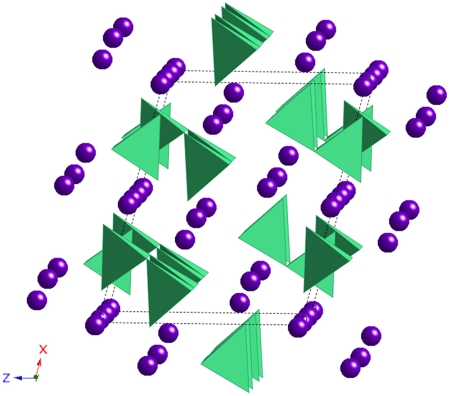
Refinement of the high-pressure and high-temperature XRD patterns allowed the identification of the high-pressure carbon-bearing structure. XRD patterns are consistent with phase II of magnesite (space group C2/m) suggested by theoretical calculations within this pressure range (15). However, the quality of the fit is considerably improved when using instead a slightly less symmetric lattice with space group P21/c (Table S1). This structure shown in Fig. 4 is made of groups of three (CO₄)^4- tetrahedra sharing one corner, which constitute (C₃O₉)^6- rings. The lattice parameters are a = 8.39 Å, b = 6.41 Å, c = 6.82 Å, β = 105.49° (V = 354.7 Å³) in the case of MgO + CO₂ at P = 82 GPa and T = 2,350 ± 150 K and a = 8.37 Å, b = 6.37 Å, c = 6.80 Å, β = 104.57° (V = 351.7 Å³) in the case of MgCO₃ at P = 85 GPa and T = 2,400 ± 150 K (Table S2). In that latter case, assuming a number of formula unit per cell of 12 (15), a density of 4.76 g/cm³ is obtained corresponding to a density difference of about +10% with respect to the low-pressure structure at the same P-T conditions. Because of the incorporation of relatively smaller Fe^(III) atoms, the volume of the new Fe-bearing phase is about 10% smaller than the one of the magnesian end member (Table S2) for which we obtained a = 7.72 Å, b = 6.41 Å, c = 6.57 Å, β = 101.31° (V = 319.0 Å³) in the case of (Mg_0.6Fe_0.4)O + CO₂ at P = 105 GPa and T = 2,850 ± 150 K and a = 7.83 Å, b = 6.37 Å, c = 6.73Å, β = 101.97° (V = 328.9 Å³) in the case of (Mg_0.25Fe_0.75)CO₃ at P = 80 GPa and room temperature.

Fig. 4.

Structure of the new high-pressure phase in space group P21/c related to phase II of magnesite proposed by theoretical calculation (15). (CO₄)^4- tetrahedra appear in green and magnesium atoms are shown as violet spheres.

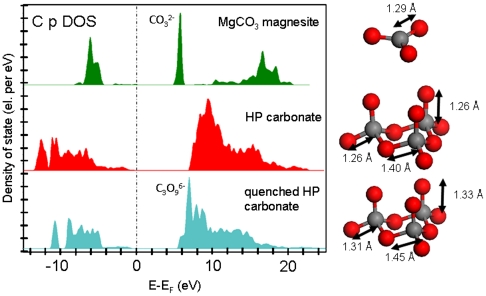
Because no reference of EELS spectra exist for that new high-pressure phase, density functional theory (DFT) calculations of the unoccupied electronic density of state have been performed. The magnesite density of state shows a narrow peak at around 5 eV above the Fermi level that corresponds to the observed C K-edge and its “molecular” style (CO₃)^2- signature (Fig. 5). The density of state obtained for the new high-pressure carbon-bearing phase does not show any molecular (CO₃)^2- peak but rather a broad band at higher energy (from 7 to 11 eV). The crystal density is of 4.79 g·cm^-3 at a pressure of 80 GPa. The geometry of (C₃O₉)^6- rings can be seen on the right-hand side of Fig. 5.

Fig. 5.

DFT calculations for electronic density of state of the carbon atoms (p orbital symmetry). This unoccupied density of state roughly corresponds to the excitation probed by EELS at the C K-edge (excitonic effects are neglected in the calculation).

In order to see how the tetrahedral (C₃O₉)^6- rings change during the decompression, structures have been relaxed at ambient conditions. The result obtained is shown at the bottom (density is 3.60 g·cm^-3) and the C-O bond lengths increase. From 80 GPa to 0 GPa the C-O-C angle also evolves from around 110–112° to 115–118°, which are values in agreement with published tetrahedral distortion (15). These structural changes have a strong influence on the unoccupied density of state. Indeed, as expected for less dense structures, the overall unoccupied density of state shifts to lower energy. Narrow peaks are present and correspond to tetrahedral (C₃O₉)^6- rings, whose molecular signatures are similar to those observed by EELS in samples recovered from high-pressure experiments (i.e., a peak observed at around 290.7 eV).

In Fe-bearing experiments, a large amount of Fe^(III) is incorporated in the new structure. No Pt was present in these experiments, and thus Pt had no interference with this redox reaction. The redox partner for Fe^(III) formation could eventually be Fe⁽⁰⁾ as observed for high-pressure silicates such as perovskite (9). Fe⁽⁰⁾ may have been an intermediate partner; however, no evidence of Fe⁽⁰⁾ was observed in the recovered samples. We argue that the incorporation of Fe^(III) is more likely due to an oxidized carbon partner. We propose that oxidation of iron is balanced by partial reduction of carbon-bearing molecular structures such as (CO₃)^2- or CO₂, according to the following chemical reaction:

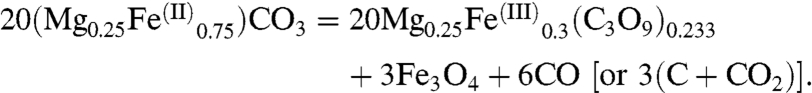[1]

This reaction implies an elemental ratio of Fe/C ∼ 0.43 and Fe/O ∼ 0.14 in the new Fe^(III)-bearing phase, in reasonable agreement with EELS estimations on the recovered sample.

Conclusion

Our study provides direct evidence for the recombination of CO₂ with other oxides to form a high-pressure carbon-bearing phase at P-T conditions close to the lower mantle geotherm. This suggests a strong stability of this phase against dissociation into simple oxides. Also, the preference of the new high-pressure phase for Fe^(III) implies reduction of part of the carbon, following the chemical reaction 1. It shows experimentally the coexistence of oxidized and reduced species of carbon at lower mantle conditions. This behavior might be due to a strong thermodynamic stability of the new carbon-bearing phase. However, for this new phase to be actually present in the deep lower mantle, carbonates must be preserved during deep subduction. Although the lower mantle assemblage is speculated to induce reducing conditions (9), carbonates could remain stable at depths if isolated from the surrounding mantle, for instance, in a relatively cold subducted slab where oxygen fugacity, as controlled by the local mineral assemblage, is locally higher (10, 26). This fraction of surviving carbonates may be transported beyond 1,800-km depth, where transformation into the newly observed Fe^(III)-bearing phase would occur.

Materials and Methods

Two types of experiments have been conducted, with starting materials being either natural carbonate samples or a stoichiometric intimate assemblage of pure oxides. Grounded natural carbonates of two compositions on the iron-magnesium join, MgCO₃ magnesite and (Fe_0.75Mg_0.25)CO₃ siderite, were provided by the mineralogical collection of University of Pierre et Marie Curie and loaded in symmetric Mao-type diamond-anvil cell without a pressure-transmitting medium. Clear inclusion-free crystals were chosen and analyzed by electron microprobe showing very little minor elements content (Table S3). Moreover, in order to test the recombination of oxides, synthetic periclase (MgO) and ferropericlase (M_0.6,Fe_0.4)O were loaded into CO₂ gas. For Mg end-member experiments using MgCO₃ and MgO as starting material, finely ground powdered platinum (platinum black) was incorporated and used as infrared absorber. Samples were pressurized at ambient temperature and then heated using the double-sided heating system available on the high-pressure beam line ID-27 at the European Synchrotron Radiation Facility (ESRF) (27). Hot spots developed on the sample (and transformed areas) are of the order of 20 μm in diameter. Angle dispersive XRD pattern were collected in situ at high pressure and at high temperature, with a beam focused down with Kirkpatrick–Baez mirrors to 1.7 × 2.3 μm FWHM at 33.3 keV (wavelength of 0.3738 Å), so as to minimize the influence of lateral temperature gradients in X-ray diffraction patterns. Typical exposure time was about 90 s at high pressure–high temperature. About 2 h of heating at 2,000–2,500 K were applied to transform the samples. Pressure was measured using ruby fluorescence at room temperature (28) and the thermal equation of state of platinum (29) at high temperature. Temperatures were measured by spectroradiometric analysis of thermal emission spectra (30). The diffraction images were integrated with the Fit2d software (31), and the one-dimensional diffraction patterns were processed with the GSAS software package (32) using the LeBail method to identify phases and determine lattice parameters.

Analyses of recovered samples were carried out on carefully selected regions of interest, at the center of transformed area. The recovered samples were then thinned to electron transparency (∼100 nm) by the focused ion beam (FIB) method prior to observations in scanning transmission electron microscopy (STEM) and TEM. FIB milling was performed with a FEI STRATA DB 235 at Institut d’Electronique, de Microélectronique et de Nanotechologie (IEMN) and Zeiss Crossbeam Neon40 at Institut de Minéralogie et de Physique des Milieux Condensés (IMPMC). To protect the sample during the milling process, a linear strap of platinum was deposited across the heated area, localized by the electronic imaging capabilities of the FIB. A 30-kV Ga⁺ beam operating at ∼20 nA was used to excavate a thin foil, removing sample material on both sides of the platinum layer to a depth of 5–10 μm. The thin cross-sections (15 μm × 5 μm × 1 μm) were extracted using a micromanipulator and welded to a TEM copper grid. Final thinning down to a thickness of less than 100 nm was achieved using low incident angles and low Ga ion currents (approximately 50 pA). A further description of the FIB sample preparation technique can be found in Heaney et al. (33).

Transmission electron microscopy was done with a JEOL 2100-F operating at 200 kV with a field effect gun as electron source. STEM-EELS measurements were done with a dedicated scanning transmission electron microscope Vacuum Generators HB 501 microscope. All EELS spectra were recorded in STEM mode with 100-keV incident electrons focused on the specimen. The probe size was of ca. 1 nm and the current intensity of 100 pA. The collection semiangle and the convergent semiangle of this microscope are, respectively, of 24 mrad and 7 mrad. The electronic structures of each element were investigated using EELS spectra collected at the C K-, O K-, and Fe L_2,3-edges with an energy dispersion of 0.2 eV per channel. The final energy resolution measured as the width of the zero-loss peak at half height was of 0.6 eV. We used the Hitchcock gas core excitation database and already published fingerprint of EELS data for identification and interpretation of fine structure EELS spectra of the different elements (Fe and C).

DFT has also been performed in order to interpret the C K-edges of the newly reported structure. The DFT calculations were performed for the Mg end-member carbonate using a pseudopotential method (valence electrons are C 2s² 2p², O 2s² 2p⁴, and Mg 2p⁶ 3s²) and a plane wave basis with an energy cutoff at the order of 1,000 eV (34, 35). Because no iron atoms were included in the structure, non-spin-polarized local density approximation has been used as an exchange-correlation functional, and site and symmetry projected density of state has been computed using the tetrahedron method. Structural models have been relaxed (residual atomic forces below 5.10^-3 eV/Å) in order to obtain the quenched structure for the high-pressure phase. An indicative stoichiometry of the new phases was obtained using a conventional extraction and Hartree–Slater cross–section calculation (36). This method provides us cation ratios such as Fe/C, Fe/O, and C/O. The reliability of this method was first verified on different natural carbonates composition, and the measured stoichiometries were in good agreement with electron microprobe analysis.