Resolving variation in the reproductive tradeoff between sperm size and number

Abstract

Spermatozoa are amongst the most variable cells, and three factors are thought to account for this variation in design: fertilization mode, phylogeny, and postcopulatory sexual selection. In addition, it has long been assumed that a tradeoff exists between sperm size and number, and although postcopulatory sexual selection affects both traits, empirical evidence for a tradeoff has so far been elusive. Our recent theoretical model predicts that the nature of a direct tradeoff between sperm size and number varies with sperm competition mechanism and sperm competition risk. We test these predictions using a comparative approach in two very different taxa with different sperm competition mechanisms: passerine birds (mechanism: simple raffle) and Drosophila fruit flies (sperm displacement). We show that in both groups, males increase their total ejaculate investment with increasing sperm competition risk, but whereas passerine birds allocate disproportionately to sperm number, drosophilids allocate disproportionately to sperm size. This striking difference between the two groups can be at least partly explained by sperm competition mechanisms depending on sperm size relative to the size of the female reproductive tract: in large animals (passerines), sperm numbers are advantageous in sperm competition owing to dilution inside the female tract, whereas in small animals (drosophilids), large sperm are advantageous for physical competition (sperm displacement). Our study provides two important results. First, we provide convincing evidence for the existence of a sperm size–number tradeoff. Second, we show that by considering both sperm competition mechanism and dilution, can we account for variation in sperm size between different taxa.

The seemingly unlimited number of tiny sperm produced by males compared with the few large eggs produced by females (i.e., anisogamy) has shaped our understanding of sexual selection and the evolution of mating systems (1–3). However, although the males of most animals produce huge numbers of tiny sperm, some produce few, giant sperm (4), suggesting that males trade off sperm size and sperm number. Theoretical models of sperm size evolution in the context of sperm competition assume either a direct or indirect tradeoff between sperm size and sperm number. Under a direct tradeoff (5), males have a fixed energy budget, M, to invest in an ejaculate, so if each sperm has size m, the sperm number will be s = M/m; any change in one strategic parameter (m or s) trades off directly against the other. Under an indirect tradeoff (6), a fixed resource budget, R, is allocated between the ejaculate and effort spent acquiring a mating, C, where the number of matings, n, obtained by a male is given by R/(C + Dsm) and where Dsm defines the amount of energy invested into the ejaculate. Thus, a male can effectively now vary three strategic parameters: n, s, and m. Our recent theoretical model (7) shows that at a given level of R and sperm competition risk q (i.e., at a given level β; Box 1), a direct tradeoff between sperm size and number effectively still operates even under the indirect tradeoff model. However, empirical evidence for such a tradeoff has been equivocal (8–11). The present study couples data with theoretical predictions of our recent model (7) (Box 1) to generate insights into sperm size/number evolution. It introduces the concepts of the mechanisms of sperm competition and dilution to explain observed interspecific variation in sperm size. Only by considering both of these factors are we able to account for the relationship between body mass and sperm size, as well as for sperm gigantism in Drosophila.

Box 1. Overview of Theory of Parker et al. (7).

We here summarize our recent theoretical developments (7); m = mass of each sperm, and s = number of sperm per ejaculate. The model examines the risk range of sperm competition (47): females choose to mate with two different males with probability q, and mate once with probability (1 – q). A male’s total reproductive expenditure, R, is allocated between each ejaculate (expenditure proportional to product, ms) and investment into gaining matings. The ESS for sperm size and number (m*, s*) at a given risk level of sperm competition q obey:

where β = (R/D)[2q/(1 + q)], G′(s*) = the marginal gains through increasing sperm numbers, G′(m*) = the marginal gains through increasing sperm size, and D = the cost of one unit of ejaculate. Hence

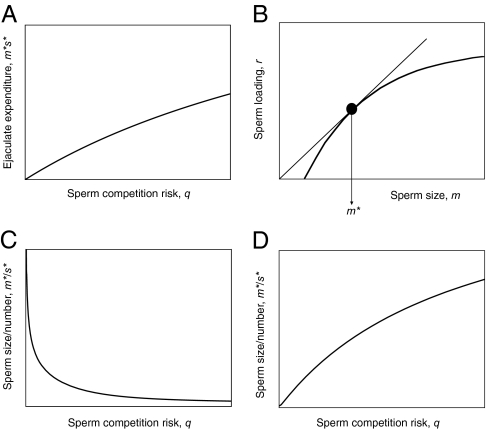
(6, 7). Using explicit forms for G(s) and G(m) for three different sperm competition mechanisms, sperm expenditure (product m*s*) always increased with sperm competition risk, q (Fig. 1A) but was invariant at any given value of β, at which a direct sperm size–number tradeoff must therefore apply. How sperm size and number are allocated as m*s* increases with q across populations depends on G′(s*), G′(m*), in Eq. 2.

We (7) studied two mechanisms relevant to our present results. In Scenario 1, there is no space constraint for fertilization, and sperm compete in a raffle loaded by sperm size. In Scenario 2, sperm from the last male to mate displace sperm stored in the female’s fixed-volume spermatheca; those remaining in store after displacement then compete as in Scenario 1. Scenario 1 is most relevant to external fertilizers or large internal fertilizers, such as vertebrates with low sperm densities (and hence to passerines), and Scenario 2 to insects or other invertebrates with fixed-volume sperm-storage organs and high sperm densities (and hence to Drosophila). The loading due to sperm size was modeled by function r(m), so that Male 1 competing against Male 2 has a fertilization probability of r(m₁)s₁/[r(m₁)s₁ + r(m₂)s₂]. For an intermediate ESS sperm size (rather than a maximum or minimum), r(m) must allow a tangent to be drawn from the origin (Fig. 1B) following the marginal value theorem (56).

If r does not vary with sperm competition risk, ESS sperm size m* remains constant with q, so the increase in m*s* with q (Fig. 1A) is due entirely to increased sperm numbers s*, and the ratio m*/s* decreases with q (i.e., generating the “default expectation” that sperm numbers increase more rapidly than sperm size with q) (Fig. 1C). However, because m* increases with q, m* can vary with q if the fertilization loading factor r(m) changes with competing sperm density: m* and s*, then depend on precisely how sperm density alters r(m). Sperm size can increase with sperm competition risk if (i) sperm density decreases the slope of r(m), and/or (ii) sperm density increases the intercept of r(m) (Fig. 1B). Both can theoretically generate an increase in the ratio m*/s* with q (Fig. 1D), although Scenario 2 does this more readily than Scenario 1. Opposite effects, or insufficient strength of (i) and (ii), give the typical default expectation (Fig. 1C). In Scenario 1, effects of sperm density on r(m) (if they occur at all) are likely to be weak, and hence generate the default expectation (Fig. 1C), as in passerines. Scenario 2 can cause m*/s* to increase with q (Fig. 1D) quite readily through effect (ii), most plausibly by sperm–sperm interactions becoming increasingly important with increased sperm density, as is likely in Drosophila.

To clarify the logic, we give an overview of our recent theoretical model of sperm size–number tradeoffs and its main predictions in Box 1; the full account is complex and is presented elsewhere (7). It differs from previous models (6) in predicting how absolute and relative expenditure on sperm size and number should vary in relation to sperm competition risk, q, in both sperm mixing and sperm displacement systems, under varying sperm density: (i) sperm number, s, should always increase with q, but sperm size (defined here as mass), m, may be constant, increasing, or decreasing with q, (ii) total ejaculate investment, ms, should always increase with q, and (iii) the ratio m/s (which indicates how allocation within ms is skewed toward size or number as q increases) can increase or decrease with q depending on the influence of sperm density (the density of sperm in the set from which fertilizations are drawn) on sperm competition; specifically, (iv) if sperm size has no effect (or only a moderate effect) on sperm competitive ability with increasing sperm density (e.g., in systems with a raffle mechanism, such as external fertilizers and internally fertilizing vertebrates), then sperm number is favored over sperm size with increasing risk of sperm competition (thus as ms increases with q, the ratio m/s decreases), or (v) if sperm competitive ability is strongly affected by increases in sperm density, (e.g., where sperm displacement is an important mechanism), then sperm size is favored over sperm number with increasing risk of sperm competition (thus as ms increases with q, m/s may also increase). Here we examine the above predictions in two taxonomic groups with internal fertilization, which differ considerably in their sperm competition mechanisms and sperm densities: passerine birds, in which sperm competition obeys a simple raffle mechanism (12), and Drosophila fruit flies, in which sperm competition success relies on displacement mechanisms (13, 14).

To examine relationships between sperm size and number and sperm competition across species, we use relative testis size as an index of sperm competition risk (a causal positive correlation between the two has been demonstrated in numerous experimental and comparative studies) (15–23). Relative testis size is also typically a direct reflection of male investment in sperm production (24, 25) and therefore likely to correlate with the cost of each ejaculate, proportional to the product of the evolutionarily stable strategy (ESS) sperm size and number in our model (i.e., m*s*: as expected, our data demonstrate such a positive relationship in both birds and flies) (see below). Our focus here, however, is on how the tradeoff balance between sperm size and number changes with increasing sperm competition risk (and hence increasing m*s*) and how this balance is affected by systems with different sperm competition mechanisms and sperm densities (see below). In particular, from the predictions above, we expect passerines, with their low sperm density raffle mechanism, to show a decreasing relationship between m*/s* and risk q (Box 1 and Fig. 1C). In sharp contrast, the drosophilids, with their high-density sperm displacement mechanism, are predicted to show an increasing relationship between m*/s* and risk q (Box 1 and Fig. 1D).

Fig. 1.

Theoretical predictions for sperm size–number relationship with increasing risk of sperm competition. (A) The ESS total sperm expenditure (product of sperm size and number, m*s*) always increases across the risk range sperm competition risk, q, as observed in passerine birds and Drosophila (Fig. 3 A and B). (B) Sperm loading factor, r, determines a sperm’s competitive ability and must increase at a decreasing rate with m. The tangent to the curve r(m) gives the marginal value theorem solution for ESS sperm size, m*, at a given level of sperm competition risk, q. If sperm density increases the intercept of r(m), or decreases its slope, a higher ESS sperm size is generated. (C) The “default expectation” (as observed in passerine birds; Fig. 3C)—a decreasing relationship between the ratio of sperm size/number, m*/s*, and sperm competition risk, q, is expected when (i) r(m) is unaffected by the sperm density, or where (ii) increasing sperm density decreases the intercept of r(m) or increases the slope of r(m), or where (iii) increasing sperm density only generates weak increases in the intercept of r(m) or weak decreases in the slope of r(m). (D) An increasing relationship between the ratio of sperm size/number, m*/s*, and sperm competition risk, q (as observed in Drosophila; Fig. 3D), is expected only when increasing sperm density sharply decreases the slope or increases intercept of r(m) and is more likely to occur in sperm displacement systems such as those found in insects.

We next present a hypothesis that arises (a priori) from our theoretical models, basic biology, and empirical data on sperm competition in different groups; these collectively enable strong quantitative predictions that can be compared with patterns within animal groups. Our rationale is as follows. Vertebrate systems with internal fertilization typically have low sperm densities around the egg during fertilization, owing to reproductive tracts that are large relative to sperm size (26–28). Consequently, competitive advantages of increased sperm size in the region of the ESS are likely to be relatively weak across wide ranges of natural sperm densities and related mainly to effects of size on sperm motility and survival. Further, in birds, the sperm competition mechanism obeys the raffle principle (12, 29), which requires strongly escalating competitive benefits of sperm size with sperm density to generate disproportionate allocation to sperm size with increased sperm competition risk. It is difficult to envisage that passerines could fulfill these requirements, and so we predict that m*/s* should decrease with q (Box 1 and Fig. 1C). The same applies to externally fertilizing organisms. In contrast, in insects and other invertebrates with internal fertilization, longer (or larger) sperm have been shown to have a competitive fertilization advantage against shorter (or smaller) sperm of rival males through enhanced displacement or other competitive abilities (13, 20, 30, 31). In insects, sperm are stored at high density in the female sperm-storage organs (13, 32), which in Drosophila have fixed volume so that new ejaculates displace previously stored sperm. At fertilization, sperm compete at high density around the proximal region of the sperm store duct to enter the micropyle of the egg as it passes down the oviduct. Longer sperm seem to provide a competitive advantage mediated through location rather than swimming speed (13). For this scenario, our models predict sperm size to increase more than sperm number with increasing risk of sperm competition (m*/s* increasing; Box 1 and Fig. 1D) only under special circumstances, most easily met in displacement systems, when sperm size has special and strong competitive advantages in skewing fertilization, notably if the minimum successful sperm size escalates as sperm density increases (7, 13). The propensity for increasingly escalating competitive benefits of sperm size with sperm density in systems such as Drosophila is considerable, and some of the largest sperm described to date are found in small-bodied invertebrate taxa (33, 34).

The well-known phenomenon of sperm density declining as the female reproductive tracts become larger (the “sperm dilution” effect) (15, 35–37) may act in a manner that reinforces our predictions. In large animals, the dilution effect hypothesis suggests a compensating increase in sperm number at the expense of sperm size as body size—and hence female tract dimensions—increases (assuming that female reproductive tract size scales directly with body size). In tiny animals, by contrast, dilution constraints on the evolution of longer sperm are largely absent because sperm size is relatively large compared with body size (33), and furthermore, sperm are typically stored in small, fixed-volume storage organs.

Using a comparative approach, we tested our predictions by quantifying the relationship between sperm size, sperm number, and the total investment in spermatogenesis (m*s*) in passerines (Aves, Passeriformes) as a relatively large-bodied taxon [5.7–589 g body mass (BM)] obeying the raffle principle, and in Drosophila (Insecta, Diptera) as a small-bodied taxon (176–1,020 mg BM) obeying sperm displacement. These two taxa certainly differ in many biological aspects, which are not taken into account here, and we caution that a comparative analysis of two lineages cannot establish causation. However, because sperm competition mechanisms are well understood in both taxa, we believe that the differences between sperm size and number in the two groups are likely to be at least partly determined by the selective forces outlined above. Our results generally supported our theoretical predictions and provide intriguing information about mechanisms involved in postcopulatory sexual selection and animal reproduction in general.

Results

For passerines, we collected data on sperm size, combined testis mass (CTM), and BM for a total of 196 species (Table S1), and sperm number for 23 of these species. As a proxy for ejaculate size we used the number of sperm counted in the seminal glomera (i.e., the extragonadal male sperm-storage organs). Sperm numbers in the seminal glomera are directly related to testis size (17), which in turn is related to ejaculate size (16). Although the use of this proxy may add random noise due to measurement errors, it will not bias our results in a systematic way and hence does not jeopardize the overall conclusions we can draw from our results. We performed multiple regression analyses in a phylogenetic framework [PGLS (38–40); details in Materials and Methods] starting with a model including CTM and BM to control for the allometric relationship between the two, as well as a quadratic term, CTM², and an interaction term, CTM*BM.

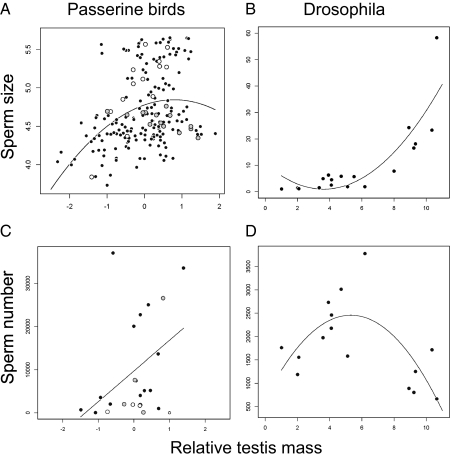
Identifying the best-fitting model using the Akaike information criterion, we found a significant positive, nonlinear relationship between sperm size and relative testis size (CTM: estimate = 1.50, t = 4.34, P < 0.00001; CTM² = −1.01, t = 3.32, P = 0.001; Fig. 2A), but also a significant negative relationship between sperm size and BM (estimate = −0.35, t = 4.19, P < 0.0001) and a significant CTM*BM interaction term (estimate = 0.21, t = 2.69, P = 0.008; model: r² = 0.19, λ = 0.82^**,ns), suggesting that sperm size decreases with decreasing sperm density through the dilution effect. In addition, the negative association between sperm size and body size supports the hypothesis that larger-bodied species have relatively smaller sperm, supporting the prediction from the dilution effect. A positive linear relationship between sperm number and relative testis mass best fits the data (CTM: estimate = 1.44, t = 3.32, P = 0.003; Fig. 2C), whereas the relationship with body size was not significant (BM: estimate = −0.49, t = 1.23, P = 0.23; model: r² = 0.50, λ < 0.0001^ns,**); there also was no significant quadratic term CTM² or interaction term CTM*BM, and hence the latter two terms were excluded to obtain the minimal adequate model. As expected (see above), the sperm size and number product (m*s*) increased with increasing relative testis mass (CTM: estimate = 441.74, t = 4.12, P = 0.0005; BM: estimate = −198.49, t = 2.02, P = 0.06; model: r² = 0.55, λ < 0.0001^ns,**; Fig. 3A). The reduced major axis (RMA) slope between m*s* and CTM was significantly larger than 1 (t₂₂ = 5.52, P < 0.001), which indicates that m*s* increases at a faster rate than relative testis mass. Importantly, m*/s* decreased with increasing relative testis mass (CTM: estimate = −1.29, t = 2.77, P = 0.01; BM: estimate = 0.20, t = 0.47, P = 0.65; model: r² = 0.51, λ < 0.0001^ns,**; Fig. 3C), confirming our theoretical expectation that in passerines, sperm numbers should increase more rapidly than sperm size with increasing risk of sperm competition (according to Scenario 1 in Box 1; Fig. 1C).

Fig. 2.

Sperm size and sperm number in relation to risk of sperm competition. Sperm size is significantly associated with relative testis mass (A) following a nonlinear relationship in passerine birds (presented as ln-transformed sperm total length and residual testes mass from a regression between CTM and BM) and (B) with an accelerating increase in Drosophila (presented as sperm total length and relative testes mass as CTM over BM). Sperm number is significantly associated with relative testis mass (C) following a linear relationship in passerine birds and (D) following a single-peaked curve in Drosophila. The relative position of species belonging to Fringillidae (white circles) and Sylviidae (gray circles) confirm previous findings of opposite patterns in the two families for the relationship between sperm size and risk level of sperm competition. Figures are not controlled for phylogeny.

Fig. 3.

Sperm size–number relationship with increasing risk of sperm competition. In both (A) passerine birds and (B) Drosophila, the overall investment in sperm size (m*) and number (s*) increases with increasing risk of sperm competition (compare with theoretical prediction in Fig. 1A). As predicted (Box 1) (C; compare with Fig. 1C), in passerine birds sperm number increases at the expense of sperm size, whereas (D; compare with Fig. 1D) in Drosophila sperm size increases at the expense of sperm number. Figures are not controlled for phylogeny.

For Drosophila, we obtained data on sperm size, CTM, and BM for 18 species and sperm number for 15 of these species. We performed equivalent multiple regression analyses in a phylogenetic framework (details in Materials and Methods) and found a significant positive, accelerating relationship between sperm size and relative testis mass but not body size (CTM: estimate = −0.25, t = 0.58, P = 0.57; CTM²: estimate = 0.26, t = 3.2, P = 0.006; BM: estimate = −0.13, t = 0.35, P = 0.73; model: r² = 0.88, λ = 0.87^ns,ns; Fig. 2B). In contrast, the relationship between sperm number and relative testis mass followed an inverted U-shaped curve (CTM: estimate = 0.81, t = 1.93, P = 0.08; CTM²: estimate = −0.23, t = 2.80, P = 0.02; BM: estimate = 0.74, t = 1.86, P = 0.09; model: r² = 0.78, λ < 0.0001^ns,**; Fig. 2D). As expected, m*s* increased with relative testis mass (CTM: estimate = 0.56, t = 3.12, P = 0.009; BM: estimate = 0.92, t = 2.53, P = 0.28; model: r² = 0. 38, λ = 0.92^{ns, ns}; Fig. 3B). The RMA slope between m*s* and CTM was smaller than 1, albeit marginally nonsignificant (t₁₄ = 2.13, P = 0.05), which indicates that m*s* increases at a slower rate than relative testis mass. Most interestingly, m*/s* increased with relative testis mass and hence risk of sperm competition (CTM: estimate = 1.21, t = 2.70, P = 0.02; BM: estimate = −0.22, t = 0.25, P = 0.81; model: r² = 0.66, λ < 0.0001^ns,**; Fig. 3D) as we predicted to be a possibility for this system (according to Scenario 2 in Box 1; Fig. 1D). Thus, in Drosophila, sperm size increases more rapidly than sperm number with increasing risk of sperm competition. We suggest that this phenomenon will be mainly restricted to displacement systems in which sperm size plays an increasingly crucial role in sperm competition as sperm density increases.

Thus, in support of our theoretical predictions (Box 1): (i) total ejaculate investment, m*s*, increases with relative testis size (sperm competition risk) in both passerine birds and fruit flies, (ii) relative investment in sperm size, m*/s*, decreases with sperm competition risk in passerines but increases in Drosophila, and (iii) sperm numbers, s*, increase with risk in passerines and also across the low-risk range in Drosophila. Only the decline in sperm numbers across the high-risk range in Drosophila fails to concur with our expectations.

Discussion

Our findings suggest that males are forced to trade off sperm size against sperm number and that this tradeoff may go either way. These results have important implications for our understanding of sexual selection and the evolution of mating systems, because the difference in size and number between male and female gametes determines to a large extent the strength of sexual selection (20). In addition, our evidence for a tradeoff between sperm size and number supports the idea that sperm production is costly and that males are under pressure to adaptively allocate their reproductive energy, particularly under high risk levels of sperm competition. Our results are compatible with our theoretical predictions of a tradeoff between sperm size and number (7) (Box 1) and that as sperm competition risk increases, the balance between sperm size and number can shift in either direction. We postulate that the difference we find between passerine birds and Drosophila is based on the sperm competition mechanism, which in turn depends on sperm density and hence on body size and the volume of the female reproductive tract.

In the large-bodied taxon (passerine birds), the advantages of sperm size with increasing sperm density are unlikely to accelerate sufficiently strongly to favor sperm size rather than sperm numbers, and hence sperm number increases more rapidly than (or instead of) sperm size (the “default” expectation in Scenario 1 in our model; Fig. 1C). In contrast, the fact that sperm size increases disproportionately to sperm numbers in Drosophila supports the notion that in this taxon sperm size can play a major role in sperm competition, owing to displacement and direct competition between sperm at the site of fertilization (according to Scenario 2 in our model) (12, 13). Sperm in such species are commonly longer than any distance they travel within the female reproductive tract (19, 41). Moreover, experimental evolution studies of Drosophila have demonstrated a positive association between sperm length and postcopulatory sexual selection intensity (19) and revealed that longer sperm are better at displacing shorter sperm—and resisting being displaced by them—from the site of fertilization (12, 13). These findings provide an intriguing explanation for the evolution of “giant” sperm observed in some Drosophila species (4, 20). However, we recognize that factors other than sperm competition mechanisms, such as physiological differences (e.g., poikilotherm vs. ectotherm), may certainly also influence the evolution of sperm size and number and contribute to the variation in the evolution of sperm size and number across taxa.

In addition, our study provides a plausible explanation for some of the seemingly contradictory results of previous studies, which have shown no relationship (41, 42), a positive relationship (43–45), or a negative relationship between sperm size and sperm competition (44, 46). This variation across studies can be explained in terms of how the competitive benefits of sperm size, r(m) (Fig. 1B), change with sperm density (Box 1). The differential impact of r(m) may explain the previous findings of a positive relationship between sperm size and risk of sperm competition in the family of Fringillidae and a negative relationship in the Sylviidae (44) (Fig. 2A). The theoretical predictions for the raffle mechanism are that species with an overall low risk of sperm competition q will show a sharply increasing positive relationship between sperm size and q, whereas species with high q will exhibit little or no relation between sperm size and q, because the predicted relation asymptotes quickly with q (7). Our data support these predictions in two ways. First, comparing two families: the Fringillidae have relatively low levels of sperm competition and show a positive relationship between sperm size and q, whereas the Sylviidae have a higher level of sperm competition and show a negative relationship between sperm size and q (SI Text). Second, the empirical data for all 196 passerine species also suggests an inverted U-shaped pattern where, after reaching a peak, sperm size decreases at very high levels of sperm competition risk (Fig. 2A).

The second important implication of our study is the previously unreported discovery that the relationship between absolute sperm numbers (in Drosophila) and sperm competition risk may be nonmonotonic. The inverted U-shaped relation in Drosophila between sperm number and relative testis size (Fig. 2D) suggests that sperm number peaks at intermediate sperm competition risk levels and diminishes at high risk levels. Theory suggests that sperm numbers will increase monotonically across sperm competition risk levels, although a decrease is possible at high intensities (i.e., where more than two ejaculates compete) (7, 47). Risk levels of sperm competition are probably high in some Drosophila species. However, under such circumstances, our present model would predict a corresponding similar peak in sperm size; the continued increase in sperm size across decreasing sperm numbers at high risk levels is therefore currently unexplained by the theory in Box 1. A further limitation of the model (Box 1) is that potential female influences are omitted, although female reproductive biology plays a major role in the evolution of sperm size and number in Drosophila (19). Thus, further theoretical developments are needed to obtain a complete picture of the evolution of sperm size and number in Drosophila.

Sperm size is one of the most rapidly diversifying traits (33), yet the selective basis for this phenomenon has remained poorly understood. For example, why giant sperm have evolved in invertebrate compared with vertebrate lineages has been a long-standing question (33). Resolving taxonomic variation in the tradeoff between sperm quality and quantity, and identifying competing sperm density as a likely physiological constraint contributing to this variation, provides an important focus for future investigations of postcopulatory sexual selection and reproduction in the animal kingdom.

Materials and Methods

Sperm Size Measurements.

Sperm samples were collected from passerine males in breeding condition: (i) from fecal samples (48), (ii) by collecting sperm from the caudal end of seminal glomera dissected from males caught under license, and (iii) by “cloacal massage” (49). Sperm collected in different ways do not differ significantly in morphometry (48). Samples were processed as described by Immler and Birkhead (48). Sperm size was measured as total sperm length. For Drosophila, measures of total sperm length were obtained from Pitnick et al. (50).

Sperm Number Measurements.

For passerines, the two seminal glomera were obtained by dissection from males at the peak of the breeding season. Sperm were extruded from each glomerus separately by squeezing and macerating the tissue in a known volume of PBS and sperm number counted in an Improved Neubauer Chamber (17).

For Drosophila, sperm number estimates were obtained for 10 species from Pitnick (23); five further species were added using the same methods [the number of sperm cysts simultaneously undergoing development in a midtestis cross-section of reproductively mature and active males (n = 12 per species) was multiplied by the number of sperm per cyst; see ref. 51].

Testis Mass and BM Data.

For passerines, CTM and BM for 196 species was obtained (i) from the literature (23), (ii) from museum databases, and (iii) from dissected males in breeding condition. For guidelines, see Calhim and Birkhead (23). Body mass was obtained from the literature (23, 52) and from dissected males collected under license. For Drosophila, measures of dry testes and BM were obtained for 10 species from Pitnick (24); values for eight further species were obtained using methods described in Pitnick (24).

Statistical Analyses.

To account for the statistical nonindependence of data points due to shared ancestry we used a generalized least-squares (GLS) approach in a phylogenetic framework (PGLS; 38–40) to perform multiple regression analyses. The phylogenetic GLS is based on the use of maximum likelihood (ML) models and takes phylogeny into account by referring to an internal matrix of expected covariances among species based on their degree of shared ancestry. In addition, the ML approach allows the estimation of the phylogenetic dependence parameter λ, which ranges between 0 and 1, indicating the relative importance of phylogeny in explaining the similarities between traits. Values of λ close to 0 indicate that the underlying phylogeny explains little of the observed trait variation, whereas values of λ close to 1 indicate strong phylogenetic association of the traits. Analyses were performed using a code developed by Freckleton for the statistical package R V.2.10.1 (53). The phylogenetic topology for passerine birds was inferred from published sources (Fig. S1), and the phylogenetic topology for Drosophila species was adopted from two published sources (54, 55) (Fig. S2). We included sperm traits (size or number) as response variables and in all models testis size and body size as independent variables. We also added a quadratic term for testis size and an interaction term between testis size and BM into the model; however, these were removed if not significant. To optimize the fit of the model, data were transformed accordingly using ln or square-root transformations. For comparisons of relationships with a slope of 1, we calculated the RMA slope and performed a one-sided t test on the RMA slope compared with 1.