Entropic effect on the rate of dislocation nucleation

Abstract

Dislocation nucleation is essential to our understanding of plastic deformation, ductility, and mechanical strength of crystalline materials. Molecular dynamics simulation has played an important role in uncovering the fundamental mechanisms of dislocation nucleation, but its limited timescale remains a significant challenge for studying nucleation at experimentally relevant conditions. Here we show that dislocation nucleation rates can be accurately predicted over a wide range of conditions by determining the activation free energy from umbrella sampling. Our data reveal very large activation entropies, which contribute a multiplicative factor of many orders of magnitude to the nucleation rate. The activation entropy at constant strain is caused by thermal expansion, with negligible contribution from the vibrational entropy. The activation entropy at constant stress is significantly larger than that at constant strain, as a result of thermal softening. The large activation entropies are caused by anharmonic effects, showing the limitations of the harmonic approximation widely used for rate estimation in solids. Similar behaviors are expected to occur in other nucleation processes in solids.

Nucleation plays an important role in a wide range of physical, chemical, and biological processes (1–6). In the last two decades, the nucleation of dislocations in crystalline solids has attracted significant attention, not only for the reliability of microelectronic devices (7), but also as a responsible mechanism for incipient plasticity in nanomaterials (8–10) and nanoindentation (11–13). However, predicting the nucleation rate as a function of temperature and stress from fundamental physics is extremely difficult. Because the critical nucleus can be as small as a few lattice spacings, the applicability of continuum theory (14) becomes questionable. At the same time, the timescale of molecular dynamics (MD) simulations is about ten orders of magnitude smaller than the experimental timescale. Hence MD simulations of dislocation nucleation are limited to conditions at which the nucleation rate is extremely high (15, 16).

One way to predict the dislocation nucleation rate under common experimental loading rates (17) is to combine the transition state theory (TST) (5, 18) and the nudged elastic band (NEB) method (19). TST predicts that the nucleation rate per nucleation site in a crystal subjected to constant strain γ can be written as

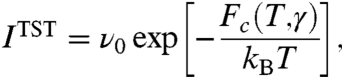[1]

where F_c is the activation free energy, T is temperature, and k_B is Boltzmann’s constant. The frequency prefactor is ν₀ = k_BT/h, where h is Planck’s constant. Note that F_c(T,γ) = E_c(γ) - TS_c(γ), where E_c and S_c are the activation energy and activation entropy, respectively. Here we assume the dependence of E_c and S_c on T is weak, which is later confirmed numerically for T ≤ 400 K. For a crystal subjected to constant stress σ, F_c(T,γ) in Eq. 1 should be replaced by the activation Gibbs free energy G_c(T,σ) = H_c(σ) - TS_c(σ), where H_c is the activation enthalpy. Because the NEB method only computes the activation energy, the contribution of S_c is often ignored in rate estimates in solids. Recently, an approximation of S_c(σ) = H_c(σ)/T_m is used (17), where T_m is the surface disordering temperature. This approximation was questioned by subsequent MD simulations (20). The magnitude of S_c remains unknown because none of the existing methods for computing activation free energies (21–23) has been successfully applied to dislocation nucleation.

We successfully applied the umbrella sampling (21) method to compute the activation free energy for homogeneous and heterogeneous dislocation nucleation in copper. Based on this input, the nucleation rate is predicted using the Becker–Döring theory (24). Comparison with direct MD simulations at high stress confirms the accuracy of this approach. Both F_c(T,γ) and G_c(T,σ) show significant reduction with increasing T, corresponding to large activation entropies. For example, S_c(γ = 0.092) = 9k_B and S_c(σ = 2 GPa) = 48k_B are observed in homogeneous nucleation. We found that S_c(γ) is caused by the anharmonic effect of thermal expansion, with negligible contribution from the vibrational entropy. The large difference in the two activation entropies, ΔS_c ≡ S_c(σ) - S_c(γ), is caused by thermal softening, which is another anharmonic effect. Similar behaviors are expected to occur in other nucleation processes in solids.

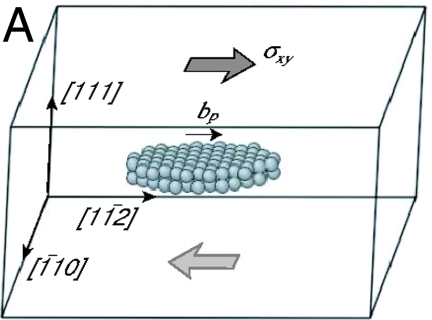
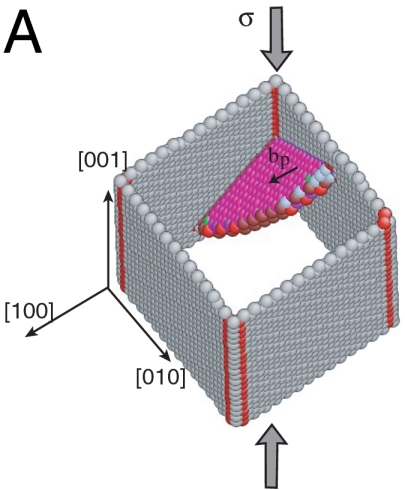
For simplicity, we begin with the case of homogeneous dislocation nucleation in the bulk. Even though dislocations often nucleate heterogeneously at surfaces or internal interfaces, homogeneous nucleation is believed to occur in nanoindentation (11) and in a model of brittle–ductile transition (25). It also provides an upper bound to the ideal strength of the crystal. Our model system is a copper single crystal described by the embedded atom method (EAM) potential (26). As shown in Fig. 1A, the simulation cell is subjected to a pure shear stress along 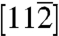. 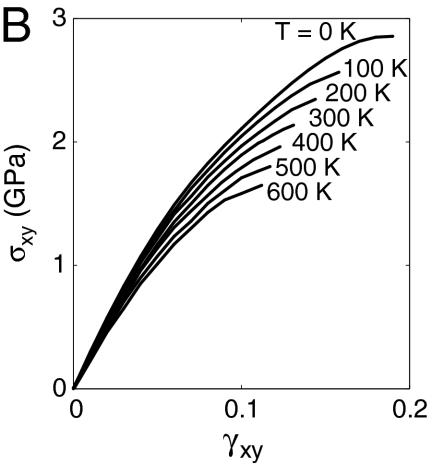The dislocation to be nucleated lies on the (111) plane and has the Burgers vector of a Shockley partial (27), 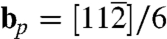. Fig. 1B shows the shear stress strain relationship of the perfect crystal at different temperatures (before dislocation nucleation).

Fig. 1.

(A) Schematics of the simulation cell. The spheres represent atoms enclosed by the critical nucleus of a Shockley partial dislocation loop. (B) Shear stress–strain curves of the Cu perfect crystal (before dislocation nucleation) at different temperatures.

In this work, we predict the nucleation rate based on the Becker–Döring (BD) theory, which expresses the nucleation rate per nucleation site as

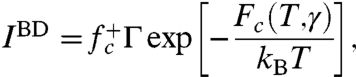[2]

where 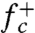is the molecular attachment rate, and Γ is the Zeldovich factor (Materials and Methods). The BD theory and TST only differs in the frequency prefactor. Whereas TST neglects multiple recrossing over the saddle point by a single transition trajectory (5), the recrossing is accounted for in the BD theory through the Zeldovich factor.

First, we establish the validity of the BD theory for dislocation nucleation by comparing it against direct MD simulations at a relatively high stress σ = 2.16 GPa (γ = 0.135) at T = 300 K, which predicts I^MD = 2.5 × 10⁸ s^-1 (Materials and Methods). The key input to the BD theory is the activation Helmholtz free energy F_c(T,γ), which is computed by umbrella sampling. The umbrella sampling is performed in Monte Carlo simulations using a bias potential as a function of the order parameter n, which is chosen as the number of atoms inside the dislocation loop (Materials and Methods).

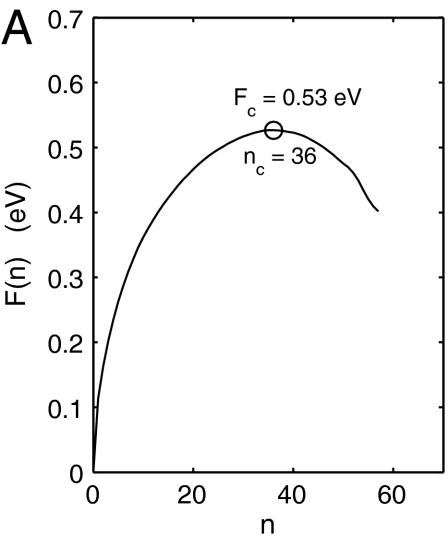
Fig. 2A shows the free energy function F(n) obtained from umbrella sampling for the specified (T,γ) condition. The maximum of F(n) gives the activation free energy F_c = 0.53 ± 0.01 eV and the critical nucleus size n_c = 36. The Zeldovich factor (28), Γ = 0.055, is obtained from 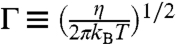, where η = -∂²F(n)/∂n²|_n=nc.

Fig. 2.

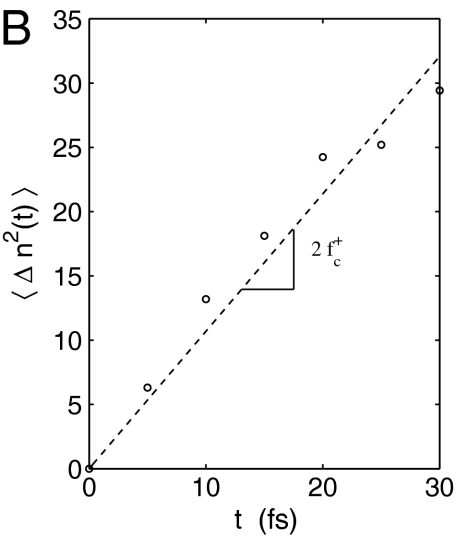
(A) Free energy of dislocation loop during homogeneous nucleation at T = 300 K, σ_xy = 2.16 GPa (γ_xy = 0.135) from umbrella sampling. (B) Size fluctuation of critical nuclei from MD simulations.

Using the configurations collected from umbrella sampling with n = n_c as initial conditions, MD simulations give the attachment rate 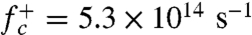(Materials and Methods). Because the entire crystal is subjected to uniform stress, the number of nucleation sites is the total number of atoms, N_atom = 14,976. Combining these data, the Becker–Döring theory predicts the total nucleation rate to be N_atomI^BD = 5.5 × 10⁸ s^-1, which is within a factor of three of the MD prediction. The difference between the two is comparable to our error bar. This agreement is noteworthy because no adjustable parameters (such as the frequency prefactor) is involved in this comparison. It shows that the Becker–Döring theory and our numerical approach are suitable for the calculation of the dislocation nucleation rate.

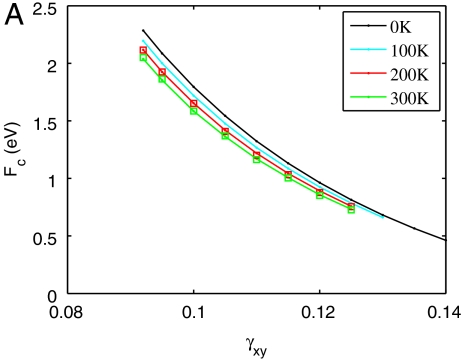
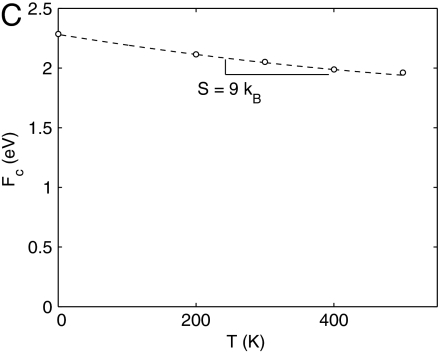
We now examine the dislocation nucleation rate under a wide range of temperature and strain (stress) conditions relevant for experiments and beyond the limited timescale of MD simulations. Fig. 3A shows the activation Helmholtz free energy F_c(T,γ) as a function of γ at different T. The zero temperature data are obtained with a minimum energy path (MEP) search using a modified version of the string method, similar to that used in refs. 29 and 17. The downward shift of F_c curves with increasing T and is the signature of the activation entropy S_c. Fig. 3C plots F_c as a function of T at γ = 0.092. For T ≤ 400 K, the data closely follow a straight line, whose slope gives S_c = 9k_B. This activation entropy contributes a significant multiplicative factor, exp(S_c/k_B) ≈ 10⁴, to the absolute nucleation rate, and cannot be ignored.

Fig. 3.

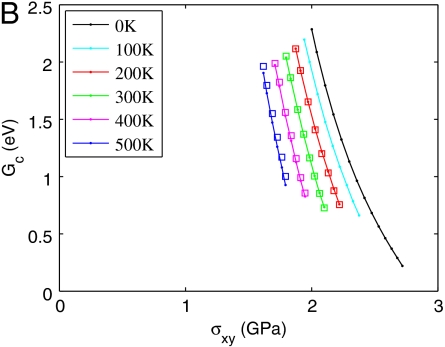
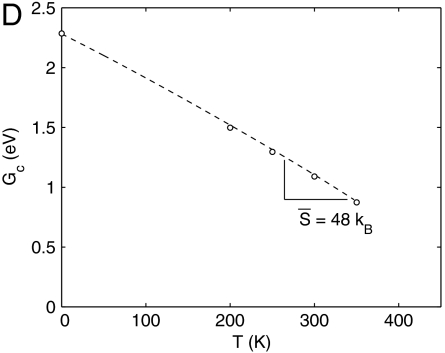
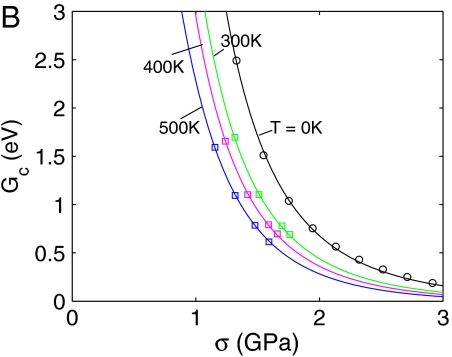
Activation free energy for homogeneous dislocation nucleation in copper. (A) F_c as a function of shear strain γ at different T. The data for T = 400 K and T = 500 K are shown in the SI Appendix. (B) G_c as a function of shear stress σ at different T. Squares represent umbrella sampling data and lines represent zero temperature MEP search results using simulation cells equilibrated at different temperatures. (C) F_c as a function of T at γ = 0.092. Circles represent umbrella sampling data and the dashed line represents a polynomial fit. (D) G_c as a function of T at σ = 2.0 GPa from polynomial fit.

What causes this rapid drop of activation free energy with temperature? Thermal expansion and vibrational entropy are two candidate mechanisms. To examine the effect of thermal expansion, we performed a zero temperature MEP search at γ = 0.092, but with other strain components fixed at the equilibrated values at T = 300 K. This approach is similar to the quasi-harmonic approximation (QHA) (30, 31) often used in free energy calculations in solids, except that, unlike QHA, the vibrational entropy is completely excluded here. The resulting activation energy, 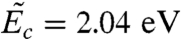, is indistinguishable from the activation free energy F_c = 2.05  ± 0.01 eV at T = 300 K computed from umbrella sampling. Because atoms do not vibrate in the MEP search, this result shows that the dominant mechanism for the large S_c(γ) is thermal expansion, whereas the contribution from vibrational entropy is negligible. As temperature increases, thermal expansion pushes neighboring atoms further apart and weakens their mutual interaction. This expansion makes crystallographic planes easier to shear and significantly reduces the free energy barrier for dislocation nucleation. In the widely used harmonic approximation of TST, the activation entropy is often attributed to the vibrational degrees of freedom as 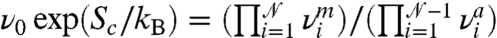, where 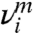and 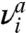are the positive normal frequencies around the local energy minimum and activated state, respectively (5, 18, 32). However, here we see that S_c(γ) arises entirely from the anharmonic effect for dislocation nucleation. At T = 400 K and T = 500 K, we observe significant differences between F_c computed from umbrella sampling and 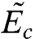computed from MEP search in the expanded cell (SI Appendix). These differences must also be attributed to anharmonic effects.

Although it is easier to control strain γ than stress σ in atomistic simulations, it is usually easier to apply stress in experiments, and experimental results are often expressed as a function of σ and T. To bridge between simulations and experiments, it is important to establish a connection between the constant stress and constant strain ensembles. In the constant strain ensemble, the system is described by the Helmholtz free energy F(n,T,γ), where n is the size of the dislocation loop and the activation Helmholtz free energy is defined as F_c(T,γ) ≡ F(n_c,T,γ) - F(n = 0,T,γ). In the constant stress ensemble, the system is described by the Gibbs free energy G(n,T,σ), from the Legendre transform G = F - σγV, with σ ≡ V^-1∂F/∂γ|_n,T. Similarly, G_c(T,σ) ≡ G(n_c,T,σ) - G(n = 0,T,σ). We have proved that G_c(T,σ) = F_c(T,γ) in the thermodynamic limit of V → ∞, when σ and γ satisfies the stress–strain relation of the perfect crystal, σ(γ,T). The difference between F_c and G_c when σ = σ(T,γ) is of the order 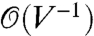. The details of the proof will be published separately.

Combining the activation Helmholtz free energy F_c(T,γ) shown in Fig. 3A and the stress–strain relations shown in Fig. 1B, we obtain the activation Gibbs free energy G_c(T,σ), which is shown in Fig. 3B. We immediately notice that the curves at different temperatures are more widely apart in G_c(T,σ) than that in F_c(T,γ), indicating a much larger activation entropy in the constant stress ensemble. For example, Fig. 3D plots G_c as a function of T at σ = 2.0 GPa, from which we can obtain an averaged activation entropy of 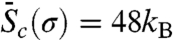in the temperature range of [0,300 K]. This activation entropy contributes a multiplicative factor of 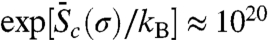to the absolute nucleation rate.

The dramatic difference between S_c(γ) and S_c(σ) may seem surprising. Indeed, they are sometimes used interchangeably (33, 34), although the conceptual difference between the two has been pointed out in the context of chemical reactions (35, 36). It is well-known that the entropy is independent of the ensemble of choice, i.e., S(n,T,γ) ≡ ∂F(n,T,γ)/∂T|_n,γ and S(n,T,σ) ≡ ∂G(n,T,γ)/∂T|_n,σ equal to each other as long as σ = V^-1∂F/∂γ|_n,T, which is true by definition. At the same time, the activation entropy is just the entropy difference between the activated state and the metastable state, i.e., S_c(T,γ) = S(n_c,T,γ) - S(n = 0,T,γ) and S_c(T,σ) = S(n_c,T,σ) - S(n = 0,T,σ). If the entropies in two ensembles can equal each other, it may seem puzzling how the activation entropies can be different.

The resolution of this apparent paradox is that under the constant applied stress, the nucleation of a dislocation loop causes a strain increase, i.e., σ(n = 0,T,γ) = σ(n_c,T,γ⁺), with γ⁺ > γ. Based on this result, one can show that the difference in the activation entropies, ΔS_c ≡ S_c(σ) - S_c(γ), equals S(n = 0,T,γ⁺) - S(n = 0,T,γ), which is the entropy difference of the perfect crystal at two slightly different strains. We can further show that ΔS_c = -Ω_c(σ)∂σ/∂T|γ, where Ω_c ≡ -∂G_c/∂σ|_T is the activation volume and -∂σ/∂T|γ describes the thermal softening effect. Hence ΔS_c is always positive for nucleation processes in solids driven by shear stress. In the case of homogeneous dislocation nucleation ΔS_c as large as 39k_B is observed for homogeneous dislocation nucleation, which is mainly caused by its large activation volume Ω_c. The numerical results enable us to examine the approximation (17) based on the so-called thermodynamic “compensation law” (37), which states that the activation entropy is proportional to the activation enthalpy (or energy). We find that S_c(γ) can be roughly approximated by E_c(γ)/T^∗ with T^∗ ≈ 3,000 K, whereas S_c(σ) is not proportional to H_c(σ) (SI Appendix).

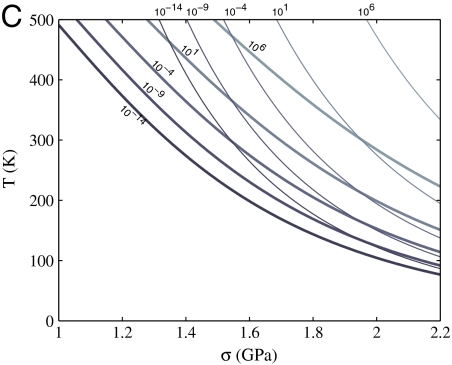
To assess the applicability of these conclusions in heterogeneous nucleation, we studied dislocation nucleation from the corner of a [001]-oriented copper nanorod with {100} side surfaces under axial compression (Materials and Methods). Fig. 4B plots the activation free energy barrier as a function of axial compressive stress σ, which shows significant reduction of the activation free energy with temperature. For example, at the compressive elastic strain of ϵ = 0.03, the compressive stress is σ = 1.50 GPa at T = 0 K. The activation entropy S_c(ϵ) at this elastic strain equals 9k_B, whereas the activation entropy S_c(σ) at this stress equals 17k_B. Fig. 4C plots the contour lines of the predicted dislocation nucleation rate (per nucleation site) as a function of T and σ. To show the physical effect of the large activation entropies, the dashed lines plot the rate predictions if the effect of S_c(σ) were completely neglected. Significant deviations between the two sets of contour lines are observed, especially for T≥300 K and σ ≤ 1.5 GPa. For example, at T = 300 K and σ = 1.5 GPa (where a thick and a thin contour line cross), the neglect of activation entropy would cause an underestimate of the nucleation rate by 10 orders of magnitude.

Fig. 4.

(A) Heterogeneous dislocation nucleation in a copper nanorod under compression, visualized by AtomEye (38). (B) G_c as a function compressive stress σ at different T. (C) Contour lines of dislocation nucleation rate per site I as a function of T and σ. The predictions with and without accounting for activation entropy S_c(σ) are plotted in thick and thin lines, respectively. The nucleation rate of I ∼ 10⁶ s^-1 per site is accessible in typical MD timescales whereas the nucleation rate of I ∼ 10^-4 - 10^-9 is accessible in typical experimental timescales, depending on the number of nucleation sites.

In summary, we have shown that the Becker–Döring theory combined with free energy barriers determined by umbrella sampling can accurately predict the rate of homogeneous dislocation nucleation. In both homogeneous and heterogeneous dislocation nucleation, a large activation entropy at constant elastic strain is observed, and is attributed to the weakening of atomic bonds caused by thermal expansion. An even larger activation entropy is observed at constant stress, caused by thermal softening. Both effects are anharmonic in nature, and emphasize the need to go beyond harmonic approximation in the application of rate theories in solids. We believe our methods and the general conclusions are applicable to a wide range of nucleation processes in solids that are driven by shear stress, including cross slip, twinning, and martensitic phase transformation.

Materials and Methods

Molecular Dynamics.

The simulation cell for homogeneous dislocation nucleation has dimension 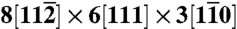. Periodic boundary conditions (PBC) are applied to all three directions. To reduce artifacts from periodic image interactions, the applied stress is always large enough so that the diameter of the critical dislocation loop is smaller than half the width of the simulation cell.

The shear strain γ is the x-y component of the engineering strain. The following procedure is used to obtain the pure shear stress–strain curve shown in Fig. 1B. At each temperature T and shear strain γ_xy, a series of 2 ps MD simulations under the canonical, constant temperature-constant volume (NVT) ensemble are performed. After each simulation, all strain components except γ_xy are adjusted according to the average virial stress until σ_xy is the only nonzero stress component. The shear strain is then increased by 0.01 and the process repeats until the crystal collapses spontaneously. The shear stress–strain data are fitted to a polynomial function, 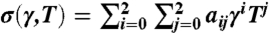in the range of 0.09 ≤ γ ≤ 0.12 and 0 ≤ T ≤ 500 K.

To obtain average nucleation time at σ_xy = 2.16 GPa (γ = 0.135) at 300 K, we performed 192 independent MD simulations using the NVT ensemble with random initial velocities. Each simulation ran for 4 ns. If dislocation nucleation occurred during this period, the nucleation time was recorded. This information is used to construct the function P_s(t), which is the fraction of MD simulation cells in which dislocation nucleation has not occurred at time t. P_s(t) can be well fitted to the form of exp(-I^MDt) to extract the nucleation rate I^MD.

To compute the attachment rate 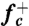, we collected from umbrella sampling an ensemble of 500 atomic configurations for which n = n_c, and ran MD simulations using each configuration as an initial condition. The initial velocities are randomized according to Boltzmann’s distribution. The mean square change of the loop size, 〈Δn²(t)〉, as shown in Fig. 2B, was fitted to a straight line, 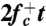, to extract 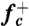(39).

Free Energy Barrier Calculations.

The reaction coordinate n is defined for each atomic configurations in the following way. An atom is labeled as “slipped” if its distance from any of its original nearest neighbors has changed by more than the critical distance d_c (40). We chose d_c = 0.33, 0.38, and 0.43 A for T ≤ 400 K, T = 500 K, and T = 600 K, respectively. The slipped atoms were grouped into clusters; two atoms belong to the same cluster if their distance was less than the cutoff distance r_c (3.4 A). The reaction coordinate n is the number of atoms in the largest cluster divided by two.

To perform umbrella sampling, a bias potential 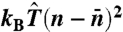is superimposed on the EAM potential, where 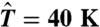and 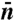is the center of the sampling window. We chose 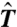empirically so that the width of the sampling window on the n-axis would be about 10. The activation Helmholtz free energy data for homogeneous nucleation can be fitted very well by a polynomial function, 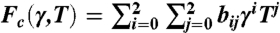in the range of 0.09 ≤ γ ≤ 0.12 and 0 ≤ T ≤ 500 K.

For heterogeneous dislocation nucleation, the size of the copper nanorod (17) is 15[100] × 15[010] × 20[001] with PBC along [001]. The activation Gibbs free energy data for heterogeneous nucleation is fitted to an empirical form G_c(σ,T) = A[(σ/σ₀)^p - 1]^q - Bσ^rT.

The error bar of activation free energies is about 0.5k_B. Hence the error bar of activation entropies is about 0.5k_B.