Extracellular Volume and Glomerular Filtration Rate in Children with Chronic Kidney Disease

Summary

Background and objectives

Extracellular volume (ECV) is the fluid contained in all noncellular compartments of the body and is a quantity tightly controlled by the kidney. Thus, there is a strong link between ECV and kidney function.

Design, setting, participants & measurements

The Chronic Kidney Disease in Children (CKiD) study uses injected iohexol to obtain direct measures of GFR. Direct calculation of ECV was viable from GFR studies using descriptors of the disappearance curves. Using linear regression methods on the log-transformed variables, markers of size (height and weight) and biomarkers of kidney disease (serum creatinine, blood urea nitrogen, and cystatin C) were assessed for their relationships with ECV normalized to body weight (ECV/wt). The relationship to hypertension (systolic BP >95th percentile for age, sex, and height) was also assessed.

Results

Data from 790 iohexol studies with medians for GFR = 43.4 ml/min per 1.73 m², weight = 35 kg, and height = 1.4 m were used. The median ECV was 8.6 L, and the median ECV/wt was 0.23 L/kg. ECV was found to be a function of height (m) and weight (kg) according to the relationship ECV = $\sqrt{weight}$ × height. Biomarkers of kidney disease yielded significant relationships with ECV/wt, but the strength of association was small. No significant association between ECV/wt and hypertension was found.

Conclusions

ECV has relevance to studies of chronic kidney disease, is related to biomarkers, and can be easily estimated from the square root of weight and height.

Introduction

Chronic kidney disease (CKD) is often seen in conjunction with hypertension. A possible mediator of the relationship is extracellular volume (ECV), the fluid contained in all noncellular compartments. ECV is tightly controlled as a critical function of the kidney. However, kidney dysfunction and disease are associated with activation of the renin-angiotensin aldosterone system, the importance of which in the regulation of blood pressure (BP) and fluid balance has long been recognized (1). Renin-angiotensin aldosterone system activation and an accompanying positive sodium balance may lead to expanded ECV and hypertension (2).

Some evidence exists to support ECV as a link between CKD, hypertension, and cardiovascular disease. A reduction in ECV using loop diuretics has been observed to effectively lower BP in patients with CKD (3). Although kidney filtration plays a primary role in adjusting ECV, the dynamics of the relationship between glomerular filtration rate (GFR) and ECV are not entirely clear (4–12). Associations among expanded ECV, obesity, hypertension, and potentially albuminuria have been noted (13–15), suggesting that an increased ECV may also predict some CKD-associated comorbidities.

In addition to possible value as a predictor of disease progression and cardiovascular morbidity, ECV is also a metric of body size. Previous investigators have suggested that ECV may serve as a physiologically and theoretically more appropriate index variable for GFR (16,17), particularly for children in whom BSA is relatively high (18).

ECV can be estimated for an individual from the time taken to clear an injected marker from the body. After equilibration, the function describing the decline in serum concentration contains information concerning the distribution volume of the marker, which approximates ECV for most markers used to assess kidney function. The estimation of ECV is accomplished using the same measured parameters as for calculation of GFR. The National Institute of Health-funded cohort study of Chronic Kidney Disease in Children (CKiD) has used the plasma disappearance of iohexol to obtain a directly measured GFR with sampling at 10, 30, 120, and 300 minutes to describe the two-compartment model (19).

In this report, we describe the distribution of ECV in the CKiD cohort and its relationship to measures of body size and markers of disease progression. We assessed the strength of association of several biomarkers of CKD severity with ECV and examined whether expanded ECV was related to the presence of hypertension in children with CKD.

Materials and Methods

Study Participants and Design

The CKiD study has been described previously (20). Briefly, children were recruited with mild to moderate CKD (30 to 90 ml/min per 1.73 m²) on the basis of the original Schwartz formula (21–23) from 43 participating pediatric nephrology centers. Eligible subjects were those 1 to 16 years of age who had never been dialyzed or undergone organ transplant. GFR was determined from plasma iohexol disappearance curves at baseline, 1 year later, and every other year thereafter. Data from participants with four-point iohexol GFR measurements performed during visits 1 and 2 were used for the calculation of ECV.

Biomarker Assays

At the study visit, an intravenous line or butterfly needle was used to administer 5 ml of iohexol. A second intravenous line was saline locked and used for obtaining blood samples for measurement of serum creatinine (SCr) and blood urea nitrogen (BUN); an aliquot was also obtained for HPLC determination of an iohexol blank. SCr (enzymatic) and BUN were analyzed centrally at the CKiD laboratory at the University of Rochester (G. Schwartz) on an Advia 2400 (Siemens Diagnostics, Tarrytown, NY) system. Blood samples were collected at four time points (10, 30, 120, and 300 minutes) after infusion for GFR and ECV calculation. Body surface area (BSA) was determined using the formula of Haycock et al. (24). Serum albumin was determined by the bromocresol green binding method, and cystatin C was determined by nephelometry (Siemens Dade-Behring).

Calculation of GFR and ECV from Plasma Disappearance Curve

The volume V_D in which a dose I of an injected marker is distributed is the product of the clearance rate (GFR) and the total clearance time (T). Expressions for GFR and T can be derived from the function c(t), which describes the concentration of the marker in a unit volume at time t after injection. Assuming a steady GFR (i.e., not dependent on t), the amount of the injected marker that is cleared at time t is given by I(t) = GFR × c(t). For a marker that is neither secreted nor absorbed, the entire injected dose I is eventually cleared and thus I = ∫₀^∞I(t) = GFR∫₀^∞c(t)dt. Hence, the clearance rate can be found from the ratio of the injected dose of the marker to the area under the concentration curve. That is,

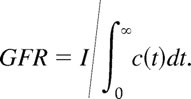The proportional decrease in concentration at each time t is c(t)/∫₀^∞c(t)dt, which describes the proportion of the molecules of the marker that is cleared at time t. Averaging across all times results in an expression for the mean transit time,

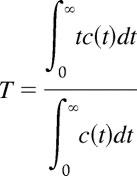or, equivalently, the total clearance time.

When describing kidney filtration, a two-compartment model is commonly used with the loss of the marker from the plasma characterized by a bi-exponential function. Thus c(t) is specified to be λ₁e^−μ₁t + λ₂e^−μ₂t, with μ₁ and μ₂ being the rate constants for the first (taken to represent exchange of the marker between plasma and the interstitial fluid of the whole body) and second (representing excretion by the kidneys) exponentials, respectively, and λ₁ and λ₂ describing the zero-time intercepts. From this representation, ∫₀^∞c(t)dt = λ₁/μ₁ + λ₂/μ₂ and ∫₀^∞tc(t)dt = λ₁/μ₁² + λ₂/μ₂². It follows that

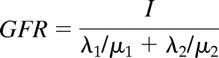and the mean transit time corresponds to

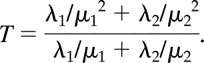This equation can also be expressed as (1 − ω)/μ₁ + ω/μ₂, where ω = (λ₂/μ₂)(λ₁/μ₁ + λ₂/μ₂), which explicitly represents T as a weighted average of the mean times the marker resides in each of the two compartments. Given an expression for GFR, the clearance rate, and for T, the clearance time, the volume of distribution of the marker then follows from

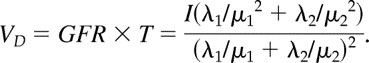The calculation for the volume of distribution comes from the work of Nosslin (25), with the mathematical model detailed by Anderson (26). The ECV is assumed to be equal to the volume of distribution. It should be noted that the volume of distribution is a function of the marker used to measure it (27). Our analysis of the CKiD population permits examining ECV over a wide range of body size, BP, and kidney function.

Statistical Analyses

After calculation of ECV, ECV was normalized to weight (ECV/wt), yielding a volume expressed as a proportion of body weight. In addition, ECV was normalized to a function of weight and height ($\sqrt{wt}$·ht), determined from regression analysis, to remove all assciation with body size (equivalent to the residuals after regression of ECV on height and weight). The relationship between the log of ECV in its unadjusted and adjusted forms was then regressed on the log of continuous markers of body size (age, weight, height, and BSA) as well as the indicator variables for sex and Tanner stage. The log of ECV was similarly regressed on the log of continuous markers of disease progression (SCr, cystatin C, and BUN) and the indicator for hypoalbuminemia (defined as albumin < 4 g/dl). The form of the regression equation was ECV = α × X^β, where X was the continuous predictor value or ECV = α × γ^I, where I was the indicator for the dichotomous trait. Thus, β was a power that qualified the value of the continuous predictor and γ was a percent change from the reference value of 1.0. Standard errors were adjusted for repeated measurements from individual participants using a robust sandwich variance estimator. Similar regressions were performed with GFR (BSA adjusted) as the dependent variable to provide a comparison for the magnitude of association between ECV and the various markers. Regression coefficients were standardized according to the formula β* = β × σ_x/σ_y, where β was the unstandardized coefficient and σ_x/σ_y was the ratio of the independent variable SD to the dependent variable SD.

The relationship between adjusted ECV and hypertension was also assessed using regression analysis and a comparison of means. Hypertension was defined as greater than or equal to the 95th percentile by age, sex, and height of systolic BP.

Results

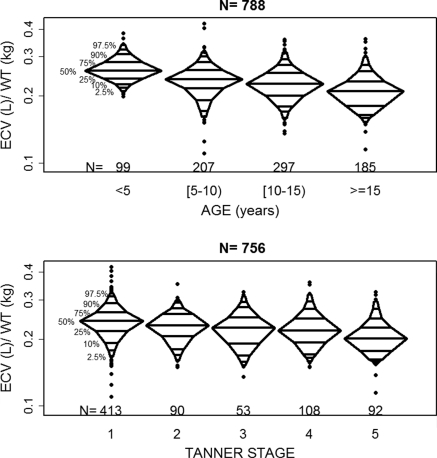
The calculated ECVs from the 790 four-point iohexol studies in 509 participants yielded a median ECV of 8.6 L (interquartile range: 5.9 to 12.2 L) and a median ECV/wt of 0.23 L/kg (interquartile range: 0.20 to 0.25 L/kg). The median age for the participant-visits was 11.3 years and the median GFR was 43.4 ml/min per 1.73 m² (Table 1). ECV and GFR are functions of body size, such that larger individuals have larger ECVs and higher absolute GFRs. The extent to which ECV and GFR are also related to kidney disease can only be assessed after removing any relationship with body size. Thus, GFR is commonly normalized to BSA and ECV is often assessed as a proportion of body weight. The effects of adjustment are clearly seen in Table 2. In Table 2, unadjusted ECV was strongly related to markers of body size and some measures of kidney function (SCr and hypoalbuminemia). When ECV was assessed as a proportion of body weight, the magnitude of association with markers of body size was attenuated but relationships were still statistically significant. The relationships with age and Tanner stage indicated that ECV as a percentage of body weight declined with increasing physical development. This trend can be seen in Figure 1. The median values of ECV/wt across categories of age were 0.26, 0.24, 0.23, and 0.21 L/kg for <5, [5 to 10), [10 to 15) and ≥15 years, respectively. Similarly the median values across categories of Tanner stage were 0.24, 0.23, 0.23, 0.22, and 0.20 L/kg for stages 1 through 5, respectively. Normalizing ECV to weight attenuated the significant relationships with 1/SCr, height/SCr, and hypoalbuminemia noted in the unadjusted ECV data.

Table 1.

Characteristics of the baseline sample of participants from the CKiD cohort and from the participant-visits taken from visit 1 and visit 2

Variable	Value
n = 509 participants, baseline assessment
male gender (%)	62.6
white race (%)	72.1
Tanner stage 1 (%)	58.0
glomerular diagnosis (%)	20.8
n = 790 participant-visits, median (interquartile range)
age (years)	11.3 (7.9 to 14.8)
height (m)	1.4 (1.2 to 1.6)
weight (kg)	38.2 (24.4 to 55.6)
BSA (m2)	1.2 (0.9 to 1.6)
BMI (kg/m2)	18.5 (16.3 to 22.1)
SCr (mg/dl)	1.3 (1.0 to 1.9)
height (m)/SCr (mg/dl)	1.0 (0.8 to 1.4)
cystatin C (mg/L)a	1.6 (1.3 to 2.2)
BUN (mg/dl)	32.1 (23.1 to 42.9)
albumin (g/dl)	4.3 (4.1 to 4.5)
iohexol GFR (ml/min per 1.73 m2)	43.4 (32.6 to 55.7)
ECV (L)	8.6 (5.9 to 12.2)
ECV (L)/weight (kg)	0.2 (0.2 to 0.3)

^an = 267.

Table 2.

Results from regressing adjusted and unadjusted ECV on markers of body size and kidney function n = 790

Variables	Regression Coefficient (β) ± SEM
	Unadjusted ECV	Weight-Adjusted ECV	$\sqrt{wt}$·ht-Adjusted ECV
Markers of body size
female gendera	0.974 ± 0.035	0.959 ± 0.013	0.975 ± 0.010
Tanner Stage 1 (reference)a	1	1	1
2a	1.650 ± 0.098	0.956 ± 0.020	1.010 ± 0.016
3a	2.030 ± 0.093	0.921 ± 0.024	1.029 ± 0.021
4a	2.258 ± 0.077	0.917 ± 0.018	1.052 ± 0.016
5a	2.411 ± 0.087	0.847 ± 0.017	1.022 ± 0.016
age (years)	0.803 ± 0.016	−0.132 ± 0.012	−0.017 ± 0.009
weight (kg)	0.823 ± 0.010	−0.177 ± 0.010	>−0.001 ± 0.009
height (m)	2.333 ± 0.032	−0.345 ± 0.031	−0.006 ± 0.025
BSA (m2)	1.242 ± 0.014	−0.251 ± 0.015	−0.001 ± 0.013
Markers of kidney function
1/SCr (mg/dl)	−0.433 ± 0.032	0.062 ± 0.013	0.022 ± 0.010
height (m)/SCr (mg/dl)	−0.097 ± 0.041	0.013 ± 0.015	0.030 ± 0.012
1.8/cystatin C (mg/L)	−0.001 ± 0.073	<0.001 ± 0.029	0.052 ± 0.022
30/BUN (mg/dl)	0.075 ± 0.039	0.033 ± 0.015	0.068 ± 0.011
Albumin < 4 (g/dl)a	1.324 ± 0.067	0.930 ± 0.018	1.004 ± 0.015

Except where indicated, regressions were of the form ECV = α × X^β, with β interpreted as the power qualifying the value of the marker to describe its effect on ECV. Bold indicates P < 0.05.

^aDichotomous and categorical variables for which the regression coefficient is a percentage of reference value (e.g., 1.1 is 10% higher than reference and 0.9 is 10% lower than reference).

Figure 1.

Distribution of ECV/wt by age (in the 788 person-visits) and Tanner stage(in the 756 person-visits) from the CKiD cohort visits 1 and 2. The median values of ECV/wt across categories of age (from left to right) were 0.26, 0.24, 0.23, and 0.21 L/kg and across categories of Tanner stage (from left to right) were 0.24, 0.23, 0.23, 0.22, and 0.20 L/kg.

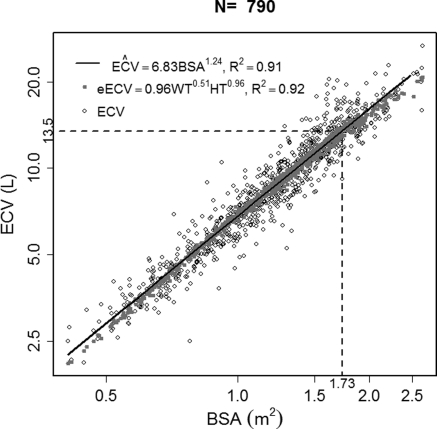
Given indications that normalizing ECV/wt did not remove all variability associated with body size, we regressed ECV on weight and height specifying an equation analogous to Haycock et al. (24) (Y = a × weight^b × height^c). Similar to the relationship between BSA and the measurements of height and weight, ECV was also well estimated from those variables (Figure 2). We found the estimated values of a, b, and c were 0.962, 0.511, and 0.963, respectively. Using this information, we removed all variability in ECV associated with height and weight using ECV/($\sqrt{wt}$·ht). This formulation resulted in the estimated regression coefficients approaching zero for all markers of body size except sex, which remained significant (Table 2). There was no longer a trend in ECV/($\sqrt{wt}$·ht) as a function of Tanner stage. However, ECV/($\sqrt{wt}$·ht) was associated with all markers of kidney function except hypoalbuminemia. The association appeared strongest with BUN, with an estimated effect of 0.068 L/($\sqrt{kg}$·m). When the regression coefficients were standardized and compared with those from regressing GFR on the biomarker values, the strength of association was much greater for the outcome of GFR as seen in Table 3.

Figure 2.

Plot of ECV versus BSA illustrating the correlation between the two measures of body size. ECV can be estimated from height and weight in a similar manner to BSA.

Table 3.

Standardized regression coefficients from regressing BSA-adjusted GFR and $\sqrt{wt}$·ht-adjusted ECV on markers of kidney function (n = 790)

Markers of Kidney Function	Standardized Effect Estimate
	BSA-Adjusted GFR	$\sqrt{wt}$·ht-Adjusted ECV
1/SCr (mg/dl)	0.110	0.004
Height (m)/Scr (mg/dl)	0.145	0.005
1.8/cystatin C (mg/L)	0.276	0.016
30/BUN (mg/dl)	0.112	0.012
Albumin < 4 (g/dl)a	0.977	1.001

Except where indicated, regressions were of the form GFR = α × X^β, with β interpreted as the power qualifying the value of the marker to describe its effect on GFR.

^aDichotomous and categorical variables for which the regression coefficient is a percentage of reference value (e.g., 1.1 is 10% higher than reference and 0.9 is 10% lower than reference).

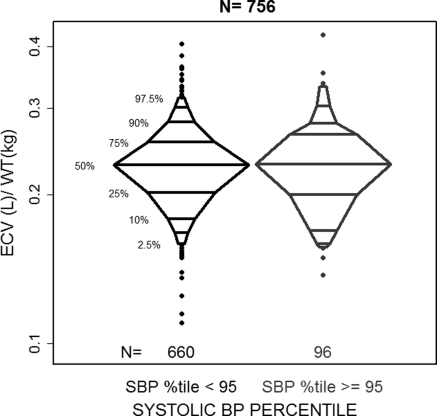
When the relationship between ECV and BP was assessed in this sample of children with CKD, we found no significant association in linear regression analysis. Comparing the median ECV/wt between hypertensives (systolic BP percentage ≥95%) and nonhypertensives (systolic BP percentage <95%) did not yield a statistically significant difference. Figure 3 compares these ECV/wt distributions for levels of hypertension. ECV/($\sqrt{wt}$·ht) was similarly unassociated with hypertension.

Figure 3.

Distribution of ECV/wt by categories of greater than the 95th percentile and less than or equal to the 95th percentile of systolic BP (normalized for height and age) in 756 person-visits from CKiD cohort visits 1 and 2.

Evaluating ECV as a marker of body size, ECV was found to be strongly correlated with BSA on the log scale (ρ = 0.95), as illustrated in Figure 2. Fitting a regression line through the data yielded a regression coefficient of 1.24 to describe the power that quantifies the predictive effect of a unit change in BSA on ECV. Using the regression equation to estimate the ECV equivalent to a BSA of 1.73 m² (the value usually considered the size of a standard adult) yielded a value of 13.5 L.

Discussion

The primary function of the kidneys is to maintain fluid balance through tight control of the chemical composition of the ECV. As kidney function declines, a loss of regulatory function may lead to expanded ECV, which could in turn lead to cardiovascular sequelae as a result of the additional loading of the system. However, although such relationships have been noted in adults, particularly in the context of obesity (13,14), evidence that ECV is related to kidney disease and hypertension is lacking in this pediatric sample. Although there was an association between ECV and several markers of kidney disease after removing the variability associated with height and weight, the direction of the relationships indicated that expanded ECV was protective. Stratifying by glomerular diagnosis revealed differences in the inferences from biomarker associations that may hint at a differential effect on ECV in the two disease processes. However, children with a glomerular diagnosis comprised a minority in our sample (approximately 20%) and thus we did not have a sufficient sample size to fully explore differences in the biomarker associations with ECV. The participants in CKiD had few reported visits with edema (25 person-visits) and thus this cohort may not have had enough individuals with large deviations in ECV and resulting sequelae.

Although there is a plausible biologic mechanism whereby expanded ECV as a result of disease progression would increase cardiovascular risk, we did not find differences in the distribution of ECV between those with and without high systolic BP. Because the number of subjects taking diuretics was small, accounting for only 8 of the 790 person-visits, this therapy was not the explanation for the failure to see expanded ECV in hypertension. However, it is possible that expanded ECV produces a small upward shift in BP that acts over time to increase cardiovascular morbidity and mortality, an effect that would not be observed in this pediatric cohort with limited follow-up.

What is clear from this analysis is that ECV is strongly related to body size, as can be seen from Table 2, which illustrated the changing regression coefficients with improved body size standardization. ECV is related to an individual's height and weight and is highly correlated with BSA, a result found by several investigators (17,28,29). Previous work has explored the exact relationship between ECV and these other measures of body size. Friis-Hansen (30) in 1961 provided a formula to estimate ECV in children that was based on percentages of weight and height. The formula was of the form ECV = a × weight^b × height^c, and he found ECV was best approximated using parameter estimates of 0.0682, 0.400, and 0.633 for a, b, and c, respectively. A similar equation was reported by Bird et al. (31) with estimates of 0.0215, 0.647,and 0.724, respectively, which the authors contrasted with the Haycock formula to estimate BSA (24). Haycock et al. found BSA best estimated using 0.024, 0.538, and 0.396 for a, b, and c, respectively. In this report, we found that height provided most of the information in the estimation of ECV, and ECV could be simply estimated from ECV = ($\sqrt{weight}$ × height). Thus, although in the study presented here we utilized the iohexol plasma disappearance protocol from the four-point GFR studies to assess ECV, a good estimation of ECV can be obtained using only height and weight measurements.

Friis-Hansen (30) has shown that ECV as a percent of body weight decreases with maturation, rapidly during the first year of life and gradually thereafter until age 10 to 15 years. Our study shows a similar decrease as a function of Tanner stage (see Figure 1), which is a surrogate for age and maturation. Indeed, the measurement they obtained for the 10- to 15-year age group was 18.7% of body weight. They note that the thiosulfate method, which estimated ECV, neglects the contribution of water in the gastrointestinal tract and other transcellular sources of transcellular water and therefore underestimates ECV by 5% to 10% in terms of percent of body weight. Thus, their estimate is probably closer to 24%, which echoes the 24% we observed in Tanner 1 to 3 subjects using iohexol distribution. Additionally, our results indicating that girls have lower ECV than boys of the same weight (Table 2) agrees with the previous findings of Friis-Hansen (30), which follows from the higher average percentage of body fat for postpuberty girls versus boys.

In summary, in this pediatric cohort, ECV was related to the disease process but to a lesser degree than to GFR and was not a clear predictor of cardiovascular morbidity. However, ECV is a quantity that can be measured in a similar fashion to GFR, is a measure of body size, and as such has some relevance to studies of CKD. Indexation of GFR to ECV abolishes many of the differences between adults and young children with respect to scaling GFR to BSA (29). This advantage may be further exploited because it is technically simple to measure simply the renal slope (μ₂), and this is equivalent to GFR per unit ECV. Further ECV may be estimated well from weight and height, yielding an easily attainable parameter. ECV may yet prove an important predictor of disease in a more edematous cohort and, should the strong relationship with height and weight found here persist in such a population, then it could be easily estimated for research or clinical purposes.

Disclosures

None.