Removal of Olefinic Fat Chemical Shift Artifact in Diffusion MRI

Abstract

Diffusion-weighted (DW) MRI has emerged as a key tool for assessing the microstructure of tissues in healthy and diseased states. Due to its rapid acquisition speed and insensitivity to motion, single-shot EPI is the most common DW imaging technique. However, the presence of fat signal can severely affect DW-EPI acquisitions because of the chemical shift artifact. Fat suppression is usually achieved through some form of chemical shift-based fat saturation. Such methods effectively suppress the signal originating from aliphatic fat protons, but fail to suppress the signal from olefinic protons. Olefinic fat signal may result in significant distortions in the DW images, which bias the subsequently estimated diffusion parameters. This paper introduces a method for removing olefinic fat signal from DW images, based on an echo time-shifted acquisition. The method is developed and analyzed specifically in the context of single-shot DW-EPI, where image phase is generally unreliable. The proposed method is tested with phantom and in vivo datasets, and compared to a standard acquisition to demonstrate its performance.

INTRODUCTION

Diffusion-weighted (DW) MRI (1) has emerged as a powerful tool for assessing the microstructure of intracerebral (2) and extracerebral (3) tissues in healthy and diseased states. The high sensitivity of diffusion-weighted MRI to tissue motion has made single-shot echo-planar imaging (EPI) the most widely used imaging technique in diffusion-weighted experiments. Although single-shot EPI acquisitions minimize the sensitivity to motion, they suffer from high sensitivity to off-resonance effects, which are caused by field inhomogeneities, susceptibility and chemical shift differences. Specifically, the low EPI bandwidth along the phase-encoding direction can cause the fat signal to be shifted into the tissue region, resulting in chemical shift artifact (CSA) (4). Therefore, since the diffusion properties of the fat are in general different from the diffusion properties of the tissue, the estimated diffusion parameters can be biased when applying diffusion-weighted imaging in tissues surrounded by fat. An example of this sort of bias is the contamination of the diffusion tensor parameters in skeletal muscle due to subcutaneous and bone marrow fat chemical shift artifacts (5, 6).

In order to eliminate fat chemical shift artifacts, diffusion-weighted acquisitions typically include some form of fat suppression. Several general methods are available for fat suppression: chemical shift selective RF pulses, short time inversion recovery (STIR), slice selection gradient reversal and water/fat separation methods. Chemical shift selection uses either spectrally selective (7) or spatial-spectral (8) RF pulses, coupled with spoiler gradients, in order to null the magnetization for spins precessing at a narrow bandwidth around a known lipid frequency. STIR techniques take advantage of the short T1 of the lipids to null the fat signal in an inversion recovery experiment (9, 10). Slice selection gradient reversal uses slice selection gradients with opposite polarity in sequences with 3 RF pulses (11). Water/fat separation methods that are based on chemical shift-encoded imaging have received considerable attention in recent years, due in part to their ability to provide robust fat suppression while maintaining good SNR efficiency (12, 13, 14, 15, 16, 17). Hybrid techniques also exist, e.g. spectral inversion recovery (SPIR), which combines the principle of STIR with chemical shift selective imaging (18).

The optimal selection of fat suppression technique is application-dependent. In imaging experiments with inherently low SNR, STIR is usually not preferred since T1 relaxation decreases the signal from the tissues of interest in the process of nulling the fat. Chemical shift selective fat suppression methods are effective at eliminating the main component of the fat signal that originates from the bulk methyl- and methylenic protons, as well as from other (aliphatic) fat protons with chemical shifts in the range 0.8-3.0 ppm. However, there is also significant fat signal due to the olefinic protons (which constitute approximately 5 – 10% of all fat protons). The chemical shift of the olefinic protons (5.4 ppm) is close to that of water protons (4.7 ppm) (19). The suppression of multiple fat peaks can be challenging. Recently proposed water-fat separation techniques are capable of separating fat at multiple frequencies (17), but they suffer from long acquisition times. However, hybrid techniques incorporating a form of fat suppression in an echo-shifted acquisition can be time efficient. Specifically, it has been proposed that the fat signal can be suppressed by a technique combining chemical shift selective fat suppression for nulling signal from aliphatic fat protons and chemical shift-encoded imaging for suppressing the signal from the olefinic fat protons (20).

In the case of diffusion-weighted single shot EPI, chemical shift-selective RF pulses are typically used for suppression of aliphatic protons. However, the signal from olefinic protons can result in significant contamination of the estimated diffusion parameters because of the combination of the following effects. First, the signal from the slower-diffusing olefinic protons becomes significant in the presence of diffusion-weighting, which greatly attenuates the water signal. Second, the olefinic fat shift can be of the order of less than 5 voxels, depending on the employed readout length, because of the low frequency separation between water and olefinic fat (0.7 ppm). This olefinic fat shift can contaminate the boundary between water and fat in the typical low resolution diffusion-weighted images, making thus the identification of the chemical shift artifact difficult in certain cases.

In this article, we propose a method based on a water/olefinic fat separation approach for removal of olefinic fat signal from DW-EPI acquisitions. This method adapts the multiple echo shift approach for the separation of water and olefinic fat signals in a DW acquisition with chemical selective suppression of aliphatic fat. The proposed method addresses two important complications encountered when incorporating water-fat separation in diffusion imaging. First, the implementation of a multiple-point water/fat separation method considerably lengthens the total scan time. In the present work, we propose to substitute the averaging commonly employed in DW acquisitions (typically 2-6 averages are needed to improve the inherently low SNR in DW acquisitions) by a water/fat separation acquisition using a set of different echo time (TE) shifts, which allow separation of the water and olefinic fat signals. Second, DW images have inherently unreliable phase, due to the sensitivity to small motions introduced by the DW gradients. This complicates water/fat separation, compared to standard, non-DW acquisitions (15), where the image phase is consistent. The proposed method performs the separation based on the magnitude DW images. Additionally, this article provides theoretical analysis of the problem of water/olefinic fat separation from magnitude images (analogous to Ref. (16) for standard water/fat separation from complex-valued images). The article is organized as follows: the Methods section contains the description of the proposed method, including the acquisition scheme and the reconstruction algorithm. In the Results section, the method is applied using phantom and in vivo data from the skeletal muscles of healthy volunteers, and a comparison with standard DW acquisition methods is provided to demonstrate its performance. In the Discussion section, we analyze the properties and limitations of the proposed method.

METHODS

Acquisition

The proposed method is based on replacing the averaging in standard DW-EPI by a TE-shifted acquisition (12, 13, 21, 14, 15). As is the practice with water/fat imaging, the TE shifts are obtained by time-shifting the refocusing pulses in a spin echo (SE) or a stimulated echo (STE) DW-EPI sequence. The proposed acquisition scheme is shown in Fig. 1.

Figure 1.

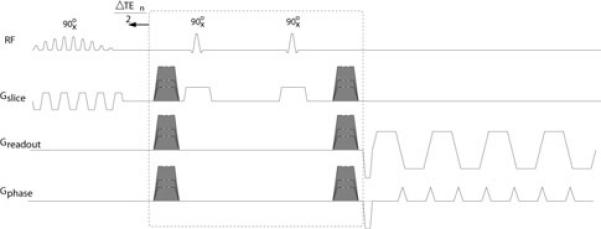
Proposed acquisition scheme, based on a stimulated echo DW-EPI acquisition. Shifting the shown block (dashed box) to the left by ΔTE_n/2 results in an effective TE shift of ΔTE_n. The shaded gradient pulses depict diffusion-weighting gradients. A similar acquisition is possible based on spin echo DW-EPI.

Due to the relatively small chemical shift between water and olefinic protons (approximately 89 Hz at 3T), longer TE shifts compared to standard water/fat imaging methods (16) are needed in order to attain sufficient phase shifts for separating the two components. In this work, we employ 6 values of ΔTE_n, equally spaced between 0 and 10 ms, which result in accumulating nearly one full cycle in the relative phase between water and olefinic protons. The SNR properties of this choice of TE shifts are analyzed theoretically and empirically in the Results section.

Postprocessing

Because of the phase distortions typical of body DW-EPI, which are caused by the motion-sensitizing DW gradients and complicate standard water/fat separation processing, we propose to perform water/olefinic fat separation using magnitude images. The signal magnitude measured at an individual voxel in a DW-EPI acquisition with a diffusion weighting b and TE shift ΔTE_n (as shown in Fig. 1) can be modeled as:

$$\mid s(\mathrm{x};b,\Delta {\mathrm{TE}}_n)\mid =\mid W(\mathrm{x};b)e^{j2\pi f_{\mathrm{B}}\left(\mathrm{x}\right)\Delta {\mathrm{TE}}_n}+F(\mathrm{x}-\Delta \mathrm{x};b)e^{j{\varphi }_F(\mathrm{x}-\Delta \mathrm{x};b)}{e}^{j2\pi \left(f_{\mathrm{B}}\right(\mathrm{x}-\Delta \mathrm{x})+f_F)\Delta {\mathrm{TE}}_n}+\nu \mid$$ [1]

where W(x; b) is the magnitude of the water signal, F (x – Δx; b) is the amplitude of the olefinic fat signal, Δx is the spatial displacement of the olefinic fat signal due to the CSA (e.g., approximately 4 voxels in the acquisitions used in this work), _ϕF (x – Δx; b) is the initial (i.e., with zero TE shift) phase of the fat signal relative to the water signal, f_F is the chemical shift of the olefinic fat signal (f_F ≃ 89Hz at 3T) (19), f_B(x) is the local frequency offset due to B₀ field inhomogeneity, and ν represents complex Gaussian noise with distribution N(0,σ²).

The field map f_B(x) is estimated from the complex-valued b = 0 data along with the b = 0 water and fat images. This is done using the algorithm proposed in (22), except modified here to account for the olefinic fat CSA (see Appendix for details).

The unknown parameters in Eq. 1 are W(x; b), F (x – Δx; b), and _ϕF (x – Δx; b). The maximum-likelihood (ML) estimates of these parameters are obtained at each voxel, accounting for the Rician distribution of the noisy MR magnitude data (23), by maximizing:

$$\begin{array}{cc}\hfill \underset{W,F,{\varphi }_F}{\max }\prod _{n=1}^N\frac{\mid s(\mathrm{x};b,\Delta {\mathrm{TE}}_n)\mid }{{\sigma }^2}& e^{-({\mid s(\mathrm{x};b,\Delta {\mathrm{TE}}_n)\mid }^2+{\mid \widehat{s}(W,F,{\varphi }_F;\Delta {\mathrm{TE}}_n)\mid }^2)∕2{\sigma }^2}\times \hfill \\ \hfill & I_0\left(\frac{\mid s(\mathrm{x};b,\Delta {\mathrm{TE}}_n)\mid \mid \widehat{s}(W,F,\varphi ;\Delta {\mathrm{TE}}_n)\mid )}{{\sigma }^2}\right)\hfill \end{array}$$ [2]

where s(x; b, ΔTE_n) is the measured signal at a given voxel, ŝ(W, F, ϕ_F;ΔTE_n) represents the signal model, i.e.,

$$\widehat{s}(W,F,{\varphi }_F;\Delta {\mathrm{TE}}_n)=W{e}^{j2\pi f_{\mathrm{B}}\left(\mathrm{x}\right)\Delta {\mathrm{TE}}_n}+F{e}^{j{\varphi }_F}{e}^{j2\pi \left(f_{\mathrm{B}}\right(\mathrm{x}-\Delta \mathrm{x})+f_F)\Delta {\mathrm{TE}}_n},$$ [3]

for known field map values f_B(x), f_B(x – Δx), and I₀ is the zeroth-order modified Bessel function of the first kind. The estimation is equivalent to minimizing the following negative log-likelihood:

$$\underset{W,F,{\varphi }_F}{\min }\sum _{n=1}^N\left[\frac{{\mid \widehat{s}(W,F,{\varphi }_F;\Delta {\mathrm{TE}}_n))\mid }^2}{2{\sigma }^2}-\log I_0\left(\frac{\mid s(\mathrm{x};b,\Delta {\mathrm{TE}}_n)\mid \mid \widehat{s}(W,F,{\varphi }_F;\Delta {\mathrm{TE}}_n)\mid )}{{\sigma }^2}\right)\right].$$ [4]

This minimization is performed using a standard iterative Newton descent-based algorithm available in MATLAB (The MathWorks, Natick, MA) (24). The proposed method is depicted graphically in Fig. 2.

Figure 2.

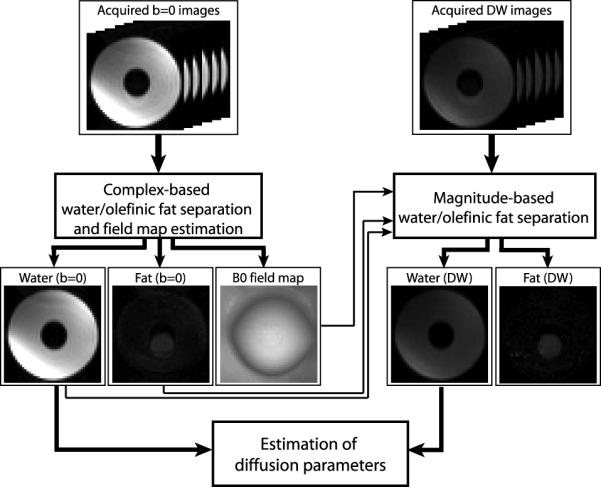
Proposed reconstruction method.

The proposed method results in locally optimal estimates, so it is important to have a good initialization. In this case, the initialization is obtained from the b = 0 images. These are also acquired using different TE shifts, and so water/fat separation is possible on them (22) (see Appendix). Note that the phase was observed to be reliable in the b = 0 images due to the lack of DW gradients. From the water/olefinic fat separated b = 0 images (W(x; 0), F(x; 0), ϕ_F(x; 0)), the initial guesses for the parameters (W, F, ϕ_F) in Eq. [4] are obtained at each location x by using approximated diffusion coefficients for the water and olefinic fat components (conservatively chosen to preserve the water signal). The specific values (W(x; 0)e^−0.0005b, F(x – Δx; 0), ϕ_F (x – Δx; 0)) are used in this work.

Experiments

All experiments were performed on a 3 T whole-body scanner (General Electric Healthcare, Waukesha, Wisconsin). Data were acquired by scanning a water/fat phantom as well as the lower extremity muscles of three volunteers, using a single-shot stimulated echo EPI sequence (25, 26). In all cases, standard fat suppression (to remove signal from methyl/methylene fat peaks near 1.4 ppm) was performed using a spatial-spectral RF pulse. The proposed acquisition was obtained using 6 values of ΔTE, equally spaced between 0.0 ms and 10.0 ms.

For the phantom dataset, seven slices were acquired with the following parameters: TR/TE=2000/72 ms, FOV=16×16 cm², slice thickness=10 mm, acquisition matrix=64×48 (6/8 partial phase encoding), with 30 diffusion directions and diffusion weighting b = 540 s/mm². For comparison, a standard acquisition (with TE=72ms) was obtained with 6 averages and no echo time shifts.

The in vivo scans included data from the right calf muscle of two volunteers and from the right lower thigh musculature of a third volunteer, using in all cases a transmit-receive single channel lower extremities coil. Twelve slices were acquired with the following parameters: TR/TE=4000/43 ms, slice thickness 7 mm, acquisition matrix=64×40 (5/8 partial phase encoding), FOV=18×18 cm² (calf) and 20×20 cm² (thigh), with 30 diffusion directions and diffusion weighting b = 522 s/mm². The diffusion timing of the stimulated-echo prepared sequence was optimized (Δ/δ =220/5.5 ms) as in Ref. (25). For comparison, a standard acquisition (with TE=43ms) was obtained with 30 diffusion directions, 6 averages and no echo time shifts.

The calf acquisitions were performed twice, by altering the direction of the phase encoding lines, so that the olefinic fat signal from the subcutaneous fat layer was shifted in a different direction each time, resulting in contamination of a different muscle region. The thigh dataset was acquired in the same way as the calf dataset, but the standard acquisition was performed with only one phase encoding direction.

RESULTS

SNR analysis

An important aspect of the proposed method is its noise performance. This can be well characterized in terms of the effective number of signal averages (NSA), which is the ratio of the noise variance in the acquired images and the noise variance in the resulting water image (13, 27, 16).

Figure 3 shows the NSA for different water/fat ratios and different initial relative phases between the two signal components (water and fat). In this work, we cannot assume an initial relative phase of 0 (as is commonly done when analyzing conventional water/fat separation), because we observe an initial relative phase (dependent on the diffusion weighting), which is unknown a priori. As can be observed, it is not possible to attain constant NSA for all water/fat ratios, unlike in standard water/fat separation (16). The varibility of NSA with fat content is due to the unreliable phase in the acquired images, so that the separation must be performed from magnitude images. Two main observations can be derived from Fig. 3:

• NSA approaches its maximum value, 6, for voxels containing mostly water. This results in good SNR for voxels containing only water, where separation is not needed in the first place.

• NSA vanishes for a water/olefinic fat ratio of 1. Note that this does not imply arbitrarily large errors in the amplitude estimates. Given a sufficiently large number of TE shifts, the signal at a voxel containing W = F will have a minimum of approximately 0 and a maximum of approximately 2W. Thus, the estimated amplitudes obtained with the proposed fitting method will both be near the correct value (so that the signal model can fit the measured signal). However, the variance of these estimates will not scale down linearly with decreasing noise variance (28). Still, it may be preferable to avoid this effect altogether, which in the context of the proposed technique can be achieved by using moderate b values so that the water amplitude is larger than the amplitude of the olefinic fat in the DW images. For instance, in the calf dataset the water/olefinic fat ratio in most of the contaminated region of the b = 0 images is nearly 6. Assuming that the diffusivity of water in muscle tissue along any direction is less than 2.3 × 10⁻³ mm²/s, the water/olefinic fat ratio of the b = 540 s/mm² images is higher than 6 × exp(−2 × 10⁻³ × 540) ≈ 1.7, so the degenerate region of the NSA can be avoided.

Figure 3.

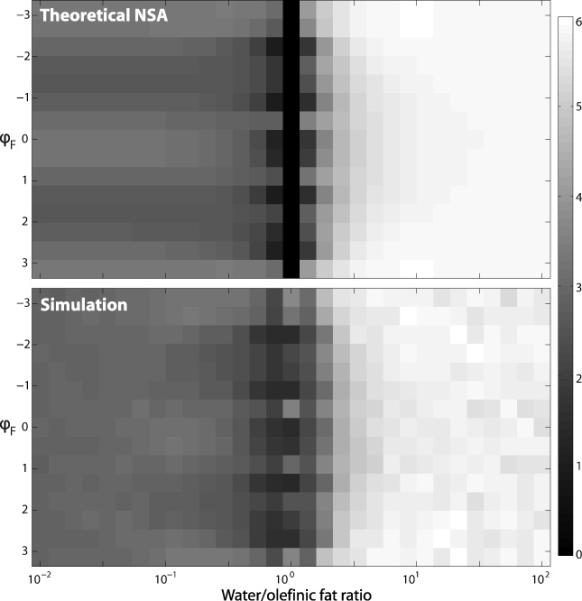
Effective number of signal averages (NSA) for water component estimation from magnitude images, using a 6-point acquisition with TE shifts evenly distributed between 0 and 10 ms. (Top) Theoretical NSA (obtained from Cramér-Rao bounds). (Bottom) Empirical NSA (obtained from MSE observed in simulation with 10,000 trials using SNR=10). Values are shown for different initial phase shifts between the water and olefinic fat components, and for different water/olefinic fat ratios.

Phantom results

Figure 4 shows representative results from a phantom scan. The imaged slice contains a circular region of fat surrounded by water. The basis for the proposed method is displayed in Fig. 4 (left box): voxels containing both water and olefinic fat components show a variation in signal magnitude with varying TE shifts (due to the varying relative phase), which allows us to separate the two components of the signal. The olefinic fat component is clearly visible in the acquired DW images, with a spatial shift of nearly 4 voxels due to the chemical shift artifact. Note that unsuppressed methylene proton signals would experience a different spatial shift (nearly 18 voxels in the opposite direction), and thus would appear elsewhere in the images. Good separation of water and olefinic fat is achieved from the DW images. Thus, the diffusion parameter estimation errors obtained with a standard acquisition are largely removed with the proposed method. Based on the proposed separation, we segmented the region of the image containing only water (“water region”), and the region containing both water and olefinic fat (“mixed region”). Table 1 shows the estimated mean diffusivity (MD) in both regions using the standard acquisition as well as the proposed method. The standard acquisition shows severely biased MD estimates in the mixed region. This bias is well removed using the proposed method. MD estimates in both regions using the proposed method are in good agreement with the standard water region estimates. Additionally, the proposed method results in a decrease of the standard deviation in MD estimation. This difference may be due to the presence of unsuppressed aliphatic signal in both acquisitions. In the standard acquisition, this unsuppressed signal appears coherently in all the averages, and results in a small but non-negligible bias in the MD estimates of a region within the image. In contrast, in the proposed acquisition, unsuppressed aliphatic signals introduce rapidly varying distortions of small amplitude to the signal, as a function of TE shift, and are treated as noise during the water/olefinic fat separation. Moreover, MD estimates in the mixed region using the proposed method also show decreased standard deviation compared to the water region. This is somewhat surprising, since according to theory (see Fig. 3), the NSA for a water/fat ratio of 4 (observed in the mixed region) should be slightly worse than for water-only voxels. This mismatch may be due to the small size of the mixed region sample, which contains 23 voxels.

Figure 4.

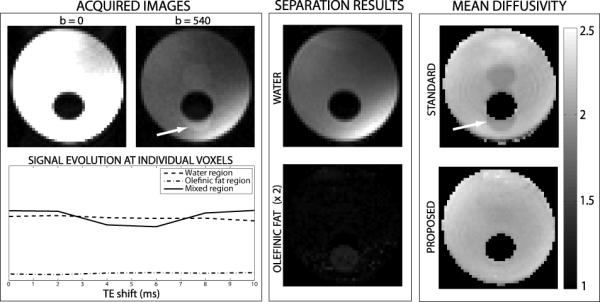
Olefinic fat removal results on a water/fat phantom. (Left box) Acquired images, with and without diffusion weighting. Note the visible signal contamination due to the olefinic fat chemical shift artifact (see arrow). Also shown is the signal magnitude evolution with TE shift at voxels within the water region, olefinic fat region, and mixed region. The proposed separation is based on the magnitude variation observed when both components are present. (Center box) Resulting DW water and olefinic fat images, obtained with the proposed method. The gray scale is common to water and olefinic fat, to highlight their relative amplitudes. (Right box) Estimated MD (×10⁻³ mm²/s) maps with a conventional acquisition (6 averages) and with the proposed method (6 TE shifts). The MD estimate obtained with the standard acquisition in the mixed region (see arrow) is significantly biased, due to the slow-diffusing olefinic fat component. This bias is largely removed with the proposed method.

Table 1.

Estimated MD (×10⁻³mm²/s) using a standard acquisition (6 averages) and the proposed acquisition (6 TEs), in the region of the phantom containing only water (“water region”), and in the region containing both water and olefinic fat (“mixed region”, where olefinic fat appears due to the chemical shift artifact).

	Standard acquisition	Proposed acquisition
Water region	2.14 ± 0.10	2.15 ± 0.08
Mixed region	2.01 ± 0.03	2.12 ± 0.04

In vivo results

Representative results from a calf DW-EPI imaging experiment are shown in Fig. 5. The acquisition was performed twice, reversing the order of the EPI phase encoding lines. This gave rise to different susceptibility-related distortions for datasets acquired with different phase encoding orderings. In order to ameliorate this inconsistency, all datasets were distortion-corrected using the field maps estimated from the b = 0 images (field maps estimated with both phase encoding orderings were averaged prior to performing distortion correction) (29).

Figure 5.

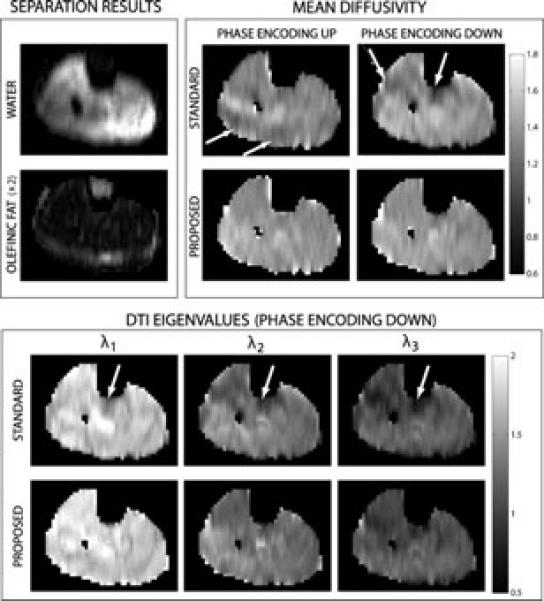
Results from a calf dataset. (Top left) Results from the proposed method for separation of water and olefinic fat from magnitude DW images. (Top right) MD estimates using the standard and proposed methods, and acquired with and without reversal of the EPI phase encoding ordering. Different phase encoding orderings give rise to different directions of the olefinic fat CSA, creating different problematic regions in the MD maps. These regions are largely fixed with the proposed method, for both phase encoding orderings. (Bottom) DTI eigenvalue maps obtained from the standard and the proposed methods.

As in the phantom case, the proposed method results in good water-only images (Fig. 5, top left box), which in turn produce improved estimates of diffusion parameters (Fig. 5, top right). The MD maps obtained with the standard acquisition show clear errors in “problematic” regions of olefinic fat contamination. The MD maps obtained with the proposed method for both phase encoding orderings are largely free of these errors. The eigenvalues of the estimated diffusion tensor are also contaminated in the region of the residual olefinic fat chemical shift artifact (Fig. 5) and the bias in the estimation of the eigenvalues is removed by employing the proposed method.

Additional results from a thigh dataset are shown in Fig. 6. The estimated water-only images obtained with the proposed method show good removal of olefinic fat (see Fig. 6, top left). The averaged images from the standard method and averaged water images from the proposed method (average taken over all diffusion directions), clearly show the presence of olefinic fat from the subcutaneous layer in the standard acquisition (see arrows Fig. 6, top right). The estimated diffusion parameters shown in Fig. 6 demonstrate the removal of errors due to olefinic fat signal, which are most visible in the region contaminated by signal from the bone marrow (see arrows).

Figure 6.

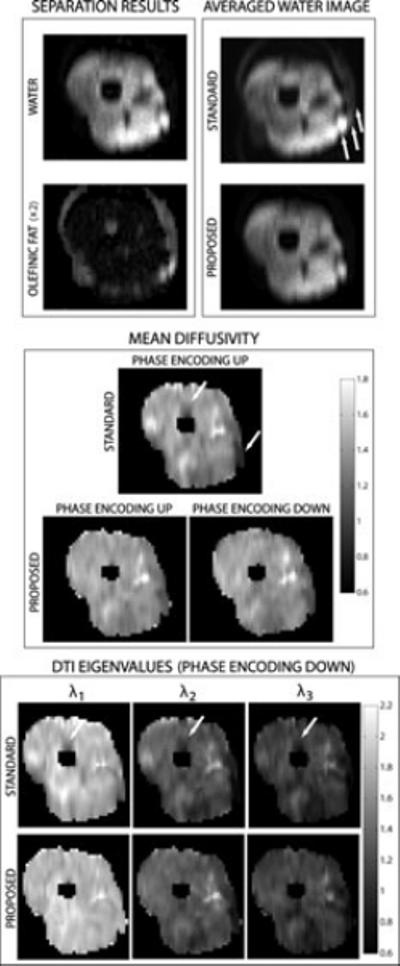
Results from a thigh dataset. (Top left) Example separated water and olefinic fat images. (Top right) Averaged images from standard acquisition, and averaged water images from proposed method (average was obtained over all diffusion directions). Note the presence of significant olefinic fat signal (ses arrows) from the subcutaneous layer. (Center) MD maps from a standard acquisition, as well as with the proposed method (for the proposed method, the images were acquired using both phase encoding directions). (Bottom) DTI eigenvalue maps obtained from the standard and proposed methods. In the parametric maps, arrows indicate MD distortions in the standard method, due to olefinic fat contamination.

DISCUSSION

In this work we have developed a novel method for removal of olefinic fat signal in DW-EPI. The proposed method is based on a combined approach for removal of aliphatic fat signals using conventional fat suppression, and removal of olefinic fat signals using a TE-shifted acquisition (20). Our algorithm seeks the ML estimates for water and olefinic fat at each voxel, and it can be viewed as an adaptation of the IDEAL algorithm (15, 30) in the case where the phase of the acquisitions is unreliable, i.e., where optimal separation is obtained from magnitude images (31, 30). The proposed method has been applied in vivo in healthy calf and thigh DW imaging applications. In these applications, the olefinic fat results in significant image contamination due to the presence of fat in the subcutaneous layer and the bone marrow region near the tissue of interest.

The proposed acquisition scheme involves replacing averages with multiple shifts of the refocusing pulses in a spin echo- or stimulated echo-based DW-EPI pulse sequence. Although the present scheme employed for the echo shifting has not been optimized, the implementation of echo shifts in a diffusion-weighted sequence places constraints on the sequence timing, affecting the minimum achievable TE. Specifically, the sequence timing needs to be such that it allows shifting the refocusing pulses (see Fig. 1) by nearly 5 ms at 3T resulting in an increase in the minimum TE by 10 ms. Furthermore, in addition to the signal loss associated with the slightly prolonged TE, the water/fat estimation process based on replacing averages with multiple echo shifts leads to a further theoretical SNR loss for the shifted sequence equal to $\sqrt{\mathrm{NSA}∕6}$ compared to the non-shifted sequence with 6 averages. Therefore, both the alteration of sequence timing and the water/fat estimation process result in an SNR loss relative to the non-echo shifted acquisition. Although this decrease in SNR can be considered as a drawback of the proposed technique, it should be noted that this SNR decrease is inherent to the ability to separate olefinic fat and water in TE-shifted diffusion-weighted acquisitions. For good NSA (that can be achieved for high water/fat ratios with the proposed TE shifts as shown in Fig. 3), the SNR loss will basically depend on the increased minimum TE and the tissue T2. However, the SNR loss of the water signal induced by the echo shifting is lower than the SNR loss of the water signal induced by using STIR to suppress olefinic fat. Specifically, if we assume T1/T2 of muscle are 1420/32 ms (32) and the T1 of olefinic fat is 537 ms (33), the required increase in the TE (by 10 ms) of the echo-shifted acquisition results in a water SNR reduction by 27% and the T1 relaxation over the inversion recovery interval (372 ms) in STIR acquisition results in a water SNR reduction by 46%.

Three important assumptions are made in the present signal model. First, even though the phase in DW-EPI images is inconsistent (so no standard water/fat separation is possible), the phase inconsistencies are assumed to be spatially smooth, so that the relative phase between olefinic fat and water signals (which originate from nearly 4 voxels apart with the current acquisition parameters) is consistent. Altough motion and eddy current effects could affect the relative phase between olefinic fat and water, the approximation of consistent relative phase appears to be good enough in the presented phantom and in vivo data to enable separation using the proposed signal model (Eq. [1]). Second, the proposed method assumes the presence of two components in the signal (water and olefinic fat), and thus, requires the use of standard fat suppression techniques to remove the aliphatic fat components. In the case of incomplete aliphatic fat suppression, the proposed method has demonstrated a moderate ability to remove residual aliphatic fat signal from the water image during the water/olefinic fat separation stage. However, a thorough characterization of this ability (e.g., to determine what levels of residual aliphatic fat signal can be tolerated) is outside the scope of this work. Third, the geometric distortions have been corrected based on the fieldmap derived by the water/fat separation results from the b=0 calf/thigh EPI images, where distortions are not severe. In regions with severe susceptibility differences, the distortion correction would require faster EPI readouts or the acquisition of a fieldmap from a separate scan.

An alternative approach to reduce the chemical shift artifact in EPI acquisitions is the reduction of the gradient readout duration by employing parallel imaging or reduced-FOV techniques. Although these techniques reduce the spatial misregistration shift of the olefinic fat (34), they do not remove the olefinic fat signal. Therefore, they can reduce the olefinic fat shift in regions close to the subcutaneous fat and the bone marrow, but they cannot suppress the olefinic fat signal in fatty infiltrated muscles and in the fascia of the intermuscular fat, where the discrimination of water from fat is more challenging. However, complete fat suppression is essential in tissues with increased fat content to monitor the mobility of the water molecules only (6). The proposed technique has the advantage of enabling water and olefinic fat separation. Therefore, the proposed technique might be preferable for suppression of the olefinic fat signal in diseased muscular tissues with homogeneous fatty infiltration or increased intermuscular adipose tissue.

The present method could be further refined both in terms of the signal model and the employed computational framework. In principle, it might be possible to perform separation jointly for all diffusion directions (e.g., by assuming isotropic diffusion of the olefinic protons). However, we have observed that the relative phase between water and olefinic fat depends on the diffusion direction, which complicates joint fitting. The causes for the varying relative phase are currently under investigation. Additionally, the proposed method uses the same initial guess for the water and olefinic fat amplitudes for all diffusion directions. In principle, it might be possible to introduce more sophisticated prior knowledge about the fiber directions in the initialization, but the proposed method is simpler and has shown to work well in the acquired data. Furthermore, the current, non-optimized Matlab implementation of the proposed method takes 60 seconds for each diffusion direction on an desktop computer based on a 3.16 GHz Intel Xeon processor. Additional accelerations are certainly possible, e.g., by switching to a compiled programming language and parallelizing the code (taking advantage of the essentially voxel-independent algorithm).

CONCLUSION

This paper introduced a simple method for the removal of olefinic fat contamination from DW-EPI acquisitions. The proposed method is based on a TE-shifted acquisition and can be viewed as an adaptation of standard water/fat separation algorithms to the case where image phase is unreliable. The method has been validated using data collected from a water/fat phantom and from the calf and thigh muscles of healthy volunteers. Potential applications of the proposed method include extracerebral DW imaging of tissues surrounded by significant amounts of fat and of tissues containing significant amounts of fat because of fatty infiltration.

APPENDIX. Water/Fat Separation from b=0 EPI Images

The complex-valued signal measured at an individual voxel in an EPI acquisition with TE shift ΔTE_n can be modeled similarly to Eq. [1]:

$$s(\mathrm{x};\Delta {\mathrm{TE}}_n)=W\left(\mathrm{x}\right)e^{j2\pi f_{\mathrm{B}}\left(\mathrm{x}\right)\Delta {\mathrm{TE}}_n}+F(\mathrm{x}-\Delta \mathrm{x})e^{j2\pi \left(f_{\mathrm{B}}\right(\mathrm{x}-\Delta \mathrm{x})+f_F)\Delta {\mathrm{TE}}_n}+\nu ,$$ [5]

where W(x) and F(x – Δx) are the complex-valued amplitudes of water and fat, respectively, observed at location x. The difference of Eq. [5] with that employed in the standard chemical-shift encoded water/fat separation (12, 13, 15) is that the olefinic fat observed at location x originates from location x – Δx due to the CSA, and is affected by the B₀ field at location x – Δx. In the EPI acquisitions used in this work, Δx was approximately 4 pixels along the phase-encoding direction. In standard water/fat separation methods (e.g., based on non-EPI cartesian acquisitions), Δx is usually less than 1 pixel and is typically neglected. Note that the shift Δx is considered fixed in this work, which assumes a relatively slow spatial variation of the field map.

In this work, we used a modified version of the method described in (22) for joint estimation of the field map and water/fat images. The proposed method is based on finding the field map, water, and fat images that best fit the acquired data in the least-squares (LS) sense, i.e., minimizing at each voxel:

$$\begin{array}{cc}\hfill R_0(& W\left(\mathrm{x}\right),F(\mathrm{x}-\Delta \mathrm{x}),f_{\mathrm{B}}(\mathrm{x}-\Delta \mathrm{x});\mathrm{s}\left(\mathrm{x}\right))=\hfill \\ \hfill & {\Sigma }_{\Delta {\mathrm{TE}}_n}{\mid s(\mathrm{x};\Delta {\mathrm{TE}}_n)-\left(W\right(\mathrm{x})e^{j2\pi f_{\mathrm{B}}\left(\mathrm{x}\right)\Delta {\mathrm{TE}}_n}+F(\mathrm{x}-\Delta \mathrm{x}\left)e^{j2\pi \left(f_{\mathrm{B}}\right(\mathrm{x}-\Delta \mathrm{x})+f_F)\Delta {\mathrm{TE}}_n}\right)\mid }^2.\hfill \end{array}$$ [6]

However, simply minimizing R₀ in Eq. [6] is known to be problematic due to the presence of ambiguities and noise (35, 22). This problem can be addressed by imposing smoothness in the field map. Our modified method seeks the solution that minimizes the regularized LS cost function:

$$\sum _{\mathrm{x}}{R}_0\left(W\right(\mathrm{x}),F(\mathrm{x}-\Delta \mathrm{x}),f_{\mathrm{B}}(\mathrm{x}),f_{\mathrm{B}}(\mathrm{x}-\Delta \mathrm{x});\mathrm{s}(\mathrm{x}\left)\right)+\sum _{\mathrm{x}}\sum _{{\mathrm{x}}^{\prime }\in {\delta }_{\mathrm{x}}}w(\mathrm{x},{\mathrm{x}}^{\prime })\left(f_{\mathrm{B}}\left(\mathrm{x}\right)-f_{\mathrm{B}}\left({\mathrm{x}}^{\prime }\right)\right),$$ [7]

where x traverses all voxels in the image, and R₀(W(x), F(x–Δx), f_B(x), f_B(x–Δx); s(x)) represents the fit residue at voxel x, and δ_x is the neighborhood of voxel x (its 8 surrounding voxels in this work). The first term in Eq. [7] imposes data fidelity, whereas the second (regularization) term imposes field map smoothness. The regularization parameters w(x, x’) are chosen as in (36).

As described in (22), the linear parameters {W(x), F(x–Δx)} can be removed from the formulation by reformulating the residue:

$$R\left(f_{\mathrm{B}}\right(\mathrm{x}),f_{\mathrm{B}}(\mathrm{x}-\Delta \mathrm{x});\mathrm{s}(\mathrm{x}\left)\right)=\underset{W\left(\mathrm{x}\right),F(\mathrm{x}-\Delta \mathrm{x})}{\mathrm{argmin}}{R}_0\left(W\right(\mathrm{x}),F(\mathrm{x}-\Delta \mathrm{x}),f_{\mathrm{B}}(\mathrm{x}),f_{\mathrm{B}}(\mathrm{x}-\Delta \mathrm{x});\mathrm{s}(\mathrm{x}\left)\right).$$ [8]

This modification leads to an equivalent version of Eq. [7], which can be now expressed in terms of R (i.e., only in terms of the field map), as minimizing

$$\sum _{\mathrm{x}}R\left(f_{\mathrm{B}}\right(\mathrm{x}),f_{\mathrm{B}}(\mathrm{x}-\Delta \mathrm{x});\mathrm{s}(\mathrm{x}\left)\right)+\sum _{\mathrm{x}}\sum _{{\mathrm{x}}^{\prime }\in {\delta }_{\mathrm{x}}}w(\mathrm{x},{\mathrm{x}}^{\prime }){\left(f_{\mathrm{B}}\left(\mathrm{x}\right)-f_{\mathrm{B}}\left({\mathrm{x}}^{\prime }\right)\right)}^2.$$ [9]

The minimization problem in Eq. [9] is then solved by iteratively updating the field map one voxel at a time, as proposed in (22). This simple optimization procedure may result in convergence to a local minimum in the presence of large field inhomogeities, so a reasonable initialization is necessary. In this work, we initialize the field map with the estimates from the graph cut-based method proposed in (36) (where the CSA is not taken into account).