Communication: Turnover behavior of effective mobility in a tube with periodic entropy potential

Abstract

Using Brownian dynamics simulations, we study the effective mobility and diffusion coefficient of a point particle in a tube formed from identical compartments of varying diameter, as functions of the driving force applied along the tube axis. Our primary focus is on how the driving force dependences of these transport coefficients are modified by the changes in the compartment shape. In addition to monotonically increasing or decreasing behavior of the effective mobility in periodic entropy potentials reported earlier, we now show that the effective mobility can even be nonmonotonic in the driving force.

Transport in systems of varying geometry has been actively studied in recent years^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} since such systems are ubiquitous in nature and technology. When the geometry variation is periodic along a certain direction, transport in this direction is effectively one-dimensional. Motion of a single particle in such a system on sufficiently large time scales, when the particle displacement significantly exceeds the period, can be characterized by effective transport coefficients.

The effective mobility μ_eff(F) of a point Brownian particle in a tube of periodically varying diameter is a function of the driving force Fdirected along the tube axis. Since periodic entropy barriers slow down the particle propagation, the effective mobility never exceeds the mobility μ₀ in space with no constraints. However, the dependence of μ_eff(F) on the driving force may be qualitatively different for different shapes of the periodic compartments that form the tube. In tubes of a smoothly varying diameter, the effective mobility monotonically increases with F from μ_eff(0) < μ₀ to μ_eff(∞) = μ₀ [Refs. ^{5a, 7a, 11c, 11d}]. In contrast, in tubes of an abruptly changing diameter μ_eff(F) decreases with the increasing driving force.^{8a, 11d}

Studying the effect of the compartment shape on the F-dependence of the effective mobility, we found that the dependence can even be nonmonotonic, namely, μ_eff(F) first decreases with the force, reaches a minimum, and then increases to approach μ₀ as F → ∞. As might be expected, the driving force dependence of the effective diffusion coefficient of the particle is also sensitive to the compartment shape. In this note, we report on a detailed study of the variation of the F-dependences of the particle effective mobility and diffusion coefficient due to variation of the shape of the tube-forming compartments.

The abovementioned nonmonotonic behavior of the effective mobility should not be confused with the nonmonotonic behavior reported recently in Ref. 5c, where the effect is due the fact that the external force has a component perpendicular to the x-direction along which the system is periodic. This component creates a periodic energy potential that affects the particle motion in the x-direction as the geometric constraints do. As a consequence, the increase of the external force leads not only to the increase of the driving force in the x-direction, but also to the increase in the height of the barriers that separate the wells of the energy potential. At certain angles between the external force and the x-axis, the interplay between the driving force, the force-dependent energy potential, and the entropy potential leads to a non-monotonic bell-shaped dependence of the mobility on the external force.

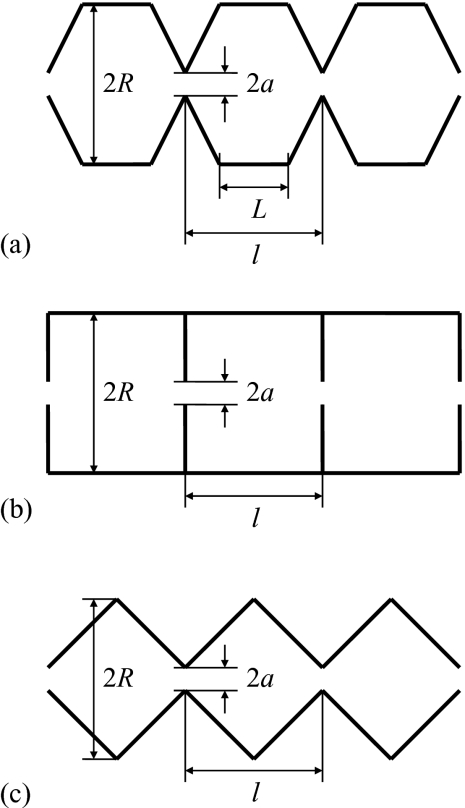
Consider a tube of periodically varying geometry schematically shown in Fig. 1a. The tube is formed by identical compartments of length l that are connected by circular openings of radius a. In the central part of the compartment there is a symmetrically located cylindrical segment of length L and radius R, L ⩽ l and a ⩽ R. This segment is connected to the left and right openings by two identical but oppositely oriented conical segments of length (l − L)/2 and the radius variation rate λ, λ = 2(R − a)/(l − L), which is a monotonically increasing function of the length of the cylindrical segment L. In the limiting case of L = l the rate goes to infinity, λ = ∞; in the opposite limiting case of L = 0 the rate is λ₀ = 2(R − a)/l. These two cases are shown in Figs. 1b, 1c. The first corresponds to a regular cylindrical tube separated into identical compartments by infinitely thin partitions with circular apertures at their centers, and the second corresponds to a tube constructed from purely conical segments. The rate λ, which will be used as the parameter to vary, determines the slope of the conical parts of the tube at fixed values of l, a, and R. As λ goes from λ = λ₀ to λ = ∞, the tube transforms from the one with a smoothly varying diameter to that of an abruptly changing diameter.

Figure 1.

Schematic representation of tubes of periodically varying diameter formed by identical compartments. In general, the compartment contains a cylindrical segment symmetrically located in its center, which is connected to the left and right openings by conical segments (panel a). Choosing the center of the compartment as the origin and directing the x-axis along the centerline of the tube, we can write the x-dependence of the tube radius within the compartment as r(x) = R, −L/2 ⩽ x ⩽ L/2, r(x) = R − λ(x − L/2), L/2 ⩽ x ⩽ l/2, r(x) = R + λ(x + L/2), −l/2 ⩽ x ⩽ −L/2. The limiting cases of tubes formed by purely cylindrical and purely conical compartments are shown in panels b and c.

The goal of the present work is to study variations of the F-dependences of the particle effective mobility and diffusion coefficient as functions of λ, μ_eff(F|λ) and D_eff(F|λ), λ₀ < λ < ∞. For tubes formed by purely cylindrical (λ = ∞) and conical (λ = λ₀) compartments, the asymptotic behaviors of μ_eff(F|λ) and D_eff(F|λ) at small and large F are known and given by^{11b, 11c}

$$\frac{{\mu }_{\mathrm{eff}}\left(0|\lambda \right)}{{\mu }_0}=\frac{D_{\mathrm{eff}}\left(0|\lambda \right)}{D_0}=\left\{\begin{array}{c}{\displaystyle \frac{\left(l∕R\right)\nu f\left(\nu \right)}{\left(l∕R\right)\nu f\left(\nu \right)+\pi ∕2},\lambda =\infty ,}\\ {\displaystyle \frac{3\nu }{\left(1+\nu +{\nu }^2\right)\sqrt{1+{\lambda }_0^2}},\lambda ={\lambda }_0,}\end{array}\right.$$ (1)

$${\left.\frac{{\mu }_{\mathrm{eff}}\left(F|\lambda \right)}{{\mu }_0}\right|}_{F\to \infty }=\left\{\begin{array}{c}{\nu }^2,\lambda =\infty ,\\ 1,\lambda ={\lambda }_0,\end{array}\right.$$ (2)

$${\left.\frac{D_{\mathrm{eff}}\left(F|\lambda \right)}{D_0}\right|}_{F\to \infty }=\left\{\begin{array}{c}{\displaystyle \frac{{\nu }^4}{4}\left[\ln \left(\frac{1}{{\nu }^2}\right)-1+{\nu }^2\right]{\left(\beta FR\right)}^2,\lambda =\infty ,}\\ {\displaystyle 1,\lambda ={\lambda }_0.}\end{array}\right.$$ (3)

Here ν = a/R, f(ν) = (1 + 1.37ν − 0.37ν⁴)/(1 − ν²)², D₀ is the particle diffusion coefficient in space with no constraints, and β = 1/(k_BT), where k_B is the Boltzmann constant and T is the absolute temperature. In addition, it is assumed that l ⩾ 2R so that λ₀ ⩽ 1.

The relations μ_eff(∞|λ₀)/μ₀ = D_eff(∞|λ₀)/D₀ = 1 are the consequence of the fact that in an alternating conical tube [Fig. 1c], as in any tube of smoothly varying diameter [Fig. 1a], at sufficiently large driving force collisions with the walls focus the particle into the cylinder connecting the openings. As a result, as F → ∞, the particle is unaware of the entropy wells and barriers since it spends all the time in this cylinder. Therefore, its effective mobility and diffusion coefficient approach their values in a purely cylindrical tube, μ₀ and D₀, respectively. This is not true for the tube formed by cylindrical compartments with partitions orthogonal to the tube axis (λ = ∞). Here the radial distribution of the particle is uniform and equal to 1/(πR²) at all F [Ref. ^11c]. The reason is that in this case collisions with the partitions do not affect the radial distribution since they do not focus the particle into the center of the tube, as they do in the case of smoothly varying diameter, corresponding to finite values of λ. This is why the large F asymptotic behaviors of μ_eff(F|∞) and D_eff(F|∞) differ from μ₀ and D₀, respectively.

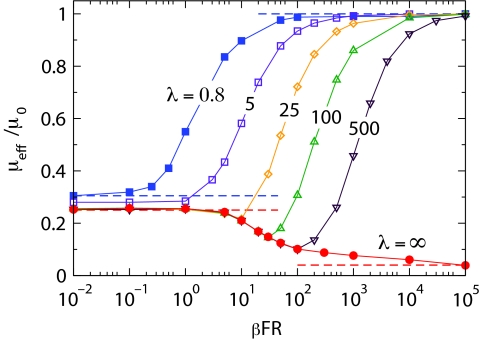
To find μ_eff(F|λ) and D_eff(F|λ), we ran Brownian dynamics simulations. Main results are shown in Figs. 23. At a fixed value of the driving force, the effective mobility monotonically decreases from μ_eff(F|λ₀) to μ_eff(F|∞) as λ increases from λ₀ to infinity (Fig. 2). As has been mentioned earlier, the F-dependences of μ_eff(F|λ₀) and μ_eff(F|∞) are qualitatively different. The former monotonically increases with F from μ_eff(0|λ₀) to μ_eff(∞|λ₀) = μ₀, while the latter monotonically decreases from μ_eff(0|∞) < μ_eff(0|λ₀) to μ_eff(∞|∞) = ν²μ₀, Eq. 2. The ratio of the asymptotic values of the effective mobility is equal to 1/ν² = R²/a². At not too large λ, the dependence of the effective mobility on the driving force follows the same pattern as μ_eff(F|λ₀): the effective mobility monotonically increases with the force. The most interesting, nonmonotonic behavior of μ_eff(F|λ) takes place at sufficiently large, but finite values of λ. In this case, the effective mobility is close to μ_eff(F|∞) and, hence, decreases with F when F is not large. However, at larger values of the force, μ_eff(F|λ) starts to increase and approaches μ₀ as F → ∞. The reason is that at finite λ and large enough F, the particle gets localized in the cylinder connecting the openings. As a consequence, the particle mobility tends to its value in a purely cylindrical tube μ₀. Similar non-monotonic behavior of the effective mobility was recently reported for a two-dimensional channel with periodically modulated boundaries in Ref. 8b.

Figure 2.

Effective mobility as a function of the driving force at different values of the radius variation rate λ = 0.8, 5, 25, 100, 500, and ∞, and a = 0.2R, l = 2R, and L = (1 − 0.8/λ) l. Thin solid curves are drawn through the symbols that represent our numerical results. Thick dashed lines show asymptotic behaviors, Eqs. 1, 2.

Figure 3.

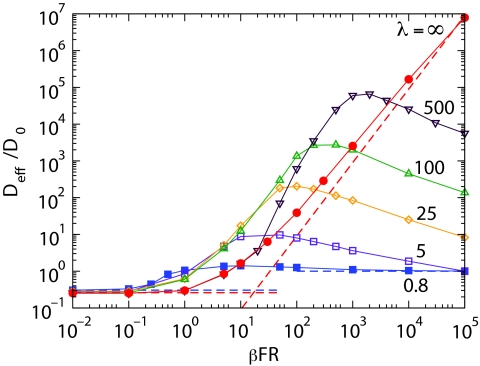
Effective diffusion coefficient as a function of the driving force at different values of the radius variation rate λ = 0.8, 5, 25, 100, 500, and ∞, and a = 0.2R, l = 2R, and L = (1 − 0.8/λ) l. Thin solid curves are drawn through the symbols that represent our numerical results. Thick dashed lines show asymptotic behaviors, Eqs. 1, 3.

The F-dependences of the effective diffusion coefficient at different values of λ are presented in Fig. 3. When λ is finite, all curves follow the same pattern as D_eff(F|λ₀): the effective diffusion coefficient first increases with F, reaches a maximum, and then decreases, approaching D₀ as F → ∞. As λ increases, the maximum value of D_eff(F|λ) becomes larger and larger, and the position of the maximum shifts to higher values of the driving force. At λ = ∞ the effective diffusion coefficient diverges as F → ∞. The large-F asymptotic behavior of D_eff(F|∞) is given in Eq. 3. At small F the effective diffusion coefficient is monotonic in λ. For larger values of the driving force, D_eff(F|λ) becomes a nonmonotonic function of λ.

In summary, in the present note we study the F-dependences of the effective mobility and diffusion coefficient in the compartmentalized tube schematically shown in Fig. 1a. As the length L of the cylindrical segment located in the center of the compartment varies from the tube period l to zero, the compartment shape changes from purely cylindrical to purely conical. Correspondingly, the radius variation rate of the conical segments, λ = 2(R − a)/(l − L), decreases from λ = ∞ to λ₀ = 2(R − a)/l. Both μ_eff(F|λ) and D_eff(F|λ) show qualitatively different behaviors as functions of F in the two limiting cases: μ_eff(F|λ₀) monotonically increases with F while μ_eff(F|∞) monotonically decreases as F increases from zero to infinity; D_eff(F|λ₀) is a nonmonotonic function of F while D_eff(F|∞) monotonically increases with F and diverges as F² as F → ∞, whereas D_eff(∞|λ₀) is finite. Dependences μ_eff(F|λ) and D_eff(F|λ) considered as functions of λ smoothly go between the two limits as shown in Figs. 23. At sufficiently large λ, μ_eff(F|λ) is nonmonotonic, it first decreases with F, following the same pattern as μ_eff(F|∞) at not too large F, and then increases and approaches the same limiting value μ₀ as μ_eff(F|λ₀). This quite unusual behavior of the effective mobility is one of the major results of the present communication.