Similarity evaluation in a content-based image retrieval (CBIR) CADx system for characterization of breast masses on ultrasound images

Abstract

Purpose: The authors are developing a content-based image retrieval (CBIR) CADx system to assist radiologists in characterization of breast masses on ultrasound images. In this study, the authors compared seven similarity measures to be considered for the CBIR system. The similarity between the query and the retrieved masses was evaluated based on radiologists’ visual similarity assessments.

Methods: The CADx system retrieves masses that are similar to a query mass from a reference library based on computer-extracted features using a k-nearest neighbor (k-NN) approach. Among seven similarity measures evaluated for the CBIR system, four similarity measures including linear discriminant analysis (LDA), Bayesian neural network (BNN), cosine similarity measure (Cos), and Euclidean distance (ED) similarity measure were compared by radiologists’ visual assessment. For LDA and BNN, the features of a query mass were combined first into a malignancy score and then masses with similar scores were retrieved. For Cos and ED, similar masses were retrieved based on the normalized dot product and the Euclidean distance, respectively, between two feature vectors. For the observer study, three most similar masses were retrieved for a given query mass with each method. All query-retrieved mass pairs were mixed and presented to the radiologists in random order. Three Mammography Quality Standards Act (MQSA) radiologists rated the similarity between each pair using a nine-point similarity scale (1=very dissimilar, 9=very similar). The accuracy of the CBIR CADx system using the different similarity measures to characterize malignant and benign masses was evaluated by ROC analysis.

Results: The BNN measure used with the k-NN classifier provided slightly higher performance for classification of malignant and benign masses (A_z values of 0.87) than those with the LDA, Cos, and ED measures (A_z of 0.86, 0.84, and 0.81, respectively). The average similarity ratings of all radiologists for LDA, BNN, Cos, and ED were 4.71, 4.95, 5.18, and 5.32, respectively. The k-NN with the ED measures retrieved masses of significantly higher similarity (p<0.008) than LDA and BNN.

Conclusions: Similarity measures using the resemblance of individual features in the multidimensional feature space can retrieve visually more similar masses than similarity measures using the resemblance of the classifier scores. A CBIR system that can most effectively retrieve similar masses to the query may not have the best A_z.

INTRODUCTION

The most effective way to reduce mortality from breast cancer is to treat the disease at an early stage. However, earlier treatment requires early diagnosis, which, in turn, requires an accurate and reliable screening and diagnostic procedure. Currently, mammography is the standard screening tool for detection of suspicious lesions. Ultrasonography (US) has been shown to be an effective modality for characterizing breast masses as malignant or benign.^{1, 2, 3} Stavros et al.³ achieved a sensitivity of 98.4% and a specificity of 67.8% by using sonography to distinguish 750 benign and malignant lesions. Taylor et al.⁴ demonstrated that the combination of US with mammography increased the specificity from 51.4% to 63.8%, the positive predictive value (PPV) from 48% to 55.3%, and the sensitivity from 97.1% to 97.9% in characterizing 761 breast masses. Real-time US is complementary to mammography in the evaluation of breast masses. In most breast imaging clinics in the United States, mammography and sonography are available for diagnostic work-up of breast masses. However, the sonographic technique described in the above studies^{1, 2, 3, 4} required extensive real-time evaluation by an experienced interpreter; this may not be practical for most clinical settings. In addition, breast cancer appearance is so heterogeneous that there is a considerable overlap in the sonographic characteristics between malignant and benign lesions. Many indeterminate solid masses are recommended for biopsy. Biopsy increases health care costs and causes anxiety and possible morbidity to the patients. Therefore, it is advantageous to improve the accuracy of noninvasive methods of distinguishing malignant from benign masses in the breast. Moreover, most biopsies might be avoidable because the current PPV for cases that undergo biopsy is about 20%–40%.^{5, 6, 7, 8, 9, 10, 11} The PPV value is low because as stated above many benign solid masses are recommended for biopsy.

Studies have shown that computer-aided diagnosis (CADx) can assist radiologists in making correct decisions by providing a second opinion.^{12, 13, 14, 15} Accordingly, CADx systems have been developed to characterize breast masses on US images as malignant or benign. Chen et al.¹⁶ used the autocorrelation feature extracted from a region of interest (ROI) containing the mass in an artificial neural network (ANN) to classify 140 pathologically proven solid nodules on US images. The area A_z under the receiver operating characteristic (ROC) curve was 0.96. Horsch et al.¹⁷ evaluated their CADx system on a database of 400 cases. The average A_z value of 11 independent experiments was 0.87. Sahiner et al.¹⁸ investigated computerized characterization of breast masses on 3D US volumetric images. By analyzing 102 biopsy-proven masses, they achieved an A_z value of 0.92. Joo et al.¹⁹ segmented the masses in a preselected ROI using an automated algorithm. An experienced radiologist reviewed and corrected the segmentation result, from which five morphological US features were extracted. An ANN classifier was trained to characterize the masses using 584 histologically confirmed cases and tested on an independent data set of 266 cases. The test A_z value was 0.98. Cui et al.²⁰ designed an automated method to segment breast masses on ultrasound images, achieving A_z values between 0.88 and 0.92.

Radiologists learn to interpret imaging features and to differentiate malignant and benign lesions by complex methods. This includes didactic teaching, clinical reading with more experienced readers, case review of lesions recommended for work-up, and biopsy. Breast radiologists are required by Mammography Quality Standards Act (MQSA) to track their positive interpretations with final pathology reports. Radiologists develop a case pattern recognition memory of specific appearances of lesions and, in fact, some of these have been labeled “Aunt Minnie”^{21, 22} to show the analogy to human recognition of facial features. Radiologists rely on their knowledge and recollection of clinically similar cases as references to make inferences for diagnostic decisions on new cases. Advances in digital technologies for computing, networking, and database storage have enabled automated search for clinically relevant and visually similar references in large medical image databases. The development of content-based image retrieval (CBIR) technology and schemes has therefore attracted wide research interest in medical imaging areas.^{23, 24} Several groups are developing methods to incorporate CBIR approaches into image database systems.^{25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37}

We are developing a CBIR system for CADx of masses in US images. A CBIR system is expected to provide additional information to the radiologist by retrieving lesions similar to the mass of interest (query mass) from the reference library and presenting the known pathology of the retrieved masses as references to assist the radiologist in making diagnosis decision of the query mass. In addition, the likelihood of malignancy of the query mass can be estimated by the CBIR system from the proportion of retrieved malignant and benign masses if the reference library is statistically representative of the population and the prevalence is properly taken into account.³⁸ Development of a CBIR system is a complex process for which many questions have yet to be answered. For example, in the image retrieval step, what similarity measure (SM) should be used and whether a similarity measure using a merged classifier score (output-score-based, see Fig. 1) or one using individual image features (input-feature-based, see Fig. 2) would be more effective in identifying similar masses; in the step of estimating the likelihood of malignancy of the lesion, whether the CBIR approach would be more accurate than the conventional classifier approach. In this study, we focused on seeking understanding of these fundamental issues by comparing seven similarity measures, two retrieval approaches (output-score-based vs input-feature-based), the accuracy of two computerized classification methods (conventional vs CBIR), and evaluating the performance of four representative similarity measures in retrieving similar masses by radiologists’ visual assessment. Although the issues that we could explore in one study are only a small fraction of those involved in the entire CBIR process, it is expected that this investigation will provide useful information for the design of a robust CBIR system for breast masses in US images.

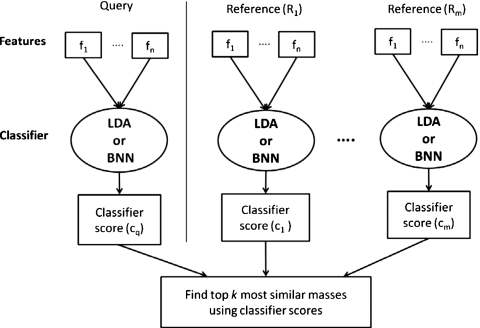
Figure 1.

The framework of output-score-based similarity measures. Linear Discriminant Analysis (LDA) and Baysiean Neural Network (BNN) were used in the current study to merge the multidimensional features into a classifier output score.

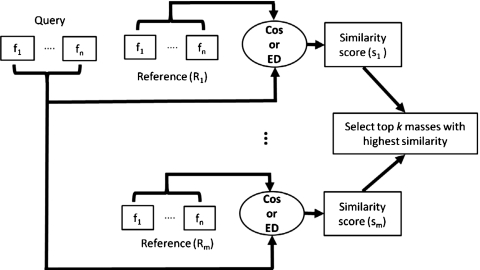
Figure 2.

The framework of input-feature-based similarity measures. Cosine distance measure (Cos) and Euclidean distance measure (ED) were chosen for the observer similarity study.

MATERIALS AND METHOD

Data set

A data set was collected with the Institutional Review Board (IRB) approval from the files of patients who had undergone breast US imaging in the Department of Radiology at the University of Michigan. All US images were acquired using a GE Logiq 700 scanner with an M12 linear array transducer by radiologists. For this study, US images of 96 malignant and 154 benign breast masses from 250 patients were obtained. The pathology of all masses was biopsy-proven. The average patient age was 52 yr (range: 14–95 yr). From the available breast US images for these masses, a total of 488 images was selected as described below.

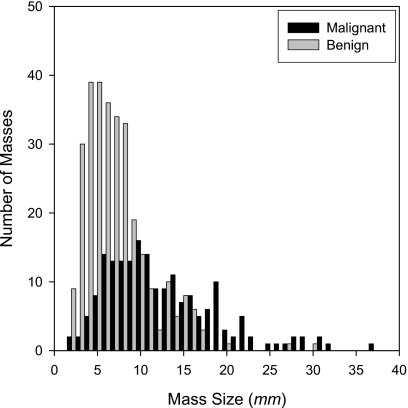
We randomly partitioned the patient cases into two subsets P1 and P2, which included 129 and 121 masses, respectively. For the set P1, after reading the pathology and radiology reports, an MQSA radiologist (R1) selected US images corresponding to the biopsy-proven mass. The radiologist was asked to select two optional orthogonal US views for each mass, where they will see the mass the best. However, for some masses, two orthogonal views were not available so that only one view was selected. The radiologist marked the mass location on every selected US image. The radiologist also measured the longest diameter of each mass using a graphic user interface. A second MQSA radiologist (R2) followed the same procedure to select and read images in the set P2. P1 included 258 images from 55 malignant and 74 benign masses, and P2 included 230 images from 41 malignant and 80 benign masses. Figure 3 shows a histogram of the mass size for both P1 and P2. The average longest diameters of the malignant and benign masses were 12.5 and 7.2 mm, respectively (total range: 1.8–37.0 mm). Both R1 and R2 provided the approximate center of the mass in each image of the P1 and P2 subsets.

Figure 3.

Histogram of mass size (longest diameter) in the entire (P1+P2) data set.

Feature extraction and selection

To segment breast masses on ultrasound images, an automated method designed by Cui et al.²⁰ was used. This method automatically estimated an initial contour based on a manually identified point approximately at the mass center using a two-stage active contour model. For every image in the P1 and P2 data sets, two different computer segmentations were obtained by using the approximate mass centers from radiologists R1 and R2.

For the design of our CBIR system, we extracted morphological features and texture features based on the automated segmentation. The taller-than-wide shape of a sonographic mass is a good indication of malignancy.³ This characteristic was defined as the width-to-height ratio (WTHR), i.e., the ratio of the widest cross section of the automatically segmented lesion shape to the tallest cross section in the segmented mass. Another feature that has been reported to be useful for differentiation of malignant and benign masses is posterior shadowing feature (PSF), which we described as the normalized average gray-level difference between the interior of the segmented mass and the darkest posterior strip.¹⁸ The texture features used in this study were extracted from the spatial gray-level dependence (SGLD) matrices or co-occurrence matrices. The (i,j)th element of the co-occurrence matrix is the relative frequency with which two pixels, one with gray level i and the other with gray level j, separated by a pixel pair distance d in a direction θ, occur in the image. Six texture feature measures—information measures of correlations 1 and 2 (IMC1 and IMC2), difference entropy (DFE), entropy (ENT), energy (ENE), and sum entropy (SME)—were extracted. The mathematical definitions of these features can be found in literature.³⁹ Since texture features extracted from the mass margins are effective for classification,⁴⁰ the texture features in this study were extracted from two disk-shaped regions containing the boundary of each mass, as well as presumably mass and normal tissue adjacent to the boundary of the mass. The areas for the upper and lower disk-shaped regions were chosen to be equal, and their sum was equal to the area of the segmented mass. The pixel pair distances used for SGLD matrix construction were chosen to be d=2, 4, and 6. Two pixel pair directions, θ=0° and θ=90°, were evaluated for each d in both regions. The number of SGLD matrices constructed for each disk-shaped region was therefore 6, and the number of texture features extracted from an image containing the segmented mass was 72 (six features extracted from six SGLD matrices in the upper and the lower disk-shaped regions). The feature extraction methods have been described in greater detail previously.¹⁸ Each feature was normalized from 0 to 1, based on its own distribution in the training data set.

A linear discriminant analysis (LDA) classifier⁴¹ with stepwise feature selection was designed to classify the masses as malignant or benign using a twofold cross validation method. Each of the two data subsets P1 and P2 described in Sec. 2A served once as the training and once as the test partition in the two cycles of twofold cross validation. The stepwise feature selection process uses three threshold values, F_in, F_out, and tolerance, based on the F statistics, for feature entry, feature elimination, and tolerance of correlation for feature selection, respectively. Since the appropriate values of these thresholds were not known a priori, they were estimated from the training set using a leave-one-case-out resampling method and simplex optimization, as described previously.⁴² The selected subset of features is used as the components of a feature vector to characterize each mass. Table 1 shows the selected feature sets for the two cycles of twofold cross validation in this study, for the mass center identified by R1 and R2, respectively. The notation of each texture feature includes the information of direction, distance, and region. For example, IMC1_90_2L is IMC1 feature at direction θ=90°, pixel pair distance d=2, and lower disk-shaped region.

Table 1.

Selected feature sets for the four combinations of test set, training set, and centroid locations.

	Test P1 (train P2), centroids by R1	Test P2 (train P1), centroids by R1	Test P1 (train P2), centroids by R2	Test P2 (train P1), centroids by R2
Selected features	WTHR	WTHR	WTHR	WTHR
	PSF	PSF	PSF	PSF
	IMC1_0_4L	IMC1_0_2L	IMC1_0_4L	IMC1_90_6L
	IMC1_90_2L	IMC1_90_2L	IMC1_0_4U	IMC2_90_6L
	IMC2_90_4U	IMC2_0_4L	IMC1_90_2L	DFE_0_4U
	IMC2_90_6U	IMC2_0_6L	IMC1_90_6U	DFE_0_6L
			IMC2_0_2L	DFE_90_2L
			ENE_90_6L	DFE_90_2U
				ENT_0_4U

Retrieval methods

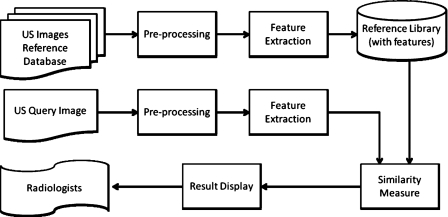
Figure 4 shows the flowchart of our CBIR scheme. The masses on the US images from the reference database are segmented and the feature vectors characterizing the masses constitute a reference feature data set stored in the reference library. When a query sample is submitted to the CBIR system to search for similar masses, the system first extracts the same feature vector as that of the reference library from this query sample. Using similarity measures, the similarity scores between the feature vectors of the query sample and those of the reference library are then computed. The system ranks the obtained similarity scores and retrieves the reference library samples that are most similar to the query sample. In this study, we evaluated the effectiveness of the CBIR system in the retrieval of similar masses by an observer study in which radiologists examined the similarities between the query and the retrieved samples by visual assessment. Because our current reference library is still small, the CBIR system can only estimate a relative malignancy rating instead of the probability of malignancy for the query mass. The capability of the system in characterizing malignant and benign masses was evaluated by ROC analysis of the relative malignancy rating estimated from the retrieved samples.

Figure 4.

The framework for our content-based image retrieval system.

We compared seven SMs used in our CBIR system. Five SMs are input-feature-based [Euclidean distance (ED), Manhattan distance, distance-weighted k-NN, correlation, and cosine measure] and two SMs are output-score-based [incorporating LDA and Bayesian neural network (BNN) classifiers]. For the input-feature-based SM, the features of a query mass are applied directly to the feature space of the samples in the reference library and the similarity between the individual features of the query mass and those of a reference mass are combined into an SM score for the pair (Fig. 2). For the output-score-based SM, the features of a query mass are combined first into a classifier score by LDA or BNN, which is then applied to the classifier scores of the samples in the reference library to calculate the SM scores (Fig. 1). In our CBIR system, the k-nearest neighbor (k-NN) algorithm is used to retrieve k reference masses that have the highest SM scores with the query mass. The seven SMs are described below.

Euclidean distance

The SM score is obtained by applying the ED between a query mass and each reference mass in a multidimensional feature space,

$$d\left(q,r_i\right)=\sqrt{\sum _{j=1}^n{\left(f_j\left(q\right)-f_j\left(r_i\right)\right)}^2},$$ (1)

where q is the query mass, r_i is a reference mass i from the reference library, f_j is the jth feature, and n is the dimensionality of the feature space.

A smaller distance indicates a higher degree of similarity between the two compared masses. From the k-NN algorithm, a characterization score that represents the relative malignancy rating of the query mass is computed as

$$p=\frac{1}{k}\sum _{i=1}^k{b}_i,$$ (2)

where k is the number of retrieved masses and b_i is a binary index indicating whether a retrieved mass is malignant (1) or benign (0) from the known pathology database in the reference library. Six (Euclidean distance, Manhattan distance, correlation, cosine measure, LDA, and BNN) of the seven similarity measures used Eq. 2 for estimating the characterization scores in the retrieval scheme.

Manhattan distance

Similarity is also measured by Manhattan distance, which is the distance between two points measured along axes at right angles,

$$d_{\text{MD}}\left(q,r_i\right)=\sum _{j=1}^n\left|f_j\left(q\right)-f_j\left(r_i\right)\right|.$$ (3)

The notations are defined as above for Eq. 1.

Distance-weighted k-NN

Several distance weighted k-NN algorithms have been investigated and tested to search for similar masses from the reference library, which include the k-NN algorithms based on distance-weighted k-NN.^{32, 43} First, the k-nearest neighbors to the query mass are determined by Eq. 1. A characterization score by the weighted k-NN algorithm is then calculated as

$$p_W=\frac{{\sum }_{i=1}^P{w}_i^{\text{Pos}}}{{\sum }_{i=1}^P{w}_i^{\text{Pos}}+{\sum }_{j=1}^N{w}_j^{\text{Neg}}},$$ (4)

where w_i=1∕d(q,r_i)² is a distance weight, $w_i^{\text{Pos}}$ and $w_j^{\text{Neg}}$ are the distance weights for the malignant (i) and benign (j) retrieved masses, respectively, P is the number of malignant retrieved masses, and N is the number of benign retrieved masses of the k nearest neighbors such that N+P=k.

Correlation

A commonly used similarity measure is Pearson’s correlation coefficient,

$$r=\frac{{\sum }_{j=1}^n\left(f_j\left(q\right)-{\overline{f}}_j\right)\left(f_j\left(r_i\right)-{\overline{f}}_j\right)}{\sqrt{{\sum }_{j=1}^n{\left(f_j\left(q\right)-{\overline{f}}_j\right)}^2}\sqrt{{\sum }_{j=1}^n{\left(f_j\left(r_i\right)-{\overline{f}}_j\right)}^2}},$$ (5)

where ${\overline{f}}_j$ is the mean value of the feature j of the reference masses in the reference library. Other notations are defined as above for Eq. 1.

Cosine measure

The cosine measure^{44, 45} (Cos) estimates the angle between two vectors corresponding to the query mass and a reference mass from the reference library. The cosine is calculated by finding the dot product and dividing it by the norm of each vector,

$$\text{Cos}=\frac{{\sum }_{j=1}^n\left(f_j\left(q\right)\right)\left(f_j\left(r_i\right)\right)}{\sqrt{{\sum }_{j=1}^n{\left(f_j\left(q\right)\right)}^2}\sqrt{{\sum }_{j=1}^n{\left(f_j\left(r_i\right)\right)}^2}}.$$ (6)

The cosine similarity measure is very closely related to Pearson’s correlation coefficient. The most notable difference is that the mean here is not subtracted from each value in order to center both sets of data at zero.

LDA

LDA has been used extensively in literature for breast cancer detection and classification. In our study, the LDA was introduced to compute a one-dimensional linear projection of the two class data (i.e., malignant and benign) that maximizes the ratio of the distance between the projected class means to the within-class covariance.

The features selected by the stepwise LDA and simplex optimization method (Sec. 2B) for the masses in the reference library are projected into one dimension to form the reference LDA classifier scores. The LDA classifier score for the query mass is calculated using the same projection. The k-NN algorithm [Eq. 1] is used for the retrieval scheme using the LDA classifier score. It simply selects the k closest scores in one dimension using the absolute difference between the query mass score and the scores of masses in the reference library.

Bayesian neural network

BNN uses Bayesian method to regularize the training process.⁴⁶ The idea behind BNN is to cast the task of training a network as a problem of inference, which is solved using Bayes’ theorem.⁴⁷ Bayesian neural network is generally more accurate and robust than conventional neural networks, especially when the training data set is small. A BNN with one hidden layer was used in this study. To avoid overfitting, we trained a set of BNNs with different numbers of hidden layer neurons N_h, found the maximum training A_z for the set, and then used N_h* that produced 98%–99% of the maximum training A_z. Table 2 shows the number of neurons in the input and the hidden layers. Similar to the LDA, for the retrieval system, the k-NN algorithm was applied to the BNN classifier scores.

Table 2.

Number of neurons in the input and hidden layers of the BNN.

Centroid by radiologist	Test set: P1		Test set: P2
	No. of inputs	No. of neurons in hidden layer	No. of inputs	No. of neurons in hidden layer
R1	6	9	6	7
R2	8	6	9	6

Evaluation methods

Evaluation of classification performance of CBIR

Six of the seven similarity measures used Eq. 2 for estimating the characterization scores in the CBIR CADx system. For the distance-weighted k-NN, the distance-weighted score [Eq. 4] was used as the characterization score. The characterization scores were then analyzed by the ROC methodology and the area under ROC curve (A_z) was calculated. As described above, for the output-score-based CBIR CADx systems, the LDA and BNN classifiers were first trained to merge the selected features into a one-dimensional classifier score (termed LDA_DI and BNN_DI scores below), which was then used for image retrieval. The performance of the output-score-based CBIR system was then obtained by analyzing the characterization scores estimated with Eq. 2.

For comparison of the classification accuracy of the CBIR approach with that of a conventional approach, the LDA_DI and BNN_DI scores of the query masses were directly subjected to ROC analysis to estimate the performance of the trained LDA and BNN classifiers without any involvement of the retrieval scheme. The A_z values from these classifiers corresponded to the performances reported for conventional classification systems and would serve as a reference to those obtained through the CBIR approaches.

Similarity evaluation by radiologists

We evaluated the similarity between the query and the retrieved masses by the CBIR CADx system based on radiologists’ visual similarity assessments. One of the four partitions (testing on set P1, training on set P2, using segmentation initialized by R1) was used. This partition was selected because its A_z is close to the average A_z (k=3) of the four partitions and the number of selected features was small. The reference library for the similarity study therefore included 121 masses on 230 (79 malignant and 151 benign) images (P2 set). Because of the constraint on the reading time available for the radiologists, the choice of the number of observers, the number of similarity measures, the number of query masses, and the number of retrieved masses (k) was a compromise among these factors in order to complete the similarity study within a reasonable time. We chose 100 query masses from P1 on 100 (49 malignant and 51 benign) images as the test set. 49 malignant and 51 benign masses were randomly selected from the P1 set, and for each mass, one view (image) was randomly selected from the available views (images) for this mass. From the seven SMs, we selected four SMs, (LDA, BNN, Cos, and ED) for the observer study. LDA and BNN were output-score-based methods and had better classification performance than other methods in our CBIR results [see Sec. 3 and Fig. 7e]. Cos and ED were selected to represent the input-feature-based methods. For each query mass, three most similar masses (k=3) were retrieved from the reference library with each method. It is possible that two of the three most similar retrieved images belong to the same mass (the orthogonal views). A total of 1200 (100×3×4) pairs of query and retrieved masses was formed for the similarity study.

Figure 7.

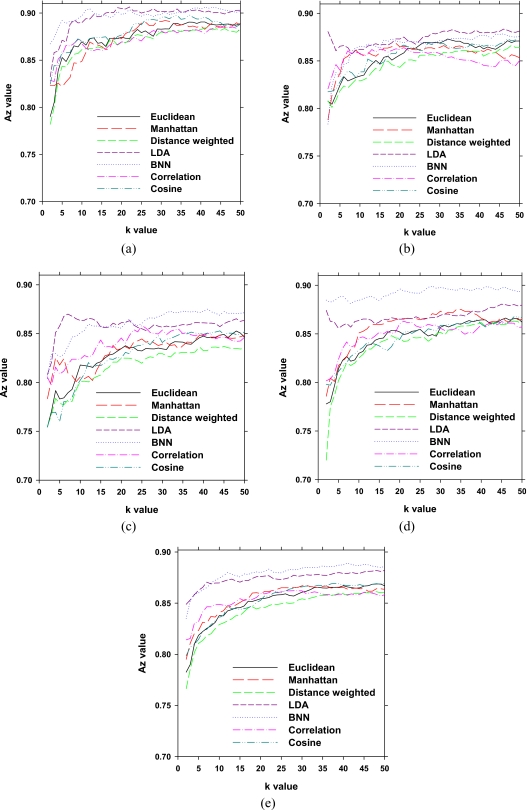
The A_z values of the area under ROC curves for top k retrievals using segmentation initialized by R1 and R2 for the two cycles of cross validation: (a) Test in set P1 (train in set P2) by R1, (b) test in set P2 (train in set P1) by R1, (c) test in set P1 (train in set P2) by R2, (d) test in set P2 (train in set P1) by R2, and (e) average of (a)–(d).

The mass pairs were mixed and presented to the radiologists in random order, one pair at a time. Three MQSA radiologists, with breast imaging experience of 8, 24, and 28 yr, rated the similarity between the query mass and the computer-retrieved masses using a nine-point similarity scale (1=very dissimilar, 3=quite dissimilar, 5=some degree of resemblance, 7=quite similar, and 9=very similar). The similarity ratings 2, 4, 6, and 8 are intermediate ratings. Figures 56 show examples of the similarity evaluation by radiologists for a malignant and a benign query mass, respectively. Two of the three radiologists (R1 and R2) were the same as the two that helped collect the data set and marked the masses on the US images and provided the centroid locations. However, the collection of the data set did not involve comparing the similarity of the masses and none of the masses were viewed in pairs during data set collection. Moreover, only ROI images were provided in the similarity study and data collection was done 1.5 yr before the similarity study. Therefore, their participation in the similarity observer study is not expected to introduce biases.

Figure 5.

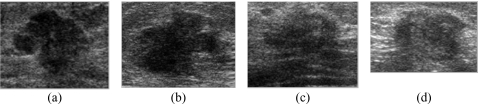
A malignant query mass and three retrieved masses (k=3) by our CBIR scheme using the ED measure: (a) A malignant query mass, (b) first retrieved mass, (c) second retrieved mass, and (d) third retrieved mass. The biopsy results of (a)–(d) are malignant. The similarity ratings from three radiologists (R1, R2, and R3) estimating the similarity between the query mass and the retrieved masses are (b) 2, 7, and 8; (c) 5, 6, and 8; (d) 7, 6, and 6.

Figure 6.

A benign query mass and three retrieved masses (k=3) by our CBIR scheme using the ED measure: (a) A benign query mass, (b) first retrieved mass, (c) second retrieved mass, and (d) third retrieved mass. The biopsy results of (a)–(d) are benign. The similarity ratings from three radiologists (R1, R2, and R3) estimating the similarity between the query mass and the retrieved masses are (b) 7, 5, and 7; (c) 6, 5, and 6; (d) 5, 7, and 7.

RESULTS

LDA_DI and BNN_DI classification accuracy

The training and test A_z values for the LDA_DI and BNN_DI obtained directly from the analysis of the classifier scores are shown in Table 3 for the different data set partitions. The average test A_z value for both the LDA and the BNN is 0.88±0.02.

Table 3.

The A_z values for LDA_DI and BNN_DI classifiers designed using features extracted from the segmented masses on US images for the two cycles of cross validation. The mass centers identified by R1 and R2 were used for initialization of segmentation by active contour model.

Data set	LDADI (train)	LDADI (test)	BNNDI (train)	BNNDI (test)
Test P1 (train P2), centroid by R1	0.91±0.02	0.91±0.02	0.91±0.02	0.91±0.02
Test P2 (train P1), centroid by R1	0.91±0.02	0.88±0.02	0.91±0.02	0.88±0.02
Test P1 (train P2), centroid by R2	0.91±0.02	0.86±0.02	0.91±0.02	0.86±0.02
Test P2 (train P1), centroid by R2	0.92±0.02	0.87±0.02	0.91±0.02	0.87±0.02
Average	0.91±0.02	0.88±0.02	0.91±0.02	0.88±0.02

Retrieval methods’ characterization accuracy

The performance accuracy of the k-NN classifier algorithm depends on the number of retrieved nearest neighbors, k. In our experiments, we varied k from 2 to 50. Figure 7 illustrates the performance of the CBIR system as measured by A_z for each data set. It shows that the CBIR-CADx system performance varies depending on the number of retrieved cases (k). Performance improves as more cases are retrieved in the range studied (k<50). In Fig. 7e, the dependence of A_z values on k averaged over four data sets is shown for all methods. The performances of the LDA and BNN based systems remain relatively unchanged for k≥10 in terms of the average A_z and those of other similarity measures do not change substantially for k≥25. On the average, LDA and BNN achieve a slightly better performance compared to other similarity measures. The average A_z values of LDA and BNN at k=25 were 0.87±0.02 and 0.88±0.02, respectively. Table 4 shows the average A_z values obtained from the seven similarity measures.

Table 4.

Average A_z values of the CBIR-CADx system using k-NN with seven different similarity measures for several k values. Results for other k values can be found in Fig. 5e.

Similarity measures	k=3	k=10	k=25	k=50
LDA	0.85±0.03	0.87±0.02	0.87±0.02	0.88±0.02
BNN	0.85±0.03	0.88±0.02	0.88±0.02	0.89±0.02
Cos	0.81±0.03	0.84±0.03	0.86±0.02	0.87±0.02
ED	0.79±0.03	0.84±0.03	0.86±0.02	0.87±0.02
Manhattan	0.81±0.03	0.84±0.03	0.86±0.02	0.86±0.02
Distance-weighted	0.79±0.03	0.83±0.03	0.85±0.03	0.86±0.02
Correlation	0.82±0.03	0.85±0.03	0.86±0.02	0.86±0.02

Number of similar masses retrieved by different methods

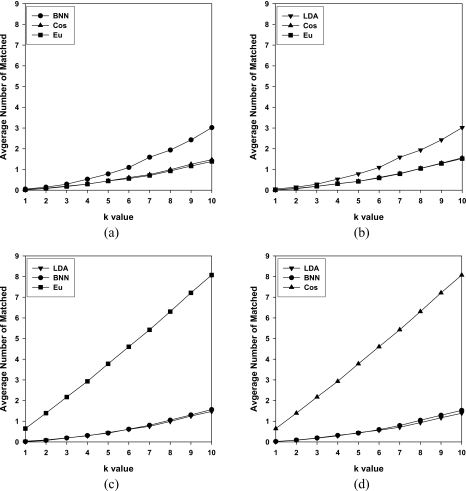
We studied the consistency of the different retrieval methods by comparing the number of identical masses retrieved by the different retrieval methods for a specified k. Figure 8 and Tables 5, 6 show the average number of identical masses retrieved by different methods for a given k (k=1,…,10). For example, BNN, Cos, and ED are compared to LDA in Fig. 8a. The BNN retrieved more masses, on the average, that were identical to those retrieved by LDA than Cos and ED, but the maximum was only 3.16 at k=10. The four comparisons in Fig. 8 show that, on the average, 8.07 of the 10 masses retrieved by Cos and ED in 10-NN (k=10) were the same. On the other hand, both LDA and BNN retrieved less than two masses, on the average, that were identical to those retrieved by Cos and ED in 10-NN.

Figure 8.

The number of retrieved masses that were identical between two similarity measures with the CBIR-CADx system. The results for k=1 to k=10 are shown. The partitions: Test P1 (train P2), centroid by R1, was used. (a) LDA compared to BNN, Cos, and ED; (b) BNN compared to LDA, Cos, and ED; (c) Cos compared to LDA, BNN, and ED; and (d) ED compared to LDA, BNN, and Cos.

Table 5.

The average number of retrieved masses from reference library that were identical when k=3 for partition: Test P1 (train P2), centroid by R1.

Similarity measures	Similarity measures
	LDA	BNN	Cos	ED
LDA	3	0.29	0.19	0.18
BNN	0.29	3	0.19	0.19
Cos	0.19	0.19	3	2.17
ED	0.18	0.19	2.17	3

Table 6.

The average number of retrieved masses from reference library that were identical when k=10 for partition: Test P1 (train P2), centroid by R1.

Similarity measures	Similarity measures
	LDA	BNN	Cos	ED
LDA	10	3.02	1.47	1.39
BNN	3.02	10	1.57	1.52
Cos	1.47	1.57	10	8.07
ED	1.39	1.52	8.07	10

Evaluation of retrieval methods by radiologists’ visual assessment

The average similarity ratings of all radiologists for the four SMs, LDA, BNN, Cos, and ED were 4.71, 4.95, 5.18, and 5.32, respectively. The radiologists’ average similarity ratings for the SMs based on ED and Cos were higher than the ones for the SMs based on LDA and BNN. Statistical comparison was performed by finding the average similarity rating for each query mass (averaged over three readers and three retrieved masses) for each retrieval method and then conducting a paired t-test of the average similarity ratings between pairs of retrieval methods. Our results indicated that the average similarity ratings were significantly (p<0.008) higher for the CBIR method based on ED than those based on a classifier score (LDA or BNN). The difference between Cos and LDA (or ED) was also statistically significant (p<0.02). However, the difference between Cos and BNN did not reach statistical significance (p=0.098). For malignant query masses, the average similarity ratings were 4.83, 5.05, 5.32, and 5.48, respectively. Table 7 shows the average similarity ratings of each radiologist for all masses and the subsets of malignant and benign query masses. One radiologist seemed to have a tendency of giving lower similarity ratings than the other two. On the average, masses retrieved by the CBIR system were moderately similar to the query masses based on radiologists’ similarity assessments. Masses of higher similarities were retrieved for the malignant than for the benign query masses.

Table 7.

The average similarity ratings of the three radiologists for all masses and the subset of malignant and benign masses retrieved by the k-NN method (k=3) using the LDA, BNN, Cos, and ED measures.

Similarity measures	R1			R2			R3
	Total	Malignant	Benign	Total	Malignant	Benign	Total	Malignant	Benign
LDA	3.96	3.94	3.98	5.05	5.16	4.94	5.12	5.38	4.88
BNN	4.33	4.19	4.46	5.20	5.54	4.86	5.34	5.42	5.26
Cos	4.47	4.43	4.50	5.47	5.66	5.28	5.61	5.86	5.37
ED	4.63	4.67	4.60	5.61	5.76	5.48	5.71	6.03	5.41

DISCUSSION

In the CBIR system, the Cos and ED measures retrieved a larger number of masses that were identical (2.17 and 8.70 for k=3 and 10, respectively, see Tables 5, 6) than other similarity measures. The masses retrieved by LDA were more similar to those retrieved by BNN (0.34 and 3.16 for k=3 and 10, respectively) than to those by the other two similarity measures. However, very few masses that were retrieved from the reference library by the input-feature-based (e.g., Cos and ED) and output-score-based (BNN and LDA) measures in the CBIR scheme were identical. This may be expected because similar merged classifier scores used in the output-score-based systems could be obtained from many different weighted combinations of the individual features in the multidimensional feature space; the retrieved masses could therefore have very different features from those of the query mass and there was also a large pool of masses with similar merged scores to be selected from. The input-feature-based systems retrieved masses based on the similarity of the individual features would tend to select masses that have features more similar to the query mass, which might therefore be different from those retrieved by the output-score-based systems. The similarity of the query and retrieved masses as evaluated by radiologists’ visual assessment in the observer study also indicated that the masses retrieved by the input-feature-based measures (Cos and ED) had higher similarity ratings than those by the output-score-based measures (LDA and BNN).

The average A_z values of the output-score-based SMs (BNN and LDA) were slightly higher than those of the five input-feature-based SMs [Table 4 and Fig. 7e]. The differences, although small, were consistent over the entire range of k values studied. Within each group, the average A_z values were similar. In addition, the classification accuracy obtained directly from the conventional classifiers (Table 3) was higher than those obtained through the CBIR process, especially for small k values [Table 4 and Fig. 7e]. These results indicated that there may be trade-offs between choosing an effective CBIR system and the best classification system. For the purpose of CADx that provides radiologist with similar lesions for visual reference and malignancy estimation, the input-feature-based type of CBIR systems may be more appropriate despite the slightly lower A_z. The results also showed that ED is the best similarity measure among the four compared in this study for searching similar masses. However, it will be prudent to further compare more sophisticated similarity measures, such as those based on supervised learning, in future studies. In this study, our focus was to design a CBIR CADx system, which included the comparison of the performance of the input-feature-based and output-score-based approaches to image retrieval. Accordingly, the features used in both types of systems were kept the same, as selected using an LDA with stepwise feature selection that was designed to classify the masses as malignant or benign, to reduce the variables in the comparison. Furthermore, we have not designed all possible features that can exhaustively describe the characteristics of a mass on US images. For example, a descriptor for echogenicity was not included in the feature pool so that it is not known if such a feature could improve retrieval or classification. However, a retrospective comparison of the masses ranked as having high similarity by radiologists to those having low similarity did not show significant difference in their echogenicity. The ultimate benchmark for a CADx system is the improvement in the performance of the radiologists when they are aided by the CADx system. The evaluation of CBIR CADx system performance is a relatively new area, and the trade-offs between the performances of the stand-alone system for retrieval and classification as they are related to this ultimate benchmark are not yet known. Future observer studies may inform us about the relative importance of these two performance criteria.

Due to the rapid increase in the number of readings required for each additional SM, we could only include four out of the seven SMs for the observer similarity study. This observer study, although limited, allowed the comparison of two different retrieval approaches (two output-score-based and two input-feature-based) and two commonly used SMs (ED and Cos). The comparison also resulted in new information that has not been reported previously based on similarity and the A_z values [Tables 7, 8].

Table 8.

The A_z values of the CBIR-CADx from 258 query masses for top k retrieval from partition: Test P1 (train P2), centroid by R1.

Similarity measures	k=3	k=10	k=25	k=50
LDA	0.86±0.03	0.89±0.02	0.90±0.02	0.90±0.02
BNN	0.87±0.02	0.90±0.02	0.90±0.02	0.90±0.02
Cos	0.84±0.03	0.87±0.02	0.89±0.02	0.89±0.02
ED	0.81±0.03	0.87±0.02	0.88±0.02	0.89±0.02

In this initial study, we included orthogonal views of the same mass in the image library due to the limited data set available. It was possible that two of the three most similar retrieved images were orthogonal views of the same mass. In our four data set combinations, the retrieval at k=3 contained orthogonal views ranged from 2.3% to 14.7% of the query masses. By analysis of the resulting classification performance with and without the retrieved masses in orthogonal views for the four SMs of interest (LDA, BNN, Cos, and ED), the differences in the A_z values were less than 0.02. However, since the image query sets were relatively small, future studies with larger data sets will be needed to further investigate this issue.

There are limitations in our similarity study. Three radiologists rated the similarity of a query mass to the top three (k=3) retrieved masses using four similarity measures. The total number of query masses was 100. Therefore, each radiologist performed 1200 (3×4×100) readings. Although the total number of readings was fairly large, the number of query masses and the number of readings for each mass were still small. In a future study, we will increase the number of observers in order to obtain more robust results. Increasing k may also produce more reliable results; however, we have to carefully choose the value of k in order to avoid excessive reading times for the radiologists. Likewise, four representative SMs were chosen from the seven for the observer study to limit the number of readings needed. Finding a good balance among the number of observers, the proper number of similarity measures, the number of query masses, and the k value will be pursued in the future.

CONCLUSION

We are developing a CBIR CADx scheme to assist radiologists in differentiating benign and malignant masses on ultrasound breast images. In this study, we compared the effectiveness of seven different similarity measures (Euclidean distance, Manhattan distance, distance-weighted k-NN, correlation, cosine, LDA, and BNN) that were derived from morphological and texture features. The performances of the CBIR CADx system using four of the similar measures were evaluated by radiologists’ visual assessment of the similarity between the query and the retrieved masses. Although the BNN and LDA measures had comparable classification performance (i.e., A_z) that were higher than the other SMs in the CBIR CADx scheme, ED exhibited higher agreement (i.e., similarity ratings) from three radiologists’ assessment than the Cos, LDA, and BNN measures for small (k=3) top retrieval masses. For larger number (k>3) of top retrieval masses, the classification performance of all similarity measures gradually leveled off. The relationship between the usefulness of the retrieved masses as references for radiologists and the accuracy of estimating the likelihood of malignancy of the query mass warrants further investigations.

Future work includes verifying the results of this study by applying the CBIR CADx system to a larger and independent data set, expanding the feature space, comparing other similarity measures, and combining the developed US characterization method with mammographic characterization methods. The major question of the impact of a CBIR system for CADx on radiologists’ characterization of breast masses as compared to a conventional CADx system that only estimates the likelihood of malignancy of the lesion will also need to be addressed in future observer studies after the CBIR system is fully developed.