An alternating focused ultrasound system for thermal therapy studies in small animals

Abstract

Purpose: To develop an alternating focused ultrasound system (AFUS) for preclinical studies of thermal and acoustic responses of tumors in small animal models. This work was motivated by the need of noninvasively creating relatively small spheroidal thermal lesions in small targets (e.g., a murine tumor) without damaging the surrounding tissues.

Methods: The AFUS consists of two lead zirconate titanate (PZT-4) spherically curved ultrasound transducers with focal zones crossing each other at a 90° angle. The transducers were independently powered following a programed alternating firing scheme. Before the device design and construction, an acoustic and biothermal model was developed to simulate the ultrasound pressure field and the resulting temperature and thermal dose distributions. A shape factor, sphericity, to quantify the roundness of the lesions was calculated based on the 240 equivalent minutes at 43 °C thermal dose contours. A prototype of the AFUS was constructed with two identical transducers of an operating frequency of 2.25 MHz, 38 mm in diameter, and F-number equal to 1.33. To evaluate the performance of the AFUS experimentally, a series of heating in polyacrylamide phantoms, ex vivo porcine liver tissues, and in implanted mouse tumors fibrosarcoma (FSaII) in vivo was conducted. In these experimental cases, the sphericity was calculated and compared based on the visible lesion (a marked change in coloration).

Results: As shown in the simulations, the lesions induced in polyacrylamide phantoms, ex vivo porcine liver tissues, and in vivo mouse tumors, the sphericities of the lesions yielded by AFUS heating were approximately 50% higher than those of single focused ultrasound heating as long as moderate intensities were used and the duty cycle pulses were distributed equally among the transducers.

Conclusions: The AFUS is a device capable of noninvasively creating spheroidal thermal lesions in small targets such as murine tumors.

INTRODUCTION

High-intensity focused ultrasound (HIFU) is a promising noninvasive thermal therapy for locally advanced cancers in the prostate,^{1, 2, 3} breast,^{4, 5, 6} liver,^{7, 8, 9, 10} and gynecological diseases.^{11, 12, 13} Ultrasound-mediated delivery^{14, 15, 16, 17, 18} has also been explored to potentially enhance or activate therapeutic effects. To translate novel ultrasound-based techniques to clinical practice, a large number of preclinical studies using small animals have to be consistently performed to understand the fundamental biological and physiological mechanisms behind the thermal and acoustic responses of normal and tumor tissues.

Small animals, such as rats and mice, are widely used models for translational research because of the relatively low cost of maintenance, ability to reproduce, availability of different small animal models of pathologies, and a number of genetic and physiological similarities to humans.¹⁹ The noninvasive nature of HIFU makes it an attractive technique for studying the effects of heating on the physiological environment without confounding tissue damage by probe insertion.²⁰ Nevertheless, challenges arise when one uses a single focused ultrasound (SFUS) to administer ultrasound energy to small animal tumors in preclinical research. One challenge is that it is difficult to position the typical SFUS elongated ellipsoidal focus inside small targets, especially when the length of the focus is comparable to the size of a tumor. For instance, a mouse fibrosarcoma tumor implanted in the thigh is approximately 8–10 mm in diameter at the time of experimentation; in such a small volume, the elongated focus of an SFUS may cause ablation of the skin proximally or the bones and other organs distally. Moreover, in order to study fundamental mechanisms of thermal ablation in combination with drugs and ionizing radiation, it is desirable to ablate specific small spheroidal subregions inside a tumor or an organ.

The purpose of this paper is to report the development and performance of an alternating HIFU system designed especially for preclinical studies using small animals (Sec. 2). The motivation for the development of the alternating focused ultrasound system (AFUS) was to have a device capable of consistently inducing small spheroidal lesions within tumors implanted in small animals. Such a device would greatly facilitate the study of molecular, cellular, and physiological effects of thermal ablation and ultrasound-mediated treatment strategies. The performance of the new ultrasound delivery system was evaluated (Sec. 3) by numerical simulations and experiments in phantoms, ex vivo porcine livers, and in vivo (FSaII) tumors implanted subcutaneously in mice thighs. In simulations, the resulting thermal lesions were characterized by temperature distributions, thermal dose contours, and sphericity. The phantom gel and ex vivo experiments and their sphericities were quantitatively evaluated. In in vivo experiments, 3D ablated regions produced by the AFUS and the SFUS were reconstructed and their sphericities were calculated and compared.

MATERIALS AND METHODS

AFUS design and fabrication

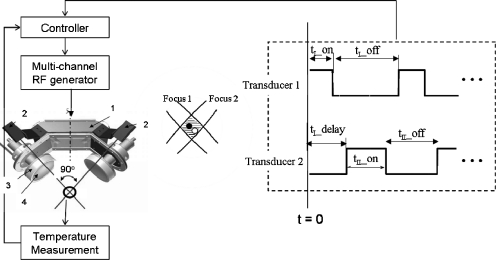
A confocal HIFU applicator incorporating an alternating powering scheme was devised, as shown in Fig. 1. The configuration of this applicator consists of two spherically curved lead zirconate titanate (PZT-4) transducers (Boston Piezo-Optics, Inc., Boston, MA), which are angularly separated by 90°. With a precise calibration and alignment (see Sec. 2D4 and Fig. 2), the centers of the two foci can be positioned at the same spot. That is, the black and white dots in the shaded area in the middle of Fig. 1 can be aligned to overlap as much as possible. Following the firing scheme depicted in the right of Fig. 1, the overlap (shaded) region is exposed almost twofold longer in time than the surrounding regions, which are exposed to lower intensity levels. Using this time-based intensity modulation, the overlap region should receive much higher thermal dose than the surrounding regions. Since the overlap region is more spheroidal than ellipsoidal, we hypothesize that a spheroidal lesion could be created using this approach.

Figure 1.

The schematic diagram of the AFUS consisting of two orthogonally mounted spherically curved ultrasound transducers, a multichannel RF generator, a temperature measurement method (e.g., thermocouple), and a controller, which includes the sonication scheme for each transducer. The basic components of the AFUS include (1) holder, (2) laser diodes, (3) acrylic frame, and (4) PZT-4 transducers. The hardware allows for adjustment of each transducer along its central axis to have both foci overlap in space, as illustrated in the middle inset.

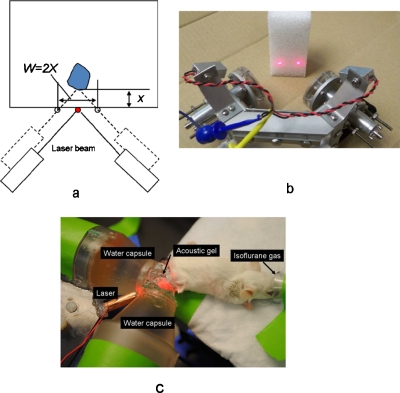
Figure 2.

The schematic diagram of a prototype design of the AFUS. (a) Targeting the ultrasound foci using lasers to a deep-seated target, where x is the desired depth and w is the distance between two laser beams on the surface. (b) Photograph of the AFUS applicator with lasers shining on an object. The two transducers are shown without capsules. (c) An experimental setup for in vivo ablations in mouse tumors showing the water-filled capsules attached to the transducers to couple the sound waves to the tumor.

In the schema of the firing scheme in the right part of Fig. 1, t_on is the power-on period, t_off is the power-off period, and t_delay is the time interval between excitations of the two transducers. The duty cycle in this paper was formatted as t_on∕t_off∕t_delay, for example, 0.3 s on∕1.1 s off∕0.7 s delay. The optimal power level and duty cycles were first studied numerically to achieve the maximal sphericity and the desired size of the thermal lesions. Experimentally, the two transducers were driven independently and in an alternating fashion (one at a time) with a multichannel RF generator (model 500-018, Advanced Surgical Systems, Tucson, AZ) capable of providing up to 100 W∕channel. The RF generator was connected to a PC via RS-232 and controlled with custom software.

The transducer parameters, such as aperture size, curvature radius, transducer thickness, and resonance frequency, were determined via acoustic and thermal modeling, as described in Sec. 2B. The radius of curvature (i.e., the focal length) of each of the spherically focused transducers was chosen to be 50 mm to provide flexibility in ablating at various depths, and the aperture size (diameter) was chosen to be 38 mm to ensure sufficient supply of acoustic power. An operating frequency of 2.25 MHz was selected based on numerical simulations.

Each piezoelectric ceramic transducer was secured in an acrylic frame with air backing and sealed using silicone to maintain watertight integrity. The transducer assemblies were mounted on custom aluminum holders to allow for easy adjustment so that the two foci could overlap each other (as described in Sec. 2D, see Fig. 2). By sonicating phantom gels, the shafts of the transducers can be adjusted longitudinally until the lesions created with both transducers overlapped. The laser beams were adjusted as well to aim at the overlapping foci.

To couple the sound waves to the small tumors, a water-filled conical extension (also called a capsule) was attached on the face of each transducer [Fig. 2b]. A Mylar membrane was glued at the end of each cone. Acoustic gel (Aquasonic, Parker Laboratories, Inc., Fairfield, NJ) was used to couple the sound from the Mylar membranes to the target, as shown in Fig. 2c. As shown in Figs. 2a, 2b, two laser diodes (wavelength: 630 nm, max. output: 4 mW) were mounted on the aluminum frame and the laser beams were adjusted so that they would intercept and point to the overlapping ultrasound foci. Electrical impedance matching was done by constructing a second-order matching circuit for each transducer together with the connecting coaxial cables so that their electrical impedances were close to 50 Ω at the operating frequency.

Acoustic and biothermal modeling

A thermoacoustic model consisting of a Rayleigh–Sommerfeld integral-based acoustic model and a finite-element biothermal model were used to simulate the transient 3D distributions of temperature and thermal dose. The spherically focused acoustic field was modeled based on the Rayleigh–Sommerfeld diffraction integral,²¹ which was solved by two-dimensional numerical integration over the surface of each transducer,

$$I\left(x,y,z\right)=\frac{1}{2\rho c}{\left|\frac{j\rho ck}{2\pi }\sum _{n=1}^N{u}_n\sum _S\frac{\Delta A_n{e}^{-(\mu +jk)r_n}}{r_n}\right|}^2,$$ (1)

where u_n is the normal particle velocity of the nth element source, c is the speed of sound in tissue, r_n is the distance between an arbitrary point (x, y, z) in the region of interest and the nth element, S is the surface area of the transducer, k is the wave number, ρ is the tissue density, and ΔA_n is the surface area of the nth element. The discretization of the transducer’s surface, i.e., the size of ΔA_n, was fine enough (<1∕10 wavelength) so that the elements can be considered as point sources. All the necessary parameters and coefficients in the acoustic and biothermal models can be found in Table 1, which were obtained from the literature.²²

Table 1.

Acoustic and thermal parameters of tissue used for simulations.

Parameters	Definition and unit	Value
ρ	Density of tissue (kg m−3)	1050
Ct	Specific heat of tissue (J kg−1 °C−1)	3639
Cb	Specific heat of blood (J kg−1 °C−1)	3639
kt	Thermal conductivity of tissue (W m−1 °C−1)	0.56
ω0	Blood perfusion rate (kg m−3 s−1)	0, 9
μ	Attenuation coefficient (Np m−1 MHz−1)	5.3
α	Absorption coefficient (Np m−1 MHz−1)	3.5
c	Sound speed (m∕s)	1500
f	Operating frequency (MHz)	2.25
k	Wave number (2πf∕c) (m−1)	9425

The transient temperature distribution in tissue was computed using the bioheat transfer equation of Pennes,²³

$$\rho C_t\frac{\partial T}{\partial t}=\nabla \left(k_t\nabla T\right)+\rho C_a{\omega }_0\left[T_a-T\right]+⟨q⟩,$$$$T\left(t=0\right)=T_b,T\left(r=\infty \right)=T_b,$$ 2

where the first term on the right hand side represents the rate of heat conduction in tissue in which k_t is the thermal conductivity, C_t is the heat capacity of tissue, and C_a is the heat capacity of arterial blood. The second term characterizes heat loss due to blood perfusion in which ω₀ is the perfusion rate coefficient and T_a is the arterial temperature. The initial and Dirichlet boundary conditions are set to be the basal temperature T_b. The third term, ⟨q⟩, represents the acoustic power deposition, i.e., the absorbed ultrasonic power in soft tissue, which can be calculated from the free-field intensity distribution I(r,z) as²⁴

$$⟨q⟩=2\alpha \left(r,z\right)I\left(r,z\right)e^{{\int }_{z0}^z-\mu \left(r,z\right)dz},$$ (3)

where α and μ are the thermal dose-dependent absorption and attenuation coefficients, respectively.²⁵ The distributions of the thermal dose (EM@43=equivalent minutes at 43 °C) were calculated from the transient temperature distributions using the Sapareto–Dewey formulation.^{26, 27} The value of 240 EM@43 was used as a therapeutic level to characterize the boundary of thermal necrosis in the soft tissue.²⁸

Numerical analysis

The acoustic pressure field modeled based on a Rayleigh–Sommerfeld integral was solved by a numerical integration [Eq. 3] that was programed in C++ and the bioheat equation [Eq. 1] was solved using COMSOL MULTIPHYSICS finite-element software (version 3.4, COMSOL, Burlington, MA). The purpose of the numerical simulations was to theoretically establish the ability of the AFUS unit to create small spheroidal thermal lesions in the soft tissue. The results would also serve as a guide to the experiments. Different heating conditions (Table 2), such as various power levels, duty cycles, and blood perfusion values, were examined. The control case (No. 1 in Table 2) was defined as a group of simulations for a single spherically focused ultrasound applicator, which was identical to one of the two AFUS transducers. For simulation, the nominal spatial peak intensity I_SP for the control cases was set to 432 W∕cm² (i.e., 3.5 MPa of the maximum focal pressure or 20 W of the acoustic power).

Table 2.

Numerical simulations of thermal ablation using the SFUS and the AFUS.

No.	Spatial peak intensity (ISP) (W∕cm2)	Blood perfusion rate (kg∕m3 s)	Sonication duty cyclest_on ∕t_off∕t_delay (s∕s/s)a	The highest sphericity	Minimum Lesion with the highest sphericityDmin (mm)	Maximum Lesion with the highest sphericityDmax (mm)b	Duration (s)b
1c	432	0, 9	0.5 ∕0.5	0.6	0.8, 0.6	0.8, 0.6	4, 4.2
2	432	0, 9	0.3 ∕1.1 ∕0.7	0.9	0.8, 0.6	2.6, 2.4	8, 8.2
3	432	0, 9	0.5 ∕1.3 ∕0.9	0.9	0.8, 0.6	2.6, 2.4	8, 8.2
4	432	0, 9	1.0 ∕1.8 ∕1.5	0.9	0.8, 0.6	2.6, 2.4	8, 8.2
5	432	0, 9	2.0 ∕2.8 ∕2.4	0.9	0.8, 0.6	2.6, 2.4	8, 8.2
6	50	0, 9	0.3 ∕1.1 ∕0.7	0.9	1.0, 0.8	6.5, 2.8	69, 84
7	100	0, 9	0.3 ∕1.1 ∕0.7	0.9	0.9, 0.8	5.5, 2.7	52, 67
8	200	0, 9	0.3 ∕1.1 ∕0.7	0.9	0.9, 0.8	4.5, 2.6	37, 53
9	300	0, 9	0.3 ∕1.1 ∕0.7	0.9	0.8, 0.7	3.6, 2.5	16, 29

^aDuty cycle: t_on(s)∕t_off(s)∕t_delay(s), refer to Fig. 1.

^bD_max and duration correspond to the maximum temperature reaching 90 °C.

^cControl case: A single transducer was considered, so there is not a delay time.

To test the effect of various duty cycles on the thermal lesions produced by the AFUS, cases 2–5 in Table 2 were simulated. Cases 6–9 were investigated to test the effect of different power levels on the AFUS ablations. For all the cases, two different blood perfusion rates (ω=0 and 9 kg∕m³ s) were used. The sonication duty cycle for the control case was a 0.5 s on∕0.5 s off alternating scheme as a standard to compare to other cases. The spatial peak intensities I_SP for the AFUS were intentionally selected to be equal to or lower than the control case, considering the two transducers involved. All the comparisons were based on the resulting temperature distributions and thermal dose contours.

To quantify how spherical a thermal lesion was, a shape factor called sphericity (ψ) was calculated as

$$\psi ={\pi }^{1∕3}{\left(6V\right)}^{2∕3}∕A,$$

where V and A were the volume and the surface area of a thermal lesion, respectively. Note that ψ=1 for a sphere. The thermal lesion was defined by the 240 EM@43 isodose contours in simulations. In the experiments described in Sec. 2D, it was defined by the observable (and manually segmented on photographs using MATLAB) physical damage in ex vivo ablated liver tissues and by the triphenyltetrazolium chloride (TTC) stained multiple sections of in vivo ablated mouse tumors, respectively. The procedure of reconstructing a 3D lesion from 2D phantom and ex vivo lesion contours was as follows: (1) We determined the lesion contour produced by each transducer and (2) then rotated each contour around the corresponding transducer axis. The entire revolved volume was assumed to be the 3D lesion volume. Finally, in MATLAB, we estimated the surfaces and volumes. In simulations, the sphericity was calculated based on the 3D thermal dose contours and plotted as a function of the exposure time.

Experiments

Measurement of pressure field

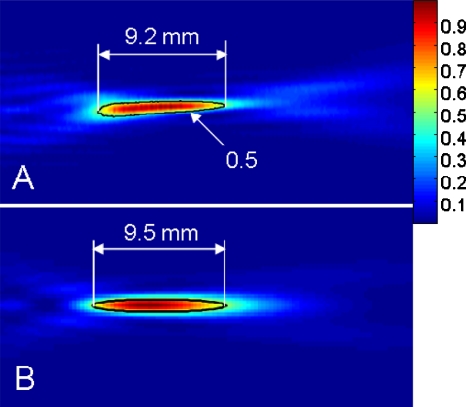
The relative acoustic pressure squared for each transducer was measured in a degassed water tank. A needle hydrophone (model Dapco #NP10-1, active diameter=0.2 mm) was moved using a computer-controlled three-axes scanning system (NF90 series stepping motor controller, Velmex Inc., Bloomfield, NY) in a rectangular focal plane (40×40 mm²). The applied sonication for these measurements was with an electrical input power of 1.0 W at a frequency of 2.25 MHz. The efficiency of energy conversion from electrical to acoustic power was measured (∼40%) using a radiation force balance. The scanning step size was set close to the diameter of the hydrophone, 0.2 mm along the x, y, and z directions. The agreement between measured and simulated pressure squared distributions was shown in Fig. 3.

Figure 3.

(a) The relative acoustic pressure squared distribution measured by a needle hydrophone (0.2 mm in diameter) in a tank filled with degassed water (applied electrical power: 1 W, frequency: 2.25 MHz). (b) The corresponding simulated relative acoustic pressure squared distribution.

Polyacrylamide phantom gel

The phantom experiments were used to test the performance of an AFUS in a homogeneous and unperfused medium. The polyacrylamide phantom gel was prepared by mixing 28.6% water, 24.4% of 40% acrylamide solution (Sigma Aldrich, St. Louis, MO), 16.8% of 2% bis acrylamide solution (Fisher Scientific, Pittsburgh, PA), 30% of egg white (local grocery store), 0.05% ammonium persulfate, and 0.02% tetramethylethylenediamine (TEMED). In order to maintain a satisfactory transparency and more uniform thermal and acoustic properties, the mixture was passed through a 70 μM cell strainer before adding the persulfate and TEMED to filter out precipitates in the egg whites. The material has acoustic properties similar to those of soft tissues and becomes opaque as the egg white is heated (T>62 °C).²⁹ This allows for identifying the ablated volume in all three spatial dimensions, and therefore, facilitated alignment and calibration of the acoustic focal spots and the laser beams. After preparation, the mixture was poured into a 5 cm×5 cm×2 cm mold. Once the material solidified, it was taken out of the mold, wrapped into a cellophane foil, and refrigerated at 4 °C until the day of the experiment.

In vivo mouse tumors

The efficacy of the AFUS to yield spheroidal lesions in heterogeneous perfused tissues was tested in seven FSaII tumors in vivo. The heterogeneous structures (e.g., tortuous blood vessels, nearby bones) present in living tumors were expected to challenge the ability of the AFUS to create spheroidal lesions. All procedures of this experimental study were approved by the university’s institutional animal care and use committee. The tumor cells were grown in RPMI-1640 medium supplemented with 10% bovine calf serum. For induction, FSaII tumor cells in exponential growth phase were harvested using 0.25% trypsin in HEPES buffered medium, washed, and counted. A subcutaneous injection of 2×10⁵ cells in 0.05 ml serum-free medium was made in the flank of female C3H mice. The implanted tumors grew for 12 days before experiments. The mouse was anesthetized using isoflurane gas during the ablations.

Thermal lesions in phantoms, ex vivo tissues, and in vivo tumors

To test that the alternating dual frequency approach of the AFUS produces thermal lesions with increased roundness relative to a single focused transducer, a series of experiments in polyacrylamide phantom gel, excised porcine livers, and murine FSaII tumors (Table 3) was carried out.

Table 3.

Focused ultrasonic heating in phantom gel, excised tissue, and in vivo tumors.

	FUS type	Peak pressure (MPa)	Sonication sequence (s)	Sonication duration (s)	No. of experiments
Phantom (polycrylamide gel)	SFUS	5.3	0.2 ∕0.2	50	3
	AFUS	3.5	0.2 ∕0.6 ∕0.4 0.1 ∕0.6 ∕0.4	140	3
		3.5	0.3 ∕1.1 ∕0.7	110	3
		3.5	0.3 ∕1.1 ∕0.7	129	3
Excised (porcine livers)	SFUS	5.3	0.2 ∕0.2	50	3
	AFUS	3.5	0.2 ∕0.6 ∕0.4	140	3
		3.5	0.3 ∕1.1 ∕0.7	110	3
		3.5	0.3 ∕1.1 ∕0.7	129	3
In vivo (FSaII) tumors	SFUS	3.5	0.3 ∕0.5	120	2
	AFUS	3.5	0.3 ∕0.5 ∕0.4	90	5

After the object (e.g., phantom, excised porcine liver, or anesthetized mouse) was placed on the platform, the entire AFUS and object were moved until the laser beams intersected on a single point on the surface of the target (Fig. 2). Next, the AFUS device was moved using micromanipulators toward the object along its main axis by a distance equal to the desired depth of the lesion. The depth is given by the distance between the two laser foci (w) on the surface of the object if the object’s surface is essentially flat over the length w, where the length w is twice the depth of the lesion (Fig. 2). Once the applicator and object were set up, acoustic gel was used for coupling. The sonications were then performed using the parameters in Table 3. The temperature histories during the phantom and ex vivo sonications near the focal zone were measured using a 0.2 mm needle thermocouple (minihypodermic thermocouple probe, model HYP-0, Omega, Stamford, CT) and recorded with a PC-controlled 8-channel thermometry unit (DI-1000TC, DataAq Instruments, Akron, OH). To avoid temperature artifacts due to viscous heating, the thermocouple was positioned 5 mm away from the focus.

Post-treatment performance evaluations

After the sonications in polyacrylamide phantom gel and excised porcine livers, the thermal lesions were manually outlined on photographs. To quantitatively evaluate the roundness of the lesions produced by the AFUS and SFUS, the sphericity for each case was calculated based on the assumption each lesion was symmetric around both its major and minor axes, which were used to estimate each lesion’s volume and surface area.

After in vivo ablations, the tumors were sectioned and completely submerged in the solution of TTC for 2 h at 37 °C and then were kept in a solution of formalin. The fixed ablated tumor samples were cut into slices with each approximately 1 mm thick. The lesions were then contoured along the boundary of the white areas that were rendered nonviable due to the ablations. Based on the 3D volumes that were reconstructed from these multislice contours, the roundness of the lesions was quantitatively evaluated between AFUS and SFUS. To confirm the heating performance of AFUS ablations, in another batch of three mice after fixations (2 days), we performed histological analysis of in vivo ablated mouse tumors with hematoxylin and eosin (H&E) to determine cell viability.

RESULTS

Simulations

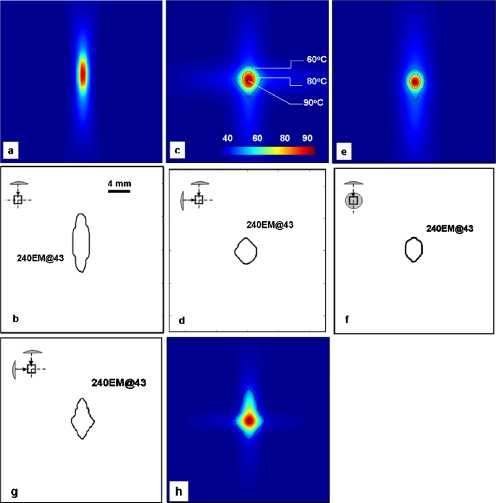
The ability of the AFUS to create spheroidal lesions was first evaluated by calculating the sphericity (ψ) of the resulting lesions under the simulation conditions specified in Table 2. The contours of temperature isotherms and 240 EM@43 thermal distributions are shown in Fig. 4. Corresponding to the control case listed in Table 2, Figs. 4a, 4b show a typical elongated ellipsoidal lesion produced by sonicating with a SFUS with peak intensity (I_SP) of 432 W∕cm² using a duty cycle of 0.5 s on∕0.5 s off for 4 s. Figures 4c, 4d, 4e, 4f showed the axial and sagittal views of the spheroidal lesions that were created with the AFUS with peak intensity (I_SP) of 432 W∕cm², a duty cycle of 0.3 s on∕1.1 s off∕0.7 s delay for 8 s. Figures 4g, 4h showed the simulation with the AFUS with I_SP=432 W∕cm² for 10 s and an unequal duty cycles for the two transducers: A duty cycle=0.2 s on∕0.6 s off∕0.4 s delay for one transducer and a duty cycle=0.1 s on∕0.6 s off∕0.4 s delay for the other transducer.

Figure 4.

Simulated temperature distribution produced by [(a) and (b)] a single transducer with I_SP=432 W∕cm² for 4 s, i.e., the first case (without perfusion) in Table 2. [(c)–(f)] AFUS with I_SP=432 W∕cm² and evenly spaced duty cycle of 0.3 s on/1.1 s off/0.7 s delay for 8 s, the second case (without perfusion) in Table 2. We also demonstrated the effect of unevenly distributed firing scheme in (g)–(h), i.e., AFUS with I_SP=432 W∕cm² and unevenly spaced duty cycles for two transducers for 10 s, without perfusion: A duty cycle=0.2 s on/0.6 s off/0.4 s delay for one transducer and a duty cycle=0.1 s on/0.6 s off/0.4 s delay for the other transducer. The relative orientation and position of the transducers are shown in the upper left corner of (b)–(g).

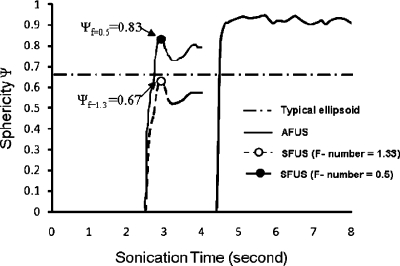
Figure 5 compares the change in sphericity as a function of time for case 1 in Table 2 for a single transducer and case 2 for the AFUS. After starting the sonications, the 240 EM@43 thermal dose contours emerge at 2.5 and 4.5 s, respectively. For reference, the sphericity corresponding to a typical ellipsoid (ψ=0.6745) is also plotted. Compared to the lesion created with a SFUS, the sphericity ψ created by the AFUS was approximately 50% larger, as shown in Fig. 5. The fluctuations of the sphericity with time were caused by the firing scheme of the AFUS and the single transducer. Particularly, the smaller variations in sphericity about ψ=0.9 for the AFUS imply that the shape of the lesion remains consistent from the beginning of lesion appearance to the end of the sonication, while the lesion (the volume of the 240 EM@43 isocontour) grows. The sphericity was calculated for the entire duration of 4 and 8 s exposures for the SFUS and the AFUS cases, respectively. The exposure times in Figs. 56 were selected so that the peak temperature in the field was less than or equal to 90 °C.

Figure 5.

The simulated sphericity of the 240 EM@43 thermal dose contour produced by the SFUS and the AFUS. As a reference, the sphericity for a typical ellipsoid (0.67, long length=10 mm and short length=3 mm), and the theoretical sphericity value for SFUS with high F-number (e.g., 1.33) and lower F-number (e.g., 0.5) was given as another reference line. The firing scheme was 0.5 s∕0.5 s for SFUS and 0.3 s∕1.1 s∕0.7 s for AFUS. The sphericity of a sphere is by definition equal to 1.0.

Figure 6.

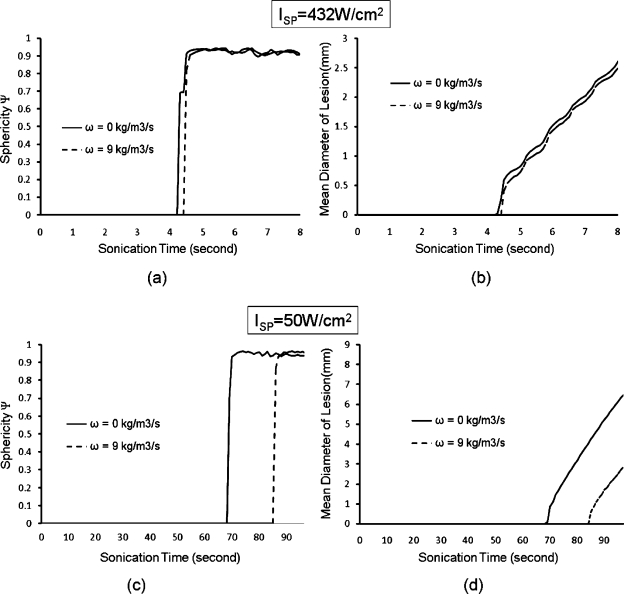
Sphericities and lesion sizes for different power levels for the AFUS. [(a) and (b)] I_SP=432 W∕cm², i.e., the maximum focal pressure=3.5 MPa, duty cycle=0.3 s on∕1.1 s off∕0.7 s delay, τ=8 s; [(c) and (d)] I_SP=50 W∕cm², i.e., the maximum focal pressure=0.4 MPa, duty cycle=0.3 s on∕1.1 s off∕0.7 s delay, τ=110 s. The exposure times were determined by the maximal temperature of 100 °C. In (a)–(d), two different perfusions (0 and 9 kg∕m³ s) were simulated.

Furthermore, the effect of different power levels and blood perfusion on sphericity was analyzed, as demonstrated in Figs. 6a, 6b, 6c, 6d. For a low peak intensity (I_SP=50 W∕cm²), a high blood perfusion (ω=9 kg∕m³ s) significantly delays the time to the beginning of lesion formation. In this case, a relatively large spherical lesion (ψ=0.9, 6.5 mm in diameter) was achieved at the cost of a long sonication duration of 100 s. For a moderate peak intensity (I_SP=432 W∕cm², i.e., the maximum focal pressure=3.5 MPa), the differences in the shape and size of the lesions between null perfusion and a high perfusion rate (ω=0 and 9 kg∕m³ s, respectively) were negligible. This finding implies that a high power level can create lesions with high sphericity (ψ=0.9) rapidly, whose sizes are independent of the blood perfusion rate.

Experiments

Thermal lesioning in phantom gels

Taking advantage of the opaque characteristic of our phantom gels and the change in color due to temperature rise, the shapes of the lesions created by an AFUS following different firing schemes were qualitatively visualized in all three spatial dimensions. The sonication with an acoustic power input of 30 W by a single spherically focused transducer continuously for 50 s produced an elongated ellipsoid lesion as expected [Fig. 7a]. In Fig. 7b, the AFUS was run with acoustic power input of 20 W (I_SP≈432 W∕cm², i.e., the maximum focal pressure≈3.5 MPa) for 140 s with unequal duty cycles for the two transducers: A duty cycle=0.2 s on∕0.6 s off∕0.4 s delay for one transducer and a duty cycle=0.1 s on∕0.6 s off∕0.4 s delay for the other transducer. Figure 7c demonstrates the results using the conditions as in Fig. 7b with a shorter duration, 110 s. In Figs. 7d, 7e, 7f, the dual transducers were excited with an acoustic power input of 20 W and the same duty cycle (0.3 s on∕1.1 s off∕0.7 s delay). The cross-sectional view of Fig. 7e displayed in Fig. 7f clearly shows a circular lesion. The sphericities of the lesion in Figs. 7a, 7b, 7c, 7d, 7e were estimated based on the visible major and minor axes. The sphericity values ranged from 0.62 of a single transducer to 0.70, 0.77, and 0.85 for the AFUS heating with unequal duty cycles, to 0.95 of the AFUS heating with equal duty cycles. The depths of all the lesions were about 2 cm along the transducer axes.

Figure 7.

Axial and cross-sectional view photographs of phantom gel thermal lesioning by (a) a single spherically focused transducer with the acoustic power input of 30 W continuously for 50 s; (b) AFUS with 20 W for 140 s with unequal duty cycles: A duty cycle=0.2 s on∕0.6 s off∕0.4 s delay for one transducer and a duty cycle=0.1 s on∕0.6 s off∕0.4 s delay for the other. (c) The same as (b) but for a shorter duration, 110 s. [(d) and (e)] AFUS with 20 W with equal duty cycles (0.3 s on∕1.1 s off∕0.7 s delay) for 129 and 110 s, respectively. (f) Cross-sectional view of (e). The depths of all the lesions (between the centers of the lesions to the surface of the phantom) were about 2 cm along the transducer axes.

Thermal ablations in ex vivo porcine livers

Thermal ablations were conducted in excised fresh porcine liver. Two elliptical lesions produced by a SFUS with an acoustic input power of 30 W and a duty cycle=0.2 s on∕0.2 s off for 50 s are shown in Fig. 8a. Figure 8b shows an axial-lateral cut (with respect to the coordinates of the ultrasound transducers) of the porcine liver ablated using the AFUS with acoustic power input of 20 W (I_sp≈432 W∕cm², i.e., the maximum focal pressure≈3.5 MPa) and duty cycle of 0.2 s on∕0.6 s off∕0.4 s delay, for 140 s. Figures 8c, 8d show lesions created at depths of 5 and 10 mm from the surface, ablated using the AFUS with 20 W, a duty cycle=0.3 s on∕1.1 s off∕0.7 s delay for 110 and 129 s, respectively. The sphericities of these lesions were estimated based on the long and short axis. The values of ψ ranged from 0.65 for the ellipsoid lesions produced by the SFUS to >0.9 for the AFUS-induced lesion in Fig. 8c. There was no tissue ablation evident between the lesion at depth and the surface of the tissue sample. For all lesions, a cross section of the ablated tissue indicated spherically shaped tissue damage. For example, a cross-sectional view of the lesion in Fig. 8b is shown in Fig. 8e.

Figure 8.

Photographs of sectioned porcine liver tissues after ablation. (a) Lesion produced by the SFUS with acoustic power input of 30 W and a duty cycle of 0.2 s on/0.2 s off for 50 s. Note: As indicated by the white arrow, a separate lesion was previously created from a different angle. (b) Lesion by the AFUS applicator with 20 W and duty cycle of 0.2 s on/0.6 s off/0.4 s delay for 140 s. (c) Lesion by the AFUS applicator with 20 W, a duty cycle of 0.3 s on/1.1 s off/0.7 s delay for 110 s at the depth of 5 mm. (d) Lesion by the AFUS applicator with 20 W, a duty cycle of 0.3 s on/1.1 s off/0.7 s delay for 129 s at the depth of 10 mm. Note: The black arrows in (a)–(d) show the approximate direction of the incoming ultrasound beams. (e) Cross-sectional cut of the same ablation as (b) to show the shape of the lesion in three dimensions.

Thermal ablations in mouse murine tumors in vivo

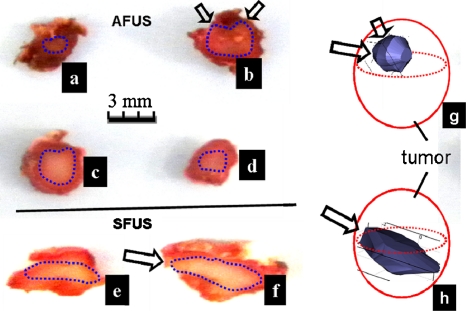
Figure 9 presents thermal ablations performed with both the AFUS and the SFUS on live tumors. We started by using firing schemes in the experiments that were close to those simulated. After a few trials, we chose firing schemes that produced good results experimentally. As shown in the in vivo cases of Table 3, the firing schemes were as follows: An AFUS 20 W of acoustic power (I_SP≈432 W∕cm², i.e., the maximum focal pressure≈3.5 MPa) for 1.5 min using a duty cycle=0.3 s on∕0.5 s off∕0.4 s delay (five mice), and a SFUS with 20 W for 2 min using a duty cycle=0.3 s on∕0.5 s off (two mice) as a reference. After the tumors were processed with TTC staining and fixed with formalin, the lesions were sectioned into multiple slices (with thickness approximately of 1 mm). Figures 9a, 9b, 9c, 9d are four TTC-stained slices of the AFUS-induced lesion, while Figs. 9f, 9g show two TTC-stained slices of the SFUS-induced lesion. Based on the segmented lesions that were defined by the white areas, 3D volumes were reconstructed and the sphericities ψ were calculated. The sphericity values were 0.40±0.03 and 0.60±0.05 (mean±S.D.) for the SFUS- and AFUS-induced lesions, respectively. Unlike the ex vivo cases, in which the 3D lesion volumes were reconstructed by rotating the 2D contours, the sphericity for in vivo experiments was calculated from volumes reconstructed based on the actual TTC-stained images. The uncertainty in sphericity calculation induced by the slice thickness and manual segmentation was estimated within 5% for both SFUS and AFUS cases as follows: The error due to slice thickness (∼2%) was estimated by comparing the sphericity of a smooth 3D simulated thermal lesion and a 3D volume of the same lesion that was linearly reconstructed from three slices of 2D contours. The bias of sphericity induced by manual segmentation was estimated by performing and comparing three independent manual segmentations; the variation in the calculated sphericity was approximately 3%. Due to the irregularity of the reconstructed surface, the sphericity was much lower than those in ex vivo experiments. Another factor, of course, was blood perfusion. However, the percentage increase in sphericity induced by using AFUS is about 50%, well above the uncertainty.

Figure 9.

Typical examples of TTC-stained slices for AFUS and SFUS ablations in FSaII tumors. (a)–(d) are four slices of tissue ablated with the AFUS. Thermal lesions in (e) and (f) were produced by the SFUS. The 3D volumes were reconstructed as shown in (g) and (h), based on which sphericities were calculated. The firing schemes were for the AFUS (acoustic power 20 W, I_SP=432 W∕cm², i.e., the maximum focal pressure=3.5 MPa) and duty cycle=0.3 s on/0.5 s off/0.4 s delay for 1.5 min, and for the SFUS 20 W and duty cycle=0.3 s /0.5 s for 2 min. The arrows indicate the directions of the ultrasound waves.

Three examples of H&E histological images of SFUS and AFUS-ablated mice tumor tissues are shown in Fig. 10, all harvested at 7 days postablation to check the viability of the ablated tumor.

Figure 10.

Viability with H&E histological image after AFUS ablations (similar results for SFUS ablations). The contour highlights ablated zone consisting of necrotic tumor debris (thick arrow) and region of additional cell death from inflammation (star). Peripheral viable tumor is present (thin arrow). Higher magnification images (200× magnification, bar is 50 μm long) of viable tumor (b), necrotic inflammatory debris (c), and ablated tumor (d).

DISCUSSION AND CONCLUSIONS

Currently, in small animal studies, HIFU systems based on a single spherically focused transducer are widely used.^{21, 29, 30, 31, 32} However, we found that with the typical elongated ellipsoidal focus produced by single transducers, it was difficult to confine the thermal lesion within the small (usually 8–10 mm in diameter) and roughly spherical tumors that are commonly grown in small experimental animals. Smaller lesions can be produced by single transducers with low F-numbers (e.g., 0.5), but at the cost of shorter focal lengths that require the transducer to be closer to the animal, which may present logistical problems. This fact motivated us to develop an instrument capable of producing spheroidal thermal ablation lesions noninvasively within small tumors without damaging the overlying tissue and skin. The AFUS therefore was designed and developed, as described in Figs. 12. Hydrophone measurements of focal pressure fields presented in Fig. 3 showed close agreement with numerical simulations for one of the two spherically focused ultrasound transducers making up the AFUS. Numerical studies and experimental characterization were performed using phantom gels and ex vivo and in vivo preparations. All of the results (Figs. 456789) demonstrated that the AFUS was able to create spheroidal lesions (1–10 mm in diameter) noninvasively without inducing damage to surrounding tissues given an adequate choice of sonication parameters (firing scheme and intensity).

Interestingly, moderate spatial peak intensities (I_SP<500 W∕cm², i.e., the maximum pressure of 4 MPa) were necessary to avoid creating ellipsoidal lesions instantaneously. For higher power levels (I_SP⪢500 W∕cm², results not shown), ellipsoidal lesions were generated immediately during the first pulse (e.g., the first 0.3 s of sonication) from one transducer, which allows no chance for constructing a spherical lesion by overlapping pulses alternatively from the two transducers. In addition, high intensities may induce nonlinear and cavitation effects that were not accounted for by the models used in this project. Numerical simulations also showed that in a homogeneous medium, the sphericity of a lesion depended on the duty cycles but not on the perfusion rate [Figs. 6a, 6b]. In other words, as long as moderate intensities are used and the duty cycle pulses are distributed equally among the transducers, a spheroidal lesion can be produced regardless of blood perfusion. It was also shown that oscillations in the sphericity vs time curves coincided with the firing schemes.

In in vivo experiments, complexities were introduced by the heterogeneities in acoustic and thermal properties, the presence of blood vessels of differing sizes, and capillary blood perfusion. In spite of these, the TTC-stained tissue slices of ablated mouse tumors demonstrated positive results: The AFUS-created lesions had larger sphericity values than the SFUS-created lesions even without monitoring temperature distributions. We understood that measuring interstitial temperature using a thermocouple was not adequate monitoring because of uncertainty in the location of the thermocouple with respect to the focus and potential viscous heating effects. We used thermocouple monitoring only to ensure that heating was occurring. Certainly, three dimensional temperature monitoring and feedback control are needed; we are currently working on a MRI-compatible AFUS system.

As mentioned in Sec. 1, we had reasons to expect the AFUS to produce more spherical lesions than a single focused transducer. By combining two identical ellipsoidal foci orthogonally, the time-averaged ultrasound absorbed energy distribution becomes “rounded” at the intersection region of the foci. At moderately intensities, the firing schemes allow time for thermal diffusion processes (heat conduction in tissues and heat convection by blood perfusion) to spread the heat energy away from the foci, thereby contributing to the creation of a spheroidal region of high temperature. This explains why the sphericities of lesions generated in phantom gels, in liver ex vivo, and in tumors in vivo were consistently of higher value for the AFUS-created than for the SFUS-created lesions. Obviously, this effect can be magnified further by adding additional transducers firing from other angles around a common focal spot. Another approach could be to use mechanical steering of an AFUS or a SFUS at a cost of increased complexity. However, as shown in this paper, two transducers seem to provide an adequate solution with a reasonable increase in complexity and cost.

In summary, this study demonstrated the concept of using a dual transducer alternating focused ultrasound system to noninvasively induce small spheroidal thermal lesions inside tumors grown in small laboratory animals. Our AFUS is currently being used to study molecular, cellular, and physiological effects of combining thermal ablation and ionizing radiation in cancer therapy.