Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Apr 1.
Published in final edited form as: J Biomol Screen. 2010 Jun 14;15(6):680–686. doi: 10.1177/1087057110372803

An Economic Framework to Prioritize Confirmatory Tests Following a High-Throughput Screen

S Joshua Swamidass 1,*, Joshua A Bittker 2, Nicole E Bodycombe 2, Sean P Ryder 3, Paul A Clemons 2,*
PMCID: PMC3069998  NIHMSID: NIHMS280503  PMID: 20547534

Abstract

How many hits from a high-throughput screen should be sent for confirmatory experiments? Analytical answers to this question are derived from statistics alone and aim to fix, for example, the false-discovery rate at a predetermined tolerance. These methods, however, neglect local economic context and consequently lead to irrational experimental strategies. In contrast, we argue that this question is essentially economic, not statistical, and is amenable to an economic analysis that admits an optimal solution. This solution, in turn, suggests a novel tool for deciding the number of hits to confirm, the marginal cost of discovery, which meaningfully quantifies the local economic trade-off between true and false positives, yielding an economically optimal experimental strategy. Validated with retrospective simulations and prospective experiments, this strategy identified 157 additional actives which had been erroneously labeled inactive in at least one real-world screening experiment.

2 Introduction

Deciding how many initial positives (“hits”) from a high-throughput screen to submit for confirmatory experiments is a basic task faced by all screeners (Storey, Dai & Leek 2007, Rocke 2004). Often, several hits are experimentally confirmed by ensuring they exhibit the characteristic dose-response behavior common to true actives. We introduce an economic framework for deciding the optimal number to send for confirmatory testing.

Many screeners arbitrarily pick the number of hits to experimentally confirm. There are, however, rigorous statistical methods for selecting the number of compounds to test by carefully considering each compound's screening activity in relation to all compounds tested (Zhang, Chung & Oldenburg 2000, Brideau, Gunter, Pikounis & Liaw 2003) or the distribution of negative (e.g., DMSO treatment) controls (Seiler, George, Happ, Bodycombe, Carrinski, Norton, Brudz, Sullivan, Muhlich, Serrano et al. 2008). In either case, a p-value is associated with each screened compound and a multi-test correction is used to decide the number of hits to send for confirmatory testing. One of the oldest and most conservative of these corrections is the Bonferroni correction, a type of family-wise error rate (FWER) correction that tests the hypothesis that all hits are true actives with high probability (van der Laan, Dudoit & Pollard 2004a, van der Laan, Dudoit & Pollard 2004b). More commonly, false discovery rate (FDR) methods are used to fix the confirmatory experiment's failure rate at a predetermined proportion (Benjamini & Hochberg 1995, Reiner, Yekutieli & Benjamini 2003). Although more principled than ad hoc methods, all multi-test correction strategies require the screener to arbitrarily choose an error tolerance without much theoretical guidance.

These methods, which balance global statistical tradeoffs based on arbitrarily chosen parameters, are not sensible in the context of high-throughput screening. In a two-stage experiment—a large screen followed by fewer confirmatory experiments—global statements about the statistical confidence of hits based on the screen alone are less useful because confirmatory tests can establish the activity (or inactivity) of any hit with high certainty, are much less expensive than the total screening costs, and are required for publication. The experimental design itself implies an economic constraint; resource limitations are the only reason all compounds are not tested for dose-response behavior. We argue, therefore, that the real task facing a screener is better defined as an economic optimization rather than a statistical tradeoff.

Tasks like this, deciding the optimal quantity of “goods” to “produce,” have a rich history and form the basis of economic optimization (Varian Hal 1992). This optimization aims to maximize the utility minus the cost: the surplus. One of the most important results from analyzing this optimization is that the globally optimal point at which to stop attempting to confirm additional hits can be located by iteratively quantifying whether the local tradeoff between true positives and false positives is sensible. A local analysis admits a globally optimal solution. This result motivates our framework.

3 Methods

Our economic framework is defined by three modular components: (1) a utility model for different outcomes of dose-response experiments, (2) a cost model of obtaining the dose-response data for a particular molecule, and (3) a predictive model for forecasting how particular compounds will behave in the dose-response experiment. After each dose-response plate is tested, the predictive model is trained on the results of all confirmatory experiments performed thus far. This trained model is then used to compute the probability that each unconfirmed hit will be determined to be a true hit if tested. Using the utility model and cost model in conjunction with these probabilities, the contents of the next dose-response plate are selected to maximize the expected surplus (expected utility minus expected cost) of the new plate, and the plate is only run if its expected surplus is greater than zero.

This framework maps directly to an economic analysis. From calculus it can be derived that the point at which a pair of supply and demand curves intersect corresponds to the point that maximizes total surplus. This point of intersection is also the last dose-response plate with a marginal surplus greater than zero. The utility model quantifies how the screener values different outcomes of the confirmatory study. This information is used to define a demand curve: the marginal utility as a function of the number of successfully confirmed actives so far. The cost model exposes the cost of obtaining a particular dose-response curve and is expressed in the same units as the utility. The predictive model forecasts the outcome of future confirmatory experiments and, together with the cost model, is used to define a supply curve: the marginal cost of discovery (MCD) as a function of the number of actives successfully confirmed as actives.

Explicitly computing the expected surplus in order to determine an optimal stop point is critically dependent on modeling a screener's utility function with mathematical formulas, a daunting task that requires in-depth surveys or substantial historical data in addition to assumptions about the screener's response to risk (Kroes & Sheldon 1988, Houthakker 1950, Schoemaker 1982). However, in practice, the expected surplus need not be explicitly computed to solve this problem. We can access the relevant summary of screeners’ preferences by repeatedly asking whether they are willing to pay the required amount to successfully confirm one more active. Iteratively exposing the MCD to the screener is like placing a price tag on the next unit of discovery, and interrogating the screener is equivalent to computing whether or not the marginal surplus is greater than zero. For illustration purposes, however, we do use mathematical utility functions to show that simple predictive models, which map screening activity to the dose-response outcome, can be constructed, and that these models admit near optimal economic decisions. To our knowledge, this is the first time formal economic analysis has informed a high-throughput screening protocol.

3.1 High-throughput screen

The technical details of the assay and subsequent analysis can be found in PubChem (PubChem AIDs 1832 and 1833). For approximately 300,000 small molecules screened in duplicate, activity is defined as the mean of final, corrected percent inhibition. After molecules with autofluorescence and those without additional material readily available were filtered out, 1,323 compounds with at least one activity greater than 25% were labeled ‘hits’ and tested for dose-response behavior in the first batch. Of these tested compounds, 839 yielded data consistent with inhibitory activity. Each hit was considered a “successfully confirmed active” if the effective concentration at half maximal activity (EC50) was less than or equal to 20μM. Using this criterion, 411 molecules were determined to be active.

3.2 Utility model

In this study, one unit of discovery is defined as a single successfully confirmed active. The utility model is defined as a function of the number of confirmed actives obtained so far, n. We consider two utility models. First, in the fixed-return model (F) we fix the marginal utility, U′(n), for each confirmed hit at $50. Second, we consider a more realistic diminishing- returns model (D) where the marginal utility of the nth confirmed hit is $(max[502 − 2n, 0]). The utility function for each model can be derived by considering the boundary condition U(0) = $0, yielding U(n) = $(50n) for F and U(n) = $(501 min[n, 250] − min[n, 250]2) for D.

3.3 Cost model

We use a fixed-cost model where each plate costs the same amount of money, C(p(n))= $(400 p(n)), where p(n) is the total number of plates required to confirm actives. Allowing for 12 positive and 12 negative controls on each plate and measuring six concentrations in duplicate, 30 dose-response curves can be tested on a single 384-well plate. We assume the first such plate tests the 30 hits with highest activity in the original screen. Subsequent plates are filled to maximize expected surplus as described in the Introduction.

Clearly, in many scenarios it is not easy or meaningful to place a dollar value on the cost of doing a confirmatory experiment. In these cases, we recommend expressing the cost function in more general units: the number of confirmatory tests (NCT) required. In our example, this is equivalent to using the cost model defined as C(p(n))= (30 p(n)) NCT. This amounts to a negligible change in the downstream analysis which only changes the y-axis of the resulting supply and demand curves without affecting their shapes. An example of how this strategy functions in practice is included in the results.

3.4 Predictive model

We consider two predictive models: a logistic regressor (LR) (Dreiseitl & Ohno-Machado 2002) and neural network with a single hidden node (NN1) (Baldi & Brunak 2001), structured to use the screen activity as the single independent variable and using the result of the associated confirmatory experiment as the single dependent variable. Both models were trained using gradient descent on the cross-entropy error. This protocol yields models whose outputs are interpretable as probabilities.

3.5 Ordering hits for confirmation

Any combination of either of the two predictive models(LR and NN1) with either of the two utility models (F and D) and a fixed-cost model will always test hits in order of their activity in the screen. The proof is as follows: the cost of screening a dose-response plate is fixed and therefore irrelevant to ordering hits. Maximizing the expected utility is exactly equivalent to maximizing the expected number of true hits in the plate. Both NN1 and LR are monotonic transforms of their input; so maximizing the expected number of confirmed hits in a plate is equivalent to selecting the hits with the highest activity. These schemes, therefore, order compounds by activity.

3.6 Experimental yield and marginal cost of discovery

Most experiments compute the expected MCD by dividing the cost of the next plate by the number of confirmed actives expected to be found within it, using either LR or NN1. The expected number of actives, the yield, is computed by summing the outputs of either LR or NN1 over all molecules tested in the plate. For the data, the MCD is computed by dividing the cost of each plate by the actual number of confirmed actives within it. When communicating the MCD to our screening team, we present the MCD as the number of confirmatory tests required to successfully confirm one more active instead of dollars. This cost is computed by dividing the number of confirmatory experiments proposed (462 in this case) by the forecast experimental yield.

4 Results

4.1 Relationship between potency and screen activity

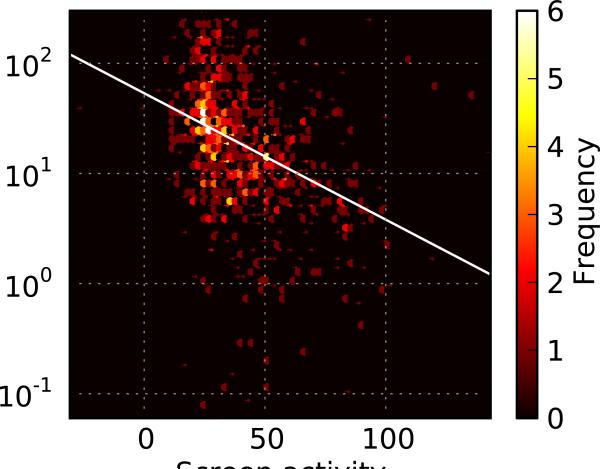
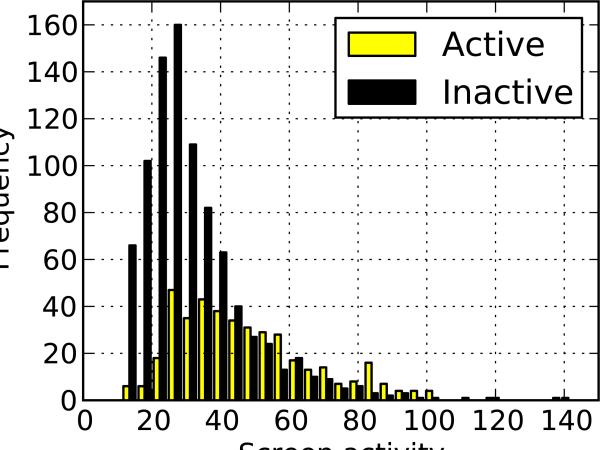
For illustration, we use the data from a fluorescence polarization screen for binding inhibitors of the C. elegans protein MEX-5 to the tcr2 element of its cognate target, glp-1 (Pagano, Farley, McCoig & Ryder 2007). Additional details are included in the Methods section. As would be expected in any successful screen, potency and screening activity are correlated (Figure 1a; N = 839 and R = 0.3656 with p < 0.0001). Similarly, actives and inactives are associated with different distributions that are not separable, overlapping substantially (Figure 1b; actives having N = 411 with 47.60 mean and 20.48 s.d. compared with inactives having N = 912 with 31.70 mean and 16.80 s.d.).

Figure 1.

Figure 1

Figure 1

Open in a new tab

Relationship between potency and activity. (a) Scatter plot demonstrating the relationship between a small molecule's confirmed potency and activity in the initial screen. (b) Distribution of molecules that were verified either active or inactive by dose-response experiments.

4.2 Feasibility of forecasting experimental yield

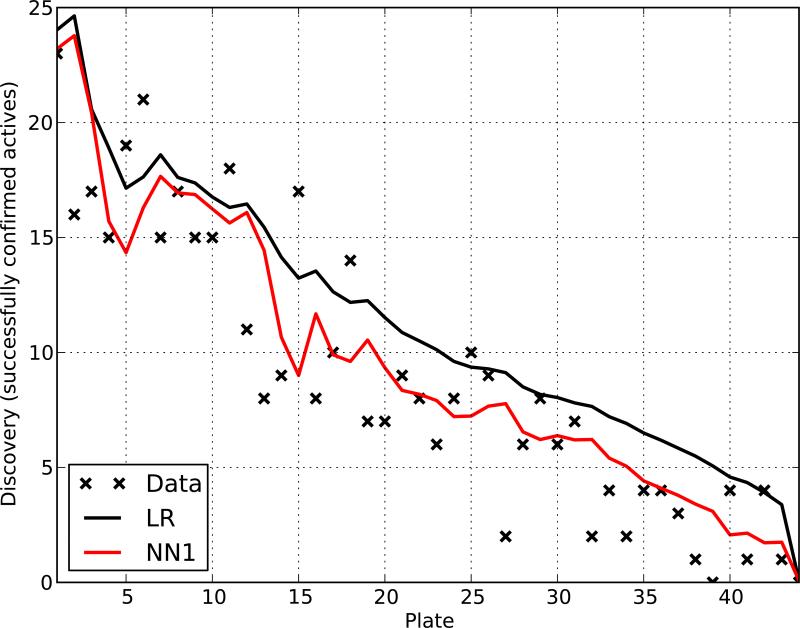
One critical test of our method's feasibility is to confirm that simple predictive models can accurately forecast the number of successfully confirmed actives in future experiments. The predictive model must extrapolate predictions on data outside the range of the training inputs. We expect that the simplest models, like LR or NN1, will extrapolate well, perhaps better than more complex models, because they will not easily overfit the data. As expected from a model with more parameters, NN1 fits the data more closely than LR (Figure 2), yielding an average residual of 2.35 compared with LR's average residual of 3.07. Certainly, there is systematic error in LR's predictions that could, possibly, be corrected. Nonetheless, both models yield curves that appear to be moving averages of the data, showing that simple models do seem to enable reasonable forecasts.

Figure 2.

Figure 2

Open in a new tab

Forecast confirmation rate. Observed and predicted (LR and NN1) number of actives for each plate. Each prediction is based on the results of all plates with lower numbers.

4.3 Prospective supply curve

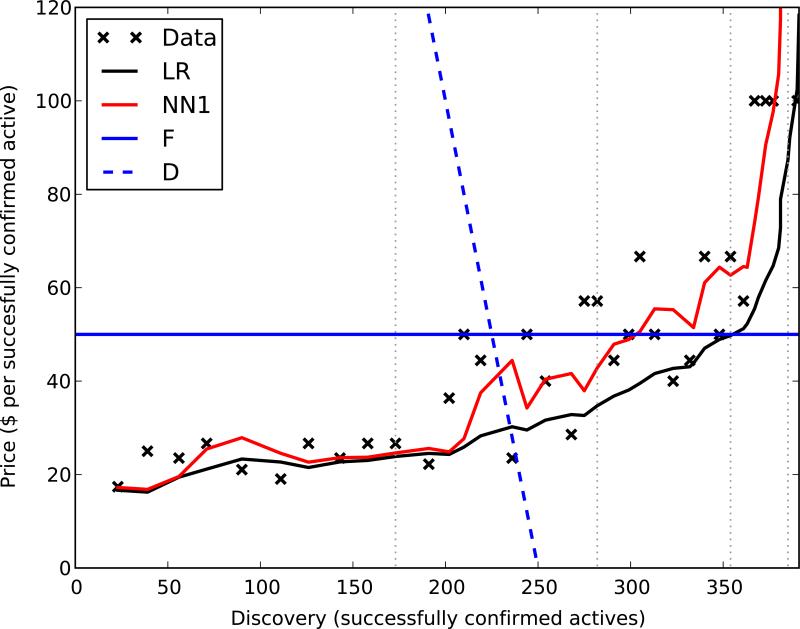
We can also evaluate this framework by considering the shape of forecast supply curves (Figure 3). Unsurprisingly, NN1 fits the data better than LR; a supply curve is the yield plotted in a particular manner. On the same graph, we can also plot demand curves derived from our two utility models. For each pair of supply and demand curves, their intersection is the predicted optimal stop point. This point is different for different demand curves, reflecting the differences amongst screeners’ budgets and projects’ value; this is exactly the behavior we hoped to observe.

Figure 3.

Figure 3

Open in a new tab

Supply and demand. Predicted supply curves (LR and NN1) plotted with demand curves (F and D) derived from two utility models. For reference, the position of every tenth plate is denoted as a vertical gridline.

4.4 Economic optimality of stop points

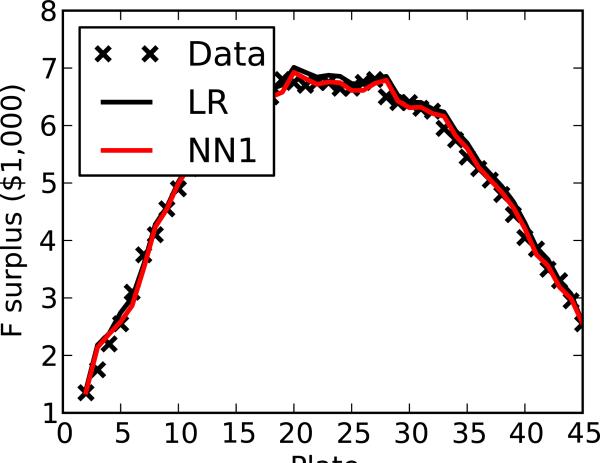
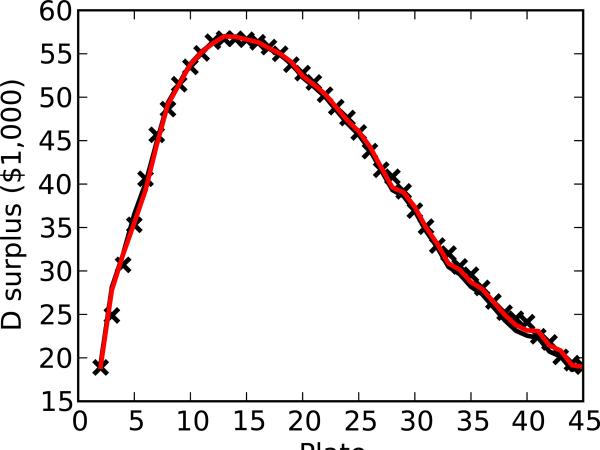
Predicted stop points can be evaluated by comparing them to the optimal stop points, those empirically found to yield the highest surplus. The surplus varies with the number of compounds tested, has several nearly equivalent plates for F, and a clearer peak for D (Figure 4). For F, the optimal stop point is either dose-response plate 19 or 27, yielding a surplus of $6,800. NN1 and LR indicate the screener should stop after plate 24 or 32 yielding surpluses of $6,750 and $6,250, respectively. For D, both NN1 and LR indicate the screener should stop after plate 15, yielding a surplus of $56,618, within 0.2% of the optimal stop point at plate 13, with a surplus of $56,738. The MCD succeeds in prospectively finding a nearly optimal solution.

Figure 4.

Figure 4

Figure 4

Open in a new tab

Surplus as a function of stop point for both (a) F and (b) D utility models, comparing observations with predictions (LR and NN1).

It is interesting to note that, with F, there are two optimal stop points, one at plate 19 and the other at plate 27. This is because stopping at either plate yields exactly the same surplus and, from the point of view of a screener with this utility function, are therefore interhangeable. Geometrically, this occurs because the true supply and demand curves intersect in two places and because the surplus has two maxima. In practice, this scenario is highly unlikely to occur because real demand curves usually slope downward and supply curves usually slope upward, thereby defining a unique optimum. In this example, however, this observation highlights that methods should be evaluated not by their ability to optimize the specific stop plate number but to optimize the computed surplus at this plate number.

4.5 Prospective validation

We further validated our methodology by presenting the MCD of the next batch of compounds to the team running the screening experiment. The MCD was presented in terms of NCT in this scenario, amounting to a simple change of units.

Predictive models were trained on the 1,323 dose response experiments performed so far; these models were then used to forecast the number of successfully confirmed actives we would expect to find by testing the next batch of compounds. The next batch of 462 compounds ranged from 19.52 to 100.25 percent activity in the original screen, over a larger window than expected because 213 of the best hits became available although they were initially unavailable when compounds for the first batch of confirmation experiments were being ordered. This batch of confirmations was predicted by LR and NN1 to yield 126.1 and 116.2 confirmed actives corresponding with an MCD of 3.66 and 3.98, respectively.

As a result of this analysis, which surprised the scientists involved, the screening team decided to obtain, and test for dose-response behavior; 157 additional compounds, which were previously presumed to be inactive, were found to be active with about 30% higher yield than predicted. This analysis proved useful to the team running the HTS experiment because they had capacity to test additional compounds and did not expect that additional actives could be retrieved at this yield. While not as accurate as forecasts on smaller batches, these forecasts provided enough information to appropriately justify testing additional compounds. In this experiment, therefore, the MCD provided the rationale to discover 157 additional actives which would otherwise have remained undiscovered. We suspect this scenario is not atypical. In HTS experiments, the cost of testing hits is low compared to the overall cost of the screen. In many cases, screeners might send more compounds for confirmatory testing with our analysis.

4.6 Comparison with FDR

It is tempting to directly compare statistical methods of error control with MCD. This comparison, however, is not straightforward because there is no correspondence between global and local error rates. However, in the context of fixed-assay cost, our fixed-utility model, F does imply a particular FDR cutoff. A maximum FDR of 0.73 would fix the average cost of confirming a hit at $50, the marginal utility for F, and also fixes the total the surplus at zero. The FDR of all dose-response plates for this example is 0.6893, below the maximum allowable FDR threshold. At least 7 additional plates of confirmatory experiments would be sent even after the screener was paying well over $50 for each additional confirmation. Confirming additional actives when their value is less than their cost, as FDR would propose, is economically irrational. Using FDR in this manner corresponds to a monopolistic supplier capturing profit at the expense of consumers by only selling their product in bundles far larger than consumers would be willing to purchase one-by-one: a well-known case from microeconomic analysis (Adams & Yellen 1976). Clearly, MCD will approximate an economically optimal solution while FDR will not.

4.7 Comparison with local FDR

There is an uncommonly used statistical method that attempts to estimate the “local” FDR from the p-values of each hit with respect to the distribution of the negative controls (Scheid & Spang 2005, Scheid & Spang 2004). Local FDR is defined as the proportion of false positives at a particular point in the prioritized list and can function as the predictive model in our framework. In the case of F, selecting the stop point at which the local FDR is 0.7333 is exactly equivalent to the economic solution we have derived. In the case of the more realistic D model, local FDR does not admit a solution by itself. There is no a priori way of determining the economically optimal local FDR threshold without knowing the utility function acceptable to the screener. So while local FDR succeeds in one simplified case, when used alone it is not capable of finding the economically optimal solution in realistic scenarios.

5 Discussion

The experiments presented here demonstrate the feasibility and power of our economic approach. For clarity, only the simplest variations have been presented. Several extensions are imaginable for each module: utility, cost, and predictive. These extensions explore how our economic analysis functions as a unified framework to quantitatively address several disparate concerns in high-throughput screening experiments.

First, more useful utility models can be derived that more accurately model the real value of screening results. As we have seen, the exact utility model can dramatically affect the economically optimal stop point, so this is a critical concern. Although the utility function of screeners remains challenging to mathematically specify, better models of the inputs into the utility function are potentially useful. For example, more meaningful definitions of a “unit of discovery,” are important because they can suggest attempting to confirm hits in different orders and increase yield even when only a fixed number of hits are to be tested. This is equivalent to change the units of the x-axis of the supply and demand curve graphs. One variation would be to define a diversity-oriented utility that measures discovery as the number of scaffolds with at least one confirmed active. Related models have been proposed in the cheminformatics literature (Clark & Webster-Clark 2008). Even more complex utility models might consider the potential of improving a downstream classifier (Danziger, Zeng, Wang, Brachmann & Lathrop 2007). We favor a “clique”-oriented utility function that counts each clique of at least three or four confirmed actives with a shared scaffold as a single unit of discovery. This models the behavior of medicinal chemists who are often only willing to optimize a lead if other confirmed actives share its scaffold. We will explore the algorithm necessary for these variations in a future study.

Second, more complex cost models can be derived that could, for example, encode the extra overhead of running smaller batch sizes. Other variations could encode the acquisition cost or the intellectual property encumbrance of particular molecules. Furthermore, in some circumstances, it may be more useful to measure cost in units of time instead of money.

Third, better predictive models are possible, including neural networks with several hidden nodes, estimates of the local FDR computed from p-values (Scheid & Spang 2005, Scheid & Spang 2004), analytic formulas based on mathematical properties of the system (Van Leijenhorst & van der Weide 2005), and predictors that take chemical information into account (Swamidass, Azencott, Lin, Gramajo, Tsai & Baldi 2009, Posner, Xi & Mills 2009). Many of these methods, however make strong assumptions about the underlying data. In contrast, our simple models make fewer assumptions and could, therefore, be more broadly applicable. Even within the structure of our simple models there are some important improvements possible. For example, adding a well-designed Bayesian prior to, for example, the logistic regressor would enable it to work appropriately even when confirmatory experiments yield no true actives, an important boundary case often encountered in HTS.

In addition to continuing to admit economically optimal experimental strategies, these extensions expose several advantages of MCD and our economic analysis over p-value based statistical methods designed to control the FDR or FWER. First, more complex predictive or utility models can reorder hits to improve the yield from confirmatory experiments while statistical methods will always prioritize compounds in the order of their screen activity. Second, the supply curve traced by MCD can be fed into higher-order models to direct more complex experimental designs while statistical methods do not yield this information. Third, MCD does not require negative or positive controls or make normality assumptions, enabling its application to datasets where calculating accurate p-values is problematic.

Finally, the immediate application of the MCD to practical HTS scenarios is straightforward, even when adaptive HTS, with plate-by-plate confirmatory experiments, is not possible. At any point after confirmatory experiments have been run, the following protocol can be applied: (1) train a predictive model on the confirmatory experiments obtained so far, (2) use this model to pick the contents of the next batch of compounds to be tested, (3) compute the MCD of this batch in terms of NCT as the number of compounds in the next batch divided by sum of the predictive model's output for each of these compounds, and (4) obtain and test these compounds if the screener feels that this MCD is an acceptable price for more confirmed actives. This analysis can even be done on publicly available HTS datasets from PubChem to discover active compounds that have yet to be discovered.

6 Conclusion

We have outlined an economic framework—from which we have derived the marginal cost of discovery (MCD)—that has applications in both science and medicine; prime candidates for its application include any experimental design where a large screen is followed up with more costly confirmatory experiments. By encoding local cost structure, MCD provides a richer, more informative analysis than statistical methods alone can provide, and yields a unified analytic framework to address several disparate tasks embedded in screening experiments.

Acknowledgements

The authors thank the Physician Scientist Training Program of the Washington University Pathology Department for supporting S.J.S.; N.E.B. and P.A.C. are supported in part by NCI's Initiative for Chemical Genetics (N01-CO-12400) and NIH Molecular Libraries Network (U54-HG005032); S.P.R. is supported by the NIH (NS-059380). We also thank Paul Swamidass and Richard Ahn for their helpful comments on the manuscript.

Footnotes

Competing Interests. The authors declare that they have no competing financial interests.

7 References

  1. Adams W, Yellen J. Commodity bundling and the burden of monopoly. The Quarterly Journal of Economics. 1976:475–498. [Google Scholar]
  2. Baldi P, Brunak S. Bioinformatics: the machine learning approach. The MIT Press; Boston: 2001. [Google Scholar]
  3. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995:289–300. [Google Scholar]
  4. Brideau C, Gunter B, Pikounis B, Liaw A. Improved statistical methods for hit selection in high-throughput screening. J Biomol Screen. 2003;8:634–647. doi: 10.1177/1087057103258285. [DOI] [PubMed] [Google Scholar]
  5. Clark R, Webster-Clark D. Managing bias in ROC curves. Journal of computer-aided molecular design. 2008;22(3):141–146. doi: 10.1007/s10822-008-9181-z. [DOI] [PubMed] [Google Scholar]
  6. Danziger S, Zeng J, Wang Y, Brachmann R, Lathrop R. Choosing where to look next in a mutation sequence space: Active Learning of informative p53 cancer rescue mutants. Bioinformatics. 2007;23(13):i104. doi: 10.1093/bioinformatics/btm166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dreiseitl S, Ohno-Machado L. Logistic regression and artificial neural network classification models: a methodology review. Journal of Biomedical Informatics. 2002;35(5-6):352–359. doi: 10.1016/s1532-0464(03)00034-0. [DOI] [PubMed] [Google Scholar]
  8. Houthakker H. Revealed preference and the utility function. Economica. 1950:159–174. [Google Scholar]
  9. Kroes E, Sheldon R. Stated preference methods: an introduction. Journal of Transport Economics and Policy. 1988:11–25. [Google Scholar]
  10. Pagano JM, Farley BM, McCoig LM, Ryder SP. Molecular basis of RNA recognition by the embryonic polarity determinant MEX-5. J. Biol. Chem. 2007;282:8883–8894. doi: 10.1074/jbc.M700079200. [DOI] [PubMed] [Google Scholar]
  11. Posner BA, Xi H, Mills JEJ. Enhanced hts hit selection via a local hit rate analysis. Journal of Chemical Information and Modeling. 2009 doi: 10.1021/ci900113d. in press. [DOI] [PubMed] [Google Scholar]
  12. Reiner A, Yekutieli D, Benjamini Y. Identifying differentially expressed genes using false discovery rate controlling procedures. Bioinformatics. 2003;19(3):368–375. doi: 10.1093/bioinformatics/btf877. [DOI] [PubMed] [Google Scholar]
  13. Rocke D. Design and analysis of experiments with high throughput biological assay data. Seminars in Cell and Developmental Biology. 2004;15(6):703–713. doi: 10.1016/j.semcdb.2004.09.007. [DOI] [PubMed] [Google Scholar]
  14. Scheid S, Spang R. A stochastic downhill search algorithm for estimating the local false discovery rate. IEEE Transactions on Computational Biology and Bioinformatics. 2004:98–108. doi: 10.1109/TCBB.2004.24. [DOI] [PubMed] [Google Scholar]
  15. Scheid S, Spang R. twilight; a Bioconductor package for estimating the local false discovery rate. Bioinformatics. 2005;21(12):2921–2922. doi: 10.1093/bioinformatics/bti436. [DOI] [PubMed] [Google Scholar]
  16. Schoemaker P. The expected utility model: its variants, purposes, evidence and limitations. Journal of Economic Literature. :529–563. (982. [Google Scholar]
  17. Seiler K, George G, Happ M, Bodycombe N, Carrinski H, Norton S, Brudz S, Sullivan J, Muhlich J, Serrano M, et al. ChemBank: a small-molecule screening and cheminformatics resource database. Nucleic Acids Research. 2008;36:D351. doi: 10.1093/nar/gkm843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Storey J, Dai J, Leek J. The optimal discovery procedure for large-scale significance testing, with applications to comparative microarray experiments. Biostatistics. 2007;8(2):414. doi: 10.1093/biostatistics/kxl019. [DOI] [PubMed] [Google Scholar]
  19. Swamidass SJ, Azencott CA, Lin TW, Gramajo H, Tsai SC, Baldi P. Influence Relevance Voting: an accurate and interpretable virtual high throughput screening method. Journal of Chemical Informatics and Modeling. 2009;49:756–766. doi: 10.1021/ci8004379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. van der Laan M, Dudoit S, Pollard K. Augmentation procedures for control of the generalized family-wise error rate and tail probabilities for the proportion of false positives. Statistical Applications in Genetics and Molecular Biology. 2004a;3(1):1042. doi: 10.2202/1544-6115.1042. [DOI] [PubMed] [Google Scholar]
  21. van der Laan M, Dudoit S, Pollard K. Multiple testing. Part II. Step-down procedures for control of the family-wise error rate. Statistical Applications in Genetics and Molecular Biology. 2004b;3(1):1041. doi: 10.2202/1544-6115.1041. [DOI] [PubMed] [Google Scholar]
  22. Van Leijenhorst D, van der Weide T. A formal derivation of Heaps’ Law. Information Sciences. 2005;170(2-4):263–272. [Google Scholar]
  23. Varian Hal R. Microeconomic Analysis. WW Norton and Co.; New York: 1992. [Google Scholar]
  24. Zhang JH, Chung TD, Oldenburg KR. Confirmation of primary active substances from high throughput screening of chemical and biological populations: a statistical approach and practical considerations. J Comb Chem. 2000;2:258–265. doi: 10.1021/cc9900706. [DOI] [PubMed] [Google Scholar]

RESOURCES