Chemical Synaptic and Gap Junctional Interactions Between Principal Neurons: Partners in Epileptogenesis

Abstract

Field potential signals, corresponding to electrographic seizures in cortical structures, often contain two components, which sometimes appear to be separable and other times to be superimposed. The first component consists of low-amplitude very fast oscillations (VFO, > 70–80 Hz); the second component consists of larger amplitude transients, lasting tens to hundreds of ms, and variously called population spikes, EEG spikes, or bursts – terms chosen in part because of the cellular correlates of the field events. To first approximation, the two components arise because of distinctive types of cellular interactions: gap junctions for VFO (a model of which is reviewed in the following), and recurrent synaptic excitation and/or inhibition for the transients. With in vitro studies of epileptic human neocortical tissue, it is possible to elicit VFO alone, or VFO superimposed on a large transient, but not a large transient without the VFO. If such observations prove to be general, they would imply that gap junction-mediated interactions are the primary factor in epileptogenesis. It appears to be the case then, that in the setting of seizure initiation (but not necessarily under physiological conditions), the gain of gap junction-mediated circuits can actually be larger than the gain in excitatory synaptic circuits.

Introduction

A critical role for recurrent synaptic excitation, in the generation of synchronized bursts of action potentials (resembling interictal spikes and ictal burst complexes in epileptic patients), has been known for upwards of 30 years now. The role of excitatory synapses was inferred, for example, by the recording of “giant” EPSPs during epileptic bursts in in vitro rodent models (Johnston & Brown, 1981; Traub & Wong, 1982), and by the ability to shorten, or entirely block, population bursts using pharmacological antagonists of AMPA/kainate or NMDA types of glutamate receptors (Lee & Hablitz, 1989; Dingledine et al., 1986; reviewed in two previous monographs: Traub & Miles, 1991; Traub et al., 1999).

Recurrent synaptic excitation, however, is not the whole story, either in human epilepsy or in experimental epilepsy models – even when one excludes so-called field bursts in low-calcium media, wherein both excitatory and inhibitory chemical synapses are blocked (Haas & Jefferys, 1982; Taylor & Dudek, 1982). Epileptiform field potentials in the disinhibited hippocampal slice, in which glutamatergic neurotransmission is intact, have long been known to contain high-frequency components, sometimes up to several hundred Hz (Schwartzkroin & Prince, 1977; Traub & Wong, 1982; Fig. 1C illustrates this phenomenon for human electrocorticographic (ECoG) data). The existence of such high-frequency components, easily visible to the naked eye and reflecting synchronized collective activity in a neuronal population, is difficult to explain via glutamatergic interactions; and, recall that in these studies, fast GABAergic inhibition was blocked, resulting in a situation wherein phasic IPSPs can not occur (unlike, for example, the case with hippocampal ripples in vivo (Ylinen et al. (1995)). The reason is that the time scale over which a single CA3 pyramidal neuron spike leads to a postsynaptic EPSP is several ms (see Fig. 2A); and, additionally, the giant EPSP, in any given pyramidal neuron during an epileptiform burst – resulting from inputs from all its presynaptic precursors – is large and smooth (see Fig. 3). As a consequence, a single EPSP alone would not allow the precise timing of a single presynaptic spike to measurably influence the timing of a postsynaptic spike: the effect of any one presynaptic spike is lost amidst the smoothed effects of the many other presynaptic spikes. Such considerations suggest that an alternative type of interaction between neurons might account for the high frequency components of the epileptiform field potential – an interaction that should be extremely fast, and in which a single action potential in one cell can produce a temporally discrete and distinguishable effect in another cell, even during a collective synchronized burst. Gap junctions between principal neurons could, in principle, provide this sort of interaction. Indeed, we shall argue that not only is epilepsy far more complex than an imbalance between synaptic excitation and inhibition, but also that gap junctions between principal neurons are likely to play a crucial role, both before and during seizure activity.

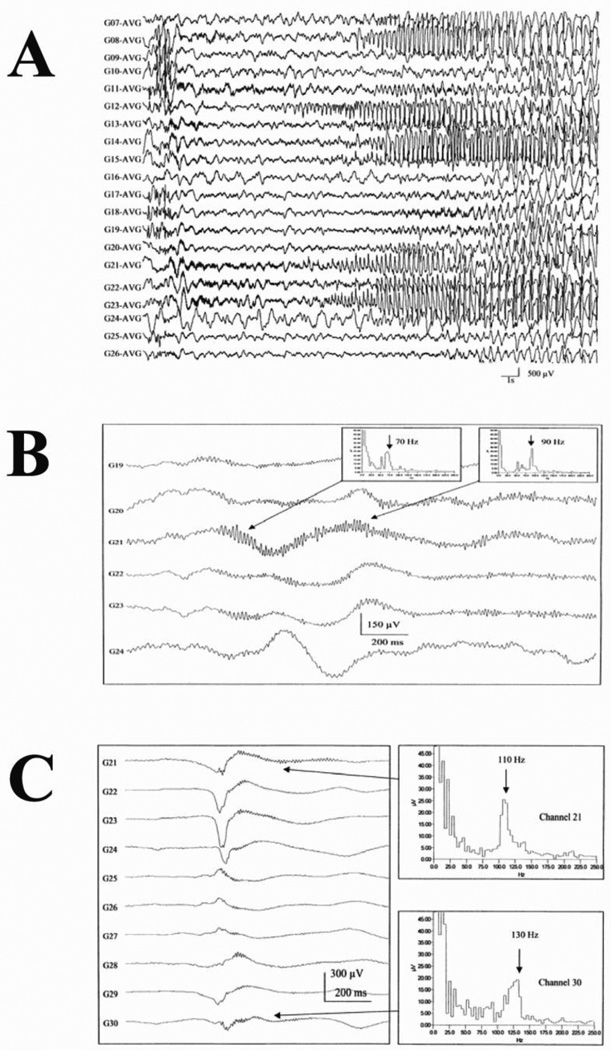
Fig. 1. Admixture of two types of population events: brief, relatively localized, VFO leading into a more extensive electrographic seizure, in a child with a subcortical dysplasia.

A focal seizure in a child is preceded by localized very fast oscillatory activity. The patient, age 13 months, had a right frontal subcortical dysplasia, subsequently removed surgically. EEG activity was recorded with a subdural grid of electrodes. (A) electrographic seizure preceded by low-amplitude very fast activity, restricted to a few recording sites (including G11, G13, G21-G23). (B) using a different recording technique, to give better signal:noise ratio, shows that the very fast activity (preceding a seizure) contains frequency components of 70 – 90 Hz. (C) an interictal burst, recorded from the same patient, contains superimposed very fast oscillations at 110–130 Hz: compare with the in vitro and in vivo interictal spikes in Fig. 3. Signals recorded and analyzed by T. Baldeweg, H. Cross and S. Boyd. (Reproduced from Traub et al. (2001).)

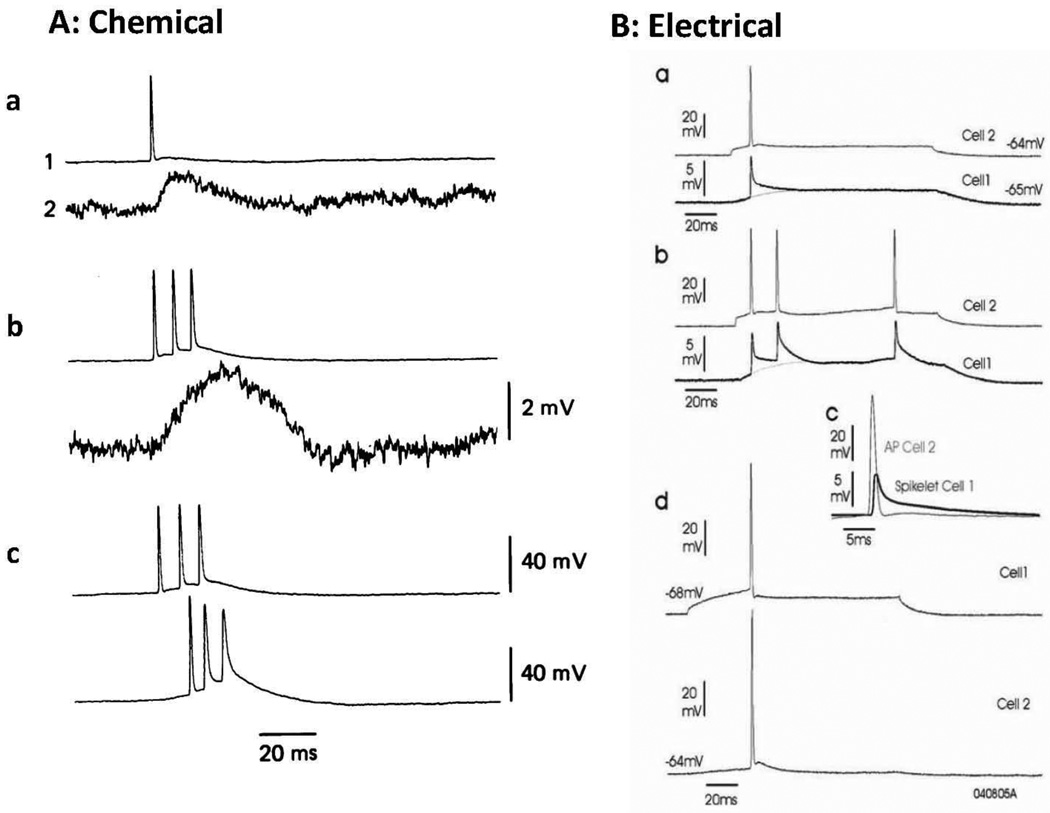
Fig. 2. Two modes of interaction between pyramidal neurons, mediated by chemical or by electrical (gap junctional) synapses.

(A) Simultaneous intracellular (sharp electrode) recordings from two monosynaptically connected CA3 pyramidal neurons in vitro, cells 1 and 2 (note the voltage scales). Cell 1 was induced to fire one or more actions potentials, with intracellular current injections. A single spike induced an EPSP (a), but a spike triplet could induce either a larger EPSP (b), or a burst (c), in the postsynaptic neuron. (B) electrical coupling between pyramidal neurons. Action potentials in CA1 pyramidal neuron can evoke spikelets in another CA1 pyramidal neuron, with latency ~0.5 ms. (Thus, if this coupling is occurring between axons, then the delay in crossing from axon to axon is <0.5 ms.) Two pyramidal neurons were somatically recorded simultaneously, with sharp electrodes, in standard bathing solution (i.e. not low Ca²⁺). a,b: current-induced spikes in cell 2 lead to spikelets in cell 1. c: the latency from spike in cell 2 to spikelet in cell 1. d: a current-induced spike in cell 1 (now shown above) leads to a spike in cell 2. [A correspondence between spikes in one CA3 hippocampal pyramidal cell with spikelets in another had previously been shown by MacVicar and Dudek (1981, 1982).] (A) from Miles & Wong (1987), (B) from Mercer et al. (2006). Electrotonic coupling between neocortical neurons is also shown in Mercer et al. (2006) and by Wang et al. (2010).

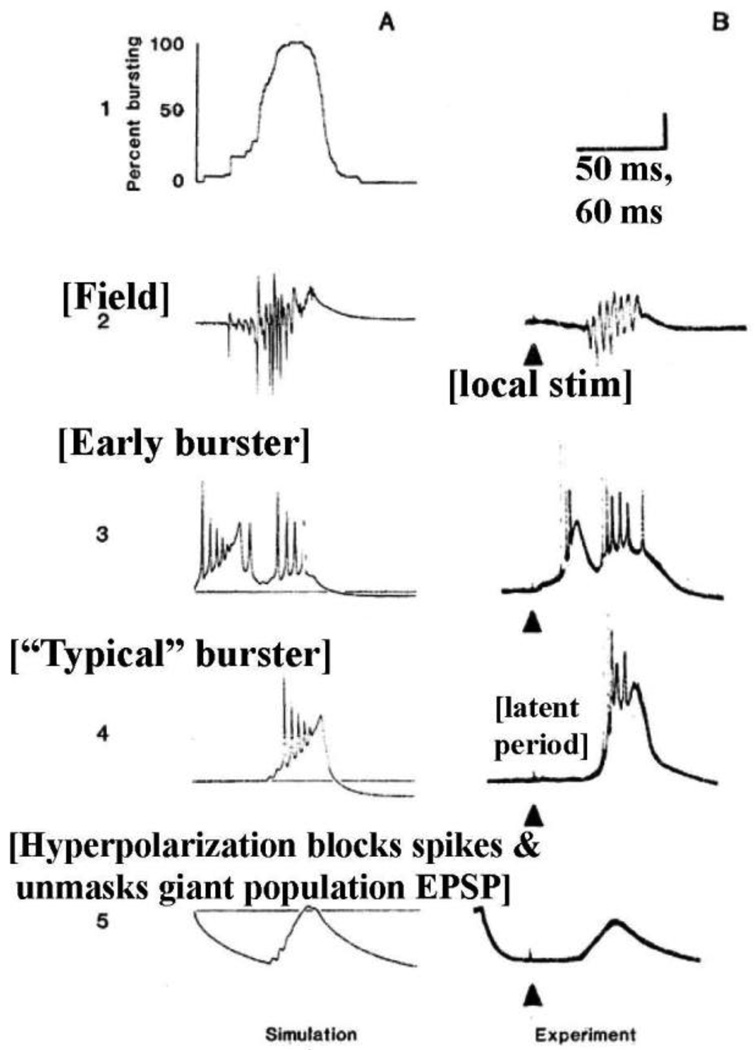
Fig. 3. Detailed mechanisms of an in vitro synchronized burst.

Recurrent chemical synaptic excitation can explain the ability of firing in a small number of neurons to recruit a large population, after a characteristic latent interval. (It does not, however, explain the high frequency signal in the epileptiform field potential, which can be accounted for by electrical coupling.) The simulation (left) was of a network of 100 intrinsically bursting neurons, with recurrent synaptic connections having two properties: a) each neuron contacted an average of 5 others; b) when a single presynaptic neuron fired a burst, it would induce bursting in a connected neuron with latency about 10 ms (see Fig. 2). There was no synaptic inhibition, corresponding to the experimental conditions (right). When 4 cells were stimulated in the model, or a small shock delivered in the experiment, population activity (i.e., the number of cells firing) increased rapidly over a period of tens of ms (line 1), leading to an epileptiform average signal (line 2). Cells receiving the initial stimulus (e.g. line 3) burst immediately, and then a second time, because of synaptic excitation received from the major population activity. Most cells fired a burst after a latent interval (e.g. line 4), corresponding to the growth of activity in the population. Hyperpolarizing such a neuron (line 5) uncovered the giant EPSP induced by the synchronized bursting of most of the population. [Calibrations: 50 ms (simulation), 60 ms (experiment); 4 mV (A2, B2); 25 mV (A3, A4, A5); 20 mV (B3, B4, B5).] Reproduced from Traub & Wong (1982).

Fig. 1 illustrates subdural grid ECoG data from a child who had a subcortical dysplasia and intractable seizures, with Fig. 1A and B showing the onset of an electrographic seizure, and Fig. 1C an interictal (i.e. between-seizure) event. From Fig. 1A,B, it is clear that in the epileptic brain, VFO can exist alone, not superimposed on burst discharges (as in Fig. 1C, and also occurred in seizure-associated burst discharges in this patient – see also Fig. 7); such an observation also suggests that VFO might not require significant glutamatergic neurotransmission. Furthermore, the common appearance of VFO just prior to a seizure (Bragin et al., 1999; Fisher et al., 1992; Traub et al., 2001; Worrell et al., 2004) suggests that distinctive tissue conditions might predispose the neural circuits to generate VFO and seizures, as part of a pathophysiology that encompasses both sorts of phenomenon together. [An example of such a possible tissue condition would be alkaline pH, which potentiates electrographic seizure activity in vitro (Traub et al., 2001, 2010), possibly by opening gap junctions.] Fig. 5, below, provides another example of VFO preceding an electrographic seizure, in a different patient.

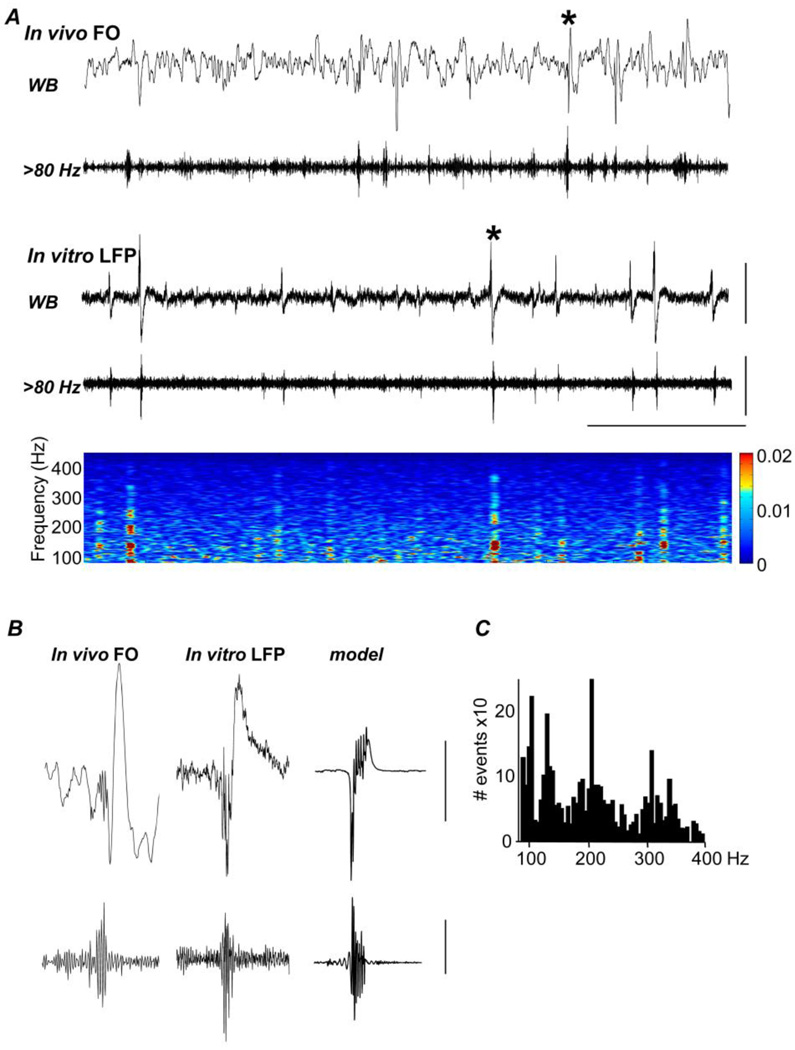
Fig. 7. Very fast oscillations (VFOs) are spontaneously generated in human temporal neocortical slices in vitro: VFO superimposes on bursts (but can also occur alone, not shown here.).

(A) Foramen ovale (FO) electrodes, implanted in a patient with right mesial temporal lobe sclerosis, demonstrate spike and wave interictal events recorded in wide band pass (WB) mode. The band pass filtered trace (20s duration) illustrates that oscillatory activity above 80 Hz is observed coincidently with the sharp wave complex. In vitro local field potential (LFP) recordings in slices of superior mediotemporal cortex (20 sec duration), resected from the same patient, demonstrate spontaneous sharp wave discharges. The band pass filtered trace reveals VFO behavior associated with the sharp wave discharges, as can be seen in the color-coded spectrogram of the activity illustrated. (B) Comparison of two selected (denoted by asterisk) events from in vivo FO and in vitro LFP - inverted for reference to the far field potential FO data - reveal a similar location of the VFO activity at the initial stage of the sharp wave event. A cortical column model, containing synaptic (excitatory and inhibitory) and gap junctional connections, reproduced the VFO and the initial low frequency envelope of the interictal discharge. Scale bars (A) 500 µV (upper), 200 µV (lower) and 5s, (B) 200 µV (upper), 100 µV (lower). Scale bars for the model ‘field’ are arbitrary. (C) Histogram displays the total number of detected VFO events from 80 to 400 Hz (n = 20, epochs of data = 60 s). Bin width of histogram was 5 Hz. From Roopun et al. (2010).

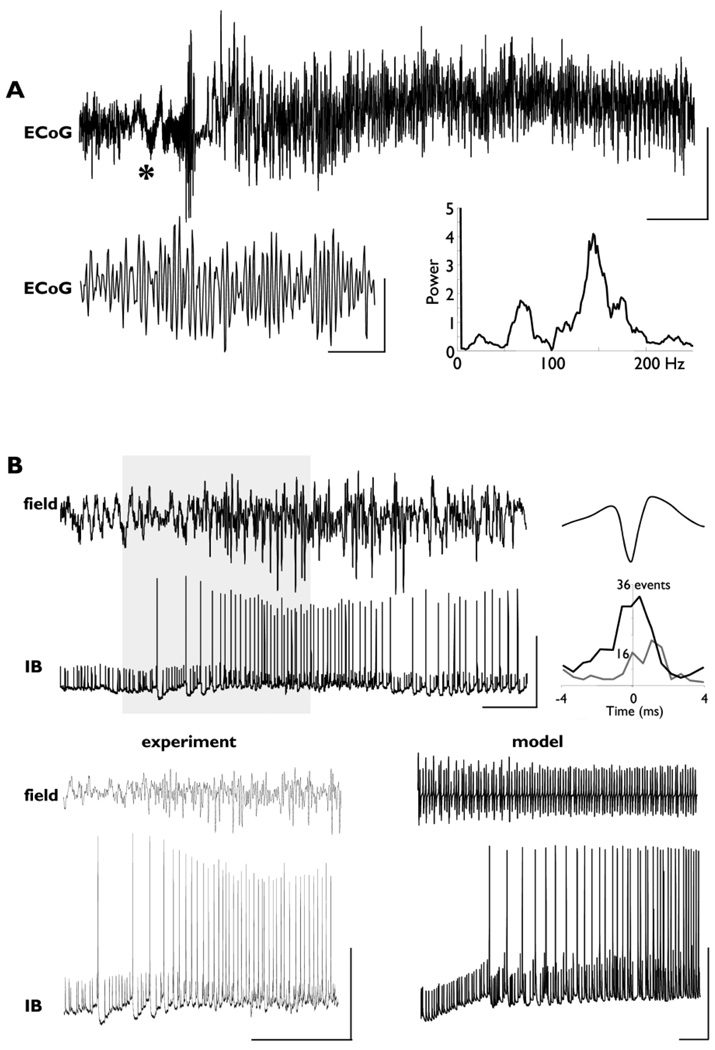
Fig. 5. Very fast oscillations (VFO) occur at the surface of human epileptic brain, in layer 5 of rat neocortex, in vitro, with chemical synapses blocked; and in a detailed network model of neurons coupled by gap junctions, without chemical synapses.

(A) ECoG recording from epileptic frontal neocortex (patient B of Roopun et al., 2009). The portion marked by * is expanded below. Power spectrum is from 1 s of data. Scale bars: 100 µV, 11 s; 10 µV, 100 ms. (B) Upper traces are field and intracellular recordings (IB, or intrinsic bursting cell), showing VFO in layer 5 of rat temporal neocortex in “non-synaptic conditions”: AMPA, NMDA and GABA_A receptors were respectively blocked with SYM2206, AP5 and gabazine. The bath contained kainate, and alkaline ACSF was pressure ejected onto the slice just before the trace begins. Scale bars; 0.1 mV (field), 50 mV (cell), 500 ms. The graph (middle right) shows pooled incidence plot (bin width 0.5 ms) for 500 field VFO periods with full spike data plotted as the gray line and spikelet data as the black line.

The data in the gray box were expanded in the lower left: scale bars 0.2 mV, 40 mV, and 400 ms. Simulation data are shown lower right: field potential of very fast network oscillation (above, spectral peak at 112 Hz), and simultaneous “intracellular recording” (below). Scale bars 50 mV (cell), 100 ms. Note the mixture of full action potentials and spikelets, as in the experiment. The model consisted of 15,000 multicompartment IB pyramidal cells, with gap junctions between axons. A ramping bias current (−0.5 nA to 0.5 nA) was applied to the illustrated cell, to show that spikelets are more common at hyperpolarized somatic membrane potentials, and full spikes at depolarized membrane potentials. From Traub et al. (2010).

VFO occurs under physiological conditions, as well as during epileptic events. For example, ~200 Hz “ripples” occur superimposed on physiological sharp waves in the normal (non-epileptic) in vivo hippocampus, and in other limbic structures (Buzsáki et al., 1992; Ylinen et al., 1995; Chrobak & Buzsáki, 1996). Such combined VFO/transient events resemble, in form, interictal bursts with superimposed VFO, although not necessarily having the same amplitude (physiological events are smaller), and certainly not the same significance for predicting the occurrence of spontaneous seizures; additionally, VFO/transient events occur in epileptic human neocortex (Fig. 1C; Roopun et al., 2010) but not, to our knowledge, in normal neocortex. VFO per se can occur, however, in non-epileptic neocortex, although – at least in the anesthetized cat – the amplitude of VFO is significantly higher in epileptic cortex than non-epileptic cortex (Edwards et al., 2010; Grenier et al., 2001, 2003). Even so, the occurrence of VFO in normal brain suggests that the structural circuit substrate of VFO is not necessarily pathological, in and of itself.

A major advance in understanding ripple physiology came with the fortuitous discovery that ripples could occur in isolation, and not just superimposed on a sharp wave, at least in vitro (Draughn et al., 1998) – although sharp wave/ripples also can occur together in vitro (see below). The evidence that in vitro ripples are mediated by electrical coupling between pyramidal cells is compelling (Draguhn et al., 1998): a) such ripples are enhanced in low calcium media, that block chemical synapses (and probably also help to open gap junctions); b) the ripples are enhanced by alkalinization of the medium, and suppressed by acidification, measures expected to open (respectively, close) gap junctions (Spray et al., 1981); c) the ripples are suppressed by octanol, halothane and carbenoxolone (Juszczak & Swiergiel, 2009), all gap junction blockers (while, unfortunately, none are completely specific, the effectiveness of each of the three agents supports specificity). Additionally, ripples are associated with somatic spikelets, or fast prepotentials, which (in hippocampal neurons) can be evoked by antidromic stimulation, depend on gap junction coupling, and are conducted along axons (Schmitz et al., 2001). As of about 10 years ago, then, the existing data suggested a novel hypothesis, that pyramidal cells were electrically coupled between their axons, and that such coupling led to VFO. We shall consider later in this review how the generation might work, and we shall describe the tissue conditions that might favor VFO vis-à-vis synchronized burst discharges.

Properties of chemical synaptic vs. electrical coupling between pyramidal neurons

Fig. 2 illustrates chemical and electrical coupling between hippocampal pyramidal neurons. For chemical synapses between CA3 pyramidal cells, Miles & Wong (1986) found unitary EPSPs of 0.6 to 1.3 mV (of course with fluctuations) and time to peak of averaged events equal to 5 to 12 ms. As Fig. 2Aa indicates, a single presynaptic action potential would not generally cause firing of the postsynaptic pyramid, although this could happen at some connections from pyramidal cells to interneurons (Gulyás et al., 1993), and could happen rarely at pyramidal/pyramidal connections (probability about 0.05, Miles & Wong, 1986). In contrast to a single action potential, however, a burst of action potentials could evoke a somewhat delayed (11 ms) postsynaptic burst, although not with perfect reliability. Latencies to postsynaptic bursting could be up to 30 ms, and the failure rate for burst propagation ranged from 0.5 to 0.7 (Traub & Miles, 1991).

As Fig. 2B demonstrates, electrical coupling between pyramidal cells is (not surprisingly) quite rapid, with latencies 0.5 ms or less, when measured with an electrode in the soma of each neuron (the latency at the coupling site might be shorter). Furthermore, a single spike could, on occasion, evoke a spike in a coupled neuron (Fig. 2Bd, Mercer et al., 2006). Such strong functional coupling – with a spike inducing a spike – is even more powerful than synaptic coupling wherein a full presynaptic burst is required to induce firing in the postsynaptic neuron. Unfortunately, in these examples the site of the coupling between the two neurons was not determined. If the coupling site were to be between axons, it is possible that the coupled axon actually fires a full spike in response to a “presynaptic” spike, but with the axonal spike conducting decrementally to the soma, where the electrode sits and sometimes records a spikelet, rather than a full spike. This issue is discussed in more detail in Schmitz et al. (2001).

The propagation of bursts of action potentials, from a neocortical pyramid to an electrically coupled pyramid, has recently been documented in a slice from a P32 rat (Wang et al., 2010). The latency from the first full spike in one cell, to the first full spike in the coupled cell, was in the tens of ms; this latter spike was, however, preceded by a series of summating spikelets. Wang et al. (2010) also showed that the “postsynaptic” (i.e. across the gap junction) somatic response in a neuron to a “presynaptic” spike – that is, whether the response was a spikelet or a full action potential – was exquisitely sensitive to membrane potential, with 2 mV making a measurable difference.

The density of connections (between pyramidal cells) also appears to be quite different for chemical synapses vs. gap junctions. Thus, in the CA3 region in vitro, a pyramidal neuron was estimated (using dual intracellular recordings) to synapse onto roughly 2% of nearby neurons (MacVicar & Dudek, 1980; Miles & Wong, 1986). The CA3 region in a slice contains some thousands of pyramidal cells, so that (on average) a pyramidal cell should synaptically connect to dozens of others; and the connectivity in vivo is doubtless higher yet. In contrast, gap junctional connectivity between pyramidal cells, as estimated by dye coupling, appears to be much sparser (Church & Baimbridge, 1991). Dye coupling probability is enhanced by alkaline pH (Church & Baimbridge, 1991) and by low-calcium media (Perez-Velazquez et al., 1994), but probably is not much over the percolation limit (i.e. wherein one cell couples to one other, on average), even in conditions optimal for coupling.

An epileptiform synchronized burst, involving relatively strong, sparse recurrent excitatory synapses

Fig. 3 (taken from Traub & Wong, 1982) illustrates an experimental model of what epileptologists call an interictal spike: a synchronized population burst occurring in the CA2/CA3 region of the hippocampal slice when GABA_A receptors are blocked. Detailed analysis of this type of event provides considerable intuition, even if this type of burst represents an extreme case, and is probably not completely typical for the cellular events during synchronized bursts in other experimental epilepsy models, or in patients.

Population events such as illustrated in Fig. 3 depend critically upon chemical synaptic transmission, as the events are suppressed by manipulation of divalent cations in the medium (to suppress chemical synaptic transmission), or by blockers of AMPA/kainate receptors (reviewed in Traub & Miles, 1991, and Traub, Jefferys & Whittington, 1999). Such data do not, however, prove that chemical synapses are the only type of between-cell interaction which is required. Let us defer consideration of this issue, however, and consider how well a model based on chemical synapses accounts for the phenomenology, which we must first describe.

In the experimental protocol for Fig. 3, GABA_A receptors were blocked with penicillin and recordings obtained in isolated CA2. A small shock to the fimbria evoked the typical epileptiform field potential (Fig. 3B2) with high-frequency components – but only after a latent period that could be over 100 ms. An occasional cell would burst relatively prematurely (line 3 of Fig. 3), but such cells fired a second burst at the long latency. More typical cells (line 4 of Fig. 3) remained near resting potential during the latent period, but then burst with the field event. Strong hyperpolarization of such “typical” cells unmasked the so-called giant EPSP (line 5 of Fig. 3), resulting from an excitatory conductance estimated at upwards of 180 nS by Johnston & Brown (1981), and reflecting the near-simultaneous bursting of many cells that are presynaptic to the recorded cell.

In using a model to account for the experimental observations, we note that the giant EPSP is straightforward: if most of the neurons are bursting simultaneously, and since they are interconnected, each neuron will receive a large excitatory synaptic input. The problem is to account for the latent period, in which augmenting intracellular depolarizations are not apparent (line 4 of Fig. 3). One possibility is simply to assume that each pyramidal neuron connects to more than one other with synaptic properties as in Fig. 2A, that is, allowing a burst in one neuron to induce a burst in a connected neuron with positive probability. [Note that this synaptic property was not actually established until after the model illustrated in Fig. 3, so that the model was predictive.] In Fig. 3, each of 100 neurons connected to an average of 5 others. A more realistic connectivity would use up to 10,000 neurons, each connecting to about 200 others. With a burst propagation probability (at any given synapse) of about 0.5, the average connectivity is more like 100 outputs per cell, and it would take only a couple of generations of growth – starting with bursting in a single neuron – to engage the whole population. With burst propagation latencies per synapse of 10 – 30 ms (see above), 2 generations of growth would account for at least part of the long latency from a small shock to the population discharge. [Note, however, that as activity in the population builds up – Fig. 3A1 – cells will start to be excited by more than one synaptic precursor simultaneously, so that burst latencies should decrease. Even so, the predicted overall latency is approximately right.]

Fig. 3A demonstrates that such a model – based on rather strong, but sparse, synaptic coupling - does generate potential traces that resemble the experimental data, with early bursters being re-excited (Fig. 3A3), and most cells quiet during the latent period (due to the exponential growth of activity). A prediction of this model was that stimulation of a single neuron should be capable of evoking a population burst. This was verified later (Miles & Wong, 1983) – although only for about 1/3 of CA3 pyramidal cells; possibly the axons of many of the cells had been damaged in preparing the slice, and the connectivity and intrinsic excitability of pyramidal neurons are likely to be heterogeneous.

Note that the model in Fig. 3 does not replicate the correct detailed shape of the epileptiform field potential. The simulated field is too noisy. This is probably due to the lack of electrical coupling between pyramids in the model; inclusion of electrical coupling leads to a more realistic simulated field, as electrical coupling – if strong enough – enables the emergence of an organized very fast oscillation, that superimposes on the epileptiform field potential (Traub et al., 1999).

Is the model illustrated in Fig. 3 generally applicable to synchronized bursts in other cortical areas, and in other conditions – particularly in patients? It certainly seems to be the case that many (or all) types of pyramidal neurons have local synaptic connectivity to other pyramids that is above the percolation limit (i.e., one cell connects to more than one other cell). This is the case even for the relatively sparsely interconnected CA1 region (Deuchars & Thomson, 1996). Nevertheless, we are not aware of other experimental examples of burst propagation from single pyramidal neuron to single pyramidal neuron, via chemical synapses. Indeed, Williams and Stuart (1999), recording from pairs of nearby layer 5 pyramidal cells, showed that presynaptic bursts evoked postsynaptic EPSPs that were subthreshold for action potential generation.

How, then, do interictal bursts, and seizures, arise? Two possibilities, which posit a predominant importance for recurrent synapses, are these:

1. interictal bursts do not, in general, arise from bursting in a single neuron, but from simultaneous (presumably repetitive) firing in many neurons, until a critical mass is built up (de la Prida et al., 2006). The critical mass would have the property that non-participating cells receive synaptic excitation from more than one firing neuron within the critical mass, so that the number of participating cells can increase over time, as a regenerative process.

2. recurrent synaptic excitation becomes augmented in disease or experimental conditions, so that bursting could then spread from neuron to neuron. An experimental model of this effect would be low-magnesium epileptogenesis, in which NMDA receptor-mediated currents are increased (although disinhibition eventually occurs as well (Traub et al., 1994; Whittington et al., 1995)).

An alternative possibility, upon which we expand below, is that recurrent excitatory synaptic connectivity can be augmented, at least under certain conditions, by electrical connectivity mediated by gap junctions. An important consideration here is that gap junction conductances are not static. Not only do the gap junction constituents themselves recycle in and out of the membrane (Wei et al., 2004), but gap junction channel conductances are modifiable by pH, Ca²⁺ ions, and connexin protein phosphorylation. The latter – at least in experimental model systems – can be controlled in turn by neuromodulators acting through tricyclic nucleotides (cAMP, etc.) (Hampson et al., 1992). Even with dual means of interconnection between pyramidal cells, however, it might still be necessary to have some degree of (transient) disinhibition – but inhibitory circuitry is also highly modifiable: excitatory synapses on interneurons can depress (Traub et al., 2005), interneuron membrane properties are modulated by metabotropic glutamate receptors or their withdrawal (Miles & Poncer, 1993), and synaptic inhibition is influenced by extracellular K⁺ concentration (Korn et al., 1987).

Gap junctions, very fast oscillations (VFO), and epileptogenesis

Fig. 1 demonstrated how VFO could precede an electrographic seizure. It is therefore necessary to consider how VFO is generated. First, however, we will show how VFO seems not to be generated.

Sharp-wave/ripples can be evoked in vitro during blockade of GABA_A receptors

There is a widespread belief that VFO must be produced by interneurons. Perhaps this belief stems from the fact that fast-spiking interneuron somata are capable of firing at high frequencies; or that very fast rhythmic inhibitory synaptic conductances have been recorded, in vivo, in pyramidal neurons during sharp waves (Ylinen et al., 1995). Nevertheless, there is compelling evidence that interneurons are not necessary for VFO. Intracellular VFO occurs in pyramidal cells during blockade of synaptic transmission (Draguhn et al., 1998), and – as Fig. 4 demonstrates – sharp wave/ripples can be evoked, in vitro, during specific blockade of GABA_A receptors. The presumed pyramidal cell in Fig. 4B exhibits either a large compound EPSP, or a burst of action potentials, during the evoked events, but no phasic IPSPs (confirming that GABA_A receptors really were blocked). Taken together, these lines of evidence suggest that – at least in physiological situations – interneurons may be recruited to fire during VFO, but that their resulting output does not consitute the mechanism underlying VFO.

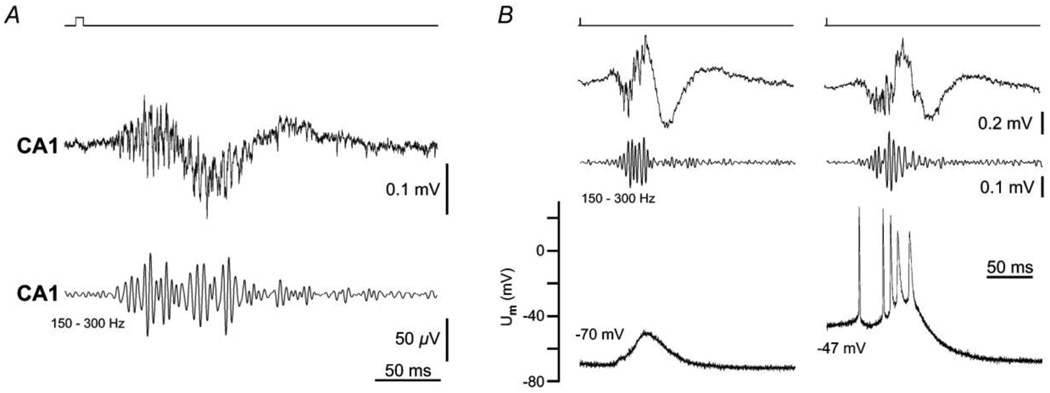
Fig. 4. Sharp wave ripple complexes in vitro (mouse hippocampal CA1 minislice) do not require GABA_A receptors.

When GABA_A receptors are blocked, the complexes can be evoked by pressure ejection of KCl (1 M) into stratum radiatum (upper traces), although they do not occur spontaneously. A: stratum radiatum field potential of KCl-evoked sharp wave ripple, in 10 µM gabazine to block GABA_A receptors. 150–300 Hz filtered trace shown below, highlighting the ripple. B: combined extracellular (above) and intracellular (putative pyramidal cell, below) recordings, during KCl-induced sharp wave ripple, with GABA_A receptors blocked. The cell was held at −70mV (left), to show the compound glutamatergic EPSP during the sharp wave, without phasic IPSPs. [Phasic IPSPs do occur in baseline conditions, in vivo (Ylinen et al., 1995) and in vitro (Maier et al., 2003).] When the cell was held depolarized at −47 mV (right), it generated a burst during the sharp wave ripple, but again without evidence of phasic IPSPs. From Nimmrich et al. (2005).

How, then, does VFO come about?

We have proposed, beginning in 1998, that VFO arises from the propagation of action potentials through plexi of axons that are interconnected by gap junctions (reviewed in Traub & Whittington, 2010). This proposal rests on a number of pieces of evidence, some amply supported, some less so. We have already provided evidence (Fig. 2) that pyramidal neurons can be electrically coupled. The remaining issues to be explained are these: what parts of the neurons are coupled – axons, somata, dendrites? And, even if pyramidal neurons are electrically coupled via their axons, how might that account for VFO?

Where are neurons coupled?

Postulating an axonal location allowed us to account for the shape of spikelets during low-calcium ripples (Draguhn et al., 1998). Electrophysiological experiments in the hippocampal slice were consistent with our postulate, and dye-coupling experiments (combined with confocal imaging in time and space) directly demonstrated passage of dye from one cell process to another – the processes being identifiable as axons, by light microscopic criteria (Schmitz et al., 2001). Freeze-fracture replica immunogold labeling (FRIL) has conclusively shown a gap junction on a hippocampal mossy fiber axon (Hamzei-Sichani et al., 2007); this gap junction contained connexin36, the most abundant known gap junction protein in the brain (Condorelli et al., 2000). [It was, however, somewhat surprising that connexin36 was present: VFO is potentiated by alkaline conditions (Draguhn et al., 1998), whereas connexin36 channels close with alkaline conditions (González-Nieto et al., 2008); additionally, VFO persists in connexin36 knockout mice (Hormuzdi et al., 2001). One would therefore expect different connexins to be present in axons.] On the other hand, so far as we are aware, there is no conclusive ultrastructural evidence for gap junctions between pyramidal cell axons (as opposed to axons of dentate granule cells), although intriguing axon-axon juxtapositions have been shown (Wang et al., 2010).

There are likely to be technical problems in developing ultrastructural evidence for pyramidal cell axonal gap junctions: first, the gap junctions may be quite small (Hamzei-Sichani et al., 2007); second, FRIL requires possession of an antibody to a gap junction protein, and that, in turn, requires knowing which connexin(s) (or other proteins) are contained in the gap junction. In the FRIL study mentioned above, antibodies were raised to connexin36, the best known neuronal connexin, and one for which highly specific antibodies are available. However, as noted above, the putative gap junctions between pyramidal cell axons may not depend on connexin36. Possibly, the putative axonal gap junctions between pyramidal cells contain connexin57, which does form axonal gap junctions between horizontal cells in the retina (Janssen-Bienhold et al., 2009), but that remains to be demonstrated (or disproved). Wang et al. (2010) have suggested that coupling between layer 5 neocortical pyramidal cells involves a pannexin (Bruzzone et al., 2003), because of the large coupling conductance. [Pannexins are vertebrate homologs of innexin proteins that from gap junctions in invertebrates.] While pannexins appear to form hemichannels in neurons (Thompson et al., 2006, 2008), that does not rule out a participation of pannexins in actual gap junctions, especially as junctions can form between oocytes (egg cells) induced to express pannexins (Bruzzone et al., 2003). We and our collaborators have observed pannexin immunolabeling in superficial layers of rat neocortex (Cunningham et al., 2004).

Because of the present paucity of ultrastructural data on gap junctions, electrophysiology and modeling assume a primary role in developing our understanding of very fast oscillations – at least for the time being.

What unusual properties might axonal electrical coupling confer on a neuronal network?

Three properties, at least, are relevant. First, as discussed above, such coupling is likely to be extremely sparse, based on dye-coupling data. Such data suggest that each axon would couple to only a few others, on average (Church & Baimbridge, 1991). Second, axonal coupling might allow an action potential in one axon to induce an action potential in a coupled axon, due to the high density/low threshold of axonal Na⁺ channels, and the locally high input resistance. [Even so, at least for CA1 pyramidal cells, in which at least some coupling sites are less than 150 µm from the soma (Schmitz et al., 2001), spike crossing could be suppressible by perisomatic synaptic inhibition (Traub et al., 2000; Munro & Börgers, 2010).] Third, if spikes do cross from axon to axon, and if the gap junctional connectivity is above the percolation limit, then collective activity could be generated, within a network of interconnected axons, in such a way that observations of somatic activities (for example with extracellular unit recordings) give a quite misleading underestimate of the axonal firing rates. The reason is that during such collective activities, spikes percolate amongst axons, without necessarily inducing corresponding rates of somatic spikes – although high rates of somatic spikelets could occur. [Spikelets, however, would be difficult to observe with extracellular recording.] This very important point is often ignored by in vivo experimentalists, who assess collective activity in the brain with unit recordings.

In the account that follows, we shall concentrate on the pyramidal cells (particularly the axons), and not consider the interneurons. The question of why interneuron firing and pyramidal cell firing are locked to each other and to the local field, in our model (and as observed experimentally during in vivo hippocampal ripples (Ylinen et al., 1995)) is considered elsewhere (Traub & Bibbig, 2000). We shall also not consider here more complex issues of ripple-related interneuron firing in vivo (Csicsvári et al., 1999; Klausberger et al., 2003).

Modeling VFO

VFO can be modeled based on the fundamental idea that temporal waves of VFO correspond to growing numbers of near-simultaneously firing neurons (or, more precisely, axons), generated by percolation of activity away from sites of spontaneous action potentials. [A low rate of spontaneous, but random, activity is required.] If the growing activity is thought of as a wave, then waves that meet will be unable to pass through each other, because of refractoriness, but can propagate into “virgin” (i.e. not refractory) directions (Lewis & Rinzel, 2000). The remarkable feature of models of this sort is that the oscillation periods, and spatial activity patterns, that are generated depend rather weakly on intrinsic membrane properties, but depend quite strongly on network topology and structure, as well as on the spontaneous activity (“noise”) rate (Traub et al., 1999, 2010; Lewis & Rinzel, 2000). Additionally, as suggested by experiments (Draguhn et al., 1998), synaptic currents do not play a role, at least not directly.

In actually constructing a model to be simulated, some critical choices need to be made. For example: what global network topology to use, and what methods to employ for simulating individual cells (or just axons). In our original proposal of this class of VFO models (Traub et al., 1999), we concentrated on a random graph topology (Erdös & Rényi, 1960) for the gap junctional network, and argued that the oscillation period was strongly influenced by the mean path length in the network (Newman et al., 2001). [In locally random, rather than globally random, networks, the oscillation period is, however, determined differently (Lewis & Rinzel, 2000; see also below).] In the 1999 paper, we employed both detailed multi-compartment multi-conductance model neurons, and also a highly simplified cellular automaton-like model. The detailed models produce potential waveforms that can usefully be compared with experimental recordings (see below). On the other hand, cellular automaton-like models allow for simulations of very large networks, contain few parameters, and allow for rapid exploration of the parameter space.

In order to correlate the output of a cellular automaton model with biological data, one needs to give a physical meaning to the model time step: it corresponds to the time required for a spike to cross from one axon to another. This time, in reality, would be expected (in real life) to depend on gap junction conductance and membrane state variables, but in the cellular automaton model is assumed to be constant, at about 0.25 to 0.5 ms.

Concerning network topology: Lewis and Rinzel (2000) pointed out that laying the network out on a grid, with a locally random connectivity, allowed for visualization of the wave patterns, which they called targets. In a random graph of given size, the statistical properties of the connectivity are specified by a single parameter (connection probability, or mean index = the expected number of nodes connected to any given node), while in a locally random graph, two parameters are required, the mean index and the “footprint”. The footprint specfies the maximal distance between two nodes that are allowed to form a connection. Locally random graphs are biologically more accurate than random graphs, for the simulation of very large cortical axon plexi; the reason is that gap junctions (at least according to available dye-coupling data in the hippocampus (Schmitz et al., 2001)) are located in proximal axons, so that widely separated neurons have no possibility of being directly coupled to each other (see also Wang et al., 2010). [The possible effects of putative gap junctions between fine axonal branches are interesting, but such putative gap junctions are difficult to demonstrate directly with available experimental methods.]

In a locally random graph, it is possible to estimate VFO period from network structural parameters, cellular refractory time, and the noise rate, provided that the noise rate is small (Traub et al., 2010). Interestingly, the period is scale-free, if the locally random network is sufficiently large: that is, oscillation periods within subregions of different size are the same as the global oscillation period (Traub et al., 2010).

In the next sections, we shall illustrate some of these ideas with specific examples.

Cellular firing patterns during VFO in neocortex

Fig. 5A shows the temporal pattern of pre-seizure VFO (~150 Hz) in a patient (compare Fig. 1). Spatial patterns of VFO from this same patient were also analyzed (see below). So far as understanding the cellular mechanisms of VFO in patients goes, however, many types of experiments are impossible to perform in situ. For example, one may not insert glass micropipettes into the human brain, in situ, for intracellular recording. Two options are then available. First, one may do in vitro experiments on human tissue that is removed during the course of a neurosurgical procedure, of course with informed consent and with approval of an Institutional Review Board (see Fig. 7). This approach has the advantage that the actual tissue pathology, causative to the patient’s neurological problem, may be present in the tissue sample studied in vitro. The approach has the disadvantages that each patient is unique, and one can not control the conditions (for example, blockade of synaptic inhibition) which might unmask the capacity of normal brain tissue to exhibit a particular sort of population activity. Second, and complimenting the first approach, one may develop animal models, either in vivo or in vitro (or both together). Often, in the animal model case, one starts with putatively normal brain tissue, and then adds drugs to the bath, or alters ion concentrations, to elicit an unusual or abnormal phenomenon. Fig. 5B is an example of this second approach.

The experimental recordings in Fig. 5B reproduce an oscillation resembling the VFO of the human ECoG data in Fig. 5A, although not the electrographic seizure that follows. To obtain these data, phasic synaptic transmission was blocked in a rat neocortical slice, and the tissue was also made alkaline (so as to open at least certain types of gap junctions). The intracellular recording, from a layer 5 intrinsically bursting neuron, demonstrates a mixture of spikelets and action potentials, with both types of event phase-locked to the field oscillation (~130 Hz). This is just the sort of behavior one expects for a network oscillation generated in the axonal plexus, given the block of synaptic transmission and alkaline conditions. Note also (Fig. 5B, lower left) that spikelets are more likely to occur (as opposed to full somatic action potentials) when the cell is relatively hyperpolarized. An extremely similar pattern of activity (~112 Hz) was observed in a network model, simulated on a computer (Fig. 5B, lower right). The network model contained 15,000 model neurons (each multi-compartment, multi-conductance), with no synaptic interconnections, but with a random pattern of gap junctions between axons (Traub et al., 2010). The mean index was 3.33.

From Fig. 5, we can conclude that a model based on axonal electrical coupling can account for VFO (at least in a slice), including cellular firing patterns, at least the signals observed with one extracellular and one intracellular electrode. But what about spatial patterns?

Spatial patterns of VFO in ECoG data from an epilepsy patient

The ECoG signal illustrated in Fig. 5A was taken from a single electrode out of 48 (in a 6 × 8 array) electrodes embedded in a subdural grid. Rectification, thresholding, and smoothing of the grid data (as in Fig. 6, left) allow the visualization of spatial patterns of VFO. Qualitatively, what one then sees (most readily apparent in movies, as in the Supplemental Data of Traub et al. (2010)) are small blobs that emerge out of the background, that then expand, and that then coalesce with other blobs. A strikingly similar pattern of activity is observed (Fig. 6, right) in a VFO cellular automaton model (Traub et al., 2010) – abstracting the principles of Fig. 5, but operating on the scale of hundreds of thousands of cells, rather than 15,000 – provided one uses a connectivity footprint that is not too large (Lewis & Rinzel, 2000). In other words, the connectivity should have a property that one would expect from dye coupling data (Gutnick et al., 1985; Ding et al., 1998).

Fig. 6. Comparison of spatiotemporal patterns in ECoG data and in cellular automaton model data.

The left shows successive frames of activity, every 2 ms, from an 8 × 6 subdural array of electrodes (with 1 cm spacing), in Patient B of Roopun et al. (2009). The right shows frames of activity every 1.25 ms, from a cellular automaton model with 480,000 “cells” in an 800 × 600 array, with sparse, localized gap junctional connectivity (mean index <i> = 1.33, connectivity footprint = 25 lattice spacings), and rare spontaneous action potentials. From Traub et al. (2010).

In summary, then, gap junctional coupling reproduces many of the experimental features of VFO, in the human brain in situ and in rat brain slices, without (to our knowledge) being clearly contradicted by available data. Unfortunately, we do not know of other experimentally plausible mathematical/computational models with which this one can be usefully compared. (We do not consider models primarily dependent on interneurons to be plausible.) That is not to say that our model is definitively established. Many extremely difficult experiments remain.

VFO in human tissue in vitro

Previous figures have shown VFO superimposed on a burst in the human brain in situ (Fig. 1), or in an experimental animal preparation in vitro, to which has been added a GABA_A receptor-blocking drug (Fig. 3). Fig. 7 demonstrates VFO/bursts in tissue from the very same patient, recorded in situ, and also in vitro (in resected tissue). Remarkably, VFO/bursts in vitro were recorded without addition of receptor-blocking drugs, or comparable manipulations (Roopun et al., 2010). Such data suggest that there are structural/functional abnormalities in the diseased human tissue.

In simulating spontaneously occurring VFO/bursts in a cortical column model (Fig. 7B), we found it necessary to transiently open, then close, axonal gap junctions (Roopun et al., 2010). (In a sense, this means that the simulated events are not truly spontaneous.) Nevertheless, the model agreed with the experimental data in a number of features: VFO continued to exist, even when chemical synapses were blocked; while keeping gap junctions closed prevented both VFO and bursts (Roopun et al., 2010). One interpretation of the data is that VFO is the “primary” event in epileptogenesis. This interpretation is consistent with the idea expressed above, that electrical coupling augments the excitatory “gain” between pyramidal neurons, and this augmentation is necessary for the expression of epileptogenesis in in situ conditions.

Alternation of VFO with sharp waves

When mouse hippocampal slices are bathed in DHPG (a metabotropic glutamate receptor agonist), the CA3 region exhibits alternating gamma (~40 Hz) oscillations and synchronized bursts (sharp waves) (Traub et al., 2005). This type of switching back and forth could be explained by dual synaptic processes occuring during the gamma epochs: a) potentiation of EPSPs between pyramidal cells, which would tend to favor synchronized bursting (Fig. 2); b) depression of EPSPs on interneurons, which would tend to disable gamma oscillations (Traub et al., 2003). Transient fragments of VFO (>70 Hz) preceded the sharp waves, as can occur in other in vitro models (Pais et al., 2003).

Human epileptic neocortex can also exhibit (spontaneously) oscillations alternating with sharp waves (Fig. 8B). In this case, however, the oscillations contained a very fast component. Interestingly, this type of alternation could be replicated in an unpublished network model, when there was disinhibition, provided recurrent synaptic exctation was not too powerful. With disinhibition, gamma oscillations did not occur in the model, but VFO was still present, provided pyramidal cell membranes were not excessively shunted. Synaptic plasticity was not required, at least in the model (Fig. 8A).

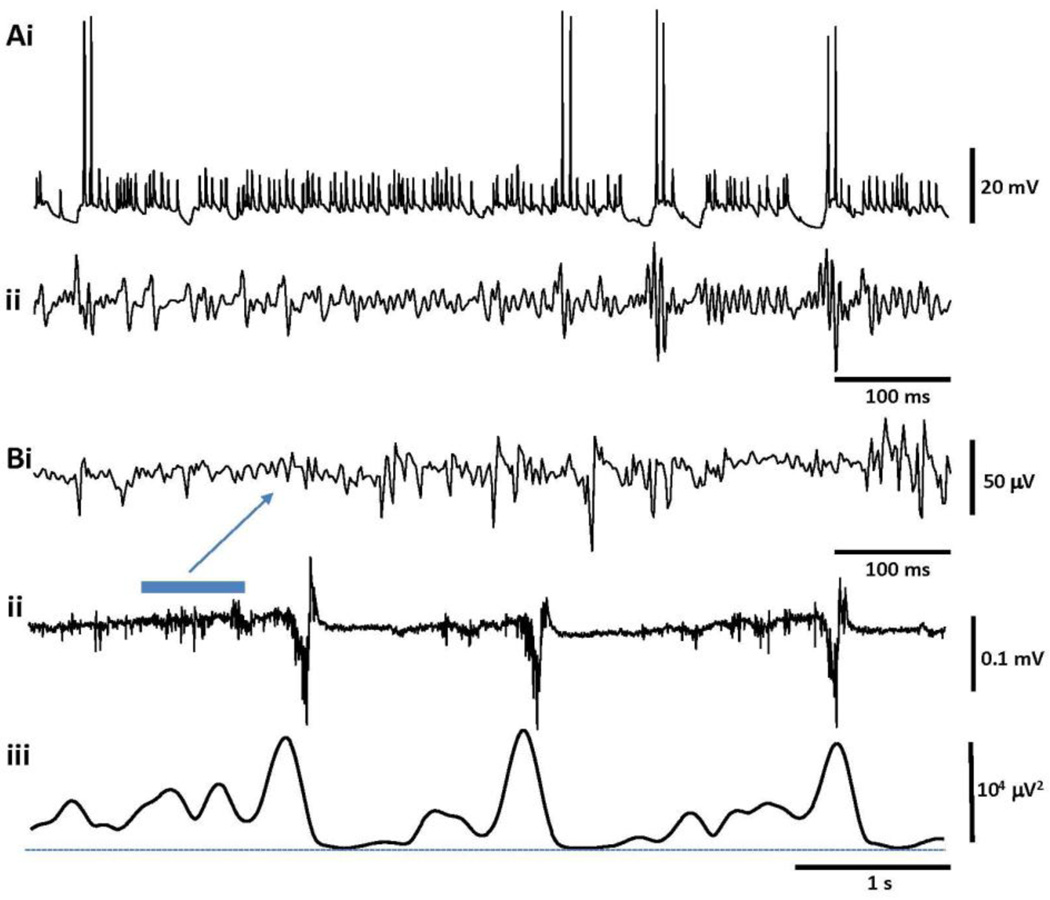
Fig. 8. Alternation of VFO and population spikes in a network model and in human epileptic cortex.

(A) simulation model intracellular record (above) and simulated field potential (below) with VFO and population spikes intermixed. Note the spikelets in intracellular record. The model contained 8,000 pyramidal cells (electrically coupled via axons), 400 basket interneurons, 100 axoaxonic interneurons, and 200 dendrite-contacting interneurons; synaptic inhibition was progressively blocked in a pattern that started at one end and spread across the quasi-1-dimensional cell array. (R.D. Traub, M.O. Cunningham, and M.A. Whittington, unpublished.) (B) Field potential recordings in layers 2/3 of human tissue, showing alternating VFO and population spikes. (i) and (ii) are broadband signals (on fast and slow time-scales, respectively), while (iii) shows VFO power (>100 Hz) in a sliding window. [Recordings from slices (450 µm) of inferior temporal gyrus obtained from a patient with secondary generalized seizures. The patient (female, 52 years old) presented with a right temporal cavernoma and underwent a right temporal lobectomy. Spontaneous inter-ictal activity was recorded using extracellular electrodes using methodologies outlined in Roopun et al., (2010).] (M.O. Cunningham, C. Nicholson, I.S. Schofield, M.A. Whittington, unpublished.)

DISCUSSION

Perhaps the most deeply entrenched idea, in the study of cellular mechanisms of epileptogenesis (and in other areas of Neuroscience as well), is that the relevant behavior of networks of neurons is dominated by a “balance between excitation and inhibition” – where “excitation” means “synaptic excitation”. There is much to this idea, so far as it goes. Experimental epilepsy models with diminished synaptic inhibition (Dichter & Spencer, 1969; Prince, 1968) or with augmented synaptic excitation (e.g. by lowering extracellular [Mg²⁺], Avoli et al., 1987) have a long and distinguished history.

Nevertheless, as the data reviewed here (particularly Fig. 5) make clear, “excitation” between principal neurons is not just synaptic, but is mediated by gap junctions as well – and not simply in an insignificant modulatory fashion, but rather in a fashion that allows (at least in some circumstances) action potentials to pass from neuron to neuron, even without chemical synapses.

Additionally, the notion of a balance of excitation and inhibition suggests (even if it does not state explicitly) that what is important are the collective firing rates of the principal neurons, which will be accelerated as inhibition declines and “excitation” increases. Yet, the actual details of cellular behavior during epileptogenesis are far richer than can be captured by changes in firing rates, with network oscillations at a wide range of frequencies (<1 Hz to over 100 Hz), and firing patterns that include spikelets, antidromic action potentials, and bursts of action potentials riding on large (but transient) depolarizations.

Finally, the richness of cellular behaviors, before and during electrographic seizures, matters. These behaviors provide clues as to possible brain tissue alterations that favor the initial and underlying events in electrographic seizure activity, which appear to be very fast oscillations that can be generated by gap junctional coupling between pyramidal neurons. Such putative tissue alterations may have even greater clinical relevance than do the abnormal neuronal activities themselves.