A Perspective on Modeling Hepatitis C Virus Infection

Abstract

By mathematically describing early HCV RNA decay after initiation of IFN-based antiviral therapy, crucial parameters of the in vivo viral kinetics have been estimated, such as the rate of production and clearance of free virus, and the rate of loss of infected cells. Furthermore, by suggesting mechanisms of action for IFN and ribavirin mathematical modeling has provided a means for evaluating and optimizing treatment strategies. Here we review recent modeling developments for understanding complex viral kinetics patterns, such as triphasic HCV RNA declines and viral rebounds observed in patients treated with the standard of care. Moreover, we discuss new modeling approaches developed to interpret the viral kinetics observed in clinical trials with direct-acting antiviral agents, which induce a rapid decline of wild-type virus but also engender a higher risk for emergence of drug resistance variants. Lastly, as in vitro systems have allowed a better characterization of the virus lifecycle, new modeling approaches that combine the intracellular and the extracellular viral dynamics are being developed and will be discussed.

Introduction

Chronic hepatitis C virus (HCV) infection has a high prevalence of about 3% worldwide (1). It is the most common cause of liver cirrhosis, hepatocellular carcinoma, end stage liver failure, liver transplantation and eventually liver failure related death around the world (2). Achieving a long term sustained virological response (SVR), defined as undetectable HCV RNA in serum 24 weeks after the end of treatment, is the most effective way to prevent disease progression. Currently, treatment outcome with pegylated interferon (peg-IFN) and ribavirin (RBV) is influenced by HCV genotype and SVR is achieved in only ~ 50% of HCV genotype 1 patients, with no effective alternative treatment for non-responders (3).

Mathematical modeling of HCV dynamics (reviewed in (4)) has played an important role in highlighting the significance of obtaining frequent viral load measurements and by providing efficient tools for early prediction of SVR for IFN-based therapies (5). Direct-acting antiviral agents (DAAs) constitute a new stage in HCV therapy. These drugs inhibit specific HCV enzymes important for viral replication, in particular the NS3 protease or the RNA dependent NS5B polymerase, and thus allow for a more profound antiviral effect than the current IFN-based therapy. Here we review viral kinetic issues related to both IFN-based and DAA-based therapies and give our current understanding of them. Lastly, we discuss how the development of in vitro systems that better characterize the intracellular virus lifecycle could allow for more comprehensive HCV modeling approaches.

Viral kinetics with IFN-based antiviral therapy

After injection of IFN, a rapid dose-dependent first phase viral decline lasting for 1-2 days followed by a slower second phase is typically observed (Figure 2, grey line). In HCV genotype 1 patients, the first phase typically leads to a reduction of HCV RNA from baseline of 0.5-2.0 logIU ml⁻¹ (6-9), and the second phase to additional reductions from 0.0-1.0 logIU mL⁻¹ week⁻¹, with large inter-patient variation (6-9). The decline kinetics in patients infected with genotypes 2 or 3 are more profound in both phases than in genotypes 1 (reviewed in (10)). The reasons for these differences are not well understood.

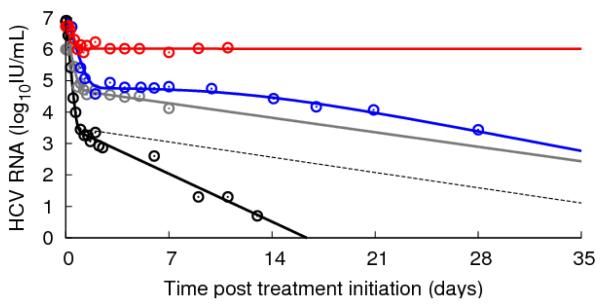
Figure 2.

Representative examples of viral kinetics patterns under treatment. HCV RNA digitalized data (circles) and their corresponding fits by the standard or extended model. Grey: biphasic responder with (daily) 10 MIU IFN (6) (ε=0.95, δ=0.16 d⁻¹, c=5.6 d⁻¹) (standard model); red: flat responder with (daily) 10 MIU IFN (70) (standard or extended model); blue: triphasic responder with (daily) 10 MIU IFN (6) (extended model); black: telaprevir plus (weekly) peg-IFNα-2a for 14 days (48) (ε=0.999, δ=0.5 d⁻¹, c=11 d⁻¹) (standard model); black dashed line: viral kinetics decline if the second phase viral decline was similar to what is observed with IFN (ε=0.999, δ=0.16 d⁻¹, c=11 d⁻¹).

The original mathematical modeling of HCV infection and treatment (Figure 1) has provided valuable insights into viral-host-IFN dynamics (6). The first phase is due to IFN acting to reduce the average rate of virion production/release per infected cell from p to (1-ε)p, where ε stands for the effectiveness of IFN. With virion production partially blocked, the virus in serum will fall at a rate close to the clearance rate c per virion, cause a decrease in the serum concentration of HCV RNA, with the magnitude viral decline depending on the degree of blockage of virion production ε. If, for example, ε = 0.99, then virion production is 99% blocked and the HCV RNA concentration will fall during the first phase until it reaches 1% of its baseline value. If ε= 0.999 then HCV RNA level will fall 3 logs until it reaches 0.1% of its baseline value, and so forth. The standard model does not distinguish, say when ε = 0.99, between each cell having its virus production reduced by 99% or 99% of cells having their viral production totally turned off and 1% of cells remaining unaffected, or various other combinations that result in the total body-wide virion production being reduced by 99%. At the end of the first phase there is less virus in serum and hence less infection of new cells. Thus as infected cells die they are less efficiently replaced by other infected cells and there is a net loss of infected cells. It is this net loss of infected cells that causes the second phase decline. The symbol δ has been used to denote the per capita rate of loss of infected cells, and according to the model of Neumann et al. (1), the second phase slope will be approximately εδ. Hence for potent therapies for which ε is close to 1, the second phase slope will be approximately δ. Since the loss rate of infected cells is smaller than the viral clearance rate (δ<c), the second phase of viral decline will be slower than the first phase (6-9).

Figure 1.

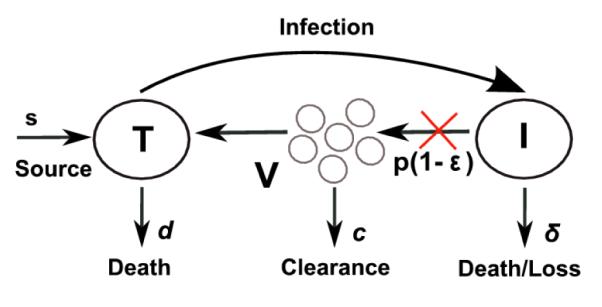
Schematic representation of the standard model (upper left), the extended model with cell proliferation (upper right) and the model with two strains of virus (bottom). The red and green X’s indicate steps in the viral lifecycle where IFN or DAAs interfere with virus production. The symbols are defined in the text.

An important question, which has not been resolved, is whether infected cells are lost by death and/or cure, i.e., loss of intracellular HCV RNA and/or other factors needed for viral production. This is an important issue as the rate of viral decline plays a critical role in determining the duration of therapy needed to attain SVR (11). We will return to this issue as viral declines with DAAs have more rapid second phases than those generated with IFN-based therapies.

The pattern of biphasic decline, while common, is not the only pattern of HCV RNA decline. Modeling has shown that a biphasic decline can occur only if the treatment effectiveness is above a certain threshold, called the critical effectiveness ε_c (12-13). If the treatment effectiveness is below the critical value, i.e. if ε<ε_c, the initial viral decline does not persist and a new on-treatment steady state level is ultimately reached in which the viral load is lower than baseline. If ε is sufficiently small these changes in HCV RNA could be negligible (14). Thus, this theory can explain non-responders. Depending on various model parameters, the theory predicts that the initial viral decline can under some circumstances go below the new on-treatment steady state and thus a rebound is observed or the decline can transition smoothly into the new on-treatment steady state giving rise to what has been called a flat second-phase (Figure 2, red line) (13).

Rebounds can also occur for other reasons, most notably changes in drug effectiveness. Not surprisingly, if for pharmacokinetic reasons or non-compliance with therapy, drug levels fall then the ability of therapy to reduce viral production is decreased and viral levels can resurge. This is the case with weekly injections of peg-IFN and viral rebounds are frequently seen towards the end of the dosing interval (15-17). Furthermore, assuming a constant effectiveness may be a poor approach when fitting HCV RNA data obtained from patients treated with peg-IFN and can lead to strong biases in the estimation of the viral parameters (18). The relationship between drug effectiveness, ε(t), and drug concentration, C(t), can be incorporated into models by using a pharmacodynamic (PD) relationship, such as the E_max model (19), $\epsilon \left(t\right)={\epsilon }_{\max }\frac{C{\left(t\right)}^n}{C{\left(t\right)}^n+E{C}_{50}^n}$, where EC₅₀ is the drug concentration in blood at which the drug is 50% effective, n is a constant called the Hill coefficient, a parameter that determines how steeply the treatment effectiveness changes with variations in drug concentration, and ε_max is the maximum effectiveness that can be attained. The drug concentration C(t) can be described by a pharmacokinetic (PK) model, such as an absorption-elimination model (20).

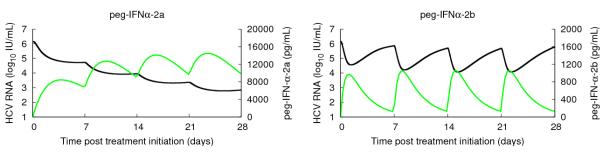
This approach was used to analyze HCV viral kinetics in HIV-HCV coinfected patients treated with peg-IFN in combination with RBV (21-22). Interestingly, in these studies drug concentration per se was not found to be associated with long-term responses whereas the pharmacodynamic parameters, such as the maximal effectiveness and the therapeutic quotient (the weekly average drug concentration divided by EC₅₀), were correlated with end-of-treatment response and SVR. The two forms of peg-IFN (peg-IFNα-2a and peg-IFNα-2b) differ widely in their PK and PD. Indeed the studies (21-22) suggested that peg-IFNα-2a is characterized by a 10-fold higher EC₅₀ (2 μg L⁻¹ vs 0.44μg L⁻¹) and a lower Hill coefficient n (n=1-2 vs n=1-4) than peg-IFNα-2b. These differences in PK/PD lead to differences in viral kinetic curves under therapy, with patients treated with peg-IFNα-2b tending to have more cases of viral load rebound toward the end of the dosing interval (23-24). Typical profiles of viral kinetics with the two peg-IFNs are shown in Figure 3.

Figure 3.

Typical PK/PD viral kinetics profiles with weekly subcutaneous injections of 180 μg of peg-IFNα-2a (left) and 1.5μg/kg of peg-IFNα-2b (right); viral load (black) and serum peg-IFN concentration (green). The PK parameters have been obtained using median values given in (23) and the PD parameters are the median values for peg-IFNα-2a and a typical patient for peg-IFNα-2b in (21-22).

The drawback of using models that incorporate PK/PD is that it requires frequent measurements of both drug and HCV RNA levels, yet often only HCV RNA is measured. Simplified approaches that take into account the drop in drug effectiveness toward the end of the dosing interval without explicitly modeling the drug concentration have been proposed. Shudo et al. (25) developed a declining effectiveness model that assumed a constant treatment effectiveness for the first days after peg-IFN injection, and then a linear or exponential decline, e.g.,

$$\epsilon =\left\{\begin{array}{c}{\epsilon }_{\max }\text{for}\mathrm{t}<{\mathrm{t}}_1\hfill \\ {\epsilon }_{\max }\exp (-\mathrm{k}(\mathrm{t}-{\mathrm{t}}_1)\text{for}\mathrm{t}>{\mathrm{t}}_1\hfill \end{array}\right\}$$

This approach was shown to provide a good approximation for estimation of parameters during the first week of peg-IFNα–2b treatment (25). However, additional parameters might be needed to model peg-IFNα–2a since it takes longer to reach its maximal effectiveness. To model viral kinetics after several injections, one might also want to distinguish between the two peg-IFNs: peg-IFNα-2a reaches a set point value after the second injection (22) and its effectiveness can be considered roughly constant afterwards, whereas for peg-IFNα-2b one needs to account for the tradeoff between accumulation and rapid drug clearance (26-28).

In some patients more complex kinetics patterns of viral decline have been observed that cannot be satisfactorily explained by the standard model, such as a triphasic decline characterized by a flat transient second phase (4-28 days) followed by a third phase of renewed of viral decline (Figure 2, blue line). Although detecting a triphasic decline requires frequent data sampling, the proportion of patients treated with IFN-based therapies that exhibit triphasic declines has been estimated to be between 25% and 50% (22, 29-31). One explanation for a triphasic decline is that the flat second phase is due to a period in which the rate of loss of infected cells, δ, is close to 0 (29). Then to account for the renewed viral decline, a delayed immunomodulatory effect (due for instance to RBV) has been suggested (29). Another potential explanation is based on the proposition that infected cells can proliferate (Figure 1), with the flat second phase being due to both proliferation of infected cells and de novo infections compensating for their loss by death (13). Because proliferation needs to be controlled to ensure that liver size is maintained, the proliferation rate of both infected and uninfected cells should slow as the total number of hepatocytes increases. In modeling a triphasic decline, Dahari et al. (13) assumed that uninfected cells proliferate faster than infected ones, since they would not have the metabolic burden of producing virus, and further such an assumption would allow uninfected cells to take over the liver under therapy as must be the case when SVR is attained. Under such an assumption the proliferation driven flat second phase would end as uninfected cells increase in number and slow the proliferation of infected cells to the point that proliferation could no longer replace cells as fast as they were being lost. At this point, the third phase of decline would ensue.

Two important predictions were derived from this model. First, triphasic patterns predominantly arise in patients with a high baseline proportion of infected cells (denoted π) and the second phase duration increases with π (32). Second, the final phase slope results from a complex interaction between π, the drug effectiveness, ε, and viral kinetic parameters (33). In particular Dahari et al. (33) found parameter regimes in which the final slope of viral decline could underestimate the actual value of the loss of infected cells, δ, by 10-fold if ε=90% and by 2-fold if ε=95%. This could account for the correlation observed between the treatment effectiveness and the final phase viral decline reported in some studies (34-35). However, if ε>99% the final phase slope predicted by the model would essentially be δ and the current interpretation of the final phase viral kinetics would not be changed.

To get agreement between the model and data, Dahari et al. (13, 22) needed to assume that both uninfected and infected hepatocytes can divide with a maximum proliferation rate >1 day⁻¹. Although the liver has a high regeneration capacity (36), the maximum per cell hepatocyte proliferation rate in vivo is not known. Further information on host cell kinetics during infection is necessary to validate the predictions of this model. From a practical point of view, the additional parameters introduced in this model makes parameter estimation by fitting the model to viral kinetic data unreliable unless a number of parameter values are set to known or assumed values.

Modeling HCV viral kinetics in the era of direct-acting antiviral agents (DAAs)

Viral kinetics observed during monotherapy with DAAs is usually characterized by an initial rapid viral decline. However, this decline may not be sustained and drug resistance, which may lead to viral breakthrough, can rapidly appear. Indeed, contrary to the complex intracellular signaling pathways involved with the response to IFN, the DAAs currently in clinical trials, which target specific HCV enzymes, seem to favor the emergence of resistance (37-38).

The selection and kinetics of drug resistant HCV variants have been studied in patients treated with DAAs (39-41). In a study with the protease inhibitor telaprevir, all four genotype 1a patients treated with monotherapy for 14 days experienced viral breakthrough (41). Virus isolated from them as early as day 2 contained 5 to 20% drug resistant variants (41) and resistant virus rapidly took over the virus population. A model has recently been developed to explain the early emergence of resistance and its rapid amplification (42)

Existence of HCV variants before therapy

Each HCV RNA molecule is made through the action of the NS5B RNA-dependent RNA polymerase, which introduces an error rate μ estimated to be 10⁻⁵ to 10⁻⁴⁵ per copied nucleotide (43-44). The entire HCV genome has approximately 9600 nucleotides. If we assume μ=10⁻⁵ per copied nucleotide, the average number of changes per genome is 0.096 per replication. According to the binomial distribution or its Poisson approximation, if a person is infected with wild-type virus that is fully sensitive to a given drug, when a new virion is generated it has a probability of 91% to carry an unmutated genome, 8.7% to carry one nucleotide substitution, 0.42% to carry two substitutions, and so on (Table 1). If μ=10⁻⁴ per copied nucleotide then even higher numbers of mutants are generated (Table 1). Thus, given that 10¹² HCV virions are produced each day in a typical untreated patient (6), 8.7×10¹⁰ and 4.2×10⁹ variants on average would be generated with single- and double-nucleotide changes, respectively. Because each nucleotide can mutate to one of three others, the total number of possible single and double mutants is 2.9×10⁴ and 4.1×10⁸, respectively. In other words, all possible single and double mutants are predicted to be generated multiple times each day (Table 1). Many of these might not be observed because they are lethal or confer reduced fitness and are eliminated (45). Because a single-nucleotide change or a number of substitution combinations may be associated with resistance (40), these calculations would predict that all viable single and double mutants that confer drug resistance preexist and may compete with the wild-type virus during therapy. Furthermore, during the early stages of therapy single and double mutants are very likely to replicate, allowing for compensatory or additional drug resistant mutations to occur. In fact, it is predicted that to avoid resistance emergence a drug combination consisting only of DAAs should carry a genetic barrier of four or more mutations (42).

Table 1.

Estimated rate of generation of HCV variants with nucleotide substitutions^*

Mutation rate	Number of nucleotide changes	Probability	Number of virions generated per day	Number of all possible mutants	Fraction of all possible mutants created per day
μ=10−5	0	0.91	9.1×1011
	1	0.087	8.7×1010	2.9×104	1
	2	0.0042	4.2×109	4.1×108	1
	3	0.00013	1.3×108	4.0×1012	3.4×10−5
μ=10−4	0	0.38	3.8×1011
	1	0.37	3.7×1011	2.9×104	1
	2	0.18	1.8×1011	4.1×108	1
	3	0.056	5.6×1010	4.0×1012	0.014

^*Daily rate of production of HCV is assumed to be 10¹² per day

Modeling the emergence of drug-resistant variants during therapy

Even if drug resistant variants pre-exist, to be observed at high frequencies as early as 2 days after treatment initiation, either the wild-type (WT) drug sensitive virus must profoundly decline or the resistant virus must grow. Current work has been examining these possibilities by extending the standard model of viral kinetics (6) to incorporate two competing viral strains, wild-type (WT) and resistant (RES) (Figure 1). The drug effectiveness in reducing viral production from cells infected with WT and RES virus is ε_WT and ε_RES, respectively, and the fitness of each strain depends on their viral production rates p_WT and p_RES in the absence of therapy. Cells infected with WT virus, I_WT generate a large majority of WT virus, V_WT as well as a small proportion of drug-resistant virus, V_RES, by mutation. Pre-treatment steady state conditions predict that resistant virus should already be present at frequency μ/[1– (p_RES / p_WT )], which depends on the mutation rate, μ, and its relative fitness, p_RES / p_WT.

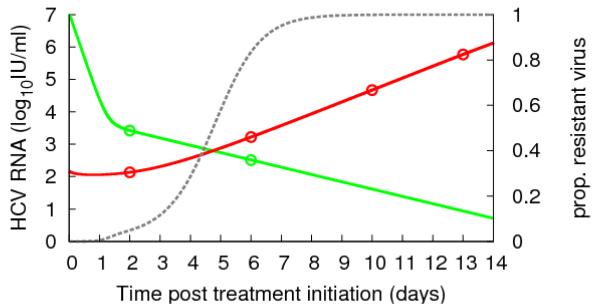
Interestingly, model analysis shows that the WT virus undergoes a more profound first phase decline than RES virus and this can uncover pre-existing drug resistant HCV variants (42). This effect can explain the high proportion of resistant virus measured by clonal sequencing during telapravir monotherapy in genotype 1a patients by Kieffer et al. (41) (Figure 4).

Figure 4.

HCV RNA data (circles, patient 1002 in (42)) during telaprevir monotherapy (green is WT, red is RES) and best-fit of the two-strain viral kinetic model (42) (solid lines). The dashed grey line is the proportion of resistant virus V_RES/ (V_WT +V_RES).

This model can also describe the rapid growth of RES virus during monotherapy (42). To account for the rapid amplification of RES virus an increase in the “replication space” (46) is needed. In the model of Rong et al. (42) the replication space is created by a high death rate of infected cells, δ= 0.32-0.52 d⁻ (or equivalently 1.3 log₁₀ IU mL⁻¹ week⁻¹ decline of the WT virus), and the proliferation of uninfected cells. These predictions still need to be validated experimentally. More complex approaches have been proposed to model the dynamics of multiple viral strains (47).

Viral kinetics during therapy with telaprevir in combination with peg-IFNα-2a for 2 weeks was also analyzed using this model (42). Assuming that peg-IFN reduces equally the production rates of RES and WT virus, the estimates of the total treatment efficacy confirmed that HCV mutants with reduced sensitivity to telaprevir still remain sensitive to peg-IFN. This prediction is consistent with the observation of continuous HCV RNA decline in most patients during 4 weeks of combination treatment (48). However, long-term studies show that during combination therapy with telaprevir and peg-IFN viral relapses are not avoided but mostly delayed (49-50).

Rapid decline of WT virus with HCV protease inhibitors: does the final phase of viral decline actually reflect the loss rate of infected cells?

The profound antiviral effect (large ε) of DAAs gives rise in most patients to a biphasic decline with a mean first phase viral decline of 2-5 logIU ml⁻¹ (i.e. 99%<ε<99.999%), larger than previously seen with IFN (51). The slope of the second phase decline is also enhanced, with a rate >1.0 logIU mL⁻¹week⁻¹ in almost all the patients treated with the protease inhibitors BILN-2061 (52), telaprevir (53) and TMC435 (54) (Figure 2, black line). Moreover, second phase slope estimates were consistent between patients (52-54) as opposed to the patient-to-patient variability seen with IFN-based treatments (6-9). Since ε is large, both the standard and the extended model with proliferation (13) attribute it to an enhanced rate of loss of infected cells. One possible explanation is that the inhibition of NS3 by a protease inhibitor may help restore IFN signaling pathways and stimulate the innate immune response (55-57), which in turn might lead to cure of infected cells as has been seen in HBV infection (58). Indeed if infected cells can be cured and become target cells again (14, 59-60), the second phase viral decline is not only due to the death rate of infected cells but is enhanced by the rate of cure of the infected cells. However, it remains to be determined whether HCV infected cells can be cured by DAAs and whether this process can explain quantitatively the observed kinetics. Modeling the kinetics of intracellular HCV RNA during therapy with DAAs might provide further insights.

Modeling intracellular HCV RNA kinetics

Dahari et al. modeled in detail the replication of subgenomic HCV RNA in Huh-7 cells (61) and studied the in vitro kinetics of intracellular genotype 1b subgenomic replicon (sg1b) RNA decline with different doses of IFN (62). They showed that sg1b RNA decline is not observed until ~12 hours after IFN dosing, similar to the delay seen in vivo (6), suggesting that the delay reflects the time needed for intracellular events to impact HCV RNA levels rather than IFN pharmacokinetics. Furthermore, sg1b RNA was found to decline rapidly in a dose dependent manner, consistent with the modeling assumption that IFN in vivo acts mainly by inhibiting HCV RNA production (6). For low doses of IFN (100 IU ml⁻¹), sg1b RNA declined initially and then reached a lower steady-state (62). Modeling showed that the kinetics of decline were consistent with sg1b RNA production under treatment simply being reduced by a constant factor (1-ε), as had previously been assumed for virion production in vivo (6). Interestingly for a higher dose of IFN (e.g. 250 IU ml⁻¹), sg1b RNA tended to decline in a biphasic (or triphasic) manner. Although experimental concerns were raised by the authors since at higher IFN doses replicon cell replication slowed or stopped before confluence was reached (62), the authors explained the biphasic decline by assuming a further on-treatment decline in the rate of viral production, possibly due to the loss of negative strand replicative intermediates.

Guedj and Neumann (unpublished data) developed a more complex intracellular model where intracellular viral RNA (vRNA) forms replication units, which in turn synthesize genomic units that are packaged and secreted as virions infecting more target cells. The model exhibited an intracellular critical effectivenessε_IC, and the implications of this threshold were investigated. The model predicts two possible modes of second phase decline for HCV RNA in serum according to the treatment effectiveness. If the antiviral effectiveness is moderate (ε < ε_IC), then the intracellular vRNA level is rapidly reduced by (1 – ε) and rapidly reaches a new steady state, lower than its pre-treatment level. Assuming that the amount of virus produced by a cell is proportional to the level of intracellular vRNA, the model predicts that viral load declines in a biphasic manner where the second phase viral decay is governed by the loss of infected cells, providedε > ε_C. On the other hand if the antiviral treatment is highly potent and ε > ε_IC, then intracellular RNA replication is more deeply destabilized and in their model intracellular vRNA vanishes over time in a biphasic exponential manner. Their model predicts that the long-term rate of intracellular vRNA decay is $\lambda =\gamma [1-\frac{1-\epsilon }{1-{\epsilon }_c}]$, where γ is the loss rate of intracellular vRNA, and that the second phase slope of serum HCV RNA decline is δ+λ. This model attributes the long-term viral decline observed with DAAs to a composite factor that depends on the loss of infected cells, the loss rate of intracellular vRNA, the treatment effectiveness and other host and viral factors involved in the determination of this intra-cellular critical threshold. Interestingly, this model predicts that the second phase viral decline could increase with the treatment effectiveness and DAAs might require shorter treatment duration to eradicate the virus. One of the limitations of this model is that all the infected cells have the same intracellular viral kinetics. However, when a cell is first infected it produces no virions for some period of time, called the eclipse phase, after which virion production would presumably ramp-up. According to the kinetics of this ramp-up and to the turnover of infected cells, the intracellular vRNA could be far from homogenously distributed and to account for this requires a more complicated model.

Methodology: fitting HCV RNA viral kinetics

To date viral kinetic models have been formulated as systems of ordinary differential equations. To evaluate such models, they are fit to data. Least-squares based methods, whereby search algorithms are used to find the set of parameter values that minimizes the discrepancy between the model prediction and viral load data from a given patient, are commonly employed. Many packages are available for that purpose in S-plus, SAS, R, Matlab or Berkeley-Madonna. Nevertheless this approach has many drawbacks. First, the information brought by data under the limit of detection (lod), whose proportion is increased in trials with new potent drugs, cannot be taken rigorously into account. Thiébaut et al. (63) showed that replacing undetectable viral load values by the lod value can lead to severe biases in the estimation of δ and ε. These biases can be dramatically reduced by likelihood-based approaches (64). Moreover the information brought by between-subject variation is ignored resulting in poor estimation of the parameters and a lack of power to identify covariates (65). An alternative approach is to use non-linear mixed effect models (NLMEM) that aim at describing the features in the population (mean of the parameters, standard deviation), rather than in each individual (66-67). Then individual parameters can be derived even if only sparse data are available that would not allow for estimation in each individual taken separately (68). By using optimally all the information, this approach allows new design of the sampling schedule that reduce substantially the number of samples needed within each individual. Free software with a viral kinetics library has been developed to address the issue of parameter estimation in NLMEM, c.f. monolix (http://software.monolix.org).

Conclusions

Mathematical models have provided detailed biologically-based explanations of HCV RNA kinetics during primary infection and under antiviral treatment. However, a complete understanding of viral kinetics is strongly limited by the lack of information on hepatocyte kinetics and intracellular viral replication dynamics. The recent finding that genetic factors, such as the polymorphism in IL-28b, critically affect IFN treatment outcome (69), suggest the need for also incorporating host cell signaling pathways into intracellular models. Ongoing development of in vitro systems should provide a better characterization of intracellular viral kinetics and motivate the development of more complex models able to provide a better picture of HCV RNA kinetics.