Modeling Competing Infectious Pathogens from a Bayesian Perspective: Application to Influenza Studies with Incomplete Laboratory Results

Abstract

In seasonal influenza epidemics, pathogens such as respiratory syncytial virus (RSV) often co-circulate with influenza and cause influenza-like illness (ILI) in human hosts. However, it is often impractical to test for each potential pathogen or to collect specimens for each observed ILI episode, making inference about influenza transmission difficult. In the setting of infectious diseases, missing outcomes impose a particular challenge because of the dependence among individuals. We propose a Bayesian competing-risk model for multiple co-circulating pathogens for inference on transmissibility and intervention efficacies under the assumption that missingness in the biological confirmation of the pathogen is ignorable. Simulation studies indicate a reasonable performance of the proposed model even if the number of potential pathogens is misspecified. They also show that a moderate amount of missing laboratory test results has only a small impact on inference about key parameters in the setting of close contact groups. Using the proposed model, we found that a non-pharmaceutical intervention is marginally protective against transmission of influenza A in a study conducted in elementary schools.

1 Introduction

In seasonal influenza epidemics, pathogens such as respiratory syncytial virus (RSV) often co-circulate with influenza and cause influenza-like illness (ILI) in human hosts (Fleming et al., 2003). Consequently, ILI alone is not a reliable indicator for the infection status of influenza. Ideally, ILI-triggered specimen collection and laboratory tests are used to ascertain the responsible pathogen. However, test results may be incomplete because of either budgetary limits or administrative difficulty. Inference may be biased if the missing infection status is not appropriately imputed or integrated out (Rubin, 1976; Little and Rubin, 2002). In situations with small close contact groups such as households, the contact groups of individuals with missing infection status may be excluded from the analysis without invalidating the inference if there is no between-group transmission and assuming the data are missing at random (MAR). By MAR we mean that whether a subject with ILI is tested or not is independent of his/her infection status given the observed data. However, with larger contact groups such as schools, it is impractical to discard a contact group because a few cases are missing laboratory test results.

The issue of incomplete laboratory test results has been addressed in the setting of influenza vaccine studies with validation sets. In these studies, surveillance cultures were obtained from a small proportion of study subjects. Under the assumption of MAR, the mean score approach can be used to estimate the vaccine efficacy (VE) (Halloran et al., 2003). In the situation of nonignorable missingness, e.g., the vaccine reduces symptom severity but cases with severe symptoms are likely to be over-sampled, an informative prior distribution can be imposed on the selection bias of the validation set to estimate the VE (Scharfstein et al., 2006). These two methods are unconditional on individual-level exposure to the risk of infection and are suitable for cumulative incidence or time-to-event (Halloran et al., 2007) data with categorical covariates. When individual-level exposure to infection is considered, missing data impose a greater challenge because of both the dependence among individuals and the continuous nature of the individual-level exposure history.

To account for individual exposure to infection and missingness in infection status, we propose a Bayesian competing-risk model for multiple co-circulating pathogens under certain pathogenicity and interference assumptions. The use of MCMC for posterior computation in the setting of transmission of infectious diseases can be traced back to the late 1990s (Gibson, 1997; Gibson and Renshaw, 1998; O’Neill et al., 2000; Auranen et al., 2000). Recent applications to influenza include analyses of household data with illness onset dates (Cauchemez et al., 2004) and asymptomatic infections identified by laboratory tests (Yang et al., 2008). However, none of this methodology has explicitly addressed missingness in infection status. For an ILI episode with unknown infection status, the evaluation of p(infection with influenza | ILI is untested) requires knowledge about p(ILI is untested | infection with a non-influenza pathogen). Therefore, it seems natural to simultaneously model the spreading of both influenza and non-influenza pathogens in the framework of competing risks. The performance of the proposed model and the effect of missing data on the inference about key parameters, such as the transmissibility of pathogens and the efficacies of an intervention, are evaluated in simulation studies. The model is used to analyze a recent study of non-pharmaceutical intervention (NPI) against influenza illness conducted in elementary schools in Pittsburgh, Pennsylvania, in the United States.

2 Methods

2.1 Data Structure

Consider a prospective clinical study to evaluate the efficacy of an intervention against influenza that is implemented in a collection of close contact groups. These groups could be households in a community or schools in a school district. The intervention could be a vaccine, an antiviral agent or a non-pharmaceutical program. Let N denote the total number of individuals under study. Starting from day 1, M different pathogens including influenza are co-circulating in the community, each imposing a hazard of community-to-person infection on susceptibles. Individuals infected with any of the pathogens can initiate within-group transmission of the same pathogen. Let day T be the stopping time of the study.

During the study period, we observe sequential ILI onset times in infected subjects. The observation is made on a daily basis with an integer day t corresponding to the continuous time scale (t − 1, t]. Each individual may have no episodes, a single episode, or multiple episodes of ILI. Let t̃_i = (t̃_i1, …, t̃_iKi) denote the ordered sequence of ILI onset days for individual i, i = 1, …, N, where K_i is the number of ILI episodes person i has during the observation period. Upon ILI onset, the individual’s specimen will be collected immediately to identify the pathogen type in the laboratory. In many studies, non-influenza pathogens are not specifically tested. When only one non-influenza pathogen is co-circulating, a negative test for influenza is equivalent to a positive test for this pathogen. When there are multiple non-influenza pathogens, one may treat all unknown ILI-causing viruses as a single hypothetical pathogen. How this simplification may affect the inference about the pathogen of primary interest, influenza in our case, will be assessed in simulation studies. Let v_i = (v_i1, …, v_iKi)′ indicate the pathogen types responsible for the ILI episodes, where v_ik = m if the pathogen at the k^th onset is type m, k = 1, …, K_i, m = 1, …, M. We assume competing risks, i.e., each ILI episode is caused by a single type of pathogen. If all ILI onsets are tested, v_i is completely observed. In reality, some components of v_i may be missing because the specimens are either not collected or not tested. Let u_i = (u_i1, …, t_iKi)′ denote the set of missingness indicators such that u_ik = I(v_ik is observed), where I(·) is the indicator function. Let x_i(t) be the covariates, including the intervention, associated with individual i on day t, and define x_i = {x_i(t) : 1 ≤ t ≤ T}. Hence, {t̃_i, u_i, x_i} is completely observed, v_i is potentially only partially observed, and the infection days, denoted by t̂_i = (t̂_i1, …, t̂_iKi)′ with t̂_i < t̃_i element-wise, are not directly observable, i = 1, …, N.

2.2 Natural History of Disease

While transmissibility of the pathogens, primarily influenza, and intervention efficacies are the major quantities of inferential interest, our parameters for transmissibility are closely related to how we define the infectious period, part of the natural history of disease. For a clear presentation of the model, we first introduce assumptions about the natural history of disease that has the following elements: the incubation period (time from infection to ILI onset), the latent period (time from infection to infectiousness onset), the infectious period for each pathogen, and the interference, or competing risk, mechanism among pathogens. The parameterization of the natural history is chosen to reduce the need for strong empirical information that may not be available for newly emerging pathogens, for example, the novel influenza A(H1N1) virus. Figure 1 presents a diagram for the type of natural history under consideration.

Figure 1.

A possible scenario of the natural history of two pathogens that infect the same individual. (a) two ILI onsets are observed at t̃_i1 and t̃_i2 for individual i. The lab-test result v_i1 (v_i2) indicates that the responsible pathogen for the first (second) ILI is pathogen 1 (2). The maximum duration of the incubation period is H_m days for pathogen m, with H₁ = 4 and H₂ = 3, and thus the 4 (3) days before t̃_i1 (t̃_i2) are possible infection times. d_jk is the duration of immunity in number of days that infection by pathogen j provides to pathogen k. The values of d_jk’s suggest that the infection of either pathogen provides long-term immunity to the same type but only short-term immunity to the other type. (b) For the second ILI episode, given that the infection occurred during day t̂_i2, the infectiousness of individual i starts at the end of day t̃_i2 and lasts for a period of Δ₂ = 7 days. During the infectious period, the relative infectiousness curve takes the shape of a beta density function with parameters a₂ and b_i2, and the infectiousness peaks at the end of the symptom onset day, t̃_i2.

2.2.1 The incubation and latent periods

Without loss of generality, we assume the actual infection and symptom onset occur at the end of the days t̂_ik and t̃_ik. We further assume that both the incubation and the infectious periods start at the beginning of day t̂_ik + 1, the day after infection, which implies that the duration of the latent period is 0. As most ILI-causing pathogens commonly seen in an influenza season have short incubation periods, we consider a discrete distribution over a duration of H_m days for pathogen m. Namely, we assume p(t̃_ik = t̂_ik + l| t̂_ik = m) = q_ml, l = 1, …, m = 1, …, M, where the q_ml are unknown parameters. If the incubation period is relatively long, it is possible to let the distribution be governed by a continuous distribution. Define q_m = (q_m1, …, q_mHm)′ and q = (q₁, …, q_m)′. Although the distribution of the incubation period is of biological importance, q can not be reliably estimated because the infection times are not observed and the posterior distribution of the infection times is governed by unknown transmission and intervention efficacy parameters. As a result, we do not make inference on q, and examine in simulation studies whether it affects inference on the parameters of interest.

2.2.2 The infectious period

While the data are generally observed on a discrete-time basis, it is more convenient to consider the infectious period in continuous-time. Yang et al. (2009) use a beta density, f_beta(·|α, β), to model the variation of infectiousness over a duration of Δ days. We refer to f_beta(α, β) as the relative infectiousness curve (RIC). Under this setting, the hazard of a secondary infection at time 0 ≤ t ≤ Δ after the primary infection is $\gamma f_{\mathit{beta}}(\frac{t}{\mathrm{\Delta }}\mid \alpha ,\beta )$, where γ is the average hazard. Daily cumulative hazards can be calculated to construct a discrete-time likelihood. However, reliable estimation of α and β is difficult with household data. The problem worsens when the distribution of the incubation period is assumed unknown. One factor contributing to this problem is the dependence between the infectious period and the incubation period: (1) both periods start from the same time point; and (2) the location of the peak infectiousness in an index case affects the possible infection time and thus the incubation period of a secondary case. A strong association between the observed ILI onset time and the infectious period can be helpful in reducing the dependence. For instance, some likelihood methods assume that the infectious period starts from ILI onset (Yang et al., 2006). In this model, we link the peak of the RIC directly to the ILI onset time. Let the duration of the infectious period of pathogen m, Δ_m, m = 1, …, M, be fixed and assumed known. The RIC for pathogen m has the shape f_beta(·|a_m, b_m) (Figure 1(b)), where the unknown parameters a_m and b_m are related to the usual shape parameters α_m and β_m via a_m = α_m + β_m and $b_m=\frac{{\alpha }_m-1}{{\alpha }_m+{\beta }_m-2}$. The parameter am represents the scale, with a larger value for a higher peak, and the parameter b_m is the mode representing the location of the peak. As a mode is forced with this parameterization, we have α_m > 1 and β_m > 1. We further assume that the mode of the RIC is specific to each ILI episode, denoted by b_ik, and is located at the end of the ILI onset day, i.e., b_ik = (t̃_ik − t̂_ik)/Δ_m if v_ik = m. This setting partially accounts for individual variation in the RIC. In addition, the number of parameters characterizing the RIC is reduced as compared to the setting in Yang et al. (2009), which makes the joint estimation of the incubation and infectious periods possible.

2.2.3 The interference mechanism via cross-immunity

Within a host, the infection by one pathogen may interfere with the infection by another pathogen via two immunological mechanisms: (1) a certain level of specific immunity to a spectrum of pathogens that share similar antigenic structures with the invaded pathogen, and (2) non-specific immunity activated by the innate and/or the complement immune system to a much broader range of pathogens. Specific immunity lasts relatively long, e.g., two influenza strains of the same type rarely infect the same person in the same season, whereas non-specific immunity often lasts for days. Epidemiological effects of biological interference among pathogens have been previously studied in simulations (Ackerman et al., 1990), but its implications for statistical inference have, to our knowledge, never been addressed.

We assume infection with pathogen m provides immunity against pathogen n from the time of infection up to and including the ILI onset day and for an additional period of d_mn days beyond. After that, the immunity against pathogen n is reduced to 0. For specific immunity, we assume d_mn = ∞. An example of immune periods is given in Figure 1(a). The assumption of short-term non-specific immunity allows two ILI episodes to be distinguishable from each other. We further assume the values of d_mn’s are known to avoid an identifiability problem, because the immunity level is confounded with the hazard of infection which is defined under complete susceptibility. In the data analysis, sensitivity to a reasonable range of d_mn’s will be investigated. We refer to D = {d_mn}_M×M as the interference matrix.

2.3 Transmission model

Let ω_m be the constant hazard of community-to-person transmission for pathogen m. It is possible to model a time-dependent community-to-person transmission hazard, e.g., multiply ω_m by a relative intensity curve varying over time. In such a case, ω_m would be interpreted as the average hazard over the season. Let δ_i(m, t) indicate whether individual i is susceptible to pathogen m on day t (1=yes, 0=no), then ${\delta }_i(m,t)=1-{\vee }_{k=1}^{K_i}I({\widehat{t}}_{ik}\le t<{\stackrel{\sim }{t}}_{ik}+d_{v_{ik}m})$, where ∨ denotes logical “or”. The covariate-adjusted transmission hazard of pathogen m from an infectious individual j with infection day t̂_jk to a susceptible individual i in the same group at time t is

$${\lambda }_{j\to i}(m,t)={\delta }_i(m,t)exp\{{\mathit{\beta }}_{S,m}^{\prime }{\mathit{x}}_i(t)+{\mathit{\beta }}_{I,m}^{\prime }{\mathit{x}}_i(t)\}{\gamma }_m{f}_{\mathit{beta}}(\frac{t-{\widehat{t}}_{jk}}{{\mathrm{\Delta }}_m}\mid a_m,b_{jk}),$$ (1)

where β_S.m and β_I,m are covariate effects associated with the susceptible and the infective, and γ_m is the average person-to-person hazard of infection specific to pathogen m. Let s_i denote the close contact group to which individual i belongs. The total instantaneous hazard of infection with pathogen m for individual i in group s_i at time t is then given by

$${\lambda }_i(m,t)={\delta }_i(m,t)exp\{{\mathit{\beta }}_{S,m}^{\prime }{\mathit{x}}_i(t)\}{\omega }_m+\sum _{\begin{array}{c}j\in s_i\\ j\ne i\end{array}}{\lambda }_{j\to i}(m,t).$$ (2)

The probability of escaping infection with pathogen m during day t is given by exp {− Λ_i(m, t)}, where ${\mathrm{\Lambda }}_i(m,t)={\int }_{t-1}^t{\lambda }_i(m,\tau )d\tau$. We assume the M pathogens are competing risks, that is, only one pathogen can infect an individual on any day. The exact probability of infection with pathogen m on day t, denoted by P_i(m, t), depends on the assumption about the mechanism of competition. A typical choice is that the earliest infection is the winner, which leads to

$$P_i(m,t)={\int }_{t-1}^t\left\{{\lambda }_i(m,\tau )\prod _{l=0}^{M}exp\{-{\int }_{t-1}^{\tau }{\lambda }_i(m,\epsilon )d\epsilon \}\right\}d\tau .$$ (3)

The evaluation of (3) requires numerical integration and hence substantially increases the computational burden. If λ_i(m, τ) is assumed constant over (t − 1, t] for all m = 1, …, M, (3) simplifies to

$$P_i(m,t)=\frac{{\mathrm{\Lambda }}_i(m,t)}{{\sum }_{l=1}^M{\mathrm{\Lambda }}_i(l,t)}\left(1-\prod _{l=1}^{M}exp\{-{\mathrm{\Lambda }}_i(l,t)\}\right).$$ (4)

The above expression implies an infection process that first selects infection from any pathogen via the probability $1-{\prod }_{l=1}^{M}exp\{-{\mathrm{\Lambda }}_i(l,t)\}$ and then chooses pathogen m via the probability ${\mathrm{\Lambda }}_i(m,t)/{\sum }_{l=1}^M{\mathrm{\Lambda }}_i(l,t)$. This mechanism of competition is computationally affordable. Consequently, although the true hazards are not constant over time, we assume (4), not (3), is the true mechanism of competition.

Let ψ = {ω_m, γ_m, β_S.m, β_I.m, a_m : m = 1, …, M} be the collection of all unknown parameters except for q. Let R_i denote the history of exposure to the risk of infection for individual i. Note that R_i is determined by the realized infections in the group s_i. Given ψ and the exposure history, the individual-level probability of transmission is

$$p({\widehat{\mathit{t}}}_i,{\mathit{v}}_i\mid \mathit{\psi },R_i)=\left(\prod _{t\notin {\widehat{\mathit{t}}}_i}\prod _{m=1}^{M}exp\{-{\mathrm{\Lambda }}_i(m,t)\}\right)\left(\prod _{k=1}^{K_i}{P}_i(v_{ik},{\widehat{t}}_{ik})\right),$$ (5)

the individual-level probability for the incubation period is

$$p({\stackrel{\sim }{\mathit{t}}}_i\mid {\widehat{\mathit{t}}}_i,{\mathit{v}}_i,\mathit{q})=\prod _{k=1}^{K_i}{q}_{v_{ik}({\stackrel{\sim }{t}}_{ik}-{\widehat{t}}_{ik})}.$$ (6)

The conditioning on R_i, the exposure history, in (5) is for notational convenience only, because the infection status of person i for each day t is really conditional only on infections occurring before t.

2.4 Prior distributions

The following flat priors are assumed:

$$\begin{array}{ll}{\omega }_m\sim \text{Uniform}({10}^{-6},10),\hfill & {\gamma }_m\sim \text{Uniform}({10}^{-6},10),\hfill \\ a_m\sim \text{Uniform}(2,10),\hfill & {\mathit{q}}_m\sim \text{Dirichlet}({\mathbf{1}}_{H_m\times 1}),\hfill \end{array}$$ (7)

m = 1, …, M. A flat prior with a wide range is adopted for most parameters to allow for assessment of the posterior with minimal prior information. For transmission parameters, the boundaries are chosen to be wide and contain historic estimates for ω_m and γ_m. Historic estimates of community-to-person and person-to-person transmission hazards for influenza have a scale of 10⁻³ – 10⁻² (Yang et al., 2006). For a_m, the lower bound is required for the existence of the mode, and the upper bound is chosen to avoid an unrealistically sharp peak. Flat priors could also be used for the covariate effects, β_S.m and β_I.m, with a range centered around the null value 0. In some situations such as intervention studies, it may be preferable to reparameterize the covariate effects, e.g., exp(β_S.m), and assign flat or other non-informative priors to the transformed parameters. Let π(ψ) be the joint prior distribution of the parameters in ψ, and let π(q) be the prior distribution of q.

2.5 The full joint probability distribution

We assume that the missingness of the laboratory test results is ignorable (MAR), i.e., the probability of u_i does not depend on v_i given the observed data. Such an assumption is reasonable because the missingness of the test result for an ILI is often driven by availability of resources for collecting specimens that largely depends on the observed onset time. An ILI case occurring near the peak of an epidemic may be less likely to have a specimen drawn.

Define t̂ = {t̂_i : i = 1, …, N}, v = {v_i : i = 1, …, N}, and t̃ = {t̃_i : i = 1, …, N}. The full joint probability distribution of t̃, v, t̂, ψ and q is given by

$$p(\stackrel{\sim }{\mathit{t}},\mathit{v},\stackrel{\sim }{\mathit{t}},\mathit{\psi },\mathit{q})=\left(\pi (\mathit{\psi })\prod _{i=1}^N\left\{p({\widehat{\mathit{t}}}_i,{\mathit{v}}_i\mid \mathit{\psi },R_i)\right\}\right)\left(\pi (\mathit{q})\prod _{i=1}^N\left\{p({\stackrel{\sim }{\mathit{t}}}_i\mid {\widehat{\mathit{t}}}_i,{\mathit{v}}_i,\mathit{q})\right\}\right)$$ (8)

The factorization in (8) suggests that, conditioning on t̃ and v, ψ and q are independent. Let C_mh be the number of episodes caused by pathogen m having an incubation period of h days, and let C_m = (C_m1, …, C_mHm)′. The nuisance parameter q can be integrated out to obtain the full joint probability distribution of t̃, v, t̂ and ψ:

$$p(\stackrel{\sim }{\mathit{t}},\mathit{v},\widehat{\mathit{t}},\mathit{\psi })=\int p(\stackrel{\sim }{\mathit{t}},\mathit{v},\widehat{\mathit{t}},\mathit{\psi },\mathit{q})d\mathit{q}=\left(\prod _{m}B({\mathit{C}}_m+\mathbf{1})\right)\left(\pi (\mathit{\psi })\prod _{i=1}^N\left\{p({\widehat{\mathit{t}}}_i,{\mathit{v}}_i\mid \mathit{\psi },R_i)\right\}\right),$$ (9)

where $B({\mathit{C}}_m+\mathbf{1})={\prod }_{h=1}^{H_m}\mathrm{\Gamma }(C_{mh}+1)/\mathrm{\Gamma }\left({\sum }_{h=1}^{H_m}(C_{mh}+1)\right)$ is the multinomial beta function with respect to the vector C_m + 1, and Π_m B(C_m + 1) = p(t̃|v, t̂). Note that ψ is also independent of t̃ given v and t̂. The posterior distribution of ψ given the full data is

$$p(\mathit{\psi }\mid \stackrel{\sim }{\mathit{t}},\mathit{v},\widehat{\mathit{t}})=p(\mathit{\psi }\mid \mathit{v},\widehat{\mathit{t}})\propto p(\mathit{v},\widehat{\mathit{t}},\mathit{\psi })=\pi (\mathit{\psi })\prod _{i=1}^N\left\{p({\widehat{\mathit{t}}}_i,{\mathit{v}}_i\mid \mathit{\psi },R_i)\right\}.$$ (10)

The posterior distribution of ψ given the observed data, p(ψ|t̃, v_obs), where v_obs is the observed components of v, is analytically intractable, but we do not need to evaluate it explicitly since we use data augmentation in the MCMC algorithm described below.

2.6 Markov chain Monte Carlo (MCMC) algorithm

All parameters in ψ are sampled using a random walk Metropolis-Hastings algorithm. We describe the sampling procedure for γ_m to illustrate. Let ψ⁻(γ_m) denote the collection of parameters excluding γ_m. To update γ_m, we draw a new value ${\gamma }_m^{★}$ from the proposal distribution $\text{Log}-\text{Normal}(log({\gamma }_m^{\#}),{\sigma }_{{\gamma }_m}^2)$, where ${\gamma }_m^{\#}$ is the current value, and accept the new sample with the probability $\mathit{min}\left\{1,\frac{{\gamma }_m^{★}p\left(\mathit{v},\widehat{\mathit{t}},{\mathit{\psi }}^{-}({\gamma }_m),{\gamma }_m^{★}\right)}{{\gamma }_m^{\#}p\left(\mathit{v},\widehat{\mathit{t}},{\mathit{\psi }}^{-}({\gamma }_m),{\gamma }_m^{\#}\right)}\right\}$. The value of ${\sigma }_{{\gamma }_m}^2$ is determined adaptively to reach an average acceptance rate of 0.25 – 0.45, and then fixed to obtain posterior samples for inference.

The data augmentation step involves sampling all infection times and missing pathogen types, if any, per individual simultaneously. Let {( ${\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i^{(l)}$) : l = 1, …, L_i} be the collection of candidate values of (v_i, t̂_i) that satisfies $p({\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i^{(l)}\mid \mathit{\psi },R_i)>0$. We sample the value of (t̂_i, v_i) from its conditional distribution:

$$\begin{array}{l}p\left({\mathit{v}}_i={\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i={\widehat{\mathit{t}}}_i^{(l)}\mid {\stackrel{\sim }{\mathit{t}}}_i,\mathit{\psi },\{{\mathit{v}}_j,{\widehat{\mathit{t}}}_j,{\stackrel{\sim }{\mathit{t}}}_j:j\in s_i,j\ne i\}\right)=\frac{\left\{{\prod }_{m}B({\mathit{C}}_m^{(l)}+\mathbf{1})\right\}p({\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i^{(l)}\mid \mathit{\psi },R_i)\left\{{\prod }_{\begin{array}{c}j\in s_i\\ j\ne i\end{array}}p({\mathit{v}}_j,{\widehat{\mathit{t}}}_j\mid \mathit{\psi },R_j^{(l)})\right\}}{{\sum }_{k=1}^{L_i}\left\{{\prod }_{m}B({\mathit{C}}_m^{(k)}+\mathbf{1})\right\}p({\mathit{v}}_i^{(k)},{\widehat{\mathit{t}}}_i^{(k)}\mid \mathit{\psi },R_i)\left\{{\prod }_{\begin{array}{c}j\in s_i\\ j\ne i\end{array}}p({\mathit{v}}_j,{\widehat{\mathit{t}}}_j\mid \mathit{\psi },R_j^{(k)})\right\}},\\ l=1,\dots ,L_i.\end{array}$$ (11)

Note that because R_j for j ≠ i and C_mh are dependent on the value of (v_i, t̂_i), we use $R_j^{(l)}$ and $C_{mh}^{(l)}$. To monitor convergence of the MCMC algorithm, we examine trace plots and compute the Gelman and Rubin’s scale reduction factor (Gelman and Rubin, 1992) for each component in ψ.

3 Simulation Study

We conduct simulations to evaluate the performance of the model and the impact of missing laboratory test results under several different settings. We simulate epidemics in a population composed of 100 households, each of size 5. Prior to the epidemics, the individuals are randomized to either vaccine or placebo, and vaccine status is the only covariate for simplicity. Let z_i denote the intervention arm, 1 for vaccine and 0 for control. Then, in equations (1) and (2), we have ${\mathit{\beta }}_{S,m}^{\prime }{\mathit{x}}_i(t)=z_{i}log({\theta }_m)$ and ${\mathit{\beta }}_{I,m}^{\prime }{\mathit{x}}_j(t)=z_{j}log({\phi }_m)$. The parameters θ_m and φ_m are related to vaccine efficacies in reducing susceptibility (VE_S) and infectiousness (VE_I) via VE_S.m = 1 − θ_m and VE_I.m = 1 − φ_m. If pathogen m is the target of the vaccine or cross-immunity exists between pathogen m and the target, we would expect 0 ≤ θ_m < 1 and 0 ≤ θ_m < 1; otherwise, we would expect θ_m = φ_m = 1 in general. The following priors are used for the vaccine effects:

$${\theta }_m\sim \text{Uniform}({10}^{-2},{10}^2),\text{and}{\phi }_m\sim \text{Uniform}({10}^{-2},{10}^2).$$

We start by evaluating the performance of the proposed model when the number of co-circulating non-primary pathogens is either correctly specified or mis-specified. We simulate epidemics of three pathogens (M=3) for this purpose, and index the primary pathogen by 1 and the non-primary pathogens by 2 and 3. The primary pathogen has transmission parameters similar to that of interpandemic influenza, with about 0.26 for the community probability of infection (CPI) during the 100-day epidemic and 0.19 for the secondary attack rate (SAR) (Yang et al., 2006). To ensure a sufficient number of cases, the two non-primary pathogens have parameters not much different from those of the primary pathogen. When simulating the epidemics, we set d_mn = 7 for m ≠ n and ∞ for m = n. Under this setting, an individual could have at most three observed ILI episodes, one caused by each pathogen.

We generate missing data under an assumption of MAR. In particular, we let the proportion of missing laboratory test results depend on the ILI onset day t̃_ik : 50% for ${\stackrel{\sim }{t}}_{ik}<\frac{T}{2}$ and 10% otherwise. Misspecification is introduced by analyzing the simulated data as if there were only two pathogens (not three), the primary one and a hypothetical non-primary one indexed by 1 and 2 respectively. We have to assume in the analysis that the non-primary pathogen does not induce specific immunity to itself, so that the misspecified model is compatible with possible situations of three ILI episodes per individual in the simulated data. For illustration, we set d₂₂ = 7 in the analysis for the scenario of misspecification.

The true parameter settings and simulation results for the primary pathogen are shown in Table 1. The estimates are very similar under the correctly specified and the misspecified scenarios, suggesting that the model is tolerant to this type of model misspecification at least when M is small. The results also imply that the transmission hazards, ω₁ and γ₁, and the vaccine effect in reducing susceptibility, θ₁, can be estimated with little or no bias even for a moderate sample size. The decreased information for φ₁ as compared to θ₁ in the household data has been reported elsewhere (Yang et al., 2006). The last two columns of Table 1 show that increasing the sample size generally leads to improved inference for all parameters, particularly for φ₁ and α₁. In addition, given an equal total sample size, having larger contact groups is preferable to having more contact groups in terms of both reducing bias and narrowing the credible sets (CS).

Table 1.

Average posterior summaries over 100 simulated epidemics of 3 co-circulating pathogens with laboratory test results missing for 30% of the ILI episodes. Estimates for the primary pathogen (m=1) are presented. Comparison is made between the scenarios that the number of non-primary pathogens (m=2, 3) is correctly specified as two versus mis-specified as one, and between a small population (100 households of size 5) versus a large population (100 households of size 10 or 200 households of size 5). True parameters generating the epidemics are given in the second column and in the footnote.

		100 households of size 5		100 households of size 10	200 households of size 5
Parameter	True Value	Correctly specified M = 3	Misspecified M = 2	Correctly specified M = 3	Correctly specified M = 3
ω1	0.003	0.0030(0.0023, 0.0039)	0.0030(0.0023, 0.0039)	0.0030(0.0025, 0.0036)	0.0029(0.0024, 0.0035)
γ1	0.030	0.029(0.020, 0.042)	0.029(0.020, 0.042)	0.030(0.025, 0.036)	0.029(0.022, 0.038)
θ1	0.70	0.70(0.50, 0.97)	0.69(0.49, 0.97)	0.69(0.57, 0.82)	0.71(0.56, 0.90)
φ1	0.70	0.74(0.37, 1.41)	0.74(0.37, 1.42)	0.70(0.51, 0.95)	0.72(0.45, 1.12)
a1	6.0	6.39(3.59, 9.47)	6.39(3.57, 9.48)	6.01(4.16, 8.75)	6.40(4.04, 9.36)

True parameters for pathogen 1 : q₁₁ = 0.2, q₁₂ = 0.6.

True parameters for pathogen 2 : ω₂ = 0.003, γ₂ = 0.015, θ₂ = 0.6, φ₂ = 1.0, a₂ = 4.0, q₂₁ = 0.8, q₂₂ = 0.3.

True parameters for pathogen 3 : ω₃ = 0.0015, γ₃ = 0.040, θ₃ = 1.0, φ₃ = 0.6, a₃ = 5.0, q₃₁ = 0.6, q₃₂ = 0.5.

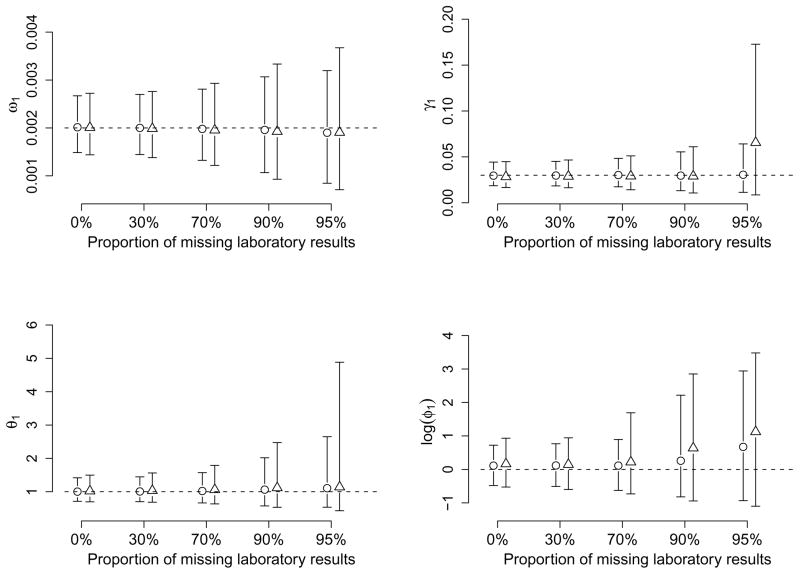
It is also of interest to investigate how the proportion of missing laboratory test results would alter inference about the primary pathogen, and whether such an effect is related to the number co-circulating pathogens. We first simulate pathogens with identical transmission characteristics and natural history. This is because any difference in parameters can help to differentiate the pathogens from each other and will thus limit the impact of missing laboratory results. In addition, we assume specific immunity within and between pathogens for simplicity. The assumption of within-pathogen specific immunity is also employed for similarity of the primary pathogen to influenza. In this simulation study, we let ω_m = 0.002, γ_m = 0.03, and θ_m = φ_m = 1 for all m, i.e., no vaccine efficacy for any pathogen. The proportion of ILI episodes with missing laboratory results takes five possible values: 0%, 30%, 70%, 90% and 95%. We show the average posterior medians and 95% credible sets over 100 epidemics in Figure 2 for ω₁, γ₁, θ₁ and φ₁ only. The 95% CS bars with circles and triangles depict results for two and three co-circulating pathogens. Estimates for φ₁ are shown on the log scale so that the bars can be shown with the same axes.

Figure 2.

Comparison of posterior estimates for parameters by the proportion of missing laboratory test results and the number of co-circulating pathogens. Bars with circles (triangles) denote average 95% credible sets, the middle point representing the average posterior medians, for the primary pathogen over 100 epidemics of two (three) equally transmissible co-circulating pathogens. The dashed lines indicate the true values of the parameters.

Overall, when two pathogens are co-circulating, a missingness proportion of 70% or less does not increase the uncertainty about the parameters by much. Dramatic increases in the length of 95% CS are observed for the efficacy parameters θ₁ and φ₁ when the proportion of missingness reaches 90%. Even more dramatic changes in the two efficacy parameters are seen at 95% missingness, but only moderate increases are observed for the transmission rates. The more co-circulating pathogens there are, the more sensitive the parameters are to the proportion of missingness. When three pathogens are co-circulating, a substantial rise in uncertainty is observed for φ₁ at the missingness proportion of 70% and for both θ₁ and φ₁ at 90% and higher. In addition, there is a large increase in the length of the 95% CS for γ₁ at 95% missingness. The reduced information about φ₁ in the simulated epidemics compared to other parameters accounts for its extreme level of sensitivity. The pattern of larger bias and higher uncertainty with increasing missingness is also obvious for all the parameters in Figure 2.

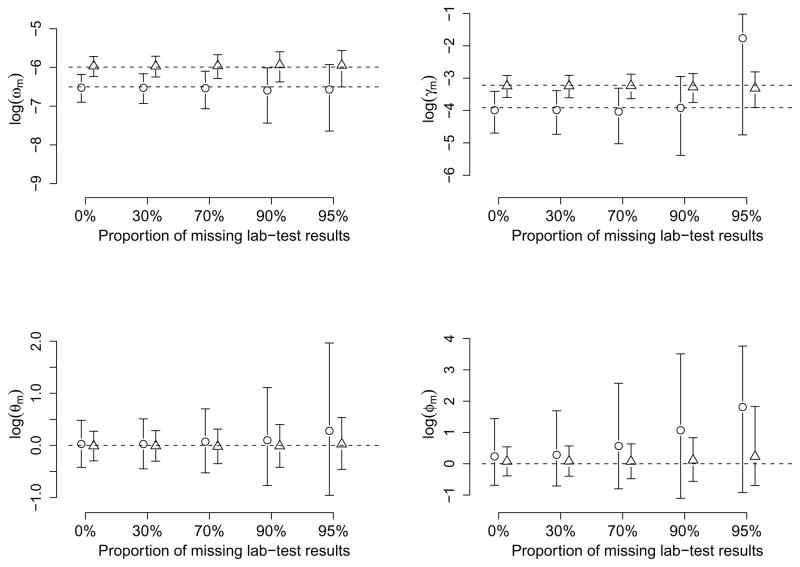
Figure 3 compares the variability in parameter estimates in response to increasing the proportion of missing laboratory test results between two co-circulating pathogens with very different transmission rates. The weaker (stronger) pathogen has ω₁ = 0.0015 (0.0025) and γ₁ = 0.02 (0.04), corresponding to a CPI of 0.14 (0.22) and a SAR of 0.13 (0.24). We index the weaker (stronger) pathogen by 1 (2) in the subscripts. The estimates for all parameters are presented on the log scale. As expected, credible sets are shorter for the stronger pathogen that generates more cases. The parameter estimates associated with the weaker pathogen are much more sensitive to the proportion of missing laboratory results compared to those of the stronger pathogen. However, for all parameters except for φ₁, uncertainty does not increase dramatically until the missingness reaches 90% even for the weaker pathogen. Similar to Figure 2, a dramatic increase in uncertainty and bias may occur for the transmission rate γ₁ when the information is decreased by an extremely high missingness rate. Among the key parameters, ω₁ and φ₁ are the parameters least and most affected by missingness respectively. Figure 3 also suggests that a fairly transmissible pathogen (with a SAR of 0.24) can provide nearly unbiased estimates for φ₁, and thus the VE_I, even at high missingness proportions.

Figure 3.

Comparison of posterior estimates for parameters by the proportion of missing laboratory test results and the two co-circulating pathogens. Bars with circles (triangles) denote 95% credible sets for the pathogen with weaker (stronger) transmissibility. The dashed lines indicate the true values of the parameters.

4 Data Analysis

The Pittsburgh Influenza Prevention Project (PIPP) is a prospective randomized study of the effectiveness of non-pharmaceutical interventions (NPI) conducted in ten public elementary schools in the city of Pittsburgh. The five schools in the intervention arm were provided with NPI training program including hand hygiene, hand etiquette, and cover your cough behaviors, as well as supplies of alcohol-based hand sanitizer for all classrooms. In addition, parents received educational materials about NPIs. Prior to and during the influenza season, absences were monitored and absentees were screened by phone for the presence of ILI. During the season, home visits were made to collect specimens for laboratory tests (rapid test and PCR). ILI is defined as fever (≥ 100°F) plus cough or sore throat.

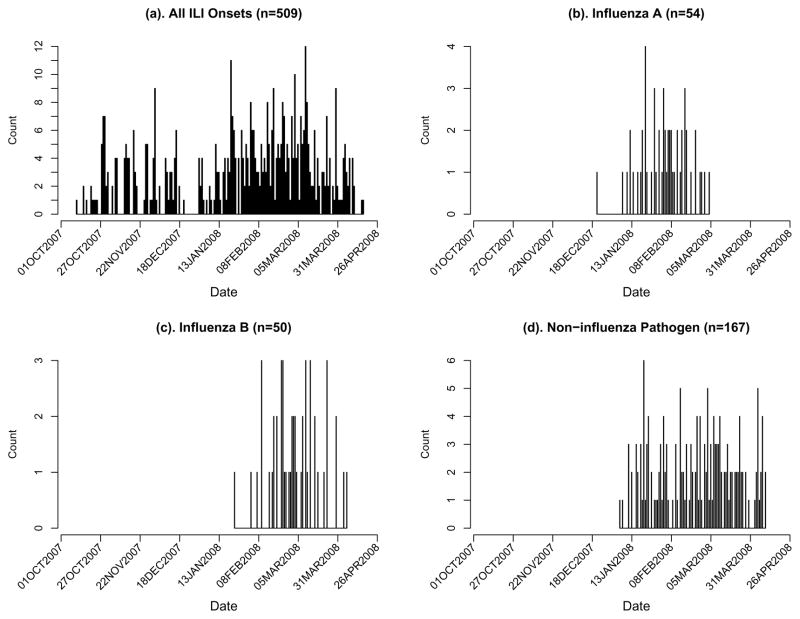
The 2007–2008 influenza season started near the end of December and ended around the end of April. The epidemic curves for overall and pathogen-specific ILI episodes are shown in Figure 4. Most ILI episodes that occurred prior to the influenza epidemic were not lab-tested by design. We restrict all analyses to the period of 12/31/2007 – 4/18/2008, during which a total of 380 ILI episodes were observed in 352 out of 3959 students. Further breakdown of these numbers by pathogen type and laboratory test is given in Table 2. The influenza B epidemic occurred slightly later than influenza A, and only a single person was infected by both influenza types. We assume that ILI episodes with negative laboratory results for both influenza types were caused by a single non-influenza pathogen. The distribution of pathogen types among infected students does not differ significantly across schools (not shown).

Figure 4.

Epidemic curves of ILI onsets in the PIPP study during the 2007–2008 influenza season. (a) All ILI onsets; (b) Influenza A; (c) Influenza B; (d) ILI episodes tested negative for influenza.

Table 2.

Summary of outcomes during 12/31/2007–4/18/2008 by intervention arm in the PIPP study of NPI effectiveness in the 2007–2008 winter season. Five schools were in each intervention arm.

Intervention Arm	Population Size	# of Subjects with ≥ 1 ILI	# of ILI episodes	Influenza Lab-test result
				A	B	Negative	Untested
NPI	1999	162	173	21	31	70	51
Control	1960	190	207	32	19	97	59

We denote the non-influenza pathogen, influenza A and influenza B as pathogens 1, 2 and 3. For a study of large contact groups, it is reasonable to assume that the community-to-person infection rate is time dependent and proportional to the number of cases in the community which may be represented by the observed number of ILI onsets in the schools. Let T₀=12/31/2007 and T₁=4/18/2008 be the starting and stopping dates. We assume each student in the study population was susceptible to the three pathogens at T₀, unless infection with either influenza A or influenza B was lab-confirmed before T₀ in the same season. If vaccination and infection history before the epidemic season were known at the individual level, prior immunity could be built into the model. Let C_m(t) be the average number of ILI onsets corresponding to pathogen m reported over the three days t − 1, t and t + 1. This smoothing step ensures a non-zero infection rate for days with zero ILI counts by chance. We assume that the community-to-person infection hazard is ω_mC_m(t)/C̄_m, where C̄_m = Σ_tI(C_m(t) > 0)C_m(t)/Σ_tI(C_m(t) > 0).

The observed numbers of influenza A and B cases in this study are relatively low, on average about 5 cases per school. To avoid non-identifiability of parameters, we assume the two types of influenza share the same natural history parameters, i.e., a₂ = a₃ and q_2l = q_3l, l = 1, 2, 3. Based on knowledge from influenza challenge studies (Murphy et al., 1980), we set Δ_m = 7 days for all m. The interference matrix used for the analysis is

$$\mathit{D}=\left\{\begin{array}{ccc}3& 3& 3\\ 3& \infty & 7\\ 3& 7& \infty \end{array}\right\},$$ (12)

which reflects that infection with influenza A (pathogen 2) or influenza B (pathogen 3) generates specific immunity to the same kind of infection. For infections with the non-influenza pathogen, the short-term nonspecific immunity against all pathogens is the only choice compatible with the data. The exact duration of non-specific immunity is arbitrarily chosen and subject to sensitivity analysis.

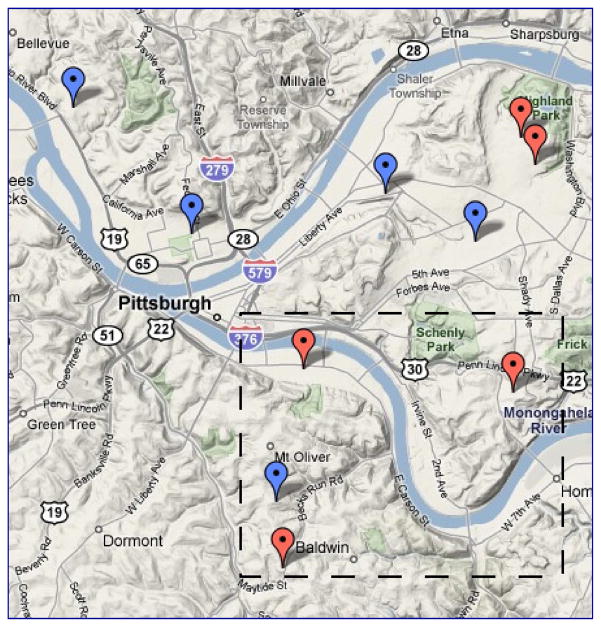
In an initial analysis assuming that all schools shared the same ω_m for all m, the estimated transmission hazard of influenza B is more than 60% higher in the intervention arm than that in the control arm with marginal statistical significance. Although the influenza B epidemic occurred later than influenza A, this counter-intuitive association is unlikely due to the depletion of susceptibles by influenza A because (1) the cross-immunity is limited, if any, between the two different influenza types, and (2) the numbers of cases are small compared to the pool of uninfected subjects. A careful examination of the data revealed that the four schools with the most frequent influenza B cases, one in the control arm and three in the intervention arm, are all located to the south of the remaining six schools (Figure 5). It is likely that schools in different geographical areas were subject to different levels of risk of influenza B from the communities. As a result, we assume that the four schools in the south had a different baseline community-to-person infection hazard of influenza B and denote it by ω_3b.

Figure 5.

Geographic location of schools in the PIPP study downloaded from google.com. Schools labeled red (blue) are in the active intervention (control) arm. The four schools in the box, three in the intervention arm and one in the control arm, have the highest influenza B attack rates.

As the intervention was implemented at the school level, only the product ξ_m = θ_m φ_m (assuming multiplicativity) is estimable, which corresponds to the total efficacy VE_T.m = 1 − ξ_m. Some features of this study warrant further consideration and yield several candidate models. First of all, the contact level of students with their home community during the holidays in which the schools were closed may differ from that during regular school days. A possible solution is to assume the community-to-person infection hazard of pathogen m is ρω_m during holidays and ω_m during school days, where ρ ∈ (0, ∞). Intuitively, one would expect ρ > 1. For a susceptible individual absent during school days for personal reasons, ρω_m also applies. Secondly, within-school contacts tend to be more frequent within grades compared to between grades. To account for this extra clustering, we may let the transmission hazard be γ_m within school but between grades and ηγ_m within grade for pathogen m, with η > 0. We used the following three models to analyze the data:

1. Model I : ρ = 1, and η = 1.

2. Model II : ρ is unknown, but η = 1.

3. Model III : both ρ and η are unknown.

A convenient criterion for model selection in the Bayesian paradigm is the deviance information criterion (DIC) (Spiegelhalter et al., 2002). However, minimal exploration has been done with the DIC in missing data problems (Celeux et al., 2006; Daniels and Hogan, 2008). Two proposals for the DIC in models with missing data are the DIC based on the observed data likelihood and the DIC based on the full data likelihood. The former is very difficult to compute for the models proposed here as the observed data likelihood cannot be expressed in closed form; the latter is computationally more tractable but has not been well studied. Alternatively, a Reversible-Jump MCMC algorithm (Green, 1995) could be used to account for uncertainty about the underlying model. Here we compare models based on posterior credible sets due to the nesting structure of the three models under consideration.

As there are 395 students for whom grade is unknown, an extra data augmentation step is necessary in Model III to incorporate these students into the analysis. Note that there are 10 schools, each with 6 grades, in the PIPP study. We assume the grade of individual i in school s follows a multinomial distribution with probability vector ξ_s = (ξ_s1, …, ξ_s6)′, where ${\sum }_{g=1}^6{\xi }_{sg}=1$, s = 1, …, 10. We specify a Dirichlet(1_6×1) prior for ξ_s, s = 1, …, 10. Let y_sg is the number of individuals in grade g of school s. The following term for grade assignment, ${\prod }_{s=1}^{10}p({\mathit{y}}_s\mid {\mathit{\xi }}_s)={\prod }_{s=1}^{10}\left\{\mathrm{\Gamma }(6){\prod }_{g=1}^6{{\xi }_{sg}}^{y_{sg}}\right\}$, is appended to the full joint probability in (8). Assuming that grades are MAR, in the MCMC algorithm we add the following: (1) sample ξ_s from Dirichlet(y_s1 + 1, …, y_s6 + 1), s = 1, …, 10; and (2) sample each missing grade G_i of individual i in school s_i from the conditional probability

$$p(G_i=G_i^{(l)}\mid \mathit{\psi },\{{\mathit{v}}_j,{\widehat{\mathit{t}}}_j,{\stackrel{\sim }{\mathit{t}}}_j:j\in s_i\})=\frac{p({\mathit{y}}_{s_i}^{(l)}\mid {\mathit{\xi }}_{s_i})\left\{{\prod }_{j\in s_i}p({\mathit{v}}_j,{\widehat{\mathit{t}}}_j\mid \mathit{\psi },R_j^{(l)})\right\}}{{\sum }_{k=1}^{6}p({\mathit{y}}_{s_i}^{(l)}\mid {\mathit{\xi }}_{s_i})\left\{{\prod }_{j\in s_i}p({\mathit{v}}_j,{\widehat{\mathit{t}}}_j\mid \mathit{\psi },R_j^{(k)})\right\}},l=1,\dots ,6,$$ (13)

if individual i had no ILI; otherwise, sample G_i together with (v_i, t̂_i) from

$$\begin{array}{l}p\left({\mathit{v}}_i={\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i={\widehat{\mathit{t}}}_i^{(l)},G_i=G_i^{(l)}\mid {\stackrel{\sim }{\mathit{t}}}_i,\mathit{\psi },\{{\mathit{v}}_j,{\widehat{\mathit{t}}}_j,{\stackrel{\sim }{\mathit{t}}}_j:j\in s_i,j\ne i\}\right)=\frac{\left\{{\prod }_{m}B({\mathit{C}}_m^{(l)}+\mathbf{1})\right\}p({\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i^{(l)}\mid \mathit{\psi },R_i^{(l)})p({\mathit{y}}_{s_i}^{(l)}\mid {\mathit{\xi }}_{s_i})\left\{{\prod }_{\begin{array}{c}j\in s_i\\ j\ne i\end{array}}p({\mathit{v}}_j,{\widehat{\mathit{t}}}_j\mid \mathit{\psi },R_j^{(l)})\right\}}{{\sum }_{k=1}^{L_i}\left\{{\prod }_{m}B({\mathit{C}}_m^{(k)}+\mathbf{1})\right\}p({\mathit{v}}_i^{(k)},{\widehat{\mathit{t}}}_i^{(k)}\mid \mathit{\psi },R_i^{(k)})p({\mathit{y}}_{s_i}^{(k)}\mid {\mathit{\xi }}_{s_i})\left\{{\prod }_{\begin{array}{c}j\in s_i\\ j\ne i\end{array}}p({\mathit{v}}_j,{\widehat{\mathit{t}}}_j\mid \mathit{\psi },R_j^{(k)})\right\}},\\ l=1,\dots ,L_i,\end{array}$$ (14)

where L_i is the number of all possible values of the triple (v_i, t̃_i, G_i). Slightly different from (11), we have $p({\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i^{(l)}\mid \mathit{\psi },R_j^{(l)})$ instead of $p({\mathit{v}}_i^{(l)},{\widehat{\mathit{t}}}_i^{(l)}\mid \mathit{\psi },R_i)$ because here the exposure history of individual i depends on his/her grade G_i.

The estimates for η, 1.91 (95% CS:0.18, 9.4), in model III do not provide strong evidence for η > 1, whereas those for ρ, 2.05 (95% CS:1.31, 3.01) in model II and 2.02 (95% CS:1.36, 2.91) in model III, do for ρ > 1. Therefore, we chose model II for the subsequent analyses. Table 3 presents results in the left and the right panels assuming that the RIC mode is located at the end of day t̃_ik and of day t̃_ik + 1, respectively, with the left panel as our primary results. We do not find statistical significance for the effectiveness of the NPI intervention in preventing influenza-related ILI. However, the NPI intervention tends to reduce the risk of symptomatic infection with influenza A by 32% (95% CS:–13%, 60%) and the risk of symptomatic infection with the non-influenza pathogen by 27% (95% CS:2%, 45%). The intervention showed no effect on the risk of symptomatic infection with influenza B.

Table 3.

Analysis of the PIPP Study with influenza A and influenza B epidemics in the 2007–2008 winter season. Posterior medians and 95% credible sets are presented.

	Mode Location of RIC
	End of day t̃ik			End of day t̃ik + 1
parameter	Non-influenza m = 1	Influenza A m = 2	Influenza B m = 3	Non-influenza m = 1	Influenza A m = 2	Influenza B m = 3
ωm(×104)	3.98(2.76, 5.53)	1.55(0.93, 2.52)	0.83(0.47, 1.39)	4.00(2.82, 5.43)	1.57(0.98, 2.41)	0.83(0.47, 1.38)
ω3b(×104)			1.65(0.84, 3.06)			1.68(0.86, 2.96)
ρ		2.05(1.31, 3.01)			2.06(1.39, 2.90)
γm(×105)	5.83(0.36, 16.27)	23.29(7.18, 44.60)	4.960.21, 18.90)	5.50(0.27, 15.76)	23.35(7.57, 46.86)	4.81(0.17, 18.61)
ξm	0.73(0.55, 0.98)	0.68(0.40, 1.13)	1.21(0.68, 2.20)	0.73(0.55, 0.96)	0.66(0.39, 1.07)	1.19(0.70, 2.12)
am	4.24(2.08, 9.61)	5.46(2.21, 9.70)		3.70(2.04, 9.49)	5.90(2.19, 9.78)
SAR(×104)†		16.29(5.03, 31.17)	3.47(0.15, 13.22)		16.33(5.30, 32.75)	3.37(0.12, 13.02)

^†SAR=1 − exp(− Δ_mγ_m).

Influenza A tended to be more transmissible person-to-person than influenza B in this epidemic, the posterior median of γ₂/γ₃ being 4.73 (95% CS: 0.77, 112.33). While the two pathogens generated about the same number of cases, the average length between successive ILI onsets within schools in the control arm is 4.4 days for influenza A and 9.7 days for influenza B. Consequently, influenza B cases are far less likely to be explained by secondary infections. The estimates for the SAR in Table 3 do not take into account the possibility of absence due to the disease or holidays. To obtain an estimate for the effective SAR adjusted for absence, we fixed the duration of the incubation period for influenza A and influenza B at two days, the average duration estimated for seasonal influenza. As a result, the infectious period is now fixed relative to the symptom onset day and can be represented by days 1–7 with day 2 being the symptom onset day. Let e_k be the probability of absence for day k of the infectious period, k = 1, …, 7, which we assume depends only on k but not the underlying pathogen. Next, we estimate (e₁, …, e₇)′ by the proportions of absence regardless of the reason among all ILI episodes, (0.488, 0.472, 0.312, 0.375, 0.436, 0.512, 0.474)′. The effective SAR can be formulated as $1-{\sum }_{k=1}^7\left\{e_k+(1-e_k)exp(-{\gamma }_m{\int }_{k-1}^k{f}_{\mathit{beta}}(\frac{t}{7}\mid a_m,\frac{2}{7})dt)\right\}$, m = 2,3, where 2/7 is the mode of the RIC. We estimate the effective SAR as 0.00093 (95% CS:0.00027, 0.0018) for influenza A and 0.00020 (95% CS:0.0000077, 0.00079) for influenza B in the PIPP study. Yang et al. (2009) reported an effective SAR of 0.00075 (95% CI: 0.00055, 0.0010) for the novel pandemic influenza A(H1N1) strain in an outbreak that occurred in a private high school in New York City. Our estimate for the PIPP study is likely higher because elementary-school students are more susceptible than high-school students.

The community-to-person infection hazard during the holidays is more than 2 times that during school days. The four schools in the south experienced twice the community-to-person hazard of influenza B compared to the six schools in the north, but the 95% CS of the difference covers zero, possibly due to the small number of cases per school.

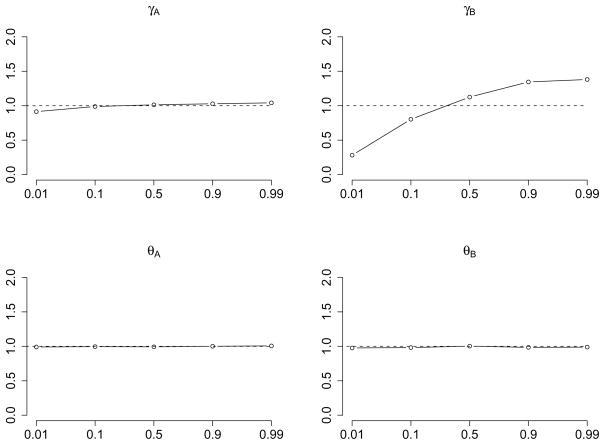
The estimates were not sensitive to the location of the mode of the RIC, as indicated by the similarity between the two panels in Table 3. Sensitivity to the natural history parameter setting was assessed assuming (1) a longer incubation period with H_m = 4; (2) a longer maximum infectious period with Δ_m = 10; and (3) a fixed one-day latent period when the incubation period is at least two days. Only mild to moderate changes were observed in the estimates for the transmission hazards, and the estimates for the intervention effects are highly robust. The key estimates are also not sensitive to moderate changes in the interference matrix. Sensitivity to the assumed prior distributions was only examined for the person-to-person transmission hazards and the intervention efficacies for the two influenza types. For each of these parameters, we replace the uniform prior with a prior that imposes high prior mass on the 1%, 10%, 50%, 90% and 99% quantiles of the posterior distribution obtained from the model using the uniform prior. Each time, the prior of only one parameter is changed. The non-flat prior is proportional to exp {−(g(x) − g(μ))²/(2σ²), where μ is the chosen quantile, σ = 2, and g(x) = logit (x − min)/(max − min) with min and max being the prior bounds of the parameter. In Figure 6, we plot the posterior medians under the non-flat priors relative to the primary estimates in Table 3. A steeper slope indicates higher sensitivity. Among the hazard and efficacy parameters for influenza A and B, only the person-to-person transmission hazard of influenza B is relatively sensitive to its prior distribution.

Figure 6.

Sensitivity to the prior distribution on the person-to-person transmission hazards and intervention effects for influenza A and B. The prior is changed by adding substantial mass at locations corresponding to 1%, 10%, 50%, 90%, and 99% quantiles of the posterior distribution based on a flat prior in the primary analysis. The vertical axes are the posterior medians under the non-flat priors relative to the primary estimates in Table 3.

5 Discussion

We have demonstrated via a simulation study the usefulness of the Bayesian approach in estimating transmissibility of co-circulating pathogens and pathogen-specific intervention efficacies with incomplete laboratory test results. Under the assumption of ignorability (MAR), a moderate amount of missing laboratory results for ILI episodes had a very limited effect on the inference for most key parameters. The reason for such insensitivity is intuitive: uncertainty about the responsible pathogen is restricted to two or three candidates, providing far more information than not observing the ILI episode at all. This finding justifies the efforts to obtain a small validation set of laboratory test results to improve statistical inference. However, the simulation study also warns that the missing results may be a concern if the number of co-circulating pathogens is high or the number of cases of the pathogen of interest is very low.

Randomized studies of large close contact groups provide unique opportunities for estimating characteristics of the natural history of infectious pathogens. Yet both our simulation study and the data analysis showed that reasonable accuracy is difficult to obtain without a sufficiently large number of secondary cases. To minimize the required amount of information for such estimation, we have assumed that the mode of the RIC is strongly associated with symptom onset. This assumption of a known location of the RIC mode can be slightly relaxed. An additional simulation study (results not shown) suggests that allowing the mode to vary uniformly over a short period, such as (t̃_ik − 1, t̃_ik + 1), does not affect the estimability of the parameters. However, the price is a substantially increased computational burden, as the sampling of the individual-level mode involves recalculation of the RIC.

We have assumed the number of co-circulating pathogens is known in the data analysis. As shown in the simulation study, the model is robust to misspecification of the number of co-circulating pathogens, M, when there are few. When M is large and unknown, a Reversible-Jump MCMC approach could be used. However, when laboratory results are not available for two or more pathogens, one or more of the following conditions must hold for identifiability of parameters for the non-tested pathogens: (1) these pathogens differ substantially in transmissibility; (2) sufficiently many clusters are infected by each pathogen; and (3) an informative prior is assumed for M. In addition, the specification of the immunity matrix and/or other natural history characteristices may be difficult for the unknown pathogens.

Our analysis also demonstrates the need for careful randomization of groups in studies like PIPP. Balance in geographical distributions between study arms is often critical to minimize the effects of unmeasured risk factors that are geographically heterogeneous. In the PIPP study, it was not possible to predict before hand that influenza B would circulate more in one area of the study. Accordingly, it is also important to examine and adjust for such potential imbalance to obtain interpretable results.

In the best scenario, the ILI cases that are confirmed biologically would be a random sample, possibly stratified by covariate values. We have assumed MAR for the missing laboratory test results, which may not necessarily hold in some studies, as discussed in Scharfstein et al. (2006). The biased selection of severe cases for surveillance culture mentioned in the introduction is such an example. Another possible scenario is that one pathogen is highly pathogenic and more likely to cause immediate hospitalization and thus prevent the collection of the specimen. A viable approach to allow for nonignorable missingness is a pattern mixture model (Rotnitzky et al., 2001; Daniels and Hogan, 2008) that assumes different transmission and competing probability structures for the two data-missing patterns: laboratory test result is available vs. missing. An example is an exponential tilt relationship: P_i(m, t̃_ik| u_ik = 0) P_i(m, t̃_ik| u_ik = 1) × exp(ζ_m)/Ω_ik, m = 1, …, M, with ζ_M = 1 and ${\mathrm{\Omega }}_{ik}={\sum }_{m=1}^M{P}_i(m,{\widehat{t}}_{ik}\mid u_{ik}=1)\times exp({\zeta }_m)$. Informative priors based on expert opinions can be elicited for the sensitivity parameters ζ_m, m = 1, …, M − 1. Further research is needed to accomodate nonignorable missing data in the complex transmission models presented here.

Unobserved pathogen types are updated individual by individual in our algorithm. In a cluster whose laboratory test results are completely missing, the MCMC algorithm can get stuck with a single pathogen. This situation is likely to occur if the cluster sizes are small, for example, in household transmission studies. Updating the infection status for a whole cluster at the same iteration could circumvent this problem. However, it would be necessary to specify a candidate distribution for proposing the set of infection status for all individuals in the cluster since enumerating all possible infection status, as we did for individual-level updating, is not computationally feasible even with a moderate cluster size. A possible approach to improve the mixing of the MCMC is the multiset sampler proposed in Leman et al. (2009), in which multisets of missing pathogen types and infection times for each cluster or the whole study population may be constructed and assigned appropriate probability densities to facilitate the move of the MCMC across potential pathogen types. The feasibility and operating characteristics of this approach in the presence of high-dimensional missing data has yet to be explored.