Heterogeneous distribution of hydrogen and bicarbonate ions during complete brain ischemia

Introduction

Heterogeneous distribution of H⁺ in brain

H⁺ exist in a non-equilibrium distribution between cells and the interstitial space in a number of tissues under normal conditions (Roos and Boron, 1981). Several methods have been used to calculate intracellular [H⁺] ([H⁺]_i) including the distribution of weak acids and bases; colorimetry or fluorometry with H⁺-sensitive dyes; ³¹P nuclear magnetic resonance. In addition H⁺-selective microelectrodes have been used to measure cytoplasmic [H⁺] (cytoplasmic is taken to mean intracellular). All of these techniques, except the use of H⁺-selective microelectrodes, derive a tissue average [H⁺]_i. Thus in tissues which consist of multiple cell types such as brain, where neurons, glia, and capillary endothelial cells are present, only an average [H⁺]_i for all cell types can be computed. Under normal steady-state conditions the histological heterogeneity of the brain may be unimportant since the [H⁺]_i is probably around pH 7 in all cells (Roos and Boron, 1981; Cohen and Kassirer, 1982).

When brain is perturbed from a resting state, however, functional changes may induce a heterogeneity in [H⁺]_i among different cell types because of varying abilities to generate or remove excess H⁺. Cell metabolic activity is associated with acidification of biological fluids either through net production of acids or carbon dioxide (CO₂). Considerable disagreement exists in the literature with regard to the overall metabolic rate of brain. Neurons (Hertz and Schousboe, 1975; Quastel, 1975), astrocytes (Hertz and Schousboe, 1975; Hertz, 1981), or capillaries (Oldendorf et al., 1977) each have their champions as a major contributor to the brain total metabolic rate. Whichever type predominates, if the metabolic rate does vary from one brain cell type to another while the physicochemical H⁺ buffer capacities are similar, [H⁺]_i might also vary during states of enhanced metabolic activity. Alternatively, [H⁺]_i could be equally heterogeneous if rates of H⁺ production in individual brain cell types are similar but H⁺ physicochemical buffer capacities differ. Furthermore, the ultimate extrusion of excess H⁺ from brain cells via plasma membrane antiport systems (see below) may vary among neurons, glia, or endothelial cells. Such differences could arise because of differences in H⁺-related counter transport or because of differences in the microenvironment to which these antiporters are exposed to during increased brain activity (Kraig et al., 1985a).

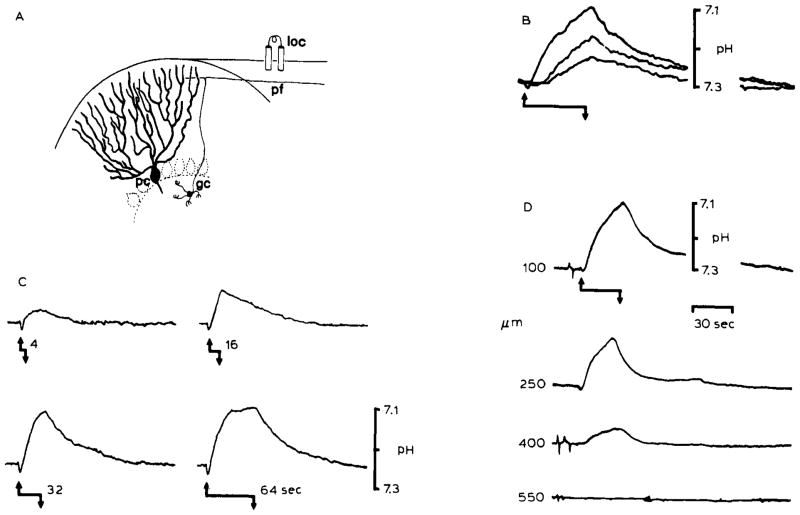
Local inhomogeneities in [H⁺] are known to occur in the brain interstitial space (Kraig et al., 1983; Nicholson et al., 1985). Repetitive surface electrical stimulation of rat cerebellar cortex produces rectilinear excitation of granule cell axons and Purkinje cell dendrites (Fig. 1A). Such activation results in a rise in [H⁺]_o directly proportional to the rate (Fig. IB), duration (Fig. 1C), and density (Fig. ID) of brain excitation. Spreading depression, a more intense activation of brain biochemical and physiological processes (see Bureš et al., 1974; Nicholson and Kraig, 1981) than repetitive electrical stimulation, similarly acidifies the interstitial space in the cerebellum (Fig. 2) and the neocortex (Fig. 3). [H⁺]_o changes are directly proportional to the proximity of the H⁺ selective microelectrode to brain involved in the wave of spreading depression (Fig. 2). Large changes in interstitial (and presumably intracellular) ion concentrations which occur during spreading depression (Kraig and Nicholson, 1978; Nicholson and Kraig, 1981) could differentially influence plasma membrane antiport mechanisms for [H⁺]_i if intracellular ion concentration changes where dissimilar in neurons and glia. In addition, should the H⁺ physicochemical buffer capacity of neurons differ from that of glia as suggested above, the rise in tissue carbon dioxide tension P_t(CO2) which occurs during spreading depression (Fig. 3) would cause [H⁺]_i to rise further in the less buffered cell type.

Fig. 1.

Changes in pH_o associated with repetitive surface stimulation in the rat cerebellar cortex. The records show that heterogeneous levels of [H⁺] can be produced in the brain interstitial space which depend on the magnitude of brain excitation. (A) Local stimulation (loc) of the cerebellar surface excites a beam of parallel fibers (pf), which are axons of granule cells (gc), that in turn induce synaptic depolarization of Purkinje cell dendrites (pc) and interneurons. The cerebellar cortex is a highly ordered and well-defined laminar brain structure. Therefore, synchronous activation of a local population of parallel fibers and Purkinje cell dendrites produces well-defined changes in interstitial electrical potentials which can be used to accurately monitor microelectrode recording positions. Field potential analyses were used to determinepH_o recording depth in (B), (C), and (D). (B) Repetitive surface stimulation produced an alkaline then acid going response. Acidification of the interstitial space was proportional to the stimulus train rate. Records showpH_o transients 100 μm down in the cerebellar molecular layer in response to 5 Hz (lower record), 10 Hz (middle record), and 20 Hz (upper record) bipolar surface stimulation for 30 seconds. The stimulus began at the upward arrow and stopped at the downward arrow. The effect of increasing the duration of the stimulus train at 20 Hz is shown in (C). pH_o records again show an initial alkaline shift with initiation of the stimulus train (upward arrow). The subsequent acid shift increased in magnitude with the stimulus duration (4, 16, 32, and 64 seconds) untilpH_o began to reach a steady-state after 64 seconds. (D) Acidification of the interstitial space was also directly proportional to the density of activated neural tissue. pH_o changes diminished in depth away from the beam of parallel fibers activated for 30 seconds at 20 Hz beginning at the upward arrow and stopping at the downward arrow. The H⁺ selective microelectrode was advanced in increments of 150 μm vertically through a folium before each stimulus train (B), (C), and (D) are modified from Kraig et al., 1983.

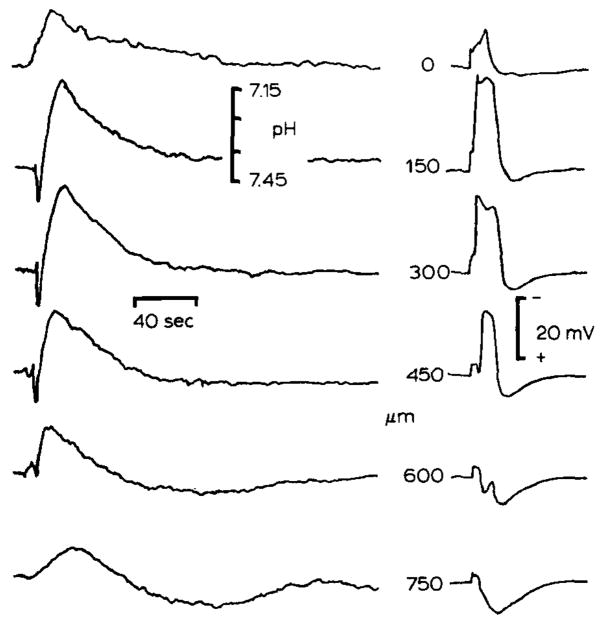
Fig. 2.

Heterogeneous changes in pH_o associated with spreading depression. Spreading depression is a pathological response of synaptically dense brain regions which consist of a cessation of spontaneous and evoked electrical activity, depolarization of brain cells, interstitial large negative d.c. signal, and massive deterioration of trans-membrane ion gradients which propagates through susceptible brain regions (see Nicholson and Kraig, 1981). pH_o and slow d.c. potentials are shown from double barrelled H⁺ selective microelectrodes. Spreading depression was evoked by 100 Hz surface stimulation for 1–5 seconds in cerebellum conditioned by exposure to proprionate Ringer solution (see Nicholson and Kraig, 1981). pH_o shifted alkaline then acid during spreading depression and reached a higher peak acid level than during repetitive surface stimulation because of more intense metabolic stimulation during spreading depression, d.c. potential records show that spreading depression was localized to 150–300 μm below the pial surface. Maximum pH_o changes occurred at this depth. Spreading depression did not propagate to 600 μm since the slow d.c. potential was positive there. Note that pH_o changes at 600 and 750 μm swing acid first and then alkaline in a damped oscillation which may suggest that pH_o changes at these depths occurred by diffusion from more superficially activated areas. (Results modified from Nicholson et al., 1985.)

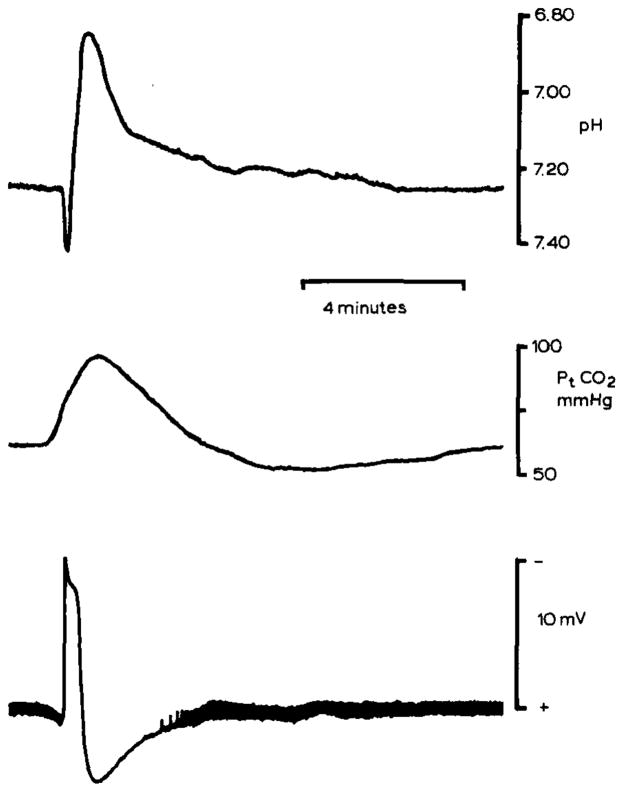
Fig. 3.

pH_o and P_t(CO2) changes during spreading depression in rat neocortex. pH_o (upper record) was recorded 500–600 μm below the pial surface in parietal neocortex with a double-barrelled H⁺ selective microelectrode. pH_o shifted initially alkaline and then acid as in the cerebellum. However, the peak acid shift reached 6.90 pH which may reflect enhanced lactic acidosis since blood glucose had been elevated to 17 mmol/l by previous intraperitoneal injection of dextrose. Spreading depression occurred spontaneously. Middle record shows simultaneous recording of P_t(CO2) from a surface carbon dioxide microelectrode. Since the time constant of the carbon dioxide microelectrode is greater than about 30 seconds, peak P_t(CO2) may be artifactually low. Nonetheless, these P_t(CO2) changes show that brain activity can crease local inhomogeneities in tissue CO₂ tension as well as [H⁺]_o. Lower record shows the slow d.c. potential negative shift associated with spreading depression. Note that the thickness of the baseline reflects spontaneous electrical activity of the cortex which stops during spreading depression and then progressively returns. These data were recorded during experiments described in Kraig et al., 1984b, 1985c.

H⁺ homeostasis in brain

H⁺ homeostasis in brain can be conceptually difficult to predict because [H⁺] is subject to several simultaneously acting physicochemical constraints in a particular compartment. In addition to physicochemical H⁺ buffers in a given brain compartment, ion transport across the compartment boundaries or metabolic production or consumption of acids and bases (Siesjö and Messeter, 1971; Siesjö, 1985) can influence [H⁺]_i. We will deal with these issues separately.

Determinants of [H⁺] in a single brain compartment

Stewart (1978, 1981, 1983) has recently presented a conceptual framework with which to solve problems of acid-base behavior in biological fluids. His approach employs the formalisms of solution chemistry to clearly define dependent and independent variables. Previously others, to varying degrees, have used a similar format (Edsall and Wyman, 1958; Siggaard-Andersen, 1963; Siesjö and Messeter, 1971).

Stewart begins by emphasizing the distinction between dependent and independent variables to an acid-base system (1978, 1981, 1983). Dependent variables are internal to a system. Furthermore, they are determined by equations relevant to a system (see Fig. 4) and by the values of externally imposed independent variables. Dependent variables include H⁺, hydroxyl ions, carbonate ions, ${\text{HCO}}_3^{-}$ ions, anions of weak acids (A⁻) as well as undissociated weak acids (HA). Independent variables, on the other hand, are parameters whose values are imposed on a system from the outside. Independent variables do not influence one another but necessarily determine the values of dependent variables. Three independent variables are defined through Stewart’s approach: the strong ion difference ([SID]), P_t(CO2), and total weak acid concentration ([A_tot]; where [A_tot] = [HA] + [A⁻]). [SID] is the value of the strong base cations minus the strong acid anions. Important strong ions include sodium (Na⁺), potassium (K⁺), calcium, magnesium, chloride (Cl⁻) and lactate. Weak acids (or bases) are represented by various ionizable groups on proteins.

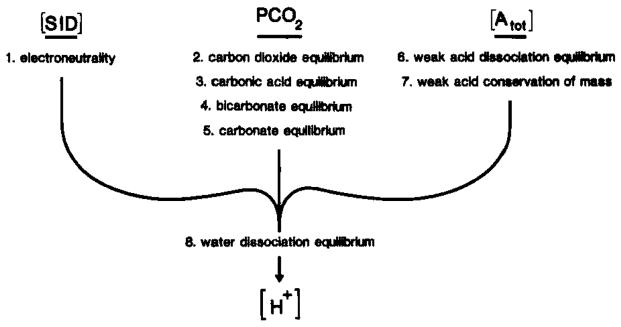
Fig. 4.

Determinants of [H⁺] in brain compartments. The putative pathogenesis of excessive acidosis during brain ischemia may be more readily defined if the [H⁺] and how it is established can be understood in important brain compartments such as the interstitial space or glia and neuronal intracellular space. In biological fluids [H⁺] is completely determined by the strong ion difference ([SID]), P_CO2, and total weak acid concentration ([A_tot]) (Stewart, 1981, 1983). It is important to recognize that [SID], P_CO2, and [A_tot] are three independent variables that completely define [H⁺] and other dependent variables, [OH⁻], [ ${\text{CO}}_3^{2-}$], [A⁻], [HA], and [ ${\text{HCO}}_3^{-}$]. In brain trans-membrane ion fluxes influence [H⁺] in a brain compartment through changes in [SID] while physicochemical H⁺ buffers which are thought to remain confined to viable cells influence [H⁺] through changes in [A_tot]. To accurately describe [H⁺] in a given compartment, equations 1 through 8 must be solved simultaneously.

[H⁺] in biological fluids is a function of the equilibria of, respectively, weak acids or bases, water dissociation, CO₂, carbonic acid, ${\text{HCO}}_3^{-}$, and carbonate solvation as well as the laws of electroneutrality and conservation of mass. Thus, to accurately describe [H⁺] in any brain compartment, all relevant equations of ion species present in that compartment must be solved simultaneously (Fig. 4). For example, in brain intracellular fluid [H⁺] is determined by [SID], P_t(CO2), and [A_tot] and requires simultaneous solutions for eight individual equations (Fig. 4). Siesjö (1984) has recently noted that the term buffer base (defined from the classical pH literature; Siggaard-Andersen, 1963) is equivalent to [SID], In brain interstitial space, where weak acids are essentially absent, [H⁺]_o is determined solely by the [SID] and P_t(CO2) and can be approximated by the following equation:

$$[{\text{H}}^{+}]=\frac{K_1^{\prime }·S^{\prime }·{\text{P}}_{\text{t}({\text{CO}}_2)}}{[\text{SID}]}$$ (1)

where $K_1^{\prime }$ is the first ionization constant for carbonic acid and S^′ is the solubility constant for CO₂ (Nicholson et al., 1985; Kraig et al., 1984b,e). Note that equation (1) is analogous to the classical Henderson equation (Henderson, 1908) since [SID] is essentially equivalent to the interstitial [ ${\text{HCO}}_3^{-}$] (Stewart, 1981).

Boundary characteristics for H⁺ regulation of brain cells and interstitial space

Brain cells to survive must ultimately expell excess H⁺, or their determinants, to the surrounding extracellular microenvironment (Kraig et al., 1985a). Primitive cells probably used a non-exclusive high energy phosphate such as adenosine triphosphate (ATP) directly to create a trans-membrane H⁺ gradient which could also be employed to conduct other energy-requiring cell activities (Fig. 5) (Wilson and Maloney, 1976). Today bacteria and mitochondria continue to so use H⁺ gradients while eukaryotic cells have evolved to employ the plasma membrane Na⁺ gradient for similar cell requirements (Wilson and Maloney, 1976). In doing so, eukaryotic cells could regulate [H⁺]_i more accurately.

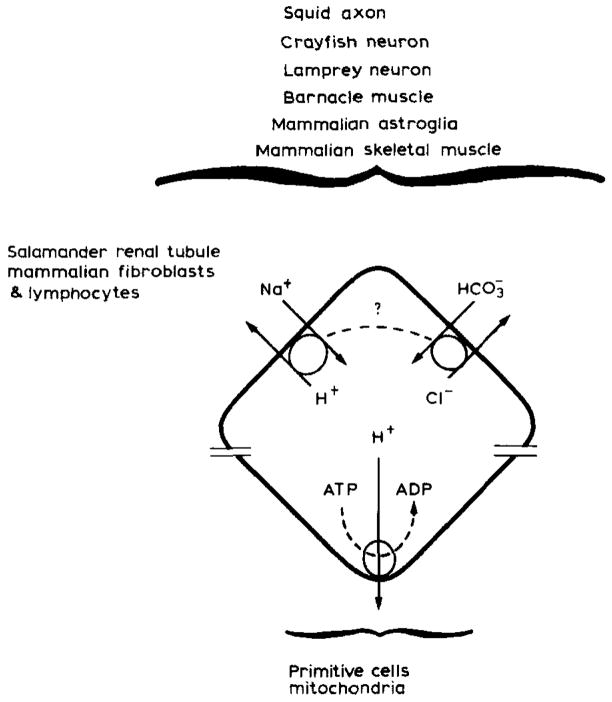
Fig. 5.

[H⁺] homeostasis in animal cells. Primitive cells may have used a proton gradient as a power source to energize vital cell activities. Today bacteria and mitochondria continue to so use proton gradients while eukaryotic cells have evolved to substitute the plasma membrane Na⁺ gradient for similar cell requirements (Wilson and Maloney, 1976). In so doing eukaryotic cells gained improved [H⁺] homeostasis which is likely to be more important to these latter cells because of their more numerous and complex enzyme systems and subcellular organelles. Today we know that excess intracellular H⁺ are ultimately removed from a number of different animal cell types through two ion antiport systems, Na⁺/H⁺ and ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$. The plasma membrane Na⁺ gradient drives Na⁺H⁺ antiport while the power source for ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport remains unclear. In squid ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport requires ATP. In barnacle muscle, squid axon, and snail or crayfish neurons ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport may be driven by the Na⁺ gradient through a variable coupling ratio (dotted line) (adapted from Thomas, 1984). For simplicity though one can regard plasma membrane H⁺ regulation as some combination of Na⁺/H⁺ and ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport.

Electrically neutral Na⁺/H⁺ and ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport in some combination are now known to remove excess H⁺ from a number of different kinds of animal cells including mammalian astroglia (Kimelberg et al., 1978; 1979; 1982; Kimelberg and Bourke, 1982) and vertebrate neurons (Chesler and Nicholson, 1985). The trans-membrane Na⁺ gradient, created by energy requiring Na⁺ pumps and a selective membrane impermeability to Na⁺, is thought to provide the energy needed for Na⁺/H⁺ antiport (Thomas, 1977; Roos and Boron, 1981; Thomas, 1984). The power source that drives ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport remains unclear. In some cells ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport may be an active process and require ATP (Boron and DeWeer, 1976). Alternatively, ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ may be driven by the Na⁺ gradient (Thomas, 1977, 1984).

In mammalian brain only astroglia are known to have Na⁺/H⁺ and ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport mechanisms. However, the fact that these H⁺ regulatory mechanisms have been conserved through a number of different cell types (Fig. 5) and have most recently been found in vertebrate (lamprey) neurons (Chesler and Nicholson, 1985) implies that they may be present in mammalian neurons as well. If so, H⁺ regulation by plasma membrane antiport systems can be schematized as in Fig. 6 (Kraig et al., 1984b).

Fig. 6.

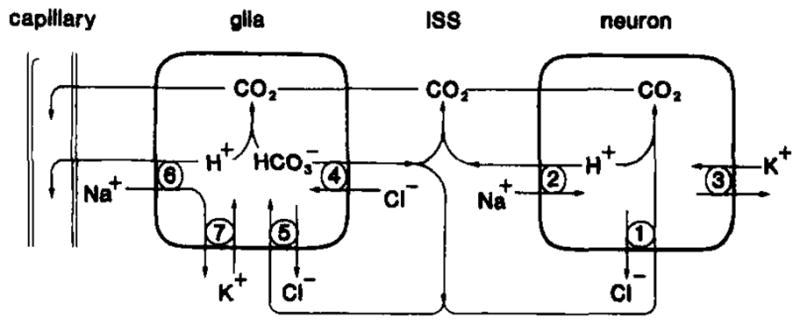
Model of plasma membrane antiport systems for brain H⁺ homeostasis under normal conditions. Excess neuronal H⁺ could be neutralized to CO₂ by intracellular ${\text{HCO}}_3^{-}$ or ${\text{HCO}}_3^{-}$ that entered through ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport (1). Otherwise, excess neuronal H⁺ could be removed to the interstitial space (ISS) by Na⁺/H⁺ antiport (2) powered by the transmembrane Na⁺ gradient created by Na⁺/K⁺ ATPase (3). Astroglia could manage excess H⁺ similarly (adapted from Kimelberg et al., 1982). Na⁺/H⁺ antiport (6) would preferentially occur at the capillary-glia border so as to create a directional flux of H ⁺ toward blood while ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport would be directed as needed to provide ${\text{HCO}}_3^{-}$ to the ISS (4) and neurons (1) or buffer excess intraglial H⁺ (5). Na⁺/K⁺ ATPase would maintain the glial Na⁺ gradient (modified from Kraig et al., 1985a).

Results and discussion

Through the work of Myers (1979) and others it is now well recognized that carbohydrate stores in brain can greatly influence the severity of outcome after nearly complete ischemia in animals (Welsh et al., 1980; Siemkowicz and Hansen, 1978; Rehncrona et al., 1981; Kalimo et al., 1981; Pulsinelli et al., 1982) and man (Pulsinelli et al., 1983). Under normoglycemic conditions only selective neurons are lost after 30 minutes of nearly complete fore-brain ischemia in rats created by occlusion of four cervical arteries (Pulsinelli and Duffy, 1983). On the other hand, equivalent ischemia under hyperglycemic conditions leads to brain infarction (Pulsinelli et al., 1982).

The above findings have led Myers (1979) and others to postulate that lactic acidosis may worsen ischemic brain injury. If so, the microphysiological mechanisms remain undefined. Nearly complete brain ischemia during normoglycemia results in selective neuronal destruction and lactate accumulation to a level up to 13 mmol/kg neocortex (Pulsinelli and Duffy, 1983). In contrast, equivalent ischemia under hyperglycemic conditions produces necrosis of all tissue elements and lactate accumulation to greater than 19 mmol/kg (Pulsinelli et al., 1982). Since H⁺ is generated in a 1:1 stoichiometric relationship with lactate during complete ischemia (Krebs et al., 1975; Alberti and Cuthbert, 1982) one might expect to find a similar narrow range or threshold of [H⁺] beyond which all brain cells are destroyed. As a first approach to disclose such a threshold we measured [H⁺] in a single brain compartment, the interstitial space, as well as the total neocortical lactate content. Furthermore, to avoid the possible exchange of H⁺ or its determinants across the blood brain barrier, we performed the experiments during complete ischemia, making the brain a closed system. If plasma membranes remain intact during complete ischemia, the brain can be considered as a three compartment system consisting of neurons, glia, and the interstitial space (Fig. 6). Pertinent aspects of the experimental paradigm are summarized in Fig. 7 and Kraig et al., 1984a,b, 1985a,b,c.

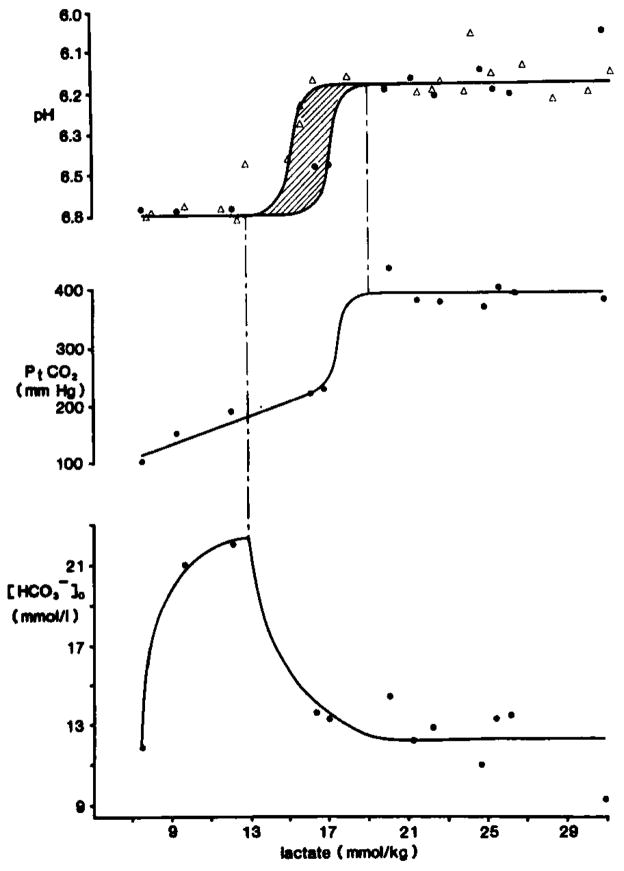
Fig. 7.

Carbonic acid buffer peak changes after complete ischemia. pH_o recordings were made with double barrelled H⁺ selective microelectrodes placed 800 μm down in parietal cortex of anesthetized rats. P_t(CO2) was measured with a surface microelectrode. Brain carbohydrate stores were modulated by pretreatment with intraperitoneal dextrose or intravenous insulin injections. Ischemia was induced by cardiac arrest caused by intravenous injection of KCl. When changes in pH_o and P_t(CO2)reached a peak, animals were decapitated and their heads frozen in liquid nitrogen for subsequent enzyme fluorometric analysis of neocortical lactate content. Upper graph shows peak pH_o compared to tissue lactate. Triangles show data from Kraig et al., 1985a and dots represent data from Kraig et al., 1984b, 1985c. The zone between 15–17 mmol/kg lactate is shaded with diagonal lines to reflect the variability in peak pH_o there. The constant peak level of pH_o between 8–13 and 16–31 mmol/kg lactate implies that [H⁺]_o is at a steady-state, but not equilibrium, with respect to [H⁺] in other brain compartments during complete ischemia. The middle graphs shows concomitant changes in P_t(CO2). P_t(CO2) initially rises linearly with increasing lactate up to about 17 mmol/kg. Then P_t(CO2) rises abruptly and remains constant at 389 ± 9 mmHg after 19 mmol/kg lactate. The constancy of peak P_t(CO2) above 19 mmol/kg lactate implies that ${\text{HCO}}_3^{-}$ stores were exhausted from acid producing cells. If [H⁺]_o continues to be determined by [SID] and P_t(CO2) (see equation 1) during complete ischemia, then the lower graph shows the concomitant changes in ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ which would be expected from the measured changes in pH_o and P_t(CO2). Notice that ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ rises from 8–13 mmol/kg lactate, when pH_o is constant at 6.81 pH and then begins to fall when pH_o and P_t(CO2) change abruptly between 13–19 mmol/kg lactate. ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ then remains constant at about 12.3 mmol/l above 19 mmol/kg lactate. Thus ${\text{HCO}}_3^{-}$ and H⁺ both remain heterogeneously distributed between the interstitial space and acid producing cells during complete ischemia.

Complete ischemia

Animals had pre-ischemic blood glucose values that ranged from 3–7 mmol/l (normoglycemia) and 17–80 mmol/l (hyperglycemia). The groups were associated respectively with brain lactate contents that ranged from 8–13 mmol/kg and 16–31 mmol/kg (Kraig et al., 1984a,b, 1985a,b,c). High energy phosphates (measured by enzyme fluorometric techniques) deteriorated to similar levels in both groups, making energy in the form of ATP-related metabolites unavailable to either group for regulation of [H⁺]. [H⁺]_o rose as soon as blood pressure fell in all animals. However, peak [H⁺]_o was bimodally distributed between the two groups. Although pre-ischemic blood glucoses in normoglycemic animals ranged from 3–7 mmol/l and brain lactates ranged from 8–13 mmol/kg, [H⁺]_o always rose by a constant amount from about 7.25 pH to a peak of 6.81 ± 0.02 pH (n = 7) (triangles in Fig. 7). Similarly, inspite of the fact that pre-ischemic blood glucoses in hyperglycemic animals ranged from 17–80 mmol/l and brain lactates ranged from 16–31 mmol/kg, [H⁺]_o again always rose by a constant, but larger amount, from 7.25 pH to a peak of 6.18 ± 0.02 pH (n = 12) (triangles in Fig. 7). In a second series of experiments where [H⁺]_o and P_t(CO2) were simultaneously monitored in a similar experimental paradigm (black dots in Fig. 7). [H⁺]_o reached peak levels of 6.79 ± 0.02 pH (n = 3) during normoglycemic ischemia and 6.19 ± 0.02 pH (n = 7) during hyperglycemic ischemia.

The constancy of peak [H⁺]_o levels for normoglycemic and hyperglycemic conditions suggests that [H⁺]_o arrives at a steady-state not in equilibrium with [H⁺] in other brain compartments. This inference stems from the conclusion that [H⁺] must be rising in some compartment other than the interstitial space because neocortical lactate content is rising (Krebs et al., 1975; Alberti and Cuthbert, 1982). Physicochemical H⁺ buffers alone can not account for the constancy of peak [H⁺]_o levels since the presence of physicochemical H⁺ buffers in any brain compartment would only reduce, but not abolish, the rate of rise and levels that [H⁺] otherwise would attain (Koppel and Spiro, 1914; Van Slyke, 1922; Bull, 1964; Stewart, 1981). Accordingly, one must invoke energy in the form of membrane barriers or residual ion gradients across plasma membranes to explain the steady-state constancy of peak [H⁺]_o.

CO₂ is a highly diffusable gas in tissues (Krogh, 1919; Gleichman et al., 1962; Kaethner and Bangham, 1977). Hence, P_t(CO2) will rise when ${\text{HCO}}_3^{-}$ is neutralized by H⁺ in any brain compartment of a closed system. Therefore, by simultaneous measurements of [H⁺]_o and P_t(CO2)during complete ischemia one can: (1) calculate remaining ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ according to equation 1; (2) calculate the amount of brain ${\text{HCO}}_3^{-}$ neutralized by lactic acidosis (where [ ${\text{HCO}}_3^{-}$] lost is equal to the change in P_t(CO2) multiplied by S^′). Our results show that peak P_t(CO2) increased linearly with lactate content until lactate reached about 17 mmol/kg. Peak P_t(CO2) then rose abruptly to 389 ± 9 mmHg (n = 7) and remained constant through 31 mmol/kg lactate (Fig. 7).

These changes in P_t(CO2) help to clarify how [H⁺]_o could remain constant between 8–13 and 16–31 mmol/kg lactate (Fig. 7) (Kraig et al., 1984b, 1985c). For [H⁺]_o to have remained constant up to 13 mmol/kg lactate while P_t(CO2) rose, ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ must have increased (Fig. 7 lower graph). Subsequently since peak levels in P_t(CO2) did not change after lactate reached 19 mmol/kg, ${\text{HCO}}_3^{-}$ stores must have been exhausted in acid producing cells. Consequently, if no changes occurred in P_t(CO2) or [SID]_o (which is essentially equivalent to ${[{\text{HCO}}_3^{-}]}_{\text{o}}$ in the interstitial space), no change in [H⁺]_o could have occurred above 19 mmol/kg lactate. If these inferences are correct, then above 19 mmol/kg lactate, remaining brain ${\text{HCO}}_3^{-}$ was segregated to the interstitial space and perhaps those cells which no longer produced lactic acid. On the other hand, excess H⁺ remained in acid producing cells. This suggests that under non-physiological conditions such as ischemia, H⁺ and ${\text{HCO}}_3^{-}$ can remain unequally distributed between cells and the interstitial space, and perhaps even unequally distributed between different cell types.

The changes in P_t(CO2) and [H⁺]_o (Fig. 7) can be further interpreted with the model of brain H⁺ homeostasis shown in Fig. 6. During complete ischemia it is known that [Na⁺]_o falls from about 154 mmol/l to about 48 mmol/l and [Cl⁻]_o declines from about 129 mmol/l to about 72 mmol/l (Hansen, 1981). The lowered [Na⁺]_o is presumably associated with a significant deterioration in the trans-membrane Na⁺ gradient across intact cell membranes. If so, this would impede H⁺ from leaving brain cells via Na⁺/H⁺ antiport. Instead, ${\text{Cl}}^{-}/{\text{HCO}}_3^{-}$ antiport alone might remain operational and powered by remaining Cl⁻ or ${\text{HCO}}_3^{-}$ gradients. CO₂ is most readily hydrated in neocortex by carbonic anhydrase containing glia (Sapirstein, 1983). Glia would, therefore, be the likely candidates to secrete ${\text{HCO}}_3^{-}$ to the interstitial space during normoglycemic ischemia (lactate of 8–15 mmol/kg in Fig. 7). Above 13 mmol/kg lactate glia would stop secreting ${\text{HCO}}_3^{-}$ and by 19 mmol/kg lactate brain ${\text{HCO}}_3^{-}$ would remain only in the interstitial space and, perhaps, some hypothetical cells which no longer produced acid.

Severe incomplete ischemia and reperfusion

We have now begun to examine the behavior of [H⁺]_o during and after severe incomplete ischemia according to the modified (Pulsinelli and Duffy, 1983) model of Pulsinelli and Brierley (1979). Under severe hyperglycemic conditions (blood glucose 17–57 mmol/l) [H⁺]_o rose as soon as blood flow fell and reached a peak of 6.1–6.2 pH after 30 minutes of ischemia (Kraig et al., 1985b) (Fig. 8). This value is similar to those of 6.18 (Kraig et al., 1984a, 1985b) and 6.19 (Kraig et al., 1984b, 1985c) found after terminal ischemia under hyperglycemic conditions (Fig. 7). It appears that brain cell impermeability to H⁺ or their ionized determinants can be maintained for at least 30 minutes of ischemia.

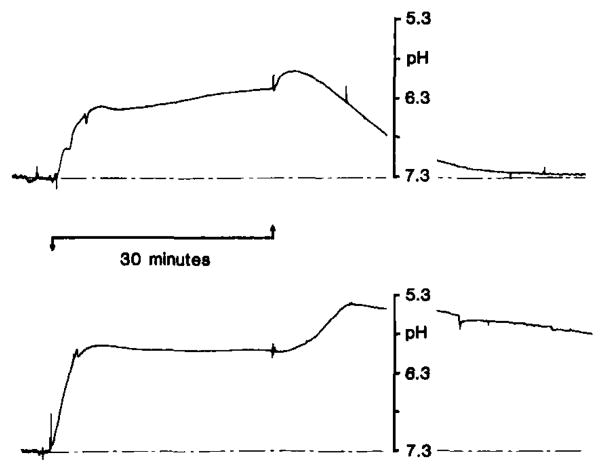
Fig. 8.

pH_o changes with severe forebrain ischemia under hyperglycemic conditions. pH_o was recorded as described in Fig. 7. Ischemia was induced by occlusion of four cervical arteries as outlined in Pulsinelli and duffy (1983). Rats were pre-treated with intravenous dextrose to raise brain carbohydrate stores. Pre-ischemic blood glucose was 17 mmol/l (upper record) and 57 mmol/l (lower record) from two representative animals. pH_o rose as soon as carotid arteries were reversibly closed (upward arrow) and reached a peak between 6.1–6.2 pH under both conditions. With the release of the carotid artery clamps and reperfusion though, pH_o reached a secondary peak acid level which was directly proportional with pre-ischemic the pre-ischemic blood glucose level. When pre-ischemic blood glucose was as high as 57 mmol/l, pH_o fell as low as 5.4–5.5 pH during reperfusion. Astroglia swell and brain becomes edematous after reperfusion from severe incomplete ischemia under hyperglycemic conditions. Plasma membranes in general may increase their permeabilities to H⁺ or their determinants under such conditions. If so, pH_o may accurately reflect brain H⁺ content and suggest that maximum deterioration of brain H⁺ buffering mechanisms occurs at this time after severe hyperglycemic ischemia (data from Kraig et al., 1985b).

A transient second rise in [H⁺]_o occurred with reperfusion. This second peak in [H⁺]_o was directly proportional to the pre-ischemic blood glucose. For example, with a pre-ischemic blood glucose of 57 mmol/l, [H⁺]_o, reached as high as 5.4–5.5 pH several minutes after reperfusion (Fig. 8). Brain is known to swell during reperfusion from severe incomplete ischemia (Kalimo et al., 1981) and membrane permeability of edematous, acid producing cells may increase. Under these circumstances, increased cell membrane permeability to H⁺ or their determinants ([SID]) could account for the further fall in ${[{\text{HCO}}_3^{-}]}_{\text{o}}$.

Previous investigations have shown that brain becomes acidotic during complete or nearly complete ischemia. Initially (Thorn and Heitmann, 1954; Crowell and Kaufman, 1961), surface H⁺-selective glass semi-microelectrodes were used to show that [H⁺]_o shifted in the acid direction during ischemia. More recently H⁺-selective glass microelectrodes have been used to show that [H⁺]_o rises to 6.80 pH after cardiac arrest (presumably under normoglycemic conditions) (Javaheri et al., 1984) or to about 6.1 pH during severe incomplete ischemia under hyperglycemic conditions (Siemkowicz and Hansen, 1981). Nemoto and Frinak (1981) recorded [H⁺]_o under similar ischemic conditions and also found that [H⁺]_o rose as high as about 6.1 pH. However, blood glucoses were not specified in these latter experiments. In addition, several indirect methods have been used to calculate ischemic [H⁺]_i including colorimetry (Kogure et al., 1980), fluorometry (Sundt et al., 1978; Welsh et al., 1982; Csiba et al., 1983), creatine kinase equilibrium and CO₂ distribution (Mabe et al., 1983), lactate content (Ljunggren et al., 1974), and ³¹P nuclear magnetic resonance (Norwood et al., 1979). Such calculations, however, fail to account for inhomogeneities in [H⁺]_i such as those implied from our studies outlined above.

H⁺-selective microelectrodes (Astrup et al., 1977; Gibson et al., 1983; Harris et al., 1984), ³¹P nuclear magnetic resonance (Thulborn et al., 1982), and the distribution of 5,5-dimethyl-2,4-oxazolidinedione-¹⁴C (Keitaro et al., 1984) have each been used to show brain acidosis during focal ischemia.

Conclusions

The enhancement by hyperglycemia of brain damage after severe incomplete ischemia is thought to result from excessive lactic acidosis in the tissue (Myers, 1979). Our results reveal an abrupt alteration in brain H⁺-buffering mechanisms at levels of lactate accumulation which previously have correlated with the transition from ischemic neuronal damage to brain infarction. Furthermore, immediately after this transition zone, at 19 mmol/kg lactate, H⁺ must remain unequally distributed between cells and the interstitial space. We propose that ${\text{HCO}}_3^{-}$ stores are exhausted in those cellular compartments which continue to produce lactic acid.

An inability of excess H⁺ to escape from brain cells may be a fundamental step in the genesis of irreversible ischemic brain injury. If ${\text{HCO}}_3^{-}$ stores in acid producing cells are exhausted (i.e. ${[{\text{HCO}}_3^{-}]}_{\text{i}}$ is at most 1 mmol/l and P_t(co2) is 389 mmHg, then [H⁺]_i in that brain compartment will drop to a pH of about 5 during ischemia, according to the isohydric principle (Cohen and Kassirer, 1982) and the Henderson-Hasselbach equation (Hasselbach, 1916). This low value exceeds the peak [H⁺]_o occurring during reperfusion, when we speculate that acid producing brain cells become more permeable to H⁺ or their determinants.

The molecular mechanisms by which such profound acidosis irreversibly damages brain cells remain unknown. However, we can now direct our attention to microphysiological processes which regulate the heterogeneous distribution of H⁺ and their determinants among different brain cell types and the interstitial space during ischemia. These pathological processes must include conditions where [H⁺]_o reaches about 6.2 pH during ischemia or about 5 pH in acid producing cells and 5.4 pH afterwards in the interstitial space during reperfusion.