Arsenate and phosphate as nucleophiles at the transition states of human purine nucleoside phosphorylase

Abstract

Purine nucleoside phosphorylase (PNP) catalyzes the reversible phosphorolysis of 6-oxypurine (2′-deoxy)ribonucleosides, generating (2-deoxy)ribose 1-phosphate and the purine base. Transition-state models for inosine cleavage have been proposed with bovine, human, and malarial PNPs using arsenate as the nucleophile, since kinetic isotope effects (KIEs) are obscured on phosphorolysis due to high commitment factors. The Phe200Gly mutant of human PNP has a low forward and reverse commitment factors in the phosphorolytic reaction, permitting the measurement of competitive intrinsic KIEs on both arsenolysis and phosphorolysis of inosine. The intrinsic 1′-¹⁴C, 1′-³H, 2′-²H, 9-¹⁵N, and 5′-³H₂ KIEs for inosine were measured for arsenolysis and phosphorolysis. Except for the remote 5′-³H₂, and some slight difference between the 2′-²H KIEs, all isotope effects originating in the reaction coordinate are the same within experimental error. Hence, arsenolysis and phosphorolysis proceed through closely related transition states. Although electrostatically similar, the volume of arsenate is greater than phosphate and supports a steric influence to explain the differences in the 5′-³H₂ KIEs. Density functional theory calculations provide quantitative models of the transition states for Phe200Gly human PNP-catalyzed arsenolysis and phosphorolysis, selected upon matching calculated and experimental KIEs. The models confirm the striking resemblance between the transition states for the two reactions.

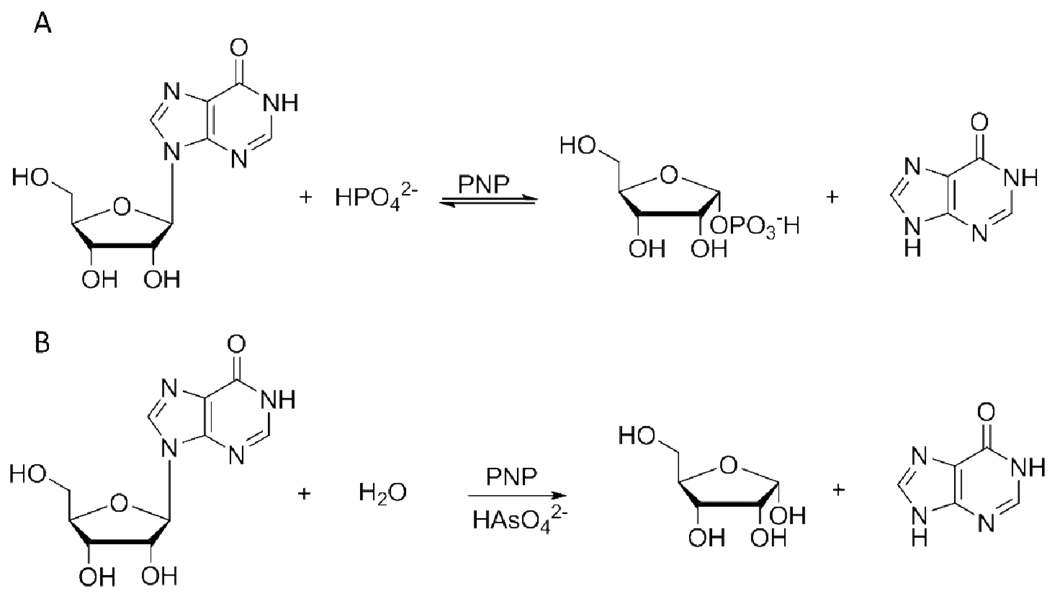
Purine nucleoside phosphorylase (PNP)¹ (EC 2.4.2.1) catalyzes the reversible phosphorolysis of 6-oxopurine (2′-deoxy)ribonucleosides to generate ribose 1-phosphate (R-1-P) and the corresponding purine base, a key step of the purine salvage pathway and an essential step in formation of uric acid in humans (1). The reaction causes inversion of configuration from β-nucleosides to α-D-(2-deoxy)ribose 1-phosphate (2) (Scheme 1A). The genetic deficiency of PNP activity in humans impairs T-cell-based immunological response, while other tissues are unaltered (3). This led to the recognition of PNP as a target for inhibitor design, aiming at the treatment of autoimmune diseases, T-cell lymphomas and gout (4). Four generations of transition state analogues designed for human PNP (HsPNP) are exemplified by immucillin-H, DADMe-immucillin-H, DATMe-immucillin-H, and SerMe-immucillin-H, with overall dissociation constants (K_i*) in the picomolar range (5).

Scheme 1.

PNP-catalyzed (A) phosphorolysis and (B) arsenolysis of inosine.

Kinetic isotope effects (KIEs) arise from differences in bond vibrational modes as a molecule goes from the ground state to the transition state. Consequently, their measurement can provide information on the nature of the transition states of chemical reactions. However, enzyme-catalyzed reactions are often affected by kinetically complicating commitment factors that obscure the expression of intrinsic KIEs (6). In the case of HsPNP, KIEs measured on phosphorolysis are near unity due to forward and reverse commitment factors. To overcome commitment factors, phosphate has been replaced by arsenate in the bovine PNP (BtPNP) reaction (7) (Scheme 1B). The chemical similarity between arsenate and phosphate makes it reasonable to use the former as a mimic of the latter. Accordingly, this strategy has been employed in several biochemical systems (8, 9). The use of arsenate in the BtPNP reaction decreased the commitment factor for the nucleoside and rendered the reaction irreversible, since α-D-ribose 1-arsenate is readily hydrolyzed. Use of arsenate allowed the measurement of intrinsic KIEs and transition state analysis indicated a dissociative, ribooxocarbenium ion-like transition state with significant bond order to the leaving group and no bond order to the approaching nucleophile (7). The same approach was also employed with HsPNP and Plasmodium falciparum PNP (PfPNP). Their isotope effects reported on the formation of a ribooxocarbenium transition state with no bond order to either the leaving group or the nucleophile (10). These studies provided the foundation for design of the powerful PNP transition state analogues mentioned above (11, 12). More recently, these properties of arsenate were used to probe the effect of remote mutations on the geometry of the transition states for Lys22Glu-His104Arg HsPNP (13) and Val39Thr-Asn123Lys-Arg210Gln BtPNP (14).

In spite of the apparent success of the method, the validity of using arsenate as a mimic of phosphate in ribosyl-transfer reactions has been questioned with the suggestion that chemical differences in the two nucleophiles would lead to distinct transition states (15). Here we test this hypothesis by taking advantage of the Phe200Gly mutant of HsPNP, which possesses low commitment factors for inosine in both arsenolysis and phosphorolysis. Phenylalanine 200 is an important catalytic site amino acid for substrate binding and catalysis in HsPNP (16). The Phe200Gly mutant has ~30 fold decreased k_cat and ~900 fold increased K_M resulting in a 27,000-fold decrease in the specificity constant (k_cat/K_M) for inosine relative to the native enzyme (17). The Phe200Gly HsPNP was used in both phosphorolysis and arsenolysis reactions and transition-state models were built based on intrinsic KIE values and gas-phase density functional theory calculations using both arsenate and phosphate. The results indicate that the transition states are remarkably similar with either nucleophile. Furthermore, the structure and geometry of the transition state for Phe200Gly HsPNP differs from those found for native or other mutant HsPNPs.

EXPERIMENTAL PROCEDURES

Materials

D-[1-³H]Ribose, D-[1-¹⁴C]ribose, D-[6-³H₂]glucose, D-[6-¹⁴C]glucose, and D-[5-³H]glucose were purchased from American Radiolabeled Chemicals, Inc. Pyruvate kinase (PK) myokinase (MK), hexokinase (HK), glucose-6-phosphate dehydrogenase (G6PDH), glutamic acid dehydrogenase (GDH), 6-phosphogluconic acid dehydrogenase (6PGDH), adenosine deaminase (ADA), and phosphoriboisomerase (PRI) were from Sigma. Alkaline phosphatase (AP) was from Roche. Ribokinase (RK) and phosphoribosyl-α-1-pyrophosphate synthetase (PRPPase) were prepared as previously described (18, 19). Hypoxanthine-guanine phophoribosyltransferase (HGPRT) and wild-type HsPNP were kind gifts from Keith Hazleton and Dr. Achelle Edwards of this laboratory. All other chemicals and reagents were obtained from commercially available sources and were used without further purification.

Expression, purification, and activity assay of Phe200Gly HsPNP

The N-terminal His-tagged mutant enzyme was expressed and purified to homogeneity, as judged by SDS-PAGE (20), according to previously described methods (17). Protein concentration was determined spectrophotometrically at 280 nm using the theoretical extinction coefficient (ε₂₈₀) of 29,800 M⁻¹ cm⁻¹ (ExPASy). Phe200Gly HsPNP activity was coupled to xanthine oxidase and measured spectrophotometricaly as previously described (11, 17), at 25 °C, in 50 mM Tris-HCl (pH 7.5), with 100 nM Phe200Gly HsPNP and 60 mU bovine xanthine oxidase. Saturation curves for Phe200Gly HsPNP with inosine were obtained by measuring initial rates at varying concentration of inosine (10 – 50 mM), and fixed, saturating concentrations of either arsenate (50 mM) or phosphate (50 mM), and fitted to the Michealis-Menten equation.

Synthesis and purification of isotopically labeled inosines

[1′-³H]IMP and [1′-¹⁴C]IMP were enzymatically synthesized at 37 °C from [1-³H]ribose and [1-¹⁴C]ribose, respectively (Scheme S1, available as Supporting Information). Each reaction mixture contained 1 mM ribose, 20 mM phosphoenolpyruvate (PEP), 0.2 mM ATP, 20 mM MgCl₂, 1.2 mM hypoxanthine, 100 mM KH₂PO₄ (pH 7.5), 50 mM KCl, 1 mM DTT, 0.2 U mL⁻¹ of PRPPase, 2 U mL⁻¹ of PK, 2 U mL⁻¹ of MK, 0.2 U mL⁻¹ of HGPRT, and 1 U mL⁻¹ of RK.

For the synthesis of [5′-³H₂]-, [4′-³H]-, and [5′-¹⁴C]IMP, D-[6-³H₂]-, D-[5-³H]-, and D-[6-¹⁴C]glucose were, respectively, utilized as precursors (Scheme S1, available as Supporting Information). Each reaction mixture contained 2 mM glucose, 20 mM PEP, 0.2 mM ATP, 20 mM MgCl₂, 2.5 mM hypoxanthine, 140 mM KH₂PO₄ (pH 7.5), 50 mM KCl, 2.5 mM DTT, 0.2 mM NADP⁺, 20 mM α-ketoglutarate (α-KG), 5.5 mM NH₄Cl, 0.2 U mL⁻¹ of PRPPase, 2 U mL⁻¹ of PK, 2 U mL⁻¹ of MK, 0.2 U mL⁻¹ of HGPRT, 1 U mL⁻¹ of G6PDH, 1 U mL⁻¹ of 6PGDH, 0.5 U mL⁻¹ of PRI, 1 U mL⁻¹ of GDH, and 0.2 U mL⁻¹ of HK. To synthesize [5′-¹⁴C,2′-²H]IMP, the reaction mix with D-[6-¹⁴C]glucose was prepared in D₂O. The deuterium was incorporated by the reaction catalyzed by PRI, and the deuterium content in the final product was determined by electrospray ionization mass spectrometry (ESI-MS).

The labeled IMPs were purified by reverse-phase HPLC (50 mM triethylamine:acetic acid, pH 5.0) using an analytical C18 Deltapak column (Waters). The solvent was evaporated in a speedvac, and the pellet was dissolved in water. The labeled IMPs were converted to labeled inosines in the AP-catalyzed reaction, and the labeled inosines were purified with the same protocol utilized for IMP purification.

The synthesis of [5′-¹⁴C,9-¹⁵N]inosine employed [5′-¹⁴C,9-¹⁵N]ATP, synthesized as previously described (13), as initial material (Scheme S2, available as Supporting Information). A solution of 10 mM glucose, 1 mM ATP, 100 mM KH₂PO₄ (pH 7.5), 20 mM MgCl₂, 2.5 mM DTT, 10 U mL⁻¹ of MK, and 6 U mL⁻¹ of HK was allowed to react overnight, after which alkaline buffer and 0.05 U mL⁻¹ of AP were added, and the reaction proceeded for a few additional hours at 37 °C. Labeled adenosine was isolated as described above for IMP, and subsequently converted to labeled inosine by incubation with 50 mM Tris-HCl (pH 7.5) and 0.5 U mL⁻¹ of ADA.

Determination of forward commitment factors

The forward commitments (C_f) for inosine with Phe200Gly HsPNP in arsenolysis and phosphorolysis reactions were measured by the isotope trapping method (21). Pulse incubation mixtures (20 µL) containing 200 µM Phe200Gly HsPNP, 5 mM [5′-¹⁴C]inosine, and 50 mM Tris-HCl (pH 7.5), at 25 °C, were chased with a solution (480 µL) consisting of 20 mM inosine, 50 mM Tris-HCl (pH 7.5), and either 0 to 30 mM arsenate or 0 to 10 mM phosphate. After 5 s, the reactions were quenched with 50 µL of 1 N HCl and loaded onto charcoal columns (14, 19). [5-¹⁴C]Ribose or [5-¹⁴C]ribose 1-phosphate was eluted with 3 mL of 10 mM ribose in 10% ethanol (v/v), dried by speedvac, and dissolved in 100 µL of water and 10 mL of scintillation fluid (Perkin-Elmer). Radioactivity was counted for 10 min in a Wallac 1414 LSC scintillation counter (Perkin-Elmer). The values obtained in the absence of arsenate and phosphate were used as background to correct the others. Forward commitments were calculated with eq 1, where C_f is the forward commitment, and Y is the asymptotic value of a hyperbolic fit of the data.

$$C_{\mathrm{f}}=Y/(1-Y)$$ eq 1

Measurement of KIEs

All KIEs were measured by the competitive radiolabel method (19), at 25 °C. A typical reaction mixture for arsenolysis contained 30 mM NaH₂AsO₄ (pH 7.5), 7 µM Phe200Gly HsPNP, 50 mM Tris-HCl (pH 7.5), and 1 mM inosine (³H-labeled, ¹⁴C-labeled, and cold carrier), while a reaction mixture for phosphorolysis consisted of 10 mM NaH₂PO₄ (pH 7.5), 50 µM Phe200Gly HsPNP, 50 mM Tris-HCl (pH 7.5), and 50 µM inosine (³H-labeled, ¹⁴C-labeled, and cold carrier). The arsenolysis was allowed to proceed to 20 to 25% completion and the phosphorolysis reaction to 10 to 15% completion, when half of each reaction mixture was loaded onto charcoal columns (14, 19). The remainder of each reaction mixture was completely converted to products by addition of 10 µM of native HsPNP and in the case of the phosphorolysis reaction, 5 mM of NaH₂AsO₄ (pH 7.5). After both reactions were complete, they were also loaded onto charcoal columns. Ribose or ribose 1-phosphate was separated from inosine and prepared for scintillation counting by the same procedures described for the commitment experiment. A sample with only [¹⁴C]inosine was also counted as a standard.

The samples were counted in dual-channel fashion, with the ³H signal appearing only in channel 1, and ¹⁴C signal, in both channels. The total ³H signal was assessed by eq 2, and the total ¹⁴C signal, by eq 3, in which ³H is the total number of counts per minute (cpm) for this isotope, ¹⁴C is the total number of cpm for this isotope, channel 1 and channel 2 are the number of cpm in each channel, and r is the channel 1 to channel 2 ratio of ¹⁴C standard (19).

$${}^3\mathrm{H}=\text{channel }1-(\text{channel }2\times r)$$ eq 2

$${}^{14}\mathrm{C}=\text{channel }2\times (1+r)$$ eq 3

Experimental KIEs were calculated and extrapolated to 0% reaction using eq 4, where R_f and R₀ are the ratios of heavy to light isotopes at partial and complete conversions, respectively, and f is the fraction of substrate conversion.

$$\text{KIE}=\text{ln}(1-f)/\text{ln}[1-f\times (R_{\mathrm{f}}/R_0)]$$ eq 4

Computational methods

The reaction of arsenate and phosphate with inosine in mutant PNP was studied in B3LYP using a 6-31G* basis set as implemented in Gaussian 03 and 09 (22, 23). Final transition structures without geometric constraints were optimized in B3LYP using a 6-31+G** basis set. All starting material structures were located as global minima and frequency calculations performed on the optimized structures contained no imaginary frequencies. Almost all transition structures that were located, with and without geometric constraints, had only one calculated imaginary frequency (structures with a second imaginary frequency were only used in the analysis if the second frequency was less than 10% of the first). The errors associated with isotope effect predictions for geometries with more than one imaginary frequency are discussed elsewhere (24). The isotope effects for each of the theoretical structures were calculated from conventional transition state theory by the method of Bigeleisen and Mayer using ISOEFF98 (25–27). from the scaled theoretical vibrational frequencies. Tunneling corrections were applied using a one-dimensional infinite parabolic barrier model (28).

RESULTS AND DISCUSSION

Steady-state apparent kinetic parameters

Phe200Gly HsPNP follows Michaelis-Menten kinetics for both inosine arsenolysis and phosphorolysis (data not shown). Fitting the data to the Michaelis-Menten equation yielded apparent values of k_cat = 0.90 ± 0.01 s⁻¹, K_inosine = 18 ± 2 mM, and k_cat/K_inosine = 50 M⁻¹ s⁻¹ with phosphate, in agreement with previously reported values (17), and k_cat = 0.30 ± 0.02 s⁻¹, K_inosine = 18 ± 3 mM, and k_cat/K_inosine = 16 M⁻¹ s⁻¹ with arsenate.

Comparison between arsenate and phosphate ions

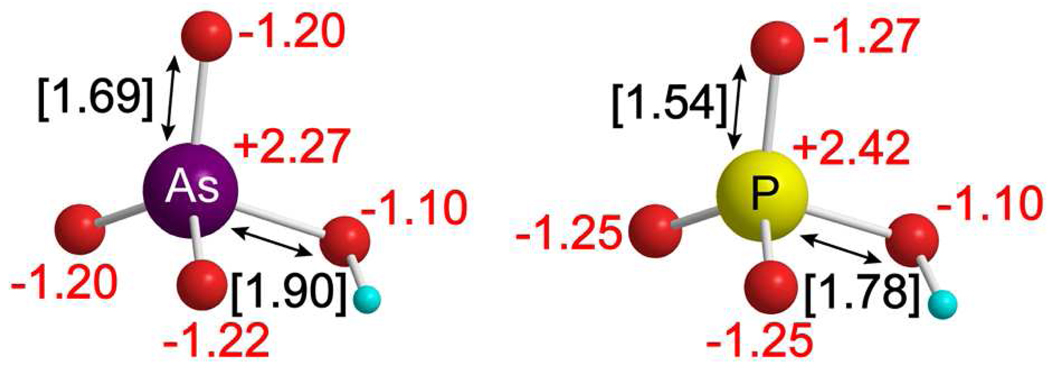
A comparison of the electronic and structural properties of phosphate and arsenate ions shows small differences in NBO charges for the nucleophilic oxygens (0.07), indicating similar electronic structure of the ions (Figure 1). The pK_a values for arsenate (pK_a1 = 2.21, pK_a2 = 6.95, pK_a3 = 11.49) and phosphate (pK_a1 = 2.16, pK_a2 = 7.21, pK_a3 = 12.32) are also similar, supporting closely related nucleophilicity. A notable difference between the ions is the longer bond lengths of the arsenate ion (greater than phosphate by 0.15 Å for the As–O bond and by 0.12 Å for the O–H bond). One possible effect of the increased size of arsenate relative to phosphate could be a change in the conformation of the enzymatic ion-binding pocket to accommodate the larger ion. However, similarities in the electronic structure and pK_a values of arsenate and phosphate support arsenate as a reasonable mimic for phosphate in the reaction of PNP.

Figure 1.

Comparison between arsenate and phosphate dianions. NBO charges for phosphate and arsenate are shown in red text. Bond distances for the P–O and As–O bonds are shown in black text with brackets. Oxygen atoms are shown in red, hydrogen in cyan, arsenic in purple, and phosphorus in yellow.

Potential energy surfaces for arsenolysis versus phosphorolysis

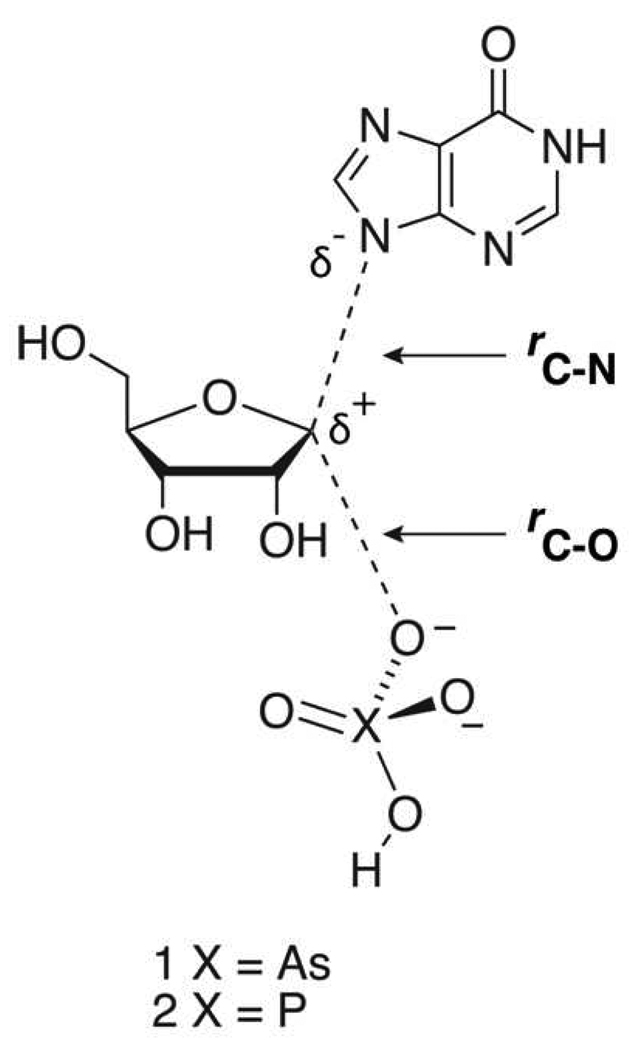
The potential energy surfaces for the reactions of arsenate and phosphate with inosine were analyzed to compare the relative landscapes for conversion of reactants to products. Scheme 2 shows general transition structures for the substitution reactions of arsenate (1) and phosphate (2) with inosine. The leaving-group bond distance between C-1′ and N-9 is defined as r_C-N and the attacking nucleophile bond distance between C-1′ and the O (of the ion) is defined as r_C-O. Energy grids were generated by varying r_C-N and r_C-O of transition structures 1 and 2 along the reaction coordinate by 0.2 Å increments. Structures for the grids were conformationally similar to the lowest energy structure of the inosine starting material and all structures were optimized using B3LYP/6-31G* calculations in the gas phase.

Scheme 2.

General transition state for arsenolysis and phosphorolysis of inosine.

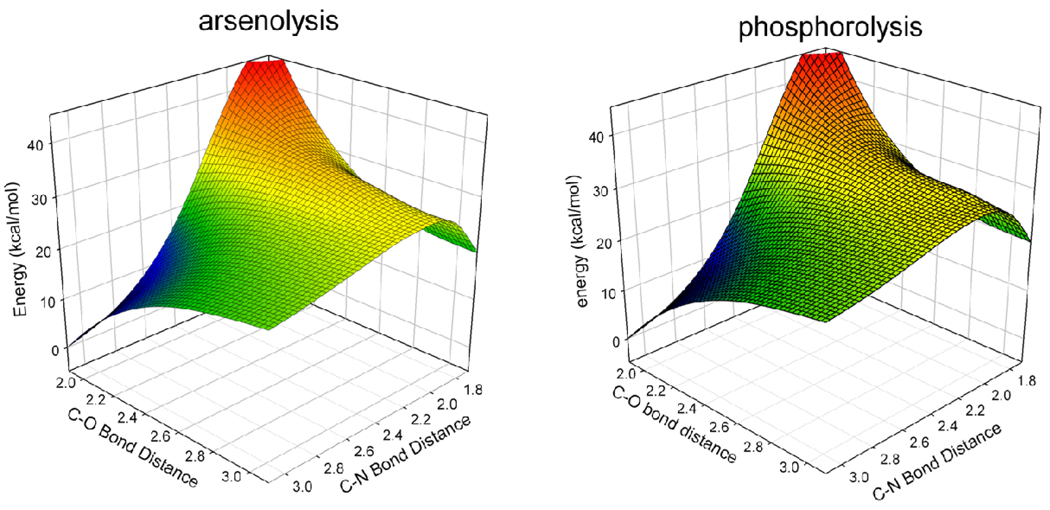
The potential energy surfaces, including zero-point energy (ZPE), for the reactions of arsenate and phosphate are virtually identical with an RMSD² of 0.982 (Figure 2). The potential energy surfaces display a flat area in the transition state region and the range is similar for both arsenolysis and phosphorolysis reactions. In the enzymatic reaction, stabilizing interactions of the substrates with the enzyme environment are known to considerably alter the position of the transition state, causing the enzymatic transition state to lie at a non-stationary point on the gas-phase surface (29). Consequently, a transition structure located for the enzymatic reaction at a non-stationary position on the analogous surfaces involving arsenate or phosphate should be similar in both reactions unless the catalytic site environment is disturbed by arsenate interactions. The similarity between the surfaces of arsenolysis and phosphorolysis provides further evidence to support the ability of arsenate to mimic phosphate in the reaction with inosine without altering the reaction coordinate.

Figure 2.

Potential energy surfaces for the reaction of arsenate with inosine and phosphate with inosine are shown above. The similarity in the surfaces (RMSD = 0.982) supports the ability of arsenate to mimic phosphate in the PNP reaction.

Transition structures of stationary points

A comparison of transition structures for the reactions of arsenolysis (1) and phosphorolysis (2), without imposing any geometric constraints upon the structure, will give an unbiased picture of the differences and similarities in the substitution reactions of the two ions with inosine. From a systematic search of the reactions of arsenate and phosphate with inosine, a total of four different transition structures were located in B3LYP calculations using a 6-31G* basis set. Variations in the transition structures primarily involve changes in the conformation of the catalytically remote 5′-OH group. Corresponding conformations of the transition structures for arsenolysis (1) and phosphorolysis (2) displayed similar KIE predictions at every position and nearly identical r_C-N and r_C-O (coordinates for all geometries are available in the Supporting Information). The lowest energy transition structures of 1 and 2 were calculated in B3LYP using a 6-31+G** basis set (Figure 3). The theoretical structures for both arsenolysis and phosphorolysis are similar with a deviation in r_C-N and r_C-O of 0.01 Å and 0.03 Å, respectively. Furthermore, the predicted KIEs are similar with the largest deviation being 0.6% at the 5′-³H₂ (Table 1). The resemblance in both the geometry and predicted KIEs of corresponding arsenolysis and phosphorolysis transition structures is striking and provides strong evidence for the similarity in reactivity of arsenate and phosphate in substitution reactions of nucleosides.

Figure 3.

Transition structures (B3LYP/6-31+G**) for the substitution reaction of (A) arsenate and (B) phosphate on the substrate inosine in gas phase without imposing geometric constraints. The numbers are measures of r_C-N and r_C-O. Carbon atoms are shown in gray, oxygen in red, hydrogen in cyan, nitrogen in blue, arsenic in purple, and phosphorus in yellow.

Table 1.

Predicted KIEs for stationary point transition states for arsenolysis and phosphorolysis of inosine in gas phase.

KIE position	Type of KIE	Predicted KIE for arsenolysis	Predicted KIE for phosphorolysis	Difference in predicted KIEs
1′-3H	α-Secondary	1.081	1.082	0.001
1′-14C	Primary	1.026	1.027	0.001
2′-2H	β-Secondary	1.097	1.101	0.004
9-15N	Primary	0.971	0.974	0.003
5′-3H2	δ-Secondary	1.134	1.141	0.007

Commitments to catalysis

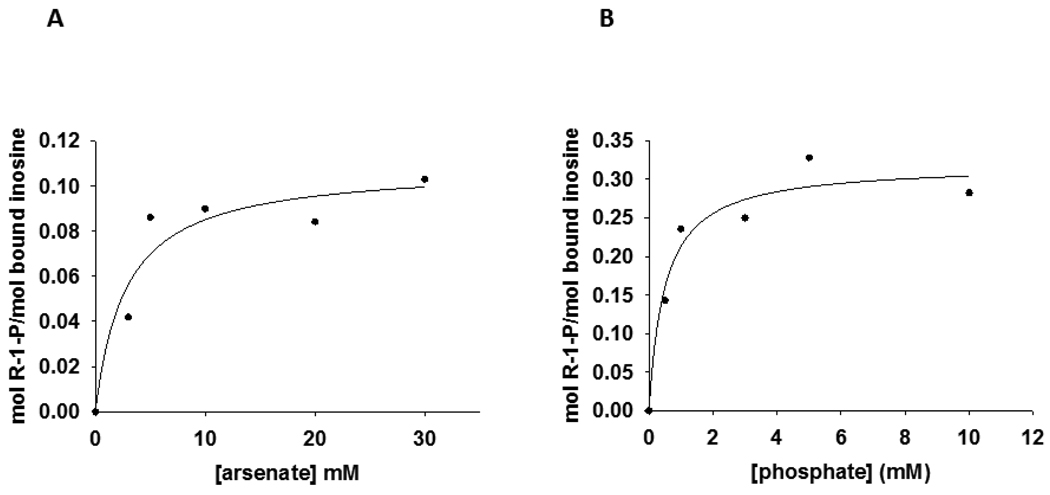
A forward commitment factor (C_f) represents the tendency of a substrate to undergo catalysis, once the Michaelis complex is formed, as opposed to dissociating to free substrate. The commitment factor is defined as the ratio of the rate constant for the isotope-sensitive step to the net rate constant of dissociation for the substrate from the catalytically competent complex (6). In the internal competition method of KIE measurement, C_f always refers to the substrate that carries the isotopic label (30), in the present case, inosine. Significant C_f masks the full expression of isotope effects in enzymatic reactions, and its value must be known to permit calculation of intrinsic KIEs (6). Accordingly, C_f upper limits were estimated for inosine with Phe200Gly HsPNP, and values of 0.115 ± 0.019 and 0.471 ± 0.058 were obtained under arsenolytic and phosphorolytic conditions, respectively (Figure 4). The C_f for Phe200Gly HsPNP-catalyzed inosine arsenolysis is the range found for native HsPNP (0.147), PfPNP (0.105) (10), and BtPNP (0.190) (7), but is smaller than the value reported for Lys22Glu-His104Arg HsPNP (0.239) (13). The C_f in the phosphorolysis reaction is in the range to permit calculation of intrinsic KIEs for the Phe200Gly HsPNP-catalyzed phosphorolysis of inosine.

Figure 4.

Isotope trapping-estimated forward commitment to catalysis for inosine with (A) arsenate or (B) phosphate as nucleophiles.

For native PNP, the C_f for inosine with phosphate is 0.687. However, the isotope effects are near unity (eg. 1.00 for [1′-¹⁴C]inosine) because of on-enzyme equilibration (reverse commitment). Enzyme-bound products on native PNP (hypoxanthine and α-D-ribose 1-phosphate) return to enzyme-bound reactants several times before product release, further reducing experimental KIE values toward equilibrium isotope effects. Both of these effects are reduced in the Phe200Gly PNP used here.

Experimental and intrinsic KIEs

Competitive KIEs were measured for Phe200Gly HsPNP-catalyzed arsenolysis and phosphorolysis reactions of inosine. Intrinsic KIEs were determined by correcting for C_f, according to eq 5, where ^LV/K is the observed KIE on V/K, and ^Lk is the intrinsic KIE (6). Terms other than the C_f are small since the values found for the primary ¹⁵N KIEs, after correction for C_f, are equal, within experimental error, to the maximum values found computationally for these isotope effects in inosine arsenolysis and phosphorolysis, as discussed below.

$${}^{\mathrm{L}}V/K=({}^{\mathrm{L}}k+C_{\mathrm{f}})/(1+C_{\mathrm{f}})$$ eq 5

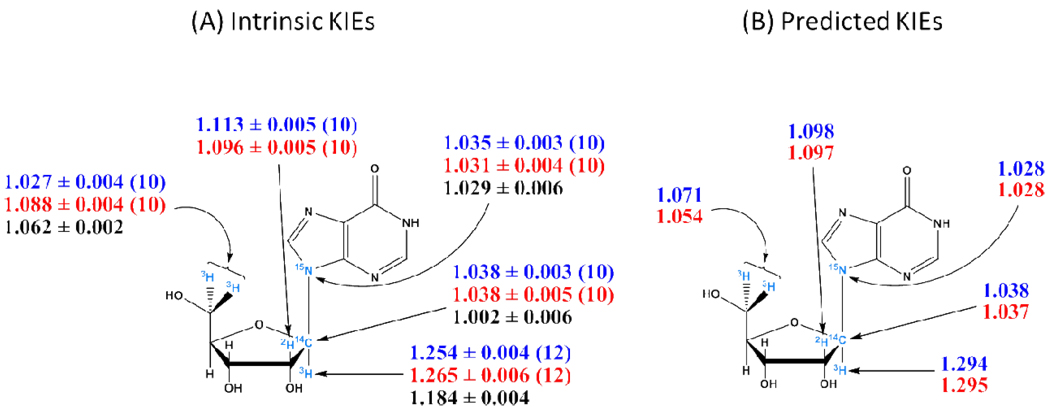
Except for the remote 5′-³H₂ KIEs and, to a much lesser extent, the 2′-²H KIEs, intrinsic KIEs for arsenolysis are the same, within experimental errors, as those for phosphorolysis, indicating that Phe200Gly HsPNP-catalyzed arsenolysis and phosphorolysis of inosine proceed through closely related transition states (Table 2) (Figure 5A). The large primary 9-¹⁵N KIEs suggest substantial C1′-N9 bond loss, and the large α-secondary 1′-³H and β-secondary 2′-²H KIEs establish a ribooxocarbenium ion-like transition state. These characteristics are also present in the transition states for native bovine, human, and malarial PNP-catalyzed reactions (7, 10). However, the primary 1′-¹⁴C KIEs are too large to support a fully formed oxocarbenium transition state as found with HsPNP (10). Thus, significant bond order between the 1′-carbon and the attacking nucleophile must exist at the transition state. Nucleophile participation in the transition state has also been reported for human and bovine PNPs carrying mutations remote from the active site (13, 14).

Table 2.

KIEs and their standard errors on arsenolysis and phosphorolysis of inosine catalyzed by Phe200Gly HsPNP.

Heavy inosine	Light inosine	Experimental KIE with AsO4	Experimental KIE with PO4	Intrinsic KIE with AsO4	Intrinsic KIE with PO4
1′-3H	5′-14Ca	1.228 ± 0.003	1.180 ± 0.003	1.254 ± 0.004	1.265 ± 0.006
1′-14C	4′-3H	1.034 ± 0.002b	1.026 ± 0.003b	1.038 ± 0.003	1.038 ± 0.005
5′-14C,2′-2H	4′-3H	1.101 ± 0.004c,d	1.065 ± 0.004c,d	1.113 ± 0.005	1.096 ± 0.005
5′-14C,9-15N	4′-3H	1.031 ± 0.002c	1.021 ± 0.003c	1.035 ± 0.003	1.031 ± 0.004
5′-3H2	5′-14C	1.024 ± 0.003	1.060 ± 0.003	1.027 ± 0.004	1.088 ± 0.004
4′-3H	5′-14C	1.022 ± 0.002	0.986 ± 0.002	-	-

^aThe remote 5′-¹⁴C KIE is assumed to be unity.

^bExperimental values corrected for remote 4′-³H KIE according to the equation KIE = KIE_obs × 4′-³H KIE.

^cExperimental values corrected for remote 4′-³H KIE according to the equation KIE = KIE_obs / 4′-³H KIE.

^dExperimental values corrected for 2′-²H content according to the equation KIE = (KIE_obs − 1 + F)/F, where F is the fraction of ²H in the substrate.

Figure 5.

(A) Intrinsic KIEs and their standard errors for Phe200Gly HsPNP-catalyzed arsenolysis (blue) and phosphorolysis (red) of inosine, and WT-HsPNP catalyzed (black) arsenolysis of inosine (10). Between parentheses is the number of replicates. (B) Predicted KIEs for the best match non-stationary point TS for arsenolysis (blue) and phosphorolysis (red) of inosine. The labels and their respective positions are shown in cyan.

Enzymatic transition structures

A match of intrinsic KIEs to theoretical predictions is a powerful technique in providing detailed information about the nature of enzymatic transition states (31). Stabilization by the enzyme alters the position of the transition state relative to the gas phase potential energy surface, necessitating the restriction of geometries and predictions from non-stationary points. This method of calculating enzymatic transition structures has provided excellent predictions in previously modeled systems resulting in powerful transition state mimics (7, 11). A detailed chemical and theoretical test of this method of transition state analysis has shown that errors are minimal (24). Transition structures for the reaction of arsenate (1) and phosphate (2) with inosine were explored from the calculated grid of structures (Figure 2). Predicted KIEs for 112 non-stationary point structures were obtained from the Gaussian 03-calculated frequencies for the heavy atom isotope effects, 1′-¹⁴C and 9-¹⁵N, along the reaction coordinate (a table of predicted KIEs is included in the Supporting Information). Several theoretical structures exhibit 1′-¹⁴C and 9-¹⁵N predicted KIEs that fit within experimental error of the measured values. Theoretical structures with a sum of r_C-N and r_C-O between 5.4–5.6 Å provided the best fit to the experimental data. The full set of KIEs, including 1′-³H, 2′-²H, and 5′-³H₂, were then predicted for this subset of grid structures. The 2′-²H position provides an accurate gauge of the electron density at the reactive center of the substitution because of the hyperconjugation effect at the 2′ position. Theoretical structures with longer r_C-N more accurately predict the measured KIEs at the 2′-²H position. Importantly, the predicted KIEs were virtually the same in geometrically similar theoretical transition state structures involving arsenate (1) and phosphate (2) (see the predicted KIEs for the grid geometries in the Supporting Information). Predictions for the 5′-³H₂ KIEs were inverse in all structures derived from the grid. To aid in the prediction of accurate KIEs and to avoid errors associated with fixed parameters, a more complete computational model was attempted incorporating several residues from the active site of HsPNP.

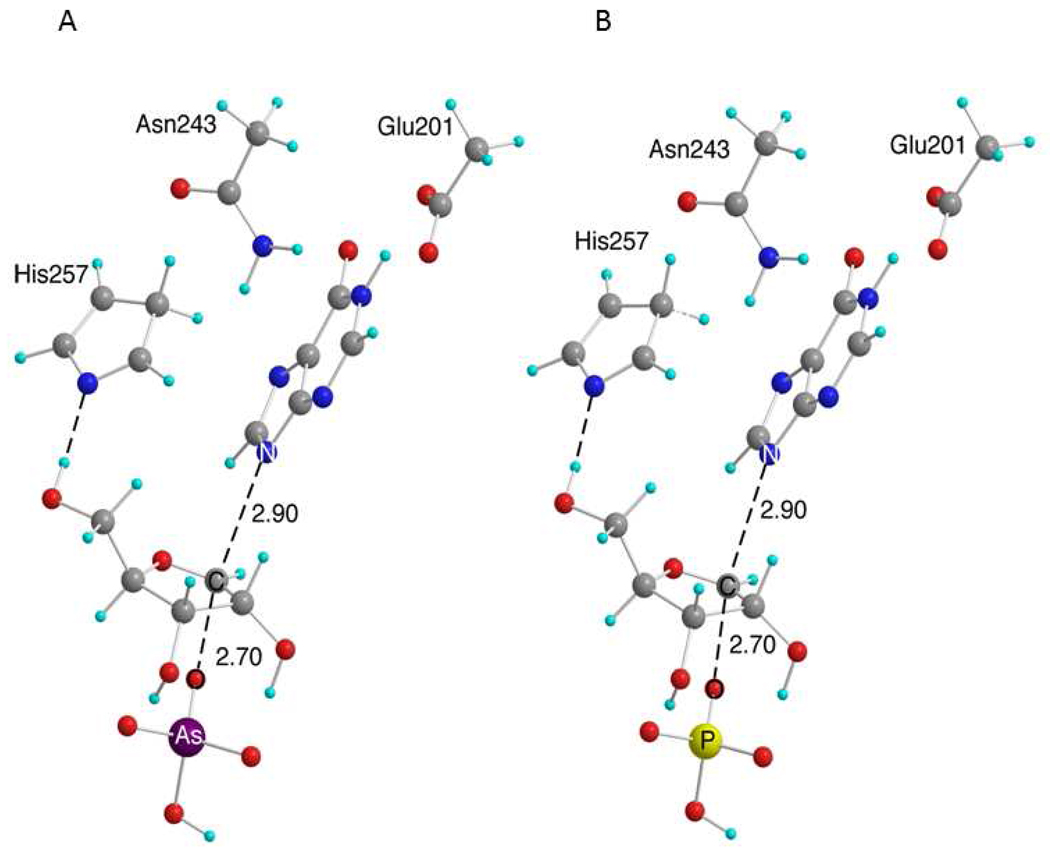
Dynamic studies have reported that the coordination of residue His257 to the 5′-OH is involved in the reaction coordinate of HsPNP (32). A pyrrole mimic of the histidine residue was added at the 5′ position of the sugar moiety in the second analysis. The pyrrole mimic was used rather than imidazole to avoid unwanted coordination of the second imidazole nitrogen. Residues Glu201 and Asn243 are also catalytically important (16) and were added to the model to mimic enzymatic stabilization of the nucleobase. New structures were explored with this more complete model containing the side chains of residues Glu201, Asn243, and the His257 mimic. All structures were calculated in B3LYP using a 6-31G* basis set. Bond distances r_C-N and r_C-O were necessarily fixed to predict the enzymatic transition structures. Several conformations of the transition structure were explored, including the position of the base, conformations of the sugar moiety, and the position of the attacking phosphate; however, the overall nucleobase and residue orientations derived from previous molecular dynamic studies were maintained (32, 33).

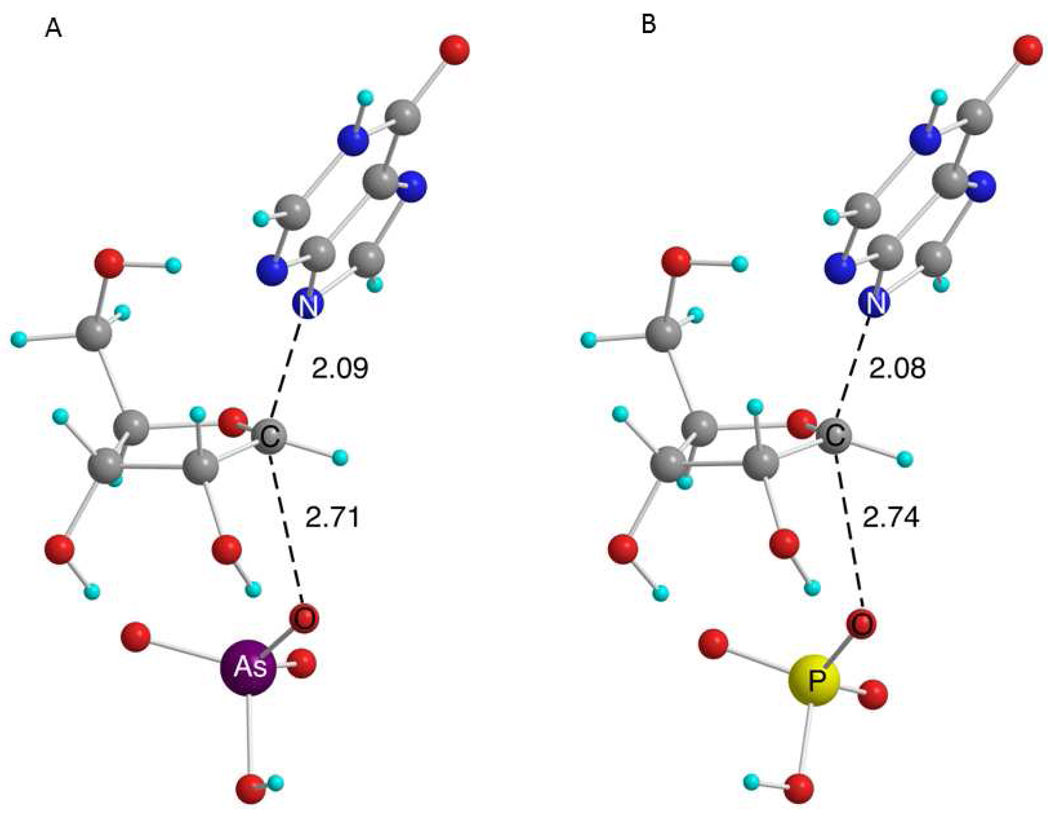
A comparison of experimental intrinsic and theoretically predicted KIEs was used to gauge the best theoretical structure to represent the enzymatic transition states for arsenolysis (1) and phosphorolysis (2) reactions. Several structures were explored with fixed r_C-N in the range of 3.0–2.8 Å and fixed r_C-O in the range of 2.7–2.5 Å (ranges were based upon previously explored structures). The transition structures for both arsenolysis and phosphorolysis exhibit r_C-N of 2.9 Å and r_C-O of 2.7 Å; however, structures within approximately 0.1 Å of each of the bond lengths give predicted values within the range of experimental error (Figure 6).

Figure 6.

Transition structures for the reaction of (A) arsenate and (B) phosphate with inosine in the reaction of Phe200Gly HsPNP. The numbers by the dashed lines are measures of r_C-N and r_C-O. Carbon atoms are shown in gray, oxygen in red, hydrogen in cyan, nitrogen in blue, arsenic in purple, and phosphorus in yellow.

The transition structures for arsenolysis and phosphorolysis represent dissociative A_ND_N transition states, exhibiting significant oxocarbenium ion character with the breaking of the r_C-N, the leaving nucleobase being advanced and with small but significant formation of the r_C-O bond with the nucleophile. The calculated transition structures exhibit remarkable similarity with either arsenate or phosphate as nucleophiles. Thus, the two ions lead to virtually the same TS in the reaction catalyzed by Phe200Gly HsPNP.

Predicted KIEs

The agreement between experimental and predicted KIEs is impressive for both arsenolysis and phosphorolysis given the simplicity of the model (Figure 5). Heavy atom predictions (1′-¹⁴C and 9-¹⁵N) are within the uncertainty of the experimental measurements, indicating that the model accurately represents the reaction coordinate. Excellent predictions of the 2′-²H KIEs support the accuracy of the ribose ring conformation of the calculated structures. The ribose ring of the inosine lies nearly flat at the transition state, allowing for strong hyperconjugation of the 2′-H into the oxocarbenium center. The 1′-³H KIEs are slightly over predicted by approximately 3–4% for both reactions; however, considering the magnitude of the effect and the difficulty in predicting 1′-³H KIEs in related reactions, the agreement is reasonable. The 9-¹⁵N KIEs are slightly under predicted in all structures explored for both reactions, and this is probably due to the sensitivity of nitrogen to the electronic environment in the active site, which differs from the gas phase calculations.

The 5′-³H₂ KIEs are predicted to be normal for both transition structures; however, the 5′-³H₂ KIEs are over predicted for arsenolysis and under predicted for phosphorolysis. The slight mismatch in predictions at this position is probably caused by differences in the coordination of the His257 mimic to the 5′-OH in the enzyme pocket as compared to the gas phase calculations (Figure 6). A dynamic study of HsPNP using transition path sampling suggests compression of the 5′-O with His257 at the transition state initiates N-ribosidic bond loss (32). A full enzymatic model involving the mode of compression at the 5′-hydroxyl group is beyond the scope of the theory used here. Nonetheless, the assumption that the 5′-³H₂ KIEs increase under this mode of compression is reasonable and explains the predicted KIEs for the reaction with phosphate. Conversely, the arsenate ion is larger than the phosphate one, and the ion-binding pocket of PNP must necessarily open to accommodate the larger ion. Molecular dynamic studies on HsPNP show that the phosphate-binding pocket interacts with the residues surrounding the 5′-OH of inosine (33). A reasonable hypothesis is that the pocket at the 5′-OH position is forced to open up in the reaction involving arsenate causing a decreased interaction between the His257 and the 5′-OH. To further examine this idea, the 5′-³H₂ KIEs were modeled as a function of the distance between the His257 mimic and the 5′-OH. The magnitude of the 5′-³H₂ KIEs were inversely proportional to the bond distance between the 5′-OH and the N of the His257 mimic. The explanation above is consistent with the reduced intrinsic KIE at the 5′-H₂ positions for the arsenolysis reaction relative to phosphorolysis. In summary, theoretical analysis of the experimentally measured KIEs for the arsenolysis and phosphorolysis reactions with mutant HsPNP has confirmed the strong similarity between the transition state structures of both reactions.

Alternative mechanisms

Only results involving an A_ND_N mechanism have been shown. However, other mechanistic possibilities were also considered. Previous studies with native HsPNP have shown that the N7 position of the nucleobase is protonated at the transition state (10). All attempts to locate a transition structure for a concerted A_ND_N mechanism with protonation at the N7 position of inosine proved to be inconsistent with the results for Phe200Gly HsPNP. The possibility of a D_N*A_N^‡ mechanism involving first the departure of the nucleobase (with or without protonation at N7) followed by rate-limiting attack of the ion, as reported for Lys22Glu-His104Arg HsPNP (13), was also explored. In that case, the isotope effect at 9-¹⁵N should represent an EIE in the case of a D_N*A_N^‡ mechanism. The isotope effect was predicted to be 1.024 and 1.028 for hypoxanthine with and without protonation at N7, respectively. The second step of the D_N*A_N^‡ mechanism, involving attack of the ion (arsenate or phosphate) to the oxocarbenium, was explored by including only the ion and the oxacarbenium (no nucleobase) and varying r_C-O. The mismatch between the predicted and intrinsic values of 1′-¹⁴C, 1′-³H, and 2′-²H KIEs at all distances of r_C-O excluded the D_N*A_N^‡ as a mechanistic possibility (all geometries and KIE predictions for the attack of arsenate and phosphate on the oxocarbenium are included in the Supporting Information).

A final mechanistic possibility is a D_N^‡*A_N mechanism involving rate-limiting dissociation of the nucleobase, followed by the attack of the ion (arsenate or phosphate) to the oxocarbenium, as reported for BtPNP (7). The D_N^‡*A_N mechanism was explored by varying r_C-N for various structures involving only the inosine (excluding the arsenate and phosphate). The mismatch between the predicted and intrinsic values of 1′-¹⁴C, 1′-³H, and 2′-²H KIEs at all distances of r_C-N, specifically the under prediction of the 2′-²H KIE, excluded the D_N^‡*A_N as a mechanistic possibility (all geometries and KIE predictions for rate-liming dissociation of the nucleobase is included in the Supporting Information). Transition structures for the dissociation of a nucleobase protonated at N7 could not be located³. Both the D_N^‡*A_N and D_N*A_N^‡ mechanisms can be excluded as mechanistic possibilities for both the arsenolysis and phosphorolysis of Phe200Gly HsPNP based on a mismatch of the predicted and experimental KIEs. The maximum predicted isotope effect at 9-¹⁵N for all investigated mechanisms was 1.035, which is equal, within experimental error, to the intrinsic values obtained for arsenolysis and phosphorolysis after correction for C_f. Thus, the reaction displays no significant terms other than C_f to influence the intrinsic KIEs.

The ability of arsenate to mimic phosphate in the reaction of Phe200Gly HsPNP has been shown using a combination of experimental and theoretical techniques. The ions of arsenate and phosphate exhibit similar electronic properties, and calculated transition structures for the reaction of arsenate and phosphate with inosine without geometric restriction are nearly identical. The strongest evidence justifying previous studies that necessarily involve the substitution of arsenate for phosphate is the similar KIE measurements at multiple positions. The results indicate the remarkable similarity between the TS reached with either arsenate or phosphate in the Phe200Gly HsPNP-catalyzed inosine cleavage, and also suggest the same is true for other nucleophilic substitution reactions of nucleosides.