Quantitative Assessment of Abdominal Aortic Aneurysm Geometry

Abstract

Recent studies have shown that the maximum transverse diameter of an abdominal aortic aneurysm (AAA) and expansion rate are not entirely reliable indicators of rupture potential. We hypothesize that aneurysm morphology and wall thickness are more predictive of rupture risk and can be the deciding factors in the clinical management of the disease. A non-invasive, image-based evaluation of AAA shape was implemented on a retrospective study of 10 ruptured and 66 unruptured aneurysms. Three-dimensional models were generated from segmented, contrast-enhanced computed tomography images. Geometric indices and regional variations in wall thickness were estimated based on novel segmentation algorithms. A model was created using a J48 decision tree algorithm and its performance was assessed using ten-fold cross validation. Feature selection was performed using the χ²-test. The model correctly classified 65 datasets and had an average prediction accuracy of 86.6% (κ = 0.37). The highest ranked features were sac length, sac height, volume, surface area, maximum diameter, bulge height, and intra-luminal thrombus volume. Given that individual AAAs have complex shapes with local changes in surface curvature and wall thickness, the assessment of AAA rupture risk should be based on the accurate quantification of aneurysmal sac shape and size.

INTRODUCTION

Abdominal aortic aneurysms (AAAs) are localized dilations that commonly form below the renal arteries. Depending on the size at the time of diagnosis, the aneurysm should either be closely monitored or repaired to prevent rupture. Traditional repair of AAAs is via open surgery, which is associated with mortality rates ranging between 2 and 4%.¹³ Endovascular aneurysms repair (EVAR), a significantly less invasive alternative to open surgical repair, involves the delivery of covered stent grafts into the aorta through the femoral artery and is associated with a mortality rate of 1.7%.¹⁰ Evaluating rupture risk is critically important as aneurysm rupture carries high mortality rates.^3,33 Currently, a maximum transverse diameter of ≥5.5 cm and an expansion rate of ≥1 cm/year are the indications for elective repair. However, studies have shown that peak wall stress is a more reliable indicator of rupture potential, which can moreover be used in the case of small aneurysms (<5.5 cm) that do not meet the maximum diameter criteria.^8,32,35 Computational approaches to assess the biomechanics and rupture risk of AAAs have applied finite element analysis and fluid–structure interaction modeling.^{6,8,25–27,35} In addition to geometric factors, numerically predicted wall stress, finite element analysis rupture index, rupture potential index (RPI), and severity parameters have been proposed as alternative approaches to assessing rupture risk.¹⁷ An RPI, which was first reported by Vande Geest et al.,³⁴ is a wall stress-to-wall strength ratio proposed as a possible indicator of rupture risk. Recently, Maier et al.¹⁵ examined the rupture-threat in a cohort of ruptured and repaired cases, and reported that maximum wall stress and maximum RPI are significantly increased for symptomatic/ruptured AAAs.

With radiologists and vascular surgeons making efficient use of CT imaging for pre-surgical planning as well as measuring AAA diameter over time during patient follow-up, it is logical to question the importance of quantifying the geometric characteristics that are routinely observed qualitatively in the images. Visual inspection of the segmented and reconstructed AAA, a process that is aided semi-automatically by most proprietary CT image processing software in the Radiology suite, can provide such qualitative assessment. However, visual inspection is insufficient to measure the degree to which the AAA wall geometry is irregular or to determine the regional variations in wall thickness, with vessel thickness being scarcely assessable from CT images by the naked eye.

The need for quantifying the shape and size of patient-specific AAAs is evident in that it can prove valuable for predicting individual rupture risks in presurgical planning, establishing index thresholds for patient selection, and for customized designs of endovascular grafts. An accurate geometrical characterization requires taking into account for the 3D complexity of the shape, tortuosity, and asymmetry of the apparently randomly formed AAA sac. In a study of 15 patient-specific AAAs, Doyle et al.⁵ demonstrated from the relationship between posterior wall stress and asymmetry that excessive bulging of one surface results in elevated wall stress on the opposite surface. In a recent study, three ruptured aneurysms analyzed by Pappu et al.²⁰ exhibited more out of plane growth than axial growth. Complex AAA geometry contributes to equivalently complex wall stress distribution over the entire AAA, with the highest stresses associated with regions of high curvature.²⁴ Moreover, it has been proposed that geometric parameters may be able to accurately predict wall stress distributions.⁷ Mean and maximum centerline curvature were shown to be highly correlated with peak wall stress⁹ and the location of maximum stress coincided with peaks in the magnitude of the Gaussian curvature, a parameter that indicates the existence of concave and convex regions on the vessel surface.¹⁹ Parameters such as the Gaussian curvature are important since they offer information unattainable with simple visual inspection and represent a measure of the degree to which the AAA wall geometry is irregular.¹

Several authors have used shape measures in the characterization of disease processes. Early studies report on the power of shape measures to distinguish between normal and abnormal brain surface shapes and to establish a relationship between the shape of the surface of the human brain and the function of the underlying tissue.² A recent study described the derivation of a set of global indices characterizing the size and shape of cerebral aneurysms for assessment of their rupture potential and for choosing the appropriate clinical treatment modality.^14,23

We previously reported on a novel, semi-automatic vessel segmentation algorithm (VESSEG v.1.0.2, Carnegie Mellon University) used to segment the CT images of 20 AAA subjects to compute wall thickness. ²⁸ Patient-specific 3D models of each AAA were constructed from the segmented data and characterized quantitatively by calculating 28 size and shape indices and local variations in aortic wall thickness.¹⁶ In this study, we discuss the potential utility of these indices as discriminators between two groups of AAAs differentiated by their status (unruptured vs. ruptured). Therefore, the objective of this investigation is to quantify the AAA geometry and wall thickness and train a learning model based on labeled data to assess the differences among geometric characteristics of the two aneurysm population subsets. In this manner, classification plays an important role in medicine, especially for medical diagnosis. However, no classification models based on statistical theory exist to diagnose AAAs. Decision trees were used to classify our data; the structure is similar to the decision-making methods that physicians normally use when they try to understand which diagnostic test is better to use or the best treatment to prescribe.¹¹

MATERIALS AND METHODS

Subjects and Image Data

Our study population consists of 76 human AAAs; 10 ruptured and 66 randomly selected unruptured aneurysms. Noteworthy is that the term “ruptured” is used in the context of this investigation to designate those aneurysms that were detected as ruptured in the last CT exam prior to emergent intervention or those that ruptured within a month after the last CT exam and prior to the intervention. All ruptured aneurysms had maximum diameters exceeding 5.5 cm. The 66 subjects with unruptured AAAs eventually underwent elective repair at Allegheny General Hospital (AGH) in Pittsburgh, PA, USA, and the last available contrast-enhanced CT scan prior to the repair was used for this study. Thirty-five of the unruptured aneurysms had maximum diameters exceeding 5.5 cm. Standard DICOM images were acquired from contrast-enhanced abdominal CT studies with the following imaging parameters: (i) scan matrix size = 512 × 512; (ii) average pixel size = 0.7693 mm (0.6172–0.9688 mm); (iii) pixel intensity = 0–2000; and (iv) average slice thickness = 3.0 mm. This study was subject to Internal Review Board approvals at CMU and AGH, and no patient consent was necessary as the data were acquired by a retrospective review of records.

Segmentation and Reconstruction

The segmentation and reconstruction methods used in this study have been previously described.^16,28 In brief, three different algorithms form the basis of the segmentation and wall thickness detection tools applied for this study. Prior to segmentation, the images are sub-selected to include those immediately below the renal arteries and before the iliac bifurcation. The lumen segmentation is performed via the intensity gradient that exists between the aortic lumen and surrounding structures. The outer wall contour can be determined either manually or automatically. In the manual method, the image is reduced to a small region containing the aorta and an array of contours, or isolines, is provided to the user to select from. In the automatic method used in this study, the outer wall is detected by using intensity thresholding and additional control rules to insure that the segmentation of the slice is discarded when no possible boundaries can be created and then the threshold is changed accordingly to attempt a new segmentation. The inner wall is detected by training a neural network to recognize regions where the inner wall could reside. Wall thickness, which we define as the shortest distance from an inner wall point to its corresponding outer wall point, was calculated for 72 points along the inner wall contour for each image in the dataset.

From the segmented images, we automatically calculate the wall thickness, 1D, 2D, and most of the 3D indices. Two 3D shape and size indices, and the four second-order curvature-based indices, are calculated by generating a surface mesh of the AAA. First, the outer wall contours are exported as a set of point clouds to generate an initial, coarse surface mesh using Delaunay triangulation. The nodes are iteratively moved into an equilibrium position with a uniform edge length between each node that is equal to the pixel spacing in the image. Due to the presence of low-quality elements, unrealistic sharp corners, and stair-shaped patterns, an iterative algorithm was developed to optimize the surface quality, via mesh refinement and smoothing. A smooth triangular surface mesh is generated based on the method described by Persson and Strang,²² adapted for AAA geometries. In brief, the boundary of the AAA wall is described using a signed distance function and triangulation is performed with a Delaunay algorithm. The irregularities on the surface are minimized by linear interpolation and the initial coarse mesh is refined by forcing mesh nodes into equilibrium positions. A surface smoothing algorithm based on a low-pass filter method³¹ is applied to remove sharp corners. The implemented algorithm produces no shrinkage or distortion of the surface topology because the low-pass filter preserves low curvature components (the underlying shape of the aneurysm) while attenuating high curvature components (sharp peaks). A smooth surface, x^N, is obtained by iteratively applying the low-pass filter to the original surface signal, x, such that

$$x^n=f{(K)}^{N}x$$ (1)

$$f{(K)}^N={((I-\mu K)(I-\lambda K))}^2,$$ (2)

where f(K) is the transfer function of the low-pass filter, N the number of iterations, and λ and μ are two scaling factors. It can be observed that f(K)N ≈ 1 for low frequencies, f(K)N ≈ 0 for high frequencies, and that the rate of decrease in the transition band is determined by the number of iterations N and the scaling factor λ in the transfer function (Eq. 2). The optimal number of iterations needed for mesh refinement and smoothing is determined by calculating an acceptable average element quality index (≥0.75) with minimal AAA sac volume change (≤1.5%).²⁹

Size and Shape Indices

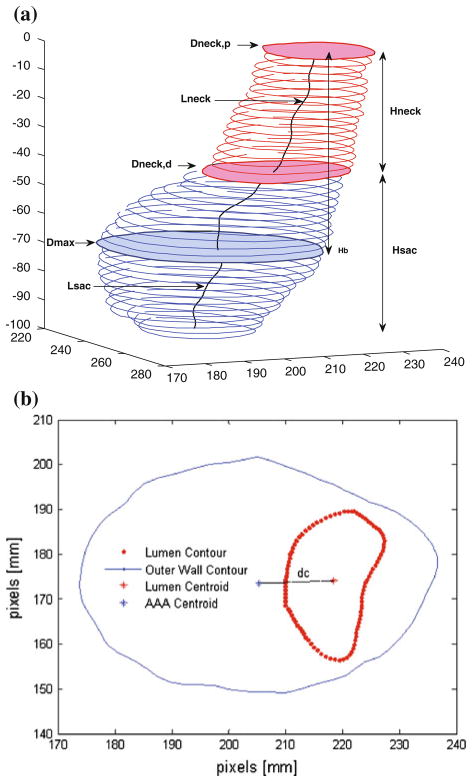
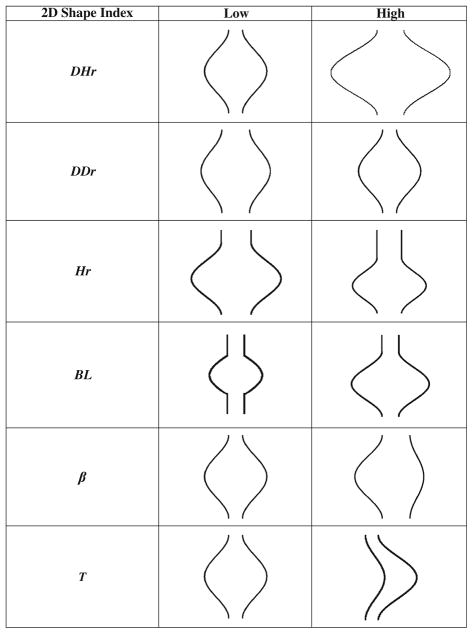
Twenty-five size and shape indices were defined and calculated for each AAA model, as described by Martufi et al.¹⁶ Nine 1D size indices (Fig. 1) were defined as follows: maximum transverse diameter (D_max), distal and proximal neck diameters (D_neck,d and D_neck,p), height of sac (H_sac), length of AAA sac centerline (L_sac), length of neck centerline (L_neck), height of neck (H_neck), the bulge height (H_b), and the distance between the lumen centroid and the centroid of the cross section where D_max is located (d_c). Six 2D shape indices (see Fig. 2) were derived from the 1D size measurements: diameter–height ratio (DHr), diameter–diameter ratio (DDr), height ratio (Hr), bulge location (BL), asymmetry factor (β), and tortuosity (T). Four 3D size indices: AAA volume (V), surface area (S), intraluminal thrombus volume (V_ILT), and γ, the ratio of AAA sac to ILT volume. Two 3D shape indices based on V and S: the isoperimetric ratio (IPR) and non-fusiform index (NFI). Four second-order curvature-based indices: area-averaged Gaussian and mean curvatures (GAA and MAA) and the L2-norms of these curvatures (GLN and MLN). All diameter measurements refer to the diameter assessed with the outer wall boundary. All indices are calculated from the segmented CT images with the following exceptions: the surface meshes are used to compute the four second-order curvature-based indices (GAA, MAA, GLN, and MLN), the two 3D shape indices (IPR and NFI), and two 3D size indices (V and S). The reader is referred to Appendix 1 and Martufi et al.¹⁶ for a complete mathematical description of the indices used in this feature-based approach for AAA geometry quantification.

FIGURE 1.

(a) 1D size indices: D_max, D_neck,p, D_neck,d, H_sac, H_neck, L_sac, L_neck, H_b; (b) 1D size index d_c.

FIGURE 2.

Schematic of 2D shape indices providing an approximate measure to construe the global AAA shape.

Wall Thickness

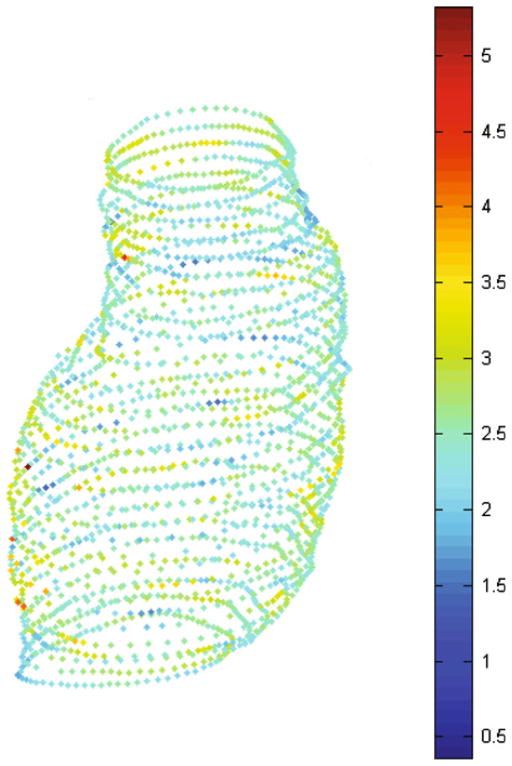
Three wall thickness parameters were calculated for each AAA model: the minimum (t_w,_min), maximum (t_w,_max), and average (t_w,_ave) wall thickness of the aneurysm sac. The average thickness was found by taking the mean of the average thickness computed at each cross section in the CT image stack. A typical wall thickness distribution projected on the inner wall surface contours is shown in Fig. 3.

FIGURE 3.

Wall thickness distribution (mm) predicted by VESSEG.

Statistical Analysis

The geometry of 76 AAAs was characterized using the above methodology. Indices were calculated for two population subgroups: ruptured aneurysms (Group 1, n₁ = 10) and unruptured aneurysms (Group 2, n₂ = 66). WEKA,¹² an open source machine learning software used for data mining, was used to perform feature selection, train a model, and assess the performance of the model. Feature selection was performed by computing the χ² statistic with respect to class, and the J48 decision tree algorithm was used to develop a model based on the data. A more detailed discussion on decision tree modeling can be found in Appendix 2.

The performance of our model was assessed using ten-fold cross validation. Stratified ten-fold cross validation is a standard method of predicting the error rate of a learning technique given a limited amount of data. The data are divided into ten parts, or folds, in which the class is represented in approximately the same proportion as in the full dataset. Each fold acts as testing data once and the learning algorithm is trained on the remaining nine-tenths. The error rate is then calculated by applying the testing data on the learned model. This process is repeated ten times on different training sets and the ten error estimates are averaged to yield an overall error estimate, which is represented as the percentage of correctly classified instances. A kappa statistic (κ) was also calculated, which is similar to percentage correct, but scaled down to account for those instances that were correctly classified by chance.

RESULTS

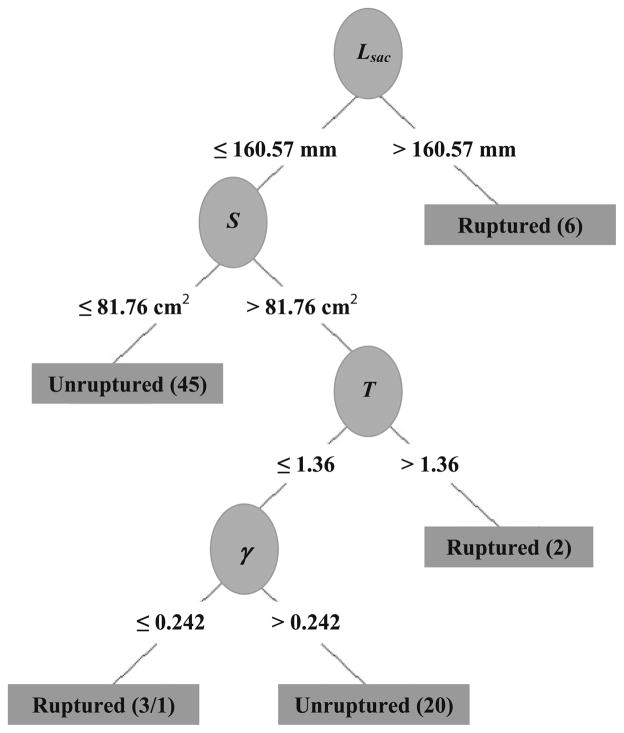
The values for the 28 indices are shown in Table 1 and are reported as mean ± standard deviation. The highest ranked indices from the feature selection algorithm are as follows: sac length (L_sac), sac height (H_sac), volume (V), surface area (S), maximum diameter (D_max), bulge height (H_b), and intra-luminal thrombus (V_ILT). The model that was constructed based on the J48 decision tree algorithm (see Fig. 4) consisted of L_sac, S, tortuosity (T), and ILT volume-to-AAA volume ratio (γ), and the performance was assessed using stratified ten-fold cross validation. The highest ranked features were chosen using a feature selection algorithm based on the χ²-test. This algorithm considers each feature in isolation from the other features, whereas the decision tree considers each chosen feature in the context of the features that have already been selected higher up in the tree. However, the highest ranked feature, L_sac, is also the feature that provides the highest information gain (IG), thus making it the first feature in the decision tree. The average prediction accuracy of the decision tree model was 86.6% with κ = 0.37. Using D_max = 5.0 cm as the predictive variable would correctly classify 19 unruptured aneurysms and all the 10 ruptured aneurysms; however, 47 of the unruptured aneurysms would be classified as ruptured, resulting in an accuracy of 38.2% (κ = 0.10).

TABLE 1.

Mean ± standard deviation for all indices for ruptured (Group 1) and unruptured (Group 2) aneurysms.

Index	Group 1	Group 2
1D size indices (mm)
Dmax	78.44 ± 13.16	54.92 ± 11.08
Dneck,p	33.01 ± 4.27	28.97 ± 4.99
Dneck,d	16.53 ± 16.70	32.50 ± 11.50
Hsac	124.40 ± 42.22	86.49 ± 22.78
Hneck	12.60 ± 16.14	17.99 ± 17.26
Lsac	166.86 ± 51.03	106.84 ± 29.15
Lneck	20.51 ± 25.66	24.58 ± 22.45
Hb	88.10 ± 25.64	66.84 ± 18.41
dc	7.95 ± 5.44	4.80 ± 3.82
2D shape indices (non-dimensional)
DHr	0.59 ± 0.08	0.69 ± 0.30
DDr	2.42 ± 0.51	1.93 ± 0.43
Hr	0.11 ± 0.15	0.28 ± 0.34
BL	0.64 ± 0.10	0.87 ± 0.43
β	0.90 ± 0.06	0.91 ± 0.06
T	1.33 ± 0.12	1.23 ± 0.11
3D size indices
V (cm3)	421.57 ± 192.40	154.87 ± 80.16
S (cm2)	154.93 ± 50.61	80.32 ± 26.14
VILT (cm3)	226.89 ± 160.22	74.43 ± 61.28
γ (non-dimensional)	0.50 ± 0.21	0.47 ± 0.16
3D shape indices (non-dimensional)
NFI	0.58 ± 0.04	0.62 ± 0.09
IPR	2.83 ± 0.15	2.89 ± 0.41
Second-order curvature-based indices
GAA (mm−1)	0.0012 ± 0.0001	0.0005 ± 0.0349
MAA (mm−1)	0.0139 ± 0.0007	0.0198 ± 0.0475
GLN (non-dimensional)	3.2645 ± 1.0802	4.3797 ± 4.7112
MLN (non-dimensional)	0.1963 ± 0.0344	0.2238 ± 0.1258
Wall thickness indices (mm)
tw,ave	1.82 ± 0.16	1.80 ± 4.17
tw,max	3.86 ± 0.47	4.17 ± 1.32
tw,min	0.68 ± 0.17	0.63 ± 0.20

FIGURE 4.

Model learned by J48 decision tree, based on highest IG. L_sac, length of sac; S, surface area; T, tortuosity; γ, ratio of intraluminal thrombus volume to aneurysm volume.

DISCUSSION

The objectives of this study were to use anatomically realistic AAA models to evaluate a proposed set of global geometric indices describing the size and shape of the aneurysm sac, and use a learning algorithm to develop a model that is capable of discriminating between ruptured and unruptured aneurysms. Modern medicine is capable of generating large amounts of data such that there is now a widening gap between data collection and data comprehension and decision making. Data mining methods and machine learning can help in identifying potentially useful patterns in the data and build models that are capable of predicting an event or the value of a categorical variable from the known values of other variables.

The results of this study show that in addition to maximum diameter (D_max), sac length (L_sac), sac height (H_sac), volume (V), surface area (S), bulge height (H_b), and ILT volume (V_ILT) were highly correlated with respect to repair status. Since ruptured aneurysms, in general, tend to have a larger maximum diameter than unruptured aneurysms, justifiably, the volume, surface area, and thrombus volume are expected to be large as well. However, other parameters such as the volume of ILT (which is not consistently correlated with AAA size) were found to be correlated with rupture.

It has been proposed that as the maximum diameter of an aneurysm increases, the risk of rupture also increases. However, this correlation may be inadequate as other geometric factors play a role in aneurysm rupture. In this study, we found that discriminating between the two groups of aneurysms cannot be determined simply from a single metric; rather, a combination of indices leads to better predictions. The decision tree model trained on the entire data (Fig. 4) shows that L_sac ≤ 160.57 mm and S ≤ 81.76 cm² correctly classified the majority of the Group 2 aneurysms (45/66). A majority of Group 1 aneurysms (6/10) were classified correctly for L_sac>160.57 mm. The remaining 25 instances were classified correctly based on different thresholds for T and γ. The decision tree trained on all the data was able to classify all the instances correctly, except for one unruptured aneurysm that was incorrectly classified as ruptured. However, it should be observed that unruptured aneurysms are aneurysms that were electively repaired, thus halting the progression of the disease. Whether the unruptured aneurysms would have eventually ruptured is unknown, though according to our model there was one instance where such an aneurysm was in a similar state as the ruptured aneurysms.

In our study, the overall classification accuracy was 86.6% (range 71.4–100%). The kappa statistic (κ), which is similar to classification accuracy but adjusted for correct predictions that occurred due to chance, was 0.37. Though each group is represented in both the training and testing sets for each fold, they are represented in approximately the same proportion as the full data. Due to the data size and skewed nature between the groups, a low κ is unavoidable. The accuracy obtained with the decision tree and a combination of features, though, had a higher accuracy than using maximum diameter alone (38.2%, κ = 0.10).

Harbaugh and co-authors^14,23 calculated geometric indices to characterize the size and shape of cerebral aneurysms. It was reported that quantified shape is more effective than size in discriminating between ruptured and non-ruptured cerebral aneurysms. In a previous study, Somkantha and Phuangsuwan³⁰ trained a Naïve Bayes classifier using three features (area, perimeter, and compactness) derived from image segmentation to discriminate between healthy and diseased aorta. They used 30 images for training (n = 15 for healthy and aneurysmal aorta, respectively) and 20 images for testing (n = 10 for healthy and aneurysmal aorta, respectively) and obtained accuracy levels of 95%. However, as the aneurysmal aorta tends to be larger than a healthy aorta, it is unsurprising that these size features can accurately classify the two categories of aorta. To the best of our knowledge, no other studies have been performed using a classification model to discriminate between ruptured and non-ruptured AAAs from a set of geometric features.

The accuracy of the geometry quantification method relies on the accuracy of the segmentation algorithm, which we addressed previously.²⁸ Additionally, this feature-based approach tends to reduce the geometric characterization to a relatively small number of indices. Without a priori knowledge of the exact discriminator among AAAs eligible for elective repair (other than D_max) a pre-conceived set of indices may omit important information necessary for evaluating shape differences between two population groups. In addition, the use of area-averaged curvatures may not address focal high and low curvature points and could exclude local gradients in curvature. A direct comparison of the spatial distributions of the Gaussian and mean curvatures could be performed although this would likely consist of a qualitative analysis. However, future study should include statistical analysis of the high and low curvature values along with correlations based on their topological location. Another limitation is the sample size of our study population. Due to the skewed nature of our data (10 ruptured vs. 66 unruptured aneurysms), the model cannot completely capture the differences between ruptured and unruptured aneurysms, which is reflected in the kappa statistic. However, a high ratio (6.6:1 in our set) of unruptured to ruptured data-sets is unavoidable when randomly selecting aneurysm repair cases and is an inherent limitation of our study as the number of ruptured aneurysms at AGH is historically low. In a review of records over the past 5 years, the ratio of emergent vs. elective AAA repairs at AGH is approximately 7.7:1 (on average 17 ruptures for every 130 elective repairs per year). This relatively low number of ruptured aneurysms may also affect the reliability of the decision tree model. Simulation studies have shown that a ratio of more than five events per variable is needed to produce reliable results in logistic regression analysis.²¹ While this ratio is not required for all multivariate modeling, future study will be targeted to include a larger number of ruptured aneurysms in our analysis. Finally, the reconstruction and feature calculation could be affected by the CT slice spacing of the datasets. Larger slice spacing requires additional interpolation masks, which could affect the reconstruction of the aneurysms and the amount of smoothing needed. However, a great majority of the datasets used in this investigation have a slice spacing of 3 mm, which is standard for patients imaged at AGH.

Our analysis differs from the more conventional use of multivariate analysis such as multiple regressions to identify ‘best fit’ variables or a multivariate analysis of variance (MANOVA). Due to the limited number of ruptured aneurysms, we would not have been able to attain full statistical power using the MANOVA since the number of features exceeds the number of instances in each group. However, the decision tree model can be considered a multivariate analysis. Although the selection of features in the decision tree is univariate in that only one feature is chosen at the leaf node, the performance of the model is multivariate in that it is assessed using all features in the tree. In addition, rather than report p-values to indicate the degree of significance, any classifier used for categorical prediction (including decision trees) measures the prediction accuracy (or kappa statistic) to assess the performance of the model. However, we acknowledge that using a multivariate decision tree may give more information regarding the relative risk at each leaf node, which is an alternative technique worth exploring when the sample sizes in each aneurysm group are approximately the same.

Previous studies have used idealized aneurysm shapes and uniform wall thickness in their attempt to characterize aneurysm shape. Although wall thickness was not one of the highest ranked features chosen with the feature selection algorithm based on the χ²-test, its effect on aneurysm rupture cannot be ignored. Other studies have reported on the role wall thickness plays in rupture risk assessment and its effect on wall stress distribution.^4,18,26 Realistic AAAs have complex, tortuous, and asymmetric shapes with local changes in surface curvature and regional variations in wall thickness. An accurate characterization of the randomly formed aneurysmal sac and the wall thickness distribution should be accounted for in the assessment of AAA rupture risk. This study demonstrates that geometry quantification of AAAs can be used to determine features and their thresholds capable of identifying aneurysms that are at high risk of rupture, with higher accuracy than using the maximum diameter criterion.

APPENDIX 1: DEFINITION OF FEATURES (I.E., GEOMETRIC INDICES) USED IN THE GEOMETRY QUANTIFICATION APPROACH

1D Size Indices

Dmax:	Maximum transverse diameter for all cross sections within the AAA sac
Dneck,p:	Proximal neck diameter immediately below the renal arteries
Dneck,d:	Distal neck diameter

Since typically arterial cross sections are non-circular in shape, the definition used for calculating D_max, D_neck,p, and D_neck,d is the fluid mechanics definition for hydraulic diameter:

$$D_i=\frac{4A_i}{P_i}$$

where A_i the cross-sectional area and P_i the perimeter of the same cross section.

H_sac is the height of AAA sac, L_sac the centerline length of AAA sac, H_neck the height of AAA neck, L_neck the centerline length of AAA neck, H_b the bulge height, and d_c the distance between the lumen centroid and the centroid of the cross section where D_max is located.

2D Shape Indices

DHr:	The diameter–height ratio, an expression of the fusiform shape of the AAA sac
	$$\mathit{DHr}=\frac{D_{max}}{H_{\text{neck}}+H_{\text{sac}}}$$
DDr:	Diameter–diameter ratio
	$$\mathit{DDr}=\frac{D_{max}}{D_{\text{neck},\text{p}}}$$
Hr:	Height ratio, an assessment of the relative neck height in comparison with the AAA height
	$$Hr=\frac{H_{\text{neck}}}{H_{\text{neck}}+H_{\text{sac}}}$$
BL:	Bulge location, provides a measure of the relative position of the maximum transverse dimension with respect to the neck
	$$BL=\frac{H_{\text{b}}}{H_{\text{neck}}+H_{\text{sac}}}$$
β:	Asymmetry factor
	$$\beta =1-\frac{d_{\text{c}}}{D_{max}}$$
T:	Tortuosity
	$$T=\frac{L_{\text{neck}}+L_{\text{sac}}}{d}$$

where d is the Euclidean distance from the centroid of the cross section where D_neck,p is located on the centroid of the cross section at the AAA distal end.

3D Size Indices

V:	Vessel volume
S:	Vessel surface area
VILT:	Volume of intraluminal thrombus contained within AAA sac
γ:	Ratio of AAA ILT volume
	$$\gamma =\frac{V_{\text{ILT}}}{V}$$

3D Shape Indices

IPR:	Isoperimetric ratio
	$$\mathit{IPR}=\frac{S}{V^{2/3}}$$
NFI:	Non-fusiform index
	$$\mathit{NFI}=\frac{\frac{S}{V^{2/3}}}{\frac{S_{\text{fusiform}}}{{V_{\text{fusiform}}}^{2/3}}}=\frac{\mathit{IPR}}{{\mathit{IPR}}_{\text{fusiform}}}$$

Second-Order Curvature-Based Indices (Calculation Described in Detail in Martufi et al.¹⁶)

GAA	Area averaged Gaussian curvature
MAA	Area averaged Mean curvature
GLN	L2 norm of the Gaussian curvature
MLN	L2 norm of the Mean curvature
	$$\begin{array}{c}\mathit{GAA}=\frac{{\sum }_{\text{all}\text{elements}}{K}_j{S}_j}{{\sum }_{\text{all}\text{elements}}{S}_j}\\ \mathit{MAA}=\frac{{\sum }_{\text{all}\text{elements}}{M}_j{S}_j}{{\sum }_{\text{all}\text{elements}}{S}_j}\\ \mathit{GLN}=\frac{1}{4\pi }\sqrt{\sum _{\text{all}\text{elements}}{S}_j·\sum _{\text{all}\text{elements}}\left(K_j^2{S}_j\right)}\\ \mathit{MLN}=\frac{1}{4\pi }\sqrt{\sum _{\text{all}\text{elements}}\left(M_j^2{S}_j\right)}\end{array}$$

Wall Thickness Indices

tw,min:	Minimum wall thickness
tw,max:	Maximum wall thickness
tw,ave:	Average wall thickness

APPENDIX 2: BRIEF DESCRIPTION OF DECISION TREE MODELS

A decision tree is a predictive machine learning model whose structure is determined by the information gain (IG) of the feature values. The IG can be calculated as:

$$\text{IG}(Y\mid X:t)=H(Y)-H(Y\mid X:t)$$

where

$$H(Y)=P(Y=\text{Ruptured})\ast {log}_{2}P(Y=\text{Ruptured})+P(Y=\text{Unruptured})\ast {log}_{2}P(Y=\text{Unruptured})$$

$$H(Y\mid X:t)=H(Y\mid X<t)\ast P(X<t)+H(Y\mid X\ge t)\ast P(X\ge t)$$

where Y the class label, which in this case is the repair status (elective vs. emergent), X the feature, and t the value of the feature. H(Y) represents the entropy prior to splitting on a certain feature and feature value and H (Y|X:t) represents the conditional entropy after splitting on a feature and feature value. Entropy is a measure of the impurity of an arbitrary collection of examples, and varies between 0 and 1 where 1 indicates that there are an equal number of examples in each group and 0 indicates that all examples are in the same group. The IG is calculated as the different between H(Y) and H (Y|X:t). A high IG is desirable as it indicates that the conditional entropy, H(Y|X:t), is low, which translates as a reduction in entropy after splitting on a certain feature and feature value.

The internal nodes of a decision tree denote the different features; the branches between the nodes provide the possible values that these features can have based on the data, while the terminal nodes yield the classification variable (ruptured or unruptured). The algorithm determines the internal nodes and branches by identifying the feature that discriminates the various instances most clearly; such feature is said to have the highest IG.

For the tree displayed in Fig. 4, the feature that provided the highest IG was L_sac. Six ruptured aneurysm had L_sac>160.57 mm and all the unruptured AAAs and the remaining four ruptured AAAs had L_sac<160.57 mm. Since the six ruptured AAAs cannot be further divided, the tree terminates at that node. The IG is recalculated using the remaining 66 unruptured AAAs and the 4 ruptured AAAs. These are then further subdivided using the feature that had the highest IG, which in this case was S.