Inference on the Strength of Balancing Selection for Epistatically Interacting Loci

Abstract

Existing inference methods for estimating the strength of balancing selection in multi-locus genotypes rely on the assumption that there are no epistatic interactions between loci. Complex systems in which balancing selection is prevalent, such as sets of human immune system genes, are known to contain components that interact epistatically. Therefore, current methods may not produce reliable inference on the strength of selection at these loci. In this paper, we address this problem by presenting statistical methods that can account for epistatic interactions in making inference about balancing selection. A theoretical result due to Fearnhead (2006) is used to build a multi-locus Wright-Fisher model of balancing selection, allowing for epistatic interactions among loci. Antagonistic and synergistic types of interactions are examined. The joint posterior distribution of the selection and mutation parameters is sampled by Markov chain Monte Carlo methods, and the plausibility of models is assessed via Bayes factors. As a component of the inference process, an algorithm to generate multi-locus allele frequencies under balancing selection models with epistasis is also presented. Recent evidence on interactions among a set of human immune system genes is introduced as a motivating biological system for the epistatic model, and data on these genes are used to demonstrate the methods.

1. Introduction

The outcome of the long-term evolution of Wright-Fisher populations with selection can be described by stationary distributions of the allele frequencies. Mathematical and statistical properties of these stationary distributions have been particularly well studied in the single-locus case (see for example Ewens [9] and references therein).

For multi-locus models, however, the analysis of stationary distributions has proven to be more difficult. Some of the assumptions leading to stationarity in the single-locus case cannot be directly extended to multi-locus models, except under the restrictive assumption of mutual independence of allele frequency distributions at different loci. When independence holds and the contribution of a locus to the overall fitness of a set of loci does not depend on the genotypes at other loci, the joint likelihood of the model parameters across loci can be expressed as the product of its marginals. In this case, the analysis effectively reduces to the single-locus case [4].

When the contribution of a genotype at a locus to the overall fitness of a set of loci depends on genotypes at nearby loci, however, independence is violated. In applying selection models to data on allele frequencies, if locus interactions are substantial, it is important to take them into account for the purpose of estimating selection accurately. Fearnhead (2006) generalized the single-locus stationary distribution of the Wright-Fisher model with selection, which was originally postulated by Wright [36] and later studied in the context of heterozygote advantage by Watterson [35]. The generalization of the stationary distribution is to a multi-locus system with a general selection model, where loci are genetically unlinked but may interact epistatically. This approach allows one to build models under complex scenarios of selection without invoking the assumption of independence, yet it maintains the ability to work with a stationary distribution. The result of Fearnhead [11] also provides a basis for development of new methods for making inference on the strength of selection in such models.

In this paper, we make use of Fearnhead’s general result on selection to build a class of multi-locus allele-based balancing selection models. Our main focus is on developing methods for estimating the strength of within-locus balancing selection, where allelic combinations at all loci determine the selective advantage of a multi-locus genotype through epistatic interactions. We begin by reviewing important features of the single-locus case. We then present our multi-locus balancing selection model, with a special emphasis on incorporating two types of epistasis into the model. A technical difficulty associated with our multi-locus model is the evaluation of the joint likelihood of the allele frequencies. This difficulty arises from complicated normalizing constants. We develop numerical and Monte Carlo methods to approximate these constants, giving us the ability to evaluate the likelihoods. In conjunction with an approximate rejection algorithm, our methods make it possible to simulate population frequencies under the model. Inference about the posterior distribution of the selection parameter is carried out via MCMC, and we assess support for different types of epistatic models using Bayes factors. Model behavior under different types of epistasis with varying strengths of selection and numbers of loci in the multi-locus group is studied by simulations. We also present the motivating biological problem for developing the methods presented in this paper: the estimation of the strength of balancing selection in a group of loci from the human immune system. In particular, we consider allele-level interactions between human leukocyte antigen (HLA) and killer-cell immunoglobulin-like receptor (KIR) gene families. We analyze a real data set to investigate whether observed allele frequencies provide evidence that HLA-A and HLA-B, essential loci in an adaptive immune response (adaptive in the immunological sense, not in the sense of natural selection), interact epistatically with KIR, a part of the innate immune system. We conclude with a short discussion on the limitations of the model.

2. Theory and setup

2.1. Single-locus case

Before proceeding with the details of the multi-locus model, we first describe symmetric balancing selection in the context of a Wright-Fisher population at a single-locus, and we emphasize some complications in extending models of balancing selection to multi-locus genotypes.

We use an abstract (and somewhat unorthodox) way of describing balancing selection as a characteristic allele frequency pattern arising through any mechanism in which variability is favored (see [31] and references therein). Examples of mechanisms that produce balancing selection include negative frequency dependence, overdominance, and types of environmental heterogeneity that lead to frequency dependence in a model with multiple niches [19]. For each of these mechanisms, balancing selection results when on average, diploid genotypes possessing a variability-promoting property possess a fitness advantage. In negative frequency dependence, we expect genotypes at low frequencies to have higher fitness relative to others in a population. Overdominance occurs when heterozygotes have higher fitness than homozygotes. For a single population, if a heterogeneous environment affects the fitness regime, so that certain genotypes are favored in some sub-environments whereas other genotypes are favored elsewhere, a balancing selection pattern can be produced in the overall environment as a result of competing selection pressures at sub-environment boundaries. Common to all of these mechanisms is promotion of genetic diversity, resulting in a balancing selection pattern in allele frequency data.

In a Wright-Fisher population possessing this variability-promoting property, an equilibrium allele frequency distribution is eventually reached. In theory, if there are k distinct allelic types in the population, it is possible to assign a selection coefficient to each of the resulting k(k + 1)/2 distinct diploid single-locus genotypes. However, the resulting equilibrium distribution will be overparameterized in such a model, since there are only k allele frequencies. To prevent overparameterization, we consider a symmetric balancing selection model of two allelic classes, as given in equation 1 below. For example, considering a heterozygote advantage scenario, equation 1 is obtained as follows [36, 35, 7]. Consider a population of N diploid individuals (2N total alleles) and k distinct allelic types, reproducing in non-overlapping generations. In each generation, 2N pairs are sampled independently from the population of existing genes. The probability of sampling a particular heterozygous diploid genotype is proportional to 1 + s (s > 0), and the probability of sampling a homozygous diploid genotype is proportional to 1. One allele is randomly sampled from the chosen pair, subjected to mutation (to one of the types, including mutation to the same type, all with equal probability) with total probability u, and the resulting allele is added to the next generation. Thus, a total of 2N alleles are added to the next generation.

If we denote the allele frequencies by [x₁, …, x_k] and set σ = 2Ns and θ = 4Nu, then the stationary distribution of the allele frequencies is given by

$$f\left(\right[x_1,\dots ,x_k]\mid \theta ,\sigma )=\frac{e^{-\sigma }\sum _{i=1}^k{x}_i^2\prod _{i=1}^k{x}_i^{(\frac{\theta }{k}-1)}}{c(\theta ,\sigma )},$$ (1)

where ${\sum }_{i=1}^k{x}_i=1$, x_i > 0, and c(θ, σ) is a normalizing constant [36, 35]. The parameters θ and σ represent the population-scaled mutation rate and the intensity (or strength) of selection, respectively. Note that in the inference methods developed later in this paper, estimates of σ can assume negative values, but that under heterozygote advantage, the parametric value of σ is positive.

The model in equation 1 captures selective differences between a favored combination of alleles and a disfavored one at a single locus (e.g., heterozygotes vs. homozygotes). The selective difference is parameterized by assigning a positive selection parameter, σ, to a variability-promoting genotype and zero to other genotypes. Estimating σ then provides information about the intensity of selection between these two genotypic classes.

In the description of the single-locus model leading to equation 1, no particular mechanism leading to a balancing selection pattern was specified. In some mechanisms leading to a balancing selection pattern, however, the assignment of a selection coefficient to a genotype is intrinsically a function of the pair of alleles at the locus. These cases, such as heterozygote advantage, require additional assumptions in a multi-locus setting. By definition, heterozygote advantage is a within-locus concept. If it is the mechanism leading to balancing selection, then the contribution of each locus to the overall selective advantage of the multi-locus genotype must be explicitly specified. The approach we take for linking within-locus selective advantages of heterozygotes to the selective advantage of a multi-locus genotype is to use a function governing the epistatic interactions among loci. Our methods do not depend on the functional form chosen. For greater generality, throughout this paper we focus on the scenario in which the selection coefficient is a function of the pair of alleles at a locus rather than a function in which the two alleles at a locus contribute separately.

2.2. The distribution of allele frequencies

We start by presenting the stationary distribution of the allele frequencies for a multi-locus genotype under selection. For m diploid loci, denote the frequencies of the k_i distinct alleles at the i^th locus by x_i = [x_1i, x_2i, …, x_kiⁱ] and the set of frequencies from all m loci by the array x = [x₁, …, x_m]. For simplicity, we assume that the selection coefficients are equal at all loci (but see Buzbas et al. [4] for a non-epistatic model in which this assumption is relaxed). Analogously to the single-locus case, let σ = 2Ns and θ_i = 4Nu_i. That is, we allow mutation parameters to vary across loci, but we use a common selection parameter for every locus. As a special case of the result of Fearnhead [11], we can obtain

$$f(\mathbf{x}\mid \theta ,\sigma )=\frac{e^{\stackrel{‒}{\sigma }\left(\mathbf{x}\right)}\prod _{i=1}^m{G}_i}{c(\theta ,\sigma )}.$$ (2)

Here, c(θ, σ) is a normalizing constant, and for notational convenience we let $G_i={\prod }_{j=1}^{k_i}{x}_{ji}^{(\frac{{\theta }_i}{k_i}-1)}=1$ and θ = [θ₁, …, θ_m]. The mean selection intensity, denoted by $\stackrel{‒}{\sigma }\left(\mathbf{x}\right)$, will be described shortly.

We examine the distribution in equation 2 in three parts. The first part, given by ${\prod }_{i=1}^m{G}_i$, poses no real difficulty in numerically computing f(x∣θ, σ), because it is the product of single-locus components [11]. The second part is the constant, c(θ, σ), which is defined as a (k₁ × … × k_m)-dimensional integral and requires substantial computation to obtain. We deal with this computation in a separate subsection below. The third part, $e^{\stackrel{‒}{\sigma }\left(\mathbf{x}\right)}$, is a function of the mean selection intensity, $\stackrel{‒}{\sigma }\left(\mathbf{x}\right)$, over all possible genotypes. This quantity, which we describe below in equation 3, is important in defining the type of epistasis. Using a multi-locus Wright-Fisher model, we can obtain all three parts of equation 2, allowing us to evaluate the stationary distribution.

Below we build a multi-locus Wright-Fisher population with balancing selection. The transmission from one generation to the next is described in terms of a population of multi-locus haplotypes, analogously to a transmission of genes in a single-locus Wright-Fisher population. However, this use of a population of haplotypes is purely for convenience. It can be shown that exactly the same model is obtained by keeping track of allele populations separately for each locus and simultaneously drawing pairs of alleles at all loci to build a multi-locus genotype, instead of drawing a pair of haplotypes.

The transmission from one generation to the next is as follows. To form an m-locus haplotype, at each locus, we sample two genes at random with replacement, such that the probability of sampling a particular multi-locus genotype is a function of three factors:

1. The within-locus selective advantage of heterozygotes over homozygotes, represented by the parameter $\frac{\sigma }{2N}=s$.

2. The total number of homozygotes in the genotype, $L={\sum }_{i=1}^m{H}_i$, where for the i^th locus we define H_i = 1 if a genotype is homozygous and H_i = 0 otherwise.

3. A decreasing function in L, denoted by g(σ, L), linking factors 1 and 2 by specifying the type of epistasis. This function satisfies boundary conditions g(σ, m) = −σm and g(σ, 0) = 0.

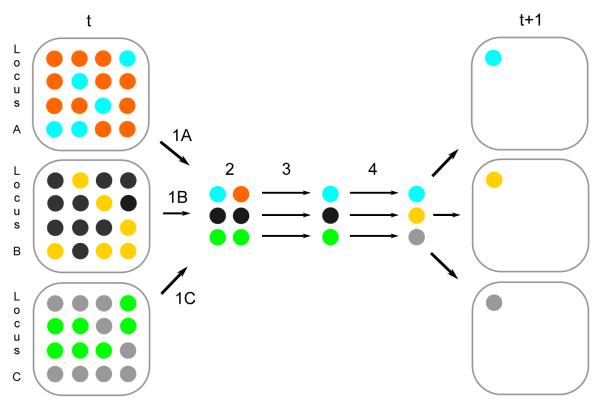
After sampling a diploid multi-locus genotype, we choose randomly (with equal probability) one of the alleles at each locus to build a new m-locus haplotype, subject each allele to mutation, independently with a locus-specific probability, so that the probability of mutating to a specific type (including mutation to the same type) is u_i/k_i. The resulting haplotype is then added to the next generation (see figure .1).

Figure .1.

A transmission in a 3-locus Wright-Fisher model with symmetric balancing selection and epistasis between loci from generation t to t + 1. Each population has two distinct alleles. The population of alleles at a locus is denoted by colored balls within a square. In Steps 1A, 1B, and 1C, single-locus genotypes are sampled, with heterozygotes having a selective advantage s = σ/(2N) over homozygotes. In step 2, the 3-locus genotype is assigned a fitness by epistatic function g(2Ns, L), where L is the number of homozygotes (2 in this case shown, from loci B and C). In step 3, an allele is randomly sampled with equal probability within each locus, independent of other loci (gamete formation). In step 4, the chosen allele is subjected to mutation at each locus, with locus-specific mutation rate u_i/k_i where u_i = θ_i/(4N). In this example, there are two mutational events (at locus B from black to yellow and at locus C from green to gray). The fitness of the 3-locus genotype in step 2 would be that of a one heterozygote (cyan-orange) and two homozygotes (black-black and green-green) if the loci were independent. If there is epistasis, depending on the form of function g, the fitness will be lower of higher.

The assumptions on the probability of sampling a multi-locus genotype can be described as follows. The first assumption states that regardless of the specific homozygous allelic type and the locus at which it is found, a homozygote has the same disadvantage with respect to a heterozygote. In other words, the within-locus symmetric heterozygote advantage that we considered in the single-locus case is preserved in this model. The second assumption extends the heterozygote advantage to a multi-locus genotype by specifying that the loci contribute to the overall fitness only through the total number of homozygous loci, L. Statistically this means that the loci are exchangeable. The third assumption guarantees that the function, g, describing the effect on fitness of homozygotes is decreasing in the number of homozygotes. Further, through the function g, it specifies the relationship between the type of epistasis and the rate of decrease in fitness. The boundary conditions imposed on g in the third assumption codify two desirable properties of g: two multi-locus genotypes containing no homozygotes are forced to be equivalent in terms of fitness, and genotypes with all loci homozygous are also equivalent, irrespective of whether the model incorporates epistasis. Finally, we define the mean selection intensity over all possible distinct genotypes as

$$\stackrel{‒}{\sigma }\left(\mathbf{x}\right)=\sum _{\ell =0}^{m}g(\sigma ,\ell )P[L=\ell \mid \mathbf{x}]=E\left[g\right(\sigma ,L)\mid \mathbf{x}],$$ (3)

where P[L = ℓ|x] is the probability of having exactly ℓ homozygous loci in the genotype (0 ≤ ℓ ≤ m). The effect of the epistasis function g on fitness and its relationship to the type of epistasis are described below.

2.3. Epistasis

Suppose we set g(σ, L) = −σL, a linear decrease in fitness with an increasing number of homozygous genotypes. Using equation 3 and assumption 2, we obtain

$$\stackrel{‒}{\sigma }\left(\mathbf{x}\right)=-\sigma \sum _{\ell =0}^m\ell P[L=\ell \mid \mathbf{x}]=E[-\sigma L\mid \mathbf{x}]$$ (4)

$$=-\sigma E\left[\sum _{i=1}^m{H}_i\mid \mathbf{x}\right]=-\sigma \sum _{i=1}^{m}E[H_i\mid \mathbf{x}]$$ (5)

$$=-\sigma \sum _{i=1}^m\sum _{j=1}^{k_i}{x}_{ji}^2.$$ (6)

Substituting the last quantity for $\stackrel{‒}{\sigma }\left(\mathbf{x}\right)$ into equation 2, the joint stationary probability density of the allele frequencies at the set of m loci can be expressed as a product of the single-locus marginal densities,

$$f(\mathbf{x}\mid \theta ,\sigma )=\prod _{i=1}^m\frac{e^{-\sigma \sum _{j=1}^{k_i}{x}_{ji}^2}\prod _{j=1}^{k_i}{x}_{ji}^{(\frac{{\theta }_i}{k_i}-1)}}{c({\theta }_i,\sigma )}.$$ (7)

Hence, a linear decrease in fitness with an increasing number of homozygotes in the genotype implies that allele frequencies are mutually independent among loci. Thus, in the linear case, epistatic interactions are absent. Further, the absolute value of the slope of the line, σ, gives the within-locus intensity of selection.

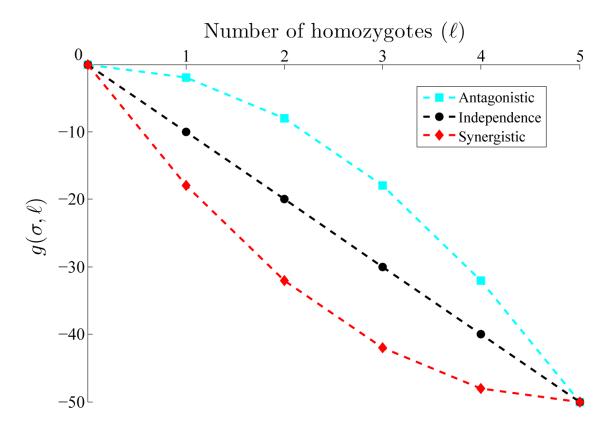
Based on these observations, we now define our epistatic models. We deal with three qualitatively distinct models: antagonistic epistasis, independence, and synergistic epistasis. Epistasis is antagonistic when each additional homozygote in the genotype decreases fitness less than would be expected in the linear case. In contrast, it is synergistic when the fitness decrease is greater than in the linear case. We refer to various quantities under the three models using the subscripts “ant”, “ind”, and “syn” respectively. When it is not necessary to distinguish between the two types of epistasis, the subscript “epi” is used to denote a generic epistatic model. Using this new notation, for example, our conclusion that a linear decrease implies independence allows us to write g_ind(σ, L) = −σL (Figure .2).

Figure .2.

Epistasis as a function of the number of homozygotes, ℓ, in a multi-locus genotype (m = 5, σ = 10). The plot shows linear and quadratic forms of the function g(σ, ℓ), describing epistasis corresponding to antagonistic interaction (cyan), independence (black) and synergistic interaction (red).

The equivalence between linear decrease and independence implies that g must be non-linear under epistasis. For illustrative purposes, we consider a quadratic form for g. However, our inference methods are general and other forms can be easily accommodated. For antagonistic epistasis, we define

$$g_{\mathrm{ant}}(\sigma ,L)=-\frac{\sigma }{m}{L}^2,$$ (8)

whereas for synergistic epistasis, we assume symmetry of g_ant(σ, L) with respect to a midpoint at g_ind(σ, L) to get

$$g_{\mathrm{syn}}(\sigma ,L)=+\frac{\sigma }{m}{L}^2-2\sigma L.$$ (9)

Models of heterozygote advantage will produce excess heterozygosity in the population with respect to what is expected under neutrality. The different epistatic models will produce different amounts of excess heterozygosity, generating different patterns in allele frequencies. On average, for a fixed σ, the synergistic model produces more excess heterozygosity in comparison to the linear model, which in turn produces more excess heterozygosity with respect to the antagonistic model. The intuition is that multi-locus genotypes carrying more homozygous loci are penalized more severely under the synergistic model in comparison to the antagonistic model, thereby inflating the probability that a genotype will be heterozygous.

3. Inference Methods

In this section, we present Bayesian methods to make inference from a model obeying equation 2 under a generic epistatic form (using notation “epi”). In practice, there is an additional source of variability in the observed allele frequencies due to sampling from the model, and therefore, the form of the sampling likelihood differs from the likelihood based on equation 2. For the single-locus case, this sampling likelihood can be written as a function of ratio of two integration constants (see [7]). For inferential purposes, however, there are at least two practical reasons for not considering the actual sampling likelihood. First, we have previously established that the variability due to sampling is negligible compared to the variability introduced by the evolutionary process, unless the sample size is small [3]. Second, because it involves a ratio of two approximated multi-dimensional integration constants, the sampling likelihood is subject to numerical instabilities, the effects of which are difficult to assess. For these reasons, we assume that the observed allele frequencies are good approximations to the population frequencies and proceed with the model likelihood based on equation 2.

In the next two subsections, we build the machinery necessary to evaluate the joint likelihood of allele frequencies under epistasis. First, we describe how to approximate the normalizing constant of the multi-locus model (equation 2). We briefly review the numerical integration method that solves the problem in the single-locus case and that enables us to generate allele frequencies under the single-locus balancing selection model [12]. We then state the problem in the multi-locus case and describe how single-locus methods can be combined with Monte Carlo integration to obtain an approximation for the constant. This approximation by naive Monte Carlo integration turns out to be inaccurate. We explain the reasons for this inaccuracy and then present a modified Monte Carlo approach that produces accurate results. We describe a rejection method (see Ripley [28]) to generate approximate multi-locus allele frequencies under epistasis. This method allows us to use simulations to study the behavior of the model. Methods for estimating the strength of selection and for performing model selection under epistasis appear in the last two subsections.

3.1. Approximating the normalizing constant

A technical problem in evaluating the likelihood function in equation 2 is calculating the normalizing constant. For the multi-locus model, under independence we have

$$f(\mathbf{x}\mid \theta ,{\sigma }_{\mathrm{ind}})=\prod _{i=1}^{m}f({\mathbf{x}}_i\mid {\theta }_i,{\sigma }_{\mathrm{ind}})=\frac{e^{{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\prod _{i=1}^m{G}_i}{\prod _{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})},$$ (10)

where c(θ_i, σ_ind) is the normalizing constant for the i^th locus. The numerical methods of Genz and Joyce [12] make it possible to calculate the multi-locus constant ${\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$ by breaking the constant for the i^th locus,

$$c({\theta }_i,{\sigma }_{\mathrm{ind}})={\int }_0^1{\int }_0^{1-x_{k_{i}i}}\cdots {\int }_0^{1-(x_{2i}+\cdots +x_{k_{i}i})}{e}^{-\sigma \sum _{j=1}^{k_i}{x}_{ji}^2}{G}_{i}d{x}_{1i}\dots d{x}_{k_{i}i},$$ (11)

into a series of iteratively defined one-dimensional integrals. However, in the epistatic case, these numerical methods are not directly applicable to constants in equation 2,

$$c_{\mathrm{epi}}(\theta ,{\sigma }_{\mathrm{epi}})\int \cdots \int e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)}\prod _{i=1}^m{G}_{i}d{\mathbf{x}}_1\dots d{\mathbf{x}}_m,$$ (12)

due to considerably more complicated integrands. Here, the integration is over the allele frequency space of all m loci, and for each locus, the limits of integration are as in equation 11.

Below we will show that equation 12 can be treated in an importance sampling framework and can be written as a weighted function of the constant under independence, ${\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$. First, we note that by the definition given in equation 3 for the independence model,

$${\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)=\sum _{\ell =0}{g}_{\mathrm{ind}}({\sigma }_{\mathrm{ind}},\ell )P[L=\ell \mid \mathbf{x}],$$

where g_ind(σ_ind, L) = −σ_indL is linear in the number of homozygotes in the multi-locus genotype, L. Here, σ_ind is an arbitrary value of the selection parameter. (Our insistence on keeping distinct subscripts for the selection parameters in the independence and epistatic models will become clear below.) Multiplying and dividing the right-hand side of equation 12 by $e^{{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}{\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$ and rearranging, we get

$$\begin{array}{cc}\hfill c_{\mathrm{epi}}(\theta ,{\sigma }_{\mathrm{epi}})=& \int \cdots \int \left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}\left(\mathbf{x}\right)}}\prod _{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})\right]\frac{e^{{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\prod _{i=1}^m{G}_i}{\prod _{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})}d{\mathbf{x}}_1\dots d{\mathbf{x}}_m\hfill \\ \hfill =& \prod _{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right],\hfill \end{array}$$ (13)

where E(·) is the expectation with respect to the joint stationary probability density of the allele frequencies under independence (i.e., equation 10). An obvious Monte Carlo estimator for the expectation part in equation 13 is

$$\frac{1}{n}\sum _{j=1}^n{e}^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)},$$ (14)

where n is the number of Monte Carlo samples. The approximation is valid for large n, with allele frequencies generated from the density in equation 10. Therefore, using equation 14 and numerical methods devised for the single-locus case, we can approximate c_epi(θ, σ_epi), at least in theory.

Unfortunately, a standard implementation of equation 14 with an arbitrary value of σ_ind does not produce accurate estimates. An intuitive explanation is that when the allele frequency distribution under epistasis is substantially different from the distribution under independence, the difference between the term ${\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$ on the right-hand side of equation 13 and c_epi(θ, σ_epi), the desired quantity on the left-hand side, is quite large. Consequently, in order to have a good approximation of c_epi(θ, σ_epi), the expectation (the second term on the right in equation 13) must be accurate in adjusting ${\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$. However, this expectation, estimated by equation 14, is itself inaccurate unless the number of samples generated is astronomical, precisely due to the difference between the epistatic and independence models. That is, when the epistatic model does not resemble the model under independence, we need to generate a large number of allele frequency sets for the estimate in equation 14 to closely approximate the true expectation. Hence, a naive Monte Carlo estimator does not produce reliable estimates of c_epi(θ, σ_epi). Our innovation to solve this problem is to implement an algorithm in which the value of σ_ind used to generate the allele frequencies under the independence model is chosen carefully to minimize the effect of the expectation $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]$ in calculating c_epi(θ, σ_epi). Briefly, σ_epi is chosen such that $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]\approx 1$, and hence, by equation 13, $c_{\mathrm{epi}}(\theta ,{\sigma }_{\mathrm{epi}})\approx {\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$. This approach allows us to produce accurate Monte Carlo estimates by keeping the Monte Carlo variance small. Details are given in Appendix A.

In summary, based on techniques more fully described in Appendix A, we first find a suitable value for σ_ind. To compute the constant of the i^th single-locus density, c(θ_i, σ_ind), we then use the numerical integration methods of Genz and Joyce [12], using a common selection parameter σ_ind, locus-specific mutation parameters θ_i, and numbers of alleles k_i. Using an inverse sampling method as described in Genz and Joyce [12] and the single-locus constants under independence, we generate n sets of allele frequencies from each single-locus density, producing n sets of frequencies under the multilocus independence model. Conditional on these sets of frequencies, we then compute an adjusted Monte Carlo estimate to obtain the multi-locus constant under epistasis by implementing equation 14.

3.2. Generating approximate samples under epistasis

A general requirement for examining the behavior of epistatic models is the ability to simulate allele frequencies under these models. To generate multi-locus allele frequencies from an epistatic model, we implement a modified rejection algorithm (details given in Appendix B) that utilizes the stochastic methods of the previous section. The efficiency of a rejection algorithm depends on choosing a proposal distribution and finding an upper bound on the ratio of target distribution to proposal distribution. First, we discuss the proposal distribution for our case.

In the rejection algorithm, random variates generated from a proposal distribution are accepted according to a probabilistic rule that guarantees that accepted values come from the distribution of interest. The proposal distribution has to be chosen carefully because if it mimics the target distribution of interest poorly, the number of values that must be proposed before accepting a sample is large, and the algorithm is computationally inefficient. In our case, we aim to generate allele frequencies x from the distribution of a multi-locus epistatic model, a distribution that has the general form in equation 2. A natural candidate family for a proposal distribution is the family of joint distributions of allele frequencies under independence given in equation 10. However, if we set σ_ind = σ_epi, the distribution under independence is very inefficient. We circumvent this problem by following the optimization given in Appendix A to determine an optimal distribution. That is, given σ_epi, we use the joint distribution under independence that has the optimal σ_ind as a proposal distribution to generate allele frequencies from an epistatic model with selection parameter σ_epi. A multi-locus allele frequency array x is proposed from the distribution in equation 10 with an optimal σ_ind, such that $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]\approx 1$. This choice contributes to the efficiency of the algorithm.

Now we turn to the upper bound on the ratio of the target and proposal distributions. This bound, which is required for rejection algorithms, is based on maximizing the ratio

$$\frac{f(\mathbf{x}\mid \theta ,{\sigma }_{\mathrm{epi}})}{f(\mathbf{x}\mid \theta ,{\sigma }_{\mathrm{ind}})}.$$ (15)

Unfortunately, the theoretical supremum on this ratio turns out to be large, making the rejection method impractical (see Appendix B). As an alternative, we substitute the theoretical bound by a (much lower) empirical maximum, B_n, from n = 10⁶ data sets simulated under independence. This approach has similarities to the empirical supremum rejection sampling method of Caffo et al. [5]. Appendix B gives an algorithm to generate an approximate sample from an epistatic interaction model with parameters θ = [θ₁, …, θ_m], σ_epi, and k = [k₁, …, k_m].

3.3. Parameter estimation

By Bayes’ theorem, we write the joint posterior distribution of the parameter vector (θ, σ) as

$$\pi (\theta ,\sigma \mid \mathbf{x})=\frac{f(\mathbf{x}\mid \theta ,\sigma )\pi (\theta ,\sigma )}{f\left(\mathbf{x}\right)},$$ (16)

where f(x∣θ, σ) is the likelihood in equation 2 and π(θ, σ) is the joint prior distribution of the parameters. We assume the prior independence of the parameters, π(θ, σ) = π(θ)π(σ), and use a diffuse uniform prior on the selection parameter, σ ~ Unif(−σ_max, σ_max), where σ_max is a fixed value chosen sufficiently large that it covers plausible values of the selection parameter. For all the analyses in this paper, we have chosen σ_max = 300. Informed prior distributions for each θ_i are obtained using only the neutral variation at each locus (i.e., synonymous mutations) and the stationary distribution of the allele frequencies under neutrality. Details on this approach to the mutation parameters, as well as the advantages of using an informative prior on the mutation parameter in Wright-Fisher models with balancing selection, appear in Buzbas et al. [4].

We sample the joint posterior distribution, π(θ, σ∣x), using Markov chain Monte Carlo (MCMC) with a componentwise Metropolis-Hastings approach for updating the parameters (Appendix C). The computational bottleneck of this algorithm is in evaluating the normalizing constant c_epi(θ, σ_epi) for given values of θ and σ_epi. In particular, an estimate of c_epi(θ, σ_epi) is required at each iteration, resulting in an evaluation of $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]$.

3.4. Support for epistatic models

We assess the support for a particular type of epistatic interaction model using Bayes factors. The case of antagonistic versus synergistic epistasis is formulated below, with a straightforward extension to any two epistatic models, including those having the same type of epistasis but different forms for the epistasis function g. Antagonistic and synergistic models will differ in the form of the function g, which is a part of the joint probability density, f, through ${\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)$. Setting the hypotheses, H_ant : g_ant(·, ℓ) and H_syn : g_syn(·, ℓ), for antagonistic and synergistic models respectively, the relevant Bayes factor, B_ant/syn, is given by

$$B_{\mathrm{ant}∕\mathrm{syn}}=\frac{P(\mathbf{x}\mid g_{\mathrm{int}}(\cdot ,\ell \left)\right)}{P(\mathbf{x}\mid g_{\mathrm{syn}}(\cdot ,\ell \left)\right)}=\frac{\int \cdots \int f(\mathbf{x}\mid \theta ,g_{\mathrm{ant}}(\sigma ,\ell \left)\right)d\theta d\sigma }{\int \cdots \int f(\mathbf{x}\mid \theta ,g_{\mathrm{syn}}(\sigma ,\ell \left)\right)d\theta d\sigma }.$$ (17)

Calculating B_ant/syn requires integrating out the nuisance parameters (θ, σ). We approximate the integrals given in equation 17 using the harmonic mean estimator [25, 18]. Thus, for example,

$$\widehat{P}(\mathbf{x}\mid g_{\mathrm{ant}}(\sigma ,\ell \left)\right)\propto {\left(\frac{1}{n}\sum _{i=1}^{n}f{(\mathbf{x}\mid {\theta }_{\mathrm{ant}}^{\left(i\right)},{\sigma }_{\mathrm{ant}}^{\left(i\right)})}^{-1}\right)}^{-1}$$ (18)

where $({\theta }_{\mathrm{ant}}^{\left(i\right)},{\sigma }_{\mathrm{ant}}^{\left(i\right)})$, are posterior samples obtained under the hypothesis g_ant(·, ℓ) by MCMC (i.e., by the algorithm given in Appendix C). The desired Bayes factor, then, is estimated by

$${\widehat{B}}_{\mathrm{ant}∕\mathrm{syn}}=\frac{\sum _{i=1}^{n}f{(\mathbf{x}\mid {\theta }_{\mathrm{syn}}^{\left(i\right)},g_{\mathrm{syn}}({\sigma }_{\mathrm{syn}}^{\left(i\right)},\ell \left)\right)}^{-1}}{\sum _{i=1}^{n}f{(\mathbf{x}\mid {\theta }_{\mathrm{ant}}^{\left(i\right)},g_{\mathrm{ant}}({\sigma }_{\mathrm{ant}}^{\left(i\right)},\ell \left)\right)}^{-1}},$$ (19)

where the values in the numerator are sampled under the synergistic model and those in denominator are sampled under the antagonistic model.

4. Simulations

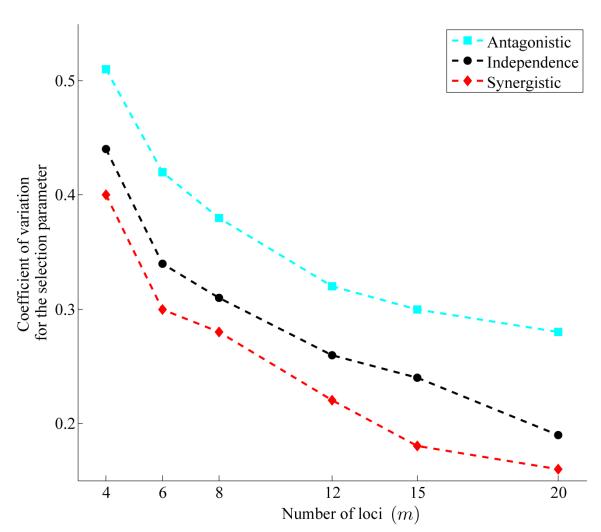
We present results from simulations under fixed locus-specific mutation parameters θ_i = 3 for each locus and k_i = 5 alleles at each locus (i = 1, 2, …, m), using the data generation methods given in Generating approximate samples under epistasis. Posterior samples are summarized for each of three models (antagonistic, independent and synergistic) for data generated under σ = {3, 12, 27, 50, 80} and m = 4. These summaries utilize the 95% highest posterior density (HPD) region by averaging the intervals obtained in 30 independent replicates, holding σ constant (Table 1). We also calculated the coefficient of variation of the selection parameter (i.e., the ratio of the sample standard deviation to the sample mean) for each posterior sample at m = {4, 6, 8, 12, 15, 20}, again using the mean coefficient of variation over 30 independent simulation replicates (the case for σ = 27 is shown in Figure .3). In the rest of this subsection we offer interpretations of the simulation results to develop intuition about the behavior of the epistatic models.

Table. 1.

95% highest posterior density intervals for σ using simulated data for a range of σ, with fixed θ_i = 3, k_i = 5 and m = 4. Each result is an average of 30 replicates.

Model	σ
	3	12	27	50	80
Antagonistic	(−4.4,23.2)	(0.6,35.5)	(8.4,80.1)	(18.0,109.2)	(45.0,172.7)
Independence	(−4.8,17.2)	(1.3,32)	(9.8,64.2)	(20.2,95.2)	(49.9,162.0)
Synergistic	(−4.5,13.4)	(1.6,31)	(9.7,53.6)	(26.5,100.9)	(50.4,161.6)

Figure .3.

Estimated coefficients of variation (the ratio of the standard deviation of the selection parameter estimates to their mean) for three models: antagonistic (cyan), independence (black) and synergistic (red). The parameters of the simulation are σ = 27, θ_i = 3, and k_i = 5 for m = {4, 6, 8, 12, 15, 20}.

A relatively large amount of uncertainty about the selection parameter is common to all three models (HPD regions in Table 1). This large variability is attributable to two sources: The first is correlation between the estimated mean and variance of the selection intensity, leading to less precision, in particular with stronger selection (Table 1 across columns). The second is the small number of loci in the multi-locus group (recall that the results in Table 1 are for m = 4). Increasing the number of loci has a sizeable effect on decreasing the variance in σ (Figure .3). Implications of this fact depend on the use of the method. If the goal is to search for signals of balancing selection along the genome, tight interval estimates for the selection parameter might be obtained by incorporating many loci in the analysis. However, when the investigation of balancing selection at a particular biological system is of interest, the number of loci in the system will be constrained a priori and will probably be small. In such cases, there will be a limit on the precision attainable for σ. The example we consider below in a real system with relatively few loci also demonstrates this point.

The large variability in the posterior sample notwithstanding, balancing selection is detectable under our model, even when the selection strength is weak (e.g., σ = 12 with θ = 3). Although when the effective population size, N, is unknown, the compound parameter σ = 2Ns does not permit direct estimation of the selection coefficient, s, the magnitude of plausible s can be obtained if the simulation is taken to represent human populations. If we assume N is on the order of 10⁴, then the mean 95% HPD regions for σ = 12 under the antagonistic and synergistic models in Table 1 correspond to intervals (0.3 × 10⁻⁴, 17.7 × 10⁻⁴) and (0.8 × 10⁻⁴, 15.5 × 10⁻⁴) for s, respectively.

For a given data set generated under balancing selection, the estimates of the strength of selection under the three different models are expected to be ordered: ${\widehat{\sigma }}_{\mathrm{ant}}>{\widehat{\sigma }}_{\mathrm{ind}}>{\widehat{\sigma }}_{\mathrm{syn}}$. In other words, a balancing selection model in which the effect of the first few homozygotes on the fitness is small (e.g., antagonistic) is expected to produce stronger estimates of selection than its alternative (e.g., synergistic), to be able to explain a given amount of variability. The intuition behind this result lies in recognizing that among the three models considered, in terms of their functional forms, the antagonistic model is the “closest” model to neutrality. This implies that to explain a given amount of variability in the data, its selection parameter, σ_ant, must be the largest. Imagine for example a model of balancing selection with an epistasis function g(σ, ℓ) ≈ 0 for all ℓ, so that the model is very similar to the neutral model. To be able to explain high variability in a given data set under balancing selection, such a model would require a very large σ because only if the selection is very strong will data with high variability have an appreciable likelihood under the model.

5. Application to data

As an application of the epistatic model, in this section we focus on balancing selection in interacting gene complexes of the human immune system. Several independent lines of evidence have suggested that gene families of the immune system experience balancing selection [15, 6, 23, 26, 16]. More recently, the existence of epistatic interactions between immunological gene families has been established [14, 32, 33, 34]. The following (necessarily simplistic) description captures the biological essentials relevant to our model. We point out that our goal is not to make any mechanistic claim about the biology of the system, but rather to demonstrate the utility of our methods in investigating population-level polymorphism data in immune system loci.

Launching a full-scale immune response, say against a pathogenic agent, requires activating both parts of the immune system: the innate component, which invokes a generic first response, and the adaptive component, which can respond to specific pathogens. Mechanisms exist by which these two parts of the immune system interact. For example, they may cooperate to perform a specific task, guaranteeing a well-coordinated immune response. Interaction exerted at the protein level relies on reciprocal recognition of specific molecular agents of both systems, facilitated by the “uniqueness” of these agents. From a population genetics perspective, single-locus estimates of the intensity of selection are somewhat unsatisfactory in such a system, because of the interactions between the parts. Our epistatic model is designed to address this problem of single-locus estimates in this system.

As an example, we consider two well-known interacting gene groups: killer-cell immunoglobulin like receptors (KIR) and human leukocyte antigen (HLA) loci. KIR are specialized receptors on natural killer (NK) cells, whose job is to destroy pathogen-infected cells. KIR are encoded by 17 genes, found on chromosome 19 of the human genome (see Vilches and Parham [34] for a review). A cell on which KIR act is a target cell, which may or may not be infected. In the presence of a target cell, KIR bind ligands presented on the target cell, and the message provided by these ligands is conveyed to NK cells. If an activating ligand is bound, NK cells kill the target cell, whereas if an inhibiting ligand is bound, the target cell is spared. KIR genes constitute the first gene family of the interacting system in which we are interested.

The second family is HLA Class I genes. Found on chromosome 6, this family contains three major genes of the adaptive immune system (see Parham and Ohta [27] for a review). HLA Class I molecules are expressed on the surfaces of all normal (uninfected) cells, but their expression is down-regulated in cells infected with pathogens.

For an effective immune response, interactions between KIR and HLA Class I genes are essential, due to the fact that the ligands to which KIR bind are HLA Class I molecules [13, 20, 21]. Recent evidence suggests that molecular products coded by specific HLA Class I alleles can cooperate only with certain products coded by specific KIR alleles [14, 32, 33, 34]. Although the nature of these interactions ultimately can be investigated with advances in molecular techniques, the specifics, particularly the consequences of these interactions for population-level polymorphism, currently remain unknown. Considering that heterozygotes of both gene families confer an advantage in performing a function within the balancing selection framework, here we assume that the number of heterozygous genotypes at a multi-locus HLA-KIR genotype gives a reasonable signal for between-locus interactions. We implement our model for the KIR-HLA system to investigate the plausibility of antagonistic and synergistic balancing selection models, based on evidence provided by population-level polymorphism data.

We consider allele frequencies at two major HLA Class I loci: A and B. We group the alleles into supertypes, classes of alleles whose protein products are known to share structural and functional similarities, such as epitope binding pockets. There are four well-identified HLA-A supertypes: A1, A2, A3 and A24, and five HLA-B supertypes: B7, B27, B44, B58 and B62 [30]. At each locus, the genotype of a diploid individual is represented by two supertypes corresponding to two alleles at that locus. In contrast to the variability in HLA, the variability in the KIR system is less well-understood and more challenging to classify. For example, certain KIR loci have perfect positive or negative linkage, and haplotypes can vary in gene content. Partly for these reasons, a common practice in KIR genetics is to classify the multilocus genotype by considering each haplotype as an allelic variant in the same way that one treats alleles at a single locus. In particular, we consider two well-identified haplotypic forms, known as A and Bx.

Our example uses previously reported HLA and KIR data on a Portuguese population [24] (Table 2). The data consist of allelic types and their frequencies for HLA and KIR loci at a population level. We have chosen the Portuguese data set for its suitability to be classified into the HLA and KIR allelic groups described above. We have excluded several rare HLA alleles that do not fall into the supertype groups and have renormalized the frequencies. Our simulations suggest that missing rare alleles have little effect on estimating the strength of balancing selection under the Wright-Fisher model (data not shown).

Table. 2.

HLA and KIR data for a Portuguese population (based on frequencies downloaded from www.allelefrequencies.net [24]). The numbers of alleles for the HLA loci are based on supertypes, as defined by Sette and Sidney [30]. For KIR, common haplotypes A and Bx are used (see e.g., Yoo et al. [37]). Het_obs is the observed heterozygosity and Het_max is the theoretical maximum heterozygosity at a locus with k distinct alleles.

Locus	Alleles	Frequencies	Hetobs	Hetmax
HLA-A	4	[0.171, 0.319, 0.315, 0.193]	0.731	0.75
HLA-B	5	[0.316, 0.150, 0.414, 0.041, 0.077]	0.698	0.80
KIR	2	[0.534, 0.466]	0.502	0.50

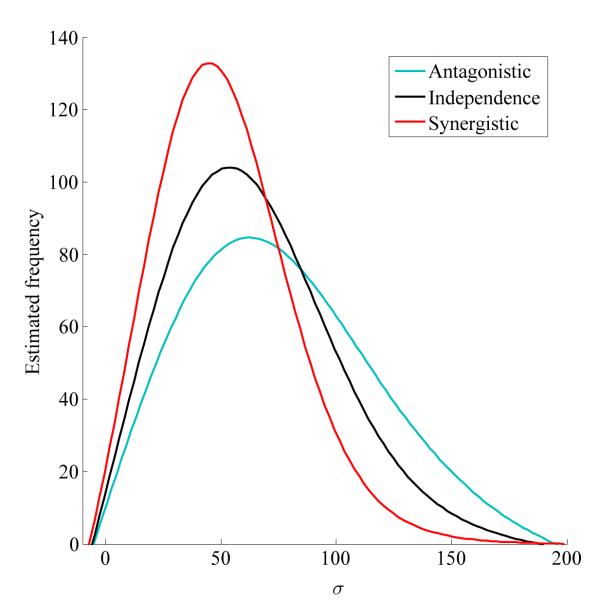
Considering a symmetric balancing selection model with three loci, two representing HLA and one representing KIR, where the observed allele frequencies are assumed to be good approximations to the population allele frequencies, the strengths of balancing selection under three models, estimated as 95% HPD intervals, are HPD_ant = {29, 143}, HPD_ind = {24, 115}, and HPD_syn = {20, 98} (Figure .4). Using Bayes factors, the antagonistic interaction model is about 7 times more likely than the synergistic alternative (B_ant/syn = 7.13). Thus, taken as a group, these loci have a polymorphic structure supporting a model in which the locus-wise fitness differences between heterozygotes and homozygotes is large and the detrimental effect of the first few homozygotes on the fitness of the whole group is small. In other words, a certain number of homozygous loci, even if homozygotes are inferior with respect to heterozygotes, can be tolerated because they only slightly decrease the fitness of the whole multi-locus genotype. In contrast, if the synergistic model had been favored, the effects would be reversed. That is, the first homozygous loci in the multi-locus genotype would not be tolerated well, since they would severely decrease the fitness of the whole multi-locus genotype, even if these homozygotes were not very inferior with respect to the heterozygotes.

Figure .4.

Kernel density estimates (using Gaussian Kernel) of posterior samples of σ under antagonistic (cyan), independence (black) and synergistic (red) models for the HLA/KIR data. The 95% HPD intervals (obtained from the original sample without density estimation) are {29, 143} for antagonistic epistasis, {24, 115} for independence, and {20, 98} for synergistic epistasis (100,000 MCMC iterations with thinning at every 100^th step).

6. Discussion

Wright-Fisher populations and distributions of allele frequencies arising from them have been central in developing theory and methodology in population genetics. In this tradition, we have taken advantage of a recent diffusion result [11] to extend previous methodology on estimating the strength of balancing selection to incorporate epistatic interactions among a set of loci. Our methods are useful in estimating the strength of selection under two qualitatively different types of epistasis. We have also presented a method that uses Bayes factors to evaluate the strength of evidence in favor of a candidate model of balancing selection. Our approach is most useful when the number of loci is large, but it has the ability to detect weak balancing selection even with relatively few loci.

The methodological innovation in this paper lies in its combination of the numerical integration techniques with Monte Carlo approaches first to compute the normalizing constants of a relatively intractable likelihood function, and then to simulate observations to make inference under a complex scenario of balancing selection. We expect that other approaches might be applicable for estimating the likelihoods without computing the normalizing constants (e.g., Beaumont [2], Andrieu and Roberts [1]) or for generating observations from models similar to ours (e.g., Fearnhead [10]); however, we have not investigated the suitability of these alternative methods.

We note that based on decisions we have made for retaining the ability to practically perform inference have generated a series of limitations. We have assumed a highly symmetrical balancing selection model, at two different levels. The first level of symmetry occurs within a locus and refers to the assumption that regardless of the particular alleles it contains, a heterozygous genotype at a locus has a higher fitness in comparison to a homozygous genotype. Further, all heterozygous and homozygous genotypes are assigned the same fitness within their class. This within-locus symmetry assumption keeps the number of parameters in the model low. A second symmetry assumption forces the selection strengths at different loci to be the same. This assumption is needed for the inference method to have power to differentiate between different types of epistasis. An alternative balancing selection model, which allows for the strength of selection to vary across loci, and which was used for estimating the mean strength of selection in a group of loci in the absence of epistasis, can be found in Buzbas et al. [4].

We conclude by discussing another important model limitation. Both our independence and epistatic models assume that the product of the frequencies of included alleles is a good proxy for the frequency of a haplotype. In a Wright-Fisher population, this amounts to assuming a sampling scheme with unlinked loci. However, when the loci of interest lie on the same chromosome, a degree of genetic linkage is expected. Genetic linkage may induce a correlation structure on the allele frequencies, which in turn may affect the frequency of heterozygotes, and hence, the estimates of the strength of selection.

Perfect linkage occurs when there is no recombination at all. This case poses no real difficulty in the perspective of the model in equation 2, since the data can be treated conceptually as generated from a single locus. Classifying haplotypes differing from each other at one or more loci as distinct allelic types, the resulting model can be analyzed using equation 1. Inferences on the strength of selection in this case must be interpreted with care, however, since they will be based on the new definition of a haplotypic locus. The case of partial linkage, on the other hand, is challenging to model. Complications introduced by partial linkage can be addressed by a model that would take into account recombination in addition to selection and mutation. However, the stationary distribution of allele frequencies has not been found in this case, even for a two-locus two-allele model [8]. Due to the difficulties of generating data under a model with partial linkage, the effects of assuming unlinked loci in estimating the strength of selection under the Wright-Fisher model when the loci of interest are actually linked remain unknown. A future direction is to design a simulation study to explore these effects.

Appendix A. The choice of σ under independence to improve the accuracy of Monte Carlo estimation

The difficulty in computing c_epi(θ, σ_epi) via Monte Carlo integration as described in Approximating the normalizing constant has the flavor of a well-known problem in stochastic sampling. This problem involves the use of an inefficient instrumental distribution, in our case, the joint distribution of allele frequencies under independence. For example, a similar problem was observed by Donnelly et al. [7], when the distribution of allele frequencies under the neutral model was used as an instrumental distribution to compute the normalizing constant under selection in the single-locus case. Even 10⁶ Monte Carlo samples generated under neutrality do not produce accurate results for the constant under selection in that case due to the dissimilarity between the neutral model and the model under selection. In our particular multi-locus model, we would like an estimate

$$\frac{1}{n}\sum _{i=1}^n{e}^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}$$ (.1)

to be an accurate estimator of $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]$. However, because of the large variability in the n replicates contributing to the sum in expression .1, the estimates are not usually accurate for values of n that are possible to implement. One way to avoid this inaccuracy is to choose σ_ind such that the values in different replicates have low variability.

Here, we exploit a special structure in the expectation of interest to accurately approximate c_epi(θ, σ_epi) with a reasonable number of simulated samples (n ≈ 10³). The key to our method is to recognize that in equations 11-14, σ_epi is not necessarily related to σ_ind in any way and we are free to simulate under independence with any value for σ_ind that we deem useful. In fact, there is an optimal σ_ind that minimizes the effect of $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]$ in the computation of c_epi(θ, σ_epi). The form of expression .1 suggests that the accuracy of the approximation for a given number of Monte Carlo samples depends on

$${\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)=\sum _{\ell =0}^m\left[g_{\mathrm{epi}}\right({\sigma }_{\mathrm{epi}},\ell )-g_{\mathrm{ind}}({\sigma }_{\mathrm{ind}},\ell \left)\right]P[L=\ell \mid \mathbf{x}],$$ (.2)

where the probability of having exactly ℓ homozygotes in the multi-locus genotype, P[L = ℓ|x], is conditional on the allele frequencies generated under independence (equation 10). An ideal σ_ind to reduce the Monte Carlo variability has the property that the sum on the right-hand side of equation .2 is close to zero, implying $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]\approx 1$. Such a choice works because it keeps the Monte Carlo variance of the expectation small, and consequently, the product of the corresponding individual locus constants c(θ, σ_ind) reproduces c_epi (θ, σ_epi) faithfully. That is, $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]\approx 1$ implies $c_{\mathrm{epi}}(\theta ,{\sigma }_{\mathrm{epi}})\approx {\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$ (equation 13).

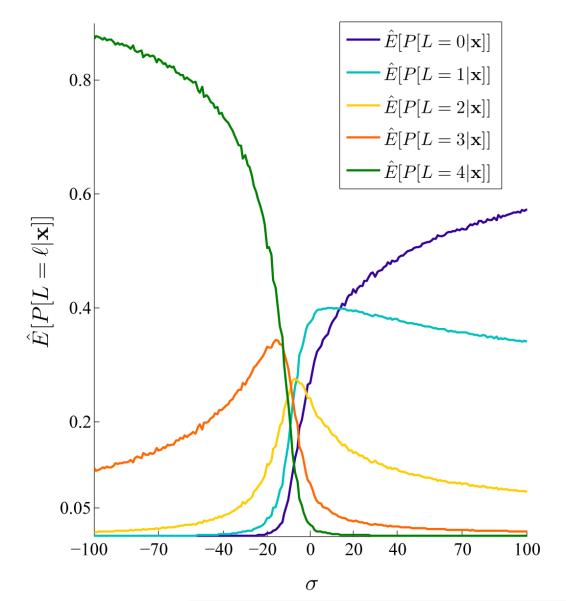
The details on optimization of σ_ind are as follows. Let x denote the multi-locus allele frequencies simulated under independence with parameters (θ, σ_ind). The right-hand side of equation .2 involves a combination of $g_{\mathrm{ind}}({\sigma }_{\mathrm{ind}},\ell )$ and x through the conditional probabilities P[L = ℓ|x]. Therefore, to choose an optimal σ_ind, we need an idea about the behavior of P[L = ℓ|x] for different σ_ind values. Figure .5 shows estimates of E[P[L = ℓ|x]] obtained by

$$E\left[P\right[L=\ell \mid \mathbf{x}\left]\right]\approx \frac{1}{n}\sum _{i=1}^{n}P[L=\ell \mid {\mathbf{x}}^{\left(i\right)}]$$ (.3)

for a range of σ values, based on n = 10³ allele frequency sets, x, generated under independence and a set of m = 4 loci. If we want to compute c_epi(θ, σ_epi) for σ_epi < 0, then generated samples contribute to the sum in equation .2 essentially through large ℓ, since E[P[L = m|x]] > E[P[L = (m−1)|x]] > … > E[P[L = 0|x]], as can be seen by comparing the plots of estimated values from equation .3 in the left part of Figure .5. In contrast, for σ_epi > 0, the samples contribute to the sum through small ℓ, since E[P[L = 0|x]] > E[P[L = 2|x]] > … > E[P[L = m|x]]. Given a value of σ_epi, the optimal σ_ind is chosen such that for values of ℓ for which E[P[L = ℓ|x]] is large, $\mid g_{\mathrm{epi}}({\sigma }_{\mathrm{epi}},\ell )-g_{\mathrm{ind}}({\sigma }_{\mathrm{ind}},\ell )\mid$ is minimized. To achieve this, we first simulate 10³ multi-locus allele frequency sets for each σ_ind value on a grid (σ ∈ [−300, 300] is chosen with a step size of δ = 1 for the analyses in this paper). We then compute equation .2 and choose as the optimal value the σ_ind for which $\mid {\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)\mid$ is closest to zero. The accuracy gained in computing the normalizing constants by optimizing σ_ind for each given value of σ_epi rather than using the value of σ_epi is particularly clear when σ_epi >> 0 (Figure .6).

Figure .5.

Estimated probability of having ℓ homozygotes in a multi-locus genotype, $\widehat{E}\left[P\right[L=\ell \mid \mathbf{x}\left]\right]$, for a range of σ values with m = 4 loci. The results are obtained by simulations (10⁶ replicates for each σ). For the homozygote advantage case (σ << 0) we have $\widehat{E}\left[P\right[L=m\mid \mathbf{x}\left]\right]>\widehat{E}\left[P\right[L=m-1\mid \mathbf{x}\left]\right]>\dots >\widehat{E}\left[P\right[L=0\mid \mathbf{x}\left]\right]$, whereas for the strong heterozygote advantage case (σ >> 0) the inequalities are reversed. We exploit the structure in $\widehat{E}\left[P\right[L=\ell \mid \mathbf{x}\left]\right]$ to find the optimal σ_ind to calculate the normalizing constant of equation 13 (see Approximating the normalizing constant and Appendix A).

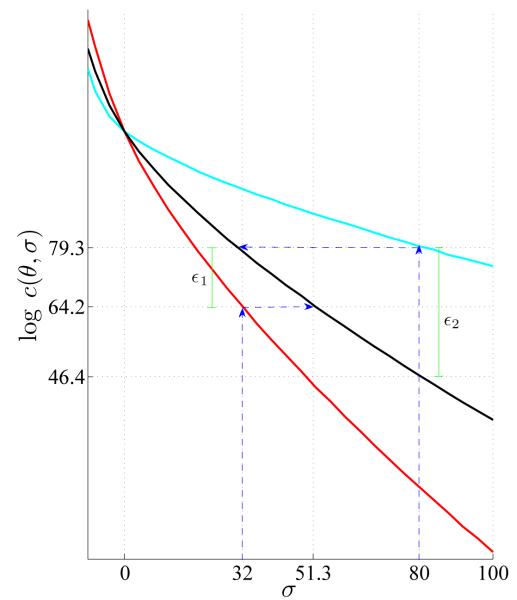
Figure .6.

Normalizing constants on a log scale for antagonistic (cyan), independence (black) and synergistic (red) models for a range of σ values, as obtained by an adjusted Monte Carlo method using equation 14 and Appendix A. The effect of choosing an appropriate σ_ind to minimize the adjustment by the estimate of $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]$ in equation 13 can be seen by comparing the difference between the constant obtained by choosing the optimal σ_ind and choosing σ_epi = σ_ind. For example, for the constant desired with σ_syn = 32, the corresponding optimal value for σ_ind(x) is 51.3. If σ_ind = 32 were used, the estimate of the expected value $E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]$ in the approximation of c(θ, σ) would have to adjust for a large discrepancy (approximately ∊₁ on the log scale). Similarly, for the constant desired with σ_ant = 80, the optimum is σ_ind = 32, and if σ_ind = 80 were used, the adjustment by the expectation in the estimate would be approximately ∊₂ (log scale). Choosing the optimal value of σ_ind minimizes the effect of the adjustment.

Appendix B. Simulating allele frequencies under the multi-locus balancing selection model

In this section we present an algorithm to generate approximate multi-locus allele frequency vectors from a set of m loci under epistasis. The ability to generate these vectors gives us the means to study the behavior of epistatic models. Quantities needed to generate data are the parameter vector (σ, θ, k, m), the type of epistasis (i.e., antagonistic, synergistic), and a form for the epistasis function g. Our modified rejection algorithm is as follows.

Algorithm B1.

1. Using Appendix A, choose σ_ind such that $c_{\mathrm{epi}}(\theta ,{\sigma }_{\mathrm{epi}})\approx {\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$.

2. For i = 1, …, m, simulate a data set from f(x_i|θ_i, σ_ind) under independence for each locus and form n multi-locus frequency arrays x^(j), j = 1, 2, …, n.

3. Accept x^(j) as a draw from the desired epistatic model if

   $$\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}({\mathbf{x}}^{\left(j\right)}-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}({\mathbf{x}}^{\left(j\right)})}\right]B_n^{-1}>U,$$

   where B_n is an upper bound (explained below) and U ~ Unif(0, 1).

A value of B_n is needed for the above algorithm to work. The efficiency of a rejection algorithm depends on an upper bound on the ratio of the target distribution to the proposal distribution. The theoretical upper bound for the ratio of the target distribution under epistasis f(x|θ, σ_epi), to the proposal distribution under independence f(x|θ, σ_ind), given in equation 15, is

$${\sup }_x\left\{\frac{f(\mathbf{x}\mid \theta ,{\sigma }_{\mathrm{epi}})}{f(\mathbf{x}\mid \theta ,{\sigma }_{\mathrm{ind}})}\right\}={\sup }_x\left\{\frac{e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)}f(\mathbf{x}\mid \theta )∕c_{\mathrm{epi}}(\theta ,{\sigma }_{\mathrm{epi}})}{e^{{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}f(\mathbf{x}\mid \theta )∕c_{\mathrm{ind}}(\theta ,{\sigma }_{\mathrm{ind}})}\right\}.$$ (.4)

By equation 13, this quantity simplifies to

$$\begin{array}{cc}\hfill {\sup }_x\left\{\frac{e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)}f(\mathbf{x}\mid \theta )∕\left[c_{\mathrm{ind}}\right(\theta ,{\sigma }_{\mathrm{ind}}\left)E\right[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\left]\right]}{e^{{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}f(\mathbf{x}\mid \theta ∕[c_{\mathrm{ind}}(\theta ,{\sigma }_{\mathrm{ind}})}\right\}=& {\sup }_x\left\{\frac{e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}}{E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]}\right\}\hfill \\ \hfill =& \frac{{\sup }_x\left\{e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right\}}{E\left[e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left(\mathbf{x}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left(\mathbf{x}\right)}\right]}.\hfill \end{array}$$

As an example, consider the synergistic case, for which it can be shown that the supremum is realized when P[L = m|x] = 1. Note that under heterozygote advantage, L = m is actually an extremely low probability event. Although an all-homozygous genotype (L = m) is part of the legitimate genotype space, it is virtually impossible under heterozygote advantage to have a population where all genotypes are all-homozygous (i.e., E[P[L = m|x]] → 0 as σ → ∞, see Figure .5). Using the theoretical bound obtained from equation .4 (realized when P[L = m|x] = 1) in the rejection algorithm results in rejections for most of the proposed values and hence, the algorithm is very inefficient. Therefore, we obtain an empirical upper bound that can be used in place of the theoretical bound as an approximation. This empirical bound can be obtained as follows.

Algorithm B2.

1. Using Appendix A, choose σ_ind such that $c_{\mathrm{epi}}(\theta ,{\sigma }_{\mathrm{epi}})\approx {\prod }_{i=1}^{m}c({\theta }_i,{\sigma }_{\mathrm{ind}})$.

2. For i = 1, …, m, simulate n = 10⁶ data sets from f(x_i|θ_i, σ_ind) under independence for each locus, and form n multi-locus frequency arrays x^(j), j = 1, 2, …, n.

3. Compute the empirical bound $B_n=\frac{{\max }_x\left\{e^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left({\mathbf{x}}^{\left(j\right)}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left({\mathbf{x}}^{\left(j\right)}\right)}\right\}}{\frac{1}{n}{\sum }_{j=1}^n{e}^{{\stackrel{‒}{\sigma }}_{\mathrm{epi}}\left({\mathbf{x}}^{\left(j\right)}\right)-{\stackrel{‒}{\sigma }}_{\mathrm{ind}}\left({\mathbf{x}}^{\left(j\right)}\right)}}$.

The calculated bound B_n can then be used with the rejection algorithm B1 to generate an approximate multi-locus allele frequency array, x.

>Appendix C. MCMC to sample the joint posterior distribution of the parameters (θ, σ)

To sample the joint posterior distribution of the parameters (θ, σ), we use a component-wise Metropolis-Hastings algorithm with independent sampler (see Robert and Casella [29] p. 276). Component-wise refers to the fact that we propose and update the elements of the parameter vector one at a time rather than updating the whole vector in one proposal. This method is more efficient than updating the whole vector because proposing a whole vector of parameters results in very few accepted updates when the parameter space is high-dimensional. The sampler is independent in the sense that the proposal distribution evaluated at the proposed value does not depend on the current value of the parameters and vice versa.

As is common in Bayesian procedures, we use prior distributions on θ and σ as proposal distributions for the respective updating steps. The acceptance probability under a component-wise Metropolis-Hastings algorithm with independent sampler is given by the ratio of the likelihood functions evaluated at the proposed value and the current value of the parameters. In our case, a slight modification from a standard component-wise Metropolis-Hastings algorithm with independent sampler is needed to accurately evaluate the constant c_epi(θ, σ) (and consequently the likelihood) for each proposed parameter value. This modification is the presence of the optimization step for σ_ind for each proposed parameter value from the prior. A sketch of the algorithm is as follows: Start with some arbitrary values of the parameters. For each update, propose a value from the corresponding prior distribution of one element of the parameter vector. Find the optimal value of σ_ind to evaluate the constant and hence the likelihood under the proposed value. Compute the ratio of posterior density (proportional to the likelihood) evaluated under the proposed value to the posterior density evaluated under the current value of the parameter. If this ratio exceeds an independently generated uniform random variate, update the chain to the proposed value; otherwise, update the chain to the current value of the parameters. Sample with thinning.

Algorithm C1. We start with arbitrary current values of the mutation and selection parameters, ${\theta }^{\left(0\right)}=[{\theta }_1^{\left(0\right)},\dots ,{\theta }_m^{\left(0\right)}]$ and σ⁽⁰⁾ respectively. We set the grid parameter to ∣σ_max∣ = 300 with a step size of δ = 1. One MCMC iteration is given by the following algorithm.

1. Calculate the current normalizing constant (in equation 13).

   1. Find the optimal σ_ind to compute the normalizing constant:

      $${\sigma }_{\mathrm{ind}}={\mathrm{argmin}}_{\sigma }\left\{\sum _{i=1}^n\mid \sum _{\ell =1}^m\left[g_{\mathrm{epi}}\right({\sigma }^{\left(0\right)},\ell )-g_{\mathrm{ind}}(\sigma ,\ell \left)\right]P[L=\ell \mid {\mathbf{x}}^{\left(i\right)}]\mid \right\},$$

      where x⁽ⁱ⁾ are samples of allele frequencies (i = 1, …, n) simulated under independence with parameter vector (θ⁽⁰⁾, σ). Here, we optimize on a grid for σ ∈ (−σ_max, σ_max) with step size δ.
   2. Compute the constant:

      $$c_{\mathrm{epi}}({\theta }^{\left(0\right)},{\sigma }^{\left(0\right)})=\prod _{j=1}^{m}c({\theta }_j^{\left(0\right)},{\sigma }_{\mathrm{ind}})\left[\frac{1}{n}\sum _{i=1}^n{e}^{\sum _{\ell =1}^m\left[g_{\mathrm{epi}}\right({\sigma }^{\left(0\right)},\ell )-g_{\mathrm{ind}}({\sigma }_{\mathrm{ind}},\ell \left)\right]P[L=\ell \mid {\mathbf{x}}^{\left(i\right)}]}\right].$$
2. Sequentially, update the mutation parameters for each locus θ₁, θ₂, …, θ_m, by applying the steps (a)-(f) below for each one.

   1. Generate ${\theta }_j^{(\ast )}\sim P_j\left(\theta \right)$, where P_j(θ) is a prior distribution of the mutation parameter for the j^th locus, obtained using the neutral variation at that locus. (See Algorithm 1 of Buzbas et al. [4] for details. Essentially, one uses the neutral version of the Wright-Fisher model with σ = 0 and obtains a posterior sample of the mutation parameter using the synonymous allele frequencies at the j^th locus. A fitted gamma distribution is then used as P_j(θ).) Set ${\theta }^{(\ast )}=[{\theta }_1^{\left(0\right)},\dots ,{\theta }_j^{(\ast )},\dots ,{\theta }_m^{\left(0\right)}]$.
   2. Repeat step 1 to find a new optimal σ_ind, but now with samples of allele frequencies simulated under independence with (θ^(*), σ). Compute c_epi(θ^(*), σ⁽⁰⁾).
   3. Set θ⁽⁰⁾ = θ^(*) if

      $$\frac{f(\mathbf{x}\mid {\theta }^{(\ast )},{\sigma }^{\left(0\right)})∕c_{\mathrm{epi}}({\theta }^{(\ast )},{\sigma }^{\left(0\right)})}{f(\mathbf{x}\mid {\theta }^{\left(0\right)},{\sigma }^{\left(0\right)})∕c_{\mathrm{epi}}({\theta }^{\left(0\right)},{\sigma }^{\left(0\right)})}>U,$$

      where U ~ Unif(0, 1).
3. Update the selection parameter:

   1. Simulate σ^(*) ~ Unif(−σ_max, σ_max).
   2. Repeat step 1 to find a new optimal σ_ind, but now with samples of allele frequencies simulated under independence with (θ⁽⁰⁾, σ). Compute c_epi(θ⁽⁰⁾, σ^(*)).
   3. Set σ⁽⁰⁾ = σ^(*) if

      $$\frac{f(\mathbf{x}\mid {\theta }^{\left(0\right)},{\sigma }^{(\ast )})∕c_{\mathrm{epi}}({\theta }^{\left(0\right)},{\sigma }^{(\ast )})}{f(\mathbf{x}\mid {\theta }^{\left(0\right)},{\sigma }^{\left(0\right)})∕c_{\mathrm{epi}}({\theta }^{\left(0\right)},{\sigma }^{\left(0\right)})}>U,$$

      where U ~ Unif(0, 1).