Detecting Phylogenetic Breakpoints and Discordance from Genome-Wide Alignments for Species Tree Reconstruction

Abstract

With the easy acquisition of sequence data, it is now possible to obtain and align whole genomes across multiple related species or populations. In this work, I assess the performance of a statistical method to reconstruct the whole distribution of phylogenetic trees along the genome, estimate the proportion of the genome for which a given clade is true, and infer a concordance tree that summarizes the dominant vertical inheritance pattern. There are two main issues when dealing with whole-genome alignments, as opposed to multiple genes: the size of the data and the detection of recombination breakpoints. These breakpoints partition the genomic alignment into phylogenetically homogeneous loci, where sites within a given locus all share the same phylogenetic tree topology. To delimitate these loci, I describe here a method based on the minimum description length (MDL) principle, implemented with dynamic programming for computational efficiency. Simulations show that combining MDL partitioning with Bayesian concordance analysis provides an efficient and robust way to estimate both the vertical inheritance signal and the horizontal phylogenetic signal. The method performed well both in the presence of incomplete lineage sorting and in the presence of horizontal gene transfer. A high level of systematic bias was found here, highlighting the need for good individual tree building methods, which form the basis for more elaborate gene tree/species tree reconciliation methods.

Introduction

The past few years have seen an explosion of phylogenomic studies, thanks to an ever-increasing sequencing power and availability of complete genomes. However, the unified term “phylogenomics” encompasses a variety of data types that may be used for phylogenetic tree reconstruction. Most often, phylogenomic studies are based on sets of putative orthologous genes, ranging from dozens to hundreds or even thousands of loci (e.g., Pollard et al. 2006; Carstens and Knowles 2007; Jansen et al. 2007; Puigbo et al. 2009; Williams et al. 2010). Other studies make use of a large portion of nuclear genetic material by considering paralogous copies in gene families, with the added complexity of dealing with gene duplications and losses (Maddison 1997; Page 1998; Maddison and Knowles 2006; Wehe et al. 2008). More recently, some studies have been able to use almost complete chromosomes or genomes for phylogenetic reconstruction (Yang et al. 2007; Schoen et al. 2008; White et al. 2009). As we believe that whole-genome alignments will become more and more prevalent in future studies, this paper focuses on the specific challenges posed by this source of data.

Much recent work acknowledges the need to shift from equating genes trees with species trees to modeling the discordance between gene trees and species trees (see Knowles [2009] and references therein). The availability of whole genomes or genome-wide alignments further allows for another paradigm shift: from estimating a unique species or population tree to estimating the whole distribution of trees along the genome: the “phylome.” Indeed, the wealth of information available from genome-wide data allows us to not only estimate the mean phylogenetic signal but also the variability around this primary phylogenetic signal. Estimating the complete distribution of gene trees across genomes can provide novel insights into the various processes that shaped this gene tree variability. Such processes include the demographic history influencing incomplete lineage sorting (ILS), chromosome-specific histories, potential selective sweeps which may have created wider phylogenetically homogeneous regions, or potential balancing selection which may have caused reduced sizes of phylogenetically homogeneous regions (Ebersberger et al. 2007). Estimating the species tree or primary concordance tree is one goal that can be achieved from genome-wide phylogenetic studies but even more insights could be obtained from the distribution of gene trees along the genome.

Several methods are now available to combine multiple loci without imposing them to share the same tree topology (Knowles and Kubatko 2010). These species tree/gene tree reconciliation methods are based on the assumption that loci are “topologically homogeneous,” that is, that all sites within a locus share the same topology. This assumption is reasonable when applied to a set of short-coding genes, for instance. In long genome-wide alignments, however, predefined homogeneous loci are no longer delimited a priori.

Detecting Recombination for Species Tree Inference

Evolution is tree-like at each site, but the underlying genealogy may vary along the genome due to recombination. In eukaryotes, recombination is achieved through meiosis. Several biological processes are recognized in prokaryotes, such as conjugation, transduction, and transformation. Whatever the biological process, recombination unlinks the genealogy of sites on either side of the recombination location. Recombination events create breakpoints in the alignment, where the tree topology or branch lengths may differ between the left side and the right side of the break. I argue here that there are different types of recombination events and that not all types are to be detected for the purpose of species tree/gene tree inference. Some recombination events do not affect the gene tree or its branch lengths, as measured in number of generations between coalescent events (Hein et al. 2005). Detecting these recombination events is of no interest for building gene trees. Indeed, it is advantageous to concatenate neighboring sites that tracked the same phylogenetic tree, regardless of the presence or absence of recombination events that may have taken these neighboring sites apart in different cells for some part of their evolutionary history. On the other hand, other recombination events did affect the tree, and those events need to be detected. Events that changed the tree topology seem more important to detect than events that only modified the tree's branch lengths. Indeed, branch lengths are typically inferred as average numbers of substitutions per site in gene trees, where time (number of generations) and substitution rate (number of substitutions per site per generation) are confounded. Selection and many biological processes other than recombination may alter substitution rates. Because substitution rates may vary across sites even when divergence times do not and because single gene tree reconstruction methods can account for complex branch length variation (e.g., Yang 1994; Huelsenbeck et al. 2008; Pagel and Meade 2008; Whelan 2008; Zhou et al. 2010), I argue that it is less important to detect recombination events that only affected generation times than to detect events affecting the tree topology, for the purpose of species tree reconstruction. I propose here a fast minimum description length (MDL) method for detecting this type of recombination events for the purpose of locus tree/species tree reconstruction. This MDL approach was applied to whole mammalian genomes (White et al. 2009), and we report here its performance from a simulation study.

Numerous methods aim to detect recombination within alignments (see reviews in Posada and Crandall 2001; Chan et al. 2006; Boussau et al. 2009), with various goals and strengths. Some detect recombination locations whereas others provide statistical significance for the presence of recombination. Many of these methods consider and aim to detect all types of recombination events.

For the purpose of reconstructing species trees from locus trees, one would like to find breakpoints where the underlying tree topology changes, thereby defining topologically homogeneous loci between breakpoints. Note that this set of breakpoints is highly taxon dependent: the same recombination event may affect the topology underlying a certain set of taxa but leave the topology intact for a reduced set of taxa. In this case, it is desirable to detect the location of this recombination event on the full taxon set but not on the reduced taxon set. As taxon sampling increases, more and more recombination breakpoints may fragment the partition into a larger number of smaller topologically homogeneous loci.

The simplest and fastest way to define loci within a chromosome alignment is to consider fixed-length intervals. Yang et al. (2007) used 100-kb intervals on 15 mouse strains for instance. It is not clear how the interval length should be chosen in general. A shorter length is expected to produce more fragments that truly admit a single underlying topology, but fewer sites per interval will mean less phylogenetic information bearing on each interval. Slatkin and Pollack (2006) showed for three species alignments that the average length of neutral loci is of the same order as linkage disequilibrium. However, adding species or populations to an alignment can only increase the number of recombination breakpoints that affect the topology, and it is not clear how the average locus length varies with the number of taxa.

Combining MDL Partitioning with Bayesian Concordance Analysis

In this paper, I propose partitioning chromosome-wide alignments using a fast MDL approach somewhat similar to the parsimony-based program RecPars (Hein 1993). The MDL approach aims to maximize the fit of breakpoints to the data while penalizing large numbers of breakpoints. Ané and Sanderson (2005) use this MDL principle, based on information theory, to find a taxon-dependent penalty parameter to appropriately weigh the cost of substitutions versus that of recombination. In this work, I consider a range of values for this penalty. A smaller penalty is expected to allow more breakpoints, therefore more homogeneous loci. On the other hand, a larger penalty is expected to reduce the number of breaks, therefore increasing the phylogenetic content of individual loci. To estimate phylogenetic variability from whole-genome alignments, I propose to combine MDL partitioning with Bayesian concordance analysis (BCA, Ané et al. 2007), which takes as input predefined loci. A key advantage of this approach is its computational tractability. It was successfully applied to whole genomes of mouse strains (White et al. 2009; Ané 2010) in which the X chromosome and all 19 autosomes were analyzed, representing a 1.8 billion site alignment across four taxa. The purpose of the present paper is to assess the performance of combining MDL partitioning with BCA. Simulations were conducted on 4 and 12 taxa. Discordance among locus trees was either caused by ILS or by horizontal gene transfer. Simulations included many processes that are known to act on sequence evolution, so that the models used to analyze the data were far simpler than the models used to simulate the data. Two questions are specifically addressed here: 1) what is the best penalty parameter in MDL partitioning for the purpose of estimating phylogenetic variability? 2) What is the gain, if any, of using MDL partitioning compared with using a fixed-length partition, for the purpose of estimating the main vertical phylogenetic signal and the genomic support of individual clades?

The MDL partitioning method and its implementation are presented in the next section. A more in-depth comparison between MDL partitioning and related methods of recombination breakpoint detection is presented in the discussion.

Materials and Methods

BCA

BCA was introduced in Ané et al. (2007) and implemented in BUCKy (Larget et al. 2010). This Bayesian approach uses the uncertainty in locus trees to tease out which loci truly have different tree topologies and which loci likely share the same topology. Like most gene tree/species tree methods, BCA assumes topologically homogeneous loci, that is, that all sites within a given locus evolved under the same underlying tree topology. BCA does not assume that a single process (like ILS) is the cause of gene tree discordance. Instead, a nonparametric approach is used to model discordance. A Dirichlet process prior models the a priori assumption that loci tend to share the same tree topology. This prior draws a random number of clusters and then randomly assigns loci to clusters. Loci in the same cluster have the same tree topology (but potentially different branch lengths and model parameters). Note that locus order is ignored by the Dirichlet process: it does not incorporate the expectation that adjacent loci belong to the same cluster more often than distant loci. The a priori number of clusters is controlled by a single parameter α, which measures the a priori level of discordance expected among locus trees. Choosing α = 0 amounts to assuming all loci share the same tree in a single cluster, so that BCA with α = 0 amounts to a concatenated Bayesian analysis with locus-specific branch lengths and locus-specific evolutionary parameters. An infinite α corresponds to assuming complete independence among locus trees, as is done in a consensus approach. Between these two extremes, information from compatible loci is combined to yield more resolution on their shared topologies. The value α = 1 is the default in BUCKy because this choice corresponds to a prior probability of about 0.5 that two randomly chosen loci share the same topology.

BCA provides posterior distribution of individual locus trees based on the combined analysis, posterior probabilities that sets of loci share the same topology, and most importantly inference on concordance factors. The genome-wide concordance factor of a clade is the proportion of loci in the genome that truly has the clade. As suggested by Baum (2007), a concordance tree built from clades with the largest concordance factors can be used to represent the dominant history of a group of taxa. Concordance factors provide genomic support for clades, as opposed to the statistical support provided by bootstrap values or posterior probabilities. For example, concordance analysis was applied to 30,040 loci aligned across human, chimpanzee, gorilla, orangutan, and rhesus from Ebersberger et al. (2007). Using BCA, it was estimated that only 76% of the human genome is sister to the chimpanzee genome (Ané 2010). Because it was significantly higher than 50% of the genome, this 76% genomic support gave full statistical support (1.0 posterior probability) for a human–chimpanzee sister relationship in the dominant history of great apes. Ané (2010) also describes the link between species trees and concordance trees, when the species history is actually tree-like, and tree discordance is due to ILS.

In order to infer concordance trees from long alignments, two steps need to be taken. First, I propose partitioning alignments into loci as a preprocessing step. An MDL approach is detailed in the next section. Second, I propose considering site-wise concordance factors: The site-wise concordance factor of a clade is the proportion of sites (rather than loci) in the alignment for which the sites’ true underlying tree has the clade. This is needed because loci may not be inferred accurately. In case a false break is used to separate two concordant neighboring loci, the site-wise concordance factors may be inferred to be identical whether the break is used or not.

MDL Partitioning

MDL is widely used as a tool for model selection (Rissanen 1978). It is based on the idea of minimizing the joint complexity—or description length—of both the model and the data (e.g., Hansen and Yu 2001, 2003 for MDL in linear and generalized linear regression). We use here the following criterion to measure the complexity (DL, for description length) of an alignment modeled as a partition of k loci:

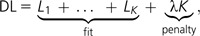where L_i is the parsimony score of the ith locus and λ is a penalty parameter that penalizes each additional break. The total parsimony score L₁+ … +L_k of the alignment measures the fit of the model, which consists of the partition and the k trees here. Note that some of the estimated maximum parsimony trees may happen to be the same for two (or more) of the k loci. Because the parsimony score is proportional to the negative log-likelihood of the alignment under a no-common mechanism model (Tuffley and Steel 1997), the DL criterion takes the form of a penalized log-likelihood, just like the Akaike (AIC) and Bayesian information criteria (Akaike 1974; Schwarz 1978). Ané and Sanderson (2005) derived a similar criterion from a compression algorithm. They showed that paying the penalty of describing a tree can help shorten the description of an alignment: the data are then described by the most parsimonious substitutions along the tree. If an alignment is made of two or more loci arising from different trees, then one might describe the data more efficiently by using two or more trees, one for each part of the alignment. They gave an exact formula for the penalty parameter λ, which depends on the size of the tree and increases with the number N of taxa: λ ∼ N. The DL criterion above is a rescaled version of theirs, although some algorithmic overhead terms have been dropped here, and a range of values is considered for λ in this work. For a given number of taxa, DL is very similar to AIC because both penalize the log-likelihood with a fixed penalty for each fragment.

The DL criterion is used to select the best partitions of an alignment. The selected number k of loci and the location of breakpoints are those that minimize the description length DL. There are a very large number of partitions to be considered. Even with a single break, there are almost as many locations for this break as there are sites in the alignment. When more breaks are allowed, the number of ways to place them grows very fast. To reduce the computational load, breakpoint locations are restricted to be every other “Nbase” sites only, where Nbase can be any integer. Breaks can be placed anywhere along the alignment if Nbase = 1, corresponding to the most thorough search. A faster search can be achieved with a higher value of Nbase, which can be defined by the user in our program. We used Nbase = 300 in the simulation study below.

The computationally demanding part of searching for the partition with smallest DL is the calculation of parsimony scores L_i for all potential loci. This was done using PAUP* (Swofford 2002) and automated using a Perl script. Once these parsimony scores are calculated, a very fast search for the best partition was implemented using dynamic programming. A C++ program is available on request.

Data Simulation

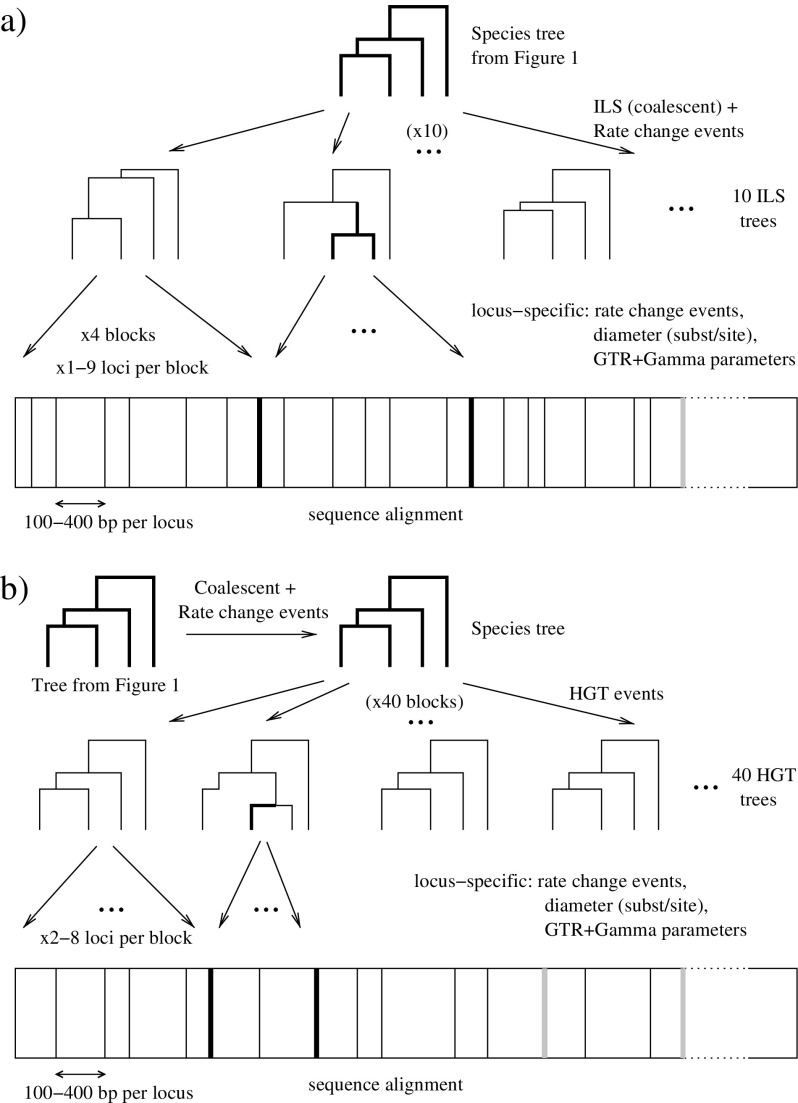
DNA sequence alignments were simulated using two species trees, one with 5 taxa and one with 12 taxa, shown in figure 1. Gene trees differed in several ways from species trees. Their topology could differ due to ILS or due to horizontal gene transfers (HGT). In addition, gene tree branch lengths were simulated by multiplying time and substitution rates. Variation in substitution rates implied that gene trees could depart from a molecular clock. One set of simulations included ILS and another set of simulations included HGT. Each alignment included 40 blocks of loci, where each locus had its own evolutionary parameters and branch lengths. Adjacent loci could share the same underlying tree topology.

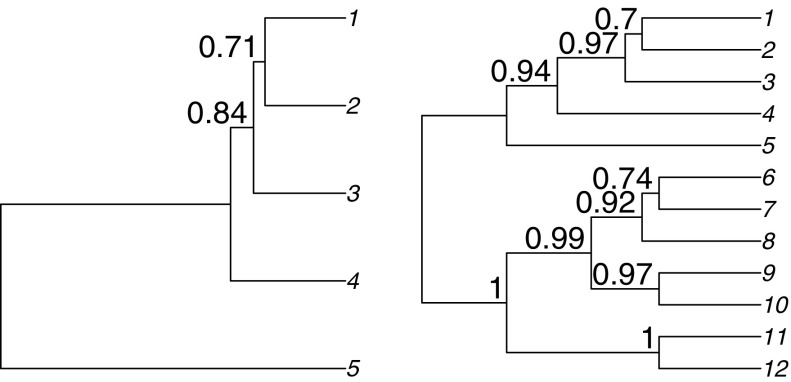
FIG. 1.—

Species trees used in simulations, with average concordance factors from ILS. Short branches, most affected by ILS, have lowest concordance factors. When ILS is the only process causing discordance, the concordance factor of minor clades conflicting with this topology is completely determined by the coalescent units.

For ILS simulations (fig. 2a), ten coalescent trees were simulated from the species tree using Serial SimCoal (Anderson et al. 2005). Numbers above branches in figure 1 indicate the average concordance factors of the clades in the species tree under ILS, showing which clades were most affected by ILS. From each of these 10 coalescent trees, 4 blocks of loci were simulated (40 blocks total), each block containing between 1 and 9 loci (uniformly). These loci had their own specific evolutionary parameters as detailed below, but all loci in the same block shared the same topology, that of the coalescent tree they were generated from. Therefore, even though branch lengths and evolutionary parameters varied along the simulated alignments, there were up to only 9 breakpoints, corresponding to 10 topologically homogeneous regions, one from each coalescent tree.

FIG. 2.—

Simulation protocol with discordance due to ILS (top) or to HGT (bottom). Branch lengths do not display rate variation across lineages. Along the alignment, thin lines represent boundaries between loci. Different loci may share the same tree topology but do not share the same evolutionary parameters. Thick lines represent boundaries between loci arising from independently generated trees. Black thick lines indicate true breakpoints, where adjacent loci have different topologies.

For HGT simulations (fig. 2b), a single coalescent tree was generated. It was used as a species tree to generate 40 HGT trees, with a HGT rate of 0.2 events per tree on average, that is, 8 transfer events on average in the 40 trees. Transfer events were mapped onto the branches of the species tree with a Poisson process, as was done in Galtier (2007): each branch in the species tree received a Poisson-distributed number of events with an average proportional to the branch duration. This process simulated the recipient lineage of each HGT event. For each event, the location of the donor lineage was drawn uniformly at random from all lineages that were contemporary or older than the recipient lineage. From each of the 40 HGT trees, one block of 2–8 loci was simulated. Again, all loci from the same block shared the same tree topology (same transfer events) even though each locus had its own evolutionary parameters and clock departure. Therefore, there were up to 39 breaks in the simulated alignments, although the actual number of simulated breaks was much smaller due to the average of eight transfer events per alignment and some of those only modified branch lengths.

For each coalescent tree, we simulated a global clock departure to be shared by all loci derived from that coalescent tree. A specific clock departure was also simulated for each locus. In both cases, clock departures were induced by changes in substitution rates, as was done in Galtier (2007). Rate change events were mapped onto trees using a Poisson process with an average of ρ = 1 global event per coalescent tree and an average of ρ′ = 2 locus-specific events. At these events, rates were multiplied by a gamma-distributed factor with shape α_l = 1. Each locus was assigned a specific average substitution rate, determined by a diameter uniformly chosen between 0.02 and 1 substitutions per site. Within loci, sites had gamma-distributed rates with shape α_s chosen uniformly between 0.3 and 1.5. The general time reversible (GTR) model was then used to simulate DNA sequences, with locus-specific parameters. Base frequencies were drawn from a gamma distribution with shape 6 and normalized to sum up to 1. GTR rates were gamma distributed with shape 2 and normalized. Finally, each locus had a random length, uniform between 100 and 400 sites.

Overall, these simulations included many complex processes that are known to govern real genomes, with rate heterogeneity among lineages, among loci, and among sites. As in real studies, the models used to analyze these data were far simpler than the models used to generate them.

Data Analysis

Simulated alignments were first partitioned using three strategies. MDL partitioning was performed with various penalty parameters, ranging from λ = 5 to λ = 12 on alignments with five taxa and from λ = 8 to λ = 15 with 12 taxa. These intervals include the theoretical value from Ané and Sanderson (2005) in each case. The second partitioning strategy used fixed-length intervals of 600 sites. This size, similar to the typical length of genes in real data, was chosen to be about twice the average length of true loci in order to limit the heterogeneity of DNA evolutionary parameters within each interval. Finally, the third partitioning strategy used the true partition defined by the breakpoints where the true topology changed. This strategy cannot be applied to real data. Of the three strategies, it is the only one that is guaranteed to meet BCA's assumption of topologically homogeneous regions.

BCA was then run on each partitioned alignment with four prior levels of discordance: α = 0.1, 0.5, 1 and α infinite using BUCKy version 1.3.0. With α = 1, any two randomly selected loci share the same tree topology a priori with a probability of 0.533 on five taxa, and 0.50 on 12 taxa (In general, the exact prior probability is (1 + α/T)/(α + 1), where T is the total number of gene tree topologies.). This probability becomes larger with smaller α's: 0.68 with α = 0.5 and 0.91 with α = 0.1. These higher probabilities seemed to better correspond to the actual simulated concordance level. With an infinite α, fragments have a priori independent trees. Therefore, the values of α span a wide range of prior values. In the first step of BCA, each part of the partition was analyzed individually in MrBayes using the Hasegawa-Kishino-Yano + G model with 5 taxa and the F81 model with 12 taxa (for faster running time). Note that like in real studies, these models were far simpler than the models used to simulate the alignments. First, the GTR + G substitution model was used in simulations. Second, most parts spanned several loci that had different branch lengths, different rates, different base frequencies, etc., if not different topologies.

The clades' concordance factors were estimated from each partitioned alignment. Under ILS, I particularly focused on clades where most of locus trees disagreed upon, namely clades (1,2) in the 5-taxon tree and clade (1,2,3) in the 12-taxon tree. The posterior distribution for each site's tree was also obtained from the joint analysis. Because the true topology was known at each site, an overall measure of accuracy was obtained as the posterior probability of the sites’ true tree averaged over all sites in the alignment.

Results

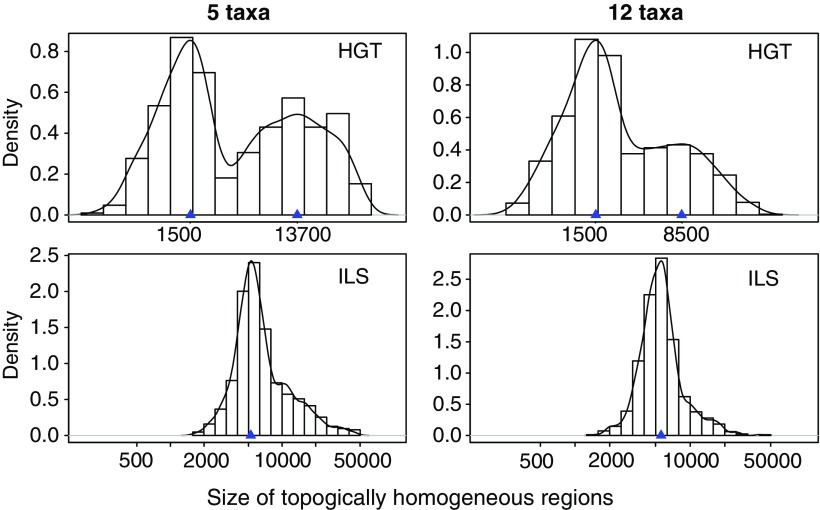
The size of regions with the same topology was comparable among alignments simulated with ILS and those simulated with HGT overall. Figure 3 shows the distribution of the size of topologically homogeneous regions, that is, regions of sites between two true breakpoints. As expected, all these regions are somewhat similar in size under ILS, with a median slightly above 5,000 sites. Under HGT, however, the regions with an HGT tree are smaller in size than the regions whose tree matches the species topology.

FIG. 3.—

Distribution of the size of topology-homogeneous regions: number of sites between two breakpoints. The same logarithmic scale is used on all graphs. Each graph represents 100 simulated alignments. The curves are nonparametric density estimates from the histograms.

The results were almost identical with the three values of α = 0.1, 0.5, and 1 on 12-taxon alignments. On five taxa, the results were also almost identical in the ILS simulations, and smaller α's (0.1 and 0.5) provided only slightly better results than α = 1 in the HGT simulations. Therefore, I only report results with α = 1 (the program's default value) and α infinite.

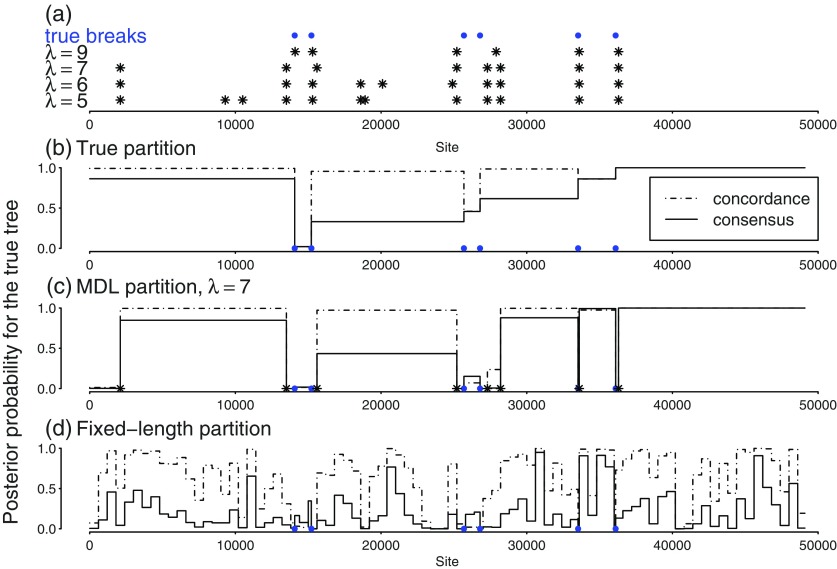
Figure 4 shows the analysis of one of the alignments simulated with five taxa and HGT. The six true breakpoints (blue circles) indicate that three regions had HGT trees, whereas the rest of the alignment had the species tree topology. MDL partitioning inferred too many breaks (12) with the low-penalty parameter λ = 5 and the correct number of breaks (6) with the higher penalty λ = 12, but in all cases, the true breaks were approximately identified. The accuracy of BCA with correctly identified regions is shown in figure 4b. The posterior distribution of trees for a given region as obtained from MrBayes is the same as that obtained from “consensus” BCA with infinite α (independence prior). Figure 4b shows the posterior probability of the site-specific true tree from the Bayesian analysis of individual regions, which is moderate or even low for many regions. For this alignment, however, the posterior probability of the true tree increases largely for all sites when BCA uses an informative prior for concordance (α = 1). Parts dominated by sites with no HGT are allowed to share information about their common topology, and those parts show the most increase in support for the true topology.

FIG. 4.—

Example of one 5-taxon simulated alignment, from the HGT case. (a) Location of true breakpoints (•) and of breakpoints inferred by MDL (*). (b–d) Posterior probability of the sites' true trees obtained from concordance analysis with prior parameter α = 1 (- - -) or α infinite (—) after three partitioning strategies: true partition (b), MDL partition with λ = 7 (c), and fixed-length intervals (d).

This alignment illustrates a pattern of systematic bias shared by the parsimony-based MDL and Bayesian methods in some areas. For instance, the first HGT region (around base 15,000) has very low support for its true tree regardless of the partitioning method. Parsimony-based MDL does detect that this region has a different evolutionary process, but Bayesian methods (individual Bayesian analysis and BCA) fail to estimate the correct tree. The individual Bayesian analysis of the region delimited by the true breakpoints gives a 0.94 posterior probability for an incorrect tree. Another example is located on the far left of the alignment. A false break is detected around base 2,000 by MDL with λ = 7 or lower. Likelihood-based analyses also fail to give high posterior probability to the true tree for sites on the left of this false break.

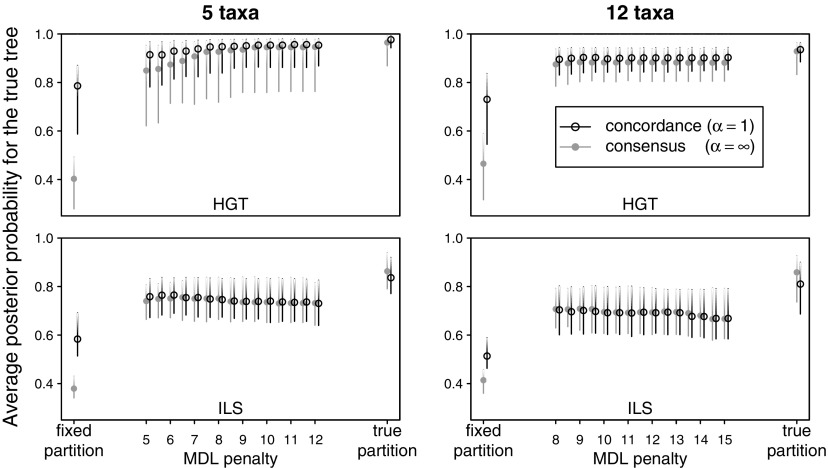
Figure 5 summarizes the various methods’ accuracies as measured by the average posterior probability for the true tree over all sites:

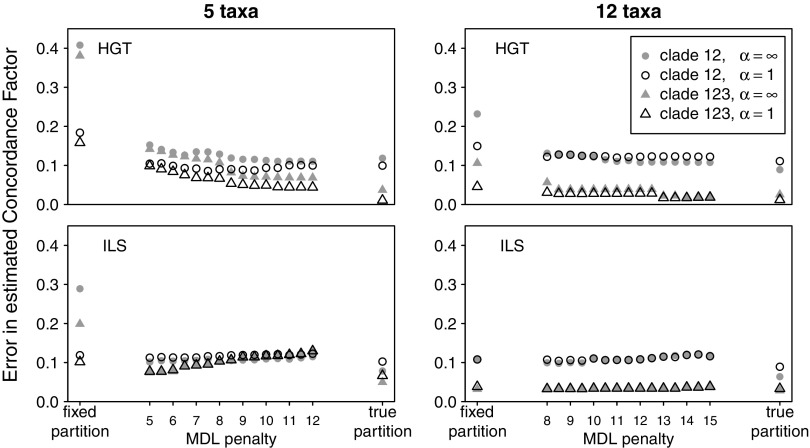
where T_j denotes the true generating tree at site j, and the formula averages the posterior probability for this site-specific true tree over all sites in the alignment. An average posterior probability of 1 occurred when a posterior probability of 1.0 was obtained for the sites’ true tree at all sites. An average posterior probability of 0.5 could be the result of an uncertain reconstruction (PP of 0.5 for the sites’ true tree) at all sites, or it could be the result of a perfect reconstruction (PP of 1.0 for the sites’ true tree) along half of the alignment and an very incorrect reconstruction (PP of 0.0 for the sites’ true tree) along the other half of the alignment. Figure 6 shows the accuracy (root mean square error) in inferring the concordance factor of clades (12) and (123), two clades in the species tree (fig. 1). The branch defining clade (12) was short and therefore difficult to reconstruct in all cases. It was especially difficult to reconstruct in the ILS case where this branch had a low concordance factor. Figures 5 and 6 show that in all cases investigated here, the informative prior α = 1 provides a significant increase in accuracy over the consensus prior (α infinite) when fixed-length partitions are used. It was not the case, however, when using MDL partitions, which typically had longer parts. On MDL partitions or on the true partition, the informative prior α = 1 provided little or no increase in accuracy over the consensus prior. Figures 5 and 6 also show that in all cases, MDL partitioning offers a significant improvement over fixed-length partitioning. Compared with the accuracy obtained with the true partition, MDL partitioning provides an almost optimal accuracy in the presence of HGT. In the presence of ILS, MDL partitioning performs better than fixed-length partitioning but was not optimal. Finally and surprisingly, the penalty parameter showed very little influence on the performance of MDL partitioning prior to BCA, over the range of penalty values explored in this study. No penalty value could be identified as being optimal.

FIG. 5.—

Average posterior probability for the true tree over all sites in the alignment. A value of 1 means that each site receives a 1.0 posterior probability for its true tree. Graphs represent 100 alignments each, on 5 (left) or 12 (right) taxa, simulated under HGT (top) or ILS (bottom) and analyzed with BCA with α = 1 (o) or α = infinity (•) after various partitioning methods (horizontal axis). Circles and bars indicate the median and interquartile range.

FIG. 6.—

Root mean square error in estimated site-wise concordance factor, for two clades in the species tree. The branch defining clade (12) had lowest concordance factor and was short, therefore difficult to reconstruct. Each point represents the average over 100 simulated alignments each, on 5 (left) or 12 (right) taxa, under either HGT (top) or ILS (bottom).

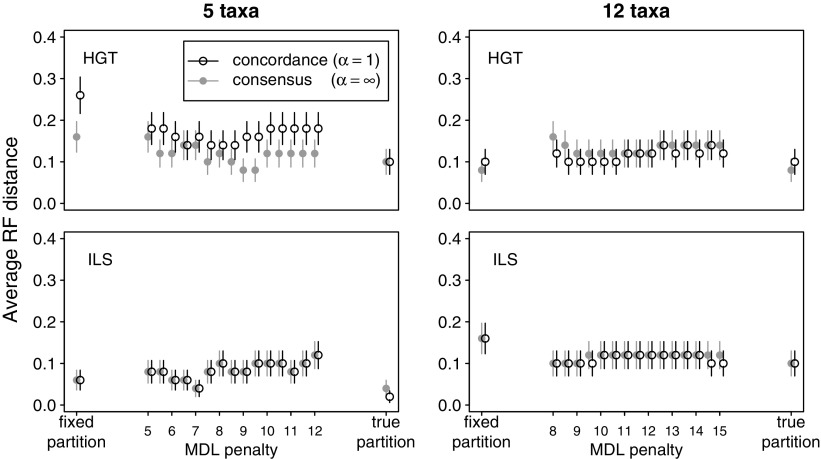
Although the informative prior (α = 1) was sometimes more accurate than the consensus prior (α = infinity) with respect to estimating concordance factors or individual sites' trees, no significant differences were found between methods regarding the accuracy of the estimated dominant history. Figure 7 shows the average Robinson–Foulds distance (Robinson and Foulds 1981) between the true concordance tree and the estimated concordance tree. These trees were reconstructed from clades with greatest estimated site-wise concordance factors. Using the true partition seemed to provide a slight increase in accuracy, but otherwise no partitioning method or concordance prior α seemed superior to another in the conditions used in this study.

FIG. 7.—

Robinson–Foulds (RF) distance between the true concordance tree and the estimated concordance tree, averaged over 100 simulated alignments, on 5 (left) or 12 (right) taxa, simulated under HGT (top) or ILS (bottom) and analyzed with BCA with α = 1 (o) or α = infinity (•) after various partitioning methods (horizontal axis). Circles and bars indicate the mean and standard error.

Discussion

In this work, I build on Ané and Sanderson (2005) and use dynamic programming to implement MDL partitioning on long alignments. I then propose to combine MDL partitioning with BCA to estimate the phylome, that is, the distribution of gene trees along the genome. This combined approach, which is applicable to extremely long alignments, is tested with simulations.

Strengths of MDL and Related Recombination Breakpoint Detection Methods

Hein (1993) introduced a parsimony-based approach, RecPars, which seeks to find loci with low parsimony scores separated by few recombination breakpoints. A user-defined value is needed to weigh the cost of recombinations and the cost of substitutions, and RecPars's accuracy is known to be sensitive to the choice of this cost parameter (Chan et al. 2006). RECOMP (Ruths and Nakhleh 2006) is another parsimony-based method, where the presence and the approximate location of recombination breakpoints is detected graphically using a user-defined threshold. Recco (Maydt and Lengauer 2006) weighs the costs of recombination and mutation with a user-defined cost ratio, similarly to parsimony-based methods. Our MDL approach belongs to this class of parsimony-based methods, but it provides a way to place the cost of recombination and of homoplasy on an equal footing, that of information complexity. Recently, Munshaw and Kepler (2008) also used the MDL principle for detecting recombination breakpoints. Their measure of fit counts different types of substitutions and is related to the parsimony score when the number of parsimony steps is small compared with the number of sites. Their method constrains the trees on either side of each breakpoint to differ by a single recombinant node, whereas our MDL criterion does not restrict the neighboring fragment topologies in any way.

MDL and AIC criteria are similar in that both try to strike a balance between the fit of the selected model to the data and the model complexity. GARD (Kosakovsky Pond et al. 2006a, 2006b) uses AIC with a likelihood-based fit. The penalty term in GARD penalizes each new breakpoint by the number of new branch length parameters: 2N − 3. This penalty is linear in the number of taxa in the tree, similarly to the penalty used here by MDL: λ ∼ N. The likelihood term in GARD is calculated on Neighbor-Joining topologies for computational tractability, and based on a traditional model of molecular evolution, which was later shown to be sensitive to substitution rate variability.

Not surprisingly, many methods for detecting recombination are sensitive to mutational “hotspots” and other substitution rate heterogeneity, when changes in branch lengths are detected as recombination (Grassly and Holmes 1997; McGuire and Wright 2000; Husmeier 2005; Minin et al. 2005). For this reason, methods based on topological changes and insensitive to branch lengths seem most appropriate for the purpose of defining loci for later use by a species tree/gene tree reconciliation method.

A number of powerful methods have used Bayesian inference or hidden Markov models (HMM) for estimating the number and location of recombination breakpoints while accounting for their uncertainty (Husmeier and McGuire 2003; Suchard, Weiss, et al. 2003; Minin et al. 2005; Bloomquist et al. 2009). Due to their computational complexity, these methods are either limited to few taxa (4 or 5 typically), or they need to be guided by a known phylogenetic tree on parental, nonrecombining sequences. Webb et al. (2009) increased the number of taxa that can be handled by combining an HMM with a Bayesian framework for the state space of this HMM. de Oliveira Martins et al. (2008) also increased the number of taxa that can be handled by adopting a prior distribution that favors small subtree-prune and regraft distances between trees at neighboring loci, thereby reducing the region of tree space that needs to be covered. The maximum likelihood approach by Boussau et al. (2009) estimates the state space of an HMM (or of a mixture model) and also scales well with the number of taxa. Because this approach uses a fixed, user-defined number of locus topologies, it seems difficult to apply to whole-genome alignments. Although these approaches do not seek species tree reconstruction, future developments seem particularly promising for the integrated inference of recombination breakpoints with species tree reconstruction. Furthermore, it is yet unknown which of these methods can scale up to very long alignments, up to hundreds of millions of sites. MDL offers a cheap and informative way to partition such long alignments.

In choosing between parsimony-based and likelihood-based phylogenetic methods, there is the typical trade-off between computational speed and estimation accuracy. This trade-off implies that parsimony-based methods might be the only approach feasible on some large data sets. Recent likelihood-based methods (Suchard, Kitchen, et al. 2003; Husmeier 2005; Minin et al. 2005; de Oliveira Martins et al. 2008) have taken an intermediate approach, by using models that are similar to the no-common-mechanism model and have a close connection to maximum parsimony (Tuffley and Steel 1997). In their Bayesian approaches, all branch lengths are integrated out analytically, thereby greatly reducing the computational burden. Husmeier and Mantzaris (2008) showed how these likelihood-based methods are also subject to long-branch attraction (LBA), just like maximum parsimony. Indeed, Huelsenbeck et al. (2008) showed that under the computationally tractable no-common-mechanism model, the posterior probability of trees is closely linked to their parsimony scores. Husmeier and Mantzaris (2008) proposed a revised model that is not subject to LBA but at the cost of a substantial computational increase.

Although the parsimony-based MDL approach described here is expected to be susceptible to LBA, it is viewed as a method to define loci rather than a method to infer trees. Widely varying substitution rates (heterotachy) and subsequent LBA are expected to cause MDL to detect extra breakpoints rather than too few, especially in fast-evolving regions. Extra false breakpoints can reveal changes in substitution rates or evolutionary constraints rather than topology changes. However, loci identified by MDL can then be analyzed with maximum likelihood or Bayesian methods, more robust to LBA. In places where MDL detects extra false breakpoints due to LBA, BCA, or other likelihood-based methods may still reconstruct the same tree topology on either side of the breakpoint.

Lessons from the Simulation Study

The simulation results presented here demonstrate that MDL partitioning provides a substantial improvement upon fixed-length partitioning, especially when combined with the consensus-like tree building method in BCA (α = infinity). Even when combined with BCA and an informative prior (α = 1) that lets short fragments share information about their trees, MDL partitioning provides improved estimates of phylogenetic trees at individual sites, compared with fixed-length partitioning. A surprising finding is that the estimates of the phylogenetic signal, both vertical (concordance tree) and horizontal (concordance factors), were insensitive to the penalty parameter in MDL. The number of inferred breakpoints was definitely sensitive to this penalty, but the resulting phylogenetic inference was not. A similar finding was reported in White et al. (2009).

The present work shows the value of fast partitioning methods. MDL partitioning can be refined in many ways but is a promising first step in the analysis of genome-wide alignment.

The concordance analysis (α = 1) improved over the consensus-like analysis especially well in two situations. The first situation is with fixed-length partitioning. With many small fragments, each fragment has few informative sites and a poorly resolved tree when analyzed individually. BCA is able to pool information across compatible fragments, thus improving the resolution of the inferred tree at each locus. The second situation is in the presence of HGT. This is not surprising because BCA does not make any particular assumption about the process of gene tree discordance. Instead, BCA attempts to group fragments into clusters, where all fragments in the same cluster share the same tree topology. The prior distribution of trees used in BCA matched our simulated distribution of trees pretty very well under HGT, where most fragments had the species tree and formed a large cluster, whereas a few fragments each had a distinct topology (due to HGT) and each formed a small cluster of their own.

Spatial Correlation among Neighboring Trees

We recognize that trees were simulated with little correlation between neighboring fragments: Conditional on the species tree, the simulated coalescent trees, and the simulated HGT events at neighboring loci were independent of each other. This simulation process mimics the assumptions in MDL or BCA, which ignore the spatial correlation of neighboring trees. To my knowledge, there is no gene tree/species tree reconstruction method that accounts for or uses the dependence across neighboring gene trees. Some recombination detection methods use this dependence (de Oliveira Martins et al. 2008) and have been used on viruses. In general, it seems reasonable to expect that the level of dependence might vary with the type of organism (viruses, bacteria, and eukaryotes) and the phylogenetic depth of the alignment, for instance.

Spatial correlation among neighboring trees could be built into BCA using a modification of its Dirichlet prior distribution on trees, in order to model a priori autocorrelated fragment trees. This is an area for future work.

Systematic Errors

An initial concern was that MDL could be led astray by systematic errors because it is parsimony-based (Felsenstein 1978). But MDL was used only to identify breakpoints, not for tree building. The tree reconstruction from the true partition with known breakpoints actually revealed a substantial amount of systematic error from MrBayes. With a consensus-like approach and when true loci are analyzed separately, any erroneous estimation can be attributed to a misspecification of the evolutionary model. The model used to simulate the sequence data was much more complex than the model used in the analysis, including rate variation across both sites and lineages (heterotachy) and a complex model (GTR) of transition rates.

Figure 5 shows an average posterior probability around 80% for the true sites’ tree in the ILS simulations. All sites having an 80% posterior probability for their true tree could explain this finding. However, we observed that a majority of sites (80% or more) had a high support for their true tree (posterior probability > 0.90) and that an average of 5% (5 taxa) and 14% (12 taxa) of sites had virtually no support for their true tree (posterior probability < 0.10). These sites were not merely in uninformative regions. Indeed, most of them (97–99%) showed a high posterior probability (>0.50) for an incorrect tree, and 79% (5 taxa) or 88% (12 taxa) of these sites had a posterior probability above 0.80 for some incorrect tree. This is a sign of systematic error for about 5–14% of sites. This high frequency of systematic errors could be explained by a substantial fraction of simulated coalescent trees with very short internal edges. It is known that the combination of a short internal edge with a mixture of branch lengths can cause of problem of long-branch attraction (Philippe et al. 2005; Matsen and Steel 2007; see also Kolaczkowski and Thornton 2009). This phenomenon may be at work here because our simulation of clock departure and heterotachy results in a mixture of branch lengths.

Therefore, this study reveals the importance of good single gene tree building methods to maximize the adequacy of the model assumptions and minimize the occurrence of systematic errors. Even in the phylogenomics era when huge amounts of sequence data can be combined, complex gene tree/species tree methods rely at their core on basic evolutionary models for individual tree reconstruction. The sophistication of gene tree/species tree methods should not side step the refinement of individual gene tree reconstruction methods because the rate of systematic error might be higher than desired. Efforts continue to be made in this direction, with the development of models that explain an increasing complexity of rate variation across sites and across lineages (Lartillot et al. 2007; Zhou et al. 2010) and with the study of the theoretical limitations of these models (e.g., Steel 2010).