Skip to main content
PMC home page
Frontiers in Physiology logoLink to Frontiers in Physiology
. 2011 Feb 24;2:4. doi: 10.3389/fphys.2011.00004

A Computational Systems Biology Software Platform for Multiscale Modeling and Simulation: Integrating Whole-Body Physiology, Disease Biology, and Molecular Reaction Networks

Thomas Eissing 1, Lars Kuepfer 1, Corina Becker 1, Michael Block 1, Katrin Coboeken 1, Thomas Gaub 1, Linus Goerlitz 1, Juergen Jaeger 1, Roland Loosen 1, Bernd Ludewig 1, Michaela Meyer 1, Christoph Niederalt 1, Michael Sevestre 1, Hans-Ulrich Siegmund 1, Juri Solodenko 1, Kirstin Thelen 1, Ulrich Telle 1, Wolfgang Weiss 1, Thomas Wendl 1, Stefan Willmann 1, Joerg Lippert 1,*
PMCID: PMC3070480  PMID: 21483730

Abstract

Today, in silico studies and trial simulations already complement experimental approaches in pharmaceutical R&D and have become indispensable tools for decision making and communication with regulatory agencies. While biology is multiscale by nature, project work, and software tools usually focus on isolated aspects of drug action, such as pharmacokinetics at the organism scale or pharmacodynamic interaction on the molecular level. We present a modeling and simulation software platform consisting of PK-Sim® and MoBi® capable of building and simulating models that integrate across biological scales. A prototypical multiscale model for the progression of a pancreatic tumor and its response to pharmacotherapy is constructed and virtual patients are treated with a prodrug activated by hepatic metabolization. Tumor growth is driven by signal transduction leading to cell cycle transition and proliferation. Free tumor concentrations of the active metabolite inhibit Raf kinase in the signaling cascade and thereby cell cycle progression. In a virtual clinical study, the individual therapeutic outcome of the chemotherapeutic intervention is simulated for a large population with heterogeneous genomic background. Thereby, the platform allows efficient model building and integration of biological knowledge and prior data from all biological scales. Experimental in vitro model systems can be linked with observations in animal experiments and clinical trials. The interplay between patients, diseases, and drugs and topics with high clinical relevance such as the role of pharmacogenomics, drug–drug, or drug–metabolite interactions can be addressed using this mechanistic, insight driven multiscale modeling approach.

Keywords: systems biology, PBPK, software, multiscale, modeling, simulation, oncology, signal transduction

Introduction

Most properties of a biological organism result from complex interactions between biological scales from the molecular level to the whole body. They are emergent properties not evident at individual biological scales. Today, systems biology is aiming for a holistic description and understanding of biological processes (Chong and Ray, 2002) by an integration of analytical experimental approaches with synthetic computational models.

The holistic claim of systems biology is progressively influencing science and leading to the mergence of previously largely separated fields of investigation and modeling. In the context of pharmaceutical research and development it is relevant not only to investigate drug action at the target site (pharmacodynamics, PD), but also to understand how the drug reaches the target and what effective concentrations result from a given dose (pharmacokinetics, PK). When taking a mechanistic view of the involved processes, PK/PD models inevitably merge with approaches to model molecular signaling and metabolic networks (Kuepfer, 2010).

Besides the different physiological scales involved in life science and pharmaceutical research, the latter is also organized into multiple project stages of research spanning from early target identification and lead optimization to late clinical development and life-cycle management of marketed drugs. Systems biology approaches are progressively entering several of these stages and promise to accompany and support projects along the development process by integrating and testing available knowledge and data as well as translating this knowledge to new settings and patient groups (Butcher et al., 2004). However, there is still a clear demand to better relate, translate, and merge results between the different physiological scales as well as research and development processes involved.

A large number of software solutions have been developed in the systems biology area supporting scientists in model building and analysis. The Systems Biology Markup Language (SBML) homepage1 provides a growing compilation of different software tools with a main focus on metabolic and signaling networks reflecting the non-clinical focus of systems biology so far. General physiology modeling tools focusing on the dynamics of human physiology across multiple organ systems as well as PK software tools focusing on physiologically-based approaches to describe xenobiotic absorption, distribution, metabolization, and elimination (ADME) have been reviewed by different authors, e.g. (Hester et al., 2010) and (Nestorov, 2007; Espie et al., 2009), respectively. Most of the available tools focus on selected aspects and physiologically-based PK (PBPK) models are neither easily extendable nor customizable. Moreover, model implementations using flexible general purpose simulation environments are generally time consuming, error prone, and difficult to assess considering their non-standard formulation.

In the following, the concept, architecture, realization, and functionality of a software platform for biological multiscale modeling and simulation is introduced and illustrated. The software platform is designed to support the integration of the different physiological levels from the whole-body scale to the molecular level and fields of research as shown in Figure 1. First, the platform concept and its realization including common components, different graphical user interfaces (PK-Sim® and MoBi®), import and export functionalities, as well as command line options via interfaces to computing environments (R and MATLAB®) will be explained. Second, the use of the software will be illustrated with an exemplary multiscale model that combines the description of tumor growth and signal transduction at the cellular level with a chemotherapeutic intervention, where a prodrug is bioactivated by a polymorphic enzyme, at the whole-body level. In a virtual clinical study, the individual outcome of the therapy with the prodrug is simulated based on realistic genetic predispositions of the virtual patients in a large virtual population.

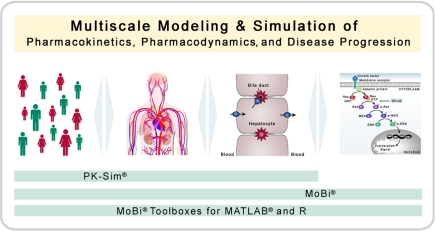
Figure 1.

Figure 1

Open in a new tab

Multiscale modeling and simulation. The software platform is designed for modeling and simulation of biological process with a focus on pharmacokinetics, pharmacodynamics, and disease progression (including biochemical reaction networks). Thereby, the platform allows the combination of multiple organizational and physiological scales. PK-Sim® has a focus on whole-body physiology and its variability in populations, whereas MoBi® has a focus on the cellular and molecular level.

Materials and Methods

Software

The software platform presented in the Section “Results” comes along with about 400 pages of documentation in the form of handbooks. Further information can also be found at www.systems-biology.com/products. The platform is available to academic researchers via a free non-commercial license, please contact info@systems-biology.com.

Software and trademark information: Excel® is a registered trademark of Microsoft Inc., Redmond, USA; R is a product of the R Foundation for Statistical Computing, Vienna, Austria2; MATLAB® is a registered trademark of The MathWorks, Inc., Natick, USA3; PK-Sim® and MoBi® are registered trademarks of Bayer Technology Services GmbH, Leverkusen, Germany4.

Application example model building

The tumor model presented in the Section “Results” considers resting (Q), dividing (P), and dead (D) cells. The Q–P transition rate is given by p × Q/(ProLayer + Q) × ERKPP, with p as the proliferation rate constant (value of 0.01 cell/molecules × min−1), Q as the number of resting cells (initial condition of 1), ProLayer as a constant accounting for the relative size of the proliferative layer (value of 1), and ERKPP as the concentration of ERKPP, which is provided through the signal transduction model described below. The P–Q transition rate is given by ln(2)/cyclelength × P, with ln as the natural logarithm, cyclelength as a constant accounting for the length of a cell division cycle (value of 1440 min), and P as the number of dividing cells (initial condition of 0). The Q–D transition is given by the simple first-order rate a_n × Q, with a_n as the rate constant (value of 5 × 10−6 min−1), and Q as the number of resting cells (see above).

The signal transduction model has been described in detail by Brightman and Fell (2000) and was imported via the SCAMP import functionally of MoBi®. The only modification/extension made, is a reversible binding of Raf to the active metabolite as expressed by kon × Rafst × ActMet × fu/Kcellpls − koff × RafstComplex, with kon as the binding rate constant (value of 100 min−1μM−1), Rafst as the concentration of the activated Raf (initial condition of 0 molecules/cell), ActMet as the concentration of active metabolite in the pancreas (initial condition of 0 μM) as provided through the PBPK model described below, as a correction factor to account for unspecific protein binding and partitioning of the active metabolite as is typical for PBPK models (value of 0.0721), koff as the dissociation rate constant (value of 5 min−1), and RafstComplex as the complex of active Raf and the active metabolite (initial condition of 0 μM). The unit differences between the signal transduction model in molecules/cell and the PBPK model in μM is accounted for by a stoichiometry entry of 600,000 for Rafst, i.e., 1 μM corresponds to 600,000 molecules/cell based on the assumption of a cell volume of 1 pl. The species ERKPP, which is part of the signal transduction model, is used in the tumor cell model, as described above.

The basis PBPK model was build using the PK-Sim® default settings for a 30-year-old male virtual individual with a body weight of 73 kg. The derivation of physiological parameter is detailed in Willmann et al. (2003a, 2005). Compound-specific inputs for the virtual prodrug were: log lipophilicity = 3.0, fraction unbound = 0.112, and molecular weight = 400 g/mol. Compound-specific inputs for the active metabolite were: log lipophilicity = 2.2, fraction unbound = 0.200, and molecular weight = 417 g/mol. The application scheme for the prodrug was: bi-daily oral administration of 1 mg. For both compounds, intrinsic hepatic clearances of 50 l/min were defined. In addition, a hepatic clearance via cytochrome P450 2D6 (CPY2D6) specific for the prodrug was implemented as a link that serves as a source for the active metabolite and thereby couples the two PBPK models via the first-order rate equation CL2D6 × ProDrug × , with CL2D6 as the clearance rate constant [value of 100 l−1 for extensive metabolizers (EMs)], ProDrug as the prodrug concentration in liver cells (initial condition of 0 μM), and as a correction factor to account for unspecific protein binding and partitioning of the prodrug as is typical for PBPK models (value of 0.0135).

CYP2D6 activity and population simulation parameter settings

The activity differences for CYP2D6 between poor (PM), intermediate (IM), extensive, and ultra-rapid (UM) metabolizers were derived according to Zanger et al. (2001). For population simulations, variability was superimposed with a geometric SD of 1.6 according to Zanger et al. (2001). The frequency of the different metabolizers within a population was according to Sistonen et al. (2007) for Europeans. Where indicated, physiological parameters (organ volumes and composition, blood flows, etc.) were varied independent of the metabolizers’ phenotype. The derivation of physiological parameter distributions in virtual populations is detailed in Willmann et al. (2007b, 2009a) and implemented in the PK-Pop module of PK-Sim®. For the population generation the settings were: European population (ICRP), age range between 18 and 40, gender male, and without further restrictions. Where indicated, variability in the protein levels of the signal transduction pathway was superimposed with a geometric SD of 1.25, which is in the range reported in similar settings (Sigal et al., 2006; Spencer et al., 2009).

Results

Platform concept and realization

The modular architecture of the software platform is outlined in Figure 2. The common core components consist of a specification of the mathematical model in XML-file format and the simulation kernels. The XML file is configured in a hierarchical manner and does not only include information on the different parts of the mathematical model, but also meta-information related to simulation and solver parameters, simulation results, experimental data, and information for documentation purposes. The simulation kernel currently contains the CVODE solver for (stiff) ordinary differential equations (Cohen and Hindmarsh, 1996)5 and the MATLAB®-derived ddesd solver for delay differential equations (Shampine, 2005)6. A plug-in interface allows the straightforward integration of further ODE and DDE solvers. The XML model can be formulated with different software tools of the platform.

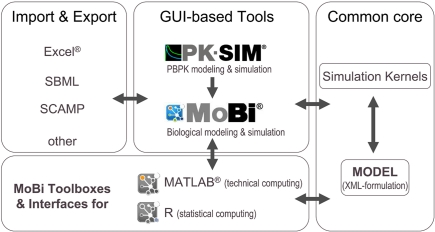
Figure 2.

Figure 2

Open in a new tab

Modular structure of the software platform. In the center of the platform are PK-Sim®, MoBi®, and the MoBi® toolboxes for R and MATLAB®. While all tools allow simulation and result visualization, PK-Sim® and MoBi® are designed for modeling and low through-put simulations, while the toolboxes allow batch simulations and additional analysis tasks. A common XML-file format can be interpreted by the different programs. Additional flexibility is provided through import and export functions. (Trademark information: see Materials and Methods).

PK-Sim®

The first graphical user interface based tool is PK-Sim®, a whole-body PBPK modeling software. PBPK modeling has been used for decades in the field of toxicological risk assessment (Loizou et al., 2008) and has in recent years been extended toward the application in the drug research and development area (Willmann et al., 2003b, 2004, 2005, 2007a,b, 2009b; Edginton et al., 2006a,b,c, 2008; Vossen et al., 2007; Edginton and Willmann, 2008). PK-Sim® allows rapid access to all relevant anatomical and physiological parameters for humans and the most common laboratory animals (mouse, rat, minipig, dog, and monkey) that are contained in the integrated database (Willmann et al., 2003b). In the example below, virtual patients with pancreatic tumors are constructed based on the whole-body model.

An exemplary screenshot of the stand-alone software is shown in Figure 3A. The software's user interface is structured according to the ADME paradigm which ensures ease-of-use and a straightforward identification of parameter input requirements. Different prediction methods for deducing drug-dependent parameters relevant for absorption and distribution, based on simple physico-chemical properties of the substance under investigation, can be chosen. These include the distribution models for small molecules as developed by Willmann et al. (2003a), Rodgers et al. (Rodgers et al., 2005a,b; Rodgers and Rowland, 2006, 2007), Poulin et al. (Poulin et al., 2001; Poulin and Theil, 2002a,b), Berezhkovskiy (2004), Schmitt (2008), as well as a newly developed proprietary distribution model dedicated to biologicals. A typical PK-Sim® whole-body model includes 17 organs and tissues, which are subdivided into the compartments vascular plasma and red blood cells, tissue interstitial and cellular space. The organs are connected via a blood flow from an arterial blood pool to a venous blood pool. An inverse flow for the lung represents the small circulation and closes the mass balance. Convective and diffusive uptake into tissue is explicitly represented in the model and an arbitrary number of specific active transport and metabolization processes in specific organs can be defined by the user to reflect substrate properties of a compound. The implemented whole-body model also includes a gastrointestinal tract to simulate oral applications of various formulation types (Willmann et al., 2003b, 2004) and allows administration of drugs into any other organ, e.g., to describe subcutaneous, transdermal, or respiratory drug administration.

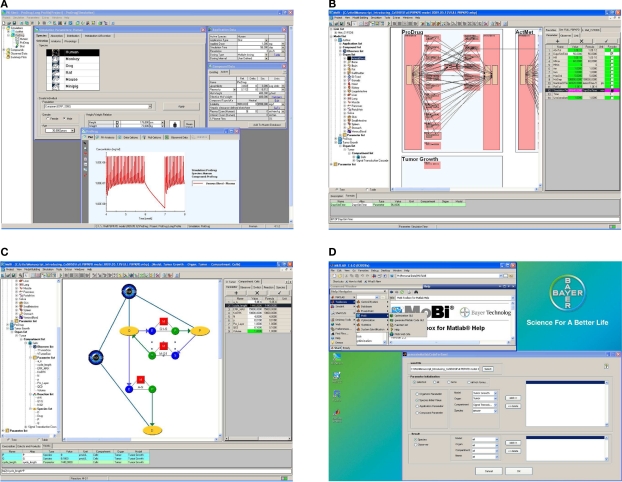
Figure 3.

Figure 3

Open in a new tab

Graphical user interface examples. The software is build to allow an efficient building, processing, and analysis of computational systems biology models. While assisting the user through graphical interfaces, full programming flexibility is provided through the interfaces to R and MATLAB®. (A) PK-Sim® screenshot. (B) MoBi® screenshot at whole body level. (C) MoBi® screenshot at the sub-compartment level. (D) MATLAB® help and GUI screenshot to assist in code generating for MoBi® model processing. Additional details describing the four subfigures as well as enlarged versions of these are available as Supplementary Material.

For humans, the database for anatomical and physiological parameters allows the individualization of the virtual human depending on his ethnicity, gender, age, body weight, and height (Willmann et al., 2007b, 2009a). For pediatric applications metabolization and excretion processes are automatically scaled to children of a given age using prior knowledge about the age-dependence of organ volumes and blood flow rates (growth) as well as the age-dependence of enzyme activities and renal or hepatobiliary excretion capacities (maturation; Edginton et al., 2006a,c). Besides average values for the anatomical and physiological parameters, prior information about the inter-individual variability has also been integrated allowing an automated simulation of virtual populations including pediatric populations down to term and even pre-term neonates. Diverse visualization options for simulation results and, if available, imported experimental data are included in the software tool as well as routines to derive relevant PK parameters and an export of all simulated results to MS Excel®. Altogether, PK-Sim® is designed for rapid and efficient PBPK model building and simulation for both, modeling experts and modeling non-experts.

MoBi®

The second major component of the platform is MoBi®, a flexible, stand-alone, general purpose graphical modeling tool. MoBi® is fully compatible with PK-Sim®, i.e., it can load and simulate any PK-Sim® model. In addition, it allows to make structural modifications of the PBPK model as, for example, the addition of further tissues or tissue sub-compartments, the dynamic coupling of multiple PBPK models established in PK-Sim® to represent drug-metabolite or drug–drug interaction scenarios (Vossen et al., 2007), but also the integration of metabolic or signaling network models as PD effect models of arbitrary complexity. Alternatively, MoBi® can also be used to build models “from scratch”. Exemplary screenshots are shown in Figures 3B,C. MoBi® can simultaneously simulate interacting PBPK models for multiple substances (“species,” e.g., drugs or endogenous substances such as plasma proteins, hormones, etc.) and offers predefined structural objects for model building such as organs, compartments, links (that define the transfer of a species between compartments), and reactions (that define interactions between different species such as specific binding). Parameters of a model can either be defined as constants or as formulas to account for dependencies on other parameters or species. The structural objects organism, organ, and compartment are inspired by mammalian anatomy. With these structural objects MoBi® allows the hierarchical organization of models and the representation of the whole-body, organ, and tissue and sub-cellular level in a graphical working environment. Reactions and links couple the different species using parameters and functional relations that the user can freely define, e.g., transport kinetics, rate laws such as mass action, Michaelis–Menten, Hill, or more sophisticated kinetics. Species appear in a reaction or link as educts, products, or modifiers. Reactions between educts and products are balanced by a stoichiometry that can be assigned by the user, while in contrast modifiers represent catalytic species that are neither produced nor consumed in a reaction. The above mentioned information is assembled by MoBi® to establish a set of differential equations that describe the rate and parameter dependent changes of species over time. In addition, all models can be extended by so-called observers. Observers are derived from state-variables of the differential equation system (species) and parameters by user-defined formulas. Furthermore, a model can be extended to represent distinct events using so-called switches. A switch consists of a conditional expression and two lists of assignments for species and parameters that are either processed, if the conditional expression is met, or not processed. It can be used to represent changes of (for example experimental) conditions or to model rapid processes implicitly rather than explicitly as a part of the differential equation. During simulation, i.e., integration of the differential equation, when a switch condition is met, MoBi® stops the integration, changes the species and parameter values according to the switch definition, and then restarts the integration. In addition to its graphical model building capabilities, MoBi® offers import functionalities for two common modeling formats frequently used in computational biology (SCAMP; Sauro, 1993 or SBML; Hucka et al., 2003). As in case of PK-Sim®, simulation results can be visualized in MoBi® and exported to MS Excel®. Also, the differential equation system can be exported to MATLAB®.

While MoBi® allows full access to all properties of a model and provides consistency checks for rate equations and other tools, e.g., for checking mass balances, it is truly flexible and will also accept models breaching mass balance (unlike PK-Sim®). As a consequence, model building in MoBi® requires a higher level of expertise than the use of PK-Sim®.

MoBi® toolboxes for R and MATLAB®

A third component of the software platform are interfaces to R and MATLAB® that are useful to analyze and interpret PK-Sim® and MoBi® models in an fast and automated manner. Advanced model analysis may, for example, involve statistical analysis of the results obtained or the calculation of local or global sensitivity measures to assess model robustness and quality (Kacser and Burns, 1973; Heinrich and Rapoport, 1974; Heinrich and Schuster, 1996; Sobol’, 2001; Zi et al., 2008). Also, repeated simulations in an automated manner are useful, for example, to identify uncertain model parameters based on a numerical minimization of the error between experimental and simulation results or to investigate population behavior. The so-called MoBi® toolboxes for R® and MATLAB® contain basic functions for parameter access and manipulation as well as simulation result retrieval. The MoBi® toolbox for MATLAB® also contains extended analysis functionalities, e.g., to perform sensitivity analysis. For several tasks, both command line functions and graphical user interfaces are available within MATLAB®. Also, example and help files are integrated into the MATLAB® environment. An exemplary screenshot is shown in Figure 3D. Tools developed in R and MATLAB® that are frequently used, have also been compiled and integrated into the MoBi® user interface, for example, to perform parameter identification or population simulation tasks without the need to install the additional software.

Application example – pharmacogenomic impact on cancer therapy

To illustrate the scope of the software platform concept and the performance of the current implementation in a case study, we present an exemplary multiscale model of a virtual patient with a pancreatic tumor and the treatment by a virtual chemotherapeutic agent (Figure 4). The chemotherapeutic agent is administered in the form of a prodrug, and the active metabolite is formed from this prodrug in the liver of the virtual patient by an enzyme that has a known polymorphism that alters the metabolization rate (CYP2D6). The model is then applied to simulate a virtual clinical study scenario, where the individual therapeutic outcome of the treatment is simulated based on realistic genetic predispositions of CYP2D6 of the virtual patients. While the test case is truly virtual, as the properties of the modeled drug are, the preceding scenario is prototypical for the application of the platform in pharmaceutical R&D.

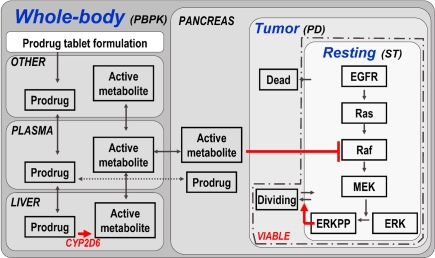
Figure 4.

Figure 4

Open in a new tab

Model structure of multiscale PBPK–PD–signal transduction (ST) application example. The figure outlines the most relevant processes captured in the multiscale model. Details (e.g., additional organs, sub-compartments, and proteins) are omitted for clarity. A whole-body PBPK model is constructed for a prodrug and its active metabolite. The two substances are coupled via a hepatic CYP2D6 clearance of the prodrug, which is the source for the active metabolite. A tumor (PD) model is contained in the pancreas of the whole-body model, considering resting, dividing, and dead cell populations. Within the resting cells an EGFR signal transduction model is nested. Raf, a kinase participating in the signal transduction process, is the target of the active metabolite. ERKPP, a transcription factor, drives the transition into the dividing population. The sum of resting and dividing cells constitutes the viable tumor mass and serves as a primary output. For additional details, see Materials and Methods.

First, a tumor model is established by creating a tumor compartment containing three sets of cells constituting the virtual tumor, i.e., quiescent (resting), proliferative (dividing), and apoptotic or necrotic (dead) cells. For each cell type, initial conditions and transition rates are defined (see Materials and Methods). For example, only those quiescent cells contained in a so-called proliferative layer can become proliferative. The transition rate of cells from the quiescent to the proliferative state is assumed to be proportional to the concentration of a transcription factor of special interest, i.e., phosphorylated extracellular-signal regulated kinase (ERKPP).

Second, a published epidermal growth factor (EGF) signal transduction model (Brightman and Fell, 2000) describing ERK activation is imported and coupled to the tumor model by the above assumption.

Third, whole-body PBPK models of the two substances of interest, the chemotherapeutic prodrug and its active metabolite, are established using PK-Sim®. The prodrug is administered bi-daily (in the form of an oral tablet) in two cycles starting in weeks 5 (2-week duration) and week 8 (1-week duration). The two PBPK models are coupled within MoBi® by defining a link that describes the bioactivation of the prodrug via hepatic enzymatic transformation to the active metabolite catalyzed by CYP2D6. This sink for the prodrug serves as the source for the active metabolite. The tumor model is (arbitrarily) located in the pancreas. Consequently, the time course of the active metabolite in the pancreas determines the PD effect. The PD effect in this model is mediated by a reversible binding of the active metabolite to the Raf kinase in pancreatic tumor cells, which is part of the imported signal transduction pathway, and its subsequent inhibition. Raf inhibition leads to a decrease in ERKPP activation. The transcription factor ERKPP promotes tumor growth and, consequently, an inhibition slows or stops tumor growth (see Materials and Methods for additional details).

The full model, containing more than a hundred ordinary differential equations and several hundred parameters (including initial conditions and derived parameters), can be established in >1 h by a trained modeling expert. It is important to mention that nearly all parameters of the model are either taken from PK-Sim®’s database of anatomical and physiological information, calculated using prediction models from a small set of drug-dependent parameters, or contained in the literature-based and imported signal transduction model. Establishing a similar model in a programming environment de novo including equation formulation, literature research on anatomical and physiological parameters, as well as their implementation and validation, would take months even for highly experienced individuals. A single simulation on a time scale of 4 weeks takes about 1 s (for a single intravenous drug application) to 1 min (for multiple oral drug administrations) on a single processor core of a state-of-the-art laptop. For large numerical tasks, an interface to the German D-Grid7 has been established allowing distributed computing in a fully scalable cloud computing infrastructure.

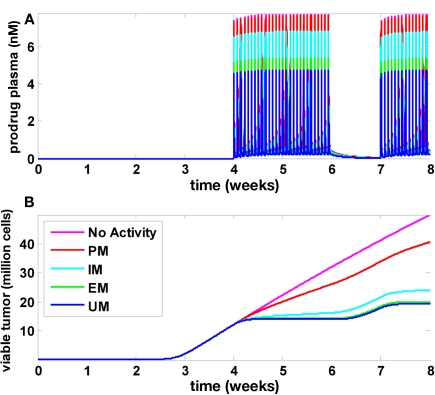
Results of the multiscale PBPK/PD model are presented in Figure 5. Figure 5A shows the plasma concentration time profile of the prodrug that was administered during weeks 5, 6, and 8. Figure 5B shows tumor growth without drug treatment (magenta line). In this case, tumor growth is biphasic: as the tumor size increases, the growth regimen switches from exponential to linear after approximately 3 weeks. In individuals undergoing chemotherapy, growth retardation or even stagnation is observed during the treatment periods (week 5, 6, and 8), and the simulations indicate a fast relapse upon treatment interruption (week 7). The four curves in Figure 5B refer to individuals with different CYP2D6 phenotypes termed UM, EM, IM, and PM (Zanger et al., 2001). As can be seen, the treatment efficacy decreases with decreasing CYP2D6 activity. While the drug is effective for CYP2D6 activities found in UM, EM, and, to a lesser extend, IM, the treatment efficacy is drastically reduced in PM. In order to investigate whether this indeed reflects a strong and specific pharmacogenomic impact or just a generally high sensitivity of the model toward model parameters, and in order to investigate if a typical variability in CYP2D6 activities or other physiological parameters can mask the pharmacogenomic impact in a realistic population, population simulations were performed.

Figure 5.

Figure 5

Open in a new tab

Tumor development, treatment, and CYP2D6 activity influence. Time courses for the prodrug plasma concentration (A) as well as viable tumor cells (B) are shown for five different values of CYP2D6 activity. Without CYP2D6 activity (magenta), no active metabolite will be generated. Regarding tumor growth, this scenario is identical to a scenario without drug treatment. The activity differences for CYP2D6 between PM, IM, EM, and UM were derived according to Zanger et al. (2001).

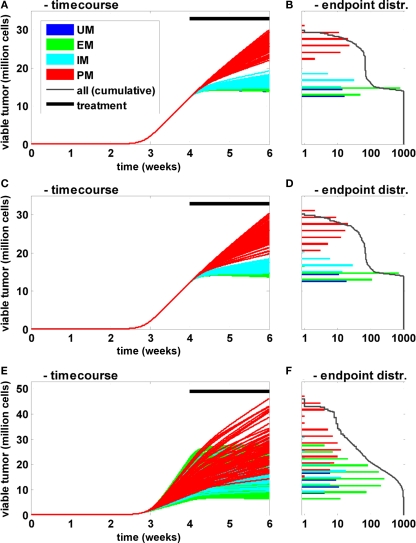
In these population simulations, only the CYP2D6 activity was varied between the individuals with reference values and a superimposed variability according to Zanger et al. (2001; Figures 6A,B). A European population composition was chosen according to Sistonen et al. (2007). Second, in addition to the clearance variability, standard physiological parameters (organ volumes and composition, blood flow rates, etc.) were varied according to Willmann et al. (2007b, 2009a; Figures 6C,D). Third, in addition to clearance and physiological variability, natural biological noise at the signal transduction level was considered (Elowitz et al., 2002; Rao et al., 2002; Sigal et al., 2006; Cohen-Saidon et al., 2009; Spencer et al., 2009). In all settings 1000 individuals were simulated and the tumor size (expressed as the number of viable cells) at the end of the simulation was used as the primary endpoint. The population simulations shown in Figures 6A,B indicate that inter-individual variability has a strong influence on the time course and thereby on treatment efficacy. However, the CYP2D6 phenotype remains the main determinant for variability within a population: even the most efficiently treated PM shows less response to the treatment than the least efficiently treated IM. Further, the clearance variability propagates most effectively through the network for small clearance values, i.e., the sensitivity toward this parameter is anti-proportional to its magnitude. A comparison of Figures 6A,B versus Figures 6C,D shows that physiological variability increases the overall variability. However, the CYP2D6 clearance phenotypes remain the dominating source of variability in the given setting. When the proteins of the signal transduction pathway are varied in addition (Figures 6E,F), the clear separation appears to be lost. However, when treatment efficacy is not simply judged by the primary endpoint but, for example, by the endpoint normalized to the tumor size at the beginning of the treatment (week 4), PM and IM phenotypes again separate from each other and from the two other groups (data not shown). This indicates that variability in the signal transduction process mainly influences tumor growth prior to treatment but hardly treatment efficacy itself in the current setting.

Figure 6.

Figure 6

Open in a new tab

Influence of CYP2D6 activity on the population level. Time courses (A,C,E) of viable tumor and frequency distribution of endpoints on a logarithmic scale (B,D,F) after 4 weeks of untreated tumor growth followed by a 2-week bi-daily treatment period are shown for a population of 1000 individuals. The activity differences for CYP2D6 between PM, IM, EM, and UM were derived according to Zanger et al. (2001). The frequency of the different metabolizers was according to Sistonen et al. (2007) for Europeans. In (A) only clearance was varied between the individuals. In (C) additional physiological parameters (organ volumes and composition, blood flows, etc.) were varied independent of the metabolizers’ phenotype according to Willmann et al. (2007b, 2009a). In (E) the concentrations of the proteins involved in EGFR signal transduction were varied in addition to the two before mentioned sources of variability.

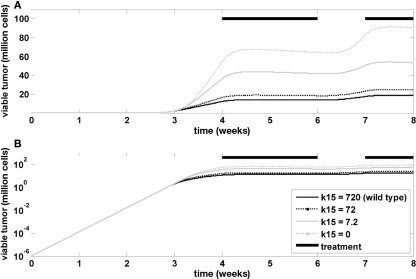
Finally, the model was used to investigate the influence of Ras mutations on tumor growth and treatment efficacy. A Ras mutation was introduced in the model by changing the rate constant in the tumor model that determines the inactivation of GAP-bound Ras. This is a formal representation of the changes associated with GAP-insensitive (G12V) mutants, which are frequently found in many cancers (Stites et al., 2007). Figure 7 indicates that the mutation has no impact on the exponential tumor growth phase, but a strong impact on the linear growth phase. The impact during tumor treatment is also minor.

Figure 7.

Figure 7

Open in a new tab

Influence of RAS mutation. Time course of viable tumor mass on a linear (A) and logarithmic (B) scale for different values of k15, which is the rate constant determining the inactivation kinetics of GAP-bound, RAS. Bi-daily treatment is indicated by thick black lines.

Discussion

We present a concept and the implementation of a software platform for multiscale modeling and simulation of biological processes along with a clinical application example spanning multiple physiological scales.

The model presented includes whole-body PBPK models of a virtual prodrug and its active metabolite generated via hepatic CYP2D6, coupled to a PD tumor and a signal transduction model at the cellular level. The untreated virtual tumor shows a switch from exponential to linear growth as has been described before (Greenspan, 1976; Marusic et al., 1994; Bru et al., 2003; Araujo and McElwain, 2004; Block et al., 2007; Radszuweit et al., 2009). Investigations on the influence of GAP-insensitive Ras mutations indicate that this mutation mainly impacts on the linear growth phase in the current setting, potentially reflecting the important role of growth-factor signaling during this phase to further promote cell division although limiting environmental conditions do not support exponential growth any more. Treatment success in this virtual clinical study is strongly dependent on the CYP2D6 phenotype, which would likely also have fundamental implications for optimal therapeutic dosing. Comparable findings have been reported for, e.g., the chemotherapeutic prodrug tamoxifen (Briest and Stearns, 2009; Rae et al., 2009).

Overall, the example illustrates the complexity of problems that can efficiently be addressed with a powerful modeling platform. It covers relevant biological phenomena exemplary for pharmaceutical R&D. The observed non-linear phenomena cannot be identified without systems-level thinking and modeling. Such investigations can help to contain risks for drug development as well as pave the road to individualized therapeutic designs (Kalow, 2006; Tomalik-Scharte et al., 2008; Deisboeck, 2009). In real-world application projects, the model structure and parameterization is adjusted to experimental data. The PBPK models are pre-parameterized by drug properties and refined using PK profiles. On the PD level (disease and signal transduction) models are adapted also to the specific situation of interest. For example, other signal transduction pathways or detailed models of drug induced processes such as apoptosis or inhibition of angiogenesis may have to be considered.

The model presented contains more than a hundred ordinary differential equations with several hundred parameters reflecting diverse anatomical and physiological properties and processes such as lipid content in a certain organ with a specific size and blood flow, or catalytic properties of an enzyme. In the face of considerable effort for model building and identification it becomes clear that efficient tools are of utmost importance in order to decrease the time needed for technical implementation. The potential reward is considerable. The integration and translation of knowledge can enhance the understanding and speed up experimentation and thereby research, discovery and development, both in academic and industrial settings. The presented software platform is geared toward these needs, enabling the efficient integration of different levels and disciplines to accelerate modeling. MoBi® in combination with PK-Sim® allows full flexibility regarding the modeling to consider both physiologically-based and classical PK and PD models, as well as mixtures of both. Models can be built efficiently, adopted, and combined across multiple hierarchical levels to support translational research and medicine. For example, a whole-body model established based on data in one animal species can be re-parameterized to provide predictions for another species with a single mouse-click retrieving the relevant information from the integrated anatomy and physiology database.

The toolboxes for R and MATLAB® provide flexible programming and analysis environments that allow the coding of customized functionalities addressing specific user needs. They provide an environment for large scale simulation studies in an automated manner and the implementation of routines and work-flows helping in the standardization of tasks accelerating the modeling process and making results more reproducible. One example is an established work-flow to automatically simulate and analyze pediatric populations of different age based on validated adult models and using age-dependent scaling information on physiological parameters (e.g., organ volumes and composition, blood flow rates) and involved enzymatic processes (e.g., cytochrome P450 isoform ontogenies) contained in the PK-Sim® database. Other examples are the calculation of local (e.g., flux control coefficients; Kacser and Burns, 1973; Heinrich and Rapoport, 1974; Heinrich and Schuster, 1996) or global (e.g., Sobol indices; Sobol’, 2001; Zi et al., 2008) sensitivity measures. Via the interface to R, also the application of non-linear mixed effect modeling techniques is possible, offering the option for classical PK/PD analysis (Tornoe et al., 2004).

The whole-body model structures that are part of the software describe physiological parameters such as organ volumes or blood flows using constant parameters, which is sufficient for many questions of interest. However, specific questions can be thought of, where a dynamic implementation of such parameters or processes could be of interest. Here, MoBi® offers the full flexibility to modify or extend a given model structure. Nevertheless, modeling with the presented platform is currently limited to ordinary and delay differential equations and spatial effect, for example, can only be modeled in a compartmental approximation. Extensions toward stochastic or partial differential equations might be desirable for specific modeling tasks. Also, additional prior knowledge and information should be integrated into the database to increase the level of physiological detail represented. Tissue specific expression of proteins is a typical example.

The application example chosen for demonstration purposes here comes from the area of pharmaceutical therapies. The software platform itself is, of course, not restricted to systems biology and pharmaceutical research but can as well be applied to fields such as risk assessment or environmental toxicology (Krishan and Johanson, 2005; Loizou et al., 2008).

The software platform concept, and its realization through the components PK-Sim®, MoBi®, and the toolboxes for R and MATLAB®, thus presents a versatile and powerful framework allowing fast and reliable model building, simulation, and model analysis across multiple physiological scales. The platform is designed for the needs of life science and pharmaceutical research allowing the integration of physiologically-based and classical approaches to model drug PK and PD as well as metabolic and signaling networks.

Conflict of Interest Statement

All authors are employed by Bayer Technology Services GmbH, the company owning the presented software platform.

Supplementary Material

The Supplementary Material for this article can be found online at http://www.frontiersin.org/Computational_Physiology_and_Medicine/10.3389/fphys.2011.00004/abstract

Acknowledgments

The authors acknowledge financial support by the FORSYS-Partner project “A Systems Biology Approach toward Predictive Cancer Therapy” (0315280F), the QuantPro Initiative (0313853B) and the Services@MediGrid project (01|G07015A) funded by the German Federal Ministry of Education and Research (BMBF).

Footnotes

References

  1. Araujo R. P., McElwain D. L. (2004). A history of the study of solid tumour growth: the contribution of mathematical modelling. Bull. Math. Biol. 66, 1039–1091 [DOI] [PubMed] [Google Scholar]
  2. Berezhkovskiy L. M. (2004). Volume of distribution at steady state for a linear pharmacokinetic system with peripheral elimination. J. Pharm. Sci. 93, 1628–1640 [DOI] [PubMed] [Google Scholar]
  3. Block M., Scholl E., Drasdo D. (2007). Classifying the expansion kinetics and critical surface dynamics of growing cell populations. Phys. Rev. Lett. 99, 248101. [DOI] [PubMed] [Google Scholar]
  4. Briest S., Stearns V. (2009). Tamoxifen metabolism and its effect on endocrine treatment of breast cancer. Clin. Adv. Hematol. Oncol. 7, 185–192 [PubMed] [Google Scholar]
  5. Brightman F. A., Fell D. A. (2000). Differential feedback regulation of the MAPK cascade underlies the quantitative differences in EGF and NGF signalling in PC12 cells. FEBS Lett. 482, 169–174 10.1016/S0014-5793(00)02037-8 [DOI] [PubMed] [Google Scholar]
  6. Bru A., Albertos S., Luis Subiza J., Garcia-Asenjo J. L., Bru I. (2003). The universal dynamics of tumor growth. Biophys. J. 85, 2948–2961 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Butcher E. C., Berg E. L., Kunkel E. J. (2004). Systems biology in drug discovery. Nat. Biotechnol. 22, 1253–1259 10.1038/nbt1017 [DOI] [PubMed] [Google Scholar]
  8. Chong L., Ray L. B. (2002). Whole-istic biology. Science 296, 166112040188 [Google Scholar]
  9. Cohen S. D., Hindmarsh A. C. (1996). CVODE, a stiff/nonstiff ODE solver in C. Comput. Phys. 10, 138–143 [Google Scholar]
  10. Cohen-Saidon C., Cohen A. A., Sigal A., Liron Y., Alon U. (2009). Dynamics and variability of ERK2 response to EGF in individual living cells. Mol. Cell 36, 885–893 [DOI] [PubMed] [Google Scholar]
  11. Deisboeck T. S. (2009). Personalizing medicine: a systems biology perspective. Mol. Syst. Biol. 5, 249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Edginton A. N., Schmitt W., Voith B., Willmann S. (2006a). A mechanistic approach for the scaling of clearance in children. Clin. Pharmacokinet. 45, 683–704 10.2165/00003088-200645070-00004 [DOI] [PubMed] [Google Scholar]
  13. Edginton A. N., Schmitt W., Willmann S. (2006b). Application of physiology-based pharmacokinetic and pharmacodynamic modeling to individualized target-controlled propofol infusions. Adv. Ther. 23, 143–158 10.1007/BF02850355 [DOI] [PubMed] [Google Scholar]
  14. Edginton A. N., Schmitt W., Willmann S. (2006c). Development and evaluation of a generic physiologically based pharmacokinetic model for children. Clin. Pharmacokinet. 45, 1013–1034 10.2165/00003088-200645100-00005 [DOI] [PubMed] [Google Scholar]
  15. Edginton A. N., Theil F. P., Schmitt W., Willmann S. (2008). Whole body physiologically-based pharmacokinetic models: their use in clinical drug development. Expert Opin. Drug Metab. Toxicol. 4, 1143–1152 [DOI] [PubMed] [Google Scholar]
  16. Edginton A. N., Willmann S. (2008). Physiology-based simulations of a pathological condition: prediction of pharmacokinetics in patients with liver cirrhosis. Clin. Pharmacokinet. 47, 743–752 10.2165/00003088-200847110-00005 [DOI] [PubMed] [Google Scholar]
  17. Elowitz M. B., Levine A. J., Siggia E. D., Swain P. S. (2002). Stochastic gene expression in a single cell. Science 297, 1183–1186 10.1126/science.1070919 [DOI] [PubMed] [Google Scholar]
  18. Espie P., Tytgat D., Sargentini-Maier M. L., Poggesi I., Watelet J. B. (2009). Physiologically based pharmacokinetics (PBPK). Drug Metab. Rev. 41, 391–407 [DOI] [PubMed] [Google Scholar]
  19. Greenspan H. P. (1976). On the growth and stability of cell cultures and solid tumors. J. Theor. Biol. 56, 229–242 [DOI] [PubMed] [Google Scholar]
  20. Heinrich R., Rapoport T. A. (1974). A linear steady-state treatment of enzymatic chains. General properties, control and effector strength. Eur. J. Biochem. 42, 89–95 [DOI] [PubMed] [Google Scholar]
  21. Heinrich R., Schuster S. (1996). The Regulation of Cellular Systems. New York: Chapman and Hall [Google Scholar]
  22. Hester R. L., Iliescu R., Summers R. L., Coleman T. G. (2010). Systems biology and integrative physiological modeling. J. Physiol. [Epub ahead of print]. 10.1113/jphysiol.2010.201558 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hucka M., Finney A., Sauro H. M., Bolouri H., Doyle J. C., Kitano H., Arkin A. P., Bornstein B. J., Bray D., Cornish-Bowden A., Cuellar A. A., Dronov S., Gilles E. D., Ginkel M., Gor V., Goryanin I. I., Hedley W. J., Hodgman T. C., Hofmeyr J. H., Hunter P. J., Juty N. S., Kasberger J. L., Kremling A., Kummer U., Le Novère N., Loew L. M., Lucio D., Mendes P., Minch E., Mjolsness E. D., Nakayama Y., Nelson M. R., Nielsen P. F., Sakurada T., Schaff J. C., Shapiro B. E., Shimizu T. S., Spence H. D., Stelling J., Takahashi K., Tomita M., Wagner J., Wang J. (2003). The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 19, 524–531 10.1093/bioinformatics/btg015 [DOI] [PubMed] [Google Scholar]
  24. Kacser H., Burns J. A. (1973). The control of flux. Symp. Soc. Exp. Biol. 27, 65–104 [PubMed] [Google Scholar]
  25. Kalow W. (2006). Pharmacogenetics and pharmacogenomics: origin, status, and the hope for personalized medicine. Pharmacogenomics J. 6, 162–165 10.1038/sj.tpj.6500361 [DOI] [PubMed] [Google Scholar]
  26. Krishan K., Johanson G. (2005). Physiologically-based pharmacokinetic and toxicokinetic models in cancer risk assessment. J. Environ. Sci. Health 23, 31–53 [DOI] [PubMed] [Google Scholar]
  27. Kuepfer L. (2010). Towards whole-body systems physiology. Mol. Syst. Biol. 6, 409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Loizou G., Spendiff M., Barton H. A., Bessems J., Bois F. Y., d'Yvoire M. B., Buist H., Clewell H. J., III, Meek B., Gundert-Remy U., Goerlitz G., Schmitt W. (2008). Development of good modelling practice for physiologically based pharmacokinetic models for use in risk assessment: the first steps. Regul. Toxicol. Pharmacol. 50, 400–411 [DOI] [PubMed] [Google Scholar]
  29. Marusic M., Bajzer Z., Vuk-Pavlovic S., Freyer J. P. (1994). Tumor growth in vivo and as multicellular spheroids compared by mathematical models. Bull. Math. Biol. 56, 617–631 [DOI] [PubMed] [Google Scholar]
  30. Nestorov I. (2007). Whole-body physiologically based pharmacokinetic models. Expert Opin. Drug Metab. Toxicol. 3, 235–249 [DOI] [PubMed] [Google Scholar]
  31. Poulin P., Schoenlein K., Theil F. P. (2001). Prediction of adipose tissue: plasma partition coefficients for structurally unrelated drugs. J. Pharm. Sci. 90, 436–447 [DOI] [PubMed] [Google Scholar]
  32. Poulin P., Theil F. P. (2002a). Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J. Pharm. Sci. 91, 129–156 10.1002/jps.10005 [DOI] [PubMed] [Google Scholar]
  33. Poulin P., Theil F. P. (2002b). Prediction of pharmacokinetics prior to in vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. J. Pharm. Sci. 91, 1358–1370 10.1002/jps.10128 [DOI] [PubMed] [Google Scholar]
  34. Radszuweit M., Block M., Hengstler J. G., Scholl E., Drasdo D. (2009). Comparing the growth kinetics of cell populations in two and three dimensions. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 79(Pt 1),051907. [DOI] [PubMed] [Google Scholar]
  35. Rae J. M., Sikora M. J., Henry N. L., Li L., Kim S., Oesterreich S., Skaar T. C., Nguyen A. T., Desta Z., Storniolo A. M., Flockhart D. A., Hayes D. F., Stearns V. (2009). Cytochrome P450 2D6 activity predicts discontinuation of tamoxifen therapy in breast cancer patients. Pharmacogenomics J. 9, 258–264 10.1038/tpj.2009.14 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Rao C. V., Wolf D. M., Arkin A. P. (2002). Control, exploitation and tolerance of intracellular noise. Nature 420, 231–237 10.1038/nature01258 [DOI] [PubMed] [Google Scholar]
  37. Rodgers T., Leahy D., Rowland M. (2005a). Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J. Pharm. Sci. 94, 1259–1276 [DOI] [PubMed] [Google Scholar]
  38. Rodgers T., Leahy D., Rowland M. (2005b). Tissue distribution of basic drugs: accounting for enantiomeric, compound and regional differences amongst beta-blocking drugs in rat. J. Pharm. Sci. 94, 1237–1248 [DOI] [PubMed] [Google Scholar]
  39. Rodgers T., Rowland M. (2006). Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J. Pharm. Sci. 95, 1238–1257 [DOI] [PubMed] [Google Scholar]
  40. Rodgers T., Rowland M. (2007). Mechanistic approaches to volume of distribution predictions: understanding the processes. Pharm. Res. 24, 918–933 [DOI] [PubMed] [Google Scholar]
  41. Sauro H. M. (1993). SCAMP: a general-purpose simulator and metabolic control analysis program. Comput. Appl. Biosci. 9, 441–450 [DOI] [PubMed] [Google Scholar]
  42. Schmitt W. (2008). General approach for the calculation of tissue to plasma partition coefficients. Toxicol. In Vitro 22, 457–467 10.1016/j.tiv.2007.09.010 [DOI] [PubMed] [Google Scholar]
  43. Shampine L. F. (2005). Solving ODEs and DDEs with residual control. Appl. Num. Math. 52, 113–127 [Google Scholar]
  44. Sigal A., Milo R., Cohen A., Geva-Zatorsky N., Klein Y., Liron Y., Rosenfeld N., Danon T., Perzov N., Alon U. (2006). Variability and memory of protein levels in human cells. Nature 444, 643–646 10.1038/nature05316 [DOI] [PubMed] [Google Scholar]
  45. Sistonen J., Sajantila A., Lao O., Corander J., Barbujani G., Fuselli S. (2007). CYP2D6 worldwide genetic variation shows high frequency of altered activity variants and no continental structure. Pharmacogenet. Genomics 17, 93–101 [DOI] [PubMed] [Google Scholar]
  46. Sobol’ I. M. (2001). Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comp. Simul. 55, 271–280 10.1016/S0378-4754(00)00270-6 [DOI] [Google Scholar]
  47. Spencer S. L., Gaudet S., Albeck J. G., Burke J. M., Sorger P. K. (2009). Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature 459, 428–432 10.1038/nature08012 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Stites E. C., Trampont P. C., Ma Z., Ravichandran K. S. (2007). Network analysis of oncogenic Ras activation in cancer. Science 318, 463–467 10.1126/science.1144642 [DOI] [PubMed] [Google Scholar]
  49. Tomalik-Scharte D., Lazar A., Fuhr U., Kirchheiner J. (2008). The clinical role of genetic polymorphisms in drug-metabolizing enzymes. Pharmacogenomics J. 8, 4–15 10.1038/sj.tpj.6500462 [DOI] [PubMed] [Google Scholar]
  50. Tornoe C. W., Agerso H., Jonsson E. N., Madsen H., Nielsen H. A. (2004). Non-linear mixed-effects pharmacokinetic/pharmacodynamic modelling in NLME using differential equations. Comput. Methods Programs Biomed. 76, 31–40 10.1016/j.cmpb.2004.01.001 [DOI] [PubMed] [Google Scholar]
  51. Vossen M., Sevestre M., Niederalt C., Jang I. J., Willmann S., Edginton A. N. (2007). Dynamically simulating the interaction of midazolam and the CYP3A4 inhibitor itraconazole using individual coupled whole-body physiologically-based pharmacokinetic (WB-PBPK) models. Theor. Biol. Med. Model. 4, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Willmann S., Edginton A. N., Dressman J. B. (2007a). Development and validation of a physiology-based model for the prediction of oral absorption in monkeys. Pharm. Res. 24, 1275–1282 10.1007/s11095-007-9247-y [DOI] [PubMed] [Google Scholar]
  53. Willmann S., Hohn K., Edginton A., Sevestre M., Solodenko J., Weiss W., Lippert J., Schmitt W. (2007b). Development of a physiology-based whole-body population model for assessing the influence of individual variability on the pharmacokinetics of drugs. J. Pharmacokinet. Pharmacodyn. 34, 401–431 10.1007/s10928-007-9053-5 [DOI] [PubMed] [Google Scholar]
  54. Willmann S., Edginton A. N., Kleine-Besten M., Jantratid E., Thelen K., Dressman J. B. (2009a). Whole-body physiologically based pharmacokinetic population modelling of oral drug administration: inter-individual variability of cimetidine absorption. J. Pharm. Pharmacol. 61, 891–899 10.1211/jpp/61.07.0008 [DOI] [PubMed] [Google Scholar]
  55. Willmann S., Edginton A. N., Coboeken K., Ahr G., Lippert J. (2009b). Risk of codeine treatment during breastfeeding – a quantitative mechanistic modeling study. Clin. Pharmacol. Ther. 86, 634–643 10.1038/clpt.2009.151 [DOI] [PubMed] [Google Scholar]
  56. Willmann S., Lippert J., Schmitt W. (2005). From physicochemistry to absorption and distribution: predictive mechanistic modelling and computational tools. Expert Opin. Drug Metab. Toxicol. 1, 159–168 [DOI] [PubMed] [Google Scholar]
  57. Willmann S., Lippert J., Sevestre M., Solodenko J., Fois F., Schmitt W. (2003a). PK-Sim®: a physiologically based pharmacokinetic ‘whole-body’ model. Biosilico 1, 121–124 10.1016/S1478-5382(03)02342-4 [DOI] [Google Scholar]
  58. Willmann S., Schmitt W., Keldenich J., Dressman J. B. (2003b). A physiologic model for simulating gastrointestinal flow and drug absorption in rats. Pharm. Res. 20, 1766–1771 10.1023/B:PHAM.0000003373.72652.c0 [DOI] [PubMed] [Google Scholar]
  59. Willmann S., Schmitt W., Keldenich J., Lippert J., Dressman J. B. (2004). A physiological model for the estimation of the fraction dose absorbed in humans. J. Med. Chem. 47, 4022–4031 [DOI] [PubMed] [Google Scholar]
  60. Zanger U. M., Fischer J., Raimundo S., Stuven T., Evert B. O., Schwab M., Eichelbaum M. (2001). Comprehensive analysis of the genetic factors determining expression and function of hepatic CYP2D6. Pharmacogenetics 11, 573–585 10.1097/00008571-200110000-00004 [DOI] [PubMed] [Google Scholar]
  61. Zi Z., Zheng Y., Rundell A. E., Klipp E. (2008). SBML-SAT: a systems biology markup language (SBML) based sensitivity analysis tool. BMC Bioinformatics 9, 342. 10.1186/1471-2105-9-342 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Frontiers in Physiology are provided here courtesy of Frontiers Media SA

RESOURCES