The Effects of Weak Genetic Perturbations on the Transcriptome of the Wing Imaginal Disc and Its Association With Wing Shape in Drosophila melanogaster

Abstract

A major objective of genomics is to elucidate the mapping between genotypic and phenotypic space as a step toward understanding how small changes in gene function can lead to elaborate phenotypic changes. One approach that has been utilized is to examine overall patterns of covariation between phenotypic variables of interest, such as morphology, physiology, and behavior, and underlying aspects of gene activity, in particular transcript abundance on a genome-wide scale. Numerous studies have demonstrated that such patterns of covariation occur, although these are often between samples with large numbers of unknown genetic differences (different strains or even species) or perturbations of large effect (sexual dimorphism or strong loss-of-function mutations) that may represent physiological changes outside of the normal experiences of the organism. We used weak mutational perturbations in genes affecting wing development in Drosophila melanogaster that influence wing shape relative to a co-isogenic wild type. We profiled transcription of 1150 genes expressed during wing development in 27 heterozygous mutants, as well as their co-isogenic wild type and one additional wild-type strain. Despite finding clear evidence of expression differences between mutants and wild type, transcriptional profiles did not covary strongly with shape, suggesting that information from transcriptional profiling may not generally be predictive of final phenotype. We discuss these results in the light of possible attractor states of gene expression and how this would affect interpretation of covariation between transcriptional profiles and other phenotypes.

FUNCTIONAL genomic research is dominated by two paradigms that derive their conceptual foundations from computer science and statistical genetics, respectively. Network biologists are interested in the patterns of connectivity between genes and gene products and in the consequences that these patterns impose on properties of biological systems, such as metabolic flux or phenotypic robustness (Reeves et al. 2006; Yakoby et al. 2008; Yan et al. 2009; Zartman et al. 2009). Quantitative geneticists tend to be more linear in their search for association between genotypes and phenotypes (including gene expression), and their models generally assume a preponderance of additive effects of individual variants (Passador-Gurgel et al. 2007; Ayroles et al. 2009; Edwards et al. 2009). A major challenge for systems biologists is to unify these two frameworks through their studies of the genomic consequences of genetic perturbation.

An additional obstacle is that there are also two conceptually different approaches to perturbation analysis used to address questions relating to genotype–phenotype mappings. One is to introduce large mutational or pharmacological changes to relatively homogeneous systems such as cell lines or clones of organisms in a highly controlled manner. While experimentally appealing, the perturbations are often well beyond the range of physiological or functional relevance, so the results may be difficult to generalize to actual biological circumstances. The alternative is to harness natural genetic or ecological variation, either in cross-sectional studies or in pedigrees and crosses (Passador-Gurgel et al. 2007; Rockman 2008; Ayroles et al. 2009; Edwards et al. 2009; Harbison et al. 2009). An advantage is that perturbation effects are averaged, and potentially replicated, over different genetic backgrounds, but the genomic effects of individual loci are generally subtle and detected only by statistical methods. They then require functional validation in more controlled experimental systems. Neither genome-wide association studies nor whole-genome expression profiling have yet proven capable of consistently describing more than a fraction of the underlying genetic basis of phenotypic variation. Nevertheless, it is of interest to bridge these conceptual gaps by studying how local perturbations of gene function ramify throughout the complex of genetic pathways operating in cells, tissues, and organisms. One common theme across paradigms is that transcriptional profiling studies, whether focused on large-scale perturbations or on comparisons across inbred lines derived from natural populations, often lead to lists of differentially expressed genes that can number in the thousands. However, it can be difficult to determine when changes in gene expression will actually influence the phenotype of interest directly. Thus it is clear that additional approaches must be sought out to ameliorate such observations.

Here we describe one model system for attempting such integration, namely the developing wing of the fruit fly Drosophila melanogaster. The wing imaginal disc is a well-studied complex tissue from which the adult wing and parts of the thorax are derived (Held 2002). Genetic and environmental perturbations can result in both qualitative (Waddington 1939; Garcia-Bellido and Santamaria 1972; Lawrence and Morata 1976; Held 2002; Blair 2007) and quantitative morphological effects (Palsson and Gibson 2000; Mezey et al. 2005; Weber et al. 2005; Debat et al. 2006; Dworkin and Gibson 2006). There is considerable segregating variation for adult wing size and shape in natural populations, and ecologically relevant variables such as temperature and nutrition contribute to the overall pattern of phenotypic variation observed for this species (Zimmerman et al. 2000; Palsson and Gibson 2004; Dworkin et al. 2005; Debat et al. 2009; Shingleton et al. 2009). Wing shape in particular is an ideal “complex” trait. It represents a highly integrated multivariate phenotype (Klingenberg and Zaklan 2000; Dworkin and Gibson 2006; Klingenberg 2009), given that wing development re quires the incorporation of information from numerous signaling pathways. These control not only the patterning of the wing blade (Garcia-Bellido and Santamaria 1972; Lawrence and Morata 1976; Brower 1986; Tabata and Kornberg 1994; Sanicola et al. 1995; Zecca et al. 1995) and cell growth, proliferation, and survival (Martin et al. 2004), but also the specification, determination, and maintenance of the wing veins whose placement provides the landmarks that are used to measure wing shape (Blair 2007).

To quantify the effect of weak genetic perturbations (mutations generating subtle quantitative phenotypic variation) on the transcriptome, we have profiled gene expression in a panel of 27 heterozygous mutants (introgressed into a common genetic background) known to quantitatively perturb wing shape (Dworkin and Gibson 2006), in addition to the co-isogenic wild-type strain (Samarkand), and one additional wild-type strain (Oregon-R). A custom Illumina bead array was designed to interrogate the abundance of 1150 genes that are expressed in late third instar imaginal wing discs at the time of patterning of the future wing blade, when the wing margin, veins, and intervein regions are specified. The mutations, listed and annotated in Table 1, are due to P-element insertions in the genes, most of which have well-defined roles in mediating signals through the Dpp (TGF-β) and Egfr (receptor-tyrosine kinase) pathways. We have previously shown that wing phenotypes of the lines are significantly different from one another, but that they do not clearly correlate with the nature of the signal transduction pathway that is perturbed (Dworkin and Gibson 2006). The gene expression profiles are considered in relation to four possible hypotheses.

TABLE 1.

List of mutations used in this study and evidence that these mutations downregulate their own expression

Gene symbol	Allele	Transcript reduced in mutants?	Location of TE insertion	Illumina probe ID
aos	W11	Yes	5′-most exon near transcription  start site	2027
ast	KG07563	Yes	Boundary of transcription start  site and 5′-UTR	2208
babo	k16912	Yes	Intron–exon boundary	509, 910 (weak)
brk	KG08470	No	5′ of transcription start site
Bs/DSRF	k07909	Yes	Unknown	4271, 2932
cbl	KG03080	Weakly	5′-UTR	4976
Dad	J1E4	Yes	Intron	3923
Dpp	KG08191	No	3′ of the gene
drk	k02401	Yes	Unknown	1182, 2166
ed	k01102	Yes	First intron	3366, 1309
Egfr	k05115	Yes	Unknown	2165, 1775
Gap1	mip-w[+]	No	Unknown
ksr	J5E2	No	50 kb upstream of ksr
mad	k00237	No	CDS
mad	KG00581	No	CDS
mam	BG02477	No	Intron
mam	KG02641	No	Intron
pnt	KG04968	No	Intron
ptc	k02507	Yes	Intron	4087
rho-6	KG05638	No transcripts on array
rho	KG07115	No	5′ noncoding
S	k09530	No	Unknown
sax	KG07525	No	5′-UTR
sbb/mtv	BG01610	No	Intron or 5′-UTR depending  on transcript
spi	s3547	Yes	Unknown	5854, 3941
tkv	k16713	Yes	Intron/5′ noncoding, depends  on transcript	79, 5076 (weak)
tkv	KG01923	Yes	tkv intron, CG14033 transcript	79, 5076 (weak)

Evidence for reduced expression was based on the linear model presented in materials and methods. P-value <0.001 was considered strong evidence that the mutations caused the reduction in the expression of their own transcripts, while P-value <0.01 was considered weak evidence. CDS, coding sequence.

The null hypothesis, H_0A, is that despite showing morphological shape differences in the wing, the mutants do not demonstrate any evidence of differential expression. This unlikely null hypothesis needs to be considered carefully with respect to a more likely null, H_0B, which states that any expression differences between the mutant measured as a heterozygote and its co-isogenic wild type will be too small to detect with the array platform. The phenotypic differences among lines typically involve slight displacements of the overall shape of the wing, or vein positioning, which are too subtle to see by eye and require careful quantitative, morphometric measurement to detect. Microarray technology resolves differences in expression as small as 1.2-fold with high confidence, but if the functionally important changes in expression occur in just a few percent of the cells of the developing imaginal disc at a precise time of development, or if expression differences are largely spatial, the experiment may be unable or underpowered to detect differences.

The first alternate hypothesis, H₁, is that each mutant line is different from the others for some fraction of the transcriptome. The differences may involve different genes in different lines or involve the same genes whose expression is modulated to varying degrees. A priori, we would predict this includes changes in the expression of genes that are known targets of each specific mutation. Transcript abundance might also be correlated with aspects of the adult phenotype, leading to the identification of key mediators of phenotypic variation. Line-specific expression differences can be detected by analysis of variance of the ratio of the within-to-between line variance, noting that in this experiment, each microarray hybridization required scores of imaginal discs to obtain sufficient mRNA, so the within-line variance is mainly technical rather than biological.

The second alternate hypothesis, H₂, is that rather than each line being unique, there is a high correlation structure to the profiles of lines that either share a common biochemical perturbation or give rise to similar adult wing shapes. For example, mutations that disrupt Dpp signaling ought to result in similar downstream effects on expression, and the differences between these lines may provide hints to the ordering of gene effects, akin to classical epistasis analysis. Alternatively, lines with a relatively enlarged posterior compartment of the wing may differentially express a common suite of genes involved in posterior patterning. Such effects can be detected by cluster analysis of the average profiles of transcriptomes of each of the mutant lines, followed by supervised tests of correlation between expression and the genotypes or phenotypes.

Our analyses failed to lend strong support for either of these alternate hypotheses and lead us to propose a third, H₃, that there is a significant correlation structure among lines, but that it suggests the existence of “attractor states” of gene expression (Huang et al. 2005; Mar and Quackenbush 2009). Almost 20 years ago, Stuart Kauffman in The Origins of Order (Kauffman 1993) proposed that the logical structure of gene networks will typically promote the channeling of development or physiology into alternate relatively stable states. The underlying logic of his mathematical models assumed Boolean on–off switches, and hence the attractor states could be visualized as matrices of on or off patterns of gene activity. Perhaps because gene expression is so clearly quantitative in nature, this idea has not been subject to empirical evaluation on the genome scale. Our data indicate that suites of hundreds of genes in perturbed wing discs adopt common expression profiles that do not clearly correlate either with the genetic perturbation or with the adult phenotype and lead us to reconsider the notion of stable genomic attractor states.

MATERIALS AND METHODS

Fly lines, rearing, and dissection:

All of the mutants used are listed in Table 1. For each mutation the DNA lesion is caused by a P-element transgenic insertion with a w+ rescue construct. As described previously (Dworkin and Gibson 2006), each mutation was introgressed via backcrossing into a common isogenic wild-type genetic background Samarkand (SAM) marked with a w− allele, a genetic background commonly used for quantitative genetic studies. Following introgression, each mutation was balanced against a balancer chromosome containing either p{w+, Ubi-GFP} or p{w+, act-GFP}. These balancer chromosomes were themselves repeatedly crossed into the SAM background (six to seven generations) prior to use to not introduce any additional segregating genetic variation. When measured as a heterozygote, each of these mutations has subtle quantitative effects on the shape of the wing, but does not generally appear to cause qualitative disruptions to the final structure of the wing (Dworkin and Gibson 2006).

For each line bearing the mutation (and corresponding balancer) males were crossed to virgin females of the w⁻; SAM isogenic background. Larvae of each genotype were reared in low-density conditions at 25°. At the wandering third instar stage, male larvae were rinsed in PBS and then scored for the absence of GFP expression (indicating they were mutant/SAM). From these individuals, ∼45–50 wing imaginal discs were dissected out and stored in RNAlater at −72°. For each line two (biological) replicate sets of dissections were performed on different days. The one exception is the isogenic wild-type w; SAM line where 6 independent dissections as outlined above were performed. In total ∼4500 wing imaginal discs were used for the experiments described in this study. Biological replicates showed correlations (for gene expression) between 0.95 and 0.99 in all cases.

Morphometric data acquisition and analysis:

The data used for the geometric morphometric analysis in this current study represent a subset of the wings used previously in Dworkin and Gibson (2006). Details of the methods used for rearing the flies, dissection, microscopy, and landmark acquisition can be found in that study. Briefly, flies from each line were reared at low density after generations 9 and 14 of backcrossing to the Samarkand wild type (marked with w⁻). Adult progeny (generation 10 and 15) were stored in 70% ethanol, prior to dissection. For dissection, a single wing from each fly was mounted in glycerol (10 wings per sex/genotype/replicate), and images of the wing were captured using a SPOT camera mounted on a Nikon Eclipse microscope. Landmarks were digitized using the tpsDIG v. 1.39, (Rohlf 2003a) software. Generalized Procrustes superimposition of landmarks was performed to remove the effects of isometric scale, location, and rotation on the data using tpsRelW (Rohlf 2003b).

RNA extraction, amplification, and labeling:

RNA extraction was performed using a modified protocol for the RNAeasy kit (QIAGEN, Valencia, CA) as described previously (Dworkin et al. 2009). Following RNA extraction and purification, all samples were quality checked for 260/280 and 260/230 ratios using a NanoDrop spectrophotometer (Thermo Scientific, Wilmington DE).

We used the Illumina (San Diego) TotalPrep RNA amplification kit (Ambion, Palo Alto, CA) and followed the manufacturer's protocol. Briefly, for each biological sample, two replicate sets of 500 ng of total RNA was used in a reverse-transcription reaction, followed by second-strand synthesis of the cDNA. Following cDNA clean-up, an in vitro transcription reaction was performed overnight with biotin-labeled NTPs. Samples were then quantified and purity of the cRNA was confirmed.

Array design and processing:

Given that the primary goal of these experiments was to examine a candidate set of genes that influence wing development as opposed to gene discovery, we designed a custom content array using the Illumina focused array platform. This array contained genes known to affect wing development via direct loss-of-function phenotypes or their interacting partners. In addition we included genes that appear to be expressed in the developing wing imaginal discs and in particular show evidence of differential expression on the basis of previous studies. (Klebes et al. 2002, 2005; Butler et al. 2003; Li and White 2003; Dworkin et al. 2009). See supporting information, Table S1 for a list of genes included on this array, as well as probe sequences. Several hundred genes have two probes representing their expression. While these probes were designed to represent independent measures, and in particular to reduce any bias of gene expression for a given transcript, in some cases the probes overlap partially in sequence.

Given that the total number of samples hybridized (240) was far larger than the number of samples per array (16), we utilized an incomplete blocking strategy (with each 16-array slide representing a block) during hybridization to avoid confounding the effects of any mutation with slide effects. Hybridization was performed following the manufacturer's protocol for the 16-sample Sentrix bead-array (Illumina). Briefly, 500 ng of biotin-labeled cRNA was mixed with hybridization buffer and formamide, and the sample was applied to the slide. Hybridization was performed overnight at 55° with samples revolving in the chamber. Samples were then washed, blocked, and incubated with strepavidin-Cy3 prior to a final washing and drying. The slide containing all 16 samples was scanned on an Illumina BeadStation. In total 240 samples were prepared and hybridized, including several samples that were rehybridized when the first sample failed. This includes three technical replicates per biological replicate for each mutant allele.

Despite the fact that each probe was represented by on average 30 independent beads randomly positioned on the array, large-scale spatial artifacts or hybridization issues can always lead to potentially misleading results with solid-state microarrays. Therefore, each of the 240 array images was visually inspected for any large-scale artifacts. In addition, several samples failed to provide any signal and were excluded from the analysis. Funnel (MA) plots of log-transformed expression data were also examined for each array and were in general quite linear. Any arrays that demonstrated obvious signs of poor hybridization were excluded. Conservatively we used 216 of the arrays for analysis, of which 16 were for the replication of the study of Dworkin et al. (2009), to assess the general performance of the custom array platform. Thus 200 arrays were used for analyses described in this study, leading to an unbalanced design.

Analysis of the Illumina Sentrix array data:

Given that the Illumina array platform is single channel, with 16 arrays per slide, data normalization is required to account for both issues with scanning (slide-level variation) and any issues with labeling or hybridization (sample level). We examined both median and quantile normalized data (normalized at the level of the individual array), which both produced very similar results (not shown). As median normalization provides a robust and simple approach, this was used for all analyses included here in the following probe (or gene) level models:

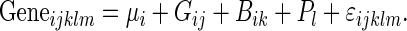The model terms represent effects of the ith replicate of the jth genotype and the kth block (slide), and P represents l different probes used to assess transcript abundance. Only the effect of block (slide) was treated as random, with all other factors treated as fixed. For probe-level models we used the same model as above, but without probe as an explanatory term. For validation of the array platform, we compared the results of the Illumina custom platform with cDNA array data reported previously (Dworkin et al. 2009). Given that the Illumina expression data set for this comparison was somewhat smaller than the original experiment (four samples per genotype/background), we adopted a liberal q-value of 0.01 as our nominal cutoff for including genes deemed differentially expressed (Storey and Tibshirani 2003), for this particular comparison. Analyses were performed in both SAS (v9.1) and R v2.8 (R Development Core Team 2009), using custom scripts (File S1).

Patterns of covariation between gene expression and shape:

To assess variation for shape between the mutations used in this study, we used canonical variates analysis to explore the data. Canonical variates constructs a new coordinate system and provides scores that are linear combinations of the original variables scaled by the loadings that describe the between-group differences, with the first canonical axis describing the vector in which the groups are best discriminated, with subsequent (and independent) axes each describing additional vectors of discrimination. This is done by scaling the between-group covariation by the within-group covariation. Canonical variates was performed using MorphoJ (Klingenberg 2011).

To assess covariation between wing shape and gene expression, we utilized two related approaches. First we used a multivariate linear model, regressing wing shape onto relative transcript abundance, fitting individual models for each probe. For this we used means of gene expression and shape for each genotype, as no individual measure for gene expression is possible from the data generated in this study. Given the statistical limitations of treating gene expression as predictor variables when only a small proportion of the total variation is accounted for, we also utilized two-block partial least-squares analysis (Klingenberg and Zaklan 2000; Rohlf and Corti 2000). Two-block partial least squares performs a singular value decomposition on the matrix of covariances between two blocks of variables, in this study represented by gene expression and shape variables (but without including variances and covariances from within the sets of either gene expression data or shape data). Mathematically, this can be represented as

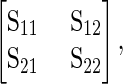where S₁₁ and S₂₂ represent the variance–covariance matrices for shape variables and gene expression variables, respectively. S₁₂ (with S₂₁ being its transpose) represents the covariation of variables between shape and gene expression. S₁₂ is decomposed using singular value decomposition (SVD) to extract vectors for each set of the original variables that represent loadings used to generate linear combinations of the original variables creating new set of variables that maximally covary (between shape and gene expression). Thus, the first singular value represents the maximal degree of covariation between the blocks of variables, which can be visualized by plotting the scores generated using the linear combinations described above. Each additional set of new variables represents statistically independent (orthogonal) sets of shape and gene expression variables that covary (that are each successively smaller than the last one). This procedure is analogous to principal components analysis; however, instead of extracting axes of maximal variation within a data set, the partial least-squares (PLS) analysis extracts axes of maximal covariation between blocks of variables (gene expression and shape). Analysis and visual shape descriptors from two-block PLS were generated using morphoJ (Klingenberg 2011), using “line” means for each genotype for both shape and gene expression with 1000 permuted data sets of the shape variables against gene expression variables, to generate an approximate null sampling distribution for comparison against the observed patterns. Results for the two-block PLS were verified using custom scripts in R (Claude 2008). As a simple, scalar measure of degree of covariation between shape and gene expression variables we utilized the RV coefficient

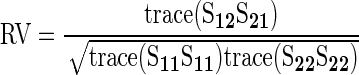(Escoufier 1973; Robert and Escoufier 1976), where the numerator can be interpreted as the total amount of covariation between the shape and gene expression (Rohlf and Corti 2000). This differs from the first singular value from the two-block PLS that represents the maximum amount of covariation between the two original sets of variables as described by a single vector for each set of original variables. The denominator can in turn be interpreted as the total amount of variation in the two sets of variables, thus scaling the numerator (Klingenberg 2009). The RV coefficient simplifies to the Pearson correlation coefficient for the bivariate case. RV was calculated using custom scripts in R v2.10.1 (R Development Core Team 2009).

Modulated modularity clustering (MMC) was used as previously described (Ayroles et al. 2009; Stone and Ayroles 2009). Briefly, MMC is an approach that seeks to identify latent structures (communities) from sets of covarying genes that estimate so-called “transcriptional modules.” In particular, the MMC approach does not require setting of explicit thresholds, or parameter tuning, which is done adaptively. For our study we utilized the transcript means (averaged across multiple probes) for the 486 transcripts with evidence for differential expression. This yielded an estimate of modularity (the quantity to be maximized) of Q = 0.784 and k (number of estimated modules) = 25.

RESULTS

Validation of the custom gene expression platform:

Given that the mutational effects employed by this study are relatively weak perturbations (as they reduce gene activity/expression by at most 50% and have only subtle quantitative phenotypic effects on wing shape), it was expected that the impact on gene expression would be modest. Therefore, we felt it was important to first demonstrate that the custom Illumina bead array was sufficient to detect such changes in transcript abundance. We have validated the custom Illumina bead array by testing specific expectations in two ways, first by examining mutations that a priori would be expected to reduce transcription and, second, by replicating published experimental results for validated (microarray and in situ hybridization) gene expression differences examining the interaction between genetic background and a mutation in the scalloped gene.

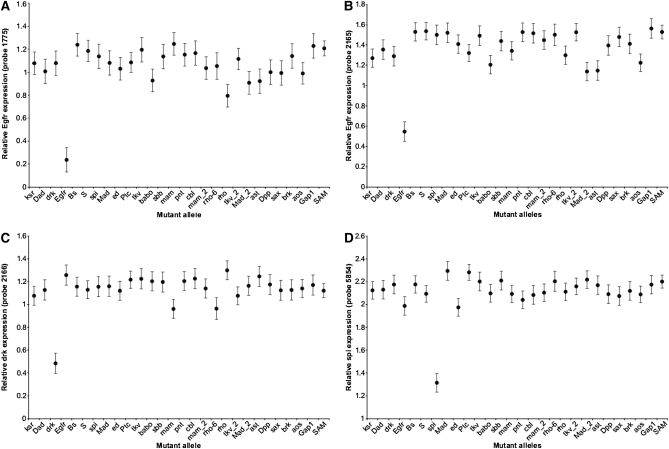
Of the 27 mutations used for this study, 17 were known to be located in putative noncoding regulatory regions of the genes of interest (Table 1). Thus we expected that, measured across this subset of 17 mutants and their isogenic wild type, the transcript abundance of the disrupted gene would be at a minimum in the line that carried the mutation. This was the case for 14 of the mutants, where the mutation reduces the expression of its own gene product (Figure 1 and Table 1), providing good evidence that the microarray accurately quantifies the transcriptome. In the case of one gene (Dad), one of two different probes was most highly expressed in the mutant line, implying upregulation of gene expression, while the other was the least expressed. By and large these results are consistent with the demonstration that despite the use of modest perturbations of gene function, the Illumina focused array platform was sufficient to detect expression changes.

Figure 1.—

Reduction in expression for select mutants. Illumina custom array-based transcriptional profiling is sufficiently sensitive to observe small quantitative differences in expression due to weak mutational perturbations. Despite the small effects of the mutational perturbation (reducing transcription by <50%), the arrays were able to clearly demonstrate reduction via the mutation. (A and B) Two independent probes of Egfr demonstrating reduced expression in the Egfr heterozygous mutant. (C and D) Similarly reduced expression for the drk probes for a drk mutation (C) and spi probes for a spi mutation (D).

We recently published a detailed analysis of wing imaginal disc expression using the Bloomington Drosophila Genome Resource Center's whole-genome PCR amplicon-based expression array to compare expression in scalloped mutants in two different genetic backgrounds (Dworkin et al. 2009). The core results of this experiment were replicated using the Illumina platform used in this study. In particular, those genes whose expression differences were verified (Dll, vg, sd, and Omb/bi) using in situ hybridization in the previous study showed similar changes in gene expression using the current platform (Figure S1). Results for specific transcripts were broadly comparable between the two platforms, with similar trends in relative abundance; however, differences in statistical power, probe sequence, and labeling methods make it difficult to make more quantitative comparisons of the two platforms. Taken together, the good agreement between these two experiments, and the internal consistency of the Illumina array, validates the use of the bead array for quantification of imaginal disc gene expression.

Refutation of the null hypothesis of no differential expression:

A first-pass analysis of the effect of each mutation was performed by pairwise comparison of the gene expression profiles of each mutant strain against the Samarkand co-isogenic wild type. As the strains were all generated by at least 15 generations of backcrossing, each one differs from Samarkand only at a few percent of the genome surrounding the mutations. On average, only 1.4% (1.0% median) of the transcripts were observed to be differentially expressed (P < 0.001) in any of these pairwise comparisons. Using a “q-value” FDR approach yielded similar results with evidence for 4.3% (0.9% median) of transcripts being differentially expressed. Thus, despite a clear indication that the effective reduction in gene expression can be detected for the transcripts of a given gene (given a mutation in that gene), individually, the weak effects of the perturbation have subtle influences on the transcriptome, much smaller than those seen for large-scale perturbations or between wild strains (sensu Dworkin and Gibson 2006).

Nevertheless, there is evidence for several potential novel interactions that are worth considering on the basis of reciprocal patterns of misregulation. For example, in a Gap1/+ mutant heterozygote, there is evidence for an increase in expression of the Dad transcript relative to the Samarkand wild type, 2.53 ± 0.17 (SE) on a log2 scale (corresponding to 5.7-fold difference). Reciprocally, in a Dad/+ mutant heterozygote there is a 1.1 ± 0.13 (SE) increase in expression of Gap1 transcript, corresponding to a 2.14-fold difference, suggesting negative feedback between these genes. In addition, Hsp67Ba appears to be upregulated in 14 of the comparisons of heterozygous mutants to their Samarkand wild type, indicating the possibility of the activation of a stress response. There are several other patterns of common alteration in expression that emerge when the effects on the transcriptional profile are examined on a gene-by-gene basis. Seven of the mutations (bs, sbb/mtv, babo, Mad, aos, ast, and ksr) show evidence for influencing the expression of CG30069. This gene has been shown to be upregulated in the wing imaginal disc (Butler et al. 2003), and RNAi knockdown of this gene induces a blistering phenotype, similar to the bs gene (Jacobsen et al. 2006). In addition, 10 of the mutants (bs, Egfr, sbb, Gap1, ptc, aos, babo, Mad, ast, and ksr), modulate the expression of X-box binding protein-1 (Xbp1). Mutations of Xbp1 over a deficiency result in larvae without imaginal discs. Thus despite the small number (and small magnitude) of effects on gene expression, it is clear that these perturbations of small effect are sufficient to modulate expression of known regulatory genes in the developing wing imaginal disc.

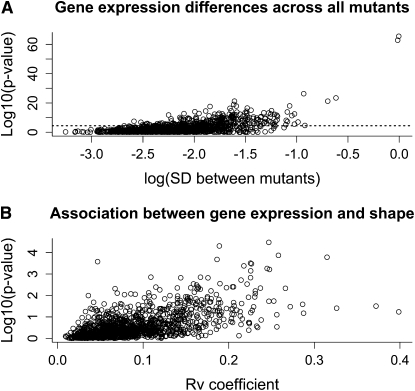
Increased statistical power for detecting differential expression of genes among lines was gained by performing analysis of variance, contrasting the ratio of variance within lines (measured on between four and six arrays derived from paired discs manually dissected from 30 larvae each) to variance between them. Figure 2A shows the relationship between significance of differential expression and the standard deviation between mutants. Evidence for differential expression can be observed across all levels of abundance. Adopting a sequential Bonferroni approach allowing for 1398 probes on the array, 270 probes were found to vary among mutants and their co-isogenic wild-type Samarkand. This number increased to 540 probes at the false discovery rate of q < 0.01 (Storey and Tibshirani 2003), demonstrating differential expression among lines of at least one-third of the genes on the microarray and clearly refuting H₀. When the second wild type (Oregon-R) is included in the analysis, the number of probes deemed to be significantly different on the basis of a sequential Bonferroni procedure is 324, or 528 at a q-value <0.01 (Figure 2A). The genes are listed in Table S1.

Figure 2.—

Gene expression differences across all mutants and associations with shape. Global transcriptional profiles and associations between wing shape and gene expression are shown. (A) transcriptional profiles for 1398 probes representing ∼1000 genes across all genotypes. The vertical axis is the transformed P-value for the overall linear model, while the horizontal axis represents the standard deviations between the genotypic means. The dashed horizontal line represents traditional Bonferroni correction for multiple comparisons. (B) Association of gene expression and variation for wing shape. The vertical axis is the transformed P-values from multivariate regression of shape onto gene expression. The horizontal axis is the RV coefficient, a measure of covariation between gene expression and shape. The RV coefficient is bounded between 0 (no covariation) and 1 (complete covariation).

There is no obvious pattern of enrichment for probes corresponding to the 27 mutant genes in the list of most highly differentially expressed probes, suggesting that transcription in the two major signaling pathways downstream of the Dpp and the Egfr is not grossly disrupted in the lines. However, it should be noted that genes that are differentially expressed in only one or a few of the mutants will typically not be detected by ANOVA across the full panel. Thus, it is possible that substantial disruption of signaling in these pathways does occur in a small subset of the lines. Three of the genes did show a marginally significant tendency for differential expression in the Egfr-pathway mutant lines relative to the Dpp mutant lines (ast was downregulated and babo and Mad were upregulated), but the trend was weak in each case.

Weak evidence for covariation between transcriptional variance and wing shape:

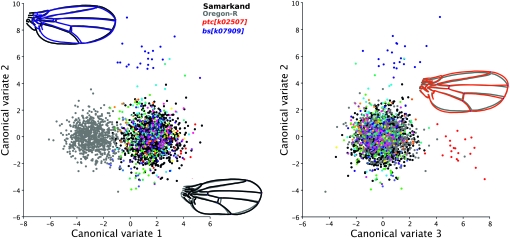
The subtle genetic perturbations caused via the heterozygous effects of the mutations can be discerned using geometric morphometric techniques, as shown in Figure 3. Despite the fact that >80% of the mutations in the original study demonstrated a significant effect on shape (Dworkin and Gibson 2006), these effects are small relative to the differences between the two wild-type strains used in both the previous and the current study. Indeed, Figure 3A demonstrates that the first canonical variate is largely due to the differences between the Samarkand and the Oregon-R backgrounds and not due to any individual mutations. By contrast, the second and third canonical variates separate bs and ptc mutant phenotypic expression, as seen in Figure 3b.

Figure 3.—

Canonical variates (CVAs) for wing shape between select mutants. CVAs of the genotypes for wing shape variation are shown. The left panel shows that CVA 1 represents the differences between the two wild-type strains compared in this study (Oregon-R and Samarkand), while CVA 2 is largely due to the differences between the shape of the Bs/DSRF allele and all other genotypes. The right panel similarly demonstrates differences between the Ptc allele and the other genotypes. The illustrations represent the shape differences along the CV axis for the nine landmarks with the remaining wing extrapolated using splines.

Given these observations, we considered patterns of covariation between gene expression and wing shape. Association of gene expression with wing shape was assessed using a subset of our previously reported wing shape data (Dworkin and Gibson 2006) corresponding to the mutations and genetic background used for gene expression profiling in the current study. First, we utilized a multivariate regression approach, regressing shape onto relative gene expression for each probe. As shown in Figure 2B, while there is some evidence for associations between wing shape and expression, in general the degree of association is weak, as measured using both the P-value from probe-specific models and the RV coefficient, a multivariate extension of the Pearson correlation coefficient for covariation between blocks of variables (Escoufier 1973). Indeed only the probe for the gene Star survived Bonferroni corrections for the multivariate regression, although two independent probes for Bs/Dsrf and a probe for Delta were among those with the highest RV coefficients. We also utilized an alternative (but related) technique to assess patterns of covariation between groups of genes and aspects of wing shape, two-block partial least-squares analysis (Klingenberg and Zaklan 2000; Rohlf and Corti 2000). For statistical inference, 1000 permutations were performed to assess whether the observed patterns of covariation between the blocks of wing shape and gene expression were extreme relative to the sampling distribution under the null model of no association, generated by permutation. When the full matrix of covariation for the shape variables was examined for association with the set of genes that were deemed to vary significantly across the weak genetic perturbations used in this study, only marginal evidence for an association was observed, none of which survived Bonferroni correction. This analysis refutes the strong version of H₁, that each mutant produces a characteristic expression profile that covaries with subtle aspects of the wing phenotype.

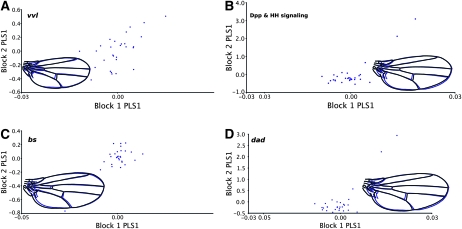
However, it is well known (Held 2002) that considerable temporal and spatial variation occurs for gene expression in the wing imaginal discs, which would make it more difficult to profile the expression of the genes at the precise times that their expression covaries with wing shape. Thus it was highly unlikely that we would observe an overall pattern of covariation between wing shape and the entire set of coexpressed genes. Consequently, we adopted a supervised exploratory approach in which we compared patterns of covariation between shape and subsets of differentially expressed genes (as determined above) considered a priori on the basis of their known functions. In Figure 4 we demonstrate the results from two-block PLS analysis for a number of candidate transcripts or signaling pathways that have suggestive patterns of covariation with shape. While none are formally significant after correcting for multiple comparisons, these represent candidates for future study. Given that two-block PLS analysis can be used for blocks of variables of arbitrary dimensions, we could theoretically scan all groups of transcripts in various block sizes and configurations for association with shape; however, it is unclear how any valid statistical inference could be made from such a large number of comparisons. Despite this, we examined a subset of genes that were differentially expressed that are all known to be involved with Dpp and Hh signaling, which help to specify the anterior–posterior patterning of the wing disc. As shown in Figure 4, the strongest associations with shape were observed for Bs and dad transcripts, as well as for a composite measure of Dpp and Hh signaling, although these effects appear to be driven by a few data points. Interestingly, genes involved explicitly with vein specification did not appear to associate with shape, nor did genes involved with insulin or TOR signaling (not shown).

Figure 4.—

PLS analysis between shape and gene expression for select groups of transcripts. Associations between variation for wing shape and gene expression using two-block partial least-squares analysis are shown. To further describe the covariation between wing shape and expression, we examined specific blocks of genes and shape. While few were significant, after correcting for the number of comparisons, several demonstrated interesting patterns worthy of description. Each panel represents the axes of maximal covariation for shape and expression: (A) ventral veinless, RV = 0.17; (B) Dpp signaling components that demonstrated significant expression differences across genotypes (bi, bs, dad, Gli, kni, and Mad), RV = 0.33; (C) both probes of bs, with the largest RV coefficient between shape and any transcript (RV = 0.43); and (D) dad, RV = 0.31. P-values (via permutation) are all P ≤ 0.05.

We also examined the correlation between the number of genes deemed to be significantly expressed between mutants and their co-isogenic wild type and measures of distance between the mean shapes of the mutant and wild type (Procrustes and Mahalanobis distances). In both cases the correlations were at best weakly suggestive (0.21 and 0.28, respectively), and the confidence intervals for both included zero. These results in general indicate that there is little evidence for covariation between gene expression and shape, when profiling transcript abundance (but not spatial distribution) in late third larval instar wing imaginal discs.

Clustering of expression profiles identifies at least five networks of coexpressed genes:

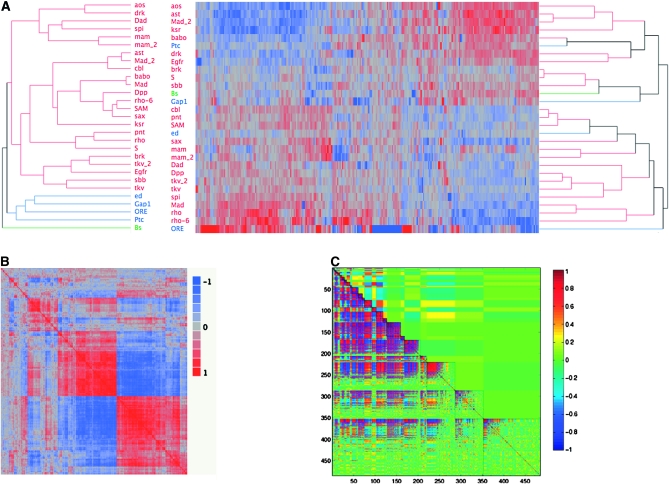
Figure 5A (right side) shows two-way hierarchical clustering used to examine the overall coexpression structure, illustrated by the heat map in Figure 5A with probes represented by columns and the 27 mutant lines as well as the 2 wild-type lines used in this study in rows. Each major grouping of mutant lines with similar profiles includes mutations in both the Dpp and the EGF pathways. There is a hint of enrichment of the Egfr mutations in the top half of the plot and Dpp in the bottom half, but permutation indicates that this partitioning is not significant. This is consistent with observations from hierarchical clustering on shape itself based on the effects of the mutations (Dworkin and Gibson 2006). Notably, the dendograms generated via hierarchical clustering for the shape variables and for the transcripts deemed to be significantly different between lines do not show a great deal of similarity (Figure 5A). This further confirms that there is no evidence for a high degree of covariation between shape and transcript abundance measured in these heterozygous mutants. There may, however, be some smaller patterns linking small numbers of mutants since some similar profiles do fit prior expectations. Examples include the groupings of Dpp, Dad, the two tkv introgressions, and the two alleles of mam that are adjacent for both shape and gene expression. On the other hand, there are also many couplings that do not separate out the pathways, such as brk, S, sbb/mtv, and bs. The two alleles of Mad do not cluster together either for shape or for gene expression; however, interestingly, Mad^kg00581 clusters with ast for both expression and shape.

Figure 5.—

Clustering of mutants on the basis of shape or gene expression. Strong covariation within gene expression is shown, despite little similarity in clustering between expression and wing shape. (A) Topologies for dendograms for shape (left) and expression (right) do not correspond. Multiple agglomeration rules and algorithms were utilized, which, varying in specific topology, always demonstrated the lack of correspondence between shape and transcript abundance. Colors (red, blue, and green) represent the clusters observed for the shape variables, which differ from those of the gene expression data. (B) Correlations between transcripts among the mutant lines show considerable amounts of covariation in gene expression in the wing imaginal disc. The symmetric matrix of probe-by-probe correlations for each of the 540 significant probes is shown. Red represents a correlation at or near 1, while blue represents the degree of negative correlation. As is observed, there are large blocks of positively and negatively correlated genes among the mutants. (C) Modularity in gene expression profiles as determined by MMC suggests covariation within and between estimated modules. The diagonal region, enclosed in solid lines, represents the estimated modules, on the basis of the average correlation within modules. Those with the greatest average correlations within modules are at the top, with decreased average correlations moving down the diagonal. The lower off-diagonal represents average cross-module correlations, while above the diagonal represents the correlation for individual transcripts (as in B, but arranged differently). Colors: red, correlation of 1; blue, −1; and green, 0.

The strong correlation structure observed in Figure 5, A and B, involves five or six groupings of mutants that cluster largely according to the expression of at least five sets of hundreds of genes. These mutant clusters are [argos, asteroid, ksr, Mad^kg00581, babo, Egfr, drk, and Ptc], [brk, S, sbb/mtv, bs, and Gap1], [Cbl, pnt, SAM, (wild-type), ed, and the two mam alleles], [Dad, Dpp, spi, and both tkv alleles], and [rho, rho-6, and Mad^k00237]. The alternative wild type, Oregon-R, as expected appeared at the farthest distance from all of the mutations that shared a common genetic background with Samarkand. These results suggest that clustering for shape, gene expression, or both appears to occur on a fairly small scale, across several mutant genotypes, but not across the whole data set.

A more formal modularity analysis was conducted using the MMC algorithm (Stone and Ayroles 2009) to simultaneously optimize the number of modules and linkages within transcripts. From the 486 transcripts that showed evidence of differential expression, MMC identified 25 modules ranging in size from 2 to 75 genes (Figure 5C), with intramodule correlations ranging from 0.94 to 0.24 (mean of 0.75), which is higher than that previously observed (Ayroles et al. 2009; Kocher 2010). This is likely due to the fact that the set of genes on the array represents a focused set of genes involved with similar biological processes. As demonstrated in the upper diagonal of Figure 5C, the amount of covariation between modules is low, despite high correlation between individual transcripts within the modules (in part due to the MMC algorithm itself). While specific gene ontology classes such as anterior–posterior lineage restriction or cuticle constituents were observed for most modules, in the majority of cases these involved <10 genes and in no cases was significant enrichment observed after adjusting for multiple comparisons. We also utilized the MMC-based clusters to reexamine the relationship between such modules and variation for shape. Focusing on the first 10 clusters, we performed two-block PLS, as described above. In no situation were the singular values or the correlations across blocks significant after correcting for genome-wide comparisons. However, this is unlikely to reflect the overall biology as much as the fact that the focused array used for this was already highly enriched for genes that likely influenced wing development, and thus the whole set of probes is “preenriched.” Indeed, Figure 5B demonstrates the very high degree of covariation between transcript abundance across hundreds of genes among the set of genes that are differentially expressed.

DISCUSSION

The motivation for this study was to combine controlled perturbation analysis with gene expression profiling to characterize the genetic networks that may underlie quantitative differences in wing shape. We hypothesized that expression of a subset of genes active in the wing imaginal disc during a crucial patterning phase of wing development would be associated with adult wing shape differences (H₁) and/or reflect the perturbation of the specific developmental pathway to which each mutation belongs (H₂). Despite overwhelming evidence for differential expression—one-third of the genes showing differences among lines—both of these hypotheses are rejected and it appears instead that the coregulation of gene expression from third larval instar wing imaginal discs follows a different structure from that observed for the morphological effects for the mutations. Here we discuss the possible reasons for rejection of the alternate hypotheses and the implications of the possible existence of attractor states of expression.

Reasons for lack of association between gene expression and wing phenotype or mutant pathway:

In retrospect it is perhaps not surprising that gene expression in mature third instar imaginal discs is not clearly correlated with subtle aspects of adult wing shape. Noting that wing shape is largely invariant to size differences between the sexes and growth temperatures (after accounting for allometry), we previously proposed that the placement and growth of the wing veins are a major determinant of wing shape and that these act as a scaffold or mold for morphogenesis (Birdsall et al. 2000; Palsson and Gibson 2000). This suggests that gene expression in the relatively small subset of the primordium that constitutes the vein fields is what is important, but quantitative changes in such cells may not be detectable by whole imaginal disc microarrays. By analogy, an aerial photograph of the foundations of a building under construction should indicate whether the structure will be square or rectangular and low-rise or high-rise, but probably will not indicate whether a skyscraper is 40 or 45 stories tall or whether the same floor plan carries through each story. Detailed expression profiling throughout the course of development may be necessary to detect associations with wing shape.

The rejection of the second alternate hypothesis, that expression differences would be most similar among lines that perturb the same developmental pathway, likely also relates to the complexity of the biology of the developing wing. It is known, for example, that the roles of genes in the Egfr pathway in specifying vein and intervein cellular identity switch in a matter of hours and over small sections of the disc (reviewed in Held 2002). Subtle expression differences in one set of cells are likely to be obscured by events occurring across the primordium: the wing disc is not like a population of uniform yeast cells or a mature tissue at equilibrium. Furthermore, patterning of the epithelium depends on interactions between multiple signaling pathways including those mediated by the EGF, TGF, HH, and WNT growth factors, with extensive feedback and cross-talk. The network of gene expression across the imaginal disc is thus likely to reflect the impact of each mutational perturbation on each of these pathways and may be more a function of the magnitude, location, and timing of the disruption than the pathway itself. Similarly, the analysis of covariation across perturbations on wing shape did not suggest that perturbations in signaling pathways tended to have similar effects on shape (Dworkin and Gibson 2006).

Variation for gene expression: When does it affect the “phenotype”?

One fundamental assumption of many functional genomics studies is that there will be a direct relationship between transcriptional variation and the “ultimate” phenotype that is the target of the study (Passador-Gurgel et al. 2007; Ayroles et al. 2009). More specifically, it can be stated that there is an expectation that modulation of gene expression will contribute to phenotypic variation, in a predictable (if complex) manner. However, it is as yet unclear how much of the variation observed for gene expression or other intermediate phenotypes is phenotypically relevant, in that variation in the amount or activity of gene products results in a change in the trait value. In this study we demonstrated that while the expression of only a small subset of genes varied under any given perturbation, across the full set of perturbations several hundred genes showed evidence of differential expression. Yet variation in gene expression was found to weakly covary with wing shape, despite the fact that the individual genetic perturbations substantially alter shape (Dworkin and Gibson 2006). This is contrary to other evidence that demonstrates much clearer patterns of covariation between gene expression and behavioral, physiological, or morphological phenotypes (Ayroles et al. 2009). Since in each of these cases it was a relatively small set of differentially expressed transcripts that was observed to covary with the target phenotype, it may be argued that much of the variation in gene expression is either noise or effectively filtered out before it can contribute to phenotypic variation.

In a recent study (Dworkin et al. 2009) we showed that despite a mutant in scalloped having a profound qualitative developmental defect in wing growth, the extent of gene expression variation (in terms of fold differences in expression) was much greater between two wild-type strains than between mutant and wild type. This included a number of well-known developmental regulators where two- to fourfold differences in expression would generally be expected to cause large developmental defects. Instead, the mutant phenotype was associated with a larger set of differentially expressed genes with relatively small differences in expression, compared to differences between wild-type strains. In the current study, the much smaller effect sizes of the genetic perturbation would further dilute our ability to observe such effects. It is clear that documenting differential expression of transcriptional covariation is of itself insufficient to predict phenotypically relevant transcript abundance.

Indeed it is worth considering whether gene expression should ever really be considered in a univariate context or whether it should be considered as part of a more diffuse multivariate structure. Instead of examining individual transcripts for associations with target phenotypes (Passador-Gurgel et al. 2007), we provide evidence that association between modules and target phenotypes should be evaluated (Stone and Ayroles 2009). Dpp pathway components, or wing margin determinants, collectively associate with aspects of wing shape, mirroring a recent report of association of modules of various classes of genes with behavioral attributes in adult flies (Ayroles et al. 2009; Harbison et al. 2009; Morozova et al. 2009). The same objective, unsupervised MMC approach adopted by these authors did not reveal enrichment for gene ontology classes in our data set and revealed only weak association between shape and expression.

A possible contributing factor to the weak associations observed here, in addition to any noise of the measurements, is that the variation observed for this set of perturbations is quite small both for wing shape and for gene expression. Given the design (genetic perturbations measured in an otherwise isogenic background in a controlled laboratory environment), our approach had a relatively high signal-to-noise ratio. Yet the perturbations used produced relatively little phenotypic variation. The average effect size for shape differences between any given mutational perturbation and the wild type was far smaller than that observed between two standard wild-type strains (Dworkin and Gibson 2006). We are currently testing this hypothesis by performing a similar experiment across a panel of inbred lines derived from natural populations that are segregating considerably more phenotypic variation for shape (Birdsall et al. 2000; Palsson and Gibson 2004; Dworkin et al. 2005) and for gene expression (Passador-Gurgel et al. 2007; Ayroles et al. 2009). One additional possibility is that the mutant lines display a greater degree of variation, as has been observed for many morphological traits (Dworkin 2005). Thus, if a larger number of biological replicates were used, with a reduced number of perturbations, we would potentially have increased statistical power to observe associations between shape and gene expression. We feel that for this particular study, this is unlikely, given that previous work did not demonstrate that these mutations increased overall phenotypic variance as heterozygotes (Dworkin and Gibson 2006). In addition, each biological replicate represented a pooling of wing imaginal discs from multiple individuals for the cross, likely obscuring any such effects.

In addition to this consideration, one other major contributing factor that may result in reduced covariation between gene expression and shape is the dynamic nature of gene expression in the wing imaginal disc during larval and pupal growth. Patterns of gene expression in the wing disc are highly dynamic during development, both spatially and with respect to abundance (Held 2002). It is possible that measuring gene expression in the late third instar in the wing imaginal discs does not capture important periods of wing development, with respect to their influence on wing shape. To address this hypothesis would require sampling from multiple developmental time points or stages. Given the number of genotypes sampled in the experiment outlined in this article (29), and the size of this experiment at one developmental stage (>200 arrays and ∼4500 wing imaginal discs dissected), the size of this ideal experiment may be intractable without an automated method for imaginal disc dissection or RNA extraction. Given that previous work demonstrated that the mutational target size of wing shape is quite high, on the order of ∼15% of the genome (Weber et al. 2005), it is unlikely that there is in fact a single “sensitive period” for wing shape. Indeed for many mutations, manipulating their function during late larval development is sufficient to modulate wing growth and structure; thus this alone seems like an unlikely explanation for the lack of association. However, in combination with the other factors (spatial distribution, small variance in expression), they have likely all acted synergistically to contribute to this lack of association.

Attractor states of gene expression in the developing wing primordium:

At the gross survey level described here, there is a pervasive correlation to the data set that requires explanation. The clustering of the transcriptome into four major sets of mutant lines with five major groups of hundreds of coregulated transcripts indicates a surprising degree of coordination of the activity of genes with diverse roles in cell growth and division, developmental patterning, morphogenesis, and physiology. Nuzhdin et al. (2008) described a similar phenomenon in a comparison of gene expression at two stages of embryogenesis in six lines of wild-type D. melanogaster and utilized path analysis to infer that perturbation of gap or dorsal–ventral gene expression coordinates downstream changes. In our study, the perturbation is likely due to the mutations introgressed into a common genetic background, rather than to segregating polymorphism, but it is tempting to suggest that differential expression of a small set of regulatory genes leads to the downstream changes observed in the imaginal discs. These may be transcription factors characteristic of the groups of differentially expressed genes, though studies of yeast indicate that trans-acting expression modulators can have a variety of molecular functions.

Kauffman (1993) provided a framework for considering this coordination when he proposed that gene networks generally follow a Boolean logic that leads to stable attractor states. He predicted that stable networks absorb diverse perturbations or switch between alternate states, simply as a function of the structure of the networks (Figure 5). Thus, the minor perturbations due to heterozygous mildly deleterious transposable element insertions studied here would be shaped by the pattern of response of cells across the imaginal disc, toward one of the relatively stable patterns of gene expression. It will be revealing to characterize the timing of establishment of these patterns as well as the extent to which they are maintained throughout development and in different environments.

The possible existence of attractor states of gene expression raises a number of interesting issues related to the mapping of genotype onto phenotype. For network biologists considering how to dissect regulatory pathways from the correlation structure of expression profiles, it adds the challenge of predicting under what circumstances expression can be channeled into alternate networks. Previous models (Von Dassow et al. 2000) are likely to be relevant in this regard as they have already shown that multiple different parameterizations of regulatory coefficients can support stable developmental patterning. A recent, and relevant example demonstrated this, via observing bistability between vein and intervein fates in the Drosophila wing (Yan et al. 2009). However, the context in which such a research paradigm will be successful for integrating gene expression with complex traits such as wing shape remains unclear. In the previously cited example (Yan et al. 2009), evidence for bistability among fates (with three predicted steady states, only two of which are stable attractors) was established (compared to simple positive feedback) after considerable empirical and modeling effort for a relatively simple developmental transition. Indeed, in other instances with similarly simple cell fate transitions, initial interpretations of such attractors (Huang et al. 2005, 2009) have been contested in favor of alternative models (Mar and Quackenbush 2009). For quantitative geneticists the results of such studies challenge the notion that additive genotypic effects on visible phenotypes arise via additive effects on gene expression. For the evidence presented here, there is little association between the clustering of mutant lines by transcription profiles and their clustering by phenotype, implying that the gene expression states are not affecting the adult wing shape. However, the ultimate demonstration of the influence of gene expression attractor states on cell determination, proliferation, growth, and polarity and how these cellular processes map onto wing shape (or other complex phenotypes) remains a Herculean task. Yet, by linking multiple approaches, it is conceivable that future such studies may be possible (i.e., Manu et al. 2009a,b). Indeed, perhaps it is best to consider such approaches within the context of robustness of wing shape to the subtle mutational perturbations. The genetic perturbations used in this study showed minimal influence on within-genotype variation for wing shape (Dworkin and Gibson 2006), although these results may be environmentally dependent (Debat et al. 2009). Thus it may be that relative to other morphological traits (Dworkin 2005), wing shape shows relatively low sensitivity, an idea that requires further empirical work. Despite the effort required, it is clear that the conundrum of the lack of association linking shape and gene expression states bears considerable further investigation as it impinges on the buffering capacity of developmental systems, the relationship between differential gene expression and abnormality, including disease, and the capacity for neutral genetic drift in gene expression space.