Surface Tension Gradient Driven Spreading on Aqueous Mucin Solutions: A Possible Route to Enhanced Pulmonary Drug Delivery

Abstract

Surface tension gradient driven, or “Marangoni,” flow can be used to move exogenous fluid, either surfactant dispersions or drug carrying formulations, through the lung. In this paper, we investigate the spreading of aqueous solutions of water-soluble surfactants over entangled, aqueous mucin solutions that mimic the airway surface liquid of the lung. We measure the movement of the formulation by incorporating dyes into the formulation while we measure surface flows of the mucin solution subphase using tracer particles. Surface tension forces and/or Marangoni stresses initiate a convective spreading flow over this rheologically complex subphase. As expected, when the concentration of surfactant is reduced until its surface tension is above that of the mucin solution, the convective spreading does not occur. The convective spreading front moves ahead of the drop containing the formulation. Convective spreading ends with the solution confined to a well-defined static area which must be governed by a surface tension balance. Further motion of the spread solution progresses by much slower diffusive processes. Spreading behaviors are qualitatively similar for formulations based on anionic, cationic, or nonionic surfactants, containing either hydrophilic or hydrophobic dyes, on mucin as well as on other entangled aqueous polymer solution subphases. This independence of qualitative spreading behaviors from the chemistry of the surfactant and subphase indicates that there is little chemical interaction between the formulation and the subphase during the spreading process. The spreading and final solution distributions are controlled by capillary and hydrodynamic phenomena and not by specific chemical interactions among the components of the system. It is suggested that capillary forces and Marangoni flows driven by soluble surfactants may thereby enhance the uniformity of drug delivery to diseased lungs.

Introduction

Surface tension gradients initiate “Marangoni flow,” a convective flow where fluid moves from areas of low surface tension to high surface tension. When surfactant adsorption is the trigger for Marangoni flow, fluid moves from regions of high surfactant surface excess concentration to low surface excess concentration. Surfactant–driven Marangoni flow can be utilized to move exogenous fluid through the lung^1–6. Surfactant formulations are currently administered in the human lungs in Surfactant Replacement Therapy (SRT), a treatment for the deficit of the endogenous pulmonary surfactant necessary for proper lung function, often displayed in premature infants. In SRT, a bolus of an insoluble surfactant dispersion is administered endotracheally to drive the surfactant into the alveoli, restoring proper lung function. Previous work suggests that during the latter stages of spreading, after the bolus has taken the form of thin films on the airway surfaces, Marangoni stresses become the dominant driving mechanism for thin film propagation along the lung airway surface liquid (ASL)^{2–4, 7}.

The success of SRT has spawned investigations into the use of surfactants to improve the uniformity of aerosolized drug delivery in the lungs. Current aerosol medications are typically dissolved in saline and accordingly have a high surface tension and tend not to disperse uniformly over the ASL after droplet deposition^{8, 9}. Furthermore, patients with obstructive lung diseases, such as cystic fibrosis, experience a greater concentration of delivered medication in the central airway passages than in peripheral regions, based on the unusual aerodynamics associated with partially obstructed flows^{10, 11}. Adding soluble surfactant to the aerosol formulations may cause Marangoni stresses to drive the aerosol droplets to spread along the ASL after deposition, delivering drugs more uniformly and reaching the otherwise poorly accessible regions that often are sites of disease. Direct observation of such enhanced spreading of an aerosol formulation has been achieved in vitro^{8, 9}.

These two applications, SRT and aerosol drug delivery, have motivated considerable theoretical and experimental research into Marangoni driven flows over thin liquid films or “subphases”^{1–4, 12–23}. Optimization of SRT and enhanced aerosol drug delivery requires understanding of how the complexity of the ASL influences the dynamics, and particularly the extent, of spreading. The ASL of the upper airways consists of a non-Newtonian mucus layer atop a less viscous periciliary liquid^{24, 25}. Mucus is rheologically and chemically complex. Another source of complexity, not generally addressed in previous surfactant spreading studies, is the fact that both the surfactant solution/dispersion and the ASL are aqueous, so the water solvent and the surfactant may transport directly from the bulk of the deposited droplet into the subphase during the spreading process. This could in turn locally alter the subphase rheology. Most experimental studies to date have focused on rheologically simple (Newtonian, nonpolymeric) subphases and solvent-free monolayers of insoluble surfactants, rather than droplets of aqueous surfactant solutions or dispersions. A few have treated soluble surfactant solutions spreading on simple subphases^{12, 21}, while others have treated simple fluids containing no surfactant spreading on rheologically more complex subphases^{13, 19, 22, 26}. Some theoretical treatments have begun to probe the impact of some of the rheological complexities likely present in the ASL^{14, 15, 17, 20, 23}. In all cases, prior studies focus on the mechanisms driving the initial phases of the spreading events and do not treat the factors that limit the ultimate extent of spreading. The latter is the key parameter for successful SRT and enhanced aerosol drug delivery.

A general picture of the spreading event is as follows^{12, 18, 21}: A droplet of surfactant solution is deposited on a liquid subphase. The surfactant solution has a lower surface tension than the subphase. Capillary imbalance at the contact line of the drop causes the drop to spread. If surface tension gradients form either along the interfaces bounding the drop or by surfactant moving beyond the contact line, a Marangoni shear stress pushes the surfactant and liquid subphase radially outwards from the deposition point. For the case where surfactant moves ahead of the contact line, flow in the liquid subphase creates a convective front with some of the characteristics of a shockwave. As the droplet itself spreads outwards, its surface area increases and the bulk surfactant concentration in the drop decreases as surfactants adsorb to the expanding air - droplet interface. A key characteristic of soluble surfactant solutions is that the surface tension decreases smoothly with increasing surfactant concentration until the concentration exceeds the critical micelle concentration (CMC), at which point it remains constant even as the surfactant concentration increases further. As long as the bulk surfactant concentration in the drop is above the CMC, the droplet surface tension remains constant. During this phase of the spreading event, the minimum value in the surface tension profile is held fixed. The capillary imbalance at the contact line remains constant but any Marangoni stress decreases as the surface tension gradient is stretched over a longer distance. Once the bulk concentration in the drop is diluted by adsorption to the expanding air – droplet interface to less than the CMC, the surface tension gradient diminishes both due to the increasing surface tension at the point of deposition and the increasing length of the overall gradient. The capillary imbalance at the contact line also decreases. Spreading ceases when capillary balance at the contact line is attained and Marangoni stresses finally disappear because the surface tension is uniform separately across the drop and across the subphase liquid/air interfaces.

In this paper, we study the spreading of aqueous soluble surfactant solutions over subphases composed of aqueous solutions of physically entangled polymers. We distinguish soluble surfactants from the lipids that constitute the bulk of pulmonary surfactant. The latter are generally water-insoluble and can only be dispersed in water as self-assembled aggregates such as vesicles. The surfactants used here are molecularly soluble in water. Most of the reported results focus on spreading over entangled aqueous mucin solutions, a model of the mucus in the ASL. To support these results we have made qualitative comparisons to spreading experiments on a chemically simpler aqueous solution of entangled (but not cross-linked) polyacrylamide. We focus both on the initial phase of the spreading as well as on the final state of the spread formulation. Surfactants chosen represent canonical categories of surfactant physical chemistry, i.e. anionic, cationic or nonionic, that help reveal critical physical mechanisms that must be considered in the formulation and optimization of enhanced pulmonary drug carriers. The particular surfactants are not being examined or advocated here as candidates for eventual clinical applications.

Experimental Section

Materials

The anionic surfactant sodium dodecyl sulfate (purity ≥99.0%, CAS #151-21-3, “SDS”), anionic dye erythrosine B sodium salt (CAS #568-63-8), NaCl (purity ≥ 99.5%, CAS #7647-14-5) and NaN₃ preservative (purity ≥99.5%, CAS #26628-22-8) were purchased from Sigma-Aldrich (Saint Louis, MO) and used as received. All water was purified to 18 MΩcm resistivity by reverse osmosis followed by a Millipore treatment unit. All surfactant solutions were made in 0.9 wt% NaCl, 2 mM erythrosine B. Porcine gastric mucin (type III, bound sialic acid 0.5–1.5% partially purified powder²⁷, CAS #84082-64-4, “PGM”) was also purchased from Sigma-Aldrich and used as received. PGM is used as a substitute for pulmonary bronchial mucins as it has a similar carbohydrate, amino acid, and sulfate ester composition ^28–31, and is available in the quantities needed for spreading experiments. The dehydrated PGM was stored between 2°C and 8°C and was used within a month of opening the received material. The PGM was rehydrated with 0.9 % NaCl, 0.02% NaN₃ solution, such that the final solution is 5% mucin by weight. PGM rehydration was achieved by magnetic stirring for ~12 h until the final solution appeared to the eye as homogeneous. The rehydrated PGM solution was used within a week. Measurement of the viscosity as a function of concentration showed that the solutions used in this study are above the entanglement concentration. As will be discussed later, differences in the mucin solution/air interface were found even for different samples taken from the same mucin solution. However, all results presented in this paper are robust against the day-to-day, and batch-to-batch variation of PGM solutions. All experiments were conducted at room temperature (20 to 24°C) and ambient humidities, typically between 40 and 60%. Experiments run in an enclosed chamber with humidity above 90% showed the same behaviors as at lower humidities, suggesting the local environment just above the aqueous mucin solutions was at high relative humidity even in the open experiments.

While we performed most of our studies with the above materials we also used other surfactants, dyes and polymeric subphases for qualitative comparison. Surfactants examined include: a cationic cetyltrimethylammoniuum bromide (CAS #57-09-0, “CTAB”), and the polymeric nonionic surfactant Pluronic F127 (polyoxyethylene-polyoxypropylene-polyoxyethylene (PEO-PPO-PEO), with a PEO/PPO ratio of 2:1 by weight, molecular weight of 12.6 kDa, CAS #9003-11-6) and an oligomeric nonionic surfactant, Tyloxapol (CAS #25301-02-4). Additional dye markers included cationic methylene blue (Fisher Scientific, Pittsburgh, Pa, CAS #7220-79-3), and hydrophobic Nile Red (CAS #7385-67-3). These surfactants and dyes were purchased from Sigma-Aldrich (Saint Louis, Mo) except as noted. We also prepared 1 wt % aqueous solutions of polyacrylamide (molecular weight 5,000,000 – 6,000,000 Da, CAS #9003-05-8, “PA”) in 0.9% NaCl as another, yet simpler, entangled polymer solution subphase. PA was purchased from Polysciences (Warrington, PA). Viscosity measurements also indicate these PA solutions were above the entanglement concentration.

Methods

Surface Tension Measurement

The surfactant solution surface tensions were measured using the duNouy ring method. Capillary rise measurements were used to determine the surface tension of the more complex PGM or PA solutions. Comprehensive details of this method may be found in references32–34. A 9 cm diameter Petri dish was filled with PGM or PA solution until a meniscus formed above the rim of the dish. An acid-cleaned, 1 inch diameter glass tube was centered above the middle of the Petri dish and lowered until it touched the meniscus. Time-lapse images were taken of the fluid-air interface of the meniscus forming on the outside of the glass tube. The images were obtained using a telemicroscope, Infinity model K2 (Boulder, CO) with Koehler illumination, carefully calibrated to ensure no detectable distortion of the meniscus image. From these images, the interface shape was digitized and fit to the Laplace equation, giving the surface tension of the mucin solution. By fitting the entire interface shape, the surface tension was obtained independently of the contact angle on the glass tube and we could differentiate between hydrodynamic distortions that cause a deviation from the Laplace shape and a quasi-static evolution of the surface tension.

Spreading Experiment

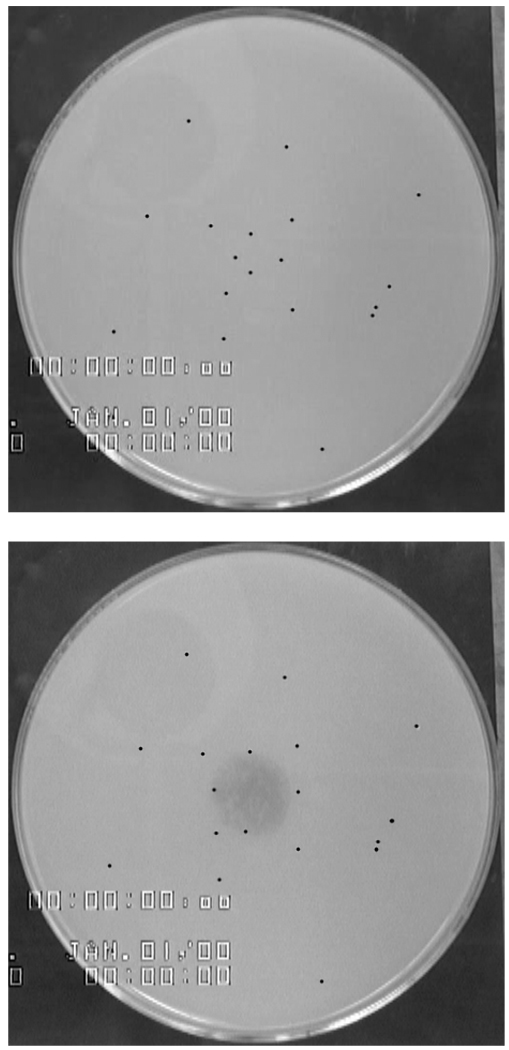
The spreading experiments were performed in a 14 cm diameter Petri dish, enclosed in a Plexiglas box to minimize air currents and filled with PGM solution to a depth of 0.5 cm. This gave a gravitational parameter (G = ρH²g/Δγ, the ratio of gravity to Marangoni forces, where ρ is the subphase density, H is the subphase thickness, g is the acceleration of gravity and Δγ is the difference in surface tension between the subphase and the surfactant solution) of order ten. In the present work, we did not probe the dependence on the subphase depth nor reached values comparable to the thickness of mucus on the lung (where the mucus is not supported by a solid surface but by another fluid layer, the periciliary layer). Rather, experiments were performed in a regime where the spreading should be insensitive to the subphase depth. Further, with G~10 the subphase should not (and did not) rupture during spreading and experiments were deeply within the regime where bidirectional flow would occur through the cross section of the subphase thus minimizing the impact of the dish diameter on the spreading¹⁶. After pouring, the PGM was left for twenty minutes to stabilize its surface tension (see Results). To track subphase movement, 0.8 – 1 mm diameter polystyrene particles (filtered MW 125,000 – 250,000 polystyrene beads, catalogue #19824 Polysciences Inc., Warrington, PA) were placed on top of the PGM. These tracer particles are not wet by the PGM and sit relatively high on the surface. The particles were placed in a fixed pattern to facilitate tracking of the subphase and to minimize capillary interaction between particles (Figure 1). The large size of the particles was chosen so they could be individually manipulated and could be imaged at the low magnification needed to image the entire spreading event in a single field of view. Varying volumes of dye-containing surfactant solution from 1 to 10 µl were gently dispensed from a micropipette onto the center of the PGM surface with as little kinetic energy as possible to initiate the spreading event. The spreading process was recorded using a video camera (XC-555/555P Sony Corporation). Particle tracking software was used to analyze the tracer particle trajectories. Image J (National Institutes of Health) image analysis software was used to measure the final spread area of the dye solution.

Figure 1.

Before and after images of a typical spreading experiment with a 2 µl droplet of a 2 mM SDS solution containing erythrosine B dye placed on the center of the PGM subphase. Each particle is marked by a black dot in the image for ease of viewing. For scale reference: the Petri dish is 14 cm in diameter. Note that innermost tracer particles are swept outward by the spread of the dye solution.

Results and Discussion

Surface Tension

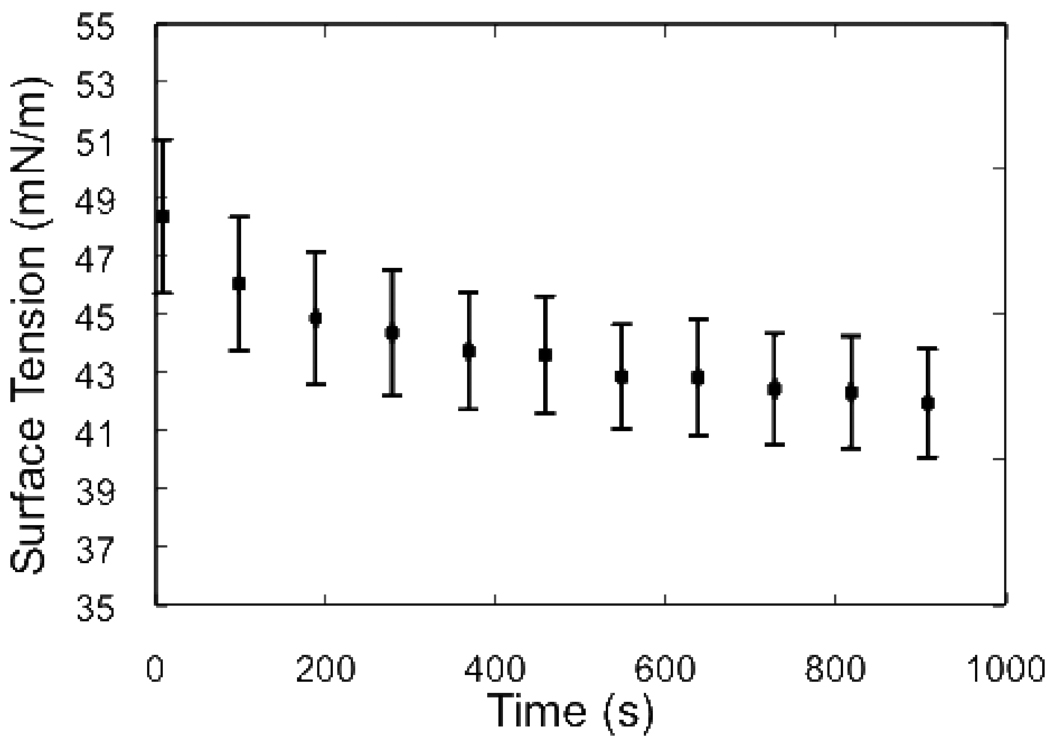
Figure 2 shows that the surface tension of the PGM solutions decreases with time after pouring. This slow variation is a consequence of the slow saturation kinetics for polymer adsorption from solution to interfaces. While the general shape of the surface tension relaxation curves is similar among all experiments, we observe variation in surface tension on the order of a few mN/m from one filling of the Petri dish to the next. To allow the transients of the surface tension to decay before we perform a spreading experiment, we wait 20 minutes after pouring before initiating spreading measurements. Because it is not possible to measure the subphase surface tension simultaneously with microscopic observation of the spreading process, we determine an initial surface tension difference between the mucin solution and spreading surfactant using an average of the observed long-time PGM solution surface tensions measured over a large number of independent experiments where no surfactant is added. Thus, we use a surface tension of 42±2 mN/m for the initial bare PGM solution surface. The timescale for the slow relaxation of PGM surface tension far exceeds that of the spreading events (discussed below) that typically conclude within ~ 10 – 30 s. We note that the 2 mN/m variability of the surface tension of the PGM is ~20% of the surface tension difference between the surface tension of the surfactant solutions just as they are placed on the PGM surface and surface tension of the bare PGM solution/air interface which must exist before any spreading can take place. This large fractional variation in the surface tension differences will cause significant variation in the initial capillary imbalance and Marangoni stresses driving the spreading in each individual experiment and is responsible for the large variation (~40%) we observe in final spread areas. We report only results that are robust against these variations which are intrinsic to the system.

Figure 2.

Relaxation of surface tension of 5 wt% PGM with 0.9% NaCl after pouring. Error bars indicate standard deviation of measurements across all samples examined.

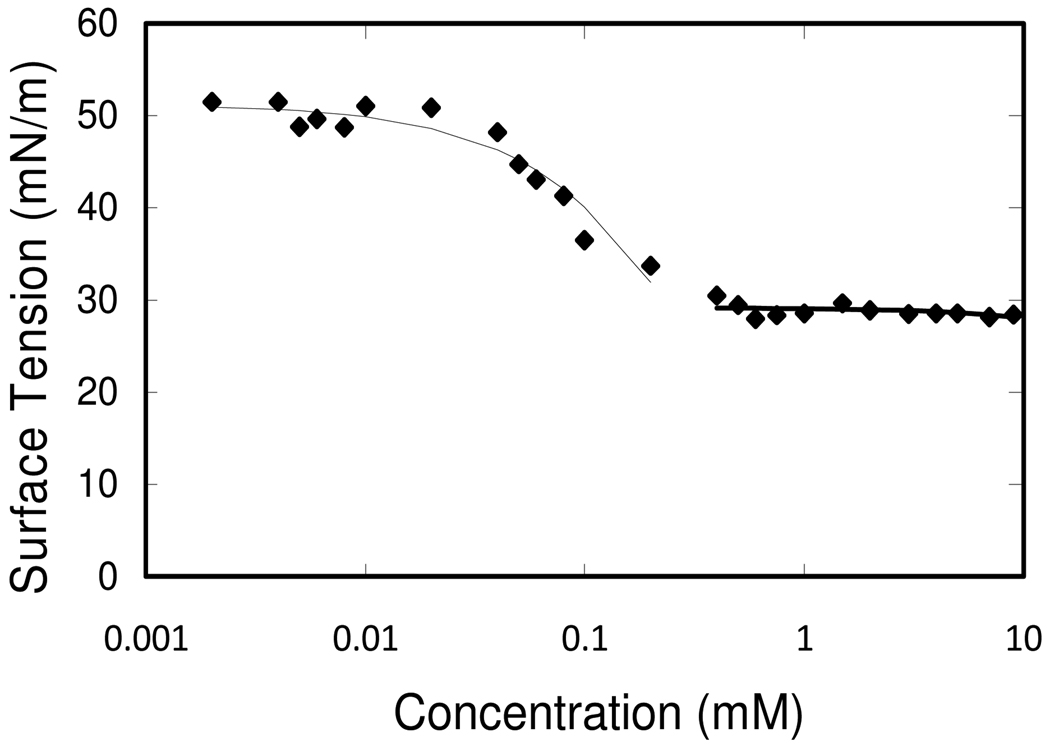
The surface tensions of SDS solutions in 0.9 wt% NaCl containing 2 mM erythrosine B dye are plotted as a function of SDS concentration in Figure 3. Below the CMC, the data was empirically fit with the Szyskowsky equation³⁵

$$\gamma =52[1-0.62\text{ln}[1+\frac{C}{0.24}\left]\right]$$ {{1]

where the SDS concentration C is in mM and surface tension γ is in mN/m. A line was fit to the data above the CMC giving a minimum surface tension of 29 mN/m. The CMC is identified by the intersection of the two regimes and is 0.24 mM for SDS under these solution conditions. This minimum surface tension above the CMC is well below the PGM surface tension.

Figure 3.

Surface tension of SDS solutions in 0.9 wt% NaCl containing 2 mM erythrosine B.

Spreading

We used both the tracer particles and the dye spot to track the extent of spreading. As shown in Figure 1, the particles move outward after the deposition of the surfactant solution droplet. The trajectories of individual tracer particles are plotted in Figure 4. Particles nearer the deposition spot move the furthest from their initial positions. We chose the size of the dish and the volume of solution deposited such that the outer particles do not move significantly, showing that the subphase far from the deposition position does not have significant surface flow during the spreading event and that the dish edges are not directly impacting the spreading event. The dye does not penetrate downward into the subphase even for times far longer than the ~ 10 – 30 s time scale of the spreading event. This long time scale for movement of the dye into the subphase is confirmed in separate experiments discussed below.

Figure 4.

Trajectories of the radial position of particles on 5% mucin solution in 0.9% NaCl after deposition of a 2 µL droplet of 1 mM SDS solution. Smaller radial positions indicate tracer particles closest to the center of the deposited droplet.

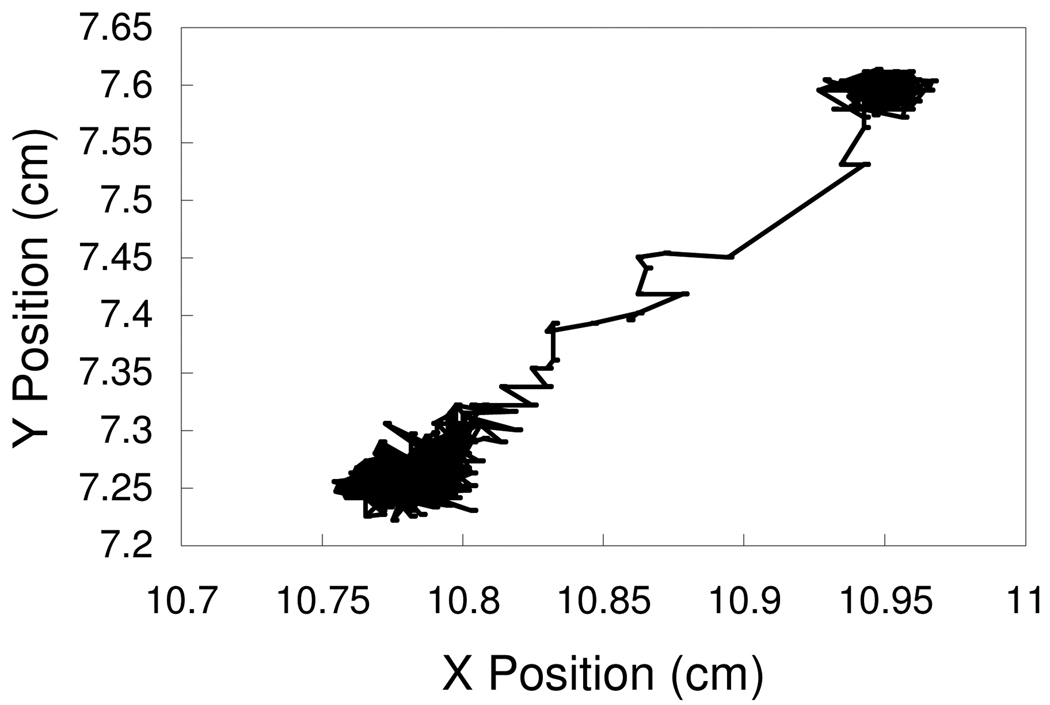
While Figure 4 shows the trajectories as radial distance from the center of the Petri dish versus time, Figure 5 shows the typical trajectory of a single tracer particle in Cartesian coordinates. The transitions from the pre-spreading diffusive movement of the particle to the convective motion during spreading and back to diffusive motion after the convection has ended are quite clear in the data. The number of observation points during the diffusive random walks are insufficient to reliably calculate a diffusion coefficient, but one can clearly see that convection dominates diffusion (i.e., the Peclet number is very large) during the spreading and that motion is clearly diffusive before and after spreading. Using the timepoint at which the tracer particle trajectory transitions from diffusive to convective motion, we determine the time required for the convective front to reach each particle as a function of its initial radial distance from the drop deposition. Thus we calculate that the convective front driven by the spreading moves radially at a speed of 5 to 10 cm/s.

Figure 5.

Motion of innermost tracer particle before and after deposition of 2 µL droplet of 1 mM SDS solution on 5% mucin solution in 0.9% NaCl. Coordinates are arbitrary and not measured relative to the drop deposition point. Initial position is (10.95, 7.6).

A key question is how the tracer particle trajectories relate to the spreading of the drop as indicated by the dye spot images. Figure 6 shows how the innermost tracer particle trajectory relates to the spread area based on image analysis of the dye spot expansion. The dye spot is at first well inside the position of the innermost particle, yet the tracer particle still begins to move at the same time (within the 30 ms time resolution of the video) as the spot starts to spread. The dye spot edge initially propagates faster than the tracer particle until it catches up with and then moves together with the particle. Further, the dye is never observed to spread past the innermost particle. This behavior suggests that the innermost particle is driven by the moving contact line of the spreading drop of surfactant solution once the spot catches up with it. Particles outside the reach of the spreading dye spot are convected only by movement of the subphase which is flowing ahead of the spreading drop.

Figure 6.

Radial position of the innermost tracer particle (black triangles) and the radius of the dye spot (grey squares) versus time on 5% mucin solution in 0.9% NaCl. Data are shown for 4 µl of 1 mM SDS solution. Error bars represent estimated uncertainty in position measurements.

Recoil of tracer particles (seen for example in the trajectories of the innermost tracer particle in Figure 4 as well as the highest concentration drop in Figure 7) is seen in some, but not all, experiments, including replicates of experiments under nominally the same conditions. The specific conditions causing this motion have not been determined and are apparently related to experimental factors we are unable to control.

Figure 7.

Position of innermost tracer particle for SDS solutions of varying concentration on 5% mucin solution in 0.9% NaCl versus time. Curves are identified by their SDS concentration and initial surface tension differences Δγ = γ_sub − γ_drop.: black, C = 2 mM and Δγ = 15 mN/m; gray, C = 0.5 mM and Δγ = 15 mN/m; light gray C = 0.006 mM and Δγ = −6 mN/m.

As has been shown in related situations^12–23, capillary forces at the drop contact line and Marangoni stresses drive the initial spreading dynamics. For these stresses to induce spreading, the initial surface tension of the subphase must be higher than that of the surfactant solution. Representative experiments presented in Figure 7 show that when the surfactant concentration is initially low enough that its surface tension is above that of the subphase, spreading does not occur. Within the limitations of our time resolution, we do not observe any power law behavior at early times as has been observed and predicted in some other cases of spreading due to capillary forces and Marangoni stresses^{12, 21}.

Figure 7 also shows that although the initial surface tension difference drives the onset of spreading, it does not control the final spread area. The two solutions that start above the CMC and therefore have the same initial surface tension difference between the subphase and the droplet, Δγ = γ_sub − γ_drop, initially move at the same rate. The spreading rate for the more dilute droplet soon decreases relative to the more concentrated drop, and the more concentrated drop spreads further. This deviation is expected as the bulk concentration in the spreading droplet falls below the CMC and the surface tension difference starts to decrease²¹. This is seen even more clearly in the spreading of a physically similar but chemically different system, shown in Figure 8. There, aqueous CTAB solutions, both of which are above the CMC, are spread on an entangled aqueous polyacylamide solution subphase. These results show that the spreading dynamics depend not only on the initial surface tension difference between the surfactant solution and the subphase but also on the evolution of that surface tension difference. As the drop spreads, the surface to volume ratio increases and the surface accumulates more surfactant through adsorption, depleting the bulk surfactant concentration in the spreading drop. Since the local equilibration of small soluble surfactants with fluid interfaces is typically rapid or comparable to the time scales of the spreading we report here (see for example reference³⁶ and references therein), this process likely occurs with surfactant on the drop surface and within the drop bulk in local equilibrium. As discussed theoretically by Starov²¹, when the initial surfactant concentration in the spreading drop is above the CMC, for some time after spreading starts, the surface tension remains fixed at a value below that of the subphase driving the Marangoni stresses. However, after the drop expands sufficiently, the surfaces deplete the bulk concentration until it falls below the CMC. As the surface tension of the drop increases, the forces driving the spreading decrease and the spreading rate begins to fall.^*

Figure 8.

Position of innermost tracer particle for CTAB solutions of varying concentration on 1 wt% polyacrylamide solution subphase. Curves are labeled by their CTAB concentrations and initial surface tension differences Δγ = γ_sub − γ_drop. black, C = 0.5 mM and Δγ = 23 mN/m; gray, C = 0.1 mM and Δγ = 23 mN/m.

State After Spreading

After ~10 to 30 seconds, convective spreading ceases. The dye spot and particle positions remain essentially static (other than Brownian motion) for times on the order of hours. Image analysis of the relative dye concentration across the spot shows that the dye concentration gradient at the spot perimeter does broaden over these long times. If we interpret the broadening of the edge as simple two-dimensional diffusion, the broadening is consistent with a dye diffusion coefficient on the order of 10⁻⁶ cm²/s.

An important factor in determining the final state of the spreading process is the fate of the water solvent in the spreading drop. Water evaporation rates for the surfactant solutions (0.001 to 0.002 µL/s0·cm² at the ambient humidities encountered in our experiments) would allow all the water in the drops to evaporate on a timescale of order 300 – 1000 seconds once the drop has reached its typical final spread area. This timescale is one to two orders of magnitude longer than the typical timescale for convective spreading.

While water could in principle move into the subphase, we find this process is much slower than the timescale of spreading. Because of the geometry of our mucin solution sample (open to expansion only on top), net flow of water into the subphase must be accompanied by movement of the entangled mucin molecules in the subphase. In recent experiments, we have seen that it takes hours for polyethylene oxide homopolymer molecules (a much simpler molecule than the complex mucin polymer molecules) in a semidilute aqueous solution to diffuse into a pure water phase in direct contact with the solution. We also have several simple visualization experiments that show that the timescale for penetration into the PGM solution or PGM dissolution into surfactant solutions is far longer than the spreading events. First, a thin (~1 mm) layer of surfactant solution containing erythrosine dye was gently placed on top of a PGM solution in a small sealed vial. A meniscus was formed and the less dense surfactant solution remained on top of the PGM solution. Imaging the thin film/PGM solution interface at 50 µm resolution by telemicroscope showed no sign of dye penetration into the PGM subphase for as long as 10 h. Assuming the dye tracks the water movement, it suggests water penetration into the subphase is slower than the spreading rate on top of the subphase. In a second experiment, a drop of PGM solution was gently placed on the bottom of a Petri dish filled with surfactant solution. No sign of PGM dissolution was observed again for as long as 10 h. Finally, when a 5 µl drop of pure saline was placed on top of the mucin, it did not spread but sat on the PGM surface. We visually observed the drop sitting undissolved on the surface of the PGM for at least 5 to 10 min. Mucin molecule penetration into the solution drop is controlled by the timescale for the polymer network to disentangle and swell, and this evidently limits the rate of droplet mixing with the subphase.

While the spreading event is clearly initiated and driven at early times by capillary and Marangoni stresses, the surface tension balances that control the final quasi-static state when diffusive movement becomes the dominant transport mechanism are less clear. To determine the nature of this balance, we must know the spatial distribution of each of the components of the formulation as spreading ends. Most of the dye is contained in the visible spot throughout the experiment. As discussed above, during the spreading event, the dye spot boundary meets, and then moves together with the innermost subphase surface tracer particles, suggesting that at least throughout spreading, the dye and innermost tracer particles are moved by the contact line of the spreading surfactant formulation. Surfactant has been observed to cross contact lines during spreading events on solid surfaces,^37–39 and this may be occurring in the present case. Modeling of Marangoni driven spreading predicts when G, the gravitational parameter, is as high as in our experiments, there is convective movement of the subphase ahead of the end of the surfactant surface gradient¹⁶. Consequently, our observations of tracer particle movement beyond the spreading dye spot does not necessarily mean surfactant has reached those distances during spreading. Thus, the surfactant inventory in the area where dye exists is not certain and estimates of area per molecule and thus surface tensions at the end of spreading are not possible. Further, we cannot be certain that the classic picture of Marangoni stresses arising from surfactant monolayers with smoothly varying surface concentrations on the subphase interface applies in this case. There may be an abrupt change in surface excess concentration at the boundary of the quasi-static spread drop if surfactant does not migrate ahead of the contact line.

Our results on other surfactants of widely differing chemistries and mucin-binding tendencies reported below clearly show there is little interaction between the mucin chains and surfactant molecules at the PGM/surfactant solution interface during the spreading event. In other words, the spreading occurs as if it were on an inert, non-adsorptive subphase. Absent any specific mucin-surfactant binding, the lack of surfactant at the metastable subphase - droplet interface would be consistent with the ultralow (transient) interfacial tension that exists between the aqueous solution and the PGM which is 95% water.^*

The fate of the water solvent as the drop spreads is more complex. The existence of a contact line able to transport the innermost particle differently than the other particles (as discussed above) requires the solvent to be present in the droplet during spreading. The rate of this solvent loss due to evaporation increases as the area covered by the formulation increases but our measured evaporation rates suggest that the time to evaporate all the water from the drop is much longer than the spreading event. The long dissolution times of mucin chains into surfactant solutions compared to the spreading timescale suggest that the spreading occurs as if the surfactant solution and the PGM subphase are immiscible. The same assumption has been validated by experiments for SDS solutions spreading over a pure water subphase²¹. In the latter stages of the spreading, even though the time scale of the PGM dissolution into the layer of solution is long compared to the spreading time, the layer is thin (~10 microns during the latest stages of spreading), and we do not know to what extent mucin chains have moved into the layer.

Results on other materials

The results of the spreading experiments presented above are not unique to SDS spreading on a PGM subphase. For the wide variety of systems shown in Table 1 all the basic features of the spreading are similar including (a) initiation of spreading only when the initial surface tension of the solution is below that of the subphase, (b) initial spreading rates being equal for solutions of different initial concentration but all above the CMC, (c) spreading ending in a quasi-static state, (d) the area of spot after spreading not simply determined by the initial surface tension difference between the droplet and subphase, and (e) dissolution of the drop into the subphase occurring on a much longer timescale than the spreading event. The only substantial difference was that the polymeric Pluronic F127 and oligomeric Tyloxapol surfactant formulations have a significantly longer time scale of spreading compared to the SDS and CTAB formulations, tens of minutes versus tens of seconds at comparable absolute concentrations or concentrations relative to their CMC. An example is shown in Figure 9.

Table 1.

Systems observed to show similar spreading behavior.

Surfactants	Dyes	Subphases
SDS   (anionic)	Erythrosine*   (hydrophilic, anionic)	Entangled Mucin solutions
CTAB   (cationic)	Methylene Blue*   (hydrophilic, cationic)	Entangled Polyacylamide   solutions
Tyloxapol   (nonionic, oligomeric)	Nile Red   (hydrophobic)
Pluronic F127   (nonionic, polymeric)

^*Anionic dye not used with cationic surfactant to prevent precipitation. Similarly, cationic dye not used with anionic surfactant to prevent precipitation.

Figure 9.

Position of innermost tracer particle for 0.56 mM Pluronic F127 on a 1 wt% polyacrylamide solution subphase.

Summary

Our results show that capillary and Marangoni stresses drive spreading of water-soluble surfactant solutions across aqueous entangled, polymer solution subphases even as complex as mucin solutions that serve as a mimic of the lung airway surface liquid. We observe that the spreading is not initiated if the original surfactant concentration is such that its initial surface tension is above that of the subphase. As seen by others for non-polymeric subphases²¹, we have also seen that different concentration surfactant solutions above the CMC first spread at the same rate and then spread at different rates only later as the bulk is depleted. This result is consistent with the timescale for surfactant equilibration between the bulk of the drop and its interface being rapid or comparable to the spreading times. After the convective spreading event ends, on a timescale of a few seconds to minutes, only diffusive transport of material continues. The final area – the parameter most critical to the efficacy of such solutions as enhanced pulmonary drug delivery vehicles – must depend on a balance of surface tensions. These surface tensions in turn depend on the final distribution of surfactant and water from the droplet after spreading has ceased.

The independence of our results from surfactant and dye marker chemistry strongly suggests that surfactant enhanced spreading using surfactants will be applicable to drug delivery in the lungs. We do not suggest that ionic surfactants such as SDS or CTAB would be suitable candidates for pulmonary drug delivery. The conclusion from the generality of our observations on different surfactants and entangled polymer subphases is that any soluble surfactant could suffice, provided it creates a sufficiently low surface tension at concentrations suited for aerosolization. The key to optimizing the final spread area of formulations will be determining the surfactant characteristics controlling the disposition of the water and surfactant after spreading has ceased.