Specification of absorbed-sound power in the ear canal: Application to suppression of stimulus frequency otoacoustic emissions

Abstract

An insert ear-canal probe including sound source and microphone can deliver a calibrated sound power level to the ear. The aural power absorbed is proportional to the product of mean-squared forward pressure, ear-canal area, and absorbance, in which the sound field is represented using forward (reverse) waves traveling toward (away from) the eardrum. Forward pressure is composed of incident pressure and its multiple internal reflections between eardrum and probe. Based on a database of measurements in normal-hearing adults from 0.22 to 8 kHz, the transfer-function level of forward relative to incident pressure is boosted below 0.7 kHz and within 4 dB above. The level of forward relative to total pressure is maximal close to 4 kHz with wide variability across ears. A spectrally flat incident-pressure level across frequency produces a nearly flat absorbed power level, in contrast to 19 dB changes in pressure level. Calibrating an ear-canal sound source based on absorbed power may be useful in audiological and research applications. Specifying the tip-to-tail level difference of the suppression tuning curve of stimulus frequency otoacoustic emissions in terms of absorbed power reveals increased cochlear gain at 8 kHz relative to the level difference measured using total pressure.

INTRODUCTION

Assessment of auditory function based on a sound stimulus delivered into the ear canal typically requires specification of the level of the sound stimulus. This input pressure level is measured at one or more locations in the ear canal, which may include a location adjacent to the tympanic membrane. Ambiguities in relating pressure between an arbitrary mid-canal location and the tympanic membrane exist due to the presence of longitudinal acoustical standing waves, which produce significant effects above 1 kHz in the adult ear canal. Even when sound pressure is referenced to the tympanic membrane, further ambiguities may exist at even higher frequencies due to the presence of transverse acoustic modes in the ear canal that interact with the inhomogeneous motion of the tympanic membrane (Khanna and Stinson, 1985). Rosowski et al. (1988) and Shaw (1988) emphasized the importance of the external and middle ears as collectors of sound power in a diffuse free field, and the power absorption characteristics of the human ear in a diffuse free field was measured by Keefe et al. (1994). For hearing experiments, Keefe and Levi (1996) proposed that the ear-canal sound stimulus be specified in terms of the acoustic power absorbed by the ear, which would eliminate effects of longitudinal standing waves, and thus the strong dependence of the stimulus magnitude on measurement location in the ear canal. To the extent that losses at the ear-canal walls are negligible, this power equals the power absorbed by the middle ear at the tympanic membrane. Neely and Gorga (1998) investigated the use of in-the-ear calibration based on total acoustic intensity, i.e., the acoustic power per unit area absorbed over a reference area, and reported that the sound intensity level has advantages for specifying stimulus level compared to sound pressure level (SPL) at frequencies from 4 to 8 kHz. This report describes absorbed power using a decomposition of ear-canal pressure into a forward wave traveling toward the tympanic membrane and a reverse wave traveling away from the tympanic membrane. Similarities and differences are described between in-the-ear calibration procedures based on total pressure, forward pressure, acoustic intensity, and absorbed-sound power. An application of power calibration to the suppression of otoacoustic emissions (OAEs) is described. The results improve the non-invasive assessment of the gain of the cochlear amplifier at high frequencies in the human ear.

High-frequency acoustic measurements in audiological testing require careful calibration of the sound stimulus. Two commonly used pressure calibration procedures in OAE experiments calibrate the sound stimulus eliciting the OAE across frequency either by maintaining the drive voltage constant across frequency to the sound source or maintaining the measured SPL constant at the probe microphone that is inserted into the ear canal (Siegel, 2007). These procedures lead to ear-canal stimulus levels that may vary by as much as 15–20 dB across frequency when acoustic standing waves are significant (Siegel, 1994). Another recommended pressure calibration procedure is to place the sound source next to the tympanic membrane (Siegel, 1994), which eliminates standing-wave effects, although such a placement may be problematical in routine measurements with human subjects. A fourth pressure calibration procedure for OAEs and audiometric thresholds at high frequencies maintains constant the forward pressure generated in a reflection-less tube with a similar acoustical characteristic impedance to that of the test ear (Goodman et al., 2009). Under this condition of no reverse wave, the forward pressure wave is termed the incident-pressure wave. A general procedure in our laboratory is to calculate the electrical signal that drives the sound source transducer to produce an acoustic signal with desired spectral–temporal properties. This electrical input is calculated based on an incident sound pressure measured in a reflection-less tube with characteristic impedance similar to that of the ear canal.

With the added information from a measurement of an aural acoustic transfer function such as reflectance or admittance, the sound stimulus eliciting an OAE can be specified in terms of the absorbed power. This report describes the use of such a power calibration to measure the acoustic stimulus eliciting the OAE and the additional acoustic stimuli used to suppress the OAE. Such suppression effects are studied at the cochlear, neural, and behavioral levels, and the problem of specifying the input sound stimulus level is common to all such experiments. A quantitative analysis of OAE suppression demonstrates a benefit at high frequencies of an absorbed-power calibration relative to a pressure calibration. The absorbed-power calibration is concluded to have potential advantages compared to in-the-ear calibration procedures based on total pressure, forward pressure, and sound intensity.

THEORY UNDERLYING AURAL ABSORBED POWER

Incident pressure

The sound field in the ear canal is analyzed at sufficiently low frequencies (i.e., up to 8 kHz in an adult human ear canal) that there is only a single propagating acoustic mode along the longitudinal centerline of the ear canal (Stinson and Khanna, 1989). Higher-order modes are also excited at locations near the probe and tympanic membrane and at interior locations along the ear canal for which the geometry transverse to this centerline is rapidly changing over distances greater than or equal to a quarter wavelength of sound (Rabbitt and Holmes, 1988; Hudde and Schmidt, 2009). These higher-order modes are attenuated within a distance along the longitudinal axis on the order of the radius of the ear canal, and influence acoustic measurements at locations and frequencies where the propagating mode has small amplitude. The one-dimensional model of ear-canal acoustics used in the present report is applicable to frequencies up to 8 kHz and to measurement locations that are sufficiently far from the tympanic membrane (i.e., a distance exceeding the ear-canal radius from the tympanic membrane). The model may be useful at even higher frequencies up to the maximum audible frequency of 20 kHz, although more care would be needed in interpreting responses.

A key property of ear-canal acoustics at “high” frequencies (i.e., above 1–2 kHz) is the difference between the incident-pressure spectrum and the (total) pressure spectrum in the ear canal. A useful approach to understand ear-canal acoustics is to analyze a sound field in a cylindrical tube of area A, which is chosen to be approximately equal to the cross-sectional area of the ear canal, and of fixed length between the microphone location and the tympanic membrane. (Subsequent discussion sometimes relaxes the assumption of a cylindrical-tube model to better describe the condition that the ear-canal area varies slowly along the longitudinal centerline axis of the canal.) Neglecting the power lost at the walls of the ear canal, the characteristic impedance Z_c is given in terms of the equilibrium density ρ and phase velocity c of air by

$$Z_c=\frac{\rho c}{A}.$$ (1)

Consider a sound wave traveling away from its source in a long tube of constant cross-sectional area. As long as the stimulus duration is sufficiently short that it entirely decays and no reflected wave from the opposite end of the tube has returned before the end of the measurement, the pressure waveform within the tube is equal to this incident-pressure waveform (Keefe, 1997; Goodman et al., 2009).

If the ear-canal area A differs from the reflection-less tube area used to measure the incident signal, then there is effectively a step discontinuity between the model representation of the probe and the ear canal, as further described in Keefe and Simmons (2003). At the probe surface, the incident pressure in the ear with impulse excitation is proportional to the characteristic impedance, which scales inversely with the area of the ear-canal. The ear-canal area in adults might range ±40% relative to its population mean, which would translate to a range of incident-pressure levels of 7 dB, with larger incident pressures in subjects with smaller ear-canal areas. The pressure may also vary at interior locations within the ear canal. In the long-wavelength approximation, the leading-order effect of varying area within the ear canal is that the acoustic pressure within the canal varies inversely with the square root of its area.

Forward and reverse pressure

Adopting a cylindrical model of the ear-canal, the forward pressure P_f measured at the probe for sound traveling in the “forward” direction toward the tympanic membrane is related to the incident pressure P₀ by (Keefe, 1997)

$$P_f=\frac{P_0}{1-R_{0}R}.$$ (2)

This relation includes effects on the forward pressure of the pressure reflectance R of the ear at the probe, and the source reflectance R₀ of the probe. These acoustic pressures and acoustic transfer functions vary with frequency. As a notational convenience, the explicit functional dependence with frequency is omitted in Eq. 2 and subsequent equations in this report to simplify their form, but the frequency dependence is always implicit. The relations between acoustic source reflectance and Thevenin acoustic source impedance Z_T and between incident pressure and Thevenin source pressure P_T are

$$\begin{array}{l}{Z}_T=Z_c\left(\frac{1+R_0}{1-R_0}\right),P_T=\frac{2P_0}{1-R_0}.\end{array}$$ (3)

It is straightforward to relate the waveguide parameters (R₀ and P₀) to Norton acoustic parameters by similar means.

An advantage of the waveguide relation in Eq. 2 is that it explicitly represents the causal build up of the forward pressure in response to the presentation of an incident pressure. The denominator of Eq. 2 describes the effect of multiple internal reflections within the ear canal between the tympanic membrane and the probe. Defining the transfer-function H_F0 between the forward and incident pressure by

$$\begin{array}{l}{H}_{F0}=\frac{P_f}{P_0}=\frac{1}{1-R_{0}R}\approx 1+\left(R_{0}R\right)+{\left(R_{0}R\right)}^2+\dots \end{array}$$ (4)

the geometric series decomposes the denominator into the incident, first-order internal reflection, second-order internal reflection, etc., of the incident pressure. In the cylindrical-tube approximation of ear-canal acoustics, the term R₀R is the round-trip reflectance product in which the ear reflectance R at the probe is

$$R=R_{\text{TM}}{e}^{-2\mathit{jkL}}=\left|R_{\text{TM}}\right|e^{-j\left(2\mathit{kL}-{\phi }_{\text{TM}}\right)}.$$ (5)

R is the product of the pressure reflectance R_TM at the tympanic membrane and a phasor with unit imaginary number j describing round-trip propagation between the probe and the tympanic membrane. The acoustic wavenumber is k = 2πf∕c at frequency f, and 2L is the round-trip path length between the probe and tympanic membrane (the spatial extent of the tympanic membrane over a range of longitudinal distances in the ear canal is neglected). The reflectance phase at the tympanic membrane is φ_TM.

The loading impedance Z_TM at the tympanic membrane is related to R_TM using the cylindrical model of ear-canal acoustics as follows:

$$Z_{\text{TM}}=Z_c\left(\frac{1+R_{\text{TM}}}{1-R_{\text{TM}}}\right),$$ (6)

in which Z_c is defined in Eq. 1. Both representations assume a model in which the function of the tympanic membrane may be adequately represented using a lumped circuit element at a single location in the ear canal. If the area of the tympanic membrane A_TM in this one-dimensional transmission line model differs from A for the ear canal, then the characteristic impedance used in Eq. 6 would be based on the corresponding form of Eq. 1 with A replaced by A_TM. The critical details of how to represent and measure the area of the tympanic membrane must be specified whether the model is based on the use of waveguide or Thevenin parameters. The actual motion of the tympanic membrane varies in magnitude and phase across its surface in response to a spatially distributed acoustic field in the ear canal (Cheng et al., 2010). Nevertheless, there is a net frequency-specific volume velocity swept out by the motion of the tympanic membrane that is coupled to the sound field in the ear canal in the one-dimensional transmission line approximation.

When the denominator in Eq. 4 is close to one (i.e., when |R₀R| is much less than one), the forward pressure is approximately equal to the incident pressure. When |R₀R| is close to 1, a minimum results in the denominator that produces a maximum in |P_f| relative to |P₀|. The maximum possible value of the denominator is 2, which implies that the minimum |P_f| can be no less than |P₀|∕2 at any frequency. The source reflectance of a typical OAE probe such as an Etymotic ER-10C probe, which was measured in a tube set with a similar area to an adult ear (Keefe and Abdala, 2007), has a magnitude |R₀| between 0.9 and 1.0 at frequencies up to approximately 1.4 kHz, and a magnitude of about 0.8 between 2 and 8 kHz. Its phase is close to 0 radians at low frequencies and within π∕4 radians at all frequencies up to 8 kHz. The source reflectance of a different probe assembly described in Keefe and Simmons (2003) has generally similar properties. The dominant source of frequency variability in the phase of R in Eq. 5 is the round-trip lag of 2kL, which rotates rapidly with increasing frequency. The product |R₀R| is mainly reduced at intermediate frequencies where |R| is reduced. Nevertheless, |R| has higher-frequency peaks in adult ears at 8 and 13 kHz “with considerable intersubject variability” (Stinson, 1984).

The feature in the time domain, which is complementary to Eq. 4 in the frequency domain, is a sequence of multiple internal reflections. These are observed as a set of echoes of the incident click with delays at approximate multiples of the round-trip time delay 2L∕c.

Because the reverse pressure P_r at the probe is related to the forward pressure by the ear reflectance, i.e., P_r = RP_f, the total pressure P at the probe is (Keefe, 1997)

$$\begin{array}{l}P=P_f+P_r=P_f\left(1+R\right)=P_0\frac{1+R}{1-R_{0}R}\end{array}.$$ (7)

The expression for total pressure on the right side of Eq. 7 shares the same denominator as does forward pressure in Eq. 2, so both pressures have the same set of minima in their denominators. The total pressure has an additional term 1 + R in the numerator with minima close to R = −1, which occur when its phase −2kL + φ_TM is equal to an odd multiple of −π (the term −2kL dominates the phase). An ear reflectance phase of −π is close to the frequency at which the length L is a quarter wavelength.

The click-evoked OAE measurement protocol of Goodman et al. (2009) used a fixed incident pressure of relatively constant level for the click stimulus. This is in contrast to a calibration using fixed total pressure level in the ear canal, which would be strongly influenced by ear-canal standing-wave minima associated with the 1 + R term in Eq. 7. The transfer-function H_FE of the forward pressure to the total pressure is expressed using Eq. 7 as

$$H_{\text{FE}}=\frac{P_f}{P}=\frac{1}{1+R}.$$ (8)

Its corresponding level L_FE defined as

$$L_{\text{FE}}=20{\log }_{10}\left|\frac{P_f}{P}\right|=-20{\log }_{10}\left|1+R\right|$$ (9)

has maxima at the minima of |1 + R|. The mean L_FE in adult ears was reported in Fig. 5 of Keefe and Abdala (2007) based on a typical OAE probe insertion distance: L_FE had a maximum of approximately 12 dB at approximately 3.4 kHz in adult ears. Keefe and Abdala (2007) applied this forward-to-total pressure transfer function to interpret distortion-product otoacoustic emission (DPOAE) measurements in test ears of infants and adults.

Absorbed power

An absorbed-power calibration focuses on the relative effectiveness of the middle ear at collecting sound power. This is in contrast to the measurement of incident, forward, reverse, or total pressure within the ear canal, which does not specify middle-ear effectiveness. Acoustic power flow in mammalian ears is described in Ravicz et al. (1996).

Consider an ear-canal stimulus that is stationary in time, e.g., a sinusoid or a periodically repeated transient such as a click. The power W_a absorbed from an acoustic stimulus presented in an ear canal with acoustic admittance Y = G + jB and mean-squared total pressure |P|²∕2 at the probe is (Keefe et al., 1993)

$$W_a=G{\left|P\right|}^2∕2.$$ (10)

Ear-canal wall losses are important below 1 kHz in young infants (Keefe et al., 1993); they are detectable, but remain small, below 0.4 kHz in adults [Fig. 5(b) in Margolis et al., 1999]. Otherwise, it is sufficiently accurate to neglect ear-canal losses at higher frequencies in evoked OAE responses in subjects without ear-canal or middle-ear pathology. It follows from conservation of energy in this approximation that the power absorbed at the probe is equal to the power absorbed by the middle ear at the tympanic membrane. There is no need to measure an acoustic response at a more proximal location to the tympanic membrane to specify this absorbed power.

The mean acoustic intensity is the mean energy flux flowing through a reference surface (Landau and Lifshitz, 1959), which in this application is the ear-canal area. For an ear canal with a spatially varying cross-sectional area, the acoustic intensity of the forward wave is |P_f|²∕2ρc and of the reverse wave is |P_r|²∕2ρc (Farmer-Fedor and Rabbitt, 2002) for mean-squared forward and reverse pressures of |P_f|²∕2 and |P_r|²∕2, respectively. Because energy is conserved, the acoustic intensity absorbed by the middle ear from the probe is equal to the difference between the forward and reverse intensities: the power absorbed by the ear equals the integral of this intensity difference over the ear-canal area A at the location where |P_f|² and |P_r|² are measured. These squared pressures are constant over the constant-phase surface of the area in this long-wavelength approximation, so that the power absorbed takes the form

$$W_a=\frac{A}{2\rho c}\left({\left|P_f\right|}^2-{\left|P_r\right|}^2\right)=\frac{A{\left|P_f\right|}^2}{2\rho c}\left(1-{\left|R\right|}^2\right).$$ (11)

This equation can also be obtained from Eqs. 10, 1 by transforming conductance into reflectance, and total pressure into forward and reverse components. The admittance Y and reflectance are related by

$$Y=G+\mathit{jB}=\frac{1}{Z_c}\frac{(1-R)}{(1+R)},$$ (12)

in which the susceptance B and conductance G are real, and G is non-negative. The aural absorbance α is the ratio of acoustic energy absorbed by the middle ear (and in the ear canal when significant wall loss is present) from a single click stimulus to its incident sound energy. It is expressed in terms of pressure reflectance by (Liu et al., 2008)

$$\alpha =1-{\left|R\right|}^2.$$ (13)

The conductance is related to the reflectance by

$$G=\frac{1}{Z_c}\frac{\alpha }{{\left|1+R\right|}^2},$$ (14)

and the conductance level L_G is defined by

$$L_G=10{\log }_{10}G.$$ (15)

Variations in ear-canal area with location in the ear canal are associated with variations in acoustic intensity flowing through that area, whereas absorbed power integrates contributions over the entire area and remains constant with ear-canal location as long as wall loss is negligible. Thus, its use in the long-wavelength approximation is not limited to ear canals with constant area.

The power absorbed from the sound wave by the middle ear is well defined even though the motion across different locations close to the surface of the tympanic membrane has a complicated shape, especially at higher frequencies. Such motion results in a spatially inhomogeneous pressure field close to the surface of the tympanic membrane. Use of absorbed power measured away from the tympanic membrane, as in a typical mid-canal probe location, may lessen the interpretative difficulties associated with measuring pressure close to the tympanic membrane, because any higher-order modes in a human ear canal are attenuated with distance away from the tympanic membrane at frequencies up to 20 kHz.

The power absorbed by the middle ear in Eq. 11 using Eq. 13 takes the instructive form,

$$W_a=\alpha \frac{{\left|P_f\right|}^2∕2}{\rho c}A.$$ (16)

This equation is limited to the approximation of one-dimensional acoustics and the ability to represent the function of the tympanic membrane in terms of a single transfer function. As remarked earlier, each acoustic variable or transfer-function W_a, |P_f| and α varies with frequency, and A is independent of frequency. This equation shows that the ability of the middle ear to absorb power depends on the product of (1) the size of the ear-canal area, which varies across mammals and grows post-natally in human ears, (2) the mean-squared forward pressure |P_f|²∕2 from the sound wave that impinges on the tympanic membrane, and (3) the proportion α of that forward-directed wave that is absorbed by the middle ear at the tympanic membrane, which also has comparative and developmental variability.

The form of Eq. 16 applies to the case of a cylindrical ear canal, but it is only slightly affected if the ear canal area varies between the probe and the tympanic membrane. The magnitude of these effects depends on how the absorbance is measured. To give one example, a local increase in area is associated with a local decrease in squared forward pressure, so that the acoustic intensity changes but the total power flowing through each local reference area is constant (again due to conservation of energy). In a hypothetical comparison of two ears with the same squared forward pressure at the probe and the same absorbance, the power absorbed increases with increased ear-canal area. This predicts that an adult ear absorbs more power than an infant ear (when forward pressure and absorbance are equal in the adult and infant ears). In practice, a stimulus might be used with a relatively flat incident spectrum |P₀|²∕2 or forward spectrum. To the extent that |P_f|²∕2 is constant with frequency, the absorbed power is predicted to have the same frequency dependence as the absorbance. While the calculation of absorbed power using Eq. 10 provides the same result as Eq. 16, standing waves in the ear canal produce maxima in conductance and minima in mean-squared total pressure, and vice versa, which cancel out at each frequency to produce a slowly varying absorbed power. The representation of absorbed power in Eq. 16 eliminates all standing-wave effects.

It is convenient to express the absorbed power in Eq. 16 in terms of a decibel level. A reference power W_ref is used to define 0 dB and is calculated based on a reference area A_ref and the reference root mean-squared pressure of P_ref = 0.00002 Pa, i.e., by

$$W_{\text{ref}}=P_{\text{ref}}^2{A}_{\text{ref}}∕\rho c.$$ (17)

The reference area for the calibration-tube set used in measurements described below was A_ref = 49.5 mm², which is reduced by about 17% (or 0.7 dB in level) of the median cross-sectional area of 58 mm² of the ear canal in a human adult (Keefe and Abdala, 2007). The corresponding reference power is W_ref = 47.6 aW (aW signifies attoWatt, with 1 aW = 10⁻¹⁸ W). The SPL of a pure tone is $10{\log }_{10}\left(\left({\left|P\right|}^2∕2\right)∕P_{\text{ref}}^2\right)$. The absorbed-power level L_W of a pure tone is defined by

$$L_W=10{\log }_{10}\frac{W_a}{W_{\text{ref}}}$$ (18)

and is expressed in terms of the SPL by

$$L_W=\text{SPL}+L_{\text{FE}}+L_{\alpha }+10{\log }_{10}\frac{A}{A_{\text{ref}}},$$ (19)

in which L_FE is defined in Eq. 9 and the absorbance level L_α is defined by

$$L_{\alpha }=10{\log }_{10}\alpha .$$ (20)

The power levels expressed in the admittance and reflectance representations via L_G and L_α, respectively, are related by

$$L_G=L_{\text{FE}}+L_{\alpha }+10{\log }_{10}\frac{A}{A_{\text{ref}}}.$$ (21)

If the reference area is a sufficiently close approximation to the ear-canal area, then the term 10 log₁₀A∕A_ref may be omitted in Eqs. 19, 21. This implies that

$$\begin{array}{l}{L}_W=\text{SPL}+L_{\text{FE}}+L_{\alpha },\\ L_G=L_{\text{FE}}+L_{\alpha }.\end{array}$$ (22)

The absorbed-power level is expressed as the sum of the SPL, the forward pressure transfer-function level, and the absorbance level; the conductance and absorbance levels differ by the forward-pressure transfer-function level. These relations calibrate the sound source in terms of absorbed power, yet retain a pressure specification based on SPL.

Constant stimulus-level procedures

Stimulus calibration in the ear canal is important in interpreting behavioral air-conduction threshold measurements, for which the standard (ANSI S3.6, 2004) specifies how the reference equivalent threshold sound pressure level (RETSPL) is measured in a standard coupler, artificial ear, or ear simulator. ANSI S3.6 reports that the RETSPL at 8 kHz differs by as much as 19 dB with choice of coupler, artificial ear, or ear simulator, which exemplifies the increased difficulty of high-frequency measurements. Based on the properties of incident pressure described above, Goodman et al. (2009) developed a calibrated sound source using an insert earphone for use up to 16 kHz and measured its RETSPL in normal-hearing listeners. Using incident pressure as the reference pressure and a reflection-less tube as the reference coupler, this system avoided the problems of standing waves that complicate measurements at high frequencies.

Other studies have developed calibrated sound sources based on measurements of sound pressure and aural acoustic transfer functions. Neely and Gorga (1998) compared behavioral threshold measurements between 0.5 and 8 kHz based on pressure and acoustic intensity calibration and concluded that intensity calibration in the ear was preferable above 2 kHz. Scheperle et al. (2008) reported that an in-the-ear stimulus calibration based on forward pressure level or intensity level provided more consistent DPOAE measurements between 2 and 8 kHz compared to a calibration based on total pressure. Based on analyses of measurements between 0.25 and 6 kHz, Withnell et al. (2009) proposed that either forward pressure or the fraction of total pressure at the tympanic membrane that is not reflected at the tympanic membrane be used to specify behavioral hearing threshold rather than total pressure. Calibrating the ear-canal stimulus according to forward pressure level has also been suggested for hearing-aid applications using probe-microphone measurements in the ear canal (McCreery et al., 2009; Lewis et al., 2009) and compared with calibrations using total pressure level in DPOAE measurements (Burke et al., 2010). Lewis et al. (2009) also described a calibration method based on the sum of the forward pressure magnitude and the reverse pressure magnitude.

Measuring the absorbed power delivered to the middle ear is an alternative procedure to calibrate the sound source (Keefe and Levi, 1996). For example, the variation in the power absorbed from a wideband chirp was reported for frequencies varying from 0.3 to 8 kHz as a function of the level of a contralateral tone (at 1 and 2 kHz) that activated the acoustic reflex (Feeney and Keefe, 1999). The relative level of absorbed power between activator-present and activator-absent conditions was measured at each frequency and each reflex activator level.

Absorbed power was also used to characterize reverse transmission from a spontaneous otoacoustic emission (SOAE)that was generated within the cochlea in the absence of any sound stimulus and transmitted through the middle ear into the ear canal. Burns (2009) reported that the power absorbed in the ear canal from frequency-specific SOAE components ranged from 0.1 to 400 aW in test ears of children and adults. This range straddles the W_ref of 49.5 aW for an average adult ear-canal area based on a reference P_rms of 0 dB SPL, which is close to the threshold of hearing. Such a threshold power in a human ear is in the same range as the estimated 20 aW of power absorbed by a single frog saccular hair cell for a ciliary tip deflection of 10 nm at 0.15 kHz (Geisler, 1998). While this ciliary mechanism in an amphibian ear may or may not be related to the mechanism underlying SOAE generation in the human ear, the characteristic levels of absorbed power associated with hair-bundle dynamics are of the same order of magnitude as measured SOAE power levels.

For general experiments intended to study how auditory processes vary with frequency, it might be desirable to supply a constant strength of cochlear excitation across frequency. This is difficult in practice inasmuch as non-invasive testing of human subjects must often rely on transmitting a sound stimulus via the air-conduction pathway through the ear canal and middle ear to the cochlea. Because the middle ear is closer to the cochlea than the ear canal in the forward transmission pathway, it would appear advantageous to supply a constant strength of excitation across frequency to the middle ear rather than to the ear canal. Maintaining a constant absorbed power to the middle ear accomplishes this goal. The constant absorbed-power level procedure differs from the constant forward-pressure level procedure, in that absorbed power includes the efficiency with which the middle ear collects power via the product of area and absorbance in Eq. 16, whereas the forward-pressure procedure does not. As described above, absorbed power and intensity-level calibrations are equivalent with a given test ear when a fixed reference area is used, so that a constant intensity-level procedure has the same advantages for auditory experiments as the constant absorbed-power procedure as long as any effect of ear-canal area size is adequately taken into account. The fixed acoustic intensity and fixed absorbed-sound power procedures differ when results are compared between ears with substantially different ear-canal areas. This would be the case in comparing responses in infant and adult ears and responses in ears of different species.

In human infants compared to adults, the maturational growth of the ear-canal area is a major factor in understanding reverse transmission through the middle ear and ear canal and its effect on the maturation of DPOAE responses (Keefe and Abdala, 2007). The effect of ear-canal area on the power absorption from the forward sound wave in Eq. 16 predicts that maturational growth of the ear-canal area influences the interpretation of infant and adult responses in any hearing experiment using a calibrated sound source in the ear canal. That is, maturation of the ear-canal area would influence both reverse and forward transmission. For example, a halving of the area coupled with a doubling of mean-squared forward pressure is predicted to have the same absorbed power in an ear with constant absorbance. This trading relation between ear-canal area and mean-squared pressure may be helpful in better understanding how infant and adult responses differ in a general experiment on hearing.

Aside from OAE-related issues, the power transmitted to the cochlea is equal to the power absorbed by the middle ear minus the internal power losses within the middle ear. This absorbed power within the cochlea has been measured in chinchilla (Slama et al., 2010). However, little is known about the magnitude of the internal middle-ear loss and its frequency dependence in the normal-functioning human middle ear. In the event that the internal power losses within the middle ear would turn out to be negligible compared to the absorbed power, a measurement of power absorbed by the middle ear would equal the power absorbed by the cochlea.

APPLICATION TO OAE MEASUREMENTS

Preliminary remarks

OAEs are clinically useful in detecting sensorineural hearing loss because evoked OAE levels in such ears are significantly lower on average than in ears with normal function. The initial task of stimulus selection is to generate a sufficiently large OAE for detection in a normal ear. To the extent that ear-canal and middle-ear functioning are similar in groups of ears with normal function and with sensorineural hearing loss, the average ear-canal area, absorbance, and forward-pressure level measured in the two groups using the same probe assembly would also be similar. Indeed, acoustic transfer functions such as reflectance and admittance are unable to predict the presence of sensorineural hearing loss at octave frequencies between 0.5 and 8 kHz, except for a significant but small effect at 4 kHz (Ellison and Keefe, 2005). This study reported that including an acoustic transfer-function response with a stimulus frequency otoacoustic emission (SFOAE) response at 4 kHz improved the test performance for predicting sensorineural hearing loss at 4 kHz. However, the statistical analyses were unable to determine the extent to which this was better interpreted as a main effect of energy reflectance or an interaction of energy reflectance with the SFOAE measure. To the extent that acoustic transfer functions do not predict sensorineural hearing status, major differences would not be predicted in OAE test performance when stimulus calibration methods are varied across incident pressure, forward pressure, acoustic intensity, or absorbed-power procedures. Nevertheless, any of these calibration methods may be preferable to a calibration based on total pressure near frequencies where standing-wave minima occur at the probe, especially when the dynamic range of the OAE measurement system is limited by system distortion at higher levels or measurement noise at lower levels. Burke et al. (2010) reported that a DPOAE test had slightly better test performance in predicting the presence of sensorineural hearing loss at 8 kHz when the sound source was calibrated in the ear using forward pressure than using total pressure, but there was no difference at lower frequencies and this difference at 8 kHz was not statistically significant.

Acoustic transfer-function measurements

The aural acoustic transfer functions analyzed in the present report were measured between 0.22 and 8 kHz in the same group of normal-hearing subjects who participated in a study reported by Schairer et al. (2007). Summarizing the inclusion criteria described in greater detail by Schairer et al., an ear test was included in the database based on normal otoscopy, normal 0.226-kHz tympanometry, and normal audiometric thresholds, i.e., air-conduction thresholds ≤15 dB hearing level (HL) between 0.5 and 8 kHz, and air-bone gaps ≤15 dB between 0.5 and 4 kHz. The final database was composed of 40 ear tests obtained from 21 participants ranging in age from 18 to 36 yr (mean, 27.2 yr), including 15 females and six males. Measurements were performed using an Etymotic ER-10C probe assembly, which was modified by the manufacturer to allow 20 dB higher output levels from the receivers. The stimulus for the acoustic transfer-function test was a click presented at a 61 dB SPL based on peak-to-peak amplitude. The custom software ran on a computer using the Windows operating system, in which a high quality sound card (CardDeluxe) was used to deliver and record signals at a sample rate of 22.05 kHz. The acoustic transfer-function measurement system was calibrated daily according to procedures described in Keefe and Abdala (2007), which were refinements of procedures described in Keefe and Simmons (2003). The incident click was designed to approximate a band-limited acoustic impulse with relatively flat spectral magnitude between 0.25 and 8 kHz in a recording in a long cylindrical tube that generated no reflected energy during the measurement duration. This means that the incident-pressure magnitude |P₀| [see Eq. 2] of the click was relatively constant over this frequency range.

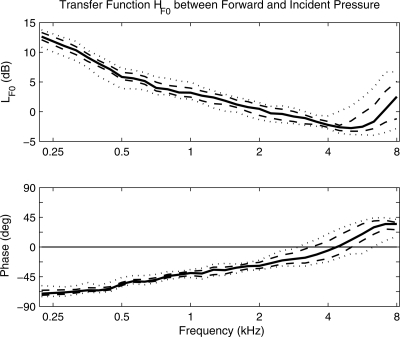
Group results for the transfer-function H_F0 of the forward pressure relative to the incident pressure, which is defined in Eq. 4, are shown in Fig. 1 for the 10th, 25th, 50th, 75th, and 90th percentiles of responses. The transfer-function level L_F0 = 20 log₁₀|H_F0| in the top panel had a median level close to 13 dB at 0.22 kHz, which decreased with increasing frequency to 4 dB at 0.7 kHz. The median L_F0 remained within ±4 dB for all frequencies from 0.7 up to 8 kHz. This quantified the median difference between the SPLs of forward- and incident-pressure waves. As expected from Eq. 4, L_F0 ≥ −6 dB for every ear. The tendency for all the percentiles of L_F0 to increase above 6 kHz was due to an increase in |R| at this frequency range, as further discussed below and consistent with previous group measurements of |R|² (e.g., Keefe et al., 1993). The phase of the transfer-function H_F0 for the percentiles shown in the lower panel of Fig. 1 was negative at low frequencies, had a zero crossing at frequencies ranging from 3 to 6 kHz, and was positive at higher frequencies. The negative phase at low frequencies implies that the internal reflections lagged the incident pressure. The tendency for wider variability in the H_F0 level above 4 kHz and phase above 2 kHz was associated with a wider variability in R at these frequencies. A larger forward-pressure level occurred near 8 kHz when |R| was close to 1 and when the round-trip phase 2kL approached 2π [see Eq. 5] from below, which is the so-called half-wavelength resonance condition.

Figure 1.

Transfer function results for H_F0, the ratio of forward pressure to incident pressure in the ear canal. The transfer-function level (top panel) and phase (bottom panel) are plotted as 10th, 25th, 50th, 75th, and 90th percentiles based on 40 adult ears with normal function.

The summary of Fig. 1 for adult ears with normal function is that (1) the forward pressure had a larger level than the incident pressure below 0.7 kHz, (2) the difference in the forward- and incident-pressure levels differed, on average, by less than 4 dB at frequencies between 0.7 and 8 kHz, and (3) the 90th percentiles of the forward-pressure level exceeded the incident-pressure level by larger amounts above 5 kHz, with a maximum of 7 dB at 8 kHz.

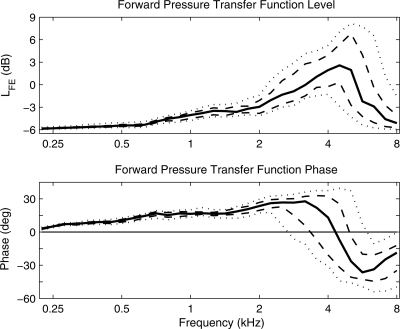
The transfer-function L_FE of forward-pressure level to total pressure level in the ear canal at the probe microphone is plotted in the top panel of Fig. 2 for the 10th, 25th, 50th, 75th, and 90th percentiles of ear tests. All percentiles of L_FE were slightly above −6 dB at 0.22 kHz and increased with increasing frequency to a maximum in the range of −1 to 8 dB at frequencies ranging from 3.9 to 5 kHz. L_FE decreased at higher frequencies out to 8 kHz. The median L_FE was about 3 dB at its maximum near 4.3 kHz, which was a boost of 8 dB higher relative to its minimum at 0.22 kHz. In terms of the model described earlier [see Eq. 8], the low-frequency asymptote of −6 dB occurred because the ear reflectance R was close to 1. The forward and reverse pressures were nearly equal in this case, and each was approximately one-half of the total pressure. This approximates the limiting case of pressure doubling at an ideal reflecting surface. The broad maximum of L_FE was due to a minimum in the total pressure (i.e., the first standing-wave minimum).

Figure 2.

Transfer function results for H_FE, the ratio of forward pressure to total pressure in the ear canal. Forward-pressure transfer-function level (top panel) and phase (bottom panel) are plotted as 10th, 25th, 50th, 75th, and 90th percentiles based on 40 adult ears with normal function.

The phase of the transfer-function H_FE between forward pressure and total pressure [see Eq. 8] is plotted in the bottom panel of Fig. 2 for the 10th, 25th, 50th, 75th, and 90th percentiles of ear tests. All of the percentiles of this phase were close to 0° at 0.22 kHz and increased with increasing frequency up to a transition region in which the phase changed from positive to negative. This means that the forward pressure slightly led the total pressure at low frequencies—because the total pressure is the sum of forward and reverse pressures, and the forward pressure led the reverse pressure at low frequencies. The zero crossing of the phase of H_FE corresponds to a phase of −π radians (i.e., 180°) in R, which is the quarter-wavelength resonance described above. The maximum L_FE generally occurred slightly above this zero-phase frequency (except for the 90th percentile). Thus, the maximum L_FE was influenced not only by this phase condition but also by the frequency dependence of |R|. The median phase was zero at 4.1 kHz. The zero-crossing frequency of the phase varied from 2.5 kHz at the 10th percentile to 5.7 kHz at the 90th percentile.

This median L_FE served as a repeatability test of the mean L_FE reported by Keefe and Abdala (2007) in a group of ten adult test ears (mean age, 27.5 yr) with one test ear per adult. Keefe and Abdala used the same measurement equipment and procedures as were used in the present report. Their mean L_FE had a similar spectral shape with frequency, with an asymptote of −6 dB at the lowest test frequency (0.25 kHz), a maximum close to 6 dB near 3.3 kHz, and a rolloff at higher frequencies to −5 dB at 8 kHz. The main difference between studies is that Keefe and Abdala reported a slightly higher maximum L_FE of 6 dB that occurred at a slightly lower peak frequency of 3.3 kHz. Factors contributing to this difference would include sampling variability, measurement-system differences that should be small, and the possibility that different testers at the sites used slightly different insertion depths. A deeper insertion would correspond to a shorter ear-canal length, and thus an increased peak frequency. Nevertheless, the maximum of the mean L_FE of 6 dB in the Keefe and Abdala (2007) study was within the inter-quartile range of the maximum L_FE in Fig. 2, for which the maximum L_FE was 6 dB at the 75th percentile. Experimental results from Withnell et al. (2009) are also generally consistent with Keefe and Abdala (2007) and the present results. Differences between studies emphasize the importance of individual variability in ear-canal acoustics, including variability in the depth of insertion of the probe.

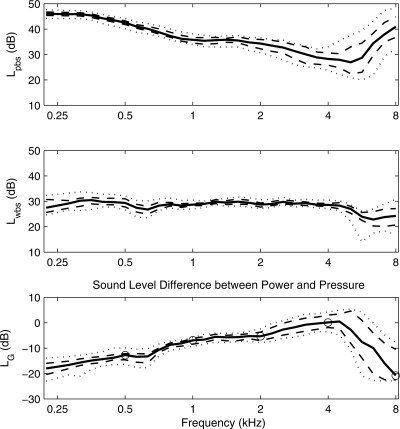
The 10th, 25th, 50th, 75th, and 90th percentiles of the band sound pressure spectrum level L_pbs and band sound absorbed-power spectrum level L_wbs (each with 1-Hz bandwidth) are compared in the top and middle panels, respectively, of Fig. 3. Spectra were measured in the normal-hearing group of ears in response to a click stimulus with a nearly constant incident-pressure spectrum level. The minimum in L_pbs occurred close to frequencies where L_FE in Fig. 2 had its maximum in the corresponding percentile. The median L_pbs varied from 47 dB at low frequencies to approximately 28 dB near 4.3 kHz, a change of 19 dB. The difference between the 10th and 90th percentiles of L_pbs ranged from approximately 3 to 5 dB from 0.22 to 2 kHz and increased to as large as 19 dB near 5.7 kHz.

Figure 3.

The band sound pressure spectrum level L_pbs (top panel) and band sound absorbed-power spectrum level L_wbs (middle panel) are plotted as 10th, 25th, 50th, 75th, and 90th percentiles based on 40 adult ears with normal function. The conductance level L_G, which is equal to the difference of L_wbs and L_pbs is plotted in the bottom panel as 10th, 25th, 50th, 75th, and 90th percentiles for the same data set. The values on the median L_G curve at octave frequencies between 0.5 and 8 kHz are identified with circle markers.

The absorbed-power level L_wbs was calculated in terms of the measured pressure and acoustic transfer functions using Eq. 22, in which the reference tube area was assumed to approximate the adult ear-canal area. L_wbs (middle panel, Fig. 3) was more nearly constant with frequency than L_pbs from 0.22 kHz up to 8 kHz. The median L_wbs varied between a minimum of 23 dB at 6.3 kHz and a maximum of 30 dB over a broad range of frequencies including 0.32–0.5 kHz and 0.71–4.5 kHz. The difference between the 10th and 90th percentiles of L_wbs covered a 6 dB range at 0.22 kHz, which narrowed to a 2 dB range between 1 and 4 kHz. This range widened between 4.3 and 8 kHz to as large as a 13 dB range at 5.7 kHz. The fact that the incident-pressure level range was constant across frequency to within about 2 dB combined with the relatively flat L_wbs in Fig. 3 shows that the acoustic power absorbed from an insert earphone in a mid-canal location in a normal-functioning adult ear had a similar frequency dependence to the incident pressure.

This finding demonstrates that a sound source calibrated to incident pressure, as in the Goodman et al. (2009) study to measure click-evoked OAEs in adult ears with normal function, would be expected to produce generally similar average results at frequencies between 0.2 and 8 kHz compared to a sound source calibrated to absorbed power. The ability to measure the absorbed power in an individual ear would control for the overall lack of constancy of the median with frequency as well as the group variability with respect to the median, which was observed in the L_wbs results.

The conductance level L_G = L_FE + L_α [see Eq. 22] is equal to the difference (L_wbs − L_pbs) between the absorbed-power level and the SPL. This is plotted in the bottom panel of Fig. 3 in terms of the group percentiles of L_G. The median L_G in adults increased approximately linearly with frequency between 0.22 and 4 kHz with a slope of about 4.5 dB∕octave. Its maximum of 0.5 dB occurred at 4.5 kHz with a rapid decrease at higher frequencies down to −21 dB at 8 kHz. This decrease was due to decreases in both L_FE (see top panel of Fig. 2) and absorbance level. Absorbance is not plotted here, but the effect is also evident in terms of an increased energy reflectance at 8 kHz relative to 5 kHz in adult norms, e.g., in Keefe et al. (1993). The variability between the 10th and 90th percentiles in L_G was larger overall than either of the corresponding variability in L_pbs or L_wbs. This variability never exceeded 10 dB at frequencies up to 4.5 kHz but was much larger at higher frequencies with a maximum of 25 dB at 5.7 kHz.

The mean L_G for a group of adult ears was reported in Fig. 15 of Keefe et al. (1993); its reference of 0 dB was based on P_ref and a reference 1 mmho, which is a typical audiological unit for conductance (the CGS unit of acoustic conductance is the mho, and 1 mmho = 0.001 mho). Keefe et al. (1993) did not report a variability measure for L_G. A reference pressure P_ref terminated by a 1-mmho conductance corresponds to an absorbed power of 4 aW, which is 10.8 dB below the reference for 0 dB of 47.6 aW in the present study. Therefore, adding 10.8 dB to the conductance levels in Keefe et al. (1993) converted them to the absolute levels used in the present study. The mean conductance level in Keefe et al. (1993) had a low-frequency slope of about 4.3 dB∕octave up to a converted maximum level of −6 dB at 5 kHz. This slope was similar to the low-frequency slope of 4.5 dB∕octave in the present study, and this maximum occurred at about the same frequency, but below the maximum of 0.5 dB at 4.5 kHz in the present study. Both studies showed an attenuation of conductance level above 5 kHz, but the attenuation at 8 kHz was greater in the present study. Thus, the agreement between the studies was reasonable, given the differences in probe assemblies used, measurement procedures, and any unknown variability between the subject groups tested. The transfer-function level L_G between absorbed power and total pressure may be broadly applicable to any hearing study in adults that requires a calibrated sound source. For example, an evoked OAE experiment in an adult ear that maintains constant SPL will produce an absorbed-power level with a frequency dependence identical to that of the conductance level, which peaks around 4 kHz.

Interpreting suppression of SFOAEs at high frequencies

This section describes effects of stimulus pressure versus absorbed power on measurements of two-tone suppression of SFOAEs that were reported by Keefe et al. (2008). Such SFOAE responses are analogous to two-tone suppression measured mechanically and neurally in non-human mammalian cochleae, although SFOAE suppression can be non-invasively measured in the human ear canal based on acoustic responses. SFOAE suppression probes the saturating nonlinearities associated with cochlear amplification on the basilar membrane.

The subject inclusion criteria and age range in this SFOAE study were similar to those in the acoustic transfer-function data set measured in the subjects tested by Schairer et al. (2007). Specifically, subjects were included in the SFOAE study only if their air-conduction thresholds were 15 dB HL or better at half-octave frequencies from 0.25 to 8 kHz, and air-bone gaps were 10 dB or less at frequencies from 0.25 to 4 kHz. The SFOAE database included responses from both ears of 24 subjects with a mean age of 28 yr. Subjects were tested using the same probe assembly (Etymotic ER-10C with the 20 dB increase in receiver levels) used in the database of acoustic transfer-function measurements.

Because the subjects in the SFOAE study did not receive acoustic transfer-function testing with this probe assembly, the present analysis combined the average results from the two studies. The constraints were that all data were measured using the same probe assembly in young normal-hearing adults with a similar average age (27–28 yr). The transfer-function level L_G between absorbed power and total pressure, which is plotted in Fig. 3, was used with Eq. 10 to calculate the absorbed power delivered by the pressure stimuli. These results were used to transform the stimulus and suppressor components from pressure level to power level in the mean SFOAE suppression responses.

The procedures used by Keefe et al. (2008) to measure SFOAE suppression are briefly described. SFOAEs were measured at five octave-spaced probe frequencies f_p between 0.5 and 4 kHz over a 40 dB range of probe levels L_p from 30 to 70 dB. Each SFOAE was suppressed using a suppressor tone with a frequency f_s ranging from two octaves below f_p to 0.7 octave above f_p, and a suppressor level L_s ranging from just-detectable to full suppression of the SFOAE. A SFOAE suppression tuning curve was constructed for fixed f_p and L_p as the suppressor level ${\widehat{L}}_s$ required to produce a criterion decrement in the SPL of the total SFOAE as a function of suppressor frequency f_s. The criterion decrement was chosen to be 10.7 dB (equal to $20{\log }_{10}\left(1-1∕\sqrt{2}\right)$). This criterion was equivalent to an amplitude increase of the magnitude of a measured nonlinear SFOAE residual by a factor of $1∕\sqrt{2}$ or 3 dB.

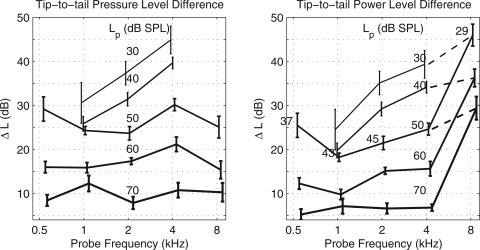
The SFOAE suppression tuning curve was parameterized in terms of the tip-to-tail pressure-level difference. This was calculated as the difference in the SPL of ${\widehat{L}}_s$ at a f_s one octave below the probe frequency (in the lower “tail” region of the tuning curve) to the SPL of ${\widehat{L}}_s$ at a f_s that was 2–3% above f_p (in the “tip” region of the tuning curve). Keefe et al. (2008) concluded that this tip-to-tail difference estimated the cochlear gain. The mean and standard error (SE) of the mean of the tip-to-tail pressure level difference are re-plotted from Keefe et al. (2008) in the left panel of Fig. 4 as a function of f_p, with separate curves parameterized by L_p. The (mean) tip-to-tail pressure level difference was largest at the lowest L_p, and uniformly decreased with increasing L_p. This is consistent with larger cochlear gain at smaller L_p. At the lowest L_p of 30 dB SPL, the tip-to-tail pressure level difference increased from 32 to 45 dB as f_p increased from 1 to 4 kHz.

Figure 4.

Left panel: Mean ± 1 SE of the tip-to-tail pressure-level difference of the SFOAE suppression tuning curve as a function of probe frequency. Each curve represents different probe levels (L_p) specified as SPL. Each curve is slightly displaced along the horizontal axis to improve clarity. Right panel: Mean ± 1 SE of the tip-to-tail power-level difference of the SFOAE suppression tuning curve as a function of probe frequency with similar plotting conventions. The SE values quantify the variability power-level differences but not including the variability of L_G that was used to calculate power-level differences. L_p is specified as SPL in the column of numbers just to the left of 4 kHz that labels each equal-SPL contour (i.e., each solid-line curve). L_p is also specified as absorbed-power level in the row of numbers along the horizontal probe frequency axis for the 50 dB SPL contour. L_p at 4 kHz on this contour has a SPL of 50 dB and absorbed-power level of 50 dB. The dashed lines between 4 and 8 kHz connect the tip-to-tail power level differences at approximately equal absorbed-power levels of L_p (±1 dB).

An unexpected high-frequency finding in the SFOAE study was that the tip-to-tail difference decreased at 8 kHz compared to 4 kHz for L_p of 50 and 60 dB SPL, and these differences were approximately equal at 70 dB SPL. In the absence of other factors, this would predict that cochlear gain is reduced at 8 kHz relative to 4 kHz, which would appear to contradict reports that human cochlear tuning is sharper at high frequencies (Shera et al., 2010). Even though suppression tuning differs from the cochlear tuning described in these reports, an attractive hypothesis is that sharper tuning results from an increased cochlear gain at high frequencies. To account for the discrepancy in the tip-to-tail difference at 8 kHz, Keefe et al. (2008) cited “lower confidence” in their 8-kHz suppression data based on an increased measurement-system distortion at 8 kHz using this probe and a smaller number of ears with valid test data compared to the numbers at lower frequencies. This lower confidence may have been overly pessimistic for the 8-kHz data plotted in Fig. 4: the SEs of the SFOAE suppression tuning curve at f_p of 8 kHz in Keefe et al. (2008) were not greatly elevated compared to the SEs at lower f_p. The comment about increased distortion was based on an observation that the off-frequency growth-of-suppression responses reported in Keefe et al. (2008) had an artifact in a larger proportion of ears at 8 kHz compared to lower frequencies. Nevertheless, the mean tip-to-tail difference inferred from the 8-kHz suppression tuning curve remained well defined and large compared to these types of errors.

On the other hand, Keefe et al. (2008) did not discuss the potential influence of ear-canal and middle-ear factors on the high-frequency SFOAE suppression responses. The current analysis takes account of these more peripheral factors and finds a significant effect on the SFOAE suppression results at 8 kHz. It is sufficient to consider stimulus-calibration effects on the tip-to-tail difference of the SFOAE suppression tuning curve, which was most closely related to cochlear gain.

The calibration approach in the present study was to apply the transfer-function L_G to transform both ${\widehat{L}}_s$ and L_p from pressure level to power level. Because a SFOAE suppression tuning curve is constructed at a fixed L_p level, any transformation of L_p simply changed its reference value labeling the entire tuning curve. In contrast, a transformation of ${\widehat{L}}_s$ affected the overall shape of the suppression tuning curve and was thus the stimulus level that had the greatest impact on calculating the tip-to-tail ratio. The transformation of ${\widehat{L}}_s$ to absorbed-power level is described first. This transformation of ${\widehat{L}}_s$ was applied by a linear interpolation of the median L_G data in Fig. 3 (bottom panel) at each f_s on the tuning curve. In particular, the tip-to-tail power-level difference at a f_p of 8 kHz was calculated as the difference in the transformed power levels of ${\widehat{L}}_s$ at a f_s of 4 kHz compared to a f_s just above 8 kHz. This amounted to a 21 dB difference between 4 and 8 kHz in L_G, as is evident in the bottom panel of Fig. 3.

The tip-to-tail power-level difference is plotted in the right panel of Fig. 4, in which the reference terminology for L_p to parameterize each curve is retained as SPL for clarity. The SPLs for L_p are in the column of numbers in a normal font just to the left of 4 kHz. The largest change between specifying the suppressor tone level using power rather than pressure occurred at 8 kHz. The tip-to-tail power-level difference, and thus the estimated cochlear gain, was larger at 8 kHz than at all lower f_p’s. This increased cochlear gain is consistent with the observation of sharper tuning at higher frequencies. Between 1 and 4 kHz, the growth in the tip-to-tail power-level difference (right panel) with increasing f_p was monotonic for L_p from 30 to 60 dB SPL, whereas the pressure level difference (left panel) was non-monotonic for a L_p of 50 dB SPL and monotonic at 30, 40, and 60 dB SPL. The data at L_p of 70 dB SPL are of lesser interest for studying suppression effects because cochlear distortion would be likely to increase at this highest probe level; such an increase would decouple the relation between tip-to-tail difference and cochlear gain (Keefe et al., 2008).

The effect of converting probe level L_p from pressure to power level is next described. After transformation of L_p to power level, each tip-to-tail level difference curve (plotted in the right panel of Fig. 4 at a constant SPL for L_p) no longer corresponded to a constant- L_p condition. The particular L_G levels used at the measured f_p octave frequencies in Fig. 4 were obtained from the median data in Fig. 3 (bottom panel), which are identified by the circle symbols. L_p expressed as power level relative to SPL was changed by −13 dB at 0.5 kHz, −7 dB at 1 kHz, −5 dB at 2 kHz, 0 dB at 4 kHz, and −21 dB at 8 kHz. Thus, the tip-to-tail difference on each constant-SPL curve was measured at the highest probe power level at 4 kHz, and at the lowest probe power levels at 0.5 and 8 kHz. The absorbed-power levels for L_p across the range of f_p are listed in the right panel of Fig. 4 on the contour line for a L_p of 50 dB SPL. Because L_G = 0 dB at 4 kHz, L_p was 50 dB on this contour whether specified as SPL or absorbed-power level, but L_p was reduced to an absorbed-power level of 29 dB at 8 kHz (and 37 dB at 0.5 kHz). Similar level offsets would apply to the other contours in the right panel of Fig. 4. If the tip-to-tail power-level difference were plotted using equal- L_p contours based on absorbed-power level rather than SPL, a smoothly increasing contour would result with frequencies increasing from 1 to 8 kHz. This is represented on the right panel of Fig. 4 between 4 and 8 kHz by the three dashed lines between L_p contours with approximately equal absorbed-power levels; e.g., the top dashed line connects the difference for L_p = 30 dB at 4 kHz to the difference for L_p = 29 dB at 8 kHz.

The tip-to-tail power-level difference was slightly higher at 0.5 kHz than at 1 kHz when compared at similar absorbed-power levels. In particular, the difference ΔL was 25 dB at 0.5 kHz at an absorbed-power level of 37 dB, whereas ΔL would be interpolated between 18 and 19 dB at 1 kHz for corresponding absorbed-power levels of 43 dB and 33 dB, the latter equal to the absorbed-power level for a L_p of 40 dB SPL. That is, the tip-to-tail power-level difference was about 6–7 dB higher at 0.5 kHz compared to 1 kHz. Whether this might be a purely cochlear effect—indicative of increased cochlear gain at 0.5 kHz or some additional cochlear process—would also depend on whether the internal power losses within the middle ear were larger at 0.5 kHz than 1 kHz. The tip-to-tail differences at 0.5 and 1 kHz were based on tail suppression measurements as low as 0.25 and 0.5 kHz, respectively, so that internal losses within the middle ear at these lower frequencies would also contribute to the tip-to-tail differences. The present analysis based on available data is inconclusive concerning the SFOAE tip-to-tail difference at 0.5 kHz.

No significance testing should be inferred from the size of the SE bars in the right panel of Fig. 4, which were derived only from the SFOAE suppression measurements, i.e., they were copied from the corresponding error bars in the left panel. The additional variability in L_G, which varied from 10 to 25 dB in the frequency range between 4 and 8 kHz in Fig. 3, was not included in calculating the error bars in the right panel of Fig. 4. This limitation exists because the SFOAE and L_G data sets were not measured in the same group of subjects.

The predicted relationship is that cochlear gain increases with increasing frequency in the human cochlea, so that the tip-to-tail power-level difference derived from SFOAE suppression is predicted to increase with increasing frequency when constant power is absorbed by the middle ear. The justification in Keefe et al. (2008) for using the tip-to-tail difference to predict cochlear gain was based on the observation that the cochlear gain is equal to the tip-to-tail level difference on the basilar membrane at the best-frequency place of the input probe tone. That study proposed that the SFOAE at the probe tone was generated as a result of two-tone suppression near the tonotopic place of the probe tone. Therefore, the tip-to-tail level difference in the SFOAE response estimated the tip-to-tail difference on the basilar membrane at the onset of compression, and thus of the cochlear gain. The SFOAE tip-to-tail power-level difference better accounted for forward ear-canal and middle-ear transmission effects between the probe and the basal end of the cochlea than did the SFOAE tip-to-tail pressure level difference. It is this difference that enabled the tip-to-tail power-level difference to predict an increased gain of the cochlear amplifier at 8 kHz. This relationship was generally confirmed between 1 and 8 kHz. It would have been preferable to measure acoustic transfer functions and SFOAE suppression at constant absorbed-power levels in the same group of subject ears to facilitate a full statistical analysis. Such an approach would be valuable in the further study of SFOAE suppression. Notwithstanding that, a shift from calibrating the SFOAE suppressor sound source using absorbed-power level rather than SPL provided an improved understanding of high-frequency suppression effects.

The improved level of agreement at 8 kHz between the SFOAE predictions of cochlear tuning by Shera et al. (2010) and of cochlear-amplifier gain in the present study is a non-trivial result, even though it is reasonable to expect sharper cochlear tuning to result from increased cochlear-amplifier gain. The two studies analyzed different types of SFOAE responses. Shera et al. combined SFOAE latencies in human ears with measured basilar membrane responses across species, whereas the present study analyzed in human ears the suppression of SFOAE levels in the presence of a second suppressor tone.

CONCLUDING REMARKS

The sound power absorbed from the probe inserted into the ear canal has advantages for calibrating a sound source to use in general types of hearing experiments. Such a calibration is based on measurements of pressure and an acoustic transfer function in the ear canal, for example, pressure reflectance or admittance. Because this power is mainly absorbed by the middle ear, except for low frequencies, this calibrates the hearing experiment to the sound power collected by the middle ear. The causal mechanism underlying power absorption is made explicit by expressing the absorbed power as proportional to the product of the mean-squared amplitude of the forward pressure, the ear-canal area, and the absorbance measured in the ear canal. This absorbance equals the middle-ear absorbance in the limit that ear-canal losses are negligible. The forward pressure differs from the incident pressure due to round-trip internal reflections of sound between the tympanic membrane and the probe surface.

Using a database of measurements of acoustic transfer functions in adult ears with normal function, the median forward-pressure level was boosted by as much as 13 dB relative to the incident-pressure level at frequencies below 0.7 kHz and was within ±4 dB of the incident-pressure level at higher frequencies. It was also increased near, or probably just above in some ears, the maximum test frequency of 8 kHz. This incipient peak region would correspond to frequencies at which the length between the tympanic membrane and the probe was approximately equal to a half wavelength.

The presence of ear-canal standing waves was revealed by the transfer function between forward pressure and total pressure. This transfer-function level varied between 5 and 14 dB across the middle 80% of the distribution of responses at the peak frequency relative to its minimum level at low frequencies. The resonance frequency based on the zero crossing in the phase, which is closely related to the quarter-wavelength frequency, varied between 3 and 6 kHz across subjects. Based on a typical probe insertion distance within the ear canal, the median transfer function between absorbed-power level and SPL had a bandpass shape with maximum levels between 4 and 5 kHz and greatly reduced levels (−13 to −21 dB) below 0.6 kHz and above 7 kHz.

Two-tone suppression of SFOAE responses showed the advantage of a high-frequency specification of the sound source in terms of absorbed-power level at the stimulus frequency of the SFOAE and at each of the suppressor frequencies. The tip-to-tail power-level difference of the SFOAE suppression tuning curve increased with increasing stimulus frequency between 1 and 8 kHz. This is consistent with increased cochlear gain associated with sharper cochlear tuning at higher frequencies. This result is in contrast with the tip-to-tail pressure level difference of the SFOAE suppression tuning curve, which was anomalously reduced in Keefe et al. (2008) of 8 kHz relative to its values at lower frequencies. It is predicted that the interpretation of DPOAE suppression measurements would also be improved by specifying the forward-directed sound stimuli in terms of their absorbed-power levels, both for the stimuli used to generate and suppress the DPOAE response.

In future studies using OAEs or auditory brainstem response (ABR) testing, it might be clinically useful to perform an initial wideband acoustic test of conductive status to assess whether conductive dysfunction is present, prior to testing for the presence of sensorineural hearing loss. A stimulus calibration procedure based on absorbed power may be advantageous for such procedures. In ears with reduced absorbance, the OAE or ABR stimulus level might be increased so as to increase the likelihood of detecting a response indicative of function within normal limits. For example, ears with otitis media with effusion (Piskorski et al., 1999; Feeney et al., 2003) and ears that referred on a DPOAE examination in a newborn hearing screening (Sanford et al., 2009) each had a reduced absorbance compared to an age-matched group of ears with normal function. A reduced absorbance is associated with an increased reflection of sound back into the ear canal, i.e., an increased energy reflectance. Depending on the relative phase of forward and reverse waves, this increase in reflected energy may increase the total pressure in the ear canal according to the model described above. Thus, a calibration based on total or forward pressure in the ear canal might decrease the sound stimulus level under these conditions in the subset of ears that need increased level to counteract the reduced absorbance of sound. A sound source calibrated according to absorbed power via Eq. 16 would increase the forward-pressure level in an ear with reduced absorbance due to any conductive disorder, i.e., there is a trading ratio between mean-squared forward pressure and absorbance.

An additional complication in an ear with conductive dysfunction is the increased likelihood of reduced reverse transmission of the OAE from the cochlea through the middle ear back to the ear canal. This problem requires further study. Irrespective of this complication, a test finding of conductive dysfunction would be relevant to the overall diagnostic assessment.

Calibrating an ear-canal sound source based on absorbed power may be useful in a variety of measurements in clinical audiology and auditory research. In addition to avoiding effects of ear-canal standing waves, a measurement of absorbed-power level captures information about the multiple internal reflection of sound within the ear canal, the increased efficiency of large ear-canal areas in collecting sound power, and the absorption properties of the middle ear. Such information is relevant to understanding post-natal development of function in the human ear, comparative function across mammalian ears, and in better identifying the presence and type of auditory dysfunction, whether of conductive or sensorineural origin, in clinical screening or diagnostic applications.