Articulatory–acoustic kinematics: The production of American English ∕s∕

Abstract

Due to its aerodynamic, articulatory, and acoustic complexities, the fricative ∕‐∕ is known to require high precision in its control, and to be highly resistant to coarticulation. This study documents in detail how jaw, tongue front, tongue back, lips, and the first spectral moment covary during the production of ∕‐∕, to establish how coarticulation affects this segment. Data were obtained from 24 speakers in the Wisconsin x-ray microbeam database producing ∕‐∕ in prevocalic and pre-obstruent sequences. Analysis of the data showed that certain aspects of jaw and tongue motion had specific kinematic trajectories, regardless of context, and the first spectral moment trajectory corresponded to these in some aspects. In particular contexts, variability due to jaw motion is compensated for by tongue-tip motion and bracing against the palate, to maintain an invariant articulatory–aerodynamic goal, constriction degree. The change in the first spectral moment, which rises to a peak at the midpoint of the fricative, primarily reflects the motion of the jaw. Implications of the results for theories of speech motor control and acoustic–articulatory relations are discussed.

INTRODUCTION

Sibilant fricatives are usually regarded as being among the most difficult segments to produce, due to the preciseness with which the vocal tract must be configured (Hardcastle, 1976; Ladefoged and Maddieson, 1996). Successful sibilant production necessitates the formation of a constriction small enough to produce a turbulent jet, but large enough to avoid full closure. An obstacle must also be placed at a precise distance from the constriction to allow for aerodynamic-to-acoustic energy conversion characteristic of sibilants (Catford, 1977; Shadle, 1985). There may also be demands on the tongue dorsum, which can groove to channel the air jet (Stone and Lundberg, 1996). Due to this preciseness of control, sibilants tend to be among the consonants most resistant to coarticulation and most aggressive in coarticulatory incursion onto surrounding segments (Recasens and Espinosa, 2009). Engwall (2000) and Mooshammer et al. (2007) have shown, in Swedish and German sibilants, respectively, that there are precise timing relations, where the jaw follows the tongue tip in the achievement of their goals. They also showed that variability is low within subject in the positioning of the tongue tip and jaw during sibilants, in contrast to other obstruents.

To produce these precisely controlled segments, one possibility is that each articulator would achieve a position appropriate for the initiation of turbulence and remain fixed in position to maintain the turbulence until the end of the sibilant. However, several articulatory studies have presented data showing that there is a consistent upward and downward trajectory of the jaw during the production of sibilants (McGowan, 2004; Mooshammer et al., 2007). Acoustic studies of fricative spectra show considerable variability in the time-varying behavior of the spectral moments and other spectral measures through a fricative, even when this temporal variability was not the focus of the study (Shadle and Mair, 1996; Jongman et al., 2000; Munson, 2001; Jesus and Shadle, 2002). For instance, using several example spectra, Munson (2001) showed that the center of gravity of the fricative (first spectral moment) can vary by 500–1000 Hz during an ∕‐∕, which may last 100–200 ms. Yet this amount of acoustic variability is surprising, arguing against the notion of sibilants as stationary segments. Further, quantal theory asserts that articulatory variability within the constriction region for either ∕‐∕ or ∕∫∕ production would not have an appreciable acoustic effect (Stevens, 1989).

The goal of this work is to investigate in detail how different articulators move during the particular sibilant ∕‐∕, and how a following vowel or consonant affects that motion. We also investigate how the output spectra are shaped by articulator motion, and whether the predictions of quantal theory are met. Earlier works that have demonstrated motion of the articulators during ∕‐∕ (McGowan, 2004; Mooshammer et al., 2007) have examined ∕‐∕ before a vowel, as opposed to before consonants. It is therefore possible that the coarticulation of ∕‐∕ and the following vowel influenced the articulator motions that were reported. By comparing articulator motion and spectral change within ∕‐∕ before vowels vs consonants, we aim to establish what aspects of that motion are due to the ∕‐∕ itself, and what aspects are due to context, since neither vocalic nor consonantal context is neutral with respect to the production of ∕‐∕. Our goal is to determine the specifics of the time-varying synergy of the various articulators in the production of ∕‐∕, and the acoustic result of this synergy, as the context of ∕‐∕ s/ varies. Specifically, we are interested in determining if any articulatory or acoustic property of ∕‐∕ is maintained through synergistic use of articulators. We also test the predictions of the degree of articulatory constraint (DAC) model of speech production (Recasens et al., 1997; Recasens and Espinosa, 2009), which holds that consonants are more resistant to surrounding segments and more aggressive in their coarticulatory behavior than vowels, since consonants have a greater DAC in their production. The model therefore predicts that a following consonant will have greater anticipatory spatial influence than a vowel on a preceding ∕s/.

In the work reported here, the production of American English sibilant ∕‐∕ and the interaction of that sibilant with its phonetic context were studied by using the Wisconsin x-ray Microbeam (XRMB) database. Articulatory and acoustic data from 24 subjects were analyzed to investigate the nature of ∕sV∕ and ∕sC∕ coproduction. In Sec. 2 the database and the measurements made on the data are described. In Sec. 3 the results using these measures are described. The main findings are discussed in Sec. 4, and Sec. 5 concludes.

METHOD

The Wisconsin XRMB database allows the study of movements of the tongue, jaw, and lips, and the simultaneously recorded acoustic output with high temporal and spatial resolution, for a total of 57 speakers. Four pellets were glued on the tongue to allow observation of its functional divisions: T1 is near the tongue tip, T2 on the tongue blade, T3 on the tongue dorsum, and T4 on the upper tongue root for some subjects and the posterior tongue dorsum for others. In addition, two pellets were placed on the upper and lower lips (UL and LL), and two on the jaw—one at the central incisor (JW) and one on a molar. The pellet movements were recorded at a frame rate of 40 Hz, which was upsampled to 145 Hz in order to smooth the signals; sound waveforms were digitized at a sampling rate of 21 739 Hz. Positions are given with respect to the maxillary occlusal plane, as shown in Fig. 1. Further details are given in Tasko and Westbury (2002) and Westbury (1994).

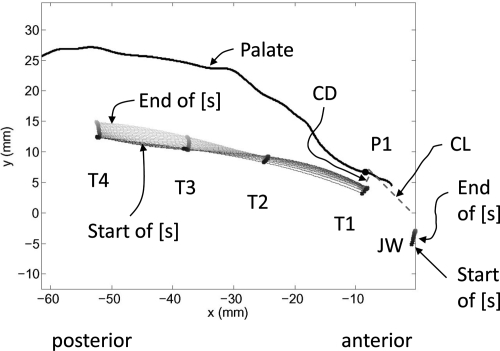
Figure 1.

(Color online) Palate outline and tongue and jaw markers for subject JW11 [s] in sad. The anterior end of the palate is to the right; the x-axis is the intersection of the midsagittal and occlusal planes, with x = 0 mm at the central incisors; the y-axis is perpendicular to the occlusal plane at x = 0 mm. Splines fitted to T1 through T4 are shown, with the black curve at the start of the [s] and palest gray curve at end of [s]. CL and CD are shown. P1 is the point on the palate closest to T1; JW is the jaw pellet.

Corpus and subjects

Data for prevocalic and preconsonantal ∕‐∕ were analyzed. The prevocalic data were obtained from task 13, in which speakers read a list of ten words of the form ∕sVd∕: “side, sewed, seed, sod, sued, sawed, sid, sad, surd, said.” Five other items in task 13 were not used in this study because not all of the subjects recorded them. Three tokens each of three words beginning with an ∕s/-stop-consonant cluster were also analyzed: special from tasks 2 and 4 (two tokens), street from tasks 2, 23, and 47, and school from tasks 1, 22, and 73.

In the XRMB database, not all subjects recorded all tasks, and pellets were sometimes mis-tracked or fell off during a session, resulting in missing data. In this study, data from 24 subjects (15 females, 9 males) were analyzed. The particular tokens and subjects used were chosen because they had the smallest amount of missing data. The male subjects are: 11, 24, 32, 45, 51, 53, 58, 59, 63. The female subjects are: 16, 20, 21, 25, 26, 31, 33, 35, 36, 37, 39, 48, 49, 60, 62. The majority of the subjects spoke an upper midwest dialect of American English. Their median age was 20.69 yr. Further demographic and dental information on the subjects is provided by Westbury (1994).

Acoustic segmentation

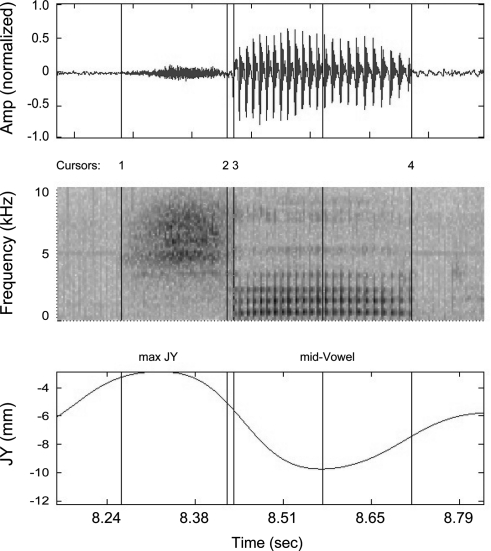
The ∕sVd∕ tokens for a given subject were segmented in two stages. The temporal limits of each word were first identified by viewing the acoustic waveform and auditing the selected segment. Then, while viewing the waveform of a single word and its spectrogram, four events were labeled, as shown in Fig. 2: (i) frication onset, (ii) frication offset, (iii) vowel onset, and (iv) vowel offset. Vowels were extracted for use in normalization, since speakers vary widely in the size of the vocal tract and in the exact location of the pellets. The exact normalization methods are discussed later. Frication onset and offset are the times at which noise appears to begin and cease, both in the time waveform and, in the spectrogram, at the frequency of the main peak (in this example, noise begins at 5000 Hz and extends to higher frequencies later in the [s]). The vowel onset was defined as the start of voicing. Vowel offset was usually taken to be the time when F1 stopped being visible on the spectrogram, but sometimes the end of the first steady region of the vowel was marked instead, as for the diphthong in side. For the ∕s/-cluster words, a similar procedure was followed, but only the first two points of frication onset and offset were identified. Automatic methods for segmentation were also explored, but were inconsistent, especially for frication offset, since high frequency energy can persist into the beginning of the vowel, so manual segmentation was used throughout. Temporal normalization was performed by uniformly sampling each articulatory and acoustic measure (to be presented in Sec. 2C) at nine points through the fricative.

Figure 2.

(Color online) Example illustrating acoustic segmentation of sad as spoken by subject JW11. Top: Speech waveform. Middle: Spectrogram. Bottom: JWy, the y-component of the jaw pellet. Vertical cursor lines in all three graphs indicate (1) frication onset, (2) frication offset, (3) vowel onset, and (4) vowel offset. Max-JY indicates the time at which JWy reaches its maximum height during the [s]; Mid-vowel indicates the midpoint between vowel onset and offset.

Articulatory and acoustic measurements

The start and end points of ∕‐∕ defined by the segmentation of the acoustic signal were then used to locate the corresponding articulatory frames. Some of the analyses to be presented compare ∕‐∕ before different vowel categories: high vs low, front vs back, and rounded vs unrounded. These categories were determined from the articulatory data for each subject rather than by phonetic classification. Articulatory parameter values were extracted at the midpoint of the following vowel in the ∕sVd∕ words and were used to split the ten ∕‐∕ tokens into two equal-sized groups (e.g., one half followed by a high vowel and the other half followed by a low vowel). The articulatory parameters used are expected to be strongly correlated with a phonetic feature of the vowel: Jaw height, the y-component of the JW pellet, was used to divide the ∕‐∕ tokens by vowel height; the x-component of T3 was used to divide by front∕backness; and the y-component of the LL marker, LY, was used to divide by rounded∕unroundedness. We have also run the analyses using the x-component of the LL to distinguish rounded from unrounded vowels, with little to no effect on the results. This means that the “high” tokens represented in graphs and tables will not necessarily contain data from the same set of words for all subjects, but will contain the five tokens with the highest vowels as measured by JWy for all subjects; the same qualification is true for “front” and “rounded” tokens.

To combine data from all subjects in Figs. 4567, the data were subject-normalized by centering for each subject before analysis. For each articulatory measure (e.g., T1y), values were determined at two points in each token, mid-[s] and mid-vowel, and averaged. The average values for all tokens for that subject were then averaged, resulting in the subject’s mean for that measure (e.g., $\overline{T1y}$). This subject mean for each measure was then subtracted from its corresponding measure ($T1y_{\text{normed}}=T1y-\overline{T1y}$). All of the articulator variables were normalized in this way, except for constriction degree (CD) and constriction location (CL), since they represent distances between points rather than positions of a pellet.

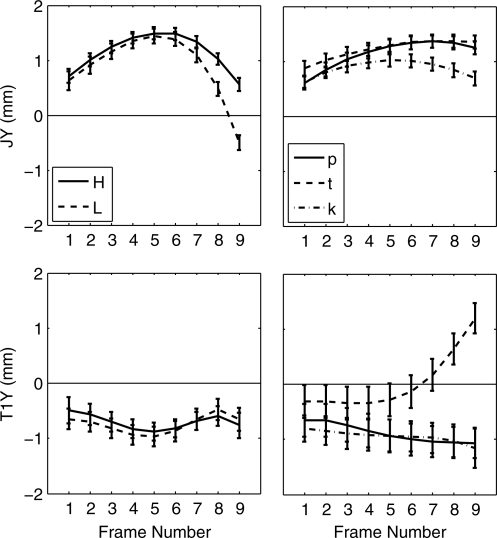
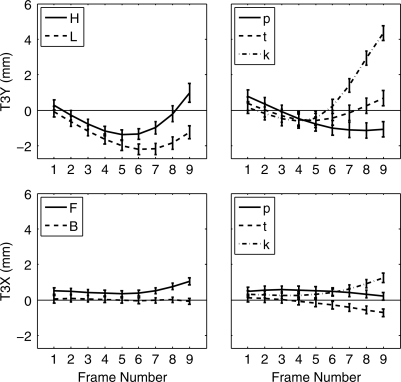
Figure 4.

Means and standard errors of JWy (JY, top row) and T1y in jaw frame (T1Y, bottom row) for nine articulatory frames during ∕s∕, split by phonetic context (see Sec. 2C). Left column: High vs low vowel contexts. Right column: ∕p, t, k∕ indicate the place of the following stop consonant.

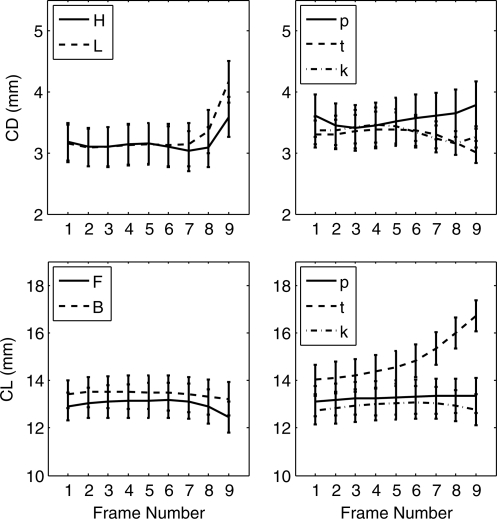
Figure 5.

Means and standard errors of CD (top row) and CL (bottom row) for nine articulatory frames during production of ∕s∕.

Figure 6.

Means and standard errors of T3 motion in jaw frame. T3Y (top row) and T3X (bottom row) for nine articulatory frames during [s].

Figure 7.

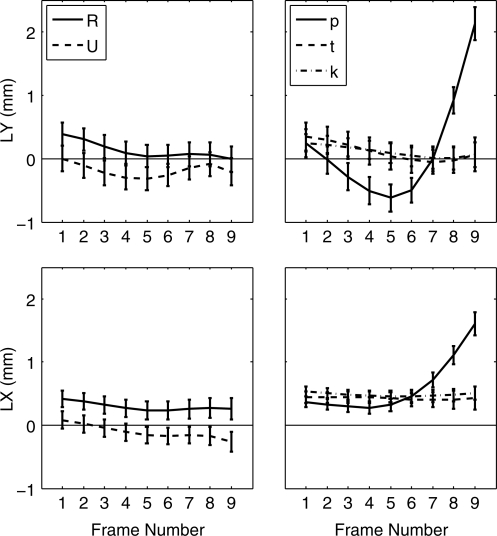
Means and standard errors of lower lip motion. LY (top row) is y-component, LX (bottom row) is x-component; both are in jaw frame, plotted for nine articulatory frames during ∕s∕.

In some analyses, tongue and lip motion with respect to the jaw are determined. This has been done by using both jaw pellets, which are mounted on the molar and on the central incisor (JW), to determine the overall jaw motion and remove it from the tongue and lip pellets. We have used the algorithm presented by Westbury et al. (2002). When this has been done, we refer to the coordinates as being in the jaw frame as opposed to the original head frame.

CD and CL are computed in the following way: (1) T1 is used as the best estimate of the tongue-tip location; (2) the midsagittal palate trace is upsampled to generate 3000 uniformly spaced points; (3) for each articulator frame, the point on the palate that is the closest to T1 is determined; this point is referred to as P1 (see Fig. 1). Then two distances are computed: CL is the Euclidean distance from P1 to the origin on the occlusal plane. CD is the distance from P1 to T1.

For the acoustic analysis, nine 30-ms intervals were distributed evenly through each [s] token. The intervals overlapped by an amount inversely proportional to the token’s duration. For each interval, pre-emphasis was applied, and, following Blacklock (2004), a multitaper (MT) spectrum was calculated, using eight orthogonal tapers, and these spectra were averaged at each frequency to obtain a single MT spectrum as a good spectral estimate for that interval. The first spectral moment (M1) was computed from the magnitude-squared values of the MT spectrum (Forrest et al., 1988). Amplitudes below 320 Hz were excluded to avoid ambient noise. The most significant peak (MSP) was also computed, and is defined as the frequency of the highest-amplitude peak in the MT spectrum over the range 320–10 870 Hz. It was intended as an estimate of the frequency of the main resonance, rather than of the center of gravity of the spectrum. The MSP and M1 results were similar enough that only M1 will be discussed in this paper. In Fig. 7, the M1 data were centered by calculating the mean M1 for each subject across all ∕‐∕ data, and subtracting that mean from each data frame.

Statistical analysis

The statistical tests used in this work examine the significance of effects of context, such as following vowel height, on the temporal trends in the time series of articulators during the ∕s/. The statistical technique we have found most appropriate for this task is the growth-curve model, which is usually used for the analysis of categorical effects on longitudinal data (Singer and Willett, 2003). Such models are instantiations of multilevel models, where some explanatory variable (here time) enters at the first level of regression, and a higher explanatory variable (here a factor such as vowel height, which takes two levels high and low) enters at a higher level to explain the coefficients of the first level model. Specifically, we used orthogonal polynomial functions to predict the variability with time at the first level. Only linear and quadratic effects were used, since higher orders were found to be consistently either insignificant, or significant but very small. The statistics we report are only for the significant (at the p < 0.01 level) temporal trends, which indicate either slopes (linear) or curvatures (quadratic). For main effects (shown in Table TABLE I.), if a parameter increases with time significantly, it will have a positive linear coefficient. If a parameter has significant uniform curvature with respect to time, it will have a positive quadratic coefficient if it is concave, that is, the trajectory is lowest mid-∕s/; a negative quadratic coefficient indicates it is convex, or highest mid-∕s/. The interactions, shown in Tables 2, TABLE III., describe how the nature of the following vowel or consonant affects the kinematic trajectory within ∕‐∕ for each measure. Linear and quadratic interaction coefficients therefore describe the change in slope or curvature due to one level vs another, e.g., following high vs low vowel. The data were not centered prior to statistical analysis, as was done for plotting; rather subject was included as a random effect in the model, to account for the intra-subject correlation in each of the measurements. The model was fit using the nonlinear mixed-effects package nlme (Pinheiro and Bates, 2000) for the statistical programming language R.

Table 1.

Main effect of time on ∕‐∕ in sV and sC. Linear (slope) and quadratic (uniform curvature) coefficients are shown for significant effects (p < 0.01).

	Linear		Quadratic
	sV	sC	sV	sC
JWy	−0.402	0.459	−1.226	−0.394
JWx	—	0.17	−0.393	−0.17
T1y	—	0.703	0.290	—
T1x	—	−0.652	—	—
CL	—	0.863	—	—
CD	0.410	—	0.431	—
T2y	—	1.61	1.67	1.63
T3y	—	1.81	1.845	2.25
T4y	—	2.55	1.012	1.31
T2x	—	—	0.328	—
T3x	—	—	0.237	—
T4x	—	—	0.319	—
LY	—	—	0.188	1.01
LX	−0.21	0.525	—	—
M1	924	443	−1258	−1065

Table 2.

Interaction between vowel effect (high∕low, front∕back, and round∕unround) and time trends (linear and quadratic). Linear and quadratic coefficients are shown for significant effects (p < 0.01). Second feature of each pair is reference case.

	H∕L		F∕B		R∕U
	L	Q	L	Q	L	Q
JWy	0.725	0.578	—	—	0.621	0.489
JWx	—	—	—	—	—	—
T1y	−0.283	—	—	—	−0.328	—
T1x	—	—	—	0.502	—	—
CL	—	0.423	—	−0.347	—	0.462
CD	−0.447	−0.309	−0.336	—	—	—
T2y	1.211	0.840	0.810	0.468	0.742	0.564
T3y	1.717	0.750	1.130	0.666	1.212	—
T4y	0.919	—	—	0.474	0.775	—
T2x	0.572	—	0.365	0.590	—	—
T3x	0.473	—	0.529	0.482	—	—
T4x	0.405	—	0.626	0.476	—	—
LY	−0.641	—	—	—	—	—
LX	—	—	—	—	—	—
M1	−302	−260	—	—	−203	−244

Table 3.

Comparison between ∕‐∕ before C and V in particular word pairs: Street vs seed, school vs sued, special vs said, and special vs sued. Coefficients are shown for results significant at level of p < 0.01. ∕sC∕ word is reference for each case.

	Street vs seed		School vs sued		Special vs said		Special vs sued
	L	Q	L	Q	L	Q	L	Q
JY	—	−0.710	—	—	−1.27	−1.019	—	—
JX	—	—	—	—	—	—	—	—
T1Y	−1.673	—	—	—	—	—	—	—
T1X	2.93	1.48	—	—	—	—	—	—
CL	−2.72	−1.381	—	—	—	—	—	—
CD	—	—	0.566	—	—	—	0.735	−0.55
T2Y	—	1.57	−2.32	—	—	—	1.81	1.60
T3Y	2.37	2.49	−5.10	−1.48	—	—	3.22	2.18
T4Y	—	—	−7.66	−2.02	—	—	2.76	—
T2X	2.28	1.48	—	—	—	—	—	—
T3X	1.46	1.0	—	—	—	—	—	—
T4X	—	—	—	—	—	—	—	—
LY	−1.23	—	—	—	−2.23	−1.48	−2.64	−1.39
LX	−1.01	—	—	—	−1.59	—	−1.26	—
M1	602	−453	—	−355	509	—	—	−362

RESULTS

Range of motion

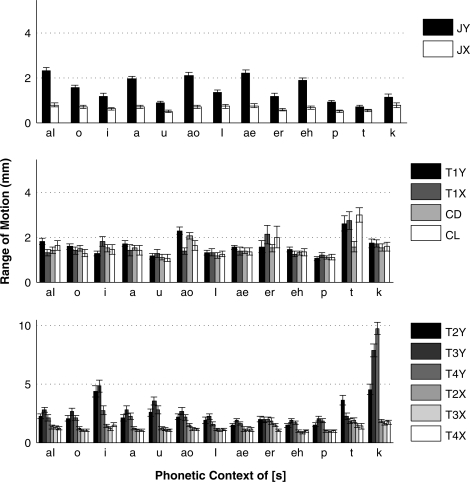
Figure 3 shows the range of motion during the production of ∕‐∕ of all articulatory measures, averaged across subjects. All parameters are in head frame and are plotted by phonetic context. The jaw moves much more in the vertical than in the horizontal direction for all contexts, and more in the low vowel context than in the high vowel and stop contexts. The T1 pellet (middle graph) has a similar range for both x- and y-components, and that range is similar to the range of motion for the vertical component of the jaw. The T1 range varies little by vowel context, but its range in ∕t/ context is larger than in any other, probably due to the following rhotic. CD and CL have similar ranges to T1 in a given context, except that CD has a smaller range in ∕t/ context. The y-components of T2, T3, and T4 ranges are all larger than their x-components; the relative size of these y-components varies with vowel context, with T3y largest for ∕i/ and ∕u/ contexts. The ranges of T2, T3, and T4 are largest of all for ∕‐∕ in school, which is expected since ∕k/ is made with a large displacement of the tongue back; the T2y range is also large in street (comparable to the ∕i/ context), again due to the rhotic. In summary, the place of articulation for the segment following ∕‐∕ has a marked effect on the amount of motion during ∕s/.

Figure 3.

The ranges of five pellet positions (not normalized, in head frame), and associated measures CD and CL, during ∕s∕ across temporal frames in different contexts, averaged across subjects.

Trajectories of motion

Jaw

The data of Fig. 3 give a general indication of the amount of motion of each of the articulators in the two dimensions. We now present details on the specific trajectories of motion of the articulators during the ∕s/. The upper row of Fig. 4 presents the trajectory of the y-component of the jaw as a function of time, split by following vowel height (left) and following consonant place of articulation (right). JX is not included in the figure, since its motion was very small and inconsistent across subjects. Regardless of the following segment, the jaw rises through about the first half of the ∕s/, indicating that the jaw continues to rise even after the sibilant noise has been initiated. This rise is small in magnitude but is consistent across speakers and contexts. The jaw starts to fall for a following vowel around the middle of the ∕s/, whereas for a following consonant, the jaw stays raised. Moreover, as expected, at the end of ∕s/, the jaw is higher before a following high vowel than before a low vowel, and higher preceding ∕t/ and ∕p/ than ∕k/.

The significance of this difference of the timing of the jaw maximum in vowels and consonants was examined using the growth-curve model tests described. Table TABLE I. shows the main effect of time on each parameter, considering ∕sV∕ and ∕sC∕ tokens separately. There is a significant negative quadratic effect on JWy for both ∕sV∕ and ∕sC∕ contexts, indicating a convex trajectory, i.e., one that moves up, then downward with time, but the effect is of larger magnitude in the ∕sV∕ context. The linear effect is significant in both contexts for JWy, but in opposite directions: the quadratic rise–fall effect is superimposed on a net fall for a following vowel, and a net rise for a following consonant, probably due to the role of the jaw for these consonants. Table TABLE II. shows the results for the statistical tests of the effect of vowel context on the time trends of the articulators. For each comparison, the second term (i.e., L, B, U) is the base case. Thus, in the columns labeled “H∕L,” the positive linear coefficient indicates that JWy trajectories of ∕‐∕ in high vowel contexts have a more positive slope than those in low vowel contexts. The positive quadratic coefficient indicates that JWy trajectories of ∕‐∕ in high vowel contexts have a more positive (steeper convex) curvature than in low vowel contexts. The same observations apply to rounded vowel contexts relative to unrounded.

To determine whether the jaw is affected significantly differently by a following consonant vs following vowel, paired comparisons were also made for particular words, so that effects of averaging across segments and the unbalanced nature of the data would not affect the significance of results. Table TABLE III. shows effects on the trends in the articulators for street vs seed and school vs sued, special vs said (same vowel in both words) and special vs sued (labial C vs rounded vowel). In each case the ∕sC∕ word is the base case, so JWy for ∕‐∕ in seed is significantly more convex than ∕‐∕ in street (negative quadratic coefficient), JWy of ∕‐∕ in said drops more and is more convex than ∕‐∕ in special (negative linear and quadratic coefficients), but ∕‐∕ in sued does not differ significantly from ∕‐∕ in special or in school.

To summarize, the jaw has a consistent upward trajectory through the first half of ∕s/, continuing on well after the initiation of frication. Whether a consonant or vowel follows the ∕‐∕ is crucial, since a following vowel forces the jaw to start descending in the middle of the frication, whereas a following consonant requires the jaw to stay in a relatively stationary position. The exception is the vowel context ∕u/; the jaw trajectories of ∕‐∕ in this context do not differ significantly from those of ∕‐∕ in special or school, probably due to the jaw’s assistance with the lip’s task for ∕u/.

Constriction region

The lower panels of Fig. 4 show T1y in jaw frame as a function of time, and as a function of following vowel height and consonant place of articulation. Interestingly, in vowel context, T1y looks somewhat like an upside-down version of the JWy trajectories, dropping mid-∕‐∕ and then rising again—a significant effect as can be seen from the positive quadratic coefficient in Table TABLE I.. Table TABLE II. shows that this quadratic effect does not differ significantly with feature of the following vowel. The amount of the drop is smaller in magnitude than the rise in JWy, so that T1y in head frame rises slightly during the ∕s/. In consonant context, T1y shows a different pattern. In ∕t/ context, T1y begins similarly to the vowel context trajectories, but then increases dramatically from mid-[s] onward, as expected for an alveolar preceding a rhotic. In general, there is no significant quadratic effect for ∕‐∕ preceding consonants.

In Fig. 5 the trajectories of CD and CL with time are shown split by context. For the ∕sVd∕ words split by vowel height, CD is constant until nearly the last frame, when it suddenly increases. The results for vowel contexts split by front∕backness and rounded∕unroundedness are similar. For the ∕sC∕ contexts, CD drops during ∕‐∕ for ∕st∕ and ∕sk∕, but rises slightly from near the beginning of ∕‐∕ for ∕sp∕, probably due to jaw raising. Table TABLE I. shows that there are significant linear and quadratic effects on CD in the vowel context, but, as can be seen from Fig. 5, these effects are due to the large increase of CD at the end of ∕s/; there is no significant fall of CD at the beginning of ∕s/.

CL also shows a different pattern in vowel and in stop-consonant context (bottom half of Fig. 5). When split by front∕backness of the following vowel, CL is nearly constant during the ∕s/; split by other vowel features (not shown), CL is nearly constant until the last articulatory frame, when front, unrounded, and low vowels have noticeably smaller CL values, implying that P1 has moved anteriorly (closer to the central incisors) relative to the back, rounded, and high vowels, respectively. The trajectories for ∕‐∕ in ∕p/ and ∕k/ context are similar to the trajectories in ∕sV∕ context. For ∕‐∕ in ∕t/ context, however, CL increases significantly from mid-∕s/. This may be due to anticipation of the ∕r/ following the cluster in street. Table TABLE I. shows that for ∕sV∕ contexts there is no main effect of time on CL; for ∕sC∕, there is a significant quadratic trend, with the positive coefficient consistent with the ∕st∕ trajectory of CL. Table TABLE II. shows that the feature of the following vowel interacts significantly over time with CL. The positive quadratic trend for H∕L and R∕U indicates that the sharp change in the last frame leads to significance. Table TABLE III. shows that, of the word-pair comparisons, only street vs seed shows a significant difference in CL, with negative coefficients for both linear and quadratic trends, indicating that ∕‐∕ in seed is significantly less concave and upward-trending than ∕‐∕ in street.

To summarize, before vowels, the vertical motion of the tongue tip during ∕‐∕ seems to be opposite to that of the jaw, with the constriction degree and location remaining nearly constant until the very end of the ∕s/, in contrast to T1. A following consonant, however, does seem to significantly affect the change in CD and CL. For ∕st∕, the tongue tip rises throughout the ∕s/, and CL increases similarly; for ∕sp∕, though the tongue tip drops slightly in apparent opposition to jaw motion, CD increases slightly from mid-∕s/. Thus, in stop-consonant context, the constriction parameters can change throughout the ∕s/, unlike in vowel context.

Tongue back and lips

Figure 6 shows the trajectories of both components of T3 in jaw frame. Regardless of the following vowel or consonant, T3y falls in the first half and T3x is stationary. The effect of time on the trajectory is significant (concave∕positive coefficients in Table TABLE I.). But from mid-∕‐∕ on, high vowel contexts rise more than low vowel contexts (significant positive coefficient in Table TABLE II.). T3x begins with front vowel contexts more anterior than back contexts, with the difference increasing by the end. T3y increases steadily in the last half in ∕sk∕ context, as expected for a velar. The statistical results in Tables 1, 2, TABLE III. confirm the observations from the figures, with a highly significant positive quadratic trend for the y-components of the tongue back, and significant interactions due to the following vowel. The x-components show effects of much smaller magnitude. In school, T3 moves up and forward substantially by the end of ∕s/, beginning in frame 6; in street, T3 moves back beginning in frame 4. In special, where the ∕p/ does not constrain tongue position, the changes are less dramatic. To summarize, in the first half of ∕s/, the tongue back lowers, but is stationary in its horizontal position, regardless of following V or C. From mid-∕‐∕ onward, the context affects the trajectory of the tongue back significantly.

Figure 7 shows that the LL, in Jaw frame, is higher and more forward for the rounded vowels. Of the ∕s/-clusters, the ∕p/ context shows the most extreme pattern, with a drop in LY and then a big rise in the last half. It might seem possible that comparing the trajectory of a single stop-consonant context, ∕sp∕, to an average of the five most rounded vowel contexts, could mask a more extreme trajectory of the most rounded vowel context. To guard against this possibility, we made additional comparisons of ∕‐∕ in special to ∕‐∕ in said (same vowel) and in sued (rounded vowel matching labial closure for ∕p/). In said, the LY trajectory was smaller throughout. In sued, LY was similar in the first frame to that of special, but then decreased gradually, remaining positive, unlike the trajectory of special. Similar results were obtained for LX comparisons to single vowel contexts. Even these more conservative measures show that the ∕‐∕ in special has a more varied lip motion than in any of the vowel contexts. The statistical tests shown in Tables 1, 2, TABLE III. reflect the differences seen in Fig. 7. Specifically, LY and LX show no significant effects for ∕sV∕ context except for a linear effect of high relative to low vowels in LY, probably due to jaw raising for a following high vowel. However, significant differences do occur when tokens of special are compared to either said or sued, with significant linear and quadratic effects. Also, Table TABLE I. shows significant quadratic effects for LY for both vowel and consonant contexts, but the coefficient is larger (more concave) for consonant contexts, probably due to special.

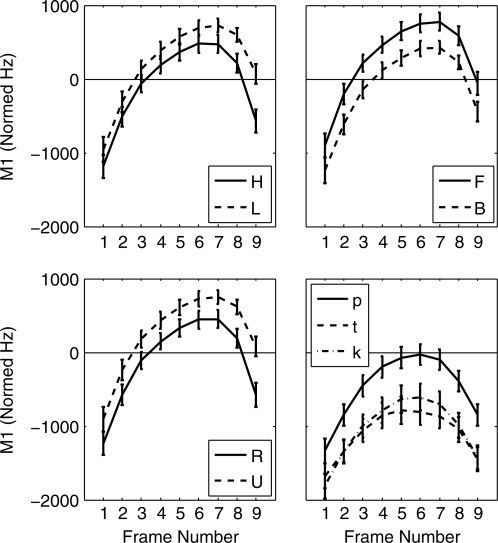
First spectral moment

Figure 8 shows one measure of the acoustic results, centered M1, of the articulatory movements discussed above. The first observation is that M1 rises through the first half, and falls by the end of ∕‐∕ in all contexts. For any subset of the vowel contexts (e.g., rounded or low vowel contexts), the total average increase is approximately 1500 Hz. For ∕‐∕ in special, the rise is approximately 1200 Hz; for ∕‐∕ in school and street the rise is less than that (approximately 800–900 Hz). There is a significant positive linear trend in M1 in all cases, but the coefficient is larger for vowel than stop-consonant context. Likewise, both vowel and consonant contexts have a significant negative quadratic coefficient, with the coefficient more negative in vowel contexts, indicating that the trajectories are more convex. Rounding and vowel height, but not frontness, significantly affect linear and quadratic effects, indicating that M1 falls more and with a more curved trajectory for the rounded than unrounded, and high than low, vowels. When we compare ∕‐∕ in special to said (Table TABLE III.), there is a significant linear effect, with ∕‐∕ in said rising more overall than in special. On the other hand, ∕‐∕ in sued does not have a significant linear trend relative to special, but is significantly more convex (negative quadratic coefficient). The ∕‐∕ in special, then, can be said to be affected by both the bilabial closure of the ∕p/ and the following front mid-vowel.

Figure 8.

First spectral moment (M1) normalized by each subject’s mean M1 during all ∕s∕ tokens, plotted for nine 30-ms intervals during ∕s∕.

The rise of M1 in the first half of ∕‐∕ seems similar to the rise of JWy, and there are some reasons why jaw movement may cause part of the M1 increases, as will be discussed below. However, the two parameters differ noticeably in the last half of ∕s/. JWy is nearly symmetric for ∕sV∕ tokens; only in the last two frames do differences appear, with JWy for low vowels dropping further than for high vowels (see Fig. 4). M1 has its maximum later in the ∕sV∕ tokens; differences between high and low contexts are apparent throughout ∕s/, and low vowel contexts have a significantly higher M1, the opposite of the JWy pattern in the last half. The ∕sC∕ contexts show a similar departure of M1 and JWy in the last half: where JWy for ∕sk∕ drops below ∕sp∕ and ∕st∕, in the M1 trajectories ∕sp∕ is higher than ∕st∕ and ∕sk∕ throughout ∕s/. Clearly M1 is affected by more than jaw height.

There are two main influences on M1: the frequency of the lowest front-cavity resonance and the amplitude of noise excitation overall. The noise amplitude builds up at the beginning of an ∕s/, increasing amplitudes at the resonance frequency and above and shifting M1 upward. The resonance itself may shift in frequency, and is strongly related to front-cavity length, lip protrusion, and lip rounding (a longer front cavity, more protrusion or more rounding will all act to lower the resonance frequency).

The differences in M1 with different vowel articulations are relatively constant throughout ∕‐∕ and much smaller than the overall increase in M1. The difference in LY for rounded vs unrounded vowel contexts is relatively constant throughout, and implies a smaller lip aperture for rounded contexts, which could explain the consistent lower M1 for rounded contexts. While some of the difference in M1 between front and back contexts is likely due to the fact that more of the back vowels are rounded, some may also be due to the difference in CL throughout: front contexts have a shorter CL, implying a shorter front cavity and higher M1. For M1 differences between high and low contexts, the combination of LY and JWy provides an explanation: the jaw frame LY is higher for high vowels at the beginning of ∕s/, and is lower at the end (not shown). Together with the JWy trajectory, these indicate that there is a relatively constant difference in lip aperture throughout, with the aperture smaller for high vowels; this would result in M1 being lower for high vowels throughout.

There is no such straightforward explanation for the overall large increase in M1 by mid-∕s/. Since CD is constant through most of the ∕‐∕ in ∕sV∕ context, one cannot argue that the constriction area continues to decrease, and thus, to produce more turbulence noise. One possibility is that as the jaw rises, the lower teeth move more into the path of the jet, and this acts to generate more noise. The distance that the jaw moves is small (of the order of 1 mm), but noise generation is very sensitive to the position of an obstacle (Shadle, 1985).

The differences in M1 with consonant context show a somewhat different pattern. CL (as defined in Fig. 1) is longer for ∕st∕, and lengthens markedly in the last half of ∕s/, which would indicate a longer front cavity and lower M1. But this explanation will not work for ∕sk∕. The drop and subsequent large rise in LY for ∕sp∕, together with the JWy trajectory, indicate that the lip aperture increases and then strongly decreases for ∕sp∕. Lip protrusion (LX) also rises toward the end of ∕‐∕ in ∕p/ context. Together these facts explain in part the higher M1 values mid-∕‐∕ and low M1 at the end of ∕‐∕ in ∕p/ context. Also, CD is slightly larger in ∕sp∕ context, and increases in the last half, which could mean that there is less noise generation in the last half of ∕‐∕ in ∕p/ context, but this explanation will not work for ∕t/ and ∕k/ contexts. Finally, the rise in T3y in ∕sk∕ context might mean that the constriction is effectively lengthened, affecting its noise-generating properties, but this is not enough to explain the overall low M1 in ∕k/ context.

GENERAL DISCUSSION

Most of the time-varying aspects of the production of ∕‐∕ depend on its context. However, there seem to be some generalizations, which are small in magnitude yet highly consistent across subjects, that are independent of context:

• (1)The jaw moves upward during the first half of ∕s/.
• (2)The tongue-back motion is greater than that of the tongue front during ∕s/, and is horizontally stationary, but moves downward in the first half.
• (3)There is an upward trend of M1 during the first half of ∕s/.

McGowan (2004) and Mooshammer et al. (2007) have noted the first generalization for cases when a sibilant precedes a vowel, but this study adds further detail and shows that the jaw-raising during ∕‐∕ also occurs in ∕‐∕ preceding stops. It is not surprising that in ∕sp∕ context, the jaw is raised by the end of ∕‐∕ to support lip closure in the stop, but that for a following vowel it falls more. What is surprising is that the jaw rises in the first half of ∕s/, regardless of the following context. It would seem that the jaw could reach its maximal height at the beginning of ∕‐∕ and then start falling for a following vowel, as long as it stayed in the range for enhancing noise. Or it could stay at the same high position from the beginning of ∕‐∕ in ∕sp∕, since the jaw is necessary for both. However, the jaw rises at the beginning of ∕‐∕ in both contexts, which seems to be an invariant aspect of the production of ∕s/. Considering all contexts, it seems that the tongue tip is sufficient to form the constriction, initiating turbulence; the jaw rises more slowly and enhances noise generation, which increases M1; the jaw then falls or stays high according to the following phonetic context. The inertia of the jaw leads to a lag between the initiation of jaw raising to reaching a maximum. But, if the speech control system does intend the jaw to reach some invariant position at the beginning of frication and remain in that position, the control signal could be timed earlier to compensate for the inertia of the jaw; this does not seem to be the case. Further investigation needs to be made of ∕‐∕ in different contexts to determine if the same trajectory is present when ∕‐∕ is not word-initial. The second generalization is expected, since the back of the tongue is not as crucial in forming ∕s/, and is consistent with the DAC model (Recasens and Espinosa, 2009), which predicts higher variability in the less constrained articulator. The third generalization has been noted indirectly in the literature (Shadle and Mair, 1996; Jongman et al., 2000; Munson, 2001; Jesus and Shadle, 2002), but this work has presented greater detail in the variation of M1 due to context, which will be explored in Sec. 4B.

Other generalizations explored in this work are restricted to ∕‐∕ in ∕sV∕ context. When the ranges of motion of the various articulators were examined, it was shown that, generally, JWy, T1y, CD, and CL have the same range. However, when the time course of articulatory events was examined, it emerged that for the prevocalic ∕s/, T1y, measured with respect to the jaw, is inversely related to JWy, and that, furthermore, CD and CL remain relatively constant through the course of the ∕‐∕ until the very end, when they change drastically for the following vowel. There are two plausible, but not mutually exclusive, explanations for the downward motion of the tip. One hypothesis is that the T1y trajectory compensates for the consistent upward and downward motion of the jaw, in order to keep the CD relatively constant throughout the ∕s/. But how can the tongue tip be lowered actively when the jaw is heading upward? This can be achieved by controlling the tongue tip through its hydrostatic link to the tongue back. Indeed it was seen in Sec. 3B3 that the back of the tongue has a downward motion of the tongue in the first half of the ∕s/, even when the following vowel is high. The first hypothesis, therefore, is that the motion of the jaw is being compensated for by the tongue tip, by controlling the tip through its hydrostatic link to the back, in order to achieve relative invariance of the constriction parameters through most of the ∕s/. The second hypothesis is that if the sides of the tongue are braced against the sides of the palate during ∕s/, then upward motion of the jaw may not be able to cause a significant upward motion of the tongue, since the side contact with the palate prevents such upward motion (Perkell et al., 2000). This would also stabilize CD. Under this possibility, the speech motor control system would be stabilizing CD by using passive properties of the structure of the vocal tract.

The data presented here are consistent with a model in which the speech motor control system is using the reaction force from the palate that is obtained by side contact, in combination with the active force of tongue tip downward motion, for CD stabilization. Evidence for the hypothesis that the tongue tip is actively recruited is that the magnitude of the motion of the back of the tongue (see Fig. 6) is about twice the magnitude of motion of the jaw. In terms of the magnitude of change, that of the tongue back is largest, followed by the jaw, the tongue tip, and CD, in that order (until the very end of the ∕s/). This largely consistent downward motion of the tongue back, even for a following high vowel, together with the linkage between tongue back and tip, suggests that the tongue back downward motion is to assist the tongue tip’s downward motion. If the stabilization of the constriction is achieved solely by the bracing against the palate, it is hard to understand the magnitude of the downward motion of the tongue back, exactly when the jaw is rising. The same downward motion of the tongue back could also serve another purpose, that of grooving the tongue back to channel the jet, but this would not be inconsistent with its use for assisting the tongue tip in stabilizing CD. We believe that both active and passive forces are recruited for constriction stabilization, and that the presence of one force does not in any way imply the absence of the other.

Consistent with DAC, a following alveolar obstruent (high DAC value) is able to effect the change in CL very early in the ∕s/, whereas a following vowel (low DAC value) is only able to affect ∕‐∕ during the last half. However, since the position of the tongue for vowels is much less resistant to coarticulation than ∕s/, it is surprising that vowels are able to affect the jaw trajectory in ∕‐∕ at all.

Compensation for natural mechanical vs phonetic perturbations

Two types of perturbation to the achievement of the articulatory, aerodynamic, and acoustic goals for ∕‐∕ were investigated in this study. The first is a phonetic or contextual perturbation due to the competition between ∕‐∕ and the following segment in determining the motion of the articulators during ∕‐∕ (Fowler and Saltzman, 1993). The second is a dynamic perturbation due to the inertial effects of a body in motion (Flash and Hogan, 1985; Laboissière et al., 2009). In this study, there is such an effect: the motion of the jaw. As stated earlier, we believe that the upward trajectory of the jaw through the first half of an ∕‐∕ is an effect of the mass of the jaw, which the speech motor control system does not compensate for in the jaw’s own motion (i.e., it does not recruit the jaw earlier to reach an invariant position), but through the motion of other articulators that can compensate for its inertia, or through the use of passive reaction force of the palate.

If we compare the two types of natural perturbations in the production of ∕‐∕ investigated in this study, it is found that natural mechanical perturbations are compensated for, whereas phonetic perturbations are largely uncompensated for. The downward motion of the tongue tip for ∕s/, together with use of the side contact against the stationary palate, seems to compensate for the jaw’s vertical motion due to its inertia, keeping CD and CL, but not M1, relatively constant. However, the sudden increase of CD at the end of ∕‐∕ for a following low vowel and the effect of a following rounded or labial segment do not seem to be compensated for by the motion of some other articulator. That context affects the ∕‐∕ at its end is not in itself surprising. What is significant is the difference in how context affects the jaw and the constriction, where the effect on the former is consistently earlier than the latter. Moreover the jaw does not lower in preconsonantal context, especially for ∕p/ and ∕t/, since jaw raising is necessary for their articulation. This effect affects tongue motion and is not compensated for. We believe that the difference in response to mechanical and phonetic perturbations is a novel type of result in speech motor control that merits further investigation.

Articulatory–acoustic relations

Based on the discussion of how various articulators affect M1 in various contexts, we conclude that all the articulators at the constriction and anterior to it (tongue, jaw, and lips) interact in determining M1. However, the lips and jaw are the articulators that affect M1 the most. Raising the jaw through the first portion of ∕‐∕ seems to have the general effect of raising M1. We believe that raising the jaw allows the lower teeth to act as an obstacle to the jet, even though the upper teeth act as an obstacle as well. Such an obstacle serves as a converter of aerodynamic-to-acoustic frication energy. Specifically, the more orthogonal to the flow and the more the jet impinges on the obstacle, the more noise is generated at all frequencies. We explained in Sec. 3B4 how increased noise production could lead to M1 increasing, and that this mechanism does not explain why M1 falls at the end of ∕s/, even when the jaw remains high. What is interesting about this effect of the rising M1 is that it is not compensated for. We have argued that the tongue tip, together with side contact against the palate, compensates for the jaw’s upward motion by moving downward, maintaining CD at a relatively constant level till the end of the ∕s/. However, this compensation for CD does not change the acoustic effect of the jaw’s upward motion on the output acoustic signal. The implication for quantal theory is that articulatory variability during ∕‐∕ does not lead to an acoustic plateau, i.e., articulatory variability emerges in acoustic variability, and is not hidden. In particular, the effect is not removed by, for instance, time-varying compensatory lip rounding that could eliminate the effect of the jaw on the output spectrum.

The implication of this result for the theory of speech motor control is to point to a particular situation, ∕‐∕ production, where compensation to achieve an articulatory–aerodynamic goal, constant CD, is not accompanied necessarily by a compensation for an acoustic effect, providing partial support for the idea of articulatory goals in speech production (Saltzman and Munhall, 1989). Rather, in this case the compensation for CD is accompanied by marked variability in M1. However, since the magnitude of variability is still not high enough for perceivers to confuse ∕‐∕ and ∕∫∕, it may be that no compensation for acoustic variability is necessary in such a case. It could also be that the acoustic goal is simply the generation of noise, not specific M1 frequency, as long as it is in the correct region. Indeed, theories of speech production that posit acoustic∕auditory regions as targets (Guenther et al., 1998) are not inconsistent with the possibility presented here, where articulatory compensation is somewhat complete for CD, but incomplete for M1, since the variability of M1 may be within the region of acceptable variability (Maniwa et al., 2009). But those same models would predict that there would also be a region of variability for CD, the articulatory–aerodynamic goal. However, that parameter seems to be achieved with high precision and remains static through almost the entire ∕s/. Further research on the extent of acoustic variation within a target window may therefore be able to use the acoustic change within a segment to establish the extent of an acoustic target window, while also measuring the extent of the underlying articulatory windows.

CONCLUSIONS

We have used the Wisconsin XRMB database to examine the articulatory production of ∕‐∕ in detail. Even though most aspects of articulator motion are context-dependent during ∕s/, we have found that there are some relatively invariant time-variable aspects: small but highly consistent upward motion of the jaw through the first half of ∕s/, reduced motion in the constriction region compared to the tongue back, and an increase in the frequency of the first spectral moment through the first half of ∕s/. Furthermore, it was found that the natural mechanical perturbation of ∕‐∕ due to the upward motion of the jaw seems to be compensated for by tongue-tip motion when ∕‐∕ is in prevocalic context, in collaboration with side contact against the palate, but that contextual phonetic perturbations are largely uncompensated for. It was also shown that in ∕‐∕ production, articulatory–aerodynamic compensation does not automatically lead to compensation for an acoustic result of articulatory motion.