Molecular Dynamics and Brownian Dynamics Investigation of Ion Permeation and Anesthetic Halothane Effects on a Proton-gated Ion Channel

Abstract

Bacterial Gloeobacter violaceus pentameric ligand-gated ion channel (GLIC) is activated to cation permeation upon lowering the solution pH. Its function can be modulated by anesthetic halothane. In the present work we integrate molecular dynamics (MD) and Brownian dynamics (BD) simulations to elucidate the ion conduction, charge selectivity and halothane modulation mechanisms in GLIC, based on recently resolved x-ray crystal structures of the open-channel GLIC. MD calculations of the potential mean force (PMF) for a Na⁺ revealed two energy barriers in the extracellular domain (R109 and K38) and at the hydrophobic gate of transmembrane domain (I233), respectively. An energy well for Na⁺ was near the intracellular entrance: the depth of this energy well was modulated strongly by the protonation state of E222. The energy barrier for Cl⁻ was found to be 3–4 times higher than that for Na⁺. Ion permeation characteristics were determined through BD simulations using a hybrid MD/continuum electrostatics approach to evaluate the energy profiles governing the ion movement. The resultant channel conductance and a near-zero permeability ratio (P_Cl/P_Na) were comparable to experimental data. Based on these calculations we suggest that a ring of five E222 residues may act as an electrostatic gate. In addition, the hydrophobic gate region may play a role in charge selectivity due to a higher dehydration energy barrier for Cl⁻ ions. The effect of halothane on the Na⁺ PMF was also evaluated. Halothane was found to perturb salt bridges in GLIC that may be crucial for channel gating and open-channel stability, but had no significant impact on the single ion PMF profiles.

INTRODUCTION

The Gloeobacter violaceus pentameric ligand-gated ion channel (GLIC) is activated to ion permeation by lowering the pH value.¹ In 2009 x-ray crystal structures for the open channel state were solved at pH=4.0 (PDB: 3EHZ)² and pH=4.6 (PDB: 3EAM)³ with resolutions of 3.1 Å and 2.9 Å, respectively. As the first open channel structures of high resolution in the pentameric ligand-gated ion channel superfamily (pLGICs), these two crystal structures from prokaryotic family provide an invaluable structural archetype for homologous eukaryotic Cys-loop receptors, which mediate fast neurotransmission in the central nervous system. Cys-loop receptors include the anion-selective glycine receptor (GlyR) and γ-aminobutyric acid type-A receptor (GABA_AR), and cation-selective serotonin receptor (5-HT₃) and neuronal acetylcholine receptor (nAChR). Members of LGICs share considerable structural similarity. Each receptor is formed by five subunits and each subunit has a large extracellular (EC) domain and four transmembrane (TM) domains with the TM2 segments forming the channel pore through which ion permeation occurs. These high-resolution open channel structures^2,3 together with an electrophysiological study of the single channel conductance of GLIC¹ have offered excellent structural models for theoretical study of ion permeation in the LGICs at the atomic level.

The time scale for ion permeation under physiological conditions is on the order of 10s of nanoseconds to μs - close to the limit of fully atomistic molecular dynamics (MD) simulation. Thus for real protein channels, especially large ones like GLIC under physiologically relevant conditions of solution ionic strength and applied voltage, some type of coarse-graining strategy^4–9 is required to simplify the calculations without compromising the essential structural and dynamical features of the channel. Among these coarse-grained methods, Brownian dynamics (BD) has extensively applied to several types of ion channels.^5,8,10,11 In these BD simulations, protein, lipids and water are treated as static dielectric continua, but the ions are treated explicitly as spherical particles, subjected to Brownian motion in the many-body force field generated by the protein channel, externally-applied membrane potential, and all other ions as well as electric charge induced at dielectric interfaces. Continuum calculations of these systematic potentials have been reliably applied to large channels,^5,12 but their applications to narrow channels are still debatable.^13,14,15 Within the highly confined region of a channel, protein fluctuations and water dynamics in response to the presence of an ion can have a significant effect on the potential of mean force (PMF) governing the ion’s motion. Such effects can in fact be assessed using equilibrium MD simulations of manageable size.^16–19 However a fully atomistic calculation of the single ion PMF in domains of large sizes, i.e. EC domains of the GLIC, is computationally costly, even along a one dimensional reaction coordinate, such as the channel centerline axis. In reality, one needs to compute this single-ion PMF in three dimensions within the EC domain, thus further exacerbating the situation.

In order to balance computational accuracy and efficiency, we have implemented in the present work a hybrid MD/continuum approach to estimate the single ion PMF for transporting Na⁺ or Cl⁻ through the GLIC receptor. The paradigm of this hybrid approach is illustrated in Fig. 1. Inside the TM domain, the ion is confined within a narrow channel pore and one may assume the lateral deviations of the PMF can be averaged to obtain an effective one-dimensional PMF,^18,19 which can be calculated via an all-atom MD-based free energy method, such as the adaptive biased force (ABF) method.^20,21 For other regions (in particular in the EC domain), a three-dimensional PMF is necessary. This can be estimated using continuum electrostatics approaches,^4–6,8 i.e. solving Poisson’s equation. The two results are then connected together at the entrances to the constricted TM channel pore. Using this hybrid approach, we calculated the effective potential energy fields for transporting Na⁺ or Cl⁻ ion through GLIC, which were then input, along with suitable estimates of the ion diffusivity profiles for Na⁺ and Cl⁻ (described in detail below), to BD simulations of channel conductance using a dynamic Monte Carlo (DMC) algorithm.^6,7 Our calculated single channel conductance as well as the permeability ratio of P_Cl/P_Na were comparable to experimental study of single channel conductance in GLIC.¹ The ion permeation characteristics predicted by the present study differ in certain aspects from a recent BD simulation of ion permeation in the GLIC.²² In the study by Song and Corry,²² the usage of default charge states (at pH=7) for titratable residues at pH values of 4~5 is questionable. Additionally, the use of static x-ray structures may not be appropriate for estimating the potential energy profiles relevant in a system where the channel protein undergoes dynamic fluctuations, especially in the constricted channel region.

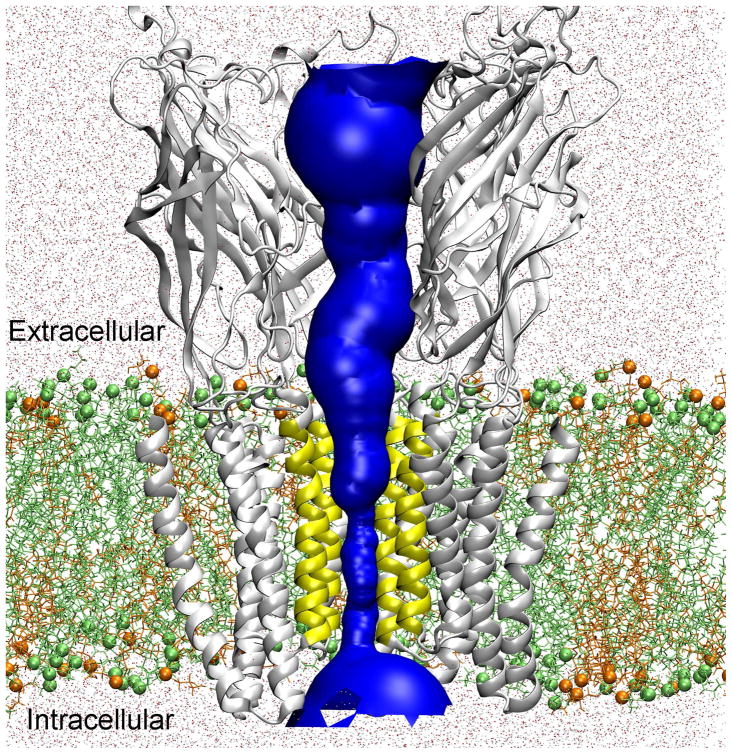
Figure 1.

Hybrid MD/continuum approach for calculating the single ion PMF through an equilibrated GLIC (PDB: 3EAM) protein. The channel pore for ion permeation is highlighted in blue. For the constricted TM pore (lined by the yellow TM2 segments), the single ion PMF was calculated via MD simulation. For other regions (i.e., the extracellular and intracellular domains), the single ion PMF was evaluated using a continuum dielectric approach. In the MD simulations, GLIC was embedded into a binary lipid containing POPE (lime) and POPG (orange) (in a ratio 3:1) and solvated by TIP3P water (dots). Lime spheres and orange spheres show the phosphorus atoms of POPE and POPG. For clarity, only four protein subunits are shown.

LGICs are molecular targets of general anesthetics, but knowledge of the underlying mechanism of anesthetic modulation remains incomplete. A recent electrophysiological study²³ has found that the whole cell current of GLIC could be inhibited by halothane, similar to that of its homologous nAChRs. However it remains unknown whether the inhibition is generated by reducing the single channel conductance or altering the channel opening. Here we integrated both MD and BD simulations to study the effects of halothane binding on the single channel conductance and protein dynamics in the GLIC. Valuable insights into anesthetic effects on the GLIC were provided, which may facilitate the understanding of anesthetic modulation mechanism in the LGICs.

METHODS

Molecular dynamics simulations

Details on system preparation are provided in Supporting Information. Briefly, the protonation state of titratable residues at pH = 4.6 was estimated based on the Henderson-Hasselbalch equation and the pKa calculations performed by Bocquet et al.³ The TM domain of the GLIC was embedded in a pre-equilibrated binary POPE-POPG (3:1) lipid mixture²⁴ and the remaining part of GLIC was fully solvated by TIP3P water (see Fig. 1). To fine-tune the protonation states of E222 residues, three different systems were constructed: in System A, two E222 residues were protonated; in System B, three E222 residues were protonated; and in System C, none of E222 residues were protonated. In all systems, Na⁺ and Cl⁻ ions were appropriately added to neutralize the system. There were one GLIC, 263 POPE, 80 POPG, and about 33,277 water molecules in each system for a total of over 168,000 atoms.

Anesthetic halothane binding sites in GLIC were predicted through flexible docking analysis using the Autodock program²⁵ (version 3.0.05) on the original crystal structure and MD-equilibrated structures of GLIC (PDB: 3EAM). Detailed results of these docking calculations are provided in Supporting Information (see Fig. S1). Two halothane systems (see Fig. S2) were constructed: 1) ten halothane molecules docked in the crystal structure (termed as 10HAL); and 2) two halothane molecules docked near W160 in a snapshot of GLIC obtained after a 5ns MD simulation (termed as HAL-Near-W160). Parameters for halothane were taken from Ref. 26. The Halothane systems were the same as System A except for the additional halothane molecules at different sites.

MD simulations were performed using the NAMD package²⁷ with the CHARMM27 force field (version 31).²⁸ Production runs were carried out without any restraint and under Nosé-Hoover constant pressure (P = 1 Bar) and temperature (T = 310 K) (NPT).^29,30 The single ion PMFs for transporting a Na⁺ or Cl⁻ ion through the GLIC channel in the various systems described above were calculated using the adaptive biased force (ABF) method^20,21 implemented in NAMD. A computation protocol for Cys-loop receptors in a previous study¹⁹ was followed. The ion diffusivities for a Na⁺ ion inside the channel were calculated using the random force autocorrelation function (FACF) method,^31–33 which has been applied to calculate the ion diffusivities in cavities or ion channels.^34,35 More details regarding the MD simulation protocol, calculation of single ion PMF and ion diffusivities can be found in Supporting Information.

Brownian dynamics simulations

Brownian dynamics (BD) simulation of ion permeation was carried out using a Dynamic Monte Carlo (DMC) algorithm.^6,7 Detailed description can be found in Refs. 6,7,10,11. Briefly, protein channel, membrane, and water were treated as continua characterized by different dielectric constants, but ions were treated explicitly, undergoing 3D Brownian motion according to the following effective potential:

$$W_k={\phi }_k^{\mathit{mem}}+{\phi }_k^{\mathit{PMF}}+\sum _{j\ne k}\frac{q_k{q}_j}{{\epsilon }_w}{\phi }^{\mathit{coul}}(r_{kj})+\sum _{j\ne k}{q}_k{q}_j{\phi }_{kj}^{\mathit{diel}}-k_{B}Tln(D(z)/D_0)$$ (1)

where q_k and q_j are the charges of ion k and j, respectively. D₀ and D(z) are the diffusion constants of an ion in the bulk and at position z, respectively. The first term in the right hand side of Eq. 1 is an externally applied transmembrane potential. The second term is the single ion potential mean force (PMF). In the present study, a hybrid MD/continuum approach was implemented, which combined all-atom MD simulations of the statistical mechanical potential of mean force in the narrow pore region of the channel with an approximate continuum electrostatics evaluation (solving Poisson’s equation) of the same quantity in the large pore regions. Full details are provided in the Results section, including the procedure for connecting the results of the two computational schemes near the entrances to the narrow TM pore region. The third and fourth terms together calculated the long-ranged Coulombic ion-ion interactions in a dielectric inhomogeneous medium⁶ and were estimated following our previous approach.^10,11,36 The last term is introduced to account for the spatial dependence of the ion diffusion constant in the Brownian dynamics simulations.^7,37 A hard-core excluded volume potential was also included. In particular, any overlap between an ion and the protein/membrane or between any two ions was not permitted. For each specified voltage ( ${\phi }_k^{\mathit{mem}}$), a total of 8 individual BD simulations were carried out with each run lasting 5.6 μs. Radii of 1.8 Å and 0.95 Å were taken for Cl⁻ and Na⁺, respectively. The ion displacement in the bulk solutions was chosen to be 1 Å and reduced accordingly with ion diffusivity inside the channel. ^7,11

Data analysis

VMD³⁸ with scripts developed in house was used for data analysis and visualization. The standard deviation for the ABF-calculated PMF was estimated from different runs and also from simulations of different lengths. The channel centerline and pore-radius profiles were computed using the HOLE program.³⁹ The ion density profiles inside the channel were estimated by counting the number of ions within the pore identified by the HOLE program.³⁹ pKa values for titratable residues were estimated using PROPKA.⁴⁰ Calculation of the continuum electrostatic potential followed our previous procedure^4,10 and used CHARMM27 force field. For details see Supporting Information.

RESULTS and DISCUSSION

Converged single ion PMFs

Using the ABF method,^20,21 we calculated the 1D PMF for transporting a Na⁺ or Cl⁻ along the channel centerline in System A, in which two of five E222 residues were neutralized. In the region of the constricted TM pore (from z=−42 Å to z=−12 Å), no lateral restraints were applied on the target ion since it was well confined inside the pore by the protein channel. Outside the TM pore, to prevent the target ion from drifting too far away from the channel centerline,^18,19 the target ion was laterally restrained along the channel centerline using harmonic restraints which restricted the lateral fluctuation of the ion to ~±4 Å around the centerline. Fig. 2 shows the calculation results for Na⁺ and Cl⁻ ions. Their PMF values fall to zero at z=−57 Å and z = 28 Å, i.e., near both entrances of GLIC. To confirm the convergence of the PMF, we performed a second set of PMF calculations on the same system for the TM pore region. Although we used different random seeds, different initial configurations and a 4-ns instead of 5-ns simulation for each window in the second set of calculations, both sets of PMF attained comparable profiles as shown in Fig. 2, suggesting that the PMFs inside the TM pore are converged fairly well.

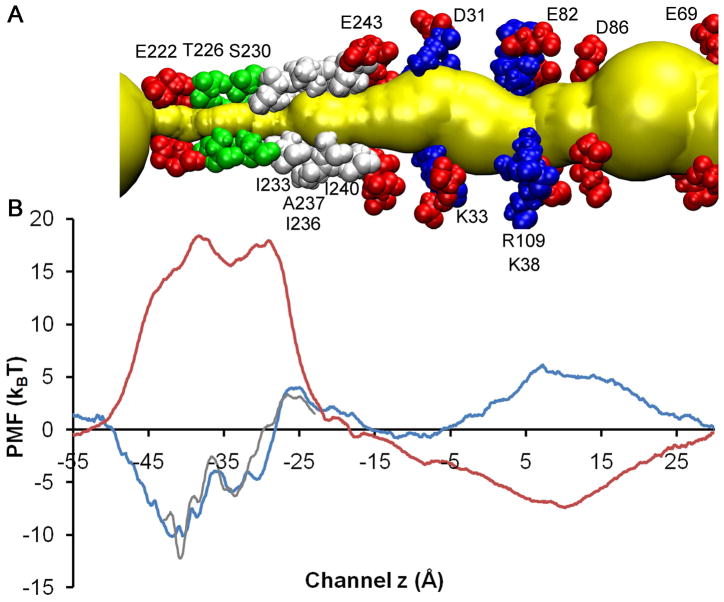
Figure 2.

A) Important pore lining residues in the MD-equilibrated GLIC. Acidic, basic, hydrophilic and hydrophobic residues are shown in red, blue, green, and white VDW format, respectively. The permeation pore is highlighted in yellow; and B) comparison of MD-calculated single ion PMFs for transporting Na⁺ (blue line) and Cl⁻ (red line) ions along the channel centerline of System A. Grey line shows another set of PMF calculations for Na⁺ using different initial configurations and slightly different MD protocols. The standard deviation for the Na⁺ PMF near the intracellular entrance (−55 Å < z < −45 Å) was high.

Na⁺ and Cl⁻ ions have distinctly different PMF profiles. Two energy barriers of equal height (18.3±2.0 k_BT) are found for Cl⁻. One is near E222, where E222 (−2′) residues from the five subunits form a charge selectivity filter. Charge selectivity filters at homologous locations also exist in other cation-selective LGICs.⁴¹ The other energy barrier for Cl⁻ is at I233 (9′), which has been proposed as part of the hydrophobic gate in the GLIC.⁴² The high energy barriers for Cl⁻ in GLIC are comparable to those found in the open-channel α4β2 nAChR (17.0 k_BT)10 and in α7 nAChR (13.6 k_BT),19 indicating that Cl⁻ ions are not permeable in GLIC as in nAChR channels. In contrast, Na⁺ has much smaller energy barriers in GLIC. The one at the hydrophobic gate near I233 (9′) is 4.0±1.5 k_BT, which is close to the Na+ energy barriers previously computed at similar regions of α4β2 nAChR (4.6 k_BT)10 and α7 nAChR (4.0 k_BT).19 Another significant Na⁺ energy barrier of 5.0±1.0 k_BT in the EC domain (near R109 and K38) is unique to GLIC, and there is no homologous energy barrier found in either α4β2 or α7 nAChRs. This extra energy barrier in the EC domain of GLIC is due to protonation of several acidic residues at a lower pH in GLIC and may be partially responsible for the much lower channel conductance in GLIC (8 pS) than found in α7 nAChR (~80 pS)⁴³ and α4β2 nAChR (40~46 pS).⁴⁴

In addition to energy barriers, energy wells can also significantly affect Na⁺ permeation in GLIC, particularly the well nearby E222 with a value of −10.2±2.5 k_BT. The depth of this energy well along with the protonation state of E222 merits discussion in a separate section.

Energy well and charge states of titratable residues: E222 determines the single ion PMF

On the basis of crystal structures resolved at pH=4.6 (PDB: 3EAM)³ and pH=4.0 (PDB: 3EHZ),² we estimated the protonation probability (using PROPKA⁴⁰) for E222 residues as 20% and 80%, respectively. MD relaxation of the x-ray structure (PDB: 3EAM) lead to a different estimation of these probabilities. Three of five E222 residues were suggested to be protonated based on pKa calculations of our MD equilibrated GLIC structures at pH=4.6. E222 plays a crucial role in the GLIC channel function, as evidenced by the strong influence of the E222 protonation state on the Na⁺ PMFs (see Fig. 3). In system C, where all five E222 residues were deprotonated, an energy well of −22.5±5 k_BT was obtained. Such a deep well will strongly trap Na⁺ and thus prevent Na⁺ dissociation from this binding site. Protonation of two (System A) or three (System B) E222 residues changed the energy well near E222 to be −10.2±3.0 k_BT and −6.3±2.0 k_BT, respectively. It is worth re-emphasizing that systems A, B, and C are identical except for their E222 protonation states.

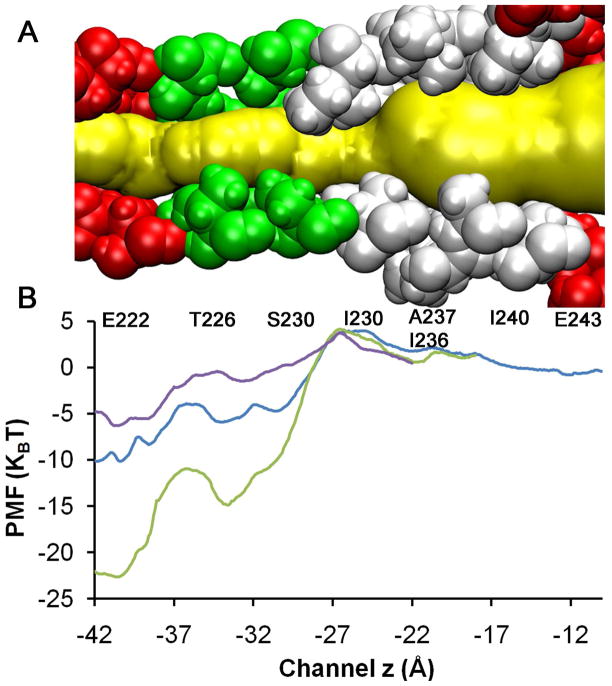
Figure 3.

The charge state of E222 strongly influences the PMF. A) Pore lining TM2 residues. Ion permeation pathway is highlighted in yellow. Hydrophobic gate region is shown in white; and B) Comparison of MD-calculated single ion PMFs for transporting Na⁺ ion through the TM pore of GLIC with different protonation probability of E222 residues. Purple, blue and green represent three, two and no protonated E222 residues, respectively. The charge states of E222 had only minor effects on the Na⁺ PMF when the z coordinate of Na⁺ was greater than −17Å (after A237 and I236).

The protonation state of E222 could affect the orientation of its side chain and thus the pore size. Asymmetric side chain orientation of E222 residues was observed in our simulation systems. The pore radius near E222 tended to become smaller as the number of protonated E222 residues increased (equivalent to reducing pH). This observation is in accord with a smaller pore radius near E222 in the crystal structure resolved at pH=4.0 (~0.5 Å; PDB: 3EHZ)² than that resolved at pH=4.6 (2.5 Å; PDB: 3EAM).³ A larger electrostatic repulsive interaction with more charged E222 residues may push the E222 side chains away from each other and enlarge the pore size. In contrast, the presence of a Na⁺ ion near E222 reduces the channel pore (near E222) through attractive electrostatic interactions. We noticed in our MD simulations that the target Na⁺ ion was fully solvated with its first hydration shell intact throughout the entire channel pore except near E222, where Na⁺ was partially dehydrated (cf. Fig. S4) and carboxyl (or carboxylate) oxygen atoms of E222 interacted directly with Na⁺.

In addition to E222 residues, we also evaluated how protonation of other titratable residues affected the GLIC channel. Whether HIS residues were protonated or not seemed to have a negligible effect on the GLIC structure and the open channel stability in our MD simulations. However, when all the acidic residues of GLIC were deprotonated at high pH, water was excluded from the hydrophobic gate region within 2ns MD simulation (data not shown), indicating a channel in the closed state.^10,42 40% more salt bridges were found in this simulation as compared to those in the crystal structures. By contrast, when the charge states of acidic residues at a lower pH (i.e. pH=4.6) were appropriately assigned in accord with pKa calculations³ (specifically, in our System A and B; see details in Materials and Methods), full water occupancy was observed inside the hydrophobic gate region. This suggested that appropriate charge states of acidic residues played an important role on the open channel stability.

Multi-level implementation of MD/continuum approaches for BD simulations of ion permeation

Ion permeation characteristics in GLIC were investigated using a DMC algorithm^6,7,10 to perform BD simulations. Differing from our previous BD simulations, here we implemented a hybrid MD/continuum approach to determine the single ion PMFs for permeant Na⁺ and Cl⁻ (the term ${\phi }_k^{\mathit{PMF}}$ in Eq. 1) for the sake of computational accuracy and efficiency. In particular, the 1D PMF calculated by the ABF method^20,21 was employed for an ion moving through the narrow pore in the TM domain; outside this region, a 3D electrostatic energy profile calculated via a continuum dielectric approach (i.e., solving Poisson’s equation)⁴ was employed. A 1D PMF has been found to reflect reasonably well the multi-dimensional energy landscape that governs single ion motion within a narrow channel pore.¹⁸ The connecting points (z positions at which the 1D MD-based PMF and 3D continuum electrostatics PMFs were joined) were chosen to be near I240 and S220 inside the narrow TM pore, where the lateral variations in the 3D electrostatic potential were small (~1 k_BT) for permeant ions, thus enabling a 3D electrostatic energy profile to be treated using a 1D PMF without sacrificing much computational accuracy. Since we are doing high-friction Brownian Dynamics simulations here, any problems that might arise from the φ (effective potential guiding the BD simulation) or its gradient being not perfectly continuous at certain points are effectively masked by the (roughly ±1 k_BT) noise of the stochastic simulation. It is worth emphasizing that even though different approaches are employed to tabulate the single ion PMFs in different regions, all permeant ions undergo 3D Brownian motion. When the ion occupies the narrow channel pore region, we assume that the PMF calculated at a given z point has the same value along the transverse (xy) direction until the “wall” created by impenetrable pore-lining protein atoms is reached, at which point the PMF becomes infinitely positive.

Fig. 4 compares the single ion PMFs calculated using different approaches for a permeant Na⁺ or Cl⁻ ion to transport along the channel centerline of System A. Inside the EC section of the channel, electrostatic energy profiles calculated by the continuum dielectric approach produced results similar to those obtained via MD calculations, but a significant difference was observed in the TM pore, where MD calculations showed a much larger energy barrier for a Cl⁻ ion. In our MD simulations, different degrees of dehydration were observed for Na⁺ and Cl⁻ ions when they permeated through the constricted TM pore. For a Cl⁻ ion, up to 15% reduction of its first hydration shell was observed, as inferred from the appropriate radial distribution function (see Fig. S5). In contrast, a Na⁺ ion was able to transport with its first hydration shell fully intact (see Fig. S4) through the entire TM pore except near E222, where oxygen atoms from E222 (or T226) substituted partially as the first hydration shell and compensated for the dehydration energy barrier.⁴⁵ Such dehydration variations for different ions greatly influence the ion permeability ratio and can only be realistically captured at the atomic level using MD simulations.

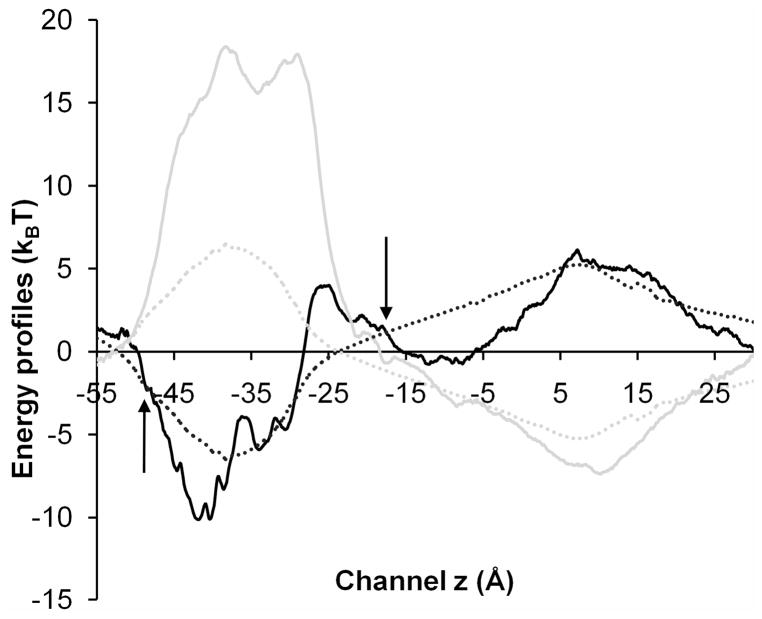
Figure 4.

Comparison of energy profiles for transporting a Na⁺ (black) or Cl⁻ (gray) ion along the channel centerline of System A. Solid lines represent the single ion PMF calculated by MD and the dotted lines show the electrostatic energy profiles calculated by continuum electrostatics approach. A hybrid MD/continuum strategy was implemented to estimate the PMF for transporting a Na⁺ or Cl⁻ ion in BD simulations. The z positions (shown via arrows) at which the MD and continuum electrostatics PMFs were joined were chosen to be z= −17.5 Å (near I240) and z= −48.0 Å (near S220), where the lateral variations of 3D electrostatic potential were small (~1 k_BT) inside the channel pore.

The ion diffusivities for Na⁺ ion inside the channel were calculated using the random force autocorrelation function (FACF) method.^31–35 (see Supporting Information for more details) The calculated ion diffusivity was highly correlated with the channel radii (see Fig. S3). In the EC domains, the ion diffusivity was roughly 0.5~1.0 (pore radii of 5~10 Å) times its bulk value. Inside the constricted TM pores, the ion diffusivity was 0.2~0.7 (pore radii of 2.5~6 Å) times of its bulk value. For simplicity, in our BD simulations diffusivities for Na⁺ and Cl⁻ were assumed 1.33×10⁻⁵ cm²/s and 2.02×10⁻⁵ cm²/s in bulk water,⁴⁶ and were reduced from their bulk values near the receptor entrances to 0.3 times these values near the TM entrances, and maintained at 0.3 times of their bulk values throughout the entire TM region (z= −54 Å to z= −18 Å).

Furthermore, in our BD simulations, the long-ranged Coulombic ion-ion interactions were calculated as in previous work.^10,11,36 The externally applied membrane potential fields were obtained by solving Poisson’s equation with specified voltages at the boundary layer.

Permeation characteristics of Na⁺ and Cl⁻ ions in GLIC: E222 may function as an electrostatic gate

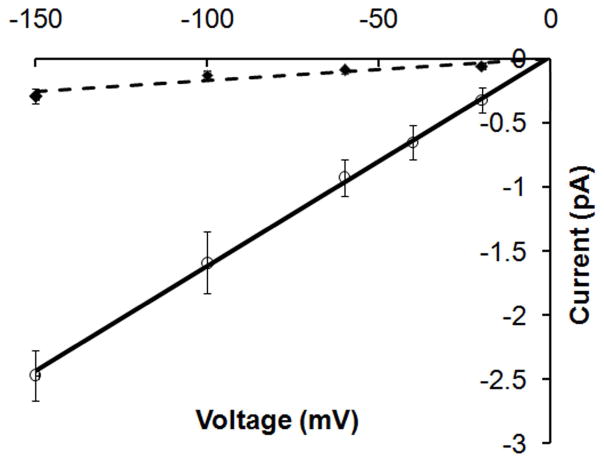
Fig. 5 compares the BD-simulated current-voltage (IV) relationship in System A and System B. A linear current-voltage relationship was obtained in both simulations, which agrees well with the single-channel measurements in GLIC.¹ The protonation state of E222 determined the channel conductance. If none of E222 residues were protonated (in System C), no Na⁺ was observed to pass E222 due to excessively strong electrostatic attractive interaction (an energy well of −22.5 k_BT) between the cation and E222. When the number of protonated E222 residues was increased from two (in System A) to three (in Sytem B), the simulated channel conductance increased from 1.9±1.0 pS to 15.8±2.5 pS. Both values are comparable to the experimentally measured single channel conductance¹ of ca. 8±2 pS in GLIC at pH=5.

Figure 5.

BD simulated current-voltage relationship in System A (diamonds with error bars) and System B (open circles with error bars). Dashed line and solid line show the least square fit to the simulation data in System A and System B, respectively. BD simulations were carried out in symmetric bathing solutions of 0.15M NaCl. The simulated currents at different applied external potentials were collected and the conductance was calculated as γ = I/V. The calculated channel conductance in System A and System B was 1.9±1.0 pS and 15.8±2.5 pS, respectively.

In our model systems, we observed that the single channel conductance was amplified when the number of protonated E222 chains was increased from 0 up to 3 (equivalent to lowering the pH). This trend generally agrees with the changes in experimentally measured whole cell currents vs. pH value.² We suggest that besides the proposed hydrophobic gate⁴² (near I233) E222 (−2′) residue may function as an electrostatic gate in GLIC. At PH=7, the channel is closed to cation permeation since no cation can leave the deep energy well generated by five deprotonated E222 residues. Lowering the pH reduces the binding site strength at the E222 site and increases the rate for a cation to dissociate from this binding site. This putative electrostatic gate may be unique to the GLIC channel. Compared to other cation-selective LGICs, the signature E-1′K0′ (or E-1′R0′) residue sequence near the intracellular entrance is replaced by E-2′A-1′N0′ in GLIC. It is interesting to note that the position of E222 (−2′) is consistent with a gating position proposed by substituted cysteine or histidine accessibility experimental studies in other LGICs.^47,48

Consistent with the experimentally measured permeability ratio¹ of P_Cl/P_Na=0, no Cl⁻ ion was observed to transport through the channel during the entire BD simulations due to the ~18.3 k_BT energy barrier it experiences near E222 and the hydrophobic gate region (near I233). The intracellular entrance homologous to the location of E222 residues in GLIC has previously been proposed as the filter for charge selectivity in other LGICs.⁴¹ In addition, we suggest that the hydrophobic gate region may also play an important role in distinguishing cation-selective from anion-selective LGICs. Cation-selective LGICs generally contain more layers (i.e., three layers at 9′, 13′ and 15′ 17′) of hydrophobic segments inside the channel pore, which may generate a higher energy barrier for the permeation of anions due to a higher dehydration energy barrier (see Fig. S4 and Fig. S5). By contrast, except at the 9′ position, highly hydrophilic pore lining segments are observed in anion-selective LGICs (i.e. GlyR and GABAR at 10′, 13′ and 17′ are hydrophilic residues), which serve as a partial hydration shell around the permeating Cl⁻ ions and facilitate the permeation of Cl⁻ ion.⁴⁹

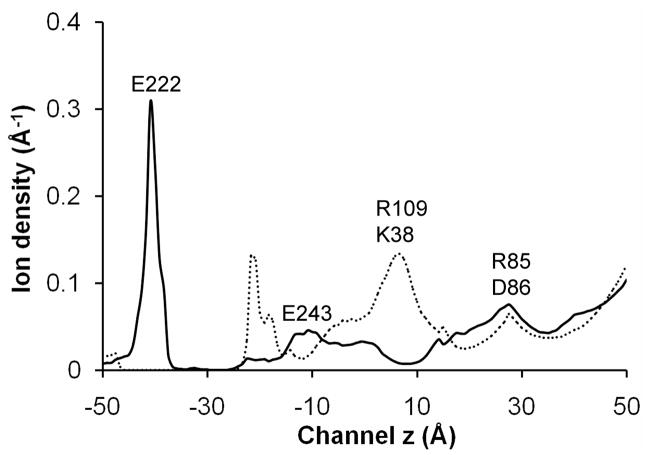
Fig. 6 shows the simulated ion density profiles for Na⁺ and Cl⁻ inside the channel pore of System B. A recent BD study of ion permeation in the GLIC²² used default charges for acidic residues (at pH =7) and found that Na⁺ had a much larger concentration in the EC domains than Cl⁻. In contrast, the present simulation suggests that the Na⁺ concentration in the EC domains is much lower than that of Cl⁻ due to neutralization of several acidic residues at a lower pH value (i.e pH=4~5). For Cl⁻ ions, the strongest binding site was found to be located near R109 and K38. The binding of Cl⁻ may reduce the energy barrier for Na⁺ and thus facilitate the Na⁺ permeation. For Na⁺ ions, the strongest binding site, which can accommodate more than 1 Na⁺ ion, occurred near E222 and T226. In addition, two comparatively weaker Na⁺ binding sites were found near E243, E82 and D86.

Figure 6.

BD simulation result for the average ion density profiles for Na⁺ (black line) and Cl⁻ (dashed line) inside the channel pore at an applied external potential of −100 mV.

Bound halothane may affect the open channel stability

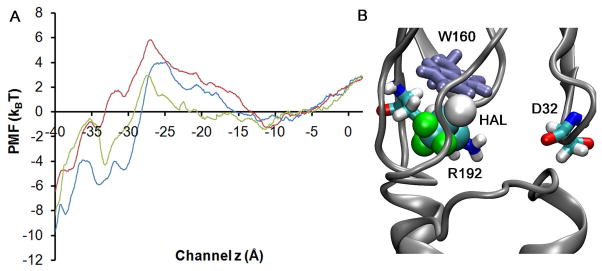
We investigated halothane binding effects on ion permeation using both MD and BD simulations. Following the same procedure as in System A, the single ion PMFs for a Na⁺ ion to transport through the TM pores of the halothane-modulated GLICs were calculated and the results presented in Fig. 7A. Due to the high degree flexibility of E222, the energy difference observed near E222 in the presence (10HAL or HAL-Near-W160 systems) versus absence of halothane was within the standard deviation of the present PMF calculations in that region. Compared to the PMF of Na⁺ ion in the System A, the energy barrier near I233 (hydrophobic gate region) was comparable in the 10HAL system, but a 2 k_BT higher energy barrier was observed in the HAL-Near-W160 system. There are several lines of MD simulation evidence that tend to suggest the existence of a higher energy barrier near I233 in the HAL-Near-W160 system. First, in the PMF calculations, the average number of waters inside the hydrophobic region (bounded by I233 and I240) was 15%~20% less in the HAL-Near-W160 system even though the initial number of water molecules was roughly the same. Second, in System A the pore radius near the most constricted hydrophobic gate I233 fluctuated around 2.6±0.5 Å when a Na⁺ ion passed through, compared to an average of 2.2±0.5 Å in the HAL-Near-W160 channel, even though at the beginning of PMF calculations, pore radii in System A and the HAL-Near-W160 system were similar.

Figure 7.

(A) comparison of the single ion PMF for transporting Na⁺ in System A (blue), 10HAL system (green), and HAL-Near-W160 (red) system. (B) Halothane binding near W160 broke salt bridges between R192 and D32.

However, our MD/BD simulations could not unambiguously distinguish the effects of halothane binding on the single channel conductance since the observed energy differences in the single-ion PMFs produce corresponding variations in single-channel conductances which are within the standard deviations of such conductance calculations. Instead, we found that the binding of halothane near W160 may affect the open channel stability. Our recent fluorescence quenching experimental study⁵⁰ confirmed halothane binding near W160 of GLIC. In our MD simulations, a bromide or chloride atom of the halothane molecule was found to interact transiently with the indole ring of W160.⁵⁰ The same halothane-binding site contains not only W160, but also D32 and R192 (see Figure 7B), whose homologous residues in the LGIC superfamily are highly conserved and have been implicated in the channel gating.⁵¹ In the crystal structures (PDB 3EAM and 3EHZ) salt-bridges of D32 and R192 were presented at all five subunits. The probability to intermittently break these salt bridges was around 30% in our control simulation and increased to 60% when halothane bound near W160. Such an increase was perhaps induced by two effects. First, in our MD simulations, halothane molecules were able to interact with residues R192 or D32. For example, we observed that halothane interacted directly with nitrogen atoms from R192 (see Fig. 7B). Such perturbations thus destabilized the salt bridges between D32 and R192 since in the absence of a halothane molecule binding here, the nitrogen atom from the side chain of R192 would form a salt-bridge with the carboxylate oxygen atom from D32. Secondly, the binding of halothane altered the local packing of the protein near D32 and R192. We observed that halothane could occupy space between (or near) D32 and R192 once the salt bridge was broken and thus made it harder to re-form a salt bridge between these two amino acids. The homologous electrostatic interaction between D32 and R192 has been implicated as critical for the open channel stability in the LGICs.² In particular, mutations that diminish the electrostatic interactions between these two homologous residues have been found to reduce the open channel stability in other LGICs. ^51,52

CONCLUSIONS

We have implemented a hybrid MD/continuum approach to estimate effective potential energy profiles acting on permeant ions in GLIC and halothane modulated GLIC. Inside the constricted transmembrane channel pore, the single ion PMF is evaluated using all-atom free energy calculations to incorporate effects of protein fluctuations and water dynamics. Outside the constricted region of the channel, energy profiles are obtained via a continuum electrostatics approach (i.e., solving Poisson’s equation). Such an implementation greatly improves computational efficiency without compromising the essential structural and dynamical features of the channel. Our simulated single channel conductance and the permeability ratio of P_Na/P_Cl in GLIC are comparable to experimental measurements.¹ This hybrid approach appears particularly suitable for the LGIC superfamily since members of LGICs all comprise a constricted TM pore connected to a large EC domain.

Our MD/BD simulations clearly demonstrate that the protonation state of E222 (near intracellular entrance) determines the ease of ion permeation through the open state of GLIC. The PMF profile with five deprotonated E222 residues in the pentamer shows a deep (multi-k_BT) energy well that may trap a Na+ ion, and that partial protonation of E222 is required for a Na⁺ ion to leave the trap. Protonating E222 in two, or more probably, three chains may partially involve into the channel opening. While we do not exclude the existence of a homologous hydrophobic gate^42,53,54 in GLIC, we suggest in addition that the E222 residue may function as an electrostatic gate, which is perhaps unique to the GLIC channel. Furthermore, our MD/BD simulations indicate that the hydrophobic gate region in the cation-selective LGICs may play an important role in determining charge selectivity due to different degrees of dehydration experienced by Na⁺ and Cl⁻ when they permeate through the constricted TM pore. The first hydration shell around a Cl⁻ ion must be partially disrupted when it transports through this region.

Since the energy differences observed in different halothane systems are well within the standard deviations of the calculations, our MD/BD analysis could not unambiguously distinguish halothane binding effects on the single channel conductance. Instead, our MD simulations suggest that halothane binding near W160 may affect the open channel stability. Halothane binding near W160 reduced the stability of salt-bridges between D32 and R192, which may inhibit the channel conductance by decreasing the open channel stability.