Abstract
Repeated Chlamydia trachomatis infections after treatment are common. One reason is reinfection from untreated partners in ongoing sexual partnerships. Mathematical models that are used to predict the impact of screening on reducing chlamydia prevalence often do not incorporate reinfection and might overestimate the expected impact. We describe a pair compartmental model that explicitly incorporates sexual partnership duration and reinfection. The pair model predicts a weaker impact of screening when compared directly with a model that does not accommodate partnerships. Effective management of sex partners to prevent reinfection might need to be strengthened in chlamydia control programs.
Repeated infections with Chlamydia trachomatis (chlamydia) after treatment are common [1, 2]. These are a potential obstacle for controlling chlamydia, the most common notifiable infection in the United States [3]. Batteiger et al used genotyping and sexual histories to show that a fraction of repeat infections among young women were reinfections from an untreated sex partner within ongoing partnerships [1]. Other reasons included infections from subsequent partners, persistent infection, and failure to receive treatment [1]. Screening to identify and treat asymptomatic cases is the intervention most often recommended to reduce chlamydia prevalence and the incidence of female complications [3]; repeated episodes of pelvic inflammatory disease increase the risk of infertility [4]. High levels of successful notification of sex partners and adherence to treatment and prevention advice might be an important component of chlamydia control strategies. In practice the contributions of screening and partner notification to chlamydia control cannot be disentangled.
Mathematical modeling is a tool for understanding the transmission and spread of infections in populations. Both individual-based [5] and compartmental models [6–9] have been used to predict the impact of chlamydia screening interventions. In published compartmental models, partnerships have not been incorporated explicitly and contacts are assumed to be instantaneous [6–9]. These models therefore cannot explore the role of partner notification as part of the screening strategy [10]. It is often assumed that omitting this feature does not matter, because adding partner notification would result in an even greater decrease in predicted prevalence [8]. However, if contacts are instantaneous, reinfection within partnerships cannot occur.
The objective of this study was to explore the specific role of chlamydial reinfection in ongoing partnerships in an intervention that includes both screening and partner notification. To allow direct comparison with a model that assumes instantaneous partnerships, we developed a pair compartmental model, which explicitly incorporates ongoing partnerships. Both models were calibrated to the same baseline prevalence by changing the transmission parameter, so the number of new cases per unit of time was the same in both. We then compared the impact of different screening and partner notification strategies.
METHODS
Description of the Models
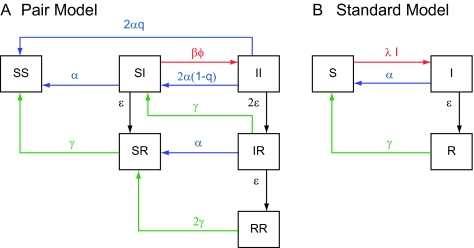
The pair model was based on work by Kretzschmar and Dietz [11] to study human immunodeficiency virus infection in men who have sex with men. We adapted the model for heterosexual contacts among young adults and incorporated a susceptible-infected-recovered-susceptible (SIRS) structure (Figure 1A; Appendix). In the model, transmission can only occur in a pair of a susceptible and an infected individual (SI). Every partnership starts with an episode of unprotected sexual intercourse with subsequent unprotected contacts once a week (ϕ), consistent with published data [12]. This allows the duration of partnerships in the model to be compared with those in empirical studies that define the start of partnerships with a sex act.
Figure 1.
Schematic overview of the chlamydia infection process in a pair model that allows for reinfection in ongoing partnerships (A) and in a standard model in which partnerships are instantaneous and reinfection is not incorporated (B). In the pair model, a compartment consists of a pair of 2 individuals which can be susceptible (S), infected (I), or recovered (R). The pair formation process is independent of the infection process and is therefore not shown in this figure. Transmission can only occur in a pair including a susceptible and an infected individual (SI) with rate βϕ (β denotes the transmission probability per sex act and ϕ the frequency of sex acts, indicated in red). After chlamydial infection, an individual can clear the infection naturally (with rate ε per year, indicated in black). After natural clearance, an individual is immune for a duration of 1/γ years (indicated in green). An individual can also be screened and treated (with rate α per year) and can notify his or her partner with probability q (indicated in blue). The partner always accepts treatment. After treatment no immunity is assumed. In the standard model, the transmission parameter λ is a combination of the number of new partners per year and the transmission probability per partnership.
The duration of the infectious period (1/ε) of chlamydia is assumed to be 1 year. This takes into account that most infections are asymptomatic and persist for >1 year [13, 14] but some infections are shorter because symptomatic individuals visit health services and are treated. We assumed a short period of immunity after clearance (1/γ = 3 months) [13].
Every individual can receive screening (at rate α per year) using a test with perfect sensitivity. Everyone with a positive test accepts treatment, which is always effective. After treatment no immunity is assumed [6]. The current partner of an infected individual can be notified with probability q, where the partner always accepts treatment. Partner notification is defined as the successful search and treatment of the current partner and adherence to a period of abstinence until infection has cleared.
We assumed that individuals have on average 1.5 new partners per year [8] and that 70% of persons are in a partnership at any time, based on published data [12]. This corresponds to a pair formation rate (ρ) of 5.0/year and an average duration of a partnership (1/σ) of 0.47 years. We assumed a baseline chlamydia prevalence of 3.5% (the average among 15–24-years-olds in Regan et al [8]) and adjusted the transmission probability (β) to achieve this, resulting in a transmission probability per sex act of 0.10. We assumed all parameters to be the same for males and females (a sensitivity analysis on this assumption was made). In the model, with prevalence at 3.5%, the percentage of women repeatedly infected (a subsequent infection from the same or another partner) 12 months after treatment was 16.2%.
We compared the pair model with a standard SIRS model with instantaneous partnerships; reinfection within the same partnership cannot occur and partner notification cannot be explored (Figure 1B; Appendix). The durations of immunity and the infectious period are the same in both models. The transmission parameter (λ) is obtained by also assuming 3.5% preintervention steady state prevalence and 1.5 new partners per year, which gives a transmission probability per partnership of 0.70 [15]. In both models the number of new infections per unit of time (incidence) is the same. The number of people screened per year is therefore the same in both models.
Analyses
We implemented screening for 5 years. We estimated the impact of screening and partner notification from the preintervention steady state prevalence in the pair model and the impact of screening alone in the standard model. We calculated the difference between the predicted relative reduction in chlamydia prevalence in the standard model and in the pair model at different levels of partner notification. We then estimated the level of successful partner notification that is necessary in a model with reinfection to achieve the same reduction in prevalence as in the model without reinfection; we call this the point of equality. Finally, we examine the effect of changing the duration of immunity after natural clearance on the point of equality for a fixed screening rate of 0.2/year. A sensitivity analysis of other parameter values was also conducted (Appendix).
RESULTS
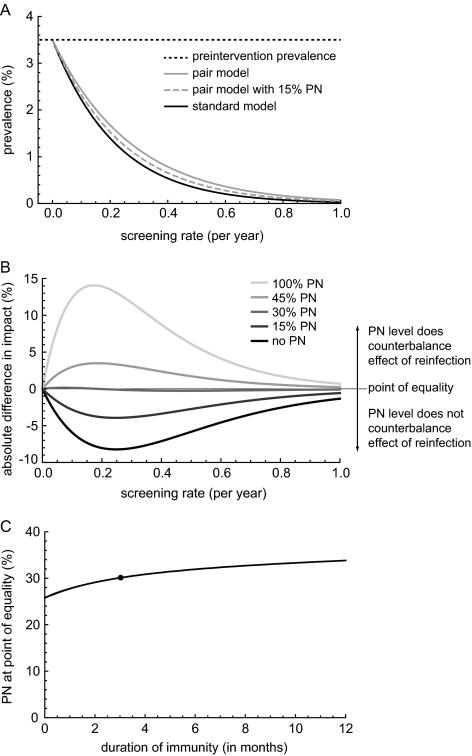
For a given screening rate, the decline in chlamydia prevalence after 5 years is more pronounced in a model with instantaneous partnerships in which reinfection cannot occur (standard model) compared with the pair model that allows for reinfection (Figure 2A). Partner notification increases the impact of the intervention in the pair model because reinfection of treated cases from infected partners in ongoing partnerships is prevented, but this does not necessarily result in a greater impact of screening than the standard model (Figure 2A).
Figure 2.
Impact of screening men and women for 5 consecutive years on chlamydia prevalence. A, Chlamydia prevalence in a pair model that allows for reinfection in the absence (gray line) or presence of partner notification (PN) (gray dashed line) and in the standard model (black line). B, Difference in the estimated relative impact of screening of the 2 models in the absence of PN (black line) and in the presence of different levels of PN (gray lines; lighter gray indicates higher levels of PN). The straight black line shows the point of equality, the level of PN needed in the pair model that allows for reinfection to estimate the same impact of screening as the standard model. C, Point of equality for different assumptions of the duration of immunity after natural clearance of chlamydia for a screening rate of 0.2/year. For all levels of immunity, the transmission probability per sex act (pair model) and the transmission parameter (standard model) is calibrated to a 3.5% baseline prevalence. The scenario used in A and B is indicated with a black dot.
The biggest difference in predicted impact between the 2 models is observed for screening rates between 0.1 and 0.4 per year (Figure 2B). As the screening rate increases, the impact of partner notification becomes less apparent. With no partner notification (Figure 2B), the peak difference in the impact of screening between the models is 8.2% at a screening rate of 0.25/year. This corresponds to a population where each individual is screened on average every 4 years. With increasing partner notification, the impact of screening in the pair model comes close to estimates from the standard model; the point of equality occurs when ∼30% of current partners are successfully notified (Figure 2B). At higher partner notification levels, the impact of screening is greater in the pair model than in the standard model.
We explored the way in which the duration of immunity after natural clearance affects the level of partner notification at the point of equality (Figure 2C). When no immunity is assumed in either model, a lower level of partner notification is needed to reach the point of equality. The longer the duration of immunity after natural clearance, the more partner notification is needed to counterbalance the effect of reinfection after screening.
We performed a sensitivity analysis of the point of equality for other parameters in all plausible ranges (Appendix). Under the ranges investigated, the model with reinfection always estimates a less pronounced impact of screening than the standard model, and the level of partner notification at the point of equality can differ between 4% and 39%. When only 1 sex is screened the magnitude of the difference between the models is similar, with the peak screening rate shifted toward higher levels and a slightly lower point of equality. Increasing the duration of screening from 5 to 20 years resulted in a peak difference between the 2 models shifted to lower screening rates and a slightly lower point of equality.
DISCUSSION
This study shows that, when reinfection by the current partner after screening and treatment for chlamydia is taken into account in a pair model, the impact of screening on reducing chlamydia prevalence is less pronounced than in a standard model that allows only for instantaneous partnerships and in which reinfection cannot happen. Even when partner notification is included in a screening strategy in the pair model, the impact on chlamydia prevalence can be less than that of screening alone in a standard model. This indicates that it is not valid to state that the predictions from a standard model of chlamydia transmission are conservative [8, 10]; in some cases such estimates can even be optimistic. This study supports the theoretical proposal that partnerships should be incorporated explicitly in mathematical models that assume that partner notification is part of a strategy for controlling chlamydia transmission [10].
This modeling study is intended to be illustrative rather than predictive so that we could focus specifically on the role of reinfection. We therefore made several simplifying assumptions. Age structure was not included. Homogeneous mixing is assumed, but we hypothesize that if a certain fraction of the population has higher partner change rates and shorter partnerships, these individuals would have a higher probability of repeated infection, and this would make notification of current partners less effective. We also assumed men and women to be the same; shortening the duration of the infectious period in men resulted in an even higher point of equality. We did not consider persistent infection because we assumed 100% treatment efficacy. The repeat infection rate in the pair model was, however, consistent with published studies [2]. For all other parameters, within the ranges studied, the pair model always estimates a less pronounced impact of screening compared with the standard model (Appendix).
There is ongoing discussion about the role of immunity in chlamydial infections [6]. We show that when immunity after natural clearance exists, more partner notification is needed to counterbalance the effect of reinfection; to achieve the same baseline steady state prevalence, the transmission probability per sex act in a model with immunity must be higher than in a model without immunity, if all other parameters are assumed equal. The probability of reinfection after screening is therefore higher in a model with immunity, and more partner notification is needed to counterbalance this. If immunity also exists after screening and treatment, less reinfection will occur after screening and lower partner notification levels are needed.
The absolute difference in the impact of screening on chlamydia prevalence between the 2 models was modest. In a large population, however, this can translate into a large number of episodes of reinfection within ongoing partnerships. Excluding reinfections from a standard model might therefore improve cost-effectiveness in favor of screening, particularly because the risk of infertility increases with each subsequent episode of pelvic inflammatory disease [4].
Our results have implications for the design of chlamydia control strategies. We found that, in a model with reinfection, ∼30% of current sex partners need to be notified to counterbalance the effect of reinfection. Although this sounds modest, it requires full compliance with identifying and informing a sex partner, treatment to be given and taken, and abstinence from sexual intercourse until infection has cleared. Continuing high chlamydia prevalence, even after regular repeated screening, early treatment, and partner notification efforts, suggests that this is difficult to achieve in practice [1]. Additional empirical studies should seek to improve partner notification effectiveness in practice, and additional modeling efforts should focus on understanding the most promising partner notification strategies. Our study suggests that effective management of sex partners to prevent reinfection might need to be strengthened in chlamydia control programs.
Financial support: Swiss National Science Foundation (grants 320030_118424 and PDFMP3_124952 to J.C.M.H. and S.A.H.); UK National Institute for Health Research (NIHR) Health Technology Assessment program (project 07/42/02 to C.L.A.). The views and opinions in this article are those of the authors and do not necessarily reflect those of the funders.
APPENDIX.
Description of the Model
We have developed a pair model with a SIRS structure. The model explicitly describes the formation of pairs (P) and the dissolution of pairs into singles (X) [16]. The model stratifies the population by sex with the labels f and m describing females and males, respectively. The male and female populations are assumed to be of equal size; thus, Nf = Nm. The infection states of the model are susceptible (S), infected (I), and recovered (R).
In the notation of singles, the first subscript defines the sex of the single, and the second subscript defines the infection state. In the notation of pairs, the first subscript defines the state of infection of the female and the second subscript defines the state of infection of the male. Thus PSI is a pair with an uninfected female and an infected male, while PIS is a pair with an infected female and an uninfected male. The distinction between PSI and PIS is only important when different screening rates are assumed for females and males, or when there are sex differences in the behavioral or infection parameters. For the modeling results and Figure 1 described in the main text, we assume that all parameters are the same in both sexes. However, we performed a sensitivity analyses in this appendix in which we screen only 1 sex.
Every infected individual can be screened at a rate α per year (with αf being the screening rate for females and αm that for males). When an individual is screened, the partner can be notified with a probability q. A person can clear the infection naturally with rate ε (with 1/εf being the duration of the infectious period for females and 1/εm that for males). After natural clearance a period of immunity (1/γ) is assumed. Pairs are formed with a pair formation rate ρ per year and separate with rate σ per year. The separation rate can be calculated as the average per capita number of new partners per year divided by the percentage of people in a partnership. The pair formation rate can be calculated as the average per capita number of new partners per year divided by the percentage of persons who are single. Transmission can occur only in partnerships, with ϕ being the number of sex acts per week, and β being the transmission probability per sex act. Every partnership starts with a single sexual contact by assuming that, on formation of a partnership between a susceptible and an infected individual, they become a pair of infected individuals with probability β, and they remain a pair of an infected and a susceptible individual with probability 1 – β until the next sex act [16].
The SIRS pair model is described by the following set of differential equations:
 |
The number of singles is given as X = Xf + Xm = Xf,S + Xf,I + Xf,R + Xm,S + Xm,I + Xm,R, and the total population size can be expressed as N = Xf + Xm + 2(PSS + PSI + PSR + PIS + PII + PIR + PRS + PRI + PRR).
The differential equations of the standard SIRS is described by the following set of differential equations:
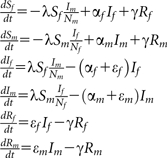 |
The transmission parameter (λ) is a combination of the transmission probability per partnership times the number of new partners per year. The transmission parameter is adjusted to obtain the same baseline prevalence as in the pair model.
Sensitivity Analyses
In the main text we showed that in a model that allows for reinfection, a substantial amount of successful partner notification is needed to estimate the same impact of screening as in a standard model that does not allow for reinfection (point of equality). In the sensitivity analyses, we explore the point of equality for all parameters used in all plausible parameter ranges. Because the point of equality is hardly affected by the screening rate (Figure 2B), the sensitivity analyses is performed for a screening rate of 0.2/year.
For all parameters ranges examined, we adjust the transmission parameter (β and λ) to obtain a baseline steady-state preintervention prevalence of 3.5%. We only explored the parameter ranges for which we could obtain a transmission probability β between 0 and 1.
In the main text it is shown that when no immunity is assumed in the model, the point of equality is at its lowest (Figure 2C). Therefore, and for simplicity, some parts of the analyses are done using a model without immunity after natural clearance (SIS model). Figures showing the results of the sensitivity analyses are available from the authors on request.
Duration of Infectious Period.
If the duration of the infectious period is varied between 0.5 and 2 years in a SIS model, the level of partner notification at the point of equality decreases from 32.4% to 17.3%. Thus, with increasing duration of the infectious period, less partner notification is needed to counterbalance the effect of reinfection. This is because increasing the infectious period results in a lower transmission rate per sex act, which results in lower reinfection rates. Therefore, less partner notification is needed to reach the point of equality.
We also explored a scenario in which men have a shorter infectious period than women. Shortening the duration of the infectious period in men to half a year and keeping the infectious period of women 1 year resulted in a higher level of partner notification at the point of equality (37.0%).
Behavioral Parameters.
We explored the effect of changing both the percentage of people in a partnership from 10% to 90% and the new number of partnerships per year from 1 partner up to 4 partners per year at steady state in a SIS model. Within the ranges explored, the level of partner notification at point of equality varies between 4.3% and 39.3%. The number of new partners per year influences the estimates more than the percentage of people in a partnership. A higher number of new partnerships per year will automatically result in shorter partnership durations. As a consequence, both models predict almost the same impact of screening, and little partner notification is needed to reach the point of equality. When the new number of partners per year is low, and the percentage of people in a partnership increases, the duration of the partnerships will automatically increase, and the differences between both models become more apparent. As a consequence, more partner notification is needed to estimate the same impact of screening in the pair model that allows for reinfection compared with a standard model.
Transmission Parameters.
In all analyses so far, we kept the baseline preintervention steady-state prevalence at 3.5%. Therefore, we also explored the effect of a different baseline prevalence on the point of equality in a SIS model. For every value of the baseline prevalence studied (0.5%–15%), we adjusted the transmission parameter β and λ. In the pair model, this can also be seen as keeping β constant but changing the frequency of sex acts between once every 7.3 and 0.6 days. For a baseline prevalence of 0.5%, the level of partner notification at the point of equality is 30.3%, and this steadily decreases to a level of 9.1% when the baseline prevalence is increased to 15%. With increasing baseline prevalence, it becomes more likely that both partners are infected, and hence partner notification becomes more efficient. Therefore, less partner notification is needed to achieve the same impact of screening without reinfection.
Screening.
We also explored the results of screening only 1 sex for 5 consecutive years. In general, when only 1 sex is screened, the impact of screening is less compared with when both sexes are screened. The magnitude of the difference in the predicted impact of screening between the model that assumes instantaneous partnership and the pair model is more or less similar as when both sexes are screened (Figure 2B). However, the peak difference between the models is shifted toward higher screening strategies. The partner notification at point of equality is slightly lower (26.5%) than when both sexes are screened.
In the main text, screening is implemented for 5 consecutive years. Increasing the duration of screening from 5 to 20 years resulted in a peak difference between the 2 models shifted toward lower screening rates and a slightly lower partner notification level at the point of equality (23.9%).
References
- 1.Batteiger BE, Tu W, Ofner S, et al. Repeated Chlamydia trachomatis genital infections in adolescent women. J Infect Dis. 2010;201:42–51. doi: 10.1086/648734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Scott LaMontagne D, Baster K, Emmett L, et al. Incidence and reinfection rates of genital chlamydial infection among women aged 16-24 years attending general practice, family planning and genitourinary medicine clinics in England: a prospective cohort study by the Chlamydia Recall Study Advisory Group. Sex Transm Infect. 2007;83:292–303. doi: 10.1136/sti.2006.022053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.US Preventive Services Task Force. Ann Intern Med. Screening for chlamydial infection: U.S. Preventive Services Task Force recommendation statement. 2007; 147: 128–34. [DOI] [PubMed] [Google Scholar]
- 4.Westrom L, Joesoef R, Reynolds G, Hagdu A, Thompson SE. Pelvic inflammatory disease and fertility: a cohort study of 1, 844 women with laparoscopically verified disease and 657 control women with normal laparoscopic results. Sex Transm Dis. 1992;19:185–92. [PubMed] [Google Scholar]
- 5.Kretzschmar M, Turner KM, Barton PM, Edmunds WJ, Low N. Predicting the population impact of chlamydia screening programmes: comparative mathematical modelling study. Sex Transm Infect. 2009;85:359–66. doi: 10.1136/sti.2009.036251. [DOI] [PubMed] [Google Scholar]
- 6.Brunham RC, Pourbohloul B, Mak S, White R, Rekart ML. The unexpected impact of a Chlamydia trachomatis infection control program on susceptibility to reinfection. J Infect Dis. 2005;192:1836–44. doi: 10.1086/497341. [DOI] [PubMed] [Google Scholar]
- 7.Gift TL, Gaydos CA, Kent CK, et al. The program cost and cost-effectiveness of screening men for chlamydia to prevent pelvic inflammatory disease in women. Sex Transm Dis. 2008;35:S66–75. doi: 10.1097/OLQ.0b013e31818b64ac. [DOI] [PubMed] [Google Scholar]
- 8.Regan DG, Wilson DP, Hocking JS. Coverage is the key for effective screening of Chlamydia trachomatis in Australia. J Infect Dis. 2008;198:349–58. doi: 10.1086/589883. [DOI] [PubMed] [Google Scholar]
- 9.Sharomi O, Gumel AB. Re-infection-induced backward bifurcation in the transmission dynamics of Chlamydia trachomatis. J Math Anal Appl. 2009;356:96–118. [Google Scholar]
- 10.Low N, Heijne JC, Kretzschmar M. Use of mathematical modeling to inform chlamydia screening policy decisions. J Infect Dis. 2009;199:767–8. doi: 10.1086/596744. [DOI] [PubMed] [Google Scholar]
- 11.Kretzschmar M, Dietz K. The effect of pair formation and variable infectivity on the spread of an infection without recovery. Math Biosci. 1998;148:83–113. doi: 10.1016/s0025-5564(97)10008-6. [DOI] [PubMed] [Google Scholar]
- 12.Johnson AM, Mercer CH, Erens B, et al. Sexual behaviour in Britain: partnerships, practices, and HIV risk behaviours. Lancet. 2001;358:1835–42. doi: 10.1016/S0140-6736(01)06883-0. [DOI] [PubMed] [Google Scholar]
- 13.Althaus CL, Heijne JCM, Roellin A, Low N. Transmission dynamics of Chlamydia trachomatis affect the impact of screening programmes. Epidemics. 2010;2:123–31. doi: 10.1016/j.epidem.2010.04.002. [DOI] [PubMed] [Google Scholar]
- 14.Molano M, Meijer CJ, Weiderpass E, et al. The natural course of Chlamydia trachomatis infection in asymptomatic Colombian women: a 5-year follow-up study. J Infect Dis. 2005;191:907–16. doi: 10.1086/428287. [DOI] [PubMed] [Google Scholar]
- 15.Quinn TC, Gaydos C, Shepherd M, et al. Epidemiologic and microbiologic correlates of Chlamydia trachomatis infection in sexual partnerships. JAMA. 1996;276:1737–42. [PubMed] [Google Scholar]
- 16.Kretzschmar M, Dietz K. The effect of pair formation and variable infectivity on the 367 spread of an infection without recovery. Math Biosci. 1998;148(1):83–113. doi: 10.1016/s0025-5564(97)10008-6. [DOI] [PubMed] [Google Scholar]