Abstract
Stimulation efficiency is an important consideration in the stimulation parameters of implantable neural stimulators. The objective of this study was to analyze the effects of waveform shape and duration on the charge, power, and energy efficiency of neural stimulation. Using a population model of mammalian axons and in vivo experiments on cat sciatic nerve, we analyzed the stimulation efficiency of four waveform shapes: square, rising exponential, decaying exponential, and rising ramp. No waveform was simultaneously energy-, charge-, and power-optimal, and differences in efficiency among waveform shapes varied with pulse width (PW) For short PWs (≤ 0.1 ms), square waveforms were no less energy-efficient than exponential waveforms, and the most charge-efficient shape was the ramp. For long PWs (≥0.5 ms), the square was the least energy-efficient and charge-efficient shape, but across most PWs, the square was the most power-efficient shape. Rising exponentials provided no practical gains in efficiency over the other shapes, and our results refute previous claims that the rising exponential is the energy-optimal shape. An improved understanding of how stimulation parameters affect stimulation efficiency will help improve the design and programming of implantable stimulators to minimize tissue damage and extend battery life.
Keywords: Charge efficiency, computational modeling, energy efficiency, implantable stimulators, power efficiency
I. Introduction
Implantable neural stimulators assist thousands of individuals with neurological disorders. The stimulation parameters of these devices are selected and programmed by physicians to treat the target condition and to minimize side effects. However, it is also important to consider the impact of stimulus parameter selection on the efficiency of stimulation. The charge delivered during a stimulus pulse (charge efficiency) contributes to the risk of tissue damage [1], [2]; the instantaneous power of a stimulus pulse (power efficiency) is important since the maximum power that can be delivered is directly proportional to the size of the battery; and the energy consumed per stimulus pulse (energy efficiency) determines the lifetime of battery-powered implanted pulse generators, which, when depleted, must be replaced through an expensive and invasive procedure. We analyzed the effects of waveform shape and duration on the charge, power, and energy efficiency of neural stimulation using computational modeling and in vivo measurements.
Stimulation efficiency is dependent on the duration (pulse width; PW) and shape of the stimulus waveform. Analysis of the strength-duration relationship for rectangular waveforms as defined by Lapicque [3] or Weiss [4] shows that shorter PWs result in greater charge efficiency, longer PWs result in greater power efficiency, and PW equal to chronaxie optimizes energy efficiency [5]. Similar conclusions regarding the relationships between PW and efficiency have been reached experimentally [6], [7]. The effects of waveform shape on stimulation efficiency have also been examined previously. In computational models of an unmyelinated Hodgkin–Huxley fiber, a rectangular waveform was more charge-efficient than waveforms that resembled postsynaptic potentials, and the energy-duration curves varied with waveform shape [8]. A recent study using a computational model of a myelinated mammalian axon concluded that each waveform shape produced unique energy-duration and charge-duration curves, demonstrating that waveform shape greatly influences stimulation efficiency [9].
One waveform shape in particular—the rising exponential—has been found to be energy-optimal. Offner [10] determined analytically that to reach threshold during neural stimulation, the waveform shape that generated the least amount of heat, i.e., required the least amount of energy, was the rising exponential. Using analytical and numerical optimization techniques, Kajimoto et al. [11], [12] also concluded that a rising exponential was the energy-optimal waveform shape, and Fishler [13] and Jezernik and Morari [14] reached the same conclusion. However, the rising exponential may not be energy-optimal because optimality was determined using a linear (passive) model of the membrane. The passive model is useful for estimating subthreshold behavior, but ignores many important traits of excitable cells, including accommodation—the increase in the threshold voltage during extended subthreshold stimulation. When models with nonlinear (active) membrane conductances are considered, the rising exponential may not be energy-optimal and may be inefficient in terms of power and charge. Therefore, we reanalyzed the efficiency of the rising exponential using nonlinear models and in vivo measurements.
There were two goals for this study: 1) to test the hypothesis that the rising exponential waveform is energy-optimal for electrical stimulation of nerve fibers, and 2) to improve the understanding of the effects of waveform shape and duration on stimulation efficiency. Using computational models of mammalian myelinated axons as well as experiments on cat sciatic nerve, we measured the energy efficiency, charge efficiency, and power efficiency for rising exponential, decaying exponential, linearly rising (ramp), and rectangular (square) waveforms. The results refute the hypothesis that the rising exponential waveform is energy-optimal. As well, no single waveform was simultaneously energy-, charge-, and power-optimal. These results will help guide the design and programming of stimulators that can deliver more efficient stimulation.
II. Methods
A. Stimulation Waveforms
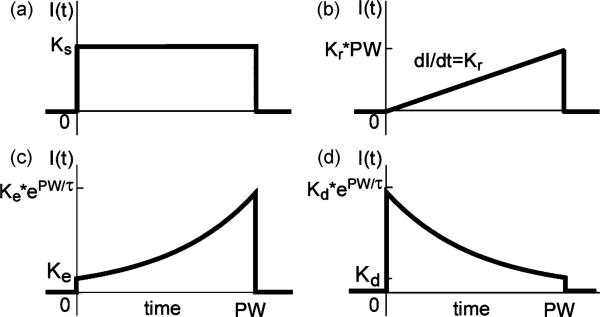
Four different waveform shapes were analyzed: rectangular (square), rising ramp, rising exponential, and decaying exponential. For all shapes, stimulation was applied at t = 0 and turned off at t = pulse width (PW). The equation for the stimulus current with the square waveform was
| (1) |
where Ks is the current amplitude, t is time, and u(t) is the unit step function [Fig. 1(a)]. The equation for the stimulus current of the ramp was
| (2) |
where Kr is the slope of the ramp [Fig. 1(b)]. The equation for the rising exponential waveform, as described by Fishler [13] and Jezernik and Morari [14], was
| (3) |
where VTHR is the transmembrane voltage threshold, gm is the specific membrane conductance, cm is the specific membrane capacitance, and the time constant τ is equal to cm/gm. Equation (3) assumes that VTHR and gm are constants, and Jezernik and Morari [14] used cm = 2 μF/cm2 and gm = 30.4 mS/cm2 [15], resulting in τ = 65.8 μs. However, these assumptions are inaccurate because gm (and thereby τ) depends strongly on the dynamics of the ion channels, which vary with time and transmembrane voltage (Vm), and VTHR depends strongly on pulse duration [16]. Since and VTHR and gm could not be determined a priori at every instant in the present computational simulations or experiments, (3) could not be applied, and the variables were lumped together into constants to produce a new equation
| (4) |
The constant Ke in the equation was the amplitude of the stimulus current at t = 0 [Fig. 1(c)]. To examine the sensitivity of the stimulation efficiency to τ, we tested five different values of τ—32.9 μs, 65.8 μs, 132 μs, 263 μs, and 526 μs.
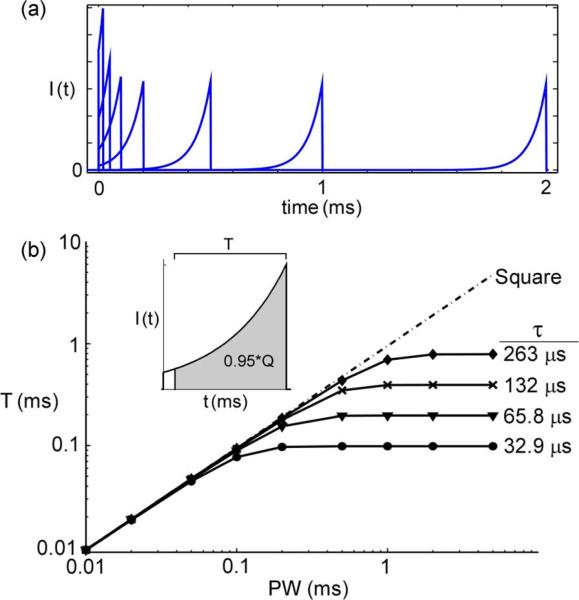
Fig. 1.
Stimulation waveform shapes. (a) Square waveform. (b) Rising ramp waveform. (c) Rising exponential waveform. (d) Decaying exponential waveform. Values of K were varied to adjust amplitude of stimulation, and values of τ were varied to alter the shape of exponential waveforms.
Decaying exponential waveforms are delivered by thousands of currently-used implanted stimulators [17]. These waveforms are described by
| (5) |
where the constant Kd was the amplitude of the stimulus current at t = PW, and we tested decaying exponential waveforms with τ = 132 μs, 263 μs, and 526 μs [Fig. 1(d)].
B. Measures of Efficiency
The different waveform shapes were compared using three measures of efficiency: maximum instantaneous power required (power efficiency), charge delivered (charge efficiency), and energy consumed (energy efficiency) to reach threshold. The instantaneous power across any electrical component, P(t), is
| (6) |
where I is the current through the component and V is the voltage across the component. In the computational models, we used the quasi-static approximation [18], and peak power (Ppeak) was reached when the current amplitude was at its peak. In the in vivo experiments, Ppeak was determined for each stimulus pulse by measuring the current through and the voltage across the working and return electrodes, multiplying the two waveforms, and determining the maximum of the product.
In the computational models and in vivo, the amount of charge delivered during a stimulus pulse was determined by integrating the current waveform over time
| (7) |
The energy in a stimulus pulse was determined by integrating the power of the stimulus waveform over time
| (8) |
In the computational models, the power was proportional to I2(t)
| (9) |
In the in vivo experiments, E was determined by measuring both and I(t) and V(t) during stimulation and integrating their product.
C. Computational Models
We conducted computational simulations of extracellular stimulation of a population of myelinated axons. All simulations were run in NEURON [19] with a time step of 0.001 ms using Backward-Euler integration. The axons were modeled with the MRG model, which represented a myelinated mammalian peripheral axon as a double cable model with a finite impedance myelin sheath and explicit representation of the nodes of Ranvier, paranodal sections, and internodal segments [20]. Axons (diameter = 11.5 μm) were randomly and uniformly distributed within a 3-mm-diameter cylinder and were aligned parallel to the cylinder's axis. Monophasic cathodic stimulation was delivered through a point current source located at the center of the cylinder with extracellular conductivity of 300 Ω – cm [15]. To simulate extracellular stimulation, the potentials generated by the source along the length of each axon were calculated and were applied to the outside of the axon.
The input-output properties generated by each of the waveform shapes were compared across a wide range of PWs (0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, and 5 ms) through the following procedure. First, for each PW that was tested, 10 individual populations of 100 axons with varying nodal positions were generated. Next, for each waveform shape, recruitment (input–output) curves were constructed for each of the 10 populations by stimulating with increasing amplitude [i.e., incrementing K in (1), (2), (4), and (5)] until all 100 axons in the population were activated. At each increment, E, Q, and Ppeak were calculated, and the number of activated axons was recorded. These data were used to construct three recruitment curves: an E recruitment curve (i.e., number of axons activated versus E), a Q recruitment curve, and a Ppeak recruitment curve. From these recruitment curves, the values of E, Q, and Ppeak required to activate 25%, 50%, and 75% of each population were calculated, and the means and standard errors of these values across the 10 populations were computed.
A single fiber model (MRG axon, 11.5-μm diameter) was used to analyze the effects of waveform shape on membrane gating parameters. The electrode was positioned 1 mm directly above the center node of Ranvier, and extracellular stimulation was delivered using each waveform shape across a wide range of PWs at threshold amplitude. Parameters were analyzed at the node beneath the electrode and included Vm , the gating variables of the sodium channel (m, h, and m3 h), and the sodium current density (iNa).
D. In Vivo Experiments
Surgical Preparation
All animal care and experimental procedures were approved by the Institutional Animal Care and Use Committees of Duke University and were followed according to The Guide to the Care and Use of Laboratory Animals, 1996 Edition, National Research Council. Experiments were performed on adult cats (n = 6). Sedation was induced with acepromazine (Vedco Inc., 0.3 mg/kg; S.Q.), and anesthesia was induced with ketamine HCl (Ketaset 35 mg/kg; I.M.) and maintained during the experiment with α-chloralose (Sigma-Aldrich, Inc., initial 65 mg/kg supplemented at 15 mg/kg; I.V.). The cat was intubated, and respiration was controlled to maintain end tidal CO2 at 3%–4%. Core temperature was monitored and maintained at ~ 39°C. Fluid levels were maintained with saline solution and lactated ringers delivered through the cephalic vein (15 ml/kg/h, I.V.). Blood pressure was monitored using a catheter inserted into the carotid artery.
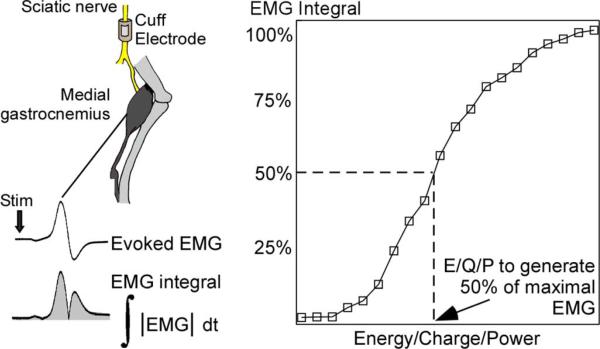
The sciatic nerve was accessed via an incision on the medial surface of the upper hindlimb. A monopolar cuff electrode, composed of a platinum contact embedded in a silicone substrate, was placed around the nerve and secured with a suture around the outside of the electrode. The return electrode was a subcutaneous needle. Two stainless steel wire electrodes were inserted into the medial gastrocnemius muscle to measure the electromyogram (EMG) evoked by stimulation of the sciatic nerve. The evoked EMG signal was amplified, filtered (1–3000 Hz), recorded at 500 kHz, rectified, and integrated to quantify the response (EMG integral) (Fig. 2).
Fig. 2.
In vivo stimulation of cat sciatic nerve. Stimulation was delivered to the sciatic nerve, and evoked electromyogram (EMG) was recorded from the medial gastrocnemius. EMG was rectified and integrated (EMG integral) to quantify the evoked response. Recruitment curves were generated for each waveform shape at each PW and were generated by measuring the EMG integral over a wide range of stimulation amplitudes. For each recruitment curve the energy, charge, and peak power required to activate 50% of the maximal EMG integral was recorded.
Stimulation and recording were controlled using Labview (DAQ: PCI-MIO-16E-1) (National Instruments, Austin, TX). Voltage-regulated stimulation was delivered at a rate of 1 Msamples/s to a linear voltage-to-current converter (bp isolator, FHC, Bowdoin, ME or 2200 Analog Stimulus Isolator, A-M Systems, Inc., Sequim, WA) and delivered through the cuff electrode. The voltage across and current through the cuff electrode and return electrode were amplified (SR560, Stanford Research Systems, Sunnyvale, CA) and recorded (fsample = 500 kHz).
Input–Output Curves
Recruitment curves of the EMG integral as a function of stimulation amplitude were measured for every combination of waveform shape and PW in two sets of experiments. In the first set (n = 3), the square, rising ramp, and rising exponential waveforms (τ = 32.9, 65.8, 132, and 263 μs) were tested for PW = 0.01–2 ms. In the second set (n = 3) the square, rising exponential (τ = 132, 263, and 526 μs), and decaying exponential waveforms (τ = 132, 263, and 526 μs) were tested for PW = 0.02–1 ms. In both sets, stimulation was delivered as single (stimulation frequency <1.4 Hz) monophasic cathodic pulses, and the order in which the combinations were presented was randomized. E, Q, and Ppeak recruitment curves were generated using a similar method as in the computational models: stimulus amplitude was incremented, three stimulation pulses were delivered at each increment, and the average values of E, Q, Ppeak, and EMG integral were recorded. Periodically during each experiment, we stimulated with the square waveform at a fixed PW to monitor shifts in threshold, and the values of E, Q, and Ppeak were scaled to account for these shifts. Changes in threshold over the course of an experiment were never greater than 37% of the initial threshold. From each recruitment curve, the values of E, Q, and Ppeak required to generate 50% of the maximal EMG were calculated (Fig. 2), and the minima of these values across PWs for the square waveform were set as baseline values. Subsequently, all values of E, Q, and Ppeak from within an experiment were normalized to their respective baseline value, and the means and standard errors across the experiments were calculated.
After log-transformation of the data, the effects of waveform shape on each measure of efficiency were analyzed. The two sets of experiments were compared to one another by examining the results for stimulation with parameters that were used in both sets: square and rising exponential waveforms (τ = 132 and 263 μs) for PWs = 0.02–1 ms. We performed an ANOVA for each measure of efficiency with E, Q, or Ppeak as the dependent variable and waveform shape, PW, and experimental set as the independent variables. The outcome of the ANOVAs revealed that experimental set had no significant effect on the results, and the interactions between experimental set and the other independent variables were not significant (p > 0.29). Therefore, data from both sets were combined for plots of in vivo measurements, but each set was analyzed separately to permit analysis using repeated measures ANOVA. A two-way repeated measures ANOVA was performed for each measure of efficiency; the dependent variable was E, Q, or Ppeak, and the independent variables were waveform shape, PW (within-subjects factors), and cat (subject). Where interactions between waveform shape and PW were found to be significant (p < 0.05), the data were subdivided by PW for one-way repeated measures ANOVA. Again, the dependent variable was E, Q, or Ppeak, and the independent variables were waveform shape (within-subjects facgtor) and cat (subject). For tests which revealed significant differences among waveforms (p < 0.05), post hoc analyses were performed using Fisher's protected least significant difference (FPLSD). Although data were log-transformed for analysis, data were plotted as average percent difference with respect to the square waveform.
III. Results
A. Computational Simulations
In the model of excitation of a population of myelinated nerve fibers, trends in the relationships between the measures of efficiency and the duration (PW) and shape of the waveform were consistent for activation of 25%, 50%, and 75% of the axons in the population, and results for 50%-activation are presented. Also, the same trends were observed for activation of a single axon with the electrode positioned 1 mm above the center node. In addition, the energy-, charge-, and power-efficiencies of the decaying exponential waveforms differed from those of the rising exponentials with corresponding τ (132, 263, and 526 μs) by less than 5.4%. Accordingly, the differences in stimulation efficiency with the square and ramp waveforms were approximately the same for both the rising and decaying waveforms.
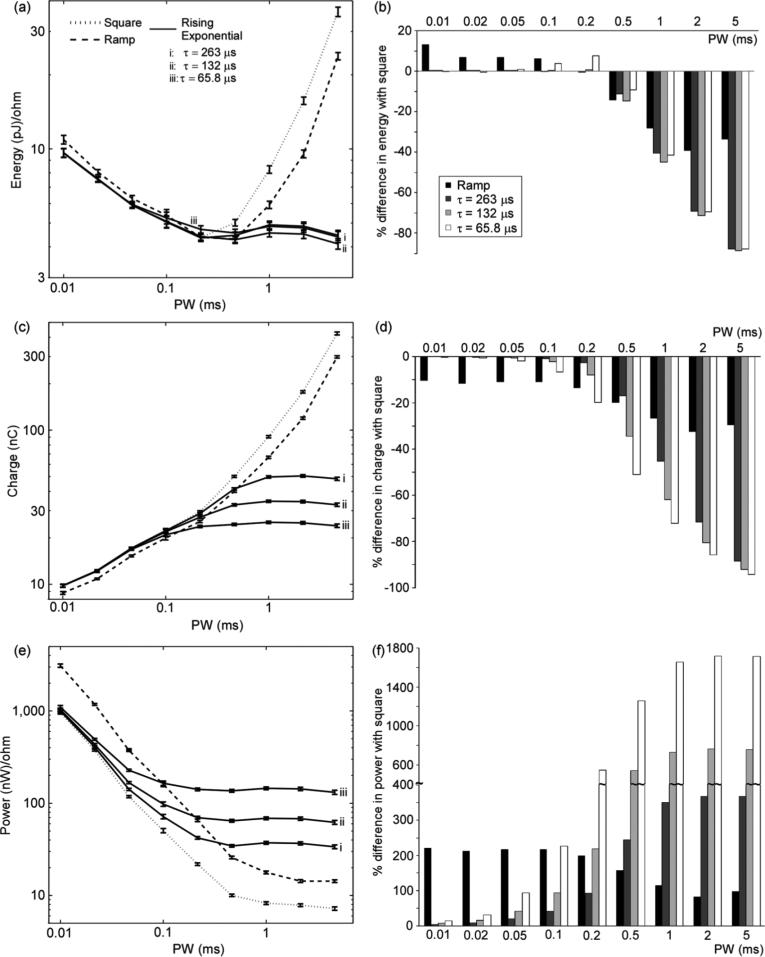
No waveform shape was energy-optimal across all PWs, but rather, the differences in energy efficiency among waveform shapes varied with PW. In contrast to previous predictions that the rising exponential waveform was energy-optimal across all PWs, the square waveform was at least as energy-efficient as the rising exponential waveforms for PW ≤ 0.2 ms [Fig. 3(a) and (b)]. However, the rising exponential waveforms were more energy-efficient than the square waveform for all but one combination of PW and τ for PW ≥ 0.5 ms. At long PWs, while E increased with PW for the square and ramp waveforms, the energy-duration curve for the exponential waveforms leveled off [Fig. 3(a)], and the exponential waveforms were substantially more energy-efficient than the square and ramp waveforms for PW ≥ 2 ms. Even though the energy-duration curves of both the square and ramp waveforms were concave up, the two waveform shapes were not equally energy-efficient. For PW ≤ 0.1 ms the square waveform was more energy-efficient than the ramp waveform, but for PW ≤ 0.5 ms the ramp waveform was more energy-efficient [Fig. 3(b)].
Fig. 3.
Energy, charge, and power efficiency in computational model of a population of 100 myelinated axons. (a) Energy-duration curves, (c) charge-duration curves, and (e) power-duration curves for activation of 50% of the axons in populations of randomly-positioned axons (mean +/- SE;n = 10). (b), (d), (f) Percent difference in E, Q, and Ppeak, respectively, between square waveform and other waveform shapes (mean; SEs were negligible). Rising exponentials with τ = 32.9 and 526 μs followed the same trends as exponential waveforms shown in these plots. Decaying exponential waveforms had approximately the same stimulation efficiency as rising exponentials with equivalent τ (ΔE < 5.4%, ΔQ < 3.7%, ΔPpeak < 5.4%).
As with energy efficiency, the differences in charge efficiency among waveform shapes were dependent on PW, and no waveform shape was charge-optimal across all PWs. For PW ≤ 0.05 ms, the rising and decaying exponential waveforms were about as charge-efficient as the square waveform [Fig. 3(d)]. However, as PW increased the exponential waveforms became increasingly more charge-efficient than the square and ramp waveforms. While the charge-duration curves of both the square and ramp waveforms increased monotonically, the charge-duration curves of the exponential waveforms leveled off at long PWs; both the Q and the PW at which the charge-duration curves leveled off were directly proportional to τ [Fig. 3(c)]. Further, the ramp waveform was more charge-efficient than the square waveform for all PWs, and for PW ≤ 0.02 ms, ramp waveform was the most charge-efficient waveform shape.
Although none of the waveform shapes was energy-optimal or charge-optimal across all PWs, the square waveform was power-optimal. The power-duration curves for all waveform shapes resembled typical strength-duration curves: Ppeak decreased monotonically as PW increased for short PWs and leveled off at long PWs [Fig. 3(e)]. However, the power-duration curves of the rising and decaying exponential waveforms leveled off at shorter PWs than those of the square and ramp waveforms. As a result, although the differences in power efficiency between square and the exponential waveforms were small at short PWs, the differences increased as PW increased [Fig. 3(f)]. On the log-scale, the power-duration curves of the square and ramp waveforms were approximately parallel, i.e., the percent-difference in power efficiency between the square and ramp waveforms was roughly constant across PWs.
B. In Vivo Measurements
Trends in the relationships between the measures of efficiency and PW/waveform shape were consistent for generation of 25%, 50%, and 75% of the maximum EMG responses, and only the results for generation of 50% of the maximum EMG are presented. Two-way repeated measures ANOVA for each measure of efficiency revealed significant interactions between PW and waveform shape (p < 0.0001). Thus, in each set the data were subdivided by PW and analyzed using one-way repeated measures ANOVA for each PW.
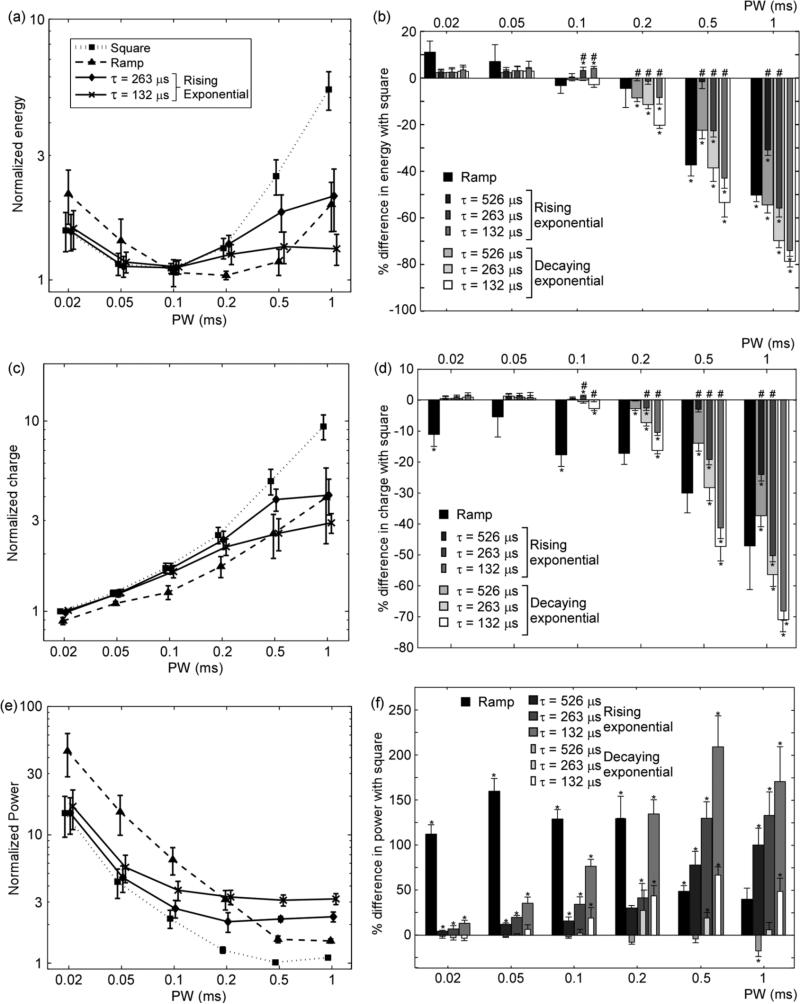
As in the computational simulations, energy efficiency varied with waveform shape and did not vary monotonically with PW. The energy-duration curves were similar to those generated in the computational model: for the square and ramp waveforms, the energy-duration curves were concave up, whereas for the exponential waveforms, E decreased with PW for short PW and did not change substatially for long PW [Fig. 4(a)]. For PW ≥ 0.1 ms, none of the waveform shapes were significantly more energy-efficient than the square waveform (repeated measures ANOVA, p > 0.05; or FPLSD, p > 0.07) [Fig. 4(b)]. However, for PW ≥ 0.5 ms the square waveform was significantly less energy-efficient than all other waveforms shapes (FPLSD; p < 0.05) for all but one combination of waveform shape and PW. One noticeable difference between the computational simulations and the experimental measurements was the difference in energy efficiency between the rising and decaying exponential waveforms with the same τ. Whereas in the simulations these differences were not substantial, the experimental results showed that the decaying exponentials were significantly more energy-efficient (<35%; FPLSD; p < 0.05) for PW ≥ 0.1 ms for most combinations of τ and PW.
Fig. 4.
Energy, charge, and power efficiency of stimulation of cat sciatic nerve. (a) Energy-duration curves, (c) charge-duration curves, and (e) power-duration curves for generation of 50% of the maximal EMG (mean +/- SE) for ramp (n = 3), square (n = 6), and rising exponential waveforms (n = 6). (b), (d), (f) Percent difference in E, Q, and Ppeak, respectively, between square waveform and other waveform shapes (mean + SE). Bars for rising and decaying exponentials with the same are superposed. Rising exponentials with τ = 32.9 and 65.8 μs followed the same trends as exponential waveforms shown in these plots. Data were analyzed as logarithmic differences using repeated measures ANOVA and post hoc Fisher's protected least significant difference test for each PW when appropriate (* p < 0.05 difference with square waveform; # p < 0.05 difference between rising and decaying exponentials with the same when τ). Decaying exponentials were significantly more power-efficient than rising exponentials with the same PWs (p < 0.05) except for τ = 263 μs at PW = 0.2 ms.
As in the computational simulations, charge-duration curves increased monotonically with PW for the square and ramp waveforms, as well as for the exponential waveforms for short PWs [Fig. 4(c)]. For PW ≥ 0.01 ms, the square waveform was generally less charge-efficient than the other waveform shapes [Fig. 4(d)]. For PW ≤ 0.02 ms, the ramp waveform was more charge-efficient than the square waveform (FPLSD; p < 0.05), but as PW increased, the exponential waveforms were generally the most charge-efficient waveform shapes. As for energy efficiency, the measurements of charge efficiency showed significant differences between the rising and decaying exponential waveforms. Specifically, for PW ≥ 0.1 ms the decaying exponential was significantly more charge-efficient (< 18%; FPLSD; p < 0.05) for most combinations of τ and PW. Thus, just as in the computational model, no waveform shape was charge-optimal across PWs.
For all waveform shapes, Ppeak decreased monotonically with PW for short PWs and leveled off for long PWs [Fig. 4(e)], as was observed in the computational simulations. For PW ≤ 0.5 ms, the ramp waveform was significantly less power-efficient than the square (FPLSD; p < 0.05), but for PW > 1 ms there were no significant differences between the two waveforms (FPLSD; p > 0.01) [Fig. 4(f)]. The square waveform was generally more power-efficient than the other waveform shapes across all PWs. However, the decaying exponential with τ = 526 μs was never significantly less power-efficient than the square waveform (FPLSD; p > 0.46), and in contrast to the computational simulations the decaying exponential was more power-efficient than the square waveform for PW = 1 ms (FPLSD; p < 0.04). Also contradicting the computational simulations, the decaying exponential waveforms were significantly more power-efficient than the rising exponential waveforms (< 59%; FPLSD; p < 0.05) across all PWs for all but one combination of PW and τ.
C. Exponential Waveforms at Long PWs
Both the computational models and in vivo results indicated that for long PWs the exponential waveforms—both rising and decaying—were much more energy- and charge-efficient and much less power-efficient than the square and ramp waveforms. However, at long PWs the efficiencies of the exponential waveforms had plateaued. To determine the cause of this behavior, rising exponential waveforms were plotted with PW between 0.02 and 2 ms and amplitude equal to threshold in the single axon model [Fig. 5(a)]. For short PWs, the shape of the exponential waveforms varied with PW, but for longer PWs, the shapes of the waveforms were insensitive to PW. While the length of the initial segment increased with PW, because of its very low amplitude this had no effect on excitation, and the main part of the exponential waveform remained the same as PW increased, thus eliciting the same neuronal response. The shape of the decaying exponentials behaved similarly as PW increased, with the length of the final segment increasing with no effect on the neuronal response.
Fig. 5.
Exponential waveforms were not unique at long PWs.(a) Rising exponential waveforms at threshold amplitude in single axon model. (b) Time from end of pulse required to deliver the last 95% of charge (T) for rising exponential waveforms and square waveform.
We approximated the PW at which rising exponential waveforms ceased to change by calculating the time required to deliver the last 95% (i.e., all but the first 5%) of the charge [Fig. 5(b)]
| (10) |
For a given PW and τ, T also calculated the time required to deliver the first 95% of the charge for decaying exponentials. After a certain PW (PWE) T leveled off, indicating that the exponential waveforms delivered almost all of their charge within the same amount of time, and beyond PWE the shapes of the exponential waveforms were no longer unique. PWE was directly proportional to τ, and exponential waveforms with shorter τ had a shorter range of PW over which they were unique in shape.
IV. Discussion
Computational simulations and in vivo experiments were used to quantify the energy, charge, and power efficiencies of square, ramp, rising exponential, and decaying exponential waveforms for extracellular stimulation. Contrary to previous studies that used passive membrane models, our results showed that rising exponential waveforms were not always more energy-efficient than the square waveform. For stimulation with short PWs (< 0.05 ms), there was little difference in efficiency between the square and the exponential waveforms, while the ramp was the least energy-efficient (computational model only), most charge-efficient, and least power-efficient waveform. For long PWs (≥0.5 ms), the square waveform was more power-efficient than most waveform shapes but was less charge- and energy-efficient. No waveform was simultaneously energy-, charge-, and power-optimal. Consistent with previous studies, the measures of efficiency were dependent on PW: all waveform shapes were charge-optimal at short PWs, power-optimal at long PWs, and energy-optimal at intermediate PWs.
A. Comparison of Waveform Shapes
Rising exponential waveforms did not provide any practical gains in efficiency over the other waveform shapes. Previously with a passive model of the membrane, rising exponential waveforms at any PW were predicted to be more energy-efficient than any other waveform shape with equivalent PW, and the difference in energy efficiency with the square waveform was predicted to increase with PW [14]. In contrast, the current results show that for short PWs the energy efficiency of the rising exponential was less than or not significantly different from the energy efficiency of the square, and for long PWs the difference in energy efficiency (<100%) was less than previously predicted (300%–1400%). In addition, for short PWs the charge and power efficiencies of the rising exponential waveforms were less than or not significantly different from those of the square waveform. For long PWs the rising exponential waveforms appeared to be much more energy- and charge-efficient than the square and ramp waveforms. However, these results were misleading because for long PWs the rising exponential waveforms did not change as PW increased (Fig. 5). Further, in the experimental measurements the decaying exponential waveforms were generally more energy-, charge-, and power-efficient when compared to rising exponentials with the same τ. Although only five values of τ were tested in this study, the results give no indication that there would be any values τ of that would substantially improve the energy, charge, or power efficiencies of the rising exponential waveforms.
The energy required by the circuitry of the stimulator should be considered to assess accurately the energy efficiency in an implantable device. Certain waveform shapes may require additional circuitry for their generation, which would consume additional energy. As a result, the most energy-efficient waveform shapes may turn out to be those that can be generated with the simplest circuits. For example, certain stimulators and pacemakers deliver stimulation using a discharging capacitor, a very energy-efficient process, and the stimulation waveforms resemble decaying exponentials. Therefore, the decaying exponentials may be highly energy-efficient in actual implantable devices, despite exhibiting the same limited range of unique PWs as the rising exponentials.
The charge and energy efficiencies of many different stimulation waveform shapes, including the shapes analyzed in the present study, were determined previously [9] in a computational model of a single mammalian axon [21]. The present study extended this approach to a population model composed of mammalian myelinated axons that more accurately reproduced the excitation properties of mammalian axons [20] than the previous model. As well, we measured stimulation waveform efficiencies in vivo. Both the previous and current results showed that Q increased monotonically with PW for short to intermediate PWs for all waveforms, the square waveform was the least charge-efficient waveform of the waveforms tested, and energy-duration curves for the ramp and square waveforms were concave up.
Unlike in the population model, the diameters of peripheral nerves and nerve fibers are nonuniform, and the conductivity of the extracellular medium is inhomogeneous and anisotropic [22]. To determine the sensitivity of the results to these parameters, we conducted additional simulations in the population model and varied the fiber diameter (5.7 μ, and 16 μm) and the diameter of the cylinder (6 mm). As well, we also modeled anisotropic extracellular conductivity (σparallel to fibers = 10 * σperpendicular to fibers) using a coordinate transformation [23]. Thresholds were sensitive to changes in these model parameters, and as a result, the absolute values of energy, charge, and power efficiencies varied. Although there were slight changes in the relative differences in efficiency among waveform shapes, which may explain the disparities between the computational and experimental models, the overall conclusions were unchanged. These alterations to the population model primarily influenced the spatial effects of stimulation: the positions of the nodes of Ranvier relative to the electrode, the dimensions of the fibers, and the spatial distribution of extracellular potential. On the other hand, waveform shape varied the temporal effects of stimulation, i.e., the dynamics of membrane ion channels. Thus, it was not surprising that varying the geometric properties had little effect on the influence of waveform shape on stimulation efficiency.
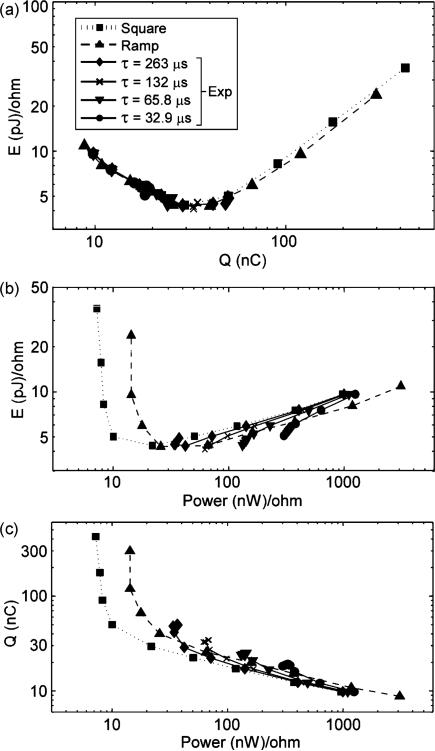
Even though stimulus waveforms are traditionally characterized by PW, PW, may not be the most appropriate parameter by which to group waveforms of different shapes for comparison. For example, the exponential waveforms were only unique over a limited range of PW, and comparing the square and ramp waveforms to exponentials at long PWs produced misleading results. An alternative method of comparing the stimulation efficiency of waveform shapes is to use the measures of efficiency as the bases of comparison. Fig. 6 shows plots of E versus Q, E versus P, and Q versus P from the population model, and this presentation provides a clearer perspective on the efficiencies across waveforms. While charge efficiency and energy efficiency varied greatly with waveform shape when compared across PW, the curves of E versus Q for all shapes overlapped substantially. The data from the rising exponentials at long PWs are represented by overlapping points, illustrating that these stimuli have the same stimulation effect. Regardless of whether a square, ramp, or exponential waveform was used, for a given amount of charge, the energy delivered was equivalent. Although the curves of E versus Q for different waveform shapes overlapped, the curves of E versus P and Q versus P did not. Thus, the analysis of stimulation efficiency of waveform shapes is dependent on the method of comparison.
Fig. 6.
Comparison of waveform shapes by efficiency rather than PW. (a) E versus Q. (b) E versus Ppeak. (c) Q versus Ppeak. Data represent means across 10 trials for activation of 50% of axons in a computational model of a population of 100 myelinated axons. Decaying exponential waveforms had approximately the same stimulation efficiency as rising exponentials with equivalent τ (difference <5.4%).
B. Different Paths to Activation
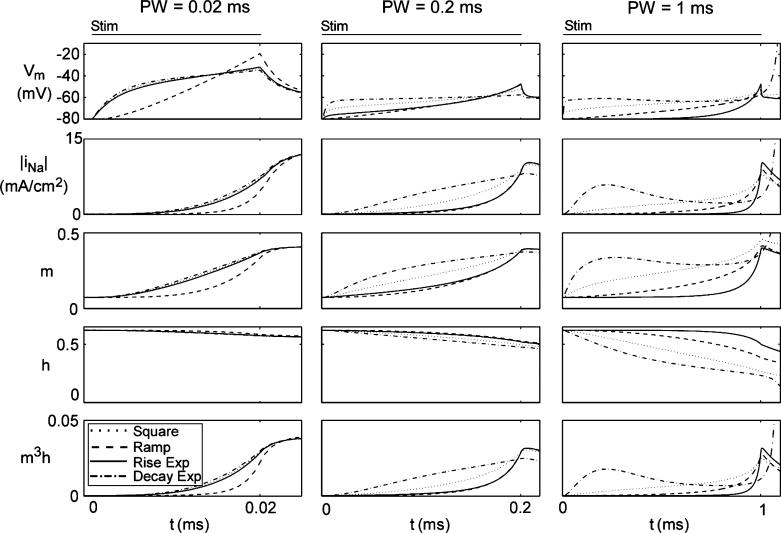
Previous claims that the rising exponential was the energy-optimal waveform shape were based upon models with fixed threshold voltages (VTHR). The assumption of a fixed VTHR is inaccurate because it fails to account for the dynamics of the ion channels, which are dependent on the stimulus waveform. For example, subthreshold stimulation for an extended duration will inactivate the sodium channels and increase VTHR [24]. We measured membrane parameters (Vm, sodium current density [INa], and sodium gating parameters [m, h]) in the single fiber model during stimulation with different waveforms. The rates at which the membrane parameters changed varied with both PW and waveform shape, as did the threshold (i.e., at the end of the pulse) values of these parameters (Fig. 7). Instead of a fixed threshold voltage, there was a wide range of threshold states, which were defined by varying levels of Vm, m, and h.
Fig. 7.
Comparison of membrane parameters during stimulation in single axon model. τ = 263 μs for exponential waveforms.
The activity of the membrane parameters during stimulation did not explain what made one waveform shape more energy-, charge-, or power-efficient than another. Different stimulus waveforms change the values of the membrane parameters at different rates, taking different paths to reach a threshold state (Fig. 7). Further, two different waveforms can have much different effects on the membrane parameters and still have similar stimulation efficiencies. For example, the rising and decaying exponentials changed the membrane parameters at much different rates for both PW = 0.2 and 1 ms (Fig. 7). Yet, their energy, charge, and power efficiencies differed by less than 5.4%. Thus, it does not appear that the stimulation efficiency of a stimulating waveform can be predicted by its effects on the membrane parameters.
C. Clinical Implications
Although the current study examined stimulation efficiency in peripheral nerves, the results may also be applicable to the stimulation of other parts of the nervous system. During spinal cord stimulation, the targets of stimulation are long axons, and the current findings would likely be relevant. As well, our results would be valid for muscular stimulation, where the targets of stimulation are motor nerve axons, not the muscle itself. The current results may also be relevant for stimulation of the brain because in both cortical stimulation [25] and deep brain stimulation [26], the targets of stimulation are thought to be axons.
Clinical stimulation typically uses biphasic waveforms, and in an efficiency-analysis of biphasic waveforms E, Q, and Ppeak of both pulses would have to be calculated. In addition, the threshold of the primary pulse can be affected by the charge recovery pulse [27], and it is unclear if changes in threshold are dependent on the waveform shape of the primary pulse. Further study is needed to analyze how waveform shape affects the stimulation efficiency of biphasic waveforms. Nonetheless, the current results are still important for understanding the effects of and waveform shape on stimulation efficiency.
Stimulation efficiency should be a major consideration in the design and programming of implantable stimulators. Energy efficiency is important to minimize the costs and risks associated with battery replacement surgery; charge efficiency is important to minimize tissue damage and electrode corrosion; and power efficiency is important to limit battery size. Most often, implantable stimulators deliver square waveforms or decaying exponential waveforms [17]. Alternative waveform shapes should also be considered since they may be more energy-, charge-, or power-efficient. When programming the stimulation parameters, clinicians should consider the stimulation efficiency alongside clinical efficacy. Although clinicians have no control over waveform shape, they still program the amplitude, PW, and frequency of stimulation. Most clinicians choose stimulation parameters based only on how well symptoms are alleviated and side effects are controlled. However, physicians may not be wise simply to set stimulation parameters based on these two criteria if only minimal benefit is gained at the cost of large increases in energy consumption or charge delivery. Unfortunately, the optimal stimulation parameters may not be obvious since no waveform was simultaneously energy-, charge-, and power-optimal, and there was no overall optimal PW. As suggested by Dean and Lawrence [28], the selection of stimulation parameters could be guided by a cost function. Expanding upon their idea, we suggest that a cost function could be used that considers the measures of efficiency, therapeutic benefit of stimulation, and side effects.
Acknowledgment
The authors would like to thank P. B. Yoo and G. Mills for assistance with the experimental work, and A. M. Kuncel and X. F. Wei for valuable insight on stimulation waveforms generated by implantable neural stimulators.
This work was supported in part by a Graduate Fellowship sponsored by the Medtronic Foundation, in part by the National Institutes of Health (R01NS040894 and R01NS050514), and in part by the National Science Foundation Graduate Research Fellowship Program.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
References
- 1.Yuen TG, Agnew WF, Bullara LA, Jacques S, McCreery DB. Histological evaluation of neural damage from electrical stimulation: Considerations for the selection of parameters for clinical application. Neurosurgery. 1981 Sep.9(3):292–299. [PubMed] [Google Scholar]
- 2.McCreery DB, Agnew WF, Yuen TG, Bullara L. Charge density and charge per phase as cofactors in neural injury induced by electrical stimulation. IEEE Trans. Biomed. Eng. 1990 Oct.37(10):996–1001. doi: 10.1109/10.102812. [DOI] [PubMed] [Google Scholar]
- 3.Lapicque L. Recherches quantitatives sur l'excitation electrique des nerfs traitee comme une polarisation. J. Physiol., Paris. 1907;9:622–635. [Google Scholar]
- 4.Weiss G. Sur la possibilite de rendre comparables entre eux les appareils servant a l'excitation electrique. Arch. Ital. Biol. 1901;35:413–446. [Google Scholar]
- 5.Kroll MW. A minimal model of the monophasic defibrillation pulse. Pacing Clin. Electrophysiol. 1993 Apr.16(4)(pt. 1):769–777. doi: 10.1111/j.1540-8159.1993.tb01657.x. [DOI] [PubMed] [Google Scholar]
- 6.Mortimer JT, Shealy CN, Wheeler C. Experimental nondestructive electrical stimulation of the brain and spinal cord. J. Neurosurg. 1970 May;32(5):553–559. doi: 10.3171/jns.1970.32.5.0553. [DOI] [PubMed] [Google Scholar]
- 7.Crago PE, Peckham PH, Mortimer JT, Van der Meulen JP. The choice of pulse duration for chronic electrical stimulation via surface, nerve, and intramuscular electrodes. Ann. Biomed. Eng. 1974 Sep.2(3):252–264. doi: 10.1007/BF02368496. [DOI] [PubMed] [Google Scholar]
- 8.Dimitrova NA, Dimitrov GV. Effect of stimulus (postsynaptic current) shape on fibre excitation. Gen. Physiol. Biophys. 1992 Feb.11(1):69–83. [PubMed] [Google Scholar]
- 9.Sahin M, Tie Y. Non-rectangular waveforms for neural stimulation with practical electrodes. J. Neural Eng. 2007 Sep.3(3):227–233. doi: 10.1088/1741-2560/4/3/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Offner F. Stimulation with minimum power. J. Neurophysiol. 1946 Sep.9:387–390. doi: 10.1152/jn.1946.9.5.387. [DOI] [PubMed] [Google Scholar]
- 11.Kajimoto H, Kawakami N, Tachi S. Optimal design method for selective nerve stimulation and its application to electrocutaneous display. Proc. 10th Symp. Haptic Interfaces Virtual Envir. Teleoperator Syst. 2002:303–310. [Google Scholar]
- 12.Kajimoto H, Kawakami N, Tachi S. Optimal design method for selective nerve stimulation. Electron. Commun. Jpn. 2004;87(9)(pt. 3):62–72. [Google Scholar]
- 13.Fishler MG. Theoretical predictions of the optimal monophasic and biphasic defibrillation waveshapes. IEEE Trans. Biomed. Eng. 2000 Jan.47(1):59–67. doi: 10.1109/10.817620. [DOI] [PubMed] [Google Scholar]
- 14.Jezernik S, Morari M. Energy-optimal electrical excitation of nerve fibers. IEEE Trans. Biomed. Eng. 2005 Apr.52(4):740–743. doi: 10.1109/TBME.2005.844050. [DOI] [PubMed] [Google Scholar]
- 15.McNeal DR. Analysis of a model for excitation of myelinated nerve. IEEE Trans. Biomed. Eng. 1976 Jul.23(4):329–337. doi: 10.1109/tbme.1976.324593. [DOI] [PubMed] [Google Scholar]
- 16.Warman EN, Grill WM, Durand D. Modeling the effects of electric fields on nerve fibers: Determination of excitation thresholds. IEEE Trans. Biomed. Eng. 1992 Dec.39(12):1244–1254. doi: 10.1109/10.184700. [DOI] [PubMed] [Google Scholar]
- 17.Butson CR, McIntyre CC. Differences among implanted pulse generator waveforms cause variations in the neural response to deep brain stimulation. Clin. Neurophysiol. 2007 Aug.118(8):1889–1894. doi: 10.1016/j.clinph.2007.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bossetti CA, Birdno MJ, Grill WM. Analysis of the quasi-static approximation for calculating potentials generated by neural stimulation. J. Neural Eng. 2008 Mar.5(1):44–53. doi: 10.1088/1741-2560/5/1/005. [DOI] [PubMed] [Google Scholar]
- 19.Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997 Aug.915(6):1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- 20.McIntyre CC, Richardson AG, Grill WM. Modeling the excitability of mammalian nerve fibers: Influence of afterpotentials on the recovery cycle. J. Neurophysiol. 2002 Feb.87(2):995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- 21.Sweeney JD, Mortimer JD, Durand D. Modeling of mammalian myelinated nerve for functional neuromuscular stimulation. Proc. IEEE 9th Annu. Conf. EMBS. 1987:1577–1578. [Google Scholar]
- 22.Geddes LA, Baker LE. The specific resistance of biological material—A compendium of data for the biomedical engineer and physiologist. Med. Biol. Eng. 1967 May;5(3):271–293. doi: 10.1007/BF02474537. [DOI] [PubMed] [Google Scholar]
- 23.Nicholson PV. Experimental models for current conduction in an anisotropic medium. IEEE Trans. Biomed. Eng. 1967;14(1):55–56. [Google Scholar]
- 24.Grill WM, Mortimer JT. Stimulus waveforms for selective neural stimulation. IEEE Eng. Med. Biol. Mag. 1995 Jul./Aug.14(4):375–385. [Google Scholar]
- 25.Nowak LG, Bullier J. Axons, but not cell bodies, are activated by electrical stimulation in cortical gray matter. I. Evidence from chronaxie measurements. Exp. Brain Res. 1998 Feb.118(4):477–488. doi: 10.1007/s002210050304. [DOI] [PubMed] [Google Scholar]
- 26.McIntyre CC, Grill WM. Excitation of central nervous system neurons by nonuniform electric fields. Biophys. J. 1999 Feb.76(2):878–888. doi: 10.1016/S0006-3495(99)77251-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.van den Honert C, Mortimer JT. The response of the myelinated nerve fiber to short duration biphasic stimulating currents. Ann. Biomed. Eng. 1979;7(2):117–125. doi: 10.1007/BF02363130. [DOI] [PubMed] [Google Scholar]
- 28.Dean D, Lawrence PD. Optimization of neural stimuli based upon a variable threshold potential. IEEE Trans. Biomed. Eng. 1985 Jan.32(1):8–14. doi: 10.1109/TBME.1985.325644. [DOI] [PubMed] [Google Scholar]