SERIAL NONRIGID VASCULAR REGISTRATION USING WEIGHTED NORMALIZED MUTUAL INFORMATION

Abstract

Vascular registration is a challenging problem with many potential applications. However, registering vessels accurately is difficult as they often occupy a small portion of the image and their relative motion/deformation is swamped by the displacements seen in large organs such as the heart and the liver. Our registration method uses a vessel detection algorithm to generate a vesselness image (probability of having a vessel at any given voxel) which is used to construct a weighting factor that is used to modify the intensity metric to give preference to vascular structures while maintaining the larger context. Therefore, our proposing method uses fully data-driven calculated weights and needs no prior knowledge for the weight calculation. We applied our method to the registration of serial MRI lamb images obtained from studies on tissue engineered vascular grafts and demonstrate encouraging performance as compared to non-weighted registration methods.

1. INTRODUCTION

Vascular registration is a critical problem in the quantitative analysis of serial images of vascular structures. It could be used to detect (via a secondary examination of the growth patterns from the displacement fields), for example, progressive stenosis in coronary artery disease and vascular growth in angiogenesis. Our target application is the quantification of the growth of tissue engineered vascular grafts within the context of congenital heart disease. Congenital heart disease (CHD) remains a leading cause of death in the newborn period. The development of tissue engineered vascular grafts is an important potential treatment for this; however there is a need for the non-invasive methods for the quantification of vascular growth over time in these tissue engineered grafts. While in principle, for example, vascular segmentation techniques could be used to measure graft volume, the definition of the exact location of the ends of the graft (i.e. where it is sutured to the native vessels) is difficult and can significantly bias the results. Our approach to this problem relies on (i) computing a non-rigid registration between the initial and subsequent time points using the method described in this paper, (ii) approximately defining the location of the graft at time point 1 and (iii) quantifying vascular growth using the integral of the determinant of the Jacobian of the transformation over the region of the graft, normalized by an equivalent measure in the nearby pulmonary arteries which is used to account for animal growth and hydration state. In this paper we focus on the non-rigid registration part of this work.

Our early attempts to attack this problem used an implementation of the work of Rueckert et al. [1]. However, the vessels of interest (the tissue engineered graft and the pulmonary artery), constitute only a small part of the image and the mutual information metric is swamped by larger structures such as the heart and the liver. To overcome this problem, we develop a spatially-weighted mutual information approach which gives higher weight to the vascular structures without requiring any prior knowledge. The weights are defined automatically using a measures of vesselness [7] which improves upon earlier work by Frangi et al. [2].

There is some work in the literature on vascular registration [12, 13]. The authors use the centerlines of presegmented vessels as part of the registration process and hence the method is critically depended on having an accurate segmentation. Penney et al.[14] perform vascular intermodal registration using the vessel probability maps directly; we note however that this work focuses on only rigid registration. Our work also relates to other previous efforts use variable spatial weighting for registration, dating back to the early optical flow work of Anandan [3] which used confidence measures for the estimation of the local weights and the work of Amini et al. [4] in cardiac deformation. This type of idea was later used within the context of non-rigid registration, e.g. [5]. An alternative approach is to compute a more-local as opposed to global metric (e.g. the work of Likar et al. [6]) defining local probabilities as a weighted combination of the probability distribution of a subimage and the global distribution. Our works differs from these approaches in that we use a spatial weight based on the significance of the underlying structure as computed using the vesselness measure. This weighting is imposed at the computation of the joint histogram itself after which we use a global unmodified mutual information metric [9].

2. METHOD

Our method consists of two steps, as shown in Fig. 1. Given two images from the same subject (animal) at different time points, we first calculate the vesselness map for each image using our recently published method [7] which improves upon earlier work by Frangi et al. [2]. Next the vesselness maps are used as weights in a weighted-NMI FFD registration method that builds upon earlier work by Rueckert [1, 11].

Fig. 1.

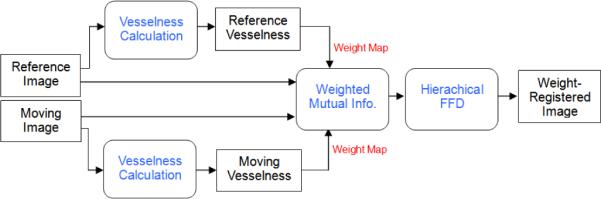
Block diagram for weighted registration using vesselness.

2.1. Weighted nonrigid registration using mutual information

Since its introduction[8] mutual information (MI) has been widely used for medical image registration. We use the normalized mutual information variant of this metric [9], which takes the form:

$$d(I_R,T\left(I_M\right))=(H\left(I_R\right)+H\left(T\left(I_M\right)\right))∕H(I_R,T\left(I_M\right))$$ (1)

where I_R and I_M are the two images, T is the (current estimate of the) transformation and H() is the image intensity entropy. All three entropy measures are computed based on the joint-histogram of the two images. In computing the joint histogram Ω(i, j) we introduce a weight term W (x) to yield the expression:

$$\Omega (i,j)=\sum _{\mathbf{x}\in V}W\left(\mathbf{x}\right)\times \delta (I_R\left(\mathbf{x}\right)=i)\times \delta (T\left(I_M\left(\mathbf{x}\right)\right)=j)$$ (2)

where x is the voxel location, V is the image volume and W(x) is the weight function. Note that if W (x) = 1 everywhere, this reduces to the conventional definition of the joint histogram. The weight function W (x) is defined as:

$$W\left(\mathbf{x}\right)=\{\begin{array}{cc}{W}_R\left(\mathbf{x}\right)\hfill & \text{if}"\text{Single}"\text{weight mode}\hfill \\ W_R\left(\mathbf{x}\right)+T\left(W_M\left(\mathbf{x}\right)\right)\hfill & \text{if}"\text{Dual}"\text{weight mode}\hfill \end{array}\phantom{\}}$$ (3)

Here, W_R(x) is a weight map depending on the reference image and T (W_M (x)) is the weight map depending on the moving image warped using the current estimate of the transformation. In “Single” weight mode we use only the reference weight image, whereas in “Dual” mode we use the sum of the two. The weight images are computed from the vesselness maps as described in the next section.

2.2. Vesselness Computation and Weight Generation

The vesselness maps are images where the intensity at each voxel corresponds to the probability of that voxel being part of a vascular structure. Our method for computing the vesselness maps has been previously published [7]. The end result of this is the vesselness image V_I(x) [2] which has range 0 to 1 and is a measure of the likelihood of having a vascular structure at location x in the image. Figure 2B is the vesselness in the region of the pulmonary artery – the original image is shown in Fig. 2A. The weight map is computed from V_I(x) as:

$$W_I\left(\mathbf{x}\right)=c_1\times (G_{\sigma }\ast V_I\left(\mathbf{x}\right))+c_2$$ (4)

Here, V_I(x) is the vesselness map for image I, G_σ is Gaussian smoothing with filter width σ, c₁ is a scaling factor and c₂ is a shift factor of intensity (× denotes multiplication and * convolution). Standard intensity based registration without weighting effectively uses c₁ = 0, c₂ = 1. In our weighted registration, we set c₁, c₂ with nonzero values in order to leverage the intensity information everywhere but weigh it more close/inside vessels. In case of “Single” weight mode we compute the overall weight by using Eq. (4) on the reference vesselness maps (i.e. the vesselness map computed from the reference image), whereas in “Dual” weight mode we compute the overall weight by using Eq. (4) on the sum of the weight images generated from the reference and moving vesselness maps.

Fig. 2.

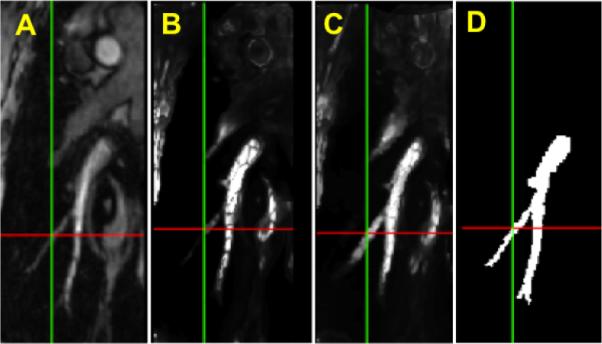
A. Original MRI image. B. Vesselness image from the reference image. C. Enhanced vesselness image by adding the reference vesselness with the registered vesselness image from the moving image. D. Manually segmentation result.

In addition to adding a degree of symmetry to the estimation, the “Dual” mode has the additional benefit of improving the effective signal-to-noise ratio of the vesselness estimator. `Single” weight mode may fail to pick up all vascular structures as shown in Fig. 2B. By using the dual weight setup, in which we utilize the vesselness of the moving image in addition to the vesselness of the reference image, we obtain a better estimate of the vesselness maps by combining the results from the two images – this combination is done dynamically during the registration using the current estimate of the transformation to warp the moving weight image to reference space. Fig. 2C shows the combined vesselness between the reference vesselness and the registered vesselness from the moving vesselness of Fig. 2A. As an aid to the comparison we show the manually segmented vessel in Fig. 2D.

3. RESULTS

We used in-vivo MRI images from a study of the growth of tissue engineered vascular grafts in a juvenile lamb model. The tissue engineered grafts were implanted as inferior vena cava (IVC) interposition grafts, i.e. they replaced part of the native IVC. The imaging protocol post surgery involved each animal being imaged bimonthly for 6 months. Magnetic resonance imaging (MRI) was performed using a Siemens Sonata 1.5 T MR Scanner. 1.5 T MRI was performed using a 3D MPRAGE acquisition with 25-cm FOV, 1.1 mm slice thickness, 128 slices, TE=3 ms, TR=24 ms, 2 averages, alpha=45°, 192×256 matrix and bandwidth=220 Hz/pixel. All images were reoriented so the IVC was parallel to the y axis of the images; the images were resampled to have dimensions 101 × 256 × 101 and isotropic voxel size equal to 0.78 mm and centered (manually) approximately on the middle of the IVC.

Data from 3 lambs and 2–3 timepoints from each lamb (a total of N=12 pairs) are used in this paper. An expert user manually segmented (painted in) the inferior vena cava (extending roughly from the heart to the liver) and one of the pulmonary arteries (PA). We use the overlaps of these segmentations for validation purposes – the manual segmentations play no role in our algorithm.

We compare 3 algorithms and note that, except for the use of the weight images, these algorithms use identical preprocessing steps, parameters and implementations (including the all-important optimization code). The first is the normal unweighted FFD NMI based method of Rueckert et al. [1] with the “fluid” extensions [11] – which is referred to as “Un-weighted”. The second method uses simply the vesselness map from the reference image to generate the weight (“Single”) whereas the final algorithm (“Dual”) uses both the reference and moving vesselness images which are added to generate the weight at each iteration using the current estimate of the transformation.

All registrations used the exact same B-Spline FFD model [1] with 5 levels (4.8mm, 2.4mm, 1.2mm, 1.2mm and 1.2mm ) and respective control point spacings (24mm, 12mm, 6mm, 6mm, 6mm) at each level. The transformations are concatenated in the same manner as in [11]. The weight images were computed from the vesselness images as described by Eq. (4) using c₁ = 100, c₂ = 10 and σ = 2 (voxels).

An example is shown in Fig. 3. Here panel A shows the reference image including IVC and B is the vesselness image calculated from the reference image. We show the result of the non-weighted registration in C, which is obviously off due to the influence of different motion/deformation of the heart and the liver nearby. Fig. 3D and E show the result of the single-weighted registration and the dual-weighted registration, respectively. The result of the dual-weighted registration looks a little better than that of the single-weighted registration. Finally Fig. 3F shows the manually segmented objectmap from the original MRI image (Fig. 3A) for the same region for comparison purpose. Fig. 4 shows the PA registration result from the same sample as Fig. 3. Fig. 4 also shows that the dual-weighted registration is superior to the non-weighted registration. Another example is shown in Fig. 5 which combines the both the IVC and PA registration results. For comparison purpose, the blue line and yellow line delineate the IVC and PA of the reference image, respectively (as obtained using manual segmentation).

Fig. 3.

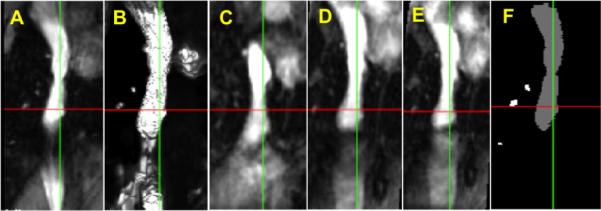
Registration result for inferior vena cava (IVC) in MRI image of lamb. A Reference blood vessel, B Vesselness image, C Result of non-weighted registration, D Result of single-weighted registration, E Result of dual-weighted registration, F Manually segmented region from A.

Fig. 4.

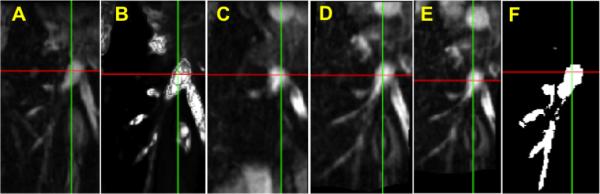
Registration result for pulmonary artery (PA) in MRI image of lamb. A Reference blood vessel, B Vesselness image, C Result of non-weighted registration, D Result of single-weighted registration, E Result of dual-weighted registration, F Manually segmented region from A.

Fig. 5.

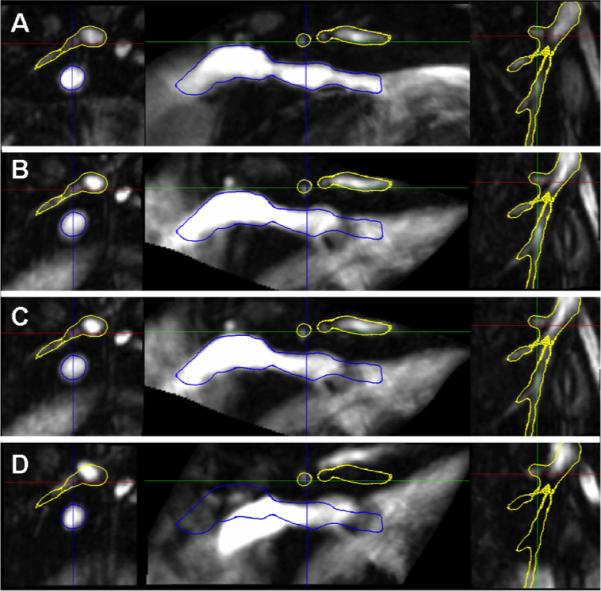
Registration result for both inferior vena cava (IVC) and pulmonary artery (PA). Blue line and yellow line delineate IVC and PA of the reference image, respectively. A Reference blood vessel, B Result of dual-weighted registration, C Result of single-weighted registration, D Result of non-weighted registration.

A more quantitative view of the results is presented in Table 1 which shows the comparison results using the overlap (Dice) as a metric, with the manual segmentations of the IVC and the PA serving as gold standards. In both cases our weighted registrations (both single and dual weight modes) are better than the unweighted registration method. We note, that the dual weighted method shows statistical significant improvements over the unweighted method for both the IVC and the PA (paired t-test p < 0.05).

Table 1.

Comparison of overlap ratios for the registration of inferior vena cava (IVC) and pulmonary artery (PA), using N=12 pairs of images.

Method	Avg. Overlap for IVC (%)	T test	Avg. Overlap for PA (%)	T test
Unweighted	41.35		30.06
Single	57.70	2.0E-03	39.63	NS
Dual	58.93	9.0E-04	44.05	0.03

4. DISCUSSION AND CONCLUSION

We presented a new fully-automated method for non-rigid vascular registration which uses spatial weighting within the context of a mutual information metric to optimize the registration. Thus, this method uses fully data-driven calculated weights and needs no prior information for the weight map. We evaluated the proposed method on vascular registration of 3D MRI lamb images. Our method is a compromise between traditional unweighted registration methods and methods relying on explicit segmentation (often manual e.g. the work of Greene et al. [10]) of key organs as constraints. The regions of high importance are highlighted but the registration process uses the whole of the image information as opposed to simply segmented structures (e.g. surface registration methods for example) and does not rely on having an accurate prior segmentation of the vessels (unlike the work in [12, 13]).