Two Archetypes of Motor Control Research

Abstract

This reply to the Commentaries is focused on two archetypes of motor control research, one based on physics and physiology and the other based on control theory and ideas of neural computations. The former approach, represented by the equilibrium-point hypothesis, strives to discover the physical laws and salient physiological variables that make purposeful coordinated movements possible. The latter approach, represented by the ideas of internal models and optimal control, tries to apply methods of control developed for man-made inanimate systems to the human body. Specific issues related to control with subthreshold membrane depolarization, motor redundancy, and the idea of synergies are briefly discussed.

The nine commentaries represent a broad spectrum of attitudes towards the central ideas of the target article, from highly positive and encouraging to strongly critical. I would like to start on a positive note and emphasize the clear shift in the general attitude towards the equilibrium-point (EP) hypothesis. It was not surprising to read the overall positive commentaries by Feldman, Levin, and Scholz. However, even the commentators who are known for their critical attitude to the EP-hypothesis (Shadmehr and Loeb) do not claim that the EP-hypothesis is meaningless and has been proven to be false. This is definitely a welcome trend, particularly when compared to the relatively recent fashion of “disproving” the EP-hypothesis and claiming that it is hopelessly wrong (Gomi & Kawato 1996; Gottlieb 1998; Hinder & Milner 2003; Popescu et al. 2003). Only five years ago, one of the commentators wrote: “…convincing evidence shows that the CNS does not use the equilibrium-point control method…” (Shadmehr & Wise, 2005; p. 143). The current commentary by Shadmehr avoids such strong statements.

The commentators raise many important issues, and, given the format of this paper, I will be unable to address them all in sufficient detail. So, I will focus on a few issues that seem to me central for the current state and the vector of development of the field of motor control.

Physics of Living Systems vs. Control Theory

Let me start with an axiomatic statement that the main goal of motor control research is to understand (to come up with a formal description operating with exactly defined variables) how the central nervous system (CNS) interacts with the rest of the body and the environment to produce coordinated, purposeful movements. The body (including the CNS) is composed of physical elements that may be expected to behave according to the laws of physics. However, physics of the inanimate nature, while being a highly developed science, has troubles dealing with typical problems of motor control. First, in contrast to movements in the inanimate world, movements of biological objects are intentional and purposeful. These two notions cannot be easily incorporated into contemporary physics. Another problem is that the body is a very complex system, maybe too complex to be studied with the currently available physical tools, and many crucial variables are not directly measurable or even identifiable. Sometimes, I call motor control “physics of unobservables” (cf. “partially-observable Markov decision processes” in the commentary by Gielen). These major problems turn motor control into a very exciting field of research that requires clever experimental designs and non-trivial theoretical constructs with the ultimate goal of turning this area into physics of living systems.

In the commentary by Houk, everything downstream from the stretch reflex is labeled as “physics”. I agree but would like to suggest that everything upstream (labeled by Houk as behavioral and neuroscience perspectives) is also physics, but we know much less about its laws and salient variables.

When researchers perform specific studies, they commonly separate the object of their interest from the rest of the body (and the environment) and assume that this object receives an input from the rest of the body that may be assigned intelligence. For example, the notions of motor programs and control variables are a poor-man way of describing a system, whose physics is unknown. These terms are nothing more but temporary substitutes reflecting our current inadequate knowledge. All researchers who accept the physical approach sin in this way, but they hope that, one day, it will be possible to describe human behavior with a set of physical laws without resorting to such notions (Gielen seems to agree with this point mentioning “if any!” with respect to control parameters).

The control theory approach is based on a different set of axioms. It views the central nervous system as a constellation of computational devices that receive information and compute control signals leading to actions executed by the rest of the body (including other computational devices). The body is equipped with sensors, and the CNS performs operations typical of many man-made control systems such as combining feed-forward and feedback control, optimal control, adaptive control etc. Within this description, physics stops at the peripheral level (as in Houk’s commentary, or even earlier), and the CNS has to deal with the complexity of the physics by performing computations. Researchers who use this approach typically do not care what physical processes underlie the presumed computations.

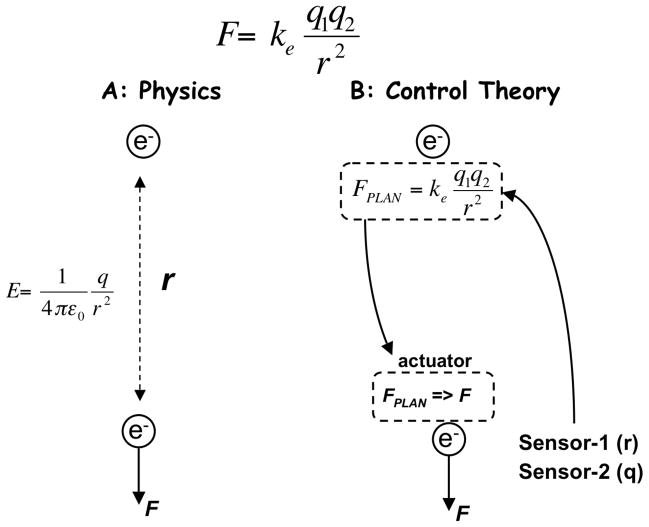
Figure 1 illustrates how the two approaches would address a well-known physical law, that is, the Coulomb law. Figure 1A illustrates the traditional physical view. A charged particle (an electron) creates an electric field. Any other charged particle experiences a force with the magnitude proportional to its charge and to the strength of the field. Figure 1B illustrates a control theory account. A particle gets information on the distance that separates it from another particle and on the charge of the other particle, it performs a relatively simple computational operation to model the force to be applied to the particle (F_PLAN) and sends a corresponding signal to an actuator, which transforms the symbolic F_PLAN into actual force acting on the particle.

Figure 1.

A: The physical account of the Coulomb law. An electron creates an electric field. Another electron experiences a force with the magnitude proportional to the charge and to the strength of the field. B: A control-theoretical (computational) account. An electron gets information on the charge and distance from the other electron, computes the force to be applied to the other electron (F_PLAN) and sends a corresponding signal to an actuator, which transforms the symbolic F_PLAN into physical force acting on the other electron.

Mathematically, both illustrations lead to the same result. However, I hope that all the readers would agree that the first one makes sense as a scientific account of the phenomenon, while the second one, at best, is good for building a model that can be used to simulate the Coulomb law for high-school students. The first illustration reflects the physics of the system, while the second one ignores it and substitutes the physics with highly questionable operations such as electrons measuring distances to other electrons and their charges, performing computations, and transforming symbolic variables into actual forces.

Certainly, neurons are not electrons, they are much more complex structures. However, the adequate language for neurons is that of synapses and membrane potentials, not of forces and mathematical operations. Assuming that neurons perform computations with mechanical variables and then somehow facilitate transformation of the symbolic results of these computations into actions represent major fallacies of the computational approach.

In his commentary, Shadmehr mentions that the optimal feedback scheme offered by Todorov (2004; also see Todorov & Jordan 2002) is mathematically equivalent to the EP-hypothesis (and later – to the uncontrolled manifold hypothesis). Even if this were true (which it is not), the EP-hypothesis tries to understand and represent the physics of the system (as in Figure 1A), while the optimal feedback control schemes could not care less about the physics, but offer methods to imitate the system’s functioning (as in Figure 1B). So, the following statement by Shadmehr seems to me misleading: “…feedback control is at the heart of both equilibrium point and optimal feedback control theory…”. Optimal feedback control theory uses feedback as a means of delivering information for the computational process, while within the EP-hypothesis, feedback is part of the physics of the system. Along similar lines, the question “how and where the computations are done?” posed by Loeb is inapplicable to the EP-hypothesis because no computations are done: It is physics at work (as in Figure 1A).

The last few statements do not mean that the notion of optimality is inapplicable to biological movement. The commentary by Feldman presents an example how a criterion of optimality can be incorporated into a theory based on physics and physiology without assuming neural computations.

To achieve a scientific, physical understanding of the system for movement production, researchers have to use adequate methods. Using methods developed for systems that have very little in common with the human body (control theory was developed for ballistic missiles and other human-built objects) may lead to important progress in building artificial systems that imitate aspects of human behavior, with substantial impact in such areas as prosthetics and robotics. But this is not motor control as defined in the opening paragraph of this section. Being artificially separated from the physics of the body (including the physics of the CNS), the control theory approach will never be able to discover how the actual system for biological movement production works.

Several years ago, Feldman and Latash (2005) stated that the mass-spring models had played their positive role in the past but had to be abandoned because they had turned from a stimulating factor into an obstacle for progress of motor control. Now the time has come to admit that the language of control theory is inadequate for studying biological objects. It played its role in the past bringing attention to certain important features of human movement, but the time has come to leave this approach behind and move forward towards an adequate description of the biological movement based on physics and physiology.

Shapiro and Körding try to reconcile the different approaches and suggest that the EP-hypothesis, optimal control, and the idea of internal models can be merged into a single coherent scheme. Given the very basic differences in the goals and axioms of the two archetypes of motor control research, I am skeptical. However, miracles happen. Two hundred years ago, it would be crazy to suggest that a wave and a particle could represent two characteristics of a single object. That miracle did happen, albeit within a single field, physics. Merging two clearly separate fields, physics and control theory, in motor control research may be not easier than breeding a mammal with a fish.

These two archetypes of motor control research have developed in parallel for about half a century. Earlier arguments in favor of the physical approach were beautifully summarized in a classical book by Kugler and Turvey (1987). In the current commentary Silva, Fonseca, and Turvey continue to support and develop this approach: “the controller creates energy gradients that direct the movement system toward the desired goal state”. Note that this phrase contains “the controller”, that is an intelligent input into the system but, as mentioned earlier, at our stage of understanding, we have to use such notions as substitutes for the currently unknown physical processes that play the role of “the controller”. I agree with Silva, Fonseca, and Turvey that it is crucial to determine what kind of signals (constraints) modulate control variables according to task demands. To proceed along this route, we first have to agree what the physical/physiological nature of the control variables is. The EP-hypothesis offers a hypothetical answer: These are subthreshold depolarization levels of neuronal pools that result in setting referent values for salient performance variables. I am unaware of another theory that would offer a comparably specific answer compatible with neurophysiology.

A Few Issues Related to the Equilibrium-Point Hypothesis

The two most critical commentaries with respect to the EP-hypothesis make statements regarding inability of the EP-hypothesis to deal with certain facts such as motor noise (Loeb) and movement patterns in humans with lost proprioception (Shadmehr). Both issues were addressed in earlier publications (Latash & Gottlieb 1990; Feldman & Levin 1995, 2009; Feldman et al. 1998). In addition, Loeb chastises the EP-hypothesis for being fixed on muscle spindles (it is not, e.g., Feldman and Latash 1982; Feldman 2009) and also makes a more general claim that “it is a conjecture, not a testable hypothesis.” The last statement had been made previously, and it deserves an answer.

Any scientific hypothesis contains established elements that have been proven beyond reasonable doubt. With respect to the EP-hypothesis, all researchers would probably agree that the following experimental facts do not need further proof. First, neurons are threshold elements. Second, voluntary muscle activation is associated with changes in the activation thresholds of corresponding alpha-motoneuronal pools. Third, muscle activation levels (and all mechanical variables) are consequences of both descending signals to the corresponding spinal segments and the external force field that affects inputs from peripheral sensory receptors.

At this level, the EP-hypothesis is indeed not disprovable, not more disprovable that the Coulomb law mentioned earlier (which does not make the Coulomb law non-scientific). However, further development of the EP-hypothesis allows to ask questions that may not have unambiguous answers at this time. Some of the commentaries point at such questions. In particular, Gielen questions whether one parameter (lambda) per muscle is sufficient to describe its functioning. This is a non-trivial question. Indeed, the notion of muscle compartments has been well established (Fleckenstein et al. 1992; Serlin & Schieber 1993). For example, the deep finger flexor (flexor digitorum profundis) has four distal tendons that attach to the distal phalanges of the four fingers. Although fingertip forces are not perfectly independent (Kilbreath & Gandevia 1994; Zatsiorsky et al. 2000), there is a lot of flexibility in involving individual fingers in multi-finger tasks (reviewed in Latash et al. 2002, 2007) suggesting that the control of the deep flexor is not limited to one variable but, more likely, involves at least four lambdas for the four major compartments. This may be true for other muscles with less obvious compartmentalization. So, Gielen’s point is well taken: The original description, “one lambda per muscle”, is a simplification that may have to be modified. This may require, in particular, accurate experimental studies of the distributions of the stretch reflex inputs across motor unit subpopulations. Changes in relative involvement of different compartments may happen across tasks performed in different external loading conditions, for example, isometric and isotonic, as pointed out by Gielen.

Loeb points at potential problems with moving from a joint-level description to more functional variables. Indeed, recent developments of the EP-hypothesis in the form of the referent configuration hypothesis try to make this important step (Feldman et al. 2007; Pilon et al. 2007). The importance of analyzing control processes that focus on functional (task) variables, not being muscle-, joint-, or limb-specific, is also emphasized by Silva, Fonseca, and Turvey. This is a less developed issue that offers a lot of exciting questions that are still without answers, that is, it leads to testable, non-trivial hypotheses, which are most definitely disprovable (for a recent study within this framework see Latash et al. 2010). The issue of linking processes at different levels of analysis that ultimately lead to purposeful movements brings us to the next main topic.

Hierarchical Schemes in Motor Control

In 1966, Bernstein and his two younger colleagues (Bassin et al. 1966; translation published in Lev Latash et al. 1999, 2000) revisited the problem of function localization within the CNS and suggested that the brain contained localized operators that could be shared among different functions (cf. Houk’s notion of distributed processing modules). Figure 1 in the target article explicitly suggests a hierarchy of operators that produce mappings of a relatively low-dimensional input (that defines the task for this particular level) to a higher-dimensional output organized to stabilize the combined action of that level at a value compatible with the input. Two commentators, Houk and Loeb, disagree and state that, according to neurophysiological data, dimensionality is decreasing, not increasing, from hierarchically higher levels to hierarchically lower ones. I agree with Loeb that we do not know how the goals of the task are represented in the CNS. So, we do not know whether the high-dimensional neurophysiological processes mentioned by Houk and Loeb are related to task representation or to results of processing of such a representation with several of the assumed few-to-many transformations. It seems natural to assume that representation of a simple, laboratory task in a reproducible environment is as low-dimensional as the task itself, as formulated by the experimenter and understood by the subject.

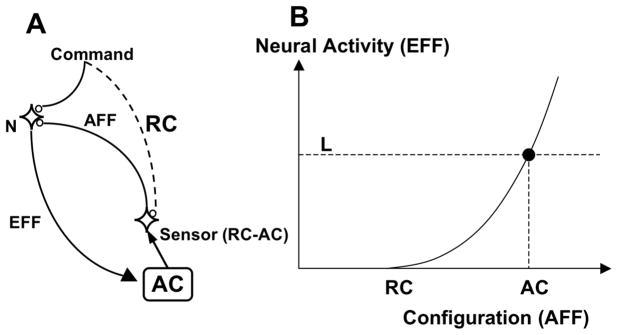
In a recent paper (Latash 2010), a generic physiological mechanism for an operator that may perform the presumed few-to-many mappings has been suggested. Figure 2 illustrates such a generic scheme using control with threshold values for neuronal activation. The controller (to remind, this word is used for a physical system whose structure and functioning are currently unknown, not for a computational system) sends a signal to a neuronal pool (N); this signal depolarizes the target cell membranes and modulates the threshold for action potential generation by N. Output of N (efferent command, EFF) is distributed along a branching tree of similar operators (not shown in the Figure) such that each output of the “top” operator serves as an input into a hierarchically lower operator. This scheme is compatible with Feldman’s notion of a hierarchy of frames of reference. To borrow another metaphor from Feldman, setting the hierarchically highest referent frame may be compared to carrying a set of objects in a box. The hierarchy suggests that there may be boxes within the larger boxes and, depending on the task, they may themselves be moved within the largest box, for example when the task is not only to move the fingertip to a target but also to produce a certain movement by one of the involved joints.

Figure 2.

An illustration of control with referent configurations. A: A command expressed in membrane potential units (V) is sent to a neuronal pool (N); this signal depolarizes the target cell membranes and modulates the threshold for action potential generation by N. Output of N (efferent command, EFF) is distributed along a branching tree of similar operators (not shown in the Figure) such that each output of the “top” operator serves as an input into a hierarchically lower operator. Ultimately, the process results in an input into alpha-motoneuronal pools and, via the tonic stretch reflex, leads to changes in muscle activations and in the actual configuration of the body (AC). Given external conditions, the signal from the controller specifies a referent configuration (RC), defined as a configuration, at which all the muscles would be at thresholds for their activation. A sensor neuron provides feedback (afferent signal, AFF) to neurons N reflecting the difference between RC and AC. B: The activation of the neurons produces a mechanical effect that moves AC towards RC. When the two coincide, N become silent, and the system stays at RC. If an external load (L) prevents AC from moving, an equilibrium state is reached corresponding to non-zero neuronal (and muscular) activation and a combination of positional and force variables.

Ultimately, the process results in an input into alpha-motoneuronal pools and, via the tonic stretch reflex, leads to changes in muscle activations and in the actual configuration of the body (AC). Given external conditions, the signal from the controller may also be viewed as specifying a referent configuration (RC), defined as a configuration, at which all the muscles would be at thresholds for their activation. A sensor neuron provides feedback (afferent signal, AFF) to neurons N reflecting the difference between RC and AC (Fig. 2A). For data compatible with this scheme see Pilon et al. 2007; Latash et al. 2010.

If AC differs from RC (to the right of RC in Fig. 2B), the neurons N are activated and this activation is higher for larger deviations of AC from RC. The activation of the neurons produces a mechanical effect that moves AC towards RC. When the two coincide, N become silent, and the system stays at RC. If something (for example, an external load, L) prevents AC from moving, an equilibrium state is reached corresponding to non-zero neuronal (and muscular) activation and a combination of positional and force variables. In the target article, I mentioned the principle of minimal final action guiding the process. Gielen criticizes this principle referring to studies that show non-zero muscle coactivation in the final state. I failed to emphasize in the target article that the notion of referent configuration involves the coactivation command (c-command, Feldman 1980). Hence, the final action is expected to be minimal given the referent configuration (including the c-command) and the external forces.

Figure 2 illustrates how control with thresholds of activation of neuronal pools may drive the body to its referent configuration. Where do all these processes happen? At this time, we do not know. So, I cannot answer Loeb’s question where to stick an electrode to measure all those variables. It is even possible that such a place does not exist, for example neurons N may be distributed over a vast area within the CNS. However, not having a place to stick an electrode is not atypical for physics (in what part of an elementary particle would you stick an electrode to measure its electric field?), and it does not make physics less scientific.

What Is a Synergy?

The term “synergy” has been used in the field of movement studies for over a century. As mentioned by Levin, in clinical studies, this word has a negative connotation implying stereotypical muscle activation patterns that differ from those observed in healthy individuals. This term had to be defined explicitly and operationally to make it useful for motor control studies. The definition offered in the target article (and in earlier papers, reviewed in Latash et al. 2007, Latash 2008) is based on several premises including the premise of motor redundancy. Although Loeb states that this premise may be false, the well documented phenomena of motor variability in laboratory tasks and the ability of humans to perform virtually any task in a variety of ways (cf. “repetition without repetition”, Bernstein 1947) suggest that motor redundancy does exist. Feldman also comments on the issue of redundancy and suggests that the size principle leading to the rank-ordered recruitment of motor units can turn the problem of sharing activation among motor units into a non-redundant one. This is a good point. However, since each motor unit can be recruited at various frequencies, the redundancy is not eliminated by the size principle but only reduced. The size principle is a good illustration of a more general principle summarized by Feldman: “The brain narrows the amount of redundancy and allows natural interactions of the system to bring about unique actions”.

Much effort has been spent recently on defining synergy in a way that allows to identify a synergy from a non-synergy and to quantify synergies (reviewed in Latash et al. 2007; Latash 2008). I believe that this effort was well spent. At a recent panel discussion during the Progress in Motor Control meeting in Marseille, one of my respected colleagues stated that researchers in motor control should stop wasting time arguing about terms (the discussion was about internal models, see the commentary by Shapiro and Körding). I could not disagree more. Arguing about the meaning of terms is not a waste of time, using terms without a clear understanding of their meaning is.

So, I view the definition of synergy as an important step in making this notion useful not only for clinicians but also for motor control researchers. As noticed by Feldman, the offered definition uses the notion of action repetition. As of now, there has been only one study that used this definition and the associated computational apparatus to study synergies within a single trial (Scholz et al. 2003). This approach is particularly important to study synergies in atypical persons who may not be able to repeat the same action many times. One problem of such analysis is that multi-element actions are usually associated with time changes of the Jacobian of the system. This introduces complications into quantitative estimation of the two components of variance (“good” and “bad”). These complications are amplified by non-independence of observations within a time series. Nevertheless, the example of the cited study shows that these complicating factors can be overcome, at least for some actions.

The notion of synergy is tightly linked to the issue of stability of important performance variables (Scholz), a feature that is ensured by flexible involvement of elementary variables (Scholz & Schöner 1999). In his commentary, Scholz makes an important point that reducing the two components of variance, “good” and “bad”, to a single index (ΔV) may be too crude. Indeed, similar changes in ΔV may be induced by changes in V_GOOD, V_BAD, or both. For example, an increase in ΔV may reflect more accurate performance with no other changes (smaller V_BAD, V_GOOD = const) or more flexible patterns of elementary variables without a change in accuracy of the important performance variable (larger V_GOOD, V_BAD = const). Within the language of the EP-hypothesis, the former scenario implies using more reproducible referent configurations across trials, while the latter one implies more variable transformations of any given referent configuration into patterns of elementary variables (see Figure 1 in the target article).

Challenges and Directions of Further Studies

The commentary by Silva, Fonseca, and Turvey suggests that the notion of synergy should be expanded to cover sensory processes. Indeed, afferent redundancy may be not as obvious as the motor one, but it is likely to be as common during most actions. In a rather old paper, Feldman and Latash (1982) discussed how position and force sense might be interpreted in the framework of the EP-hypothesis (for a recent update on this topic see Feldman 2009). They suggested that position and force sense for a muscle emerged as a point of intersection between the muscle invariant characteristic (tonic stretch reflex characteristic) and an “afferent curve” that was assumed to represent a weighted sum of afferent signals from all the proprioceptors. This mechanism allows, in particular, to make position/force sense immune to malfunctioning of any one of the sources of sensory information. The idea of a “tensegrity system” described by Silva, Fonseca, and Turvey seems to be close in spirit to the described more simplistic idea of a weighted sum of sensory signals. The issue of sensory synergies has also been discussed in one of the recent chapters (Latash 2008). The purpose of a sensory synergy was defined as creating a stable percept, in particular of the body. This idea seems close to using all afferents together in creating a coherent image of the body (in the environment).

As of now, there have been only a few attempts to link the notion of synergies, as defined in the target article, to impaired movements (Latash et al. 2003; Reisman & Scholz 2003, 2006; Olafsdottir et al. 2007). Those studies used the uncontrolled manifold toolbox to quantify synergies in a variety of motor tasks and emphasized differences in the performance of such populations as persons with Down syndrome, stroke survivors, and the healthy elderly. They did not discuss possible relations of the findings to impairments in producing patterns of control variables within the EP-hypothesis. Levin makes an excellent point emphasizing possible links between abnormal synergies and the demonstrated limitations in the range of shifts of the control variables (lambdas) in spasticity (Levin et al. 2000; Musampa et al. 2007). It may not be trivial to merge these ideas with those of hierarchical control with referent configurations, but the formulation of the problem is challenging and enticing.

In the target article, I mentioned lack of tools to measure lambda as a major challenge for development of the field. Gielen disagrees and states that such tools exist. Further he refers to tools for accurate measurement of levels of muscle activation, which are reflective of both lambda and sensory feedback. These tools may indeed be useful for analysis of thresholds of the tonic stretch reflex; however, applying these tools to extract time profiles of lambdas during movements may not be trivial.

Two commentaries, by Loeb and by Shapiro and Körding, emphasize that it is necessary to incorporate motor and sensory noise into any motor control theory. I agree, although it is not always clear what is meant under these terms. There is no argument that signals (sequences of action potentials) produced by elements of the sensory-motor system (individual receptors and motor units) are noisy. However, accuracy in some of the sensory-motor tasks is stunning. In his classic “On Dexterity and Its Development”, Bernstein (1996) estimated errors in the direction of force vector applied to a billiard ball during a successful shot as being about one angular minute. Errors of professional archers, marksmen, and pool players are probably even lower. How is this amazingly accurate performance built on noisy elements? One purpose of the notions of motor synergies and sensory synergies is indeed to allow actions to be relatively immune to noise of the elements. A few studies (Shinohara et al. 2003, 2004) have shown that multi-effector tasks can overcome the seemingly unavoidable increase in dispersion with magnitude of variables such as force (Newell & Carlton 1993; Harris & Wolpert 1998). In such tasks, each element shows the expected increase in force standard deviation with force magnitude, but the co-variation among forces of the elements allows to keep standard deviation of total force low and nearly constant over a wide range of force magnitudes.

Shapiro and Körding focus on the ability of animals to behave in a predictive fashion. A recent paper (Stepp & Turvey 2010) contrasts predictions using computational means (weak anticipation) and predictions built on physics (strong anticipation). It emphasized the insurmountable problems posed by the enormous redundancy at the level of synaptic inputs into neurons for any kind of neural prediction of mechanical variables (see Foisy & Feldman 2006). It would indeed be great to know the physics and physiology of predictive processes within the body, but at our level of knowledge this remains wishful thinking. For now, we have to resort to imprecise terms such as “neural representation” to reflect the ability of biological systems to predict and to behave in a probabilistic fashion (see the highly relevant and commonly ignored studies on “probabilistic prognosis” by Feigenberg 1969, 1998). It seems much more honest and productive to openly admit that we do not know the physics of those processes than to substitute them with computational operations assigned to brain structures.

I would like to end on a positive note by thanking the commentators for their open and honest opinions that are so rarely expressed and so badly needed in the field of motor control. I hope that “Motor Control” will continue publishing such mini-discussions on hot topics that expose different views and, hopefully, serve as important sources for both seasoned and beginning researchers.